第十章 第3节 格林公式及应用(2)
合集下载
高等数学 格林公式及其应用
D 单连通区域
D 复连通区域
2
10.3 格林公式及其应用
2. 格林公式
定理10.4(格林公式) 设闭区域D由分段光滑
的曲线L围成, 函数P(x, y)及Q(x, y)在D上具有一阶
连续偏导数, 则有
D
(Q x
P y
)dxdy
L
Pdx
Qdy
其中L是 D的取正向的边界曲线.
3
10.3 格林公式及其应用
分段光滑且不经过原点的连续闭曲线, L的方向为
逆时针方向.
解 记L所围成的闭区域为D,
令
P
y x2 y2
,
Q
x2
x
y2
则x当 2y20时 ,
有 Q x
y2 x2 ( x2 y2 )2
P y
22
10.3 格林公式及其应用
计算Lxdxy2yyd2x,
Q x
P y
D
(Q x
P y
)dxdy
L
•
A(a,0) x
Q ex cosy, P excosym
x
y
可知 Q P m 非常简单.
x y
18
10.3 格林公式及其应用
为L应不用闭格合林+公边式L＊再, 使补L充+一L＊段曲线, 使之构成
闭闭曲合线, .再因用在格补林充公的式曲.线上还要算曲线积分, 所以
补充的曲线要简单, 通常是补充与坐标轴平行的 直线段. 因而这里补加直线段 OA. y
L2
AFC , CE, L3 ,EC 及CGA构成.
B
由(2)知 D(Q xPy)dxdy
L3 E
C
L1 F A
格林公式及其应用
§10.3 格林公式及其应用一、格林公式一元微积分学中最基本的公式 — 牛顿、莱布尼兹公式'=-⎰F x dx F b F a ab ()()()表明：函数'F x ()在区间[,]a b 上的定积分可通过原函数F x ()在这个区间的两个端点处的值来表示。
无独有偶,在平面区域D 上的二重积分也可以通过沿区域D 的边界曲线L 上的曲线积分来表示,这便是我们要介绍的格林公式。
1、单连通区域的概念设D 为平面区域,如果D 内任一闭曲线所围的部分区域都属于D ,则称D 为平面单连通区域；否则称为复连通区域。
通俗地讲,单连通区域是不含“洞”(包括“点洞”)与“裂缝”的区域。
2、区域的边界曲线的正向规定设L 是平面区域D 的边界曲线,规定L 的正向为:当观察者沿L 的这个方向行走时,D 内位于他附近的那一部分总在他的左边。
简言之:区域的边界曲线之正向应适合条件,人沿曲线走,区域在左手。
3、格林公式【定理】设闭区域D 由分段光滑的曲线L 围成,函数P x y (,)及Q x y (,)在D 上具有一阶连续偏导数,则有()∂∂∂∂Q x Py dxdy Pdx Qdy DL -=+⎰⎰⎰ (1)其中L 是D 的取正向的边界曲线。
公式(1)叫做格林(green)公式。
【证明】先证 -=⎰⎰⎰∂∂Py dxdy Pdx D L假定区域D 的形状如下(用平行于y 轴的直线穿过区域,与区域边界曲线的交点至多两点)易见,图二所表示的区域是图一所表示的区域的一种特殊情况,我们仅对图一所表示的区域D 给予证明即可。
D a x b x y x :,()()≤≤≤≤ϕϕ12[]-=-=-⎰⎰⎰⎰⎰∂∂∂∂ϕϕϕϕP y dxdy dx P y dy P x y dx D a b x x abx x 1212()()()()(,)=--⎰{[,()][,()]}P x x P x x dxabϕϕ21另一方面,据对坐标的曲线积分性质与计算法有Pdx Pdx Pdx Pdx PdxLABBCCEEA⎰⎰⎰⎰⎰=+++弧弧=+++⎰⎰P x x dx P x x dx ab ba[,()][,()]ϕϕ1200=--⎰{[,()][,()]}P x x P x x dxabϕϕ21因此 -=⎰⎰⎰∂∂Py dxdy Pdx D L再假定穿过区域D 内部且平行于x 轴的直线与的D 的边界曲线的交点至多是两点,用类似的方法可证∂∂Qx dxdy Qdx D L ⎰⎰⎰=综合有当区域D 的边界曲线与穿过D 内部且平行于坐标轴( x 轴或y 轴 )的任何直线的交点至多是两点时,我们有-=⎰⎰⎰∂∂P y dxdy Pdx D L , ∂∂Q x dxdy Qdx D L ⎰⎰⎰=同时成立。
第十章 Green 公式(2)
AMB
( x y ) 2 dx ( x y ) 2 dy 和
x x2 八、试确定 ,使得 r dx 2 r dy 是某个函数 y y u( x , y ) 的全微分,其中r x 2 y 2 ,并求 u( x , y ) . k 九、设在半平面 x 0 内有力F 3 ( x i y j ) 构成力 r 2 2 k 为常数, r x y .证明在此力场中 场,其中 场力所作的功与所取的路径无关 .
xdy ydx x 2 y 2 2 其中正、负号取决于L 的方向 L
三、二元函数的全微分求积
G 设开区域 是一个单连通域, 函数 P ( x , y ), Q( x , y ) 在 内具有一阶连续偏导 G G 数, 则 P ( x , y )dx Q ( x , y )dy 在 内为某一 函数u( x , y ) 的全微分的充要条件是等式
( 3,4)
( 1, 2 )
(6 xy 2 y 3 )dx (6 x 2 y 3 xy 2 )dy 在整个 xoy 面
内与路径无关,并计算积分值 .
五、利用格林公式,计算下列曲线积分: 2 2 L 1、 L ( x y )dx ( x sin y )dy 其中 是在圆周
y 2 x x 2 上由点(0,0)到点(1,1)的一段弧；
练习题答案
一、1、 Pdx dyQ ；
L
p Q 2、 ； y x
3、10.
1 三、 . 30
3 2 四、 a . 8
五、236.
7 1 六、1、 sin 2 ； 2、-2. 6 4 七、1、当 L 所包围的区域 D 不包含原点时,0； 2、当 L 所包围的区域 D 包含原点,且 L 仅绕 原点 一圈时, 2 ； 3、当 L 所包围的区域 D 包含原点, 且 L 绕 原点 n 圈时, 2n .
第3节 格林公式及其应用
那末 Pdx Qdy Pdx Qdy
L1
L2
由于 Pdx Qdy Pdx Qdy
L2
L2
即 Pdx Qdy 0 .
L1
L
2
L1 L2 是 G内一条有向闭曲线 .
因此 , G内由曲线积分与路径无关
可推出,在 G 内沿闭曲线的积分为零 .
G
DC
x
于是我们得到与定积分中莱布尼兹公式类似的公式 ,
(x, y) Pdx Qdy U (x, y) ( x0 , y0 )
(x , y) ( x0 , y0 )
U (x, y) U (x0 , y0 )
,
其中 L 为一条无重点 ` 分段光滑
且不经过坐标原点的连续曲线 , L的方向为逆时针方向.
解 令 P y , Q x .当 x2 y2 0 时,有
x2 y2
x2 y2
? ? Q
x
y2 x2 x2 y2 2
, P y
y 2 x2 , Q P . x 2 y 2 2 x y
记 L 所围的区域为 D : (1) 当 (0, 0) D , 由格林公式
y
L D
L
xdy x2
ydx y2
D
Q x
P y
dxdy
0
D
dxdy
0
.
o
x
(2) 当 (0, 0) D ,取 r 适当小, 作小圆l
l : x2 y 2 r 2 , 记 L l 所围的区域为 D1 .
y
高等数学(同济大学)课件下第10_3格林公式
= −∫ 0⋅ dx + x∫0
1
x
y
dy x2 + y2
机动 目录 上页 下页 返回 结束
或
y (1, y) (x, y)
dy =∫ 0 1+ y2
y
o
(1,0)
( x,0)
x
x = − arctan 2 y
π
机动
目录
上页
下页
返回
结束
例7. 设质点在力场
作用下沿曲线 L : 求力场所作的功W
π 移动到 由 A( 0, )
π
π
π
L
= k 2 思考: 思考 积分路径是否可以取 AOUOB ? 为什么？
无关 !
机动 目录 上页 下页 返回 结束
π
o
Bx
注意, 本题只在不含原点的单连通区域内积分与路径
内容小结
∂Q ∂P 1. 格林公式 ∫ Pd x + Qd y = ∫∫D ∂x − ∂y d xd y L 2. 等价条件 设 P, Q 在 D 内具有一阶连续偏导数, 则有
k =1 n
n
Dk
(
∂Q ∂P − ) dxdy ∂x ∂y
Dn
o
x
= ∑∫
k =1
∂Dk
Pdx + Qdy
(∂Dk 表 Dk的 向 界) 示 正 边
证毕
= ∫ Pdx + Qdy
L
定理1
目录
上页
下页
返回
结束
∂Q ∂P − dxdy = ∫ Pdx + Qdy 格林公式 ∫∫ ∂x ∂y D L
d u(x, y) = P dx + Qdy ∂P ∂Q = . (4) 在 D 内每一点都有 ∂y ∂x
高等数学教学课件-2019 第三节 格林公式及其应 用
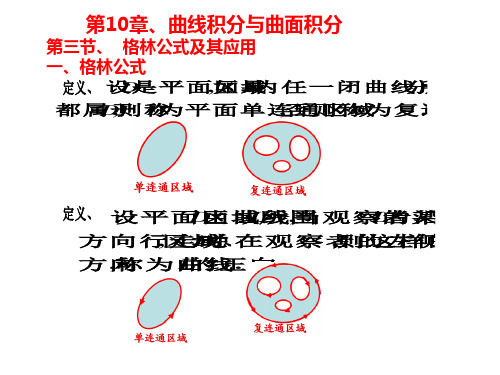
F 是
保 u (x 守 ,y)(场 x ,y) P (x ,y)d x Q (x ,y)d是 y x ,y 的
二 .
u(xx,y)u(x,y)(x 0,y0)
lim
x 0
x
l x 0 i 1 x m ( ( x x 0 ,y 0 x ) ,y ) P ( x ,y ) d Q x ( x ,y ) d ( ( x y x 0 , , y y ) 0 ) P ( x ,y ) d Q x ( x ,y ) d y
LL
(xy)3
y3x 3yx
D
x((xy)3
) ( y (xy)3
)d
xdy
3 ( x y ) 3 ( y 3 x ) 3 ( x y ) 2 3 ( x y ) 3 ( 3 y x ) 3 ( x y ) 2
[
D
( x y ) 6
( x y ) 6
] d xd
L x2y2
c x2y2
2 0 co t((c so itt))2 n s (ssiti(tn )n 2 co t)d s t022co2ts22si2ntdt
2
0 dt2.
例 3、 计算 (ey1x 2)d y x(xyecoy)d s,其 y L 是 中 L 曲y线 11x2上A 从 (1,1)到 B (1,1)一.段
则
L
P(x,
y)dxQ(x,
y)dy
D(Qx
P)dxd.y y
证明 由 引 1 理 LP(x,y)dx D P ydxdy
由引 2 理 LQ (x,y)dy D Q xdxdy
LP(x,y)d xQ (x,y)d yD Q x P y dxdy
用第二型曲线积分表示区域的面积公式：
格林公式
为顶点的三角形闭区域．
解 令 P=0，Q=x e
y2
Q P y2 ，则 ， =e ． x y
y
y2
因此，由格林公式有
∫∫ e
D
y2
dxdy =
=
OA+ AB + BO
∫ xe
y2
dy
1 x2
B(0, 1)
dx
A(1, 1)
∫ xe
OA
dy = ∫ xe
0
1 = (1 e 1 ) ． 2
u u =P(x, y)， =Q(x, y)． x y 2 u P 2 u Q = = ， ． xy y yx x
2u 2u 由于 P、Q 具有一阶连续偏导数，所以 、 连续， xy yx P Q 2u 2u = 因此 ，即 ． = xy yx y x
充分性：
P Q = 已知 在 G 内恒成立，则积分 ∫ P( x, y )dx + Q( x, y )dy L y x
y L1
恒成立，就说曲线积分 ∫ Pdx + Qdy
L
． B
在G内与路径无关，否则说与路径 有关． O A． L2 x
曲线积分与路径无关与闭曲线积分为零的等价性：
设曲线积分 ∫ Pdx + Qdy 在 G 内与路径无关，L 1 和 L 2 是 G
L
内任意两条从点A到点B的曲线，则有
∫
因为
L1
Pdx + Qdy = ∫ Pdx + Qdy ，
P Q y2 x2 2 2 = 则当 x +y ≠0 时，有 ． = 2 2 2 y x ( x + y )
记L 所围成的闭区域为D． 当(0, 0)D时，由格林公式得
高等数学10-3
第三节
格林公式及其应用
第三节 格林公式及其应用
第 十 章 曲 线 积 分 与 曲 面 积 分
一 格林公式 二 平面上曲线积分与路径无关的条件
-1-
第三节
格林公式及其应用
一 格林公式
第 十 章 曲 线 积 分 与 曲 面 积 分
为平面区域, 设D为平面区域 如果 内任一闭曲线所围成的部分 为平面区域 如果D内任一闭曲线所围成的部分 都属于D, 则称D为平面单连通区域, 否则称为复连通区 为平面单连通区域 都属于 则称 为平面单连通区域 否则称为复连通区 域.
不满足格林公式的条件， 但在 上， 2 + y 2 = a 2 所以 与 不满足格林公式的条件， 但在L上 x
( x + y )dx ( x y )dy 1 = 2 ∫ ( x + y )dx ( x y )dy 2 2 ∫L a L x +y
1 = 2 ∫∫ 2dxdy = 2π a D
-9-
例6 计算
第 十 章 曲 线 积 分 与 曲 面 积 分
其中L为一无重点且不过原点 其中 为一无重点且不过原点
的分段光滑正向闭曲线. 的分段光滑正向闭曲线 解: 令
则当x2 + y2 ≠ 0时 0时 ,
所围区域为D, ( 设 L 所围区域为 当 0,0) D时 由格林公式知 ,
y
L
o
- 12 -
x
L
D B
L2
x
L2 = BA, 则
x2
O
L A 1
∫L (2 xye
π
D
)dx + (e
0 1
x2
+ mx )dy = ∫
0
格林公式及其应用
第三节 格林公式及其应用
第 十 章 曲 线 积 分 与 曲 面 积 分
一 格林公式 二 平面上曲线积分与路径无关的条件
-1-
第三节
格林公式及其应用
一 格林公式
第 十 章 曲 线 积 分 与 曲 面 积 分
为平面区域, 设D为平面区域 如果 内任一闭曲线所围成的部分 为平面区域 如果D内任一闭曲线所围成的部分 都属于D, 则称D为平面单连通区域, 否则称为复连通区 为平面单连通区域 都属于 则称 为平面单连通区域 否则称为复连通区 域.
不满足格林公式的条件， 但在 上， 2 + y 2 = a 2 所以 与 不满足格林公式的条件， 但在L上 x
( x + y )dx ( x y )dy 1 = 2 ∫ ( x + y )dx ( x y )dy 2 2 ∫L a L x +y
1 = 2 ∫∫ 2dxdy = 2π a D
-9-
例6 计算
第 十 章 曲 线 积 分 与 曲 面 积 分
其中L为一无重点且不过原点 其中 为一无重点且不过原点
的分段光滑正向闭曲线. 的分段光滑正向闭曲线 解: 令
则当x2 + y2 ≠ 0时 0时 ,
所围区域为D, ( 设 L 所围区域为 当 0,0) D时 由格林公式知 ,
y
L
o
- 12 -
x
L
D B
L2
x
L2 = BA, 则
x2
O
L A 1
∫L (2 xye
π
D
)dx + (e
0 1
x2
+ mx )dy = ∫
0
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2 0
1
(1,t ) ( 0, 0 )
2 xydx Q( x, y) dy [1 C ( y )]dy
0
t
t C ( y )dy
0
t
t C ( y )dy t C ( y )dy
2 0 0
1
t
两边对t求导得 2t 1 C (t ) 所以 C (t ) 2t 1
x y 解：因为 P ( x , y ) 2 2 x y x y Q( x , y ) 2 2 x y 2 2
从 A(1,0)到B(1,0)的弧
Q x y 2 xy P ( x, y ) (0,0) 2 2 2 x (x y ) y
即在不含原点的单连通域，积分与路径无关。 取新路径 L*为从A(1,0)到B(1,0)的上半单位圆弧
由定理 2 可知存在原函数
y
( 1, y )
( x, y)
。
u( x , y )
x 1
( x, y)
(1, 0 )
xdy ydx 2 2 x y
y 0
o
。
( 1, 0 ) ( x, 0)
x
0 d x x
y dy arctan x x2 y2
( x 0)
(2) 对D 中任一分段光滑曲线 L , 曲线积分
Pd x Q
证明 (2) (3) 在D内取定点 A( x0 , y0 ) 和任一点B( x , y ) , 因曲线积分 与路径无关 , 设 ( x, y) B( x , y ) 。 。
u ( x, y)
证明 (3) (4) 设存在函数 u ( x , y ) 使得
则
u u du dx d y P d x Qd y x y u u P ( x, y) , Q( x , y ) x y 2 2 P u Q u , y x y x y x
二、曲线积分与路径无关的定义
如果对于区域G内的
任意两点A、B,以及起点 在A、终点在B的任意两条 曲线L1、L2，有
L1
y
B
L2
G
A
L Pdx Qdy L Pdx Qdy G 则称曲线积分 Pdx Qdy 在
1
2
o
x
L
内与路径无关,
1
否则与路径有关.
三. 平面曲线积分与路径无关等价条件
0
11
例4： 验证 (3 x 2 2 x y 3 )d x (3 x 2 y 2 2 y )d y 在整个 x0 y 平面内是全微分式，并求出它的一个原函数。 解： P 3x 2 2x y 3 Q 3x 2 y 2 2 y P Q 2 6 xy 在整个 x0 y 平面上都成立 y x 则所给出的微分式是全微分式。 利用公式： 取 M 0 x0 ,y0 O0,0为起点，动点为 M x, y
3 x 2d x (2 x y 3 d x 3 x 2 y 2 d y ) 2 ydy d ( x 3 ) d ( x 2 y 3 ) d ( y 2 ) d (x x y y )
3 2 3 2
u( x, y ) x x y y
3 2 3
2
14
方法四：
A( x0 , y 0 )
。
xu u 对D lim lim P ( x , x , y ) (2) x 中任一分段光滑曲线 L 曲线积分 P ( x , y ) x 0 x x 0 与路径无关, 只与起止点有关. u L Pd x Qd y ( x , y ) Q 同理可证 (3) P d x y y在D内是某一函数 u ( x, y ) 的全微分, 即 Qd 因此有 d u u (P,d ) P dd y Qd y d x yx Q x 4
2 3 2
u x, y x x y y C
3
15
例5. 验证 并求出它.
xdy ydx 在右半平面 ( x > 0 ) 内存在原函数, x2 y2
y x 证: 令 P 2 , Q 2 2 2 x y x y 2 2 则 P y x Q ( x 0 ) 2 2 2 x (x y ) y
18
例7 设函数 Q( x, y )在xoy 平面上具有一阶连续偏导数，
曲线积分
L
2 xydx Q( x, y )dy
(1,t ) ( 0, 0 )
与路径无关，并且对任意t恒有
( t ,1) ( 0, 0 )
2 xydx Q( x, y) dy
2 xydx Q( x, y) dy
u 2 3 u x, y 满足 P 3x 2x y x
2 3
u( x, y ) (3 x 2 xy )d x
x3 x2 y3 y
u 2 2 y Q 3 x 2 y 2 2 y 3x y y
2
y y C
x y 1
2 2
10
其参数方程为
x cos t ,
y sint , t从变到 0
（x y）dx ( x y )dy I＝ ＊ L x2 y2
＝ [(cost sint )( sint ) (cost sint ) cost ] dt
0
＝ dt
u ( x, y )
( x, y )
( x0 , y0 )
(3x 2 2 xy 3 )d x (3x 2 y 2 2 y )d y
方法一： u x, y
y M x, y
(3x 2 x0 )d x (3x y 2 y )d y
2 3 2 2
x
L2 L 2
P d x Qd y
L1 L 1 ( L 2 )
P d x Qd y
L2
B
L1
P d x Qd y
0
A
L (1) 沿 D1 中任意分段光滑闭曲线 L , 有
P d x Q d y L 2 P d x Q d y
L
Pd x Qd y 0
P k( x y ) Q 4 y r x
O
k 例6. 设质点在力场 F y , x 作用下沿曲线 L : 2 r
B
x
( x2 y2 0 )
曲线积分在除原点外的单连通开区域上与路径无关, 故积分路径可取圆弧
x cos , y sin ( : 0 ) AB : 2 2 2 0 k 2 2 W ( y d x xd y ) k (sin cos )d k AB r 2 2 2
5
证明 (4)
(1)
设L为D中任一分段光滑闭曲线, 所围区域为 D D , (如图 ), 因此在 D 上
P Q y x
D D L
利用格林公式 , 得
Q P L Pdx Qdy D ( x y )d xd y 0
P Q y x
I
L BA
( x y ) d x ( y x) d y ( x y ) d x ( y x) d y
a 2 x dx a
2
2
y
C
D
2
2
BA
D
B
o
L
0 d x d y
2 3 a 3
Ax
(利用格林公式)
9
( x y )dx ( x y )dy 例2 计 算I , 2 2 L x y 2 其中L是曲线 y 2 2 x 上
( x x , y )
( x 0 , y0 )
P dx Q d y
C ( x x , y )
则 x u u ( x x, y ) u ( x, y )
( x, y)
P dx Q d y
x x
x
P dx P ( x x , y )x
C ( y) 2 y 1
Q( x, y) x 2 y 1
2
20
2. 设 grad u( x, y) x 4 4 xy3 , 6 x 2 y 2 5 y 4 , 求 u ( x, y ).
y
x3 x 2 y 3 y 2
0
0
x
0
13 B(x,0)
方法二：
u x, y
y 0
y
x
M x, y
(3 02 y 2 2 y)d y (3x 2 2 x y 3 )d x
0
A(0, y )
x
0
x3 x 2 y 3 y 2
方法三： ( 3 x 2 2 x y 3 )d x ( 3 x 2 y 2 2 y )d y
求Q( x, y).
解：由积分与路径无关的条件知
Q ( 2 xy) 2 x x y
Q( x, y) x C ( y)
2
C ( y)待定
19
( t ,1) ( 0, 0 )
2 xydx Q( x, y ) dy [t 2 C ( y)]dy
0
1
t C ( y)dy
x0
x
x0
7
x
例1. 计算 解法1 令 P x 2 y, Q y 2 x, 则
其中L 是沿逆
时针方向以原点为中心, a 为半径的上半圆周.
1
(1,t ) ( 0, 0 )
2 xydx Q( x, y) dy [1 C ( y )]dy
0
t
t C ( y )dy
0
t
t C ( y )dy t C ( y )dy
2 0 0
1
t
两边对t求导得 2t 1 C (t ) 所以 C (t ) 2t 1
x y 解：因为 P ( x , y ) 2 2 x y x y Q( x , y ) 2 2 x y 2 2
从 A(1,0)到B(1,0)的弧
Q x y 2 xy P ( x, y ) (0,0) 2 2 2 x (x y ) y
即在不含原点的单连通域，积分与路径无关。 取新路径 L*为从A(1,0)到B(1,0)的上半单位圆弧
由定理 2 可知存在原函数
y
( 1, y )
( x, y)
。
u( x , y )
x 1
( x, y)
(1, 0 )
xdy ydx 2 2 x y
y 0
o
。
( 1, 0 ) ( x, 0)
x
0 d x x
y dy arctan x x2 y2
( x 0)
(2) 对D 中任一分段光滑曲线 L , 曲线积分
Pd x Q
证明 (2) (3) 在D内取定点 A( x0 , y0 ) 和任一点B( x , y ) , 因曲线积分 与路径无关 , 设 ( x, y) B( x , y ) 。 。
u ( x, y)
证明 (3) (4) 设存在函数 u ( x , y ) 使得
则
u u du dx d y P d x Qd y x y u u P ( x, y) , Q( x , y ) x y 2 2 P u Q u , y x y x y x
二、曲线积分与路径无关的定义
如果对于区域G内的
任意两点A、B,以及起点 在A、终点在B的任意两条 曲线L1、L2，有
L1
y
B
L2
G
A
L Pdx Qdy L Pdx Qdy G 则称曲线积分 Pdx Qdy 在
1
2
o
x
L
内与路径无关,
1
否则与路径有关.
三. 平面曲线积分与路径无关等价条件
0
11
例4： 验证 (3 x 2 2 x y 3 )d x (3 x 2 y 2 2 y )d y 在整个 x0 y 平面内是全微分式，并求出它的一个原函数。 解： P 3x 2 2x y 3 Q 3x 2 y 2 2 y P Q 2 6 xy 在整个 x0 y 平面上都成立 y x 则所给出的微分式是全微分式。 利用公式： 取 M 0 x0 ,y0 O0,0为起点，动点为 M x, y
3 x 2d x (2 x y 3 d x 3 x 2 y 2 d y ) 2 ydy d ( x 3 ) d ( x 2 y 3 ) d ( y 2 ) d (x x y y )
3 2 3 2
u( x, y ) x x y y
3 2 3
2
14
方法四：
A( x0 , y 0 )
。
xu u 对D lim lim P ( x , x , y ) (2) x 中任一分段光滑曲线 L 曲线积分 P ( x , y ) x 0 x x 0 与路径无关, 只与起止点有关. u L Pd x Qd y ( x , y ) Q 同理可证 (3) P d x y y在D内是某一函数 u ( x, y ) 的全微分, 即 Qd 因此有 d u u (P,d ) P dd y Qd y d x yx Q x 4
2 3 2
u x, y x x y y C
3
15
例5. 验证 并求出它.
xdy ydx 在右半平面 ( x > 0 ) 内存在原函数, x2 y2
y x 证: 令 P 2 , Q 2 2 2 x y x y 2 2 则 P y x Q ( x 0 ) 2 2 2 x (x y ) y
18
例7 设函数 Q( x, y )在xoy 平面上具有一阶连续偏导数，
曲线积分
L
2 xydx Q( x, y )dy
(1,t ) ( 0, 0 )
与路径无关，并且对任意t恒有
( t ,1) ( 0, 0 )
2 xydx Q( x, y) dy
2 xydx Q( x, y) dy
u 2 3 u x, y 满足 P 3x 2x y x
2 3
u( x, y ) (3 x 2 xy )d x
x3 x2 y3 y
u 2 2 y Q 3 x 2 y 2 2 y 3x y y
2
y y C
x y 1
2 2
10
其参数方程为
x cos t ,
y sint , t从变到 0
（x y）dx ( x y )dy I＝ ＊ L x2 y2
＝ [(cost sint )( sint ) (cost sint ) cost ] dt
0
＝ dt
u ( x, y )
( x, y )
( x0 , y0 )
(3x 2 2 xy 3 )d x (3x 2 y 2 2 y )d y
方法一： u x, y
y M x, y
(3x 2 x0 )d x (3x y 2 y )d y
2 3 2 2
x
L2 L 2
P d x Qd y
L1 L 1 ( L 2 )
P d x Qd y
L2
B
L1
P d x Qd y
0
A
L (1) 沿 D1 中任意分段光滑闭曲线 L , 有
P d x Q d y L 2 P d x Q d y
L
Pd x Qd y 0
P k( x y ) Q 4 y r x
O
k 例6. 设质点在力场 F y , x 作用下沿曲线 L : 2 r
B
x
( x2 y2 0 )
曲线积分在除原点外的单连通开区域上与路径无关, 故积分路径可取圆弧
x cos , y sin ( : 0 ) AB : 2 2 2 0 k 2 2 W ( y d x xd y ) k (sin cos )d k AB r 2 2 2
5
证明 (4)
(1)
设L为D中任一分段光滑闭曲线, 所围区域为 D D , (如图 ), 因此在 D 上
P Q y x
D D L
利用格林公式 , 得
Q P L Pdx Qdy D ( x y )d xd y 0
P Q y x
I
L BA
( x y ) d x ( y x) d y ( x y ) d x ( y x) d y
a 2 x dx a
2
2
y
C
D
2
2
BA
D
B
o
L
0 d x d y
2 3 a 3
Ax
(利用格林公式)
9
( x y )dx ( x y )dy 例2 计 算I , 2 2 L x y 2 其中L是曲线 y 2 2 x 上
( x x , y )
( x 0 , y0 )
P dx Q d y
C ( x x , y )
则 x u u ( x x, y ) u ( x, y )
( x, y)
P dx Q d y
x x
x
P dx P ( x x , y )x
C ( y) 2 y 1
Q( x, y) x 2 y 1
2
20
2. 设 grad u( x, y) x 4 4 xy3 , 6 x 2 y 2 5 y 4 , 求 u ( x, y ).
y
x3 x 2 y 3 y 2
0
0
x
0
13 B(x,0)
方法二：
u x, y
y 0
y
x
M x, y
(3 02 y 2 2 y)d y (3x 2 2 x y 3 )d x
0
A(0, y )
x
0
x3 x 2 y 3 y 2
方法三： ( 3 x 2 2 x y 3 )d x ( 3 x 2 y 2 2 y )d y
求Q( x, y).
解：由积分与路径无关的条件知
Q ( 2 xy) 2 x x y
Q( x, y) x C ( y)
2
C ( y)待定
19
( t ,1) ( 0, 0 )
2 xydx Q( x, y ) dy [t 2 C ( y)]dy
0
1
t C ( y)dy
x0
x
x0
7
x
例1. 计算 解法1 令 P x 2 y, Q y 2 x, 则
其中L 是沿逆
时针方向以原点为中心, a 为半径的上半圆周.