12,三角函数的综合应用
浅谈生活中三角函数的应用
浅谈生活中三角函数的应用
三角函数是数学中的重要概念，也是一种非常常见和基础的数学工具。
它在生活中有
着广泛的应用，下面我将从几个方面来谈谈生活中三角函数的应用。
三角函数在建筑和工程领域中应用广泛。
在建筑中，我们需要根据地形和建筑物的高
度来确定施工的角度和高度。
三角函数可以帮助我们计算出这些信息，从而确保建筑物的
安全和可靠。
在工程中，三角函数可以用来计算力的分解和合成，帮助我们理解物体的运
动和力学性质。
三角函数在物理学中也有着重要的应用。
在力学中，我们经常需要以角度的形式来描
述力的方向和大小，而三角函数可以帮助我们计算出这些角度。
在电磁学中，三角函数可
以用来描述电流、电压和电阻之间的关系，从而研究和解决电路中的问题。
在地理学和导航中，三角函数也有着重要的应用。
地图上的位置可以用经纬度来表示，而经纬度又可以转化为角度的形式。
通过使用三角函数，我们可以计算出两个位置之间的
距离和方向，从而帮助我们进行导航和定位。
三角函数还在天文学中有着广泛的应用。
根据天体的位置和角度，我们可以使用三角
函数计算出天体的运动轨迹和周期。
三角函数还可以用来描述天体的亮度、温度等性质，
帮助我们研究和理解宇宙的奥秘。
三角函数在计算机图形学中也发挥着重要的作用。
计算机图形学是计算机科学和数学
的交叉学科，它研究如何使用计算机来生成和处理图像。
在计算机图形学中，三角函数被
广泛应用于处理和变换图像的角度和位置信息，使得我们可以根据需要修改和处理图像。
初中数学三角函数的定义与应用
初中数学三角函数的定义与应用三角函数是初中数学中的一个重要概念，它是数学中用于研究三角形和周期性现象的函数。
三角函数有正弦、余弦和正切三种常见形式，它们在数学和实际生活中都有广泛的应用。
本文将介绍三角函数的定义和其在初中数学中的应用。
一、正弦函数的定义与应用正弦函数是三角函数中最基本的一种，通常用sin表示。
它的定义是：在直角三角形中，对于任意一个锐角α，正弦函数的值等于对边与斜边的比值，即sinα = 对边/斜边。
正弦函数在初中数学中的应用非常广泛，例如在解决直角三角形的问题中，我们可以利用正弦函数来求解未知边长或角度。
二、余弦函数的定义与应用余弦函数是另一种常见的三角函数，通常用cos表示。
它的定义是：在直角三角形中，对于任意一个锐角α，余弦函数的值等于邻边与斜边的比值，即cosα = 邻边/斜边。
与正弦函数类似，余弦函数也在解决直角三角形的问题中起到了重要作用。
三、正切函数的定义与应用正切函数是三角函数中的第三种形式，通常用tan表示。
它的定义是：在直角三角形中，对于任意一个锐角α，正切函数的值等于对边与邻边的比值，即tanα = 对边/邻边。
正切函数的应用也非常广泛，特别是在解决梯度问题、角度关系问题等方面具有重要意义。
四、三角函数的周期性三角函数具有周期性的特点，即在一定范围内呈现出重复的规律性。
正弦函数、余弦函数和正切函数的周期均为2π（弧度制下）或360°（角度制下）。
因此，我们可以利用周期性特点来简化计算，并在解决周期性问题时加以应用。
五、三角函数的图像与性质正弦函数、余弦函数和正切函数都具有特定的图像形态和性质。
例如，正弦函数的图像呈现出上下波动的曲线，余弦函数的图像则是波浪形的曲线，而正切函数的图像则是以原点为对称中心的S形曲线。
对于初中生来说，理解这些图像形态及其性质对于学习和应用三角函数非常有帮助。
六、三角函数的应用举例在实际生活中，三角函数有许多应用。
例如，利用三角函数可以解决测量高楼大厦的高度问题，通过测量垂直角和距离，可以利用三角函数计算出高楼大厦的实际高度。
应用三角函数解决实际问题
应用三角函数解决实际问题三角函数是数学中重要的概念之一，它与三角形的边长和角度之间的关系密切相关。
在实际生活中，我们可以利用三角函数解决各种实际问题，例如测量高楼的高度、计算船只与灯塔之间的距离等。
本文将通过几个具体的例子，详细介绍如何应用三角函数解决实际问题。
一、测量高楼的高度假设我们想要测量一座高楼的高度，但是无法直接测量。
此时，我们可以利用三角函数中的正切函数来解决这个问题。
我们可以站在离这座高楼较远的地方，仰望其顶部，并找到一个合适的角度。
然后，通过测量自己所站位置与地面的距离，以及仰望高楼时的角度，利用正切函数可以计算出高楼的高度。
例如，假设我们站在离高楼的位置为100米的地方，仰望高楼的角度为30度。
我们可以利用三角函数中的正切函数，根据公式tan(角度) = 高楼高度 / 100，计算出高楼的高度为100 * tan(30度) = 57.74米。
因此，高楼的高度约为57.74米。
二、计算船只与灯塔之间的距离假设我们在海上驾驶一艘船，远处有一座灯塔，我们想要知道船只与灯塔的距离。
此时，我们可以利用三角函数中的正弦函数来解决这个问题。
我们可以站在船只上，观察灯塔并记录下观察的角度。
然后，通过测量船只与海平面的高度，以及观察灯塔时的角度，利用正弦函数可以计算出船只与灯塔的距离。
例如，假设船只与海平面的高度为10米，我们观察灯塔的角度为45度。
我们可以利用三角函数中的正弦函数，根据公式sin(角度) = 灯塔的高度 / 距离，计算出船只与灯塔的距离为10 / sin(45度) = 14.14米。
因此，船只与灯塔的距离约为14.14米。
三、求解三角形的边长在一些实际问题中，给定三角形的某些角度和边长，我们需要求解其他未知边长。
这时，可以利用三角函数中的正弦、余弦、正切等函数来解决。
例如，已知一个直角三角形的直角边长分别为3和4，我们需要求解斜边的长度。
根据勾股定理，我们知道斜边的长度可以通过勾股定理计算得出：斜边的平方等于两个直角边平方和。
三角函数解三角形题型归类
三⾓函数解三⾓形题型归类三⾓函数解三⾓形题型归类⼀知识归纳：（⼀）任意⾓、弧度制及任意⾓的三⾓函数 1．⾓的概念(1)任意⾓：①定义：⾓可以看成平⾯内绕着端点从⼀个位置旋转到另⼀个位置所成的；②分类：⾓按旋转⽅向分为、和．(2)所有与⾓α终边相同的⾓，连同⾓α在内，构成的⾓的集合是S ＝．(3)象限⾓：使⾓的顶点与重合，⾓的始边与，那么，⾓的终边在第⼏象限，就说这个⾓是第⼏象限⾓；如果⾓的终边在坐标轴上，就认为这个⾓不属于任何⼀个象限． 2．弧度制(1)定义：把长度等于半径长的弧所对的圆⼼⾓叫做1弧度的⾓，⽤符号rad 表⽰，读作弧度．正⾓的弧度数是⼀个，负⾓的弧度数是⼀个负数，零⾓的弧度数是 .(2)⾓度制和弧度制的互化：180°＝π rad,1°＝π180 rad ，1 rad ＝? ????180π°.(3)扇形的弧长公式：l ＝|α|·r ，扇形的⾯积公式：S ＝12lr ＝12|α|·r 2. 3．任意⾓的三⾓函数（1）定义：设α是⼀个任意⾓，它的终边与单位圆交于点P (x ，y )，那么sin α＝，cos α＝，tan α＝．（2）任意⾓α的终边与单位圆交于点P (x ，y )时，sin α＝y ，cos α＝x ，tan α＝yx (x ≠0) 4.三⾓函数值在各象限的符号规律：⼀全正、⼆正弦、三正切、四余弦．（⼆）公式概念1．三⾓函数诱导公式? ??k 2π＋α(k ∈Z)的本质奇变偶不变(对k ⽽⾔，指k 取奇数或偶数)，符号看象限(看原函数，同时把α看成是锐⾓)．2．两⾓和与差的三⾓函数公式(1)sin(α±β)＝sin αcos β±cos αsin β； (2)cos(α±β)＝cos αcos β?sin αsin β；(3)tan(α±β)＝tan α±tan β1?tan αtan β.3．⼆倍⾓公式(1)sin 2α＝2sin αcos α；(2)cos 2α＝cos 2α－sin 2α＝2cos 2α－1＝1－2sin 2α，cos 2α＝1＋cos 2α2， sin 2α＝1－cos α2；(3)tan 2α＝2tan α1－tan 2α.（三）正、余弦定理及其变形： 1．正弦定理及其变形在△ABC 中，a sin A＝＝c sin C＝2R (其中R 是外接圆的半径)；a ＝2R sin A ，b ＝2R sin B ，c ＝2R sin C ； sin A ＝a 2R ，sin B ＝b 2R ，sin C ＝c 2R. 2．余弦定理及其变形a 2＝b 2＋c 2－2bc cos A ； cos A ＝b 2＋c 2－a 22bc.b 2＝； cos B ＝；c 2＝ . cos C ＝ .3.三⾓形⾯积公式:S △ABC ＝12ah ＝12ab sin C ＝12ac sin B ＝_________________＝abc 4R ＝12(a ＋b ＋c )·r (R是三⾓形外接圆半径，r 是三⾓形内切圆的半径)，并可由此计算R ，r .2．整体法：求y ＝A sin(ωx ＋φ)(ω>0)的单调区间、周期、值域、对称轴(中⼼)时，将ωx ＋φ看作⼀个整体，利⽤正弦曲线的性质解决．3．换元法：在求三⾓函数的值域时，有时将sin x (或cos x )看作⼀个整体，换元后转化为⼆次函数来解决．4．公式法：y ＝A sin(ωx ＋φ)和y ＝A cos(ωx ＋φ)的最⼩正周期为2π|ω|，y ＝A tan(ωx ＋φ)的最⼩正周期为π|ω|.(2016年全国卷1)4.△ABC 的内⾓A ，B ，C 的对边分别为a ，b ，c ．已知5a =，2c =，2cos 3，则b =（A ）2 （B ）3 （C ）2 （D ）3 6.将函数2sin(2)6y x π=+的图象向右平移14个周期后，所得图象对应的函数为（A ）2sin(2)4y x π=+ （B ）2sin(2)3y x π=+（C ）2sin(2)4y x π=-（D ）2sin(2)3y x π=-14.已知θ是第四象限⾓，且3sin()45πθ+=，则tan()4πθ-=————————————． (2015年全国卷1)8. 函数()cos()f x x ω?=+的部分图像如图所⽰，则()f x 的单调递减区间为（）（A ）13 (,),44k k k Z ππ-+∈（B ）13(2,2),44k k k Z ππ-+∈（C ）13(,),44k k k Z -+∈（D ）13(2,2),44k k k Z -+∈17. （本⼩题满分12分）已知,,a b c 分别是ABC ?内⾓,,A B C 的对边，2sin 2sin sin B A C =.（I ）若a b =，求cos ;B （II ）若90B =，且2,a = 求ABC ?的⾯积.(2014年全国卷1) 2.若0tan >α，则A. 0sin >αB. 0cos >αC. 02sin >αD. 02cos >α 7.在函数①|2|cos x y =，②|cos |x y = ，③)62cos(π+=x y ,④)42tan(π-=x y 中，最⼩正周期为π的所有函数为 A .①②③ B. ①③④ C . ②④D. ①③16.如图，为测量⼭⾼MN ，选择A 和另⼀座⼭的⼭顶C 为测量观测点.从A 点测得 M 点的仰⾓60MAN ∠=?，C 点的仰⾓45CAB ∠=?以及75MAC ∠=?；从C 点测学科⽹得60MCA ∠=?.已知⼭⾼100BC m =，则⼭⾼MN =________m .(2013年全国卷1)9．函数()(1cos )sin f x x x =-在[,]ππ-的图像⼤致为（）10．已知锐⾓ABC ?的内⾓,,A B C 的对边分别为,,a b c ，223cos cos 20A A +=，7a =，6c =，则b = （A ）10 （B ）9（C ）8（D ）516．设当x θ=时，函数()sin 2cos f x x x =-取得最⼤值，则cos θ=______.(2012年全国卷1)9.已知ω>0，0?π<<，直线x =4π和x =54π是函数()sin()f x x ω?=+图像的两条相邻的对称轴，则?=（A ）π4 （B ）π3 （C ）π2 （D ）3π417.（本⼩题满分12分）已知a ，b ，c 分别为ABC ?三个内⾓A ,B ,C 的对边，3sin sin c a C c A =-.(Ⅰ)求A ；(Ⅱ)若a =2，ABC ?3b ，c .三、题型归纳题型⼀、三⾓函数定义的应⽤1.若点P 在－10π3⾓的终边上，且P 的坐标为(－1，y )，则y 等于( )A.－33C.－ 3变式1．已知⾓α的终边经过点(3，－1)，则⾓α的最⼩正值是( )题型⼆、三⾓函数值的符号2．已知⾓α的终边经过点(3，－1)，则⾓α的最⼩正值是( )变式2.设α是第⼆象限⾓，P (x,4)为其终边上的⼀点，且cos α＝15x ，则tan α＝( )C ．－34D ．－43题型三、同⾓三⾓函数关系式的应⽤3.已知tan θ＝2，则sin 2θ＋sin θcos θ－2cos 2θ等于( )A ．－43 C ．－344.已知sin αcos α＝18，且5π4＜α＜3π2，则cos α－sin α的值为( )A ．－32 C ．－34变式3.已知sin α－cos α＝2，α∈(0，π)，则tan α等于( ) A ．－1 B ．－22D ．1 题型四诱导公式的应⽤5．(1)已知sin π3－α＝12，则cosπ6＋α＝________. (2)sin(－1 200°)cos 1 290°＋cos(－1 020°)sin(－1 050°)＝______变式4.已知⾓α终边上⼀点p(-4,3)，则cos()sin()2119cos()sin()22παπαππαα+---+的值为题型五、三⾓函数的图形变换6.（1）要得到函数y ＝sin 4x －π3的图象，只需将函数y ＝sin 4x 的图象( ) A ．向左平移π12个单位B ．向右平移π12个单位C ．向左平移π3个单位D ．向右平移π3个单位（2）某同学⽤“五点法”画函数f (x )＝A sin(ωx ＋φ)ω>0，|φ|<π2在某⼀个周期内的图象时，列表并填⼊部分数据，如下表：(1)f (x )的解析式； (2)将y ＝f (x )图象上所有点向左平移π6个单位长度，得到y ＝g (x )的图象，求y ＝g (x )的图象离原点O 最近的对称中⼼．变式5.已知函数y ＝2sin 2x ＋π3. (1)求它的振幅、周期、初相；(2)说明y ＝2sin 2x ＋π3的图象可由y ＝sin x 的图象经过怎样的变换⽽得到．题型六、三⾓函数的性质问题7.（1）函数y ＝2sinπ3－2x 的单调增区间为________. （2）已知函数f (x )＝cos ωx ＋φ－π2ω>0，|φ|<π2的部分图象如图所⽰，则y ＝f x ＋π6取得最⼩值时x 的集合为( )（3）函数f (x )＝sin(ωx ＋φ)ω＞0，|φ|＜π2的最⼩正周期为π，且其图象向右平移π12个单位后得到的函数为奇函数，则函数f (x )的图象( ) A.关于点π2，0对称B.关于直线x ＝5π12对称C.关于点5π12，0对称 D.关于直线x ＝π12对称（4）当x ＝π4时，函数f (x )＝A sin(x ＋φ)(A ＞0)取得最⼩值，则函数y ＝f 3π4－x 是( ) A.奇函数且图象关于点π2，0对称 B.偶函数且图象关于点(π，0)对称 C.奇函数且图象关于直线x ＝π2对称 D.偶函数且图象关于点π2，0对称变式6.已知函数f (x )＝2cos x (sin x ＋cos x )． (1)求f 5π4的值；(2)求函数f (x )的最⼩正周期及单调递增区间．题型七、最值与值域问题8.已知函数2()(sinx cosx)cos 2f x x =++。
初中数学总复习专题12 三角函数
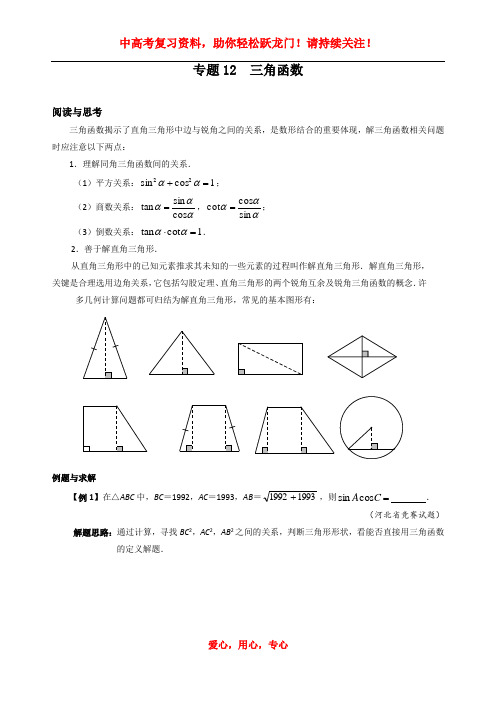
专题12 三角函数阅读与思考三角函数揭示了直角三角形中边与锐角之间的关系，是数形结合的重要体现，解三角函数相关问题时应注意以下两点：1．理解同角三角函数间的关系． （1）平方关系：1cos sin 22=+αα； （2）商数关系：αααcos sin tan =，αααsin cos cot =； （3）倒数关系：1cot tan =⋅αα．2．善于解直角三角形．从直角三角形中的已知元素推求其未知的一些元素的过程叫作解直角三角形．解直角三角形， 关键是合理选用边角关系，它包括勾股定理、直角三角形的两个锐角互余及锐角三角函数的概念．许多几何计算问题都可归结为解直角三角形，常见的基本图形有：例题与求解【例1】在△ABC 中，BC ＝1992，AC ＝1993，AB ＝19931992+，则=C A cos sin ．（河北省竞赛试题）解题思路：通过计算，寻找BC 2，AC 2，AB 2之间的关系，判断三角形形状，看能否直接用三角函数的定义解题．【例2】某片绿地形状如图所示，其中∠A ＝600，AB ⊥BC ，AD ⊥CD ，AB ＝200m ，CD ＝100m ． 求AD ，BC 的长．（精确到1m ，732.13≈）图2图1F EAE AABDDBDB解题思路：本题的解题关键是构造直角三角形，构造的原则是不能破坏∠A ，所以连结AC 不行．延长AD 和BC 交于一点E （如图1），这样既构造出了直角三角形，又保全了特殊角∠A ；或过点D 作矩形ABEF （如图2）来求解．【例3】如图，已知正方形ABCD 中，E 为BC 上一点．将正方形折叠起来，使点A 和点E 重合，折痕为MN ．若31tan =∠AEN ，DC ＋CE ＝10． （1）求△ANE 的面积； （2）求ENB ∠sin 的值．解题思路：将31tan =∠AEN 与DC ＋CE ＝10结合起来，可求出相关线段的长，为解题铺平道路．【例4】如图，客轮沿折线A —B —C 从A 出发经B 再到C 匀速航行，货轮从AC 的中点D 出发沿某一方向匀速直线航行，将一批物品送达客轮．两船同时起航，并同时到达折线A —B —C 上的某点E 处．已知AB ＝BC ＝200海里，∠ABC ＝900，客轮速度是货轮速度的2倍．（1）选择：两船相遇之处E 点（ ）A ．在线段AB 上 B ．在线段BC 上C ．可以在线段AB 上，也可以在线段BC 上（2）求货轮从出发到两船相遇共航行了多少海里？（结果保留根号）（南京市中考试题）解题思路：对于（2），过D 作DF ⊥CB 于F ，设DE =x ，建立关于x 的方程．【例5】若直角三角形的两个锐角A ，B 的正弦是方程02=++q px x 的两个根． （1）那么，实数p ，q 应满足哪些条件？（2）如果p ，q 满足这些条件，方程02=++q px x 的两个根是否等于直角三角形的两个锐角A ，B 的正弦？（江苏省竞赛试题）解题思路：解本例的关键是建立严密约束条件下的含不等式、等式的混合组，需综合运用一元二次方程，三角函数的知识与方法．C【例6】设a ，b ，c 是直角三角形的三边，c 为斜边，整数n≥3．求证：nnnc b a <+．（福建省竞赛试题）解题思路：由直角三角形的边可以转化为三角函数正余弦来解．其不等关系可以利用正弦、余弦的有界性来证明．能力训练A 级1．如图，D 是△ABC 的边AC 上一点，CD ＝2AD ，AE ⊥BC 于E ．若BD ＝8，43sin =∠CBD ，则AE ＝ ． 2．已知00900≤≤α，则ααsin sin 45+-=y 的最大值是 ，最小值是 ．（上海市理科实验班招生考试试题）3．如图，在△ABC 中，∠C ＝900，∠BAC ＝300，BC ＝1，D 为BC 边上的一点，ADC ∠tan 是方程2)1(5)1(322=+-+xx x x 的一个较大的根，则CD ＝ ．东第5题图第1题图第3题图E BAO4．已知△ABC 的两边长a ＝3，c ＝5，且第三边长b 为关于x 的一元二次方程042=+-m x x 的两个正整数根之一，则A sin 的值为 ． （哈尔滨中考试题） 5．如图，小雅家（图中点O 处）门前有一条东西走向的公路，经测得有一水塔（图中点A 处）在她家北偏东600距离500m 处，那么水塔所在的位置到公路的距离AB 是（ ） A ．250mB ．3250mC ．33500mD ．2250m6．如图，在△ABC 中，∠C ＝900，∠ABC ＝300，D 是AC 的中点，则DBC ∠cot 的值是（ ） A ．3B ．32C ．23D ．43 （大连市中考试题）7．一渔船上的渔民在A 处看见灯塔M 在北偏东600方向，这艘渔船以28海里/时的速度向正东航行．半小时后到B 处，在B 处看见灯塔M 在北偏东150方向，此时灯塔M 与渔船的距离是（ ） （黄冈市中考试题） A ．27海里B ．214海里C ．7海里D ．14海里8．如图，四边形ABCD 中，∠A ＝600，∠B ＝∠D ＝900，AD ＝8，AB ＝7，则BC ＋CD 等于（ ） A ．36B ．35C ．34D ．33第7题图第6题图第8题图东北BA OA9．如图是某品牌太阳能热水器的实物图和横断面示意图．已知真空集热管AB 与支架CD 所在直线相交于水箱横断面⊙O 的圆心，支架CD 与水平面AE 垂直，AB ＝150厘米，∠BAC ＝300，另一根辅助支架DE ＝76厘米，∠CED ＝600．（1）求垂直支架CD的长度（结果保留根号）；（2）求水箱半径OD的长度（结果保留三位有效数字，参考数据：73.13,41.12≈≈）．（扬州市中考试题）图2图1BA EOD10．若α为锐角，求证：4cossin1cos1sin1>⋅++αααα．（宁波市竞赛试题）11．如图，已知AB＝CD＝1，∠ABC＝900, ∠CBD＝300，求AC的长．（加拿大数学奥林匹克竞赛试题）12．如图，在△ABC中，∠ACB＝900，CD⊥AB于点D，CD＝1．若AD，BD的长是关于x的方程02=++qpxx的两根，且2tantan=-BA，求p，q的值并解此二次方程．ABCB 级1．若0300<<θ，且31sin +=km θ（k 为常数，k ＜0），则m 的取值范围是 ． 2．设00450<<α，1673cos sin =⋅αα，则=αsin ． （武汉市选拔赛试题） 3．已知在△ABC 中，∠A ，∠B 是锐角，且2tan ,135sin ==B A ，AB ＝29cm ，则△ABC 的面积等于 ． （“祖冲之杯”邀请赛试题）4．如图，在正方形ABCD 中，N 是DC 的中点，M 是AD 上异于D 的点，且MBC NMB ∠=∠，则有=∠ABM tan ． （全国初中数学联赛试题） 5．如图，在Rt △ABC 中，∠C ＝900, ∠CAB ＝300，AD 平分∠CAB ，则CDACCD AB -的值为（ ） A ．3B ．33C ．33-D ．326-（湖北省选拔赛试题）第4题图第5题图NBAB AMD6．如图，在梯形ABCD 中，AD//BC ，AD ⊥CD ，BC ＝CD ＝2AD ，E 是CD 上一点，∠ABE ＝450，则AEB∠tan的值等于（ ） （天津市竞赛试题） A ．23 B ．2 C ．25D ．3 7．如图，在等腰Rt △ABC 中，∠C ＝900, ∠CBD ＝300，则DCAD＝（ ） A ．33 B ．22C ．12-D ．13-（山东省竞赛试题）第7题图第6题图BA BDE8．如图是一座人行天桥的引桥部分的示意图，上桥通道是由两段互相平行并且与地面成370角的楼梯AD ，BE 和一段水平天台DE 构成．已知天桥高度BC ＝4.8米，引桥水平跨度AC ＝8米． （1）求水平天台DE 的长度；（2）若与地面垂直的平台立柱MN 的高度为3米，求两段楼梯AD 与BE 的长度之比．（参考数据：取75.037tan ,80.037cos ,60.037sin 0===） （长沙市中考试题）NA9．在△ABC 中，a ，b ，c 分别是∠A ，∠B ，∠C 的对边，且c ＝35．若关于x 的方程0)35(2)35(2=-+++b ax x b 有两个相等的实根，又方程0sin 5)sin 10(22=+-A x A x的两实数根的平方和为6，求△ABC 的面积．（武汉市中考试题）10．如图，EFGH 是正方形ABCD 的内接四边形，两条对角线EG 和FH 所夹的锐角为θ，且BEG ∠与CFH ∠都是锐角．已知,,l FH k EG ==四边形EFGH 的面积为S ．（1）求证：klS2sin =θ； （2）试用S l k ,,来表示正方形ABCD 的面积．（全国初中数学联赛试题）GF11．如图，在直角梯形ABCD 中，AD//BC ，∠A ＝900，BC ＝CD ＝10，54sin =C ． (1) 求梯形ABCD 的面积；（2）点E ，F 分别是BC ，CD 上的动点，点E 从点B 出发向点C 运动，点F 从点C 出发向点D 运动．若两点均以每秒1个单位的速度同时出发，连接EF ，求△EFC 面积的最大值，并说明此时E ，F 的位置．（济宁市中考试题）A DFB C 12．如图，甲楼楼高16米，乙楼坐落在甲楼的正北面．已知当冬至中午12时太阳光线与水平面的夹角为300，此时，求：（1）如果两楼相距20米，那么甲楼的影子落在乙楼上有多高？（2）如果甲楼的影子刚好落在乙楼上，那么两楼的距离应当是多少？（山东省竞赛试题）。
三角函数的综合应用+课件-2025届高三数学一轮复习
(2)由题意，得 f(A)＝2sin 2A－π3－ 3＝0，即 sin 2A－π3＝ 23，
∵A∈0，π2， 则 2A－π3∈－π3，23π， ∴2A－π3＝π3，∴A＝π3.
在△ABC 中， 由 a2＝b2＋c2－2bc cos A＝42＋32－2×4×3×12＝13， 可得 a＝ 13， 又∵12bc sin A＝12AD×a，即12×4×3× 23＝21AD× 13， ∴AD＝61339，故 BC 边上的高 AD 的长为61339.
(2)根据正弦定理得sina A＝sinc C＝sinb
B＝
4 ＝8 3
3
3，
2
所以
a＝8
3
3 sin
A，c＝8
3
3 sin
C.
所以
a＋c＝8
3
3 (sin
A＋sin
C).
因为 A＋B＋C＝π，B＝π3，所以 A＋C＝23π，
所以 a＋c＝8
3
3 sin
A＋sin
23π－A＝8
3
33 2sin
A＋
23cos
A
＝8sin A＋π6.
因为 0＜A＜23π，
所以 A＋π6∈π6，56π，所以 sin A＋π6∈12，1，则 a＋c∈(4，8].
所以 a＋c 的取值范围是(4，8].
【反思感悟】已知三角形一边及其对角，求取值范围的问题 的解法
(1)(不妨设已知 a 与 sin A 的值)根据 2R＝sina A求出三角形外接
∴a2＋c2 b2＝sin2Asi＋n2Csin2B＝cos22sCin＋2Ccos2C ＝(1－2sin2Cs)in2＋2C(1－sin2C)＝2＋4sins4iCn2－C 5sin2C
三角函数的性质与应用
三角函数的性质与应用三角函数是数学中重要的概念之一，广泛应用于各个领域，包括几何、物理、工程等。
本文将介绍三角函数的一些基本性质，并探讨它们在实际问题中的应用。
一、正弦函数的性质与应用正弦函数是三角函数中最基本的函数之一，它的定义域是实数集合，值域在[-1,1]之间。
正弦函数的一个重要性质是周期性，即sin(x+2π)=sin(x)，其中π是圆周率。
这个周期性质使得正弦函数在周期性变化的问题中得到广泛应用。
在几何学中，正弦函数常用于计算三角形的边长和角度。
例如，已知一个直角三角形的角度为θ，边长分别为a和b，根据正弦函数的定义可以得到：sin(θ) = a/ c，其中c为斜边的长度。
通过已知的角度和任意两个边长，我们可以使用正弦函数求解未知边长。
此外，在物理学中，正弦函数也被广泛应用于描述周期性运动。
例如，一个挂在弹簧上的质点的运动可以用正弦函数表示。
振幅、频率和初相位都可以通过正弦函数的性质进行分析和计算。
二、余弦函数的性质与应用余弦函数是三角函数中的另一个重要函数，和正弦函数类似，它的定义域是实数集合，值域也在[-1,1]之间。
余弦函数也具有周期性，即cos(x+2π)=cos(x)。
在几何学中，余弦函数常用于计算三角形的边长和角度。
例如，已知一个锐角三角形的角度为θ，边长分别为a和c，根据余弦函数的定义可以得到：cos(θ) = a/ c，其中c为斜边的长度。
通过已知的角度和两个边长，我们可以使用余弦函数求解未知边长。
在物理学中，余弦函数也被广泛应用于描述振动和波动。
例如，一个单摆的运动可以用余弦函数表示。
摆动的振幅、频率和初相位可以通过余弦函数的性质进行计算和分析。
三、正切函数的性质与应用正切函数是三角函数中的另一个重要函数，它的定义域是实数集合，但值域不再是有界的。
正切函数的周期性是π，即tan(x+π)=tan(x)。
在几何学中，正切函数常用于计算三角形的边长和角度。
例如，已知一个锐角三角形的角度为θ，边长分别为a和b，根据正切函数的定义可以得到：tan(θ) = a/ b。
三角函数：生活中的指南针
三角函数：生活中的指南针
三角函数在现实生活中有许多应用，以下是一些实例：
1.时钟：时钟的指针的运动轨迹可以通过三角函数来描述。
例如，秒针一圈的长度是60秒，分针一圈的长度是60分钟，时针一圈的长度是12小时。
当我们在时钟上表示时间时，实际上是在使用三角函数来描述各指针之间的大小关系。
2.地球运动：地球的运动如果用三角函数来描述，就可以得出地球每天的运行轨迹，以及每天的日出日落时间。
这其中就涉及到了正弦、余弦和正切等三角函数。
3.建筑：在建筑设计中，三角函数也被用来计算建筑物的抗压能力、承重能力等。
例如，通过使用三角函数，可以计算出梁的跨度和高度，以使其在满足承重要求的同时，保持足够的稳定性。
4.机械：在机械设计中，三角函数同样有广泛的应用。
例如，可以用来计算出机械的转动角度，以及机械的运动轨迹等。
5.测量：在测量建筑物或山的高度时，如果知道建筑物的位置与仰角之间的距离，则可以利用三角函数轻松地计算得到建筑物的高度。
6.游戏：在一些游戏中，如赛车游戏，当控制赛车运动的角度时，需要利用三角函数时刻计算赛车当前的位置以及运动的距离。
7.航空飞行：飞行工程师在考虑飞行路径时，需要精确地计算飞行轨道、着陆角度等，这就涉及到了大量的三角函数应用。
通过以上例子，我们可以看出三角函数在生活中的应用十分广泛，几乎在各个领域都有其用武之地。
三角函数的应用实例与解析
三角函数的应用实例与解析三角函数是数学中的重要概念之一，它在各个领域中都有广泛的应用。
本文将从几个实际问题的角度出发，探讨三角函数的应用实例与解析。
一、声波传播与三角函数声波是一种机械波，它的传播可以用三角函数来描述。
我们知道，声波的传播速度与介质的性质有关，而介质的性质又可以通过声波的频率来表征。
根据波动方程的解析解，我们可以得到声波的传播方程：y(x, t) = A * sin(kx - ωt + φ)其中，y表示波动的振幅，x表示传播的距离，t表示时间，A表示振幅的大小，k表示波数，ω表示角频率，φ表示相位差。
从这个方程中，我们可以看到三角函数的作用，它描述了声波的振幅随时间和空间的变化规律。
二、电路中的交流电与三角函数在电路中，交流电是一种周期性变化的电流或电压。
交流电的变化可以用三角函数来描述，常见的是正弦函数。
例如，交流电的电压可以表示为：V(t) = Vm * sin(ωt + φ)其中，V(t)表示电压的大小，Vm表示电压的峰值，ω表示角频率，φ表示相位差。
通过三角函数的表示，我们可以分析交流电的周期、频率、相位等特性，进而设计和优化电路。
三、航海中的三角函数应用在航海中，三角函数有着重要的应用。
例如，通过测量太阳的高度角和方位角，结合船只的观测位置和时间，可以使用三角函数计算出船只的经纬度。
这是基于三角函数的三角测量原理，通过观测角度和距离，利用三角函数的关系进行计算。
这种方法在古代航海中广泛应用，也为现代导航技术的发展奠定了基础。
四、物理学中的周期性现象与三角函数物理学中有许多周期性的现象，例如振动、波动等。
这些现象的变化规律可以用三角函数来描述。
以简谐振动为例，它的位移随时间的变化可以表示为：x(t) = A * sin(ωt + φ)其中，x(t)表示振动的位移，A表示振幅，ω表示角频率，φ表示相位差。
通过三角函数的表示，我们可以研究振动的周期、频率、相位等特性，进而深入理解物理学中的各种现象。
探讨三角函数在高考中的应用
探讨三角函数在高考中的应用三角函数是高中数学中一个重要的概念，其应用范围广泛且深入。
在高考中，三角函数的应用可以分为几个方面：几何应用、力学应用、电学应用以及数学建模等。
下面将就这些方面进行一一探讨。
首先是三角函数的几何应用。
在几何学中，三角函数主要用于解决直角三角形的问题，如计算两个已知边长的直角三角形的角度，或者计算已知角度和边长的直角三角形的缺失边长。
在高考中，这类问题通常涉及到分辨角的大小、测量长度以及计算面积等，需要运用到三角函数的概念和公式。
例如，在解决角度问题时，可以利用正弦定理、余弦定理和正切定理等来求解，而在解决边长问题时，则可以利用正弦函数、余弦函数和正切函数等来计算。
其次是三角函数的力学应用。
在物理学的力学中，三角函数广泛应用于描述物体的运动规律。
例如，当我们研究一个斜抛运动的物体时，可以利用正弦函数和余弦函数来描述抛体的水平和垂直运动。
同样地，在弹簧振动中，正弦函数也被用来描述物体的位移和速度随时间的变化。
这些力学问题往往需要使用三角函数的图像、周期和频率等概念来分析和解答。
三角函数还在电学中有着广泛的应用。
在交流电中，电流和电压的变化是呈正弦函数的，这是因为交流电信号是周期性变化的。
正弦函数不仅可以描述电流和电压的变化规律，还可以用来计算交流电的频率、周期以及最大值和最小值等。
此外，在电路中，三角函数的平均值和均方根值等概念也经常被用来描述电流的大小和能量的消耗等。
最后是三角函数在数学建模中的应用。
数学建模是将现实世界的问题抽象为数学问题，并通过数学模型进行分析和求解的过程。
三角函数在数学建模中的应用广泛，如在生物学中，可以用正弦函数或余弦函数来描述生物周期的变化；在经济学中，可以用正弦函数来分析周期性的经济波动；在环境科学中，可以利用正弦函数来建模太阳辐射的季节性变化等。
这些实际问题的建模和求解需要熟练运用三角函数的概念、公式和性质。
综上所述，三角函数在高考中有着广泛的应用。
浅谈生活中三角函数的应用
浅谈生活中三角函数的应用三角函数是数学中的一种基本函数形式，包括正弦函数、余弦函数和正切函数。
在生活中，三角函数有着广泛的应用，涉及到多个领域。
本文将从几个方面探讨生活中三角函数的应用。
三角函数在物理学中的应用非常广泛。
经典力学是物理学的重要分支之一，而三角函数是解决力学问题的基本工具。
运动学中的匀速圆周运动，可以通过正弦函数或余弦函数来描述物体在圆周上的位置随时间的变化。
动力学中的周期性运动，如弹簧振动、摆动等，也可以使用三角函数来分析和解释。
电磁波的传播也是一种周期性波动，可以使用三角函数进行数学描述。
三角函数在工程学中的应用也非常重要。
建筑工程中的梁、柱的受力分析可以使用三角函数的知识进行计算。
在土木工程中，通过三角函数可以计算斜坡的倾斜度，从而保证工程的安全和稳定。
在电子工程中，正弦函数和余弦函数是交流电信号的基础，可以用于电路分析和设计。
三角函数在音乐领域中也有着广泛的应用。
音乐中的音高和音调是通过波的震荡频率来产生的。
而三角函数可以描述这种震荡的周期性变化。
乐器演奏中的音高可以通过正弦函数描述。
音乐中的和声和音程等也可以通过三角函数进行分析和解释。
在天文学中，三角函数也有重要应用。
根据天体运动的规律，可以使用正弦函数和余弦函数来描述天体在空间中的位置和运动。
地球的公转和自转都是周期性的运动，可以通过三角函数来进行描述和计算。
天体测量中的角度测量，也离不开三角函数的知识。
三角函数在生活中有着广泛的应用，涉及到物理学、工程学、音乐、天文学等多个领域。
掌握三角函数的知识能够帮助我们更好地理解和解决实际问题。
对于学生来说，学好三角函数是非常重要的。
在实际生活和工作中，我们也可以运用三角函数的知识来解决问题，提升自己的技能和能力。
三角函数性质理解和简单应用
浅析三角函数性质理解和简单应用摘要：通过分析三角函数的图像可以掌握三角函数的性质。
在解决三角函数问题是常用数学方法有化归法、换元法、数形结合法。
关键词：三角函数性质应用前言：三角函数是基本初等函数，它是描述周期现象的重要数学模型。
在这部分内容中函数的图像和性质起着至关紧要的作用。
下面我以正弦函数为例浅谈三角函数图像和性质的理解和简单应用。
一、通过图像分析正弦函数性质1.在由正弦函数线做正弦函数曲线的过程中，明确了y=sinx的最小正周期为之后，常用作图方法即五点作图法画正弦函数曲线。
所谓的五点本质上是图像的最高点、最低点以及函数图像和x轴的交点。
在正弦函数中这五点分别是（0，0），（，1），（π，0），（，-1），（2π，0），用圆滑的曲线把它们连接起来就可以得到正弦函数y=sinx一个周期的图像。
然后再根据函数的周期性向左右两个方向再画几个周期的图像方便观察图像的规律。
如下图：2.通过分析正弦函数的图像特点，可以很容易得到正弦函数y=sinx的其它性质（1）定义域函数的图像是向左右两个方向无限延展的，所以正弦函数的定义域是。
（2）值域函数图像呈波浪形，具有周期性。
函数图像最高到达1，最低到达-1，并且函数图像是连续的，可以确定函数的值域是[-1，1]。
从函数图像可以看出函数具有周期性，所以正弦函数有无数个极值点。
距离y轴最近的最高点（，1）即当x=时，y取最大值1。
根据正弦函数的周期性可以表示出取最大值时所有的x的取值，即当y=1时，x=+2kπ，k∈z。
同样的方法就可以写出函数取最小值即y=-1时，x=-+2k，k∈z。
（3）对称轴由正弦函数图像的最高点或者最低点向x轴做垂线就会发现函数的图像会关于垂线对称。
也就是说正弦曲线有无数的对称轴，且相邻的两个对称轴的间距为π即对称周期为π。
用一条距离y轴最近的对称轴x=做参考，根据对称轴的周期性得正弦曲线的对称轴x=+k，k∈z，k的每一个取值对应一个对称轴。
三角函数的性质及其在高中数学中的应用
三角函数的性质及其在高中数学中的应用三角函数是高中数学中的重要内容，它们具有独特的性质和广泛的应用。
本文将从三角函数的定义开始，探讨它们的性质，并介绍它们在高中数学中的应用。
三角函数的定义是基于单位圆上的点坐标来进行的。
我们先来看正弦函数（sin）和余弦函数（cos）。
在单位圆上，对于任意一个角度θ，可以找到一个点P(x,y)，其中x坐标为cosθ，y坐标为sinθ。
这样，我们就得到了正弦函数和余弦函数的定义。
正弦函数和余弦函数具有很多重要的性质。
首先是周期性。
正弦函数和余弦函数的周期都是2π，也就是说，在一个周期内，函数的值会重复。
其次是奇偶性。
正弦函数是奇函数，即sin(-θ)=-sinθ；余弦函数是偶函数，即cos(-θ)=cosθ。
再次是界限性。
正弦函数和余弦函数的值都在-1和1之间，即-1≤sinθ≤1，-1≤cosθ≤1。
最后是对称性。
正弦函数和余弦函数关于y轴对称，即sin(-θ)=-sinθ，cos(-θ)=cosθ。
接下来，我们来讨论正切函数（tan）和余切函数（cot）。
正切函数定义为tanθ=sinθ/cosθ，余切函数定义为cotθ=cosθ/sinθ。
正切函数和余切函数也具有周期性、奇偶性和界限性。
它们的周期是π，即在一个周期内，函数的值会重复。
正切函数是奇函数，余切函数是偶函数。
它们的值可以是任意实数。
三角函数在高中数学中有广泛的应用。
首先是在几何中的应用。
三角函数可以用来计算三角形的边长和角度。
例如，已知一个直角三角形的一个角度和一个边长，可以利用正弦函数、余弦函数或正切函数来计算其他边长或角度。
其次是在物理中的应用。
三角函数可以用来描述波的性质，例如声波和光波。
正弦函数和余弦函数可以表示周期性的波动，而正切函数可以表示非周期性的波动。
再次是在工程中的应用。
三角函数可以用来计算力的分解、电路中的交流电和振动系统等。
在这些应用中，三角函数可以帮助我们理解和解决实际问题。
高中数学三角函数的基本关系与应用概率与统计的重要概念与计算方法
高中数学三角函数的基本关系与应用概率与统计的重要概念与计算方法高中数学三角函数的基本关系与应用、概率与统计的重要概念与计算方法随着高中数学的深入学习，我们将接触到许多重要的数学概念和计算方法。
其中，三角函数与概率统计是高中数学中非常重要的内容。
本文将分别介绍三角函数的基本关系与应用，以及概率统计中的重要概念与计算方法。
一、三角函数的基本关系与应用三角函数是数学中的重要工具，它们在几何学、物理学和工程学等领域有着广泛的应用。
下面将介绍三角函数的基本关系与应用。
1. 正弦函数与余弦函数在直角三角形中，正弦函数和余弦函数是最基本的两个三角函数。
以角A为例，若已知直角三角形的斜边为c，对边为a，邻边为b，则有以下基本关系：sin A = a / ccos A = b / c这两个基本关系在解决直角三角形的边长和角度问题时非常有用。
同时，在物理学领域中，正弦函数和余弦函数也被广泛应用于波动和周期运动的描述中。
2. 正切函数与余切函数正切函数和余切函数是另外两个重要的三角函数。
同样以角A为例，有以下基本关系：tan A = a / bcot A = b / a正切函数和余切函数常常用于解决斜三角形相关问题，尤其在物理学和工程学中，它们被广泛应用于分析倾斜物体的运动与力学特性。
3. 基本关系的应用除了直角三角形和斜三角形的应用外，三角函数还可以应用于解决几何学中的各种问题。
比如，通过利用正弦定理和余弦定理，我们可以确定任意三角形的边长和角度。
此外，三角函数还在物理学和工程学中扮演着重要的角色。
如在物理学中，我们可以通过正弦函数和余弦函数来描述物体的周期性振动，而在工程学中，三角函数的应用则涉及到建筑、测量和计算问题。
二、概率统计的重要概念与计算方法概率统计是一门研究随机事件的产生规律和统计规律的学科。
它在实际生活中的应用非常广泛，从市场调查到风险评估，几乎无处不在。
下面将介绍概率统计中的重要概念与计算方法。
1. 概率的基本概念概率是指在一次随机事件中，某一特定结果发生的可能性大小。
高中三角函数常见题型与解法
三角函数的题型和方法一、思想方法1、三角函数恒等变形的基本策略。
（ 1）常值代换：特别是用“ 1”的代换，如 1=cos 2θ +sin 2 θ=tanx · cotx=tan45 °等。
（ 2）项的分拆与角的配凑。
如分拆项： sin 2x+2cos 2x=(sin 2x+cos 2x)+cos 2x=1+cos 2x ；配凑角：α =（α + β）－β，β =－等。
2 2（ 3）降次与升次。
即倍角公式降次与半角公式升次。
（ 4）化弦（切）法。
将三角函数利用同角三角函数基本关系化成弦（切）。
（ 5）引入协助角。
asin θ +bcos θ = a 2 b 2 sin(θ + )，这里协助角 所在象限由 a 、b 的符号确立，角的值由 tan = b确立。
a（ 6）全能代换法。
巧用全能公式可将三角函数化成 tan的有理式。
22、证明三角等式的思路和方法。
（ 1）思路：利用三角公式进行假名，化角，改变运算结构，使等式两边化为同一形式。
（ 2）证明方法：综合法、剖析法、比较法、代换法、相消法、数学概括法。
3、证明三角不等式的方法：比较法、配方法、反证法、剖析法，利用函数的单一性，利用正、余弦函数的有界性，利用单位圆三角函数线及鉴别法等。
4、解答三角高考题的策略。
（ 1）发现差别：察看角、函数运算间的差别，即进行所谓的“差别剖析”。
（ 2）找寻联系：运用有关公式，找出差别之间的内在联系。
（ 3）合理转变：选择适合的公式，促进差别的转变。
二、注意事项对于三角函数进行恒等变形，是三角知识的综合应用，其题目种类多样，变化仿佛复杂，办理这种问题，注意以下几个方面：1、三角函数式化简的目标：项数尽可能少，三角函数名称尽可能少，角尽可能小和少，次数尽可能低，分母尽可能不含三角式，尽可能不带根号，能求出值的求出值。
2、三角变换的一般思想与常用方法。
注意角的关系的研究，既注意到和、差、倍、半的相对性，如1() ( ) 22 ．也要注意题目中所给的各角之间的关系。
高一第12讲 三角函数定义及运用(教师版)
(2)设 90° α<180°， 角 α 的终边上一点为 P(x， 5)， 且 cosα＝ 的值； 解析：(1)∵r＝ x ＋5，∴cosα＝
2
2 x， 求 sinα 与 tanα 4
x 2 x ，从而 x＝ 2 ，解得 x＝0 或 x＝± 3. 2 4 x ＋5 x ＋5
5 10 ∵90° α<180°，∴当 x＝－ 3时 r＝2 2，sinα＝ ＝ ， 4 2 2 5 15 tanα＝ ＝－ .当 x 0 时，sinα= 5 ，tanα 不存在。 3 － 3 例 4 角α终边上的点 P 与 A(a,2a)关于 x 轴对称(a＞0)，角β终边上的点 Q 与 A 关于直线 y＝x 对称，求 sin α²cos α＋sin β²cos β＋tan α²tan β的值． 解析 由题意得，点 P 的坐标为(a，－2a)，点 Q 的坐标为(2a，a)． －2a 2 a 1 所以，sin α＝ 2 ＝－ ，cos α＝ 2 ＝ ， 2 2 a ＋－2a 5 a ＋－2a 5 －2a a 1 2a 2 tan α＝ ＝－2，sin β＝ ＝ ，cos β＝ ＝ ， 2 2 2 2 a 2a ＋a 5 2a ＋a 5 a 1 tan β＝ ＝ ，故有 sin α²cos α＋sin β²cos β＋tan α²tan β 2a 2 －2 1 1 2 1 ＝ ³ ＋ ³ ＋(－2)³ ＝－1. 2 5 5 5 5 课堂小结：任意角的三角函数值与终边所在的位置有关，与点在终边上的位置无关，故要首 先判定 P 点所在的象限，确定 r，最后根据定义求解．
y x
α 的终边不能与 y 轴重合，故正切函数的定义域为α|α≠kπ＋ ，k∈Z.
π 2
[3] 三角函数线是三角函数的几何表示 (1)正弦线、正切线的方向同纵轴一致，向上为正，向下为负． (2)余弦线的方向同横轴一致，向右为正，向左为负． (3)当角 α 的终边在 x 轴上时，点 T 与点 A 重合，此时正切线变成了一个点，当角 α 的终边在 y 轴上时，点 T 不存在，即正切线不存在． (4)在“数”的角度认识任意角的三角函数的基础上，还可以从图形角度考察任意角的 三角函数， 即用有向线段表示三角函数值， 这是三角函数与其他基本初等函数不同的地 方．
三角函数综合应用
解 (1)m·n＝ 3sin x4·cos x4＋cos2x4
＝
3 2 sin
x2＋1＋c2os
x 2＝sinx2＋π6＋12，
∵m·n＝1，∴sinx2＋π6＝12. cosx＋π3＝1－2sin2x2＋π6＝12， cos23π－x＝－cosx＋π3＝－12. (2)∵(2a－c)cos B＝bcos C，
[4 分]
(2)解 |b＋c|2＝(b＋c)2＝b2＋c2＋2b·c＝sin2β＋16cos2β＋cos2β＋
16sin2β＋2(sin βcos β－16sin βcos β)
＝17－30sin βcos β＝17－15sin 2β，
最大值为 32，所以|b＋c|的最大值为 4 2.
[9 分]
(3)证明 由 tan αtan β＝16，得 sin αsin β＝16cos αcos β，
答题模板
平面向量与三角函数的结合问题
(14 分)设向量 a＝(4cos α，sin α)，b＝(sin β，4cos β)，c＝(cos β， －4sin β)． (1)若 a 与 b－2c 垂直，求 tan(α＋β)的值； (2)求|b＋c|的最大值； (3)若 tan αtan β＝16，求证：a∥b.
因为 α 是第一象限角，故 sin α＝1123.
所以，cossin4απ＋＋π42α＝sicnoαs ＋2απ4
＝2cos
2 α－sin
α＝－1134
2.
三角形中的三角恒等变换
例 2 设锐角三角形 ABC 的内角 A，B，C 的对边分别为 a，b， c，a＝2bsin A. (1)求 B 的大小； (2)求 cos A＋sin C 的取值范围．
变式训练 1
三角函数最值及其综合运用知识点总结及经典高考题解析
三角函数最值及其综合运用【考纲说明】1、了解三角函数的最值（值域），理解三角函数取最值的条件，掌握求三角函数最值的常用方法。
2、结合三角函数的性质，会求形如函数)0>,0≠)(+sin(=w A φwx A y 、)0>,0≠)(+cos(=w A φwx A y 、)0>,0≠)(+tan(=w A φwx A y 的综合问题。
【知识梳理】一、三角函数的最值 1、定义 （1）当2-2=ππk x )∈(Z k 时，x y sin =取最小值1-；当2+2=ππk x )∈(Z k 时，x y sin =取最大值1；正弦函数x y sin =)∈(R x 的值域为[]1,1-。
（2）当ππk x +2=)∈(Z k 时，x y cos =取最小值1-；当πk x 2=)∈(Z k 时，x y cos =取最大值1；余弦函数x y cos =)∈(R x 的值域为[]1,1-。
（3）)2+≠,∈(tan =ππk x R x x y 的值域为R 。
2、常用方法（1）求三角函数最值的常用方法①配方法（主要利用二次函数理论及三角函数的有界性）；②化为一个角的三角函数（主要利用和差角公式及三角函数的有界性）；③数形结合法（常用到直线的斜率关系）；④换元法（如万能公式，将三角问题转化为代数问题）；⑤基本不等式法等。
（2）三角函数的最值都是在给定区间上取得的，因而特别要注意题设中所给出的区间。
①求三角函数最值时，一般要进行一些代数变换和三角变换，要注意函数有意义的条件及弦函数的有界性②含参数函数的最值问题，要注意参数的作用和影响。
（3）具体方法：①y =a sin x +b cos x 型函数最值的求法：常转化为y （x +ϕ） ②y =a sin 2x +b sin x +c 型：常通过换元法转化为y =at 2+bt +c 型： ③y =dx c b x a ++cos sin 型：i 当x R ∈时，将分母与y 乘转化变形为sin （x +ϕ）＝()f y 型。
高考数学总复习教案39三角函数的综合应用
------精品文档!值得拥有！------第三章 三角函数、三角恒等变换及解三角形第9课时 三角函数的综合应用(对应学生用书(文)、(理)57～59页)ac ＝、题改编1. (必修5P 例题4)设△ABC 的三个内角AB 、C 所对的边分别是a 、b ，、c ，且9sinCcosA ＝________．则A π 答案： 4πacaaca. ＝＝，即sinAcosA ，所以A ，得＝解析：由，＝＝4cosAsinAcosAsinCsinCsinAy2. (必修个单位后，得到函数)φ<2sinx 将函数题改编)y ＝的图象向左平移φ(0≤π第习题4P1.3845π?? ．φ＝________的图象，则＝sin －x ??611 答案：π 611＝．只有＋＝个单位得到函数π≤向左平移＝将函数解析：ysinx φ(0φ<2)ysin(x φ)φπ时有＝y6??11π????πx ＋sin. sin ＝－x ??6 ??6------值得收藏！!珍贵文档------ ------------精品文档!值得拥有！π1 －＝________．3. (必修4P 习题3.3第6(2)题改编)tan 10912πtan 12 －32答案：??ππππ??－22sincos－sincos??12121212解析：原式＝－＝ππππcossinsincos12121212πcos－63. ＝＝－2π1sin62π1??2上在区间cosx＋(x∈R)，则4. (必修4P复习题第13题改编)已知函数f(x)f(x)＝3sinxcosx－，0??11524 的值域是________．31??答案：，－??22π??????π13πππ31????????.∈，故值域为－时，解析：f(x)＝sin2x－cos2x＝sin2x.当x∈，－，2x－－0，??62222 ??????4366 ．BC上的高为°，则边2，B＝60________5. 在△ABC中，AC＝7，BC ＝33答案：23322BC上的高h＝，所以边3sin60°＝.3－2c－＝0，解得c＝得解析：由余弦定理，7＝c2c＋4－，即c32sinα22α＝1，tanα＝1. 同角三角函数的基本关系式：sin.α＋cos cosααsinβ，cos(α±β)cos＝cosαcos βsinα2. 两角和与差的正弦余弦和正切公式：sin(α±β)＝sincosβ±βtantanα±.＝，tan(α±β)αsinββtantanα12222＝αα，1－1＝－2sintan2αcosα3. 二倍角公式：sin2＝2sinαα，cos2＝cosα－sinα＝2cosαα2tan.2α－tan1 4. 三角函数的图象和性质5. 正弦定理和余弦定理：cba ．为三角形外接圆的半径＝＝2R(R)＝正弦定理：(1) sinCsinAsinB------值得收藏！!珍贵文档------------值得拥有！------精品文档!222＝＋ccosA－余弦定理：(2) a2bccosA＝b，222a－＋cb .2bc题型1三角恒等变换πππ27????.，例1已知sinA∈＝，A＋????10244 (1) 求cosA的值；5 ＝cos2x＋sinAsinx的值域．(2) 求函数f(x)2πππππ3????272ππ????cos，且sin＝－.＝，所以<A＋<，解：(1) 因为<A<＋AA＋102441042????44??π??π??所以cosA＝cos??－＋A4????4ππ????ππ????sin＝cos＋sincos＋A＋A44????44322227＝.·＋·＝－10210254(2) 由(1)可得sinA＝.55所以f(x)＝cos2x＋sinAsinx221313??2－sinx2＋2sinx2sinx＝－sinx＝时，f(x)取最大值；＝1－，sinx＋，x∈R.因为∈[－1，1]所以，当??2222当sinx＝－1时，f(x)取最小值－3.3??，3－的值域为所以函数f(x). ??2备选变式（教师专享）12(2013·上海卷)若cosxcosy＋sinxsiny＝，sin2x＋sin2y＝，则sin(x＋y)＝________．232答案：31解析：由题意得cos(x－y)＝，sin2x＋sin2y＝sin[(x＋y)＋(x－y)]＋sin[(x＋y)－(x－y)]＝2sin(x＋y)cos(x222sin(x＋y)y)－＝＝. 33题型2三角函数的图象与性质------值得收藏！!珍贵文档------------!值得拥有！------精品文档ππ??分Qf(x)的部分图象如图所示，P、A>0，0<φ<f(x)例2已知函数＝Asin，y＝，，x∈Rφx＋??23 ．的坐标为(1，A)别为该图象的最高点和最低点，点P 的值；求f(x)的最小正周期及φ(1)π2 的值．＝，求AR的坐标为(1，0)，∠PRQ(2) 若点3π26.T＝＝解：(1) 由题意得π3??π??的图象上，，A)在y＝Asin因为P(1φx＋??3??π??sin所以＝1.φ＋??3ππ＝.因为0<φ<，所以φ62A)．Q的坐标为(x，－(2) 设点0π3ππ，，得x＝4由题意可知x＋＝00263．Q(4，－A)所以π2PRQ＝，由余弦定理得连结PQ，在△PRQ中，∠3222222）＋－（RQ9－PQ4AA＋9＋ARP ＋＝∠PRQ＝＝cos RQ2RP·2＋A2A·912＝3.又A>0A，所以A＝3. ，解得－2备选变式（教师专享）已知函数f(x)＝sin(ωx＋φ)(ω>0，0≤φ≤π)为偶函数，且其图象上相邻两对称轴之间的距离为π.(1) 求函数f(x)的表达式；------值得收藏！!珍贵文档------------!值得拥有！------精品文档π??12sin＋－2α??42 的值．f(α)＝，求(2) 若sinα＋3αtan1＋∵φ＝0，又，即2sinωxcosφ＝0恒成立，∴cosφ)解：(1) ∵f(x)为偶函数，∴sin(－ωx＋φ)＝sin(ωx＋ππ，T＝20≤φ≤π，∴φ＝. 又其图象上相邻对称轴之间的距离为π，∴2f(x)＝cosx. ∴ω＝1，∴1α－cos2α＋sin242ααcos＋2sinαcosα＝，即2sinα＋(2) ∵原式＝＝2sinαcosα，又∵sincosα＝，∴193αtan1＋55.，故原式＝－＝－99 正弦定理、余弦定理的综合应用题型33b. ＝a、b、c，且2asinB中，内角例3(2013·浙江)在锐角△ABCA、B、C的对边分别为的大小；(1) 求角A 的面积．b＋c＝8，求△ABC(2) 若a＝6，π3ba＝.＝.因为A是锐角，所以解：(1) 由2asinB＝3b及正弦定理＝，得sinAA3sinB2sinA2822222.，所以bc＝＝－bc＝36.又ba(2) 由余弦定理＋＝bc＋c－2bccosA，得b8＋c3371.ABC由三角形面积公式S＝bcsinA，得△的面积为32备选变式（教师专享）π3.＝，△5ABC的面积为10，C中，角A，B，的对边分别为a，b，cC＝，a在△ABC 3 (1) 求b，c的值；π??求cos的值．(2) －B??3π1，S＝，a＝5，因为＝absinC由已知，解：(1) C△ABC23π1，解得b8.＝·10即3＝b5sin32π27.c49, 80cos64＋＝由余弦定理可得：c25－＝所以＝3------值得收藏！!珍贵文档------------------精品文档!值得拥有！6425＋49－3142，所以B＝是三角形的内角，易知sinB1＝－cos(2) 由(1)有cosB＝＝，由于B 7707ππ??13343π11??.＝＝cosBcos＋cossinBsin＝×＋×－B14337227??3 题型4三角函数、平面向量、解三角形的综合应用1??，sinA＝A是△ABC的内角．例4已知向量与nm＝(3，sinA＋3cosA)共线，其中??2 的大小；(1) 求角A 的形状．，求△ABC面积S的最大值，并判断S 取得最大值时△ABC(2) 若BC＝2∥nm，解：(1) 因为30.所以sinA·(sinA＋3cosA)－＝2cos2A－133，＋所以sin2A－＝022213即1，sin2A－cos2A＝22??π??即sin1.＝－2A??6π??ππ11??.2A－∈因为A∈(0，π)，所以，－6??66πππ＝，A＝.故2A－36222bc.c(2) 由余弦定理，得4＝b－＋31，＝bc又S＝bcsinA△ABC4222)，4(当且仅当b＝c＋c时等号成立≥42bcbc＋≥2bcbc≤而b313＝3.bc≤×4bcsinA所以S＝＝△ABC442当△ABC的面积取最大值时，b＝c.π又A＝，故此时△ABC为等边三角形．3备选变式（教师专享）已知△ABC的角A、B、C所对的边分别是a、b、c，设向量m＝(a，b)，n＝(sin B，sin A)，p＝(b－2，------值得收藏！!珍贵文档------------值得拥有！------精品文档!a－2)．∥n，求证：△ABC为等腰三角形；(1) 若mπ⊥，边长c＝2，角C＝，求△ABC(2) 若m的面积．p3ba∥ABC △a＝b.∴∴n，∴asin A＝bsin B，即a·＝b·，其中R是△ABC 外接圆半径，证明：(1) ∵m2R2R为等腰三角形．22＝＋babab(a－2)＝0.∴＋b＝ab.由余弦定理可知，4＝a－＋m·(2) 解：由题意可知p＝0，即a(b－2)22，＝－1)3ab，即(ab)ab－3ab－4＝0，∴＝4(舍去(a＋b)ab－π113.sin ＝∴S＝absin C＝×4×322在已知值求角中，应合理选择三角函数形式进行求解，避免增根．分)【示例】(本题模拟高考评分标准，满分14105 ＋β，sinβ的值．＝，且α、β若sinα均为锐角，求＝α105 学生错解：522.α为锐角，∴cosα＝1－sin＝解：∵α51032. cos β＝1－sin＝又ββ为锐角，∴102＝αsin βsinαcosβ＋cos＝，∵sin(α＋β)2 β<90°，<90°，0°<α由于0°< 180°，°<α＋β<∴0.°＝45°或135β故α＋在已知值求角中，角的范围常常被忽略或不能发现隐含的角的大小关系而出现增根不能审题引导：排除．要避免上述情况的发生，应合理选择三角函数形式进行求解，根据计算结果，估算出角的较精确的取值范围，并不断缩小角的范围，在选择三角函数公式时，一般已知正切函数值，选正切函数，已知正余??ππ??，则一般选正弦函数．弦函数值时，若角在(0，π)时，一般选余弦函数，若是，－??22252.(2＝分) －＝cosα∵解：规范解答：为锐角，∴α1sinα5------值得收藏！!珍贵文档------------值得拥有！------精品文档!1032) β＝又β为锐角，∴cosβ.(4＝1－sin分102＝sinββ－sinα，(10分) 且cos(α＋β)＝cosαcos2ππ，所以0<α＋β<π，由于0<α<，0<β<22π][π0，)α因为y＝cosx在＋.(14分β＝上是单调递减函数，故4没有注意挖掘题目中的隐含条件，忽视了对角的范围的限制，造成出错．错因分析：152，α135°是正确的，但题设中sin＝β<<α＋180°而得到α＋事实上，仅由sin(α＋β)＝β＝45°或，0°<225110°，故上述结论是错误的．在已知值求角中，应60°<α＋β<0<α<30°，°<β<30°从而0，使得0°<＝sinβ210][在cosx，因为y＝合理选择三角函数形式进行求解，避免增根．本题中0<α＋β<ππ，0上是单调函数，不易出错．＋β)cos所以本题先求(α）1π（x－πx ．coscos的最小正周期为________1. (2013·常州期末)函数f(x)＝22答案：2πxπx2πxπ（x－1）π12.T＝＝＝cos·sinsinπx，最小正周期为解析：f(x)＝coscos＝22222π1ππ??????1－，的值域是f(x)，若，其中sin，则a的2. (2013·北京期末)已知函数f(x)＝x∈a－x＋，??????236 ________．取值范围是??π??答案：，π??3π7πππππππ??1π??，所以＝＝－或x＋＝时，sin＋≤解析：若－≤x≤a，则－x＋≤a＋，因为当x＋x266366666??6ππ7ππ??1π????1，－的值域是aa≤π，即的取值范围是要使f(x). ≤a，则有≤＋≤，即，π??23662??3 ．________3cosC＝，则△ABC的面积为sinC1，＝中，)3. (2013·北京期末已知△ABCAB3BC ＝，3答案：2------值得收藏！!珍贵文档------------------值得拥有！精品文档!πABBC，.根据正弦定理可得解析：由sinC3cosC＝，得tanC＝＝3>0，所以C＝sinCsinA3ππ113，所以三角形为直角B＝因为即＝＝2，所以sinA＝.AB>BC，所以A<C，所以A＝，即22sinA63231.×1三角形，所以S＝＝×3△ABC22 ________．f(x)4. (2013·新课标Ⅰ卷)设当x＝θ时，函数＝sinx－2cosx取得最大值，则cosθ＝52答案：－5552??5.＝sinx－2cosx解析：∵＝f(x)cosxsinx－??55552＝sinφ＝－，则f(x)令cosφ＝，55φ)，cosx)＝5sin(x＋5(sinxcosφ＋sin φπππ＋2k－φ，x当＋φ＝2kπ＋，k∈Z，即x＝22π∈Z，π＋k∈Z时，f(x)取最大值，此时θ＝2k－φ，k2??5π2??.∴cosθ＝cos＝sinφ＝－φ2kπ＋－5??2n cosB)、b、c.向量m＝(1，，B(2014·1. 扬州期末)在锐角△ABC中，角A、、C所对的边长分别为a⊥.＝(sinB，－3)，且mn的大小；(1) 求角B ，求此三角形周长．ABC面积为103，b＝7(2) 若△n m·＝，0 解：(1) m·n＝sinB－3cosB，∵m⊥n，∴cosB≠，0ABCsinB∴－3cosB＝0.∵△为锐角三角形，∴ππB＝.＝∴tanB3.∵0<B<，∴3231322222ca，得49＝＋2accosBa由＝，得10ac＝＝acsinB∵(2) Sac，由题设＝3ac40.7＝＋c－△ABC244------值得收藏！!珍贵文档------------------精品文档!值得拥有！22213＝，169.∴a－ac，∴(a＋c)＋＝(ac＋cac)－＋3ac＝49＋120＝20.三角形周长是∴2sinC. ＝，2＋2且sinA＋、2. 在△ABC中，a、bc分别是角A、B、C的对边，△ABCsinB的周长为c的长；(1) 求边1 C的度数．(2) 若△ABC的面积为sinC，求角3c＝2ca＋b＋c∵解：(1) 在△ABC中，sinA＋sinB＋＝2sinC，由正弦定理，得a＋b ＝2c ，∴2. ＝2＝1)c(2＋＋＝，c2. a＋b＝2∴11△ABC中，S，absinC＝sinC＝(2) 在△ABC32211.ab＝∴ab＝，即332222222ab＋b）a－＋b－c－（a1ABC△，又在cosC＝＝＝又a＋b＝2，在△ABC中，由余弦定理，得22ab2ab，∈(0，π)中∠C.C＝60°∴∠1. ＝＋C)、A、BC对应的边分别是a、b、c.已知cos2A－3cos(B湖北卷3. (2013·)在△ABC中，角A的大小；(1) 求角sinBsinC的值．(2) 若△ABC的面积S＝＝53，b5，求12∠，解得cosA＝，∴A＝60°.，∴解：(1) 由已知条件得：cos2A＋3cosA＝1 2cos2A＋3cosA－＝0225bc1a22.sinBsinC，∴＝53＝＝(2R)c＝4，由余弦定理，得a＝21，＝＝28bcsinA(2) S＝2274Rsin2AA. ∠B＝2ABC北京卷)在△中，a＝3，b＝26，∠4. (2013·求cosA的值；(1) 求c的值．(2)2sinAcosA263所以A.所以在△ABC中，由正弦定理得＝.2ba解：(1) 因为＝3，＝62，∠B＝∠sinAsinAsin2A626.故. ＝cosA＝33362.A＝－1＝(1)(2) 由知cosAsinA，所以＝cos33------值得收藏！!珍贵文档------------值得拥有！------精品文档!22122cos所以.sinB＝＝B. 1＝∠又因为B＝2∠A，所以cosB2cos－A－1＝3335＝. cosAsinBsinAcosB＋中，sinC＝sin(A＋B)＝在△ABC9a sin C＝5. 所以c＝sin A1. 三角变换的基本策略是化异为同，即将函数名称、角、次数等化异为同．2. 对于函数y＝Asin(ωx＋φ)＋B，常用“五点法”画图象，运用整体思想研究性质．3. 求三角函数的单调区间、周期，及判断函数的奇偶性，要注意化归思想的运用，通过恒等变换转化为基本三角函数类型，注意变形前后的等价性．4. 解三角函数的综合题时应注意：(1) 与已知基本函数对应求解，即将ωx＋φ视为一个整体X；(2) 将已知三角函数化为同一个角的一种三角函数，如y＝Asin(ωx＋φ)＋B或y＝asin2x＋bsinx ＋c；(3) 换元方法在解题中的运用．请使用课时训练(B)第9课时(见活页)．[备课札记]------值得收藏！!珍贵文档------。
三角函数一般形式及其应用
2
2
（2）求ω，已知函数的周期 T，则 2π ． T
（3）求φ，常用方法有：
①代入法：把图象上的一个已知点代入(此时，A，ω，B 已知)．
②五点法：确定φ值时，往往以寻找“五点法”中的第一个零点
(
,
0)
作为突破口，具体
如下：
“第一点”(即图象上升时与 x 轴的交点中距原点最近的交点)为ωx＋φ=0； “第二点”(即图象的“峰点”)为ωx＋φ= π ；
（1）函数 y＝sin x 到 y＝sin(x＋φ)的图象变换称为相位变换；
（2）函数 y＝sin x 到 y＝sin ωx 的图象变换称为周期变换；
（3）函数 y＝sin x 到 y＝Asin x 的图象变换称为振幅变换．
（4）函数 y＝sin x 到 y＝Asin(ωx＋φ)的图象的变换途径为相位变换→周期变化→振幅变 换或周期变换→相位变化→振幅变换．
T 4
＝
7 12
－
π 3
＝
4
，所以
T＝π，ω＝
2 T
＝2．
又函数图象经过点( π ，0)，所以 2× π ＋φ＝π，则φ＝ π ，
3
3
3
故函数的解析式为 f(x)＝
2
sin(2x＋
π 3
)，
所以 f(0)＝
2
sin
π 3
＝
6． 2
【名师点睛】根据函数图象确定函数解析式，关键是准确把握解析式中的各个参数在图象
三角函数一般形式及其应用专题介绍
内容简介
帮助高一学子对三角函数一般形式知识进行理解和运用，介绍了三角函数一般形式的各种应用 形式.对三角函数一般形式的各知识点进行详细介绍，同时运用例题加深学生印象.例举出该知 识可能出现的考点，针对考点设置例题供学生快速提升，并设置了详细的解析让学生参考，快 速提升解答能力.
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
实用文档 §4.8三角函数的综合应用 【复习目标】 1． 理解三角函数中自变量的两面性——角与实数，将三角函数问题与几何、代数联系起来； 2． 三角恒等变型与三角函数的图象与性质是综合应用的两个方面。
【课前预习】
1. ⊿ABC 的内角满足tan sin 0A A -<，cos sin 0A A +>，则A 的范围是 。
2. 若111cos sin θθ-=，则sin 2θ= 。
3. 由函数52sin 3()66y x x ππ=≤≤与函数2y =的图象围成一个封闭图形，这个封闭图形
的面积是 。
4. 已知()f x 是定义在（0，3）上的函数，图象如图所示，那
么不等式()cos 0f x x <的解集是
（ ）
A ．()()0,12,3⋃
B ．(1,)(,3)22ππ
⋃ C ．
()0,1,32π⎛⎫⋃ ⎪⎝⎭ D ．()()0,11,3⋃ 5. 函数|sin |,[,]y x x x ππ=+∈-的大致图象是
（ ）
【典型例题】
实用文档
例1 已知函数2()sin sin f x x x a =-++.
（1） 当()0f x =有实数解时，求a 的取值范围；
（2） 若x R ∈，有
171()4f x ≤≤，求a 的取值范围。
例2 （2003上海卷·22）已知集合M 是满足下列性质的函数()f x 的全体：存在非零常
数T ，对任意x ∈R ，有()f x T +=T ·()f x 成立.
（1）函数()f x = x 是否属于集合M ？说明理由；
（2）设函数()f x =a x （a >0,且a ≠1）的图象与y=x 的图象有公共点，证明：()f x =a x ∈M ；
（3）若函数()f x =sin kx ∈M ,求实数k 的取值范围.
实用文档
【本课小结】
【课后作业】
1． （2004北京春·16）在∆ABC 中，a ，b ，c 分别是∠∠∠A B C ，，的对边长，已知a ，
b ，
c 成等比数列，且a c ac bc 22-=-，求∠A 的大小及b B
c sin 的值。
2． 求函数
111sin cos sin cos y x x x x =++，(0,)2x π∈的最小值。
3． （2000北京春·19）在△ABC 中，角A 、B 、C 对边分别为a 、b 、c ．证明：
a b c A B C 222
-=-sin()sin . 4． （2002全国·17）已知12cos cos 2sin 2sin 2=-+αααα，⎪⎭⎫ ⎝⎛∈2,0πα.求αsin 、αtan 的
值。
5． （2004北京·15）在△ABC 中，sinA+cosA=22
，AC=2，AB=3，求tgA 的值和△ABC
的面积。