matlab验证时域采样定理实验报告
实验六 matlab采样定理的建模和验证
页眉内容
实验六
题目:采样定理的建模和验证
实验目的:通过建模与仿真验证采样定理,理解采样定理的物理实质实验要求:学习和回顾采样定理内容,对采样定理作建模和仿真
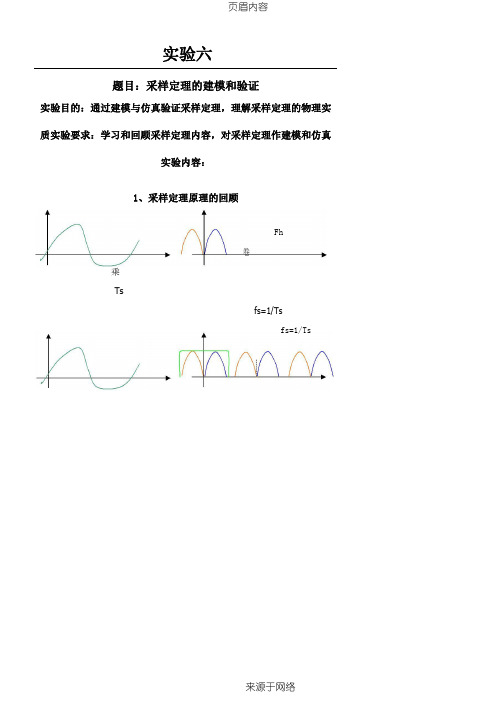
实验内容:
卷
乘
fs=1/Ts
2、建模参数要求:
设计模型,验证采样定理.
设基带波形频谱在 0Hz~200Hz 内. Fh=200Hz(信号最高频率),采样率就应该大于 400Hz 。
用窄脉冲采样,要求窄脉冲宽度是采样周期的 1/10。
从而得到系统仿真步长: 小于等于 1/4000,仿真系统的仿真步长取 1/4000。
采样器用乘法器实现. 而恢复时用低通滤波器实现. 低通滤波器的带宽等于信
号最高频率 Fh,即等于 200Hz.
4、修改基带信号最高频率,如最高频率为200Hz、250Hz 等等,观察采样前后以及恢复的
波形和频谱。
请用实验方法得到频谱混叠后的频谱图和相应的波形。
5. 将被采样信号修改为正弦波、三角波和方波,观察采样前后和恢复非波形和频谱。
实验报告内容和要求:(!!注意每部分得分情况!!)
1.建立采样和恢复模型,说明关键模块的参数设置(30分)
仿真模型建立:
参数设置:
信源与滤波器参数:
2.修改采样率,如采样率为150Hz,200Hz、300Hz等等,观察采样前后以及恢复的波形和频谱。
请用实验方法得到频谱混叠后的频谱图和相应的波形。
(40分)
150Hz:
200Hz:
300Hz:。
matlab验证时域采样定理

目录第1章摘要 (1)第2章基本原理 (2)第3章实验步骤.....................................................................5第4章 MATLAB实现编程 (5)第5章实验结果与分析 (8)5、1程序分析………………………………………………………………85、2信号得波形及幅度频谱 (8)5、3 结果分析 (9)第6章总结...........................................................................12参考文献 (13)第1章摘要一、数字信号处理数字信号处理就是将信号以数字方式表示并处理得理论与技术。
数字信号处理与模拟信号处理就是信号处理得子集.数字信号处理得目得就是对真实世界得连续模拟信号进行测量或滤波。
因此在进行数字信号处理之前需要将信号从模拟域转换到数字域,这通常通过模数转换器实现。
而数字信号处理得输出经常也要变换到模拟域,这就是通过数模转换器实现得。
数字信号处理得算法需要利用计算机或专用处理设备。
数字信号处理技术及设备具有灵活、精确、抗干扰强、设备尺寸小、造价低、速度快等突出优点,这些都就是模拟信号处理技术与设备所无法比拟得。
数字信号处理得核心算法就是离散傅立叶变换(DFT),就是DFT使信号在数字域与频域都实现了离散化,从而可以用通用计算机处理离散信号。
而使数字信号处理从理论走向实用得就是快速傅立叶变换(FFT),FFT得出现大大减少了DFT得运算量,使实时得数字信号处理成为可能、极大促进了该学科得发展。
随着大规模集成电路以及数字计算机得飞速发展,加之从60年代末以来数字信号处理理论与技术得成熟与完善,用数字方法来处理信号,即数字信号处理,已逐渐取代模拟信号处理。
随着信息时代、数字世界得到来,数字信号处理已成为一门极其重要得学科与技术领域.二、实验目得本次课程设计应用MATLAB验证时域采样定理。
基于MATLAB的信号的采样与恢复、采样定理的仿真

山东建筑大学课程设计指导书课程名称:数字信号处理课程设计设计题目:信号的采样与恢复、采样定理的仿真使用班级:电信082 指导教师:张君捧一、设计要求1.对连续信号进行采样,在满足采样定理和不满足采用定理两种情况下对连续信号和采样信号进行FFT频谱分析。
2.基本教学要求:每组一台电脑,电脑安装MATLAB6.5版本以上软件。
二、设计步骤1.理论依据根据设计要求分析系统功能,掌握设计中所需理论(信号的采样、信号的恢复、抽样定理、频谱分析),阐明设计原理。
2.信号的产生和频谱分析产生一个连续时间信号(正弦信号、余弦信号、Sa函数等),并进行频谱分析,绘制其频谱图。
3.信号的采样对所产生的连续时间信号进行采样,并进行频谱分析,和连续信号的频谱进行分析比较。
改变采样频率,重复以上过程。
4.信号的恢复设计低通滤波器,采样信号通过低通滤波器,恢复原连续信号,对不同采样频率下的恢复信号进行比较,分析信号的失真情况。
三、设计成果1.设计说明书(约2000~3000字),一般包括:(1)封面(2)目录(3)摘要(4)正文①设计目的和要求(简述本设计的任务和要求,可参照任务书和指导书);②设计原理(简述设计过程中涉及到的基本理论知识);③设计内容(按设计步骤详细介绍设计过程,即任务书和指导书中指定的各项任务)I程序源代码:给出完整源程序清单。
II调试分析过程描述:包括测试数据、测试输出结果,以及对程序调试过程中存在问题的思考(列出主要问题的出错现象、出错原因、解决方法及效果等)。
III结果分析:对程序结果进行分析,并与理论分析进行比较。
(5)总结包括课程设计过程中的学习体会与收获、对Matlab语言和本次课程设计的认识以及自己的建议等内容。
(6)致谢(7)参考文献2.附件(可以将设计中得出的波形图和频谱图作为附件,在说明书中涉及相应图形时,注明相应图形在附件中位置即可;也可不要附件,所有内容全部包含在设计说明书中。
所有的实验结果图形都必须有横纵坐标标注,必须有图序和图题。
时域采样定理(范文4篇)

时域采样定理(范文
以下是网友分享的关于时域采样定理的资料4篇,希望对您有所帮助,就爱阅读感谢您的支持。时域采样定理(1)电子信息工程学系实验报告课程名称:数字信号处理实验项目名称;时域采样定理实验时间:2013.05.08班级:通信102姓名:学号:0107052一、实验目的:熟悉并加深采样定理的理解,了解采样信号的频谱和模拟信号频谱之间的关系。二、实验环境:计算机、MATLAB软件。三、实验内容和步骤1.给定模拟信号如下:at(t)Aesin(0t)u(t) xa假设式中A444.128,2,02rad/s,将这些参数代入式中,对xa(t)进行傅立叶变换,得到Xa(j),并可画出它的幅频特性Xa(jf)~f;根据该曲线可以选择采样频率。2.按照选定的采样频率对模拟信号进行采样,得到时域离散信号x(n):x(n)xa(nT)AeanTsin(0nT)u(nT)这里给定采样频率如下:fs=1 kHz、300 Hz、200 Hz。分别用这些采样频率形成时域离散信号,按顺序分别用x1(n)、x2(n)、x3(n)表示。选择观测时间Tp50ms。3.计算x(n)的傅立叶变换X(e):jX(e)FT[x(n)]AeanTisin(0nTi)ejn(5)jn0ni1式中,i1,2,3,分别对应三种采样频率的情况111s,T2s,T3s。采样点数以下式计算:T11000300200ni式中,TpTi(6)是连续变量。为用计算机进行数值计算,改用下式计算:第1页共3页ni1n0X(e式中,kjk)DFT[x(n)]MAeanTsin(0
实验二时域采样与频域采样及MATLAB程序

实验二时域采样与频域采样及MATLAB程序时域采样与频域采样一实验目的1掌握时域连续信号经理想采样前后的频谱变化,加深对时域采样定理的理解2理解频率域采样定理,掌握频率域采样点数的选取原则二实验原理1时域采样定理对模拟信号以T进行时域等间隔采样,形成的采样信号的频谱会以采样角频率为周期进行周期延拓,公式为:利用计算机计算上式并不容易,下面导出另外一个公式。
理想采样信号和模拟信号之间的关系为:对上式进行傅里叶变换,得到:在上式的积分号内只有当时,才有非零值,因此:上式中,在数值上,再将代入,得到:上式说明采样信号的傅里叶变换可用相应序列的傅里叶变换得到,只要将自变量用代替即可。
2频域采样定理对信号的频谱函数在[0, 2]上等间隔采样N点,得到则有:即N点得到的序列就是原序列以N为周期进行周期延拓后的主值序列,因此,频率域采样要使时域不发生混叠,则频域采样点数N必须大于等于时域离散信号的长度M (即)。
在满足频率域采样定理的条件下,就是原序列。
如果,则比原序列尾部多个零点,反之,时域发生混叠,与不等。
对比时域采样定理与频域采样定理,可以得到这样的结论:两个定理具有对偶性,即“时域采样,频谱周期延拓;频域采样,时域信号周期延拓”。
在数字信号处理中,都必须服从这二个定理。
三实验内容1时域采样定理的验证给定模拟信号,式中,A二444、128,,,其幅频特性曲线如下图示:选取三种采样频率,即,300Hz, 200Hz,对进行理想釆样,得到采样序列:。
观测时间长度为。
分别绘出三种采样频率得到的序列的幅频特性曲线图,并进行比较。
2频域采样定理的验证给定信号:,对的频谱函数在[0, 2]上分别等间隔采样16点和32点,得到和,再分别对和进行IDFT,得到和。
分别画出、和的幅度谱,并绘图显示、和的波形,进行对比和分析。
四思考题如果序列的长度为M,希望得到其频谱在[0, 2]上N点等间隔采样,当时,如何用一次最少点数的DFT得到该频谱采样?五实验报告及要求1编写程序,实现上述要求,打印要求显示的图形2分析比较实验结果,简述由实验得到的主要结论3简要回答思考题4附上程序清单和有关曲线%时域采样Tp二128/1000;%观测时间128ms Fs=1000; T=l/Fs;%采样频率lKIIz M=Tp*Fs;%取样点数128 点n=0:M-l; t=n*T; A=444、128;alph=pi*50*2 0^ 5;omega=pi*50*2 0. 5;xnt=A*exp(-alph*t)、*sin(omega*t);Xk=T*fft(xnt,M);%M=128 点FFT[xnt] subplot(4,2,1);plot (n, xnt) ; xlabel (t) ; ylabel (xa(t)) ; title (原信号波形); k=0:M-l; wk=k/(Tp*Fs);%归一化处理subplot (4,2,2);plot(wk,abs(Xk));title(T*FT[xa(nT)],Fs=lKH z 幅频特性);xlabel (w/\pi) ;ylabel (幅度(III (jf)));Tp二64/1000;%观测时间64ms Fs二1000; T=l/Fs;%采样频率lKHz M=Tp*Fs;%取样点数64 点n=0:M-l;t=n*T; A=444、12&alph=pi*50*2 0^ 5;omega二pi*50*2"0、5;xnt=A*exp(-alph*t)、*sin(omega*t);Xk=T*fft(xnt,M);%M=64 点FFT[xnt] subplot (4,2,3);stem(n,xnt,); xlabel (n) ; ylabel (xa(nT)) ; title(Fs=lKllz 采样序列);k=0:M~l; wk=k/(Tp*Fs);subplot(4,2,4);plot(wk,abs(Xk));title(T*FT[xa(nT)],Fs=lKH z 幅频特性);xlabel (w/\pi) ; ylabel (幅度(III (jf)));Fs=300;T=l/Fs; M=Tp*Fs;n=0:M-l;t=n*T; A=444、128;alph=pi*50*2 0. 5;omega二pi*50*2"0、5;xnt=A*exp(-alph*t)、*sin(omega*t);Xk=T*fft(xnt,M);subplot (4,2,5); stem(n,xnt,、); xlabel(n);ylabel(x2(n)); title(Fs=300Ilz 采样序列);k=0:M-l;wk=k/(Tp*Fs); subplot (4,2,6); plot (wk, abs (Xk)) ;title (T*I?T[xa (r)T) ], Fs=300 Hz 幅频特性);xlabel(w/\pi) ; ylabel ((112 (jf)));Fs=200;T=l/Fs; M=Tp*Fs;n=0:M-l;t=n*T; A=444、128;alph=pi*50*2 0^ 5;omega二pi*50*2"0、5;xnt=A*exp(-alph*t)、*sin(omega*t);Xk=T*fft(xnt,M);subplot (4,2,7); stem(n,xnt,、); xlabel(n);ylabel(x3(n)); title(Fs=2001Iz 采样序列);k=0:M-l;wk=k/(Tp*Fs); subplot(4,2,8);plot(wk,abs(Xk));title(T*FT[xa(nT)],Fs=200 Hz 幅频特性);xlabel (w/\pi) ;ylabel ((H3 (jf))) ;%频域采样M=27;N=32;n=0:M;xn=(n>=0&n<=13)、*(n+1)+(n>=14&n<=26)、*(27-n);%产生x(n)Xk=fft(xn, 1024) ; %1024 点FFT[x(n)]X32k=fft(xn,32); %32 点FFT[x(n)]x32n=ifft(X32k); %32 点IFFT[X32(k)]得到x32(n)X16k=X32k(l:2:N);%隔点抽取X32(k)得到X16(k)xl6n=ifft (X16k,N/2) ;%16 点IFFT[X16(k)]得到xl6(n)k=0: 1023;wk=2*k/1024;%连续频谱图的横坐标取值subplot (3,2,1); plot (wk,abs(Xk));title(FT[x(n)]);xlabel('omega/'pi);ylabel( X(e j\omega)| );axis([0,1,0,200]);subplot(3,2,2);stem(n,xn,、);title(三角波序列x(n)) ; xlabel(n) ; ylabel(x(n));axis([0,32,0,20])k=0:N/2-1; %离散频谱图的横坐标取值subplot (3,2,3); stem(k, abs (X16k) ,、) ; title (16 点频域采样);xlabel(k);ylabel(|X_l_6(k)|);axis([0,8,0,200])n1=0:N/ 2-1;subplot (3,2,4);stem(nl,xl6n,. );title(16IDFT[X_1_6(k)]);x label (n) ; ylabel (x_l_6(n)) ;axis([0,32,0,20])k=0:NT ;%离散频谱图的横坐标取值subplot (3,2,5); stem(k, abs (X32k),、) ; title (32 点频域采样);xlabel(k);ylabel(|X_3_2(k)|);axis([0,16,0,200])nl=0:N1;subplot (3,2,6);stem(nl,x32n,、);title(32IDFT[X_3_2 (k)]);xlabel (n);ylabel (x_3_2(n));axis([0,32,0,20])。
基于MATLAB 的时域信号采样及频谱分析

时域信号采样及频谱分析仿真一.实验步骤:① 画出连续时间信号)()sin()(0t u t Ae t x at Ω=-的时域波形及其幅频特性曲线,其中幅度因子A =444.128,衰减因子a =222.144,模拟角频率0Ω=222.144; ② 对信号)(t x 进行采样,得到采样序列500),()sin()(0<≤Ω=-n n u nT Ae n x anT ,其中T =sf 1为采样间隔,通过改变采样频率可改变T ,画出采样频率分别为200Hz ,500 Hz ,1000 Hz 时的采样序列波形;③ 对不同采样频率下的采样序列进行频谱分析,绘制其幅频和相频曲线,对比各频率下采样序列)(n x 和)(t x 的幅频曲线有无差别,如有差别说明原因。
④ 设系统单位抽样响应为)()(5n R n h =,求解当输入为)(n x 时的系统响应)(n y ,画出)(n x , )(n h , )(n y 的时域波形及幅频特性曲线,并利用结果验证卷积定理的正确性(此内容将参数设置为A =1,a =0.4,0Ω=2.0734,T =1)。
⑤ 用FFT 对信号)(n x , )(n h , )(n y 进行谱分析,观察与④中结果有无差别。
⑥ 由采样序列)(n x 恢复出连续时间信号)(1t x ,画出其时域波形,对比)(1t x 与原连续时间信号)(t x 的时域波形,计算并记录两者最大误差。
二.实验解答:1、连续时间信号x(t)及其200Hz/500Hz/1000Hz 频率抽样信号函数x(n) %绘制信号x(n)的幅度谱和相位谱n=0:50; %定义序列的长度是50A=input('请输入A 的值 A:'); %设置信号的有关参数a=input('请输入a 的值 a:');w0=input('请输入w0的值 w0:');T1=0.005;T2=0.002;T3=0.001;T0=0.001;x=A*exp(-a*n*T0).*sin(w0*n*T0); %pi 是MATLAB 定义的π,信号乘可采用“.*”y1=A*exp(-a*n*T1).*sin(w0*n*T1); %pi 是MATLAB 定义的π,信号乘可采用“.*”y2=A*exp(-a*n*T2).*sin(w0*n*T2); %pi 是MATLAB 定义的π,信号乘可采用“.*”y3=A*exp(-a*n*T3).*sin(w0*n*T3); %pi 是MATLAB 定义的π,信号乘可采用“.*”close all %清除已经绘制的x(n)图形subplot(2,1,1);stem(n,x),grid on %绘制x(n)的图形title('离散时间信号')subplot(2,1,2);plot(n,x),grid ontitle('连续时间信号')figure(2)subplot(3,1,1);stem(n,y1),grid ontitle('200Hz理想采样信号序列'); %设置结果图形的标题subplot(3,1,2);stem(n,y2),grid ontitle('500Hz连续时间信号')subplot(3,1,3);stem(n,y3),grid ontitle('1000Hz连续时间信号')k=-25:25;W=(pi/12.5)*k;w=W/pi;Y1=y1*(exp(-j*pi/12.5)).^(n'*k);figure(3)subplot(2,1,1);plot(w,abs(Y1));grid,xlabel('w'),ylabel('幅度');title('200Hz理想采样信号序列的幅度谱');axis([-2 2 0 1000]);subplot(2,1,2);plot(w,angle(Y1));grid,xlabel('w'),ylabel('幅角');title ('200Hz理想采样信号序列的相位谱')Y2=y2*(exp(-j*pi/12.5)).^(n'*k);figure(4)subplot(2,1,1);plot(w,abs(Y2));grid,xlabel('w'),ylabel('幅度');title('500Hz理想采样信号序列的幅度谱');axis([-2 2 0 1000]);subplot(2,1,2);plot(w,angle(Y2));grid,xlabel('w'),ylabel('幅角');title ('500Hz理想采样信号序列的相位谱')Y3=y3*(exp(-j*pi/12.5)).^(n'*k);figure(5)subplot(2,1,1);plot(w,abs(Y3));grid,xlabel('w'),ylabel('幅度');title('1000Hz理想采样信号序列的幅度谱');axis([-2 2 0 1000]);subplot(2,1,2);plot(w,angle(Y3));grid,xlabel('w'),ylabel('幅角');title ('1000Hz理想采样信号序列的相位谱')分析:采样频率为1000Hz 时没有失真,500Hz 时有横线,产生失真,200Hz 时横线加长,失真增大。
时域采样与频域采样实验报告
时域采样与频域采样实验报告一、实验目的:1.理解采样定理的原理和应用;2.掌握时域采样和频域采样的方法和步骤;3.学习使用MATLAB软件进行采样信号的分析和处理。
二、实验原理:采样是指将连续时间信号转换为离散时间信号的过程。
采样过程中,时间轴被分成若干个时间间隔,每个时间间隔内只有一个采样值,即取样点,采样信号的幅度就是该时间间隔内对应连续时间信号的幅度,称为采样值。
时域采样:利用采样定理进行抽样,采样时将模拟信号保持在一个固定状态下,以等间隔时间取样,实现模拟信号的离散化。
时域采样的反变换为恢复成为原连续时间信号,称为重构。
在数字信号中,通过离散时间信号构建模拟信号。
频域采样:首先通过傅里叶变换将时域信号转换到频域,然后在频域对其进行采样,将频域采样结果再进行反傅里叶变换恢复成时域信号。
三、实验内容及步骤:1.时域采样实验①模拟信号的采样:在MATLAB软件中设计一个三角波信号和正弦波信号,并画出其时域图像。
分别设定采样频率为1.5kHz和3kHz,进行采样。
重构时域信号,并画出重构信号的时域图像。
比较原信号和重构信号,在时域和频域上进行对比和分析。
②数字信号的量化:对采集的信号进行量化处理,设量化步长分别为1、2、3。
计算量化误差和信噪比,并作图进行比较分析。
2.频域采样实验设计一个具有3kHz频率的信号,并绘制其频域图像。
设定采样率为10kHz,进行采样,同时对采样信号进行降采样处理。
恢复实验所得到的采样信号,绘制重构后的时域图像,并分析其质量。
四、实验结果与分析:1.时域采样实验:①模拟信号的采样:通过MATLAB软件设计得到的三角波和正弦波信号及其时域图像如下所示:其中,Fs1 = 1.5kHz,Fs2 = 3kHz,信号的采样频率与信号频率的比值应大于2,以保证采样后的信号不失真。
通过采样得到的信号及其重构图像如下所示:可以看出,采样和重构得到的信号与原信号的时域图像是相似的,重构后的信号和原信号之间的误差可以忽略不计。
MATLAB抽样定理验证
end
本文来自CSDN博客,转载请标明出处:/zhaojianghan888/archive/2009/09/26/4596154.aspx
要求(画出6幅图):
当TS<TN时:
1、在一幅图中画原连续信号f(t)和抽样信号fS(t)。f(t)是包络线,fS(t)是离散信号。
2、画出重构的信号y(t)。
3、画出误差图,即error=abs(f(t)-y(t))的波形。
当TS>TN时同样可画出3幅图。
%a
wm=40*pi;
wc=1.2*wm; %理想低通截止频率
2、确定Nyquist抽样间隔TN。选定两个抽样时间:TS<TN,TS>TN。
3、MATLAB的理想抽样为
n=-200:200;nTs=n*Ts;或nTs=-0.04:Ts:0.04
4、抽样信号通过理想低通滤波器的响应
理想低通滤波器的冲激响应为
系统响应为
由于
所以
MATLAB计算为
ft=fs*Ts*wc/pi*sinc((wc/pi)*(ones(length(nTs),1)*t-nTs'*ones(1,length(t))));
Ts=[0.02 0.03];
N=length(Ts);
for k=1:N;
n=-100:100;
nTs=n*Ts(k);
fs=(cos(8*pi*nTs)+2*sin(40*pi*nTs)+cos(24*pi*nTs)).*(u(nTs+pi)-u(nTs-pi));
t=-0.25:0.001:0.25;
ft=fs*Ts(k)*wc/pi*sinc((wc/pi)*(ones(length(nTs),1)*t-nTs'*ones(1,length(t))));
实验二 利用MATLAB进行时域分析报告
实验二 利用MATLAB 进行时域分析本实验容包含以下三个部分:基于MATLAB 的线性系统稳定性分析、基于MATLAB 的线性系统动态性能分析、和MATALB 进行控制系统时域分析的一些其它实例。
一、 基于MATLAB 的线性系统稳定性分析线性系统稳定的充要条件是系统的特征根均位于S 平面的左半部分。
系统的零极点模型可以直接被用来判断系统的稳定性。
另外,MATLAB 语言中提供了有关多项式的操作函数,也可以用于系统的分析和计算。
(1)直接求特征多项式的根设p 为特征多项式的系数向量,则MATLAB 函数roots()可以直接求出方程p=0在复数围的解v,该函数的调用格式为:v=roots(p)例3.1 已知系统的特征多项式为: 123235++++x x x x特征方程的解可由下面的MATLAB 命令得出。
>> p=[1,0,3,2,1,1]; v=roots(p) 结果显示:v =0.3202 + 1.7042i 0.3202 - 1.7042i -0.7209 0.0402 + 0.6780i 0.0402 - 0.6780i利用多项式求根函数roots(),可以很方便的求出系统的零点和极点,然后根据零极点分析系统稳定性和其它性能。
(2)由根创建多项式如果已知多项式的因式分解式或特征根,可由MATLAB 函数poly()直接得出特征多项式系数向量,其调用格式为:p=poly(v)如上例中:v=[0.3202+1.7042i;0.3202-1.7042i;-0.7209;0.0402+0.6780i; 0.0402-0.6780i];>> p=poly(v) 结果显示p =1.0000 0.0001 3.00002.0001 0.9998 0.9999由此可见,函数roots()与函数poly()是互为逆运算的。
(3)多项式求值在MATLAB 过函数polyval()可以求得多项式在给定点的值,该函数的调用格式为: polyval(p,v) 对于上例中的p 值,求取多项式在x 点的值,可输入如下命令:>> p=[1,0,3,2,1,1]; x=1polyval(p,x) 结果显示 x = 1 ans = 8(4)部分分式展开 考虑下列传递函数:nn n nn n a s a s a b s b s b den num s N s M +⋅⋅⋅+++⋅⋅⋅++==--110110)()( 式中0a 0≠,但是i a 和j b 中某些量可能为零。
基于MATLAB的时域抽样和频域抽样定理验证
基于MATLAB的时域抽样和频域抽样定理验证作者:吕众李彦松贾辰龙来源:《数字技术与应用》2010年第08期摘要:MATLAB 应用范围广,包括信号和图像处理、通讯、控制系统设计、测试和测量等众多应用领域,是众多领域不可获缺的工具。
本文基于MATLAB,对指数、序列信号进行不同频率的时域、频域抽样。
根据不同抽样频率下还原的信号与原信号均方差、时域逼近程度的差别来验证时域和频域抽样定理。
关键词:时域抽样定理频域抽样定理指数信号离散序列MATLAB中图分类号:TN914.3 文献标识码:A 文章编号:1007-9416(2010)08-0000-00The Verification of Time-domain sampling theorem and Frequency sampling theorem based on MATLABAbstract:This experiment will systematically verify Time-domain sampling theorem andFrequency sampling theorem,including analysis of the original signal,how to restore the original signal with sampling data,calculation of error of mean squre between original and reconstructed signal and an innovative application of MATLAB in processing matrix.With powerful Modeling and Data-processing Functions of MATLAB,original signals are discretized by different sampling frequency firstly.And with analysis of sampled data,Fourier inversion based on MATLAB and vivid figures comparing different restoring effects,this experimental can help readers understand and grasp these two theorems and applications of MATLAB in depth.Key words:Time-domain sampling theorem,Frequency sampling theorem,MATLAB,Fourier inversion1 引言时域、频域抽样定理是信号在频域、时域间转化的基础性理论,也是《信号与系统》、《数字信号处理》等多门学科的基础性理论。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
通信原理实验报告实验名称:采样定理
实验时间: 201211日年12月
指导老师:应娜
学院:计算机学院
级:班
学号:
姓名:
通信原理实验报告
一、实验名称
MATLAB验证低通抽样定理
二、实验目的
1、掌握抽样定理的工作原理。
2、通过MATLAB编程实现对抽样定理的验证,加深抽样定理的理解。
同时训练应用计算机分析问题的能力。
3、了解MATLAB软件,学习应用MATLAB软件的仿真技术。
它主要侧重于某些理论知识的灵活运用,以及一些关键命令的掌握,理解,分析等。
4、计算在临界采样、过采样、欠采样三种不同条件下恢复信号的误差,并由此总结采样频率对信号恢复产生误差的影响,从而验证时域采样定理。
三、实验步骤
1、画出连续时间信号的时域波形及其幅频特性曲线,信号为
f(x)=sin(2*pi*80*t)+ cos(2*pi*30*t);
2、对信号进行采样,得到采样序列,画出采样频率分别为80Hz,110 Hz,140 Hz时的采样序列波形;
3、对不同采样频率下的采样序列进行频谱分析,绘制其幅频曲线,对比各频率下采样序列和的幅频曲线有无差别。
4、对信号进行谱分析,观察与3中结果有无差别。
5、由采样序列恢复出连续时间信号,画出其时域波形,对比与原连续时间信号的时域波形。
四、数据分析
(1)部分程序分析:
f=[fs0*k2/m2,fs0*k1/m1]; %设置原信号的频率数组
axis([min(t),max(t),min(fx1),max(fx1)]) %画原信号幅度频谱
f1=[fs*k2/m2,fs*k1/m1]; %设置采样信号的频率数组
fz=eval(fy); %获取采样序列
FZ=fz*exp(-j*[1:length(fz)]'*w); %采样信号的离散时间傅里叶变换
TMN=ones(length(n),1)*t-n'*T*ones(1,length(t));
由采样信号恢复原信号fh=fz*sinc(fs*TMN); %.
(2)原信号的波形与幅度频谱:
fs=80Hz时原信号离散波形及频谱
(3)结果分析:
1、频率sf<max2f时,为原信号的欠采样信号和恢复,采样频率不满足时域采样定理,那么频移后的各相临频谱会发生相互重叠,这样就无法将他们分开,因而也不能再恢复原信号。
频谱重叠的现象被称为混叠现象。
时采样信号离散波形及频谱fs=80Hz
fs=80Hz恢复后信号波形及频谱
时原信号离散波形及频谱 fs=110Hz
时采样信号离散波形及频谱fs=110Hz
时原信号离散波形及频谱 fs=140Hz
时采样信号离散波形及频谱fs=110Hz(4)实验心得:
通过本实验,认识Matlab这个功能强大的仿真软件,初步了解了Matlab的操作界面以及简单的程序语言和程序运行方式,通过具体的取样和恢复信号的过程,更加深刻了解了采样定理的定义的具体含义:将模拟信号转换成数字信号,即对连续信号进行等间隔采样形式采样,采样信号的频率是原连续信号的频谱以采样频率为周期的延拓形成的,通过MATLAB编程实现对抽样定理的验证,加深了抽样定理的理解。
同时自己训练应用计算机分析问题的能力。
