反比例函数与一次函数结合
反比例函数和一次函数结合的题型

反比例函数和一次函数结合的题型
题目:
一条直线贯穿着反比例函数 $y=\dfrac{k}{x}$ 和一次函数
$y=mx+n$ 的图象,交点坐标为 $(2,3)$,求这两个函数的解析式。
解答:
设直线的解析式为 $y=ax+b$,则由于交点坐标为 $(2,3)$,所以有:
$$\begin{cases}3=2a+b \\ \dfrac{k}{2}=3a+b\end{cases}$$
解以上方程组可以得到 $a=-\dfrac{3}{4},b=\dfrac{15}{4}$。
因此,直线的解析式为 $y=-\dfrac{3}{4}x+\dfrac{15}{4}$。
将其与反比例函数 $y=\dfrac{k}{x}$ 和一次函数 $y=mx+n$ 分别相交可以得到:
$$\begin{cases}\dfrac{k}{2}=-\dfrac{3}{4}\cdot
2+\dfrac{15}{4}\\\dfrac{k}{4}=-\dfrac{3}{4}\cdot
4+\dfrac{15}{4}\end{cases}$$
解以上方程组得到 $k=12$,因此反比例函数的解析式为
$y=\dfrac{12}{x}$。
将直线与一次函数相交可以得到:
$$\begin{cases}n=3-\dfrac{3}{4}\cdot
2\\\dfrac{15}{4}=2m+n\end{cases}$$
解以上方程组得到 $m=\dfrac{13}{8},n=\dfrac{9}{4}$,因此一次函数的解析式为 $y=\dfrac{13}{8}x+\dfrac{9}{4}$。
一次函数与反比例函数综合应用教案

一次函数与反比例函数综合应用教案一、教学目标1. 让学生掌握一次函数和反比例函数的基本概念和性质。
2. 培养学生运用一次函数和反比例函数解决实际问题的能力。
3. 引导学生通过合作交流,提高解决问题的策略和思维能力。
二、教学内容1. 一次函数的基本概念和性质。
2. 反比例函数的基本概念和性质。
3. 一次函数和反比例函数的综合应用。
三、教学重点与难点1. 教学重点:一次函数和反比例函数的基本概念、性质和综合应用。
2. 教学难点:一次函数和反比例函数的综合应用。
四、教学方法1. 采用问题驱动法,引导学生主动探究一次函数和反比例函数的性质。
2. 利用案例分析法,让学生通过实际问题体会一次函数和反比例函数的应用价值。
3. 采用合作交流法,培养学生团队协作和沟通能力。
五、教学过程1. 导入新课:通过生活实例引入一次函数和反比例函数的概念。
2. 自主学习:让学生自主探究一次函数和反比例函数的性质。
3. 案例分析:分析实际问题,引导学生运用一次函数和反比例函数解决问题。
4. 合作交流:分组讨论,让学生分享解题策略和心得。
5. 总结提升:总结一次函数和反比例函数的性质及应用,提高学生解决问题的能力。
6. 课后作业:布置相关练习题,巩固所学知识。
六、教学活动设计1. 活动一:引入概念通过展示实际生活中的线性关系图片,如直线轨道上列车的运动,引导学生思考线性关系的表现形式。
引导学生提出一次函数的表达式,并解释其含义。
2. 活动二:探索性质学生通过绘制一次函数图像,观察并总结其在坐标系中的性质。
通过实际例子,让学生理解一次函数的斜率和截距对图像的影响。
3. 活动三:反比例函数的引入引导学生从比例关系出发,思考反比例函数的概念。
通过实际问题,如在固定面积内,距离与面积的关系,引入反比例函数。
七、教学评价设计1. 评价目标:学生能理解并应用一次函数和反比例函数解决实际问题。
通过设计具有挑战性的问题,如购物预算问题,让学生应用所学的函数知识。
一次函数与反比例函数相结合

3、直线y=﹣x﹣2与反比例函数y= 的图象交 于A、B两点,且与x、y轴交于C、D两点,A点的 坐标为(﹣3,k+4).(1)求反比例函数的解析 式(2)把直线AB绕着点M(﹣1,﹣1)顺时针旋 转到MN,使直线MN⊥x轴,且与反比例函数的图 象交于点N,求旋转角大小及线段MN的长.
4、已知一次函数y1=ax+b的 图象与反比例函数y2= 的图 象相交于A、B两点,坐标分 别为(﹣2,4) (4﹣2).(1)求两个函数 的解析式;(2)结合图象写 出y1<y2时,x的取值范围; (3)求△AOB的面积; (4)是否存在一点P,使以点 A﹑B﹑O﹑P为顶点的四边形 为菱形?若存在,求出顶点P 的坐标;若不存在,请说明理 由.
A M
B
O
C
N
8.(2012年衡阳市)在一次远足活动中,某班学生分成 两组,第一组由甲地匀速步行到乙地后原路返回,第二组 由甲地匀速步行经乙地继续前行到丙地后原路返回,两组 同时出发,设步行的时间为t(h),两组离乙地的距离分 别为S1(km)和S2(km),图中的折线分别表示S1、S2 与t之间的函数关系.(1)甲、乙两地之间的距离为___, 乙、丙两地之间的距离为____;(2)求第二组由甲地出 发首次到达乙地及由乙地到达丙地所用的时间分别是多少? (3)求图中线段AB所表示的S2与t间的函数关系式,并 写出自变量t的取值范围. S/km
一次函数和反比例函数的结合问题

一次函数和反比例函数的结合问题 初中阶段,我们接触的函数总共有三类:一次函数、反比例函数和二次函数。
对于二次函数,它往往会和圆、四边形等知识点结合起来去考察学生的掌握情况,相对来说比较复杂。
但是一次函数和反比例函数,通常都是在这两种函数图象结合的基础之上进行知识点的考察和运用。
具体考察的方式如下:1、已知一次函数的解析式,求反比例函数的解析式例:如图,点A 是直线2y x =与曲线1m y x -=(m 为常数)一支的交点.过点A 作x 轴的垂线,垂足为B ,且OB =2.求点A 的坐标及m 的值.解:由题意,可知点A 的横坐标是2,由点A 在正比例函数2y x =的图象上,∴点A 的坐标为()24,.又 点A 在反比例函数1m y x -=的图象上,142m -∴=,即9m =.由题目的已知条件,我们能够知道交点A 的和坐标,由于点A 既在一次函数的图象之上,又在反比例函数的图象之上,而一次函数的解析式是已知的,从而能够求出点A 的纵坐标,由于反比例函数中只有一个待定的系数,所以,我们只需要一个点的坐标就可以求出来,点A 的坐标已知,就已经具备求出反比例函数解析式的条件,用待定系数法就可以解决此类问题。
2、已知一次函数和反比例函数的两个交点坐标,求两个函数的解析式和三角形的面积例: 已知:如图,直线b kx y +=与反比例函数)0(<=x xk y 的图象相交于点A 和点B ,与x 轴交于点C ,其中A 点的坐标为(-2,4),点B 的横坐标为-4.(1)试确定反比例函数的解析式;(2)求AOC ∆的面积。
解:(1)∵ 反比例函数x k y '=(x <0)的图象相交于点A (-2,4),∴ 8-=k . ∴ 所求的反比例函数的解析式为 x y 8-=. (2)∵ 反比例函数xy 8-=(x <0)的图象相交于点B ,且点B 的横坐标为-4, ∴ 点B 的纵坐标为2,即点B 的坐标为)2,4(-.∵ 直线b kx y +=过点A )4,2(-、点B )2,4(-,∴ ⎩⎨⎧=+-=+-24,42b k b k 解得⎩⎨⎧==6,1b k . ∴ b kx y +=的解析式为6+=x y .此时,点C 的坐标为)0,6(-. ∴ △AOC 的面积为S =124621=⨯⨯ 在本题中,由于焦点坐标是已知的,所以,反比例函数和一次函数的解析式可以通过待定系数法求解出来,至于△AOC 的面积,一定要围绕面积公式底×高÷2找相关对应量。
反比例函数和一次函数结合常考题型(教学知识)

1、(本题满分10分)教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至20℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.如图为在水温为20℃时,接通电源后,水温y(℃)和时间x(min)的关系。
(1)求饮水机接通电源到下一次开机的间隔时间。
(2)在(1)中的时间段内,要想喝到超过50℃的水,有多长时间?1.2、为了预防非典,某学校对教室采用药熏消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分)成正比例,药物燃烧后y与x成反比例(如图),现测得药物8分钟燃毕,此时室内中每立方米的含药量6毫克,请根据题中所提供的信息,解答下列问题:(1)药物燃烧时,y关于x的函数关系式为_______自变量x的取值范围_____________。
(2)燃烧后,y关于x的函数关系式为__________。
(3)当空气中每立方米的含药量低于1、6毫克时,学生方可入教室,那么从消毒开始,至少需____分钟后,学生才能回到教室。
(4)当空气中每立方米含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭病菌,那么此次消毒是否有效?为什么?3、近年来,我国煤矿安全事故频频发生,其中危害最大的是瓦斯,其主要成分是CO.在一次矿难事件的调查中发现:从零时起,井内空气中CO的浓度达到4 mg/L,此后浓度呈直线型增加,在第7小时达到最高值46 mg/L,发生爆炸;爆炸后,空气中的CO浓度成反比例下降.如图11,根据题中相关信息回答下列问题:(1)求爆炸前后..空气中CO浓度y与时间x的函数关系式,并写出相应的自变量取值范围;(2)当空气中的CO浓度达到34 mg/L时,井下3 km的矿工接到自动报警信号,这时他们至少要以多少km/h的速度撤离才能在爆炸前逃生?(3)矿工只有在空气中的CO浓度降到4 mg/L及以下时,才能回到矿井开展生产自救,求矿工至少在爆炸后多少小时才能下井?1. 如图,在直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数m的图象交于A(-2,1)、B(1,n)两点。
一次函数与反比例函数图象相交的一个结论及应用
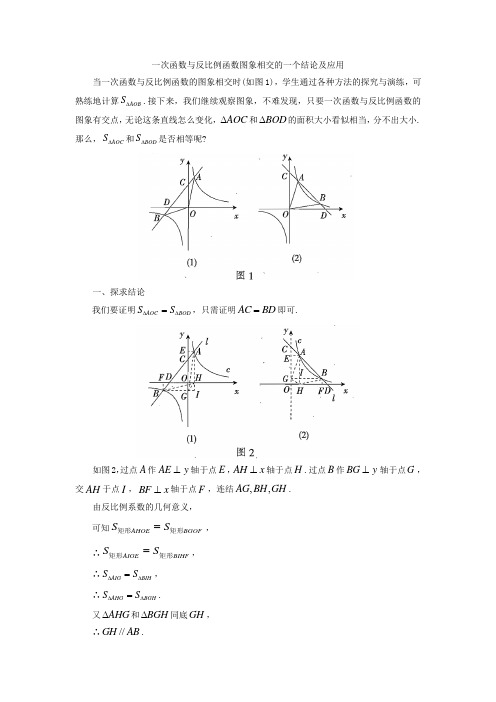
一次函数与反比例函数图象相交的一个结论及应用当一次函数与反比例函数的图象相交时(如图1),学生通过各种方法的探究与演练,可熟练地计算AOB S ∆.接下来,我们继续观察图象,不难发现,只要一次函数与反比例函数的图象有交点,无论这条直线怎么变化,AOC ∆和BOD ∆的面积大小看似相当,分不出大小.那么,AOC S ∆和BOD S ∆是否相等呢?一、探求结论我们要证明AOC BOD S S ∆∆=,只需证明AC BD =即可.如图2,过点A 作AE y ⊥轴于点E ,AH x ⊥轴于点H .过点B 作BG y ⊥轴于点G ,交AH 于点I ,BF x ⊥轴于点F ,连结,,AG BH GH .由反比例系数的几何意义,可知AHOEBGOF S S =矩形矩形, ∴AIGE BIHF S S =矩形矩形,∴AIG BIH S S ∆∆=,∴AHG BGH S S ∆∆=.又AHG ∆和BGH ∆同底GH ,∴//GH AB .∵//,//BH DH AH CG∴四边形ACGH 和四边形BGHD 均为平行四边形,∴AC GH BD ==.通过以上探究,我们得到以下结论:设直线l 与抛物线c 相交于,A B 两点,与x 轴和y 轴分别交于点D 和C (如图2),则AC BD =.二、应用举例例1 (2019年长沙中考题)如图3,函数k y x=( k 为常数,0k >)的图象与过原点O 的直线相交于,A B 两点,点M 是第一象限内双曲线上的动点(点M 在点A 的左侧),直线AM分别交x 轴,y 轴于,C D 两点,连结BM 分别交x 轴,y 轴于点,E F .现有以下四个结论:①ODM ∆与OCA ∆的面积相等;②若BM AM ⊥于点M ,则30MBA ∠=︒;③若M 点的横坐标为1,OAM ∆为等边三角形,则2k =+④若25MF MB =,则2MD MA =. 其中正确的结论的序号是 .(只填序号)本题考查反比例函数与一次函数的交点问题,三角形的面积以及平行线分线段成比例定理等知识.其中,序号①在本题中相对较难判断,但利用本文所得结论,问题就迎刃而解了.例 2 如图4,反比例函数k y x=( 0k >)与矩形OABC 相交于D ,D G 两点,则AD CG BD BG=. 证明 连结DG 交x 轴,y 轴于,E F 两点.∵//,//AB OE OA BC ,∴FADGBD GCE ∆∆∆, ∴AD FD BD GD =,CG GE BG GD=,又∵FD GE=,∴AD CG BD BG=.可见,利用本文得到的结论,我们可有效地解决反比例函数与一元函数或矩形相交的有关问题.。
反比例函数与一次函数结合

尚境导学 专题:反比例函数与一次函数结合教学目标:1.学会将反比例函数与一次函数联立,来求交点坐标;2.用函数的观点来看方程、不等式;3.能规范书写解答过程。
教学重难点:用数形结合来理解函数观点看方程、不等式。
教学流程 [活动一]基础知识回顾: 1、反比例函数y =2k+1x的图象经过点(-2,3),则k 的值为2、直线y =2x −1和双曲线y =k x(k ≠0)交点的横坐标为x =−1,则k 的值为 3、已知直线y =kx(k <0)与双曲线y =−2x 交与A(x 1,y 1),B(x 2,y 2),则3x 1y 2−8x 2y 1=4、已知一次函数y 1=ax +b 与反比例函数y 2=kx (k ≠0)的图象交于A (-4,-2)、B (2,4).若y 1>y 2,则x 的取值范围是[活动二]例题分析讲解:例:如图一次函数y 1=−x +2的图象与反比例函数y 2=kx (k ≠0)的图象相交于A 、B 两点,与x 轴相交于点C ,点B 的坐标为(m ,-21m ) (1)求反比例函数的表达式; (2)求△AOB 的面积;(3)直接写出①x < 时,y 2的取值范围 ②y 1>y 2时,x 的取值范围 ③y 2>−2时,x 的取值范围变式思考:(4)点M(x 1,y 1),N(x 2,y 2)( x 2>x 1>0)是双曲线y 2=kx上的任意两点,s =y 1+y 22,t =−16x 1+x 2,则s t(填“>”“<”或“=”)[活动三]当堂检测:如图已知反比例函数y 1=k1x 与一次函数y 2=k 2x +b 的图象交于A (1,8),B (-4,m )(1)求k 1、k 2、m 的值;(2)求△AOB 的面积; (3)直接写出当y 1<y 2时,x 的取值范围 变式思考:(4)双曲线上是否存在一点P ,使得∠PAB =,若存在请求出P 点坐标;(5)在(4)的条件下,反比例函数y =k1x在第三象限的图象上有点D 到直线AP 的距离最小时,则D 点坐标为 (6)双曲线上是否存在一点Q ,使得∠ABQ =,若存在请求出Q 点坐标.[活动四]自我测评:如图反比例函数y=kx的图象经过点A(-1,4),直线y=-x+(≠0)与双曲线交于P、Q两点,与x轴、y轴分别交于C、D两点.(1)求k的值;(2)当b=-2时,求△POQ的面积;(3)连接OQ,是否存在实数b,使得S△ODQ=S△ODC,若存在求出b的值。
反比例函数与一次函数结合19题

反比例函数与一次函数综合题【典例剖析】题型一:面积问题1.(2017成都中考)如图,在平面直角坐标系xOy 中,已知正比例函数x y 21=的图象与反比例函数xky =的图象交于()2,a A -,B 两点. (1)求反比例函数的表达式和点B 的坐标;(2)P 是第一象限内反比例函数图像上一点,过点P 作y 轴的平行线,交直线AB 于点C ,连接PO ,若POC ∆的面积为3,求点P 的坐标.2.(2016成都中考)如图,在平面直角坐标系xOy 中,正比例函数y kx =的图象与反比例函数直线my x=的图象都经过点()2,2-A . (1)分别求这两个函数的表达式;(2)将直线OA 向上平移3个单位长度后与y 轴相交于点B ,与反比例函数的图象在第四象限内的交点为C ,连接AB ,AC ,求点C 的坐标及ABC ∆的面积。
3.(2018武侯二诊)如图,一次函数b kx y +=的图象与反比例函数xmy =的图象相交于()3,n A ,()2,3-B 两点,过A 作x AC ⊥轴于点C ,连接OA .(1)分别求出一次函数与反比例函数的表达式;(2)若直线AB 上有一点M ,连接MC ,且满足AOC AMC S S ∆∆=2,求点M 的坐标.题型二:不等式问题1. (2013成都)如图,一次函数11+=x y 的图象与反比例函数xky =2(k 为常数,且0≠k )的图象都经过点()2,m A 。
(1)求点A 的坐标及反比例函数的表达式;(2)结合图象直接比较:当0>x 时,1y 和2y 的大小。
2.(2017• 成华区模拟)如图,一次函数m x y +=的图象与反比例函数xky =的图象交于B A ,两点,且与x 轴交于点C ,点A 的坐标为()1,2.(1)求一次函数和反比例函数的解析式; (2)求点C 的坐标;(3)结合图象直接写出不等式xkm x ≤+<0的解集.3.(2018高新一诊)如图,在平面直角坐标系xOy 中,一次函数b kx y +=的图象与反比例函数xy 6=的图象相交于点()3,m A 、()n B ,6-,与x 轴交于点C . (1)求一次函数b kx y +=的关系式; (2)结合图象,直接写出满足xb kx 6>+的x 的取值范围; (3)若点P 在x 轴上,且BOC ACP S S ∆∆=23,求点P 的坐标.题型三:一次函数与反比例函数交点个数问题1.2014成都)如图,一次函数5+=kx y (k 为常数,且0≠k )的图象与反比例函数xy 8-=的函数交于()B b A ,,2-两点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题:反比例函数与一次函数结合
教学目标:1.学会将反比例函数与一次函数联立,来求交点坐标;
2.用函数的观点来看方程、不等式;
3.能规范书写解答过程。
教学重难点:用数形结合来理解函数观点看方程、不等式。
教学流程 [活动一]基础知识回顾: 1、反比例函数y =
2k +1x
的图象经过点(-2,3),则k 的值为
2、直线y =2x −1和双曲线y =k
x (k ≠0)交点的横坐标为x =−1,则k 的值为 3、已知直线y =kx(k <0)与双曲线y =−2
x 交与A(x 1,y 1),B(x 2,y 2),则3x 1y 2−8x 2y 1=
4、已知一次函数y 1=ax +b 与反比例函数y 2=k x (k ≠0)的图象交于A (-4,-2)、B (2,4).若y 1>y 2,则x 的取值范围是
[活动二]例题分析讲解:
例:如图一次函数y 1=−x +2的图象与反比例函数y 2=k
x (k ≠0)的图象相交于A 、
B 两点,与x 轴相交于点
C ,点B 的坐标为(m ,-2
1
m )
(1)求反比例函数的表达式; (2)求△AOB 的面积;
(3)直接写出①x <m 时,y 2的取值范围 ②y 1>y 2时,x 的取值范围 ③y 2>−2时,x 的取值范围
变式思考:(4)点M(x 1,y 1),N(x 2,y 2)(x 2>x 1>0)是双曲线y 2=k
x 上的任意两点,s =y 1+y 22
,t =−16
x
1+x 2
,则st(填“>”“<”或“=”)
[活动三]当堂检测:
如图已知反比例函数y 1=k
1x 与一次函数y 2=k 2x +b 的图象交于A (1,8),B (-4,m )
(1)求k 1、k 2、m 的值; (2)求△AOB 的面积;
(3)直接写出当y 1<y 2时,x 的取值范围 变式思考:
(4)双曲线上是否存在一点P ,使得∠PAB =90 ,若存在请求出P 点坐标;
(5)在(4)的条件下,反比例函数y =k
1x 在第三象限的图象上有点D 到直线AP 的距离最小时,则D 点坐标为
(6)双曲线上是否存在一点Q ,使得∠ABQ =45 ,若存在请求出Q 点坐标.
[活动四]自我测评:
如图反比例函数y=k
x
的图象经过点A(-1,4),直线y=-x+b(b≠0)与双曲
线交于P、Q两点,与x轴、y轴分别交于C、D两点.
(1)求k的值;
(2)当b=-2时,求△POQ的面积;
(3)连接OQ,是否存在实数b,使得S△ODQ=S△ODC,若存在
求出b的值。
(4)求证:S
△POC
=S△BOQ
课后思考题:如图反比例函数y=
x
k(k<0)的图象与矩形
ABCO的边相交于E、F两点,且BE=2AE,
E(-1,2)
(1)求反比例函数的解析式;
(2)连接EF,AC,求△BEF的面积并证明EF//AC。
变式:如图矩形ABCO的一顶点B(a,b)在第一象限,边BA、BC分别与双曲线
y=
x
k(k>0)在第一象限交于点M、N,求证:MN//AC.
作业:1、如图点A(5
1-,5
1+)在双曲线y=
x
k(k<0)上
(1)求k的值;
(2)在y轴上取点B(0,1),问双曲线上是否存在点D,使
得以AB、AD为邻边的平行四边形ABCD的顶点C在x轴的
负半轴上?若存在求出点D的坐标,若不存在,请说明理由。
2、如图已知双曲线y=1
x
(x>0),直线L1:y-2=k(x-2)(k<0)过定
点F且双曲线交于A、B两点,设A(x1,y1),B(x2,y2)
(x1<x2),直线L2:y=-x+2
(1)若k=-1,求△AOB的面积;
(2)若AB=
2
2
5
,求k的值;。
