离散数学 群与环
离散数学--第十章群,环,域

离散数学--第⼗章群,环,域群基本定义设V=<S, ∘ >是代数系统,∘为⼆元运算,如果∘运算是可结合的,则称V为半群(代数系统的前提不要忘,详情可看第九章)如果半群中有单位元==> 含⼳半群|独异点含⼳半群还有逆元==>群通常记作G群中的⼆元运算可交换==>交换群|阿贝尔群Klein四元群特征:1. 满⾜交换律2. 每个元素都是⾃⼰的逆元3. a, b, c中任何两个元素运算结果都等于剩下的第三个元素平凡群只有单位元有限群群中元素有限⼦群如果把群看成集合,⼦群就是⼦集中能满⾜群定义的⼀个集合(可以有多个集合)群是代数系统,最基本要满⾜封闭性!真⼦群就类似真⼦集⼦群判定定理:设G为群,H是G的⾮空⼦集. H是G的⼦群当且仅当∀a,b∈H 有ab−1∈H(感觉很懵逼)证必要性显然. 只证充分性. 因为H⾮空,必存在a∈H. 根据给定条件得aa−1∈H,即e∈H. 任取a∈H, 由e,a∈H 得 ea−1∈H,即a−1∈H. 任取a,b∈H,知b−1∈H. 再利⽤给定条件得a(b−1)−1∈H,即 ab∈H. 综合上述,可知H是G的⼦群.⽣成⼦群:设G为群,a∈G,令H={a k| k∈Z},则H是G的⼦群,称为由 a ⽣成的⼦群,记作<a>例如:Klein四元群 G = {e,a,b,c}的所有⽣成⼦群是:<e>={e}, <a>={e,a}, <b>={e,b}, <c>={e,c}.则偏序集< L(G), ⊆ >称为G的⼦群格就相当于⼦群先变成偏序集然后就满⾜了格的定义?因为是⼦群所以叫⼦群格?右(左)陪集设H是G的⼦群,a∈G.令Ha={ha | h∈H}称Ha是⼦群H在G中的右陪集. 称a为Ha的代表元素.相当于右(左)乘a所得的集合?循环群设G是群,若在G中存在⼀个元素a,使得G中的任意元素都是a的幂,则称该群为循环群,元素a为循环群G的⽣成元。
离散数学 群

5 半群同态
定义7.1.5 设U=<X,ο >和V=<Y, *>是两个半群,ο和*都是 二元运算,函数f:X→Y,若对任意的x,y∈X,有:
定理 群的运算表中每一行或每一列都是G中元素的双变换。 G中每个元素在每一行必出现且仅出现一次。
例 P198习题-18 若群<G,*>中每个元素的逆是其自身, 证该群是阿贝尔群。
证 只需证运算*可交换。 对任意的a,b∈G, a*b=a-1*b-1=(b*a)-1=b*a 故<G,*>是阿贝尔群。
= x*(a*b) 故 a*b∈C; ② 可逆性:若a∈C, 证a-1∈C。明显e∈C,对任x∈G,
a-1*x = a-1*x*a* a-1 = a-1*(x*a)* a-1 = a-1*(a*x)* a-1 = (a-1*a)*x* a-1 = x* a-1
故 a-1∈C;因此C是G的子群。 (习题-25与之类似)
阿贝尔群 设<G,*>是一个群,若*是可交换的, 则称 群 <G,*>为可交换群或阿贝尔群。
例 <R,×>不是群;而 <R-{0},×>是群。
例 7.2.1 <I,+>是阿贝尔群。
例 7.2.2 G={α,β,γ,δ},验证<G,*>是群。
可验证运算*是可结合的, * α β γ
δ
离散数学第十一章群和环习题答案
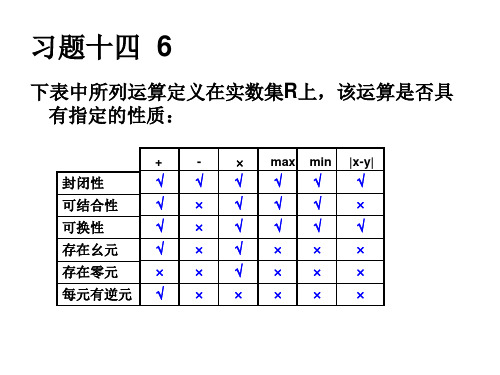
习题十五
16
证明:每个阶数大于1的群必含有阶数大于1的交换子群. 证明: 因为G的阶数大于1,必有周期大于1的元aG,构造H=(a),即 为所求。
习题十五
17
证明:循环群的子群必是循环群. 证明: 设G的生成元为a, H为G的子群,并且H中具有最小正幂的元是 ak, G=(a), HG, H={e, ak, ak2, ak3,…},设ak是H中具有最小正指数 的元, amH,证明am=(ak)* ,H=(ak), 则 amH,令m=tk+r (0r<k), 则am=(ak)t ar, 由k的选择知,r=0, 即am=(合,试确定<A, +, >是否成环、整环或域。 (1)A={x|xZ且x 0},无加法逆元,不是环 (2)A={a+b√3|a,bQ},是域 (3)A={x|(y)[yZ且x=2y]}, 由偶数构成,是环,但无法幺元, 不是整环,不是域。 (4)A={a/b|a,b为正整数,且(a,b)=1},既约分数,但无0,不构 成环。
习题十五 30
设<G, · >是群,a是G中一个固定元素,定义映射f:G → G使得对任何x G,f(x)=a· a-1. 求证:f是G的 x· 自同构映射。
证明: 容易证明f是G的同态映射, f(x· =a· y· -1 =a· a-1· y· -1 y) x· a x· a· a =f(x) ·f(y) 再证明f是双射, 证单射:f(x)=f(y), a· a-1 = a· a-1 x=y x· y· 证满射:令a· a-1 = y, x=a-1· a x· y·
c
c
c c
附加题:确定 2S,、 2S,、2S,各属于 哪一个层次?
• 2S,:闭,结,幺= S,无逆元,故含幺半群。 • 2S,:闭,结,幺= ,无逆元,故含幺半群。 • 2S,:闭,结,幺= ( A=A, AA= )A-1=A, 群。
离散数学第七章__环

n na a a a (n)a (na), 0a 0
则有:
ma na (m n)a m na mn a
0a a 0 0(0为R中零元)
n(a b) na nb
定义 一个集合(R,+,。)叫做环,假如
(a)(b) ab
a(b1 b2 bn ) ab1 ab2 abn
a b
ibn amb1 ambn
(na) b a(nb) n(ab)
规定:
n n a aa a
a0 和
ab ac ab ac 0 a(b c) 0
得
b c 0 即 b c 消去律成立。
反之,假设消去律成立,因为
ab 0 ab a 0
所以由消去律知若 a
0则 b0
所以环R没有零因子。
推论: 一个环若有一个消去律成立,则另一个消去律 也成立。
a0 1
定义(含单位元的环):(R,。)是单元半 群 常见的环:整数环,有理数环,实数环。 推论:(R,。)不可能构成群。 (因为0元无逆元)
运算规则:
(a b)c ac bc c(a b) ca cb
0a a 0 0 (0为R中零元)
(a)b a(b) ab
则对任何整数都有
a a a
m n
mn
(a ) a
m n
mn
定义:若在一个环R里
a 0, b 0 但 ab 0
则称a是环R的一个左零因子,b是环R的一个右零因子。
例 R={所有模n的剩余类}规定R中的加法和乘法如 下:
[a] [b] [a b] [a][b] [ab]
《离散数学课件》群与环3

定理的证明(续)
设G=(g)是一个n阶有限循环群,则gn=e,且对于任意的小于n 的正整数m,gm≠e。所以,对于任意的小于n大于等于0的二个 整数m1,m2,若m1≠m2,则gm1≠gm2。 即 G={g, g2, ..., gn-1, g0=e}, 而模n的整数加群为 (Zn,), 这里Zn={0, 1, 2, ..., n-1}。 作映射φ ,对于任意的i ∊ Zn, φ( i)=gi。 显然φ是一个满射且也是一个单射,即φ是一个双射。 对于任意的i,j ∊ Zn, 若i+j ≤ n-1, φ (i j)=φ (i+j)=gi+j =gi ∘ gj=φ(i)∘φ(j), 若i+j ≥ n, φ (i j)=φ (i+j-n)=gi+j-n=gi+j-n∘gn =gi+j=gi ∘ gj=φ(i)∘φ(j) 。 所以φ也即是同构映射,从而 (Zn, )同构于(G,∘)。
A2={0, 3},
A3={0, 2, 4},
和Z6本身。
14/34
例 S3= { (1), (12), (23), (13), (123), (132)}
S3的所有子群为: {(1)}
∘ (1) (12) (13) (23) (123) (132)
(1)
(12) (13) (23)
(1)
(12) (13) (23)
25/34
由子集A生成的子群(A)
设(G,· )是一个群,Ø≠A⊆G, 设想给出G的一个子群A’,有性质: ◆A’ ⊇A, ◆且若有B是G的子群,B⊇A,则B⊇A’。 这样的子群A’称为由子集A生成的子群,记 (A)=A’。
3/34
循环群
离散数学第七讲群、环、域

17
三、子群
定义7: 设〈G , *〉是一个群, S是G的非空子集, 并满足以 下条件: (1) 对任意a、b∈S有a * b∈S ; (2) 对任意a∈S有a-1 ∈S; (3) e∈S, e是〈G ,*〉的么元, 则称〈S ,*〉是〈G ,*〉的子群。 如 〈I ,+〉是〈R ,+〉的子群, 〈N ,+〉不是。
的群同态如果g一个子集k的每一元素都被映入h再没有其它元素映入e的同态h的核kerh形成群g如果abkerh那么habkerh即kerh对运算1kerh四群同态24定义10的子群我们称集合ah为元素ag所确定的子群称为左陪集ah的表示元素
6.7
一、群的定义和性质
群
定义1:群〈G , * 〉是一代数系统, 其中二元运算* 满足: (1) 运算*是可结合的; (2) 存在么元e (3) 对每一a∈G, 存在一个元素a-1 , 使 a-1 * a = a * a-1 = e 如 〈Q, ×, 1〉 不是群(0无逆元) 〈Q+, ×, 1〉 是群
16
二、置换群和循环群
定理11:设〈G, *〉是由g∈G生成的有限循环群, 如果 |G|=n,则gn =e, G = {g, g2, g3, …, gn = e} 且n是使gn =e 证: (2) 再证{g, g2, g3, …, gn}中的元素全不相同。 若有gi= gj, 不妨设i<j, 于是gj-i=e。 但j-i<n, 这与n是使gn =e 由于〈G , *〉是群, 所以G= {g, g2, g3, …, gn}, 又由(1)得gn =e。 证毕。
如 〈I, +〉是阿贝尔群。
2
一、群的定义和性质
例1:①〈Q+, ×, 1〉
离散数学第7章群、环和域

则称半群G,*为含幺半群或独异点。
第7章 群、环和域
若G,*为独异点,且*是可交换的,则称G,*为可换 的独异点。
例如,设A是任一集合,P (A)是A的幂集合。集合并运算 ∪在P (A)上是封闭的,并运算∪的单位元P (A),所以半 群<P (A),∪>是独异点;交运算∩在P (A)上也是封闭的,交运 算∩的单位元AP (A),所以半群<P (A),∩>也是独异点。显
第7章 群、环和域
⑴ (a–1)–1=a ⑵ a*b有逆元,且(a*b)–1=b–1*a–1 证明:⑴ 因a*a–1=a–1*a =e,故(a–1)–1=a ⑵ 因(a*b)*(b–1* a–1)=(a*(b*b–1)*a–1
=a*e*a–1=a*a–1=e 又
(b–1* a–1)*(a*b)=(b–1*a–1)*(a*b) =b–1*(a–1*a)*b=b–1*e*b=b–1*b=e
第7章 群、环和域
返回总目录
第7章 群、环和域
第7章 群、环和域
7.1半群和独异点
7.1.1广群和半群 代数系统<S,*>又称为广群。 定义7.1.1 设<S,*>是代数系统,*是S上的二元运算,如 果*满足结合律,则称代数系统<S,*>为半群。
例如,代数系统<I,+>、R,·、<P(a),∪>、<P(a),∩>、
则称该群为阿贝尔(Abel)群,或称可交换群。 整数加法群I,+中的加法运算是可交换的,所以,整
数加法群是阿贝尔群,群R-0,·中的乘法运算也是可交 换的,所以,R-0,·也是阿贝尔群。
离散数学环和域

a·b-a·c=0, a·b-a·c=a·b+a·(-c)= a·(b-c)=0。 由于无零因子,则b=c , 可见<R, +, ·>满足可约律。 (2) 充分性:∀b, c∈R, b·c=0, 证明b=0或c=0。
又×k可交换, 所以,乘法在加法上可分配。
一、环
定理1:设<R, +, ·>为环, 0是加法么元,那么对任意a,b,cR (1) a·0 = 0·a = 0 (加法么元必为乘法零元) (2) (-a)·b = a·(-b) = -(a·b) (3) (-a)·(-b) = a·b (4) a·(b-c) = a·b-a·c (5) (b-c)·a=b·a-c·a
例2 (b) <N6,+6,×6>不是整环,因为3×62=0, 3和2是零因子。但<N7,+7,×7> 是整环,N7= {0,1,2,3,4,5,6},根据定理2,只需证明a,源自b,cN7,
a
7
b a
a 0
7
c
b
c
反证:假如b≠c,不妨设b>c,存在整数i, j使得 ab=7i+r, ac=7j+r (0<=r<=6, i>j)
三、域
域一定是整环,但整环不一定是域
例如<I,+,·>是整环但不是域,因<I- {0},·>不是阿贝尔群。
两式相减可得,a(b-c) = 7(i-j),那么7| a(b-c),但由于0<a<7, 0<b-c<7,所 以7不可能整除a(b-c),矛盾,所以b=c。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
子群格
定义10.8 设G为群, 令 L(G) = {H | H是G的子群} 则偏序集< L(G), >称为G的子群格.
实例: Klein四元群的子群格如下:
图1
26
陪集定义与实例
定义10.9 设H是G的子群,a∈G.令 Ha={ha | h∈H} 称Ha是子群H在G中的右陪集. 称a为Ha的代表元 素. 例7 (1) 设G={e,a,b,c}是Klein四元群,H=<a>是G 的子群. H所有的右陪集是: He={e,a}=H, Ha={a,e}=H, Hb={b,c}, Hc={c,b} 不同的右陪集只有两个,即H和{b,c}.
23
典型子群的实例:子群的交
例6 设G是群,H,K是G的子群. 证明 (1) H∩K也是G的子群. (2) H∪K是G的子群当且仅当 HK 或 KH. 证 (1) 由 e∈H∩K 知 H∩K 非空. 任取a, b∈H∩K,则a∈H, a∈K, b∈H, b∈K. 必有ab1∈H 和 ab1∈K,从而ab1∈H∩K. 因此 H∩KG.
(2) 设V=<S,∘>是半群,若e∈S是关于∘运算的单位 元,则称V是含幺半群,也叫做独异点. 有时也将独 异点V 记作V=<S,∘,e>.
(3) 设V=<S,∘>是独异点,eS关于∘运算的单位元, 若aS,a1S,则称V是群. 通常将群记作G.
3
实例
例1 (1) <Z+,+>,<N,+>,<Z,+>,<Q,+>,<R,+>都是半群,+ 是普通加法. 这些半群中除<Z+,+>外都是独异点. (2) 设n是大于1的正整数,<Mn(R),+>和<Mn(R),· >都 是半群,也都是独异点,其中+和· 分别表示矩阵 加法和矩阵乘法. (3) <P(B),>为半群,也是独异点,其中为集合对 称差运算. (4) <Zn, >为半群,也是独异点,其中 Zn={0,1,…,n1},为模n加法. (5) <AA,◦>为半群,也是独异点,其中◦为函数的复 合运算. (6) <R*,◦>为半群,其中R*为非零实数集合,◦运算 4 定义如下:x, yR*, x◦y=y.
18
子群判定定理1
定理10.5(判定定理一) 设G为群,H是G的非空子集,则H是G的子群当且 仅当 (1) a,b∈H有ab∈H (2) a∈H有a1∈H.
证 必要性是显然的. 为证明充分性,只需证明e∈H. 因为H非空,存在a∈H. 由条件(2) 知a1∈H,根据 条件(1) aa1∈H,即e∈H.
r个
b 1a r b b 1eb e
从而有t | r. 另一方面,由 a = (b1)1(b1ab)b1可知 r | t. 从而 有 |b1ab| = |a|.
16
实例
(2) 设 |ab| = r,|ba| = t,则有 (ab) t 1 (ab)(ab)...(ab)
19
子群判定定理2
定理10.6 (判定定理二) 设G为群,H是G的非空子集. H是G的子群当且仅当 a,b∈H有ab1∈H. 证 必要性显然. 只证充分性. 因为H非空,必存在a∈H. 根据给定条件得aa1∈H,即e∈H. 任取a∈H, 由e,a∈H 得 ea1∈H,即a1∈H. 任取a,b∈H,知b1∈H. 再利用给定条件得 a(b1) 1∈H,即ab∈H. 综合上述,可知H是G的子群.
7
群中元素的幂
定义10.3 设G是群,a∈G,n∈Z,则a 的 n次幂.
e n 1 n a a a (a 1 ) m
n0 n0 n 0, n m
群中元素可以定义负整数次幂. 在<Z3, >中有 23 = (21)3 = 13 = 111 = 0 在<Z,+>中有 (2)3 = 23 = 2+2+2 = 6
14
群的性质:元素的阶
定理10.4 G为群,a∈G且 |a| = r. 设k是整数,则 (1) ak = e当且仅当r | k (2 )|a1| = |a| 证 (2) 由 (a1)r = (ar)1 = e1 = e 可知 a1 的阶存在. 令|a1| = t,根据上面的证明有t | r. a又是a1的逆元,所以 r | t. 从而证明了r = t,即 |a1| = |a| .
第十章 群与环
主要内容:
群的定义与性质 子群与群的陪集分解 循环群与置换群 环与域
1
10.1 群的定义与性质
半群、独异点与群的定义 半群、独异点、群的实例 群中的术语 群的基本性质
2
半群、独异点与群的定义
定义10.1 (1) 设V=<S, ∘ >是代数系统,∘为二元运算,如果 ∘运算是可结合的,则称V为半群.
实例: 例如整数加群,由2生成的子群是 <2>={2k | k∈Z}=2Z <Z6, >中,由2生成的子群<2>={0,2,4} Klein四元群 G = {e,a,b,c}的所有生成子群是: <e>={e}, <a>={e,a}, <b>={e,b}, <c>={e,c}.
22
典型子群的实例:中心C
实例
例2 设G={ e, a, b, c },G上的运算由下表给出,称 为Klein四元群
e a
e a b c e a a e b c c b
b
c
特征: 1. 满足交换律 2. 每个元素都是自己的逆元 3. a, b, c中任何两个元素运 算结果都等于剩下的第三个 元素
b c c b e a a e
10
群的性质:方程存在惟一解
定理10.2G为群,a,b∈G,方程ax=b和ya=b在G 中有解且仅有惟一解. 证 a1b 代入方程左边的x 得 a(a1b) = (aa1)b = eb = b 所以a1b 是该方程的解. 下面证明惟一性. 假设c是方程ax=b的解,必有ac=b,从而有 c = ec = (a1a)c = a1(ac) = a1b 同理可证ba1是方程 ya=b的惟一解.
8
元素的阶
定义10.4 设G是群,a∈G,使得等式 ak=e 成立的最 小正整数k 称为a 的阶,记作|a|=k,称 a 为 k 阶元. 若不存在这样的正整数 k,则称 a 为无限阶元. 例如,在<Z6,>中, 2和4是3阶元, 3是2阶元, 1和5是6阶元, 0是1阶元. 在<Z,+>中,0是1阶元,其它整数的阶都不存在.
11
群的性质:方程存在惟一解
例3 设群G=<P({a,b}),>,其中为对称差. 解下列 群方程:{a}X=,Y{a,b}={b}
解
X={a}1={a}={a}, Y={b}{a,b}1={b}{a,b}={a}
12
群的性质:消去律
定理10.3 G为群,则G中适合消去律,即对任意 a,b,c∈G 有 (1) 若 ab = ac,则 b = c. (2) 若 ba = ca,则 b = c. 例4 设G = {a1, a2, … , an}是n阶群,令 aiG = {aiaj | j=1,2,…,n} 证明 aiG = G. 证 由群中运算的封闭性有 aiGG. 假设aiGG,即 |aiG| < n. 必有aj,ak∈G使得 aiaj = aiak (j ≠ k) 13 由消去律得 aj = ak, 与 |G| = n矛盾.
21
典型子群的实例:生成子群
定义10.6 设G为群,a∈G,令H={ak| k∈Z}, 则H是G的子群,称为由 a 生成的子群,记作<a>.
证 首先由a∈<a>知道<a>≠. 任取am,al∈<a>,则 am(al)1 = amal = aml∈<a> 根据判定定理二可知<a>≤G.
15
实例
例 5 设G是群,a,b∈G是有限阶元. 证明 (1) |b1ab| = |a| (2) |ab| = |ba|
证 (1) 设 |a| = r,|b1ab| = t,则有 (b 1ab)r (b 1ab)(b 1ab)...(b 1ab)
9
群的性质:幂运算规则
定理10.1 设G 为群,则G中的幂运算满足: (1) a∈G,(a1)1=a (2) a,b∈G,(ab)1=b1a1 (3) a∈G,anam = an+m,n, m∈Z (4) a∈G,(an)m = anm,n, m∈Z (5) 若G为交换群,则 (ab)n = anbn.
5
有关群的术语
定义10.2 (1) 若群G是有穷集,则称G是有限群,否 则称为无限群.
群G 的基数称为群 G 的阶,有限群G的阶记作|G|.
(2) 只含单位元的群称为平凡群.
(3) 若群G中的二元运算是可交换的,则称G为交换 群或阿贝尔 (Abel) 群.
6
有关群的术语
实例: <Z,+>和<R,+>是无限群. <Zn,>是有限群,也是 n 阶群. Klein四元群是4阶群. <{0},+>是平凡群. 上述群都是交换群,n阶(n≥2)实可逆矩阵集合关于 矩阵乘法构成的群是非交换群.
20
子群判定定理3
定理10.7 (判定定理三) 设G为群,H是G的非空有穷子集,则H是G的子群 当 且仅当a,b∈H有ab∈H. 证 必要性显然. 为证充分性,只需证明 a∈H有a1∈H.
任取a∈H, 若a = e, 则a1 = e∈H. 若a≠e,令S={a,a2,…},则SH. 由于H是有穷集,必有ai = aj(i<j). 根据G中的消去律得 aji = e,由a ≠ e可知 ji>1,由 此得 a ji1a = e 和 a a ji1 = e 从而证明了a1 = a ji1∈H.
