华杯赛总决赛小学组数学第二试试题(无答案)
“华杯赛”决赛赛前训练模拟题小学组决赛卷-小学数学五年级下册-竞赛试题及答案-人教课标版---
“华杯赛”决赛赛前训练模拟题小学组决赛卷小学数学五年级下册竞赛试题及答案人教课标版一、填空题1、计算：=。
2、一次数学竞赛满分是100分, 某班前六名同学的平均得分是95.5分, 排第六名同学的得分是89分, 每人得分是互不相同的整数, 那么排名第三的同学最少得___________分。
3、在下面的等式中, 相同的字母表示同一数字, 不同字母表示不同的数字：若abcd－dcba=□997, 那么□中应填。
4、在梯形ABCD中, 上底长5厘米, 下底长10厘米, 平方厘米, 则梯形ABCD的面积是平方厘米。
5、已知：10△3=14, 8△7=2, △, 根据这几个算式找规律, 如果△=1, 那么x=。
6、图中共有个三角形。
7、相同的正方块码放在桌面上, 从正面看, 如图4；从侧面看, 如图5, 则正方块最多有个, 最少有个．8、有一种饮料的瓶身如下图所示, 容积是3升。
现在它里面装了一些饮料, 正放时饮料高度为20厘米, 倒放时空于部分的高度为5厘米。
那么瓶内现有饮料升。
二、解答题9、如图, 两个正方形边长分别是5厘米和4厘米, 图中阴影部分为重叠部分。
则两个正方形的空白部分的面积相差多少平方厘米？10、水桶中装有水, 水中插有A、B、C三根竹杆, 露出水面的部分依次是总长的, , 。
三根竹杆长度总和为98厘米, 求水深。
11、养猪专业户王大伯说：“如果卖掉75头猪, 那么饲料可维持20天, 如果买进100头猪, 那么饲料只能维持15天。
”问：王大伯一共养了多少头猪？12、A、B两地之间是山路, 相距60千米, 其中一部分是上坡路, 其余是下坡路, 某人骑电动车从A地到B地, 再沿原路返回, 去时用了4.5小时, 返回时用了3.5小时。
已知下坡路每小时行20千米, 那么上坡路每小时行多少千米？参考答案一、填空题1、解原式=====32、解：要想排名第三的同学得分尽量低, 则其它几人的得分就要尽量的高, 故第一名应为100分, 第二名应为99分, 因此第三、四、五名的总分为：95.5×6－100－99－89=285(分)故第三、四、五名的平均分为285÷3=95（分）, 因此第三名至少要得96分。
华杯赛试题及答案
华杯赛试题及答案1. 选择题1）以下哪个不属于华杯赛的参赛项目？A. 数学竞赛B. 语言表达C. 程序设计D. 跳高比赛2）华杯赛是哪个国家的赛事？A. 中国B. 美国C. 日本D. 英国3）以下哪个城市曾举办过华杯赛？A. 北京B. 上海C. 广州D. 香港4）华杯赛是以什么形式进行的？A. 线下比赛B. 线上比赛C. 线下与线上结合D. 每个参赛者可以自行选择5）华杯赛设立了哪些奖项？A. 一等奖、二等奖、三等奖B. 冠军奖杯、亚军奖杯、季军奖杯C. 最佳表现奖、创新奖、团队合作奖D. 所有参赛者都会获得奖励2. 填空题1）华杯赛是每年________举办一次。
2）参赛者需要先进行________报名，通过审核后方可参加比赛。
3）华杯赛的目的是________学生综合能力的培养。
4）参赛者需要在规定的时间内完成________项目的考核。
5）华杯赛的题目涵盖了多个学科，要求参赛者具备________知识。
3. 简答题请简要回答以下问题：1）你为什么想参加华杯赛？2）你认为参加华杯赛对你的个人发展有何帮助？3）你的学习方法和备考策略是什么？4）在华杯赛中，你最想获得哪个奖项，并为之付出什么努力？答案：1. 选择题1）D2）A3）B4）C5）C2. 填空题1）一次2）在线上3）促进4）指定5）跨学科3. 简答题1）参加华杯赛可以锻炼自己的能力，提高学科知识水平，同时还能通过与其他优秀学生交流，拓宽视野。
2）参加华杯赛可以提升个人的学术竞争力和综合素质，对今后的升学和就业都有积极的影响。
3）我的学习方法是注重理论与实践相结合，善于总结归纳，通过解题训练提高自己的应试能力；备考策略是提前规划时间，有针对性地复习重点知识，并进行模拟考试。
4）我最想获得的奖项是最佳表现奖，我会通过充分准备，认真完成每个项目的考核，展现出自己的才能和潜力，努力争取取得好成绩。
华杯赛试题及答案到此结束。
请注意按照华杯赛的要求认真准备，祝你取得优异的成绩！。
三年级华杯赛试题及答案
三年级华杯赛试题及答案一、选择题（每题5分，共20分）1. 下列哪一项是华杯赛的全称？A. 华罗庚数学竞赛B. 华罗庚数学奥林匹克C. 华罗庚数学邀请赛D. 华罗庚数学挑战赛答案：C2. 华杯赛的参赛对象通常是什么年级的学生？A. 一年级B. 二年级C. 三年级D. 四年级答案：C3. 华杯赛的举办周期是多久？A. 每年一次B. 每两年一次C. 每三年一次D. 每四年一次答案：A4. 华杯赛的试题难度通常如何？A. 非常简单B. 相对容易C. 适中D. 非常困难答案：C二、填空题（每题5分，共20分）1. 华杯赛的试题通常包括_______和_______两部分。
答案：选择题、填空题2. 参加华杯赛的学生需要具备一定的_______能力。
答案：数学3. 华杯赛的试题设计旨在考察学生的_______和_______。
答案：逻辑思维、解决问题4. 华杯赛的获奖者通常能够获得_______和_______。
答案：荣誉证书、奖品三、解答题（每题10分，共20分）1. 请解释华杯赛对于培养学生数学兴趣的重要性。
答案：华杯赛通过竞赛的形式激发学生对数学的兴趣，让学生在解决问题的过程中体验到数学的乐趣，从而提高他们的学习动力和数学素养。
2. 描述一下华杯赛的评分标准。
答案：华杯赛的评分标准通常依据学生解答问题的正确性、解题思路的清晰度以及解题过程的规范性来综合评定。
每道题目都有明确的得分点，评委会根据学生的答题情况给予相应的分数。
四、综合题（每题15分，共30分）1. 假设你是一名三年级的学生，你将如何准备华杯赛？答案：首先，我会定期复习数学课本中的知识点，确保基础知识的牢固。
其次，我会参加一些数学辅导班或兴趣小组，以提高解题技巧。
此外，我还会做一些历年的华杯赛试题，以熟悉题型和考试节奏。
最后，我会保持良好的心态，积极面对比赛。
2. 如果你在华杯赛中遇到了难题，你会如何应对？答案：面对难题，我会先冷静下来，仔细阅读题目，尝试从不同角度理解问题。
三年级华杯赛试题及答案
三年级华杯赛试题及答案【试题一】题目：小明有36个苹果，他决定将苹果平均分给6个小朋友。
请问每个小朋友可以得到多少个苹果？【答案】每个小朋友可以得到6个苹果。
因为36个苹果除以6个小朋友等于6个苹果。
【试题二】题目：一个长方形的长是15厘米，宽是10厘米。
请问这个长方形的周长是多少厘米？【答案】这个长方形的周长是50厘米。
根据周长的计算公式：周长= 2 × (长 + 宽)，所以周长= 2 × (15 + 10) = 2 × 25 = 50厘米。
【试题三】题目：小华有5张邮票，小刚有7张邮票。
如果小华和小刚交换了2张邮票，那么现在小华有多少张邮票？【答案】现在小华有6张邮票。
小华原本有5张邮票，交换了2张给小刚，所以剩下3张，然后从小刚那里得到了2张，所以现在总共有3 + 2 = 6张邮票。
【试题四】题目：一个班级有24名学生，如果每4名学生组成一个小组，那么可以组成多少个小组？【答案】可以组成6个小组。
因为24名学生除以每组4名学生等于6组。
【试题五】题目：一个数加上12等于36，这个数是多少？【答案】这个数是24。
因为36减去12等于24。
【试题六】题目：小丽有3个红气球，2个蓝气球，如果她又买了5个黄气球，那么她总共有多少个气球？【答案】小丽总共有10个气球。
3个红气球加上2个蓝气球等于5个气球，再加上5个黄气球，总共是5 + 5 = 10个气球。
【试题七】题目：如果一个数的3倍是18，那么这个数是多少？【答案】这个数是6。
因为18除以3等于6。
【试题八】题目：小强有40元钱，他买了一个价值15元的玩具，还剩多少钱？【答案】小强还剩25元钱。
40元减去15元等于25元。
【试题九】题目：一个班级里有22个男生和18个女生，这个班级总共有多少人？【答案】这个班级总共有40人。
22个男生加上18个女生等于40人。
【试题十】题目：如果一个数减去7等于23，那么这个数是多少？【答案】这个数是30。
第十五届华杯赛决赛试题A(小学组)、答案及详细分析解答
第十五届华罗庚金杯少年数学邀请赛决赛试题A（小学组）一、填空题（每小题10分，共80分）1．在10个盒子中放乒乓球，每个盒子中的球的个数不能少于11，不能是13，也不能是5的倍数，且彼此不同，那么至少需要个乒乓球。
2．有五种价格分别为2元、5元、8元、11元、14元的礼品以及五种价格分别为1元、3元、5元、7元、9元的包装盒。
一个礼品配一个包装盒，共有种不同价格。
3．汽车A从甲站出发开往乙站，同时汽车B、C从乙站出发与A相向而行开往甲站，途中A与B相遇20分钟后再与C相遇。
已知A、B、C的速度分别是每小时90km, 80km, 60km，那么甲乙两站的路程是km。
4．将和这6个分数的平均值从小到大排列，则这个平均值排在第位。
5．将一个数的各位数字相加得到新的一个数称为一次操作，经连续若干次这样的操作后可以变为6的数称为“好数”，那么不超过2012的“好数”的个数为，这些“好数”的最大公约数是。
6．右图所示的立体图形由9个棱长为1的立方块搭成，这个立体图形的表面积为。
7．数字卡片“3”、“4”、“5”各10张，任意选出8张使它们的数字和是33，则最多有张是卡片“3”。
8．若将算式的值化为小数，则小数点后第1个数字是。
二、解答下列各题（每题10分，共40分，要求写出简要过程）9．右图中有5个由4个1×1的小正方格组成的不同形状的硬纸板。
问能用这5个硬纸板拼成右图中4×5的长方形吗？如果能，请画出一种拼法；如果不能，请简述理由。
10．长度为L的一条木棍，分别用红、蓝、黑线将它等分为8，12和18段，在各划分线处将木棍锯开，问一共可以得到多少段？其中最短的一段的长是多少？11．足球队A，B，C，D，E进行单循环赛（每两队赛一场），每场比赛胜队得3分，负队得0分，平局两队各得1分。
若A，B，C，D队总分分别是1，4，7，8，请问：E队至多得几分？至少得几分？12．华罗庚爷爷出生于1910年11月12日。
小学六年级数学第十三届华杯赛决赛考试试卷及答案
第十三届华杯赛决赛试卷一、填空(每题10分，共80分)1、计算：416024340143214016940146+⨯+⨯+⨯+⨯= 。
2、林林倒满一杯纯牛奶，第一次喝了31，然后加入豆浆，将杯子斟满并搅拌均匀，第二次，林又喝了31，继续用豆浆将杯子斟满并搅拌均匀，重复上述过程，那么第四次后，林林共喝了一杯纯牛奶总量的 (用分数表示)。
3、下图是小明用一些半径为1厘米、2厘米、4厘米和8厘米的圆、半圆、圆弧和一个正方形组成的一个鼠头图案，图中阴影部分的总面积为 平方厘米。
4、悉尼与北京的时差是3小时，例如：悉尼时间12:00时，北京时间是9:00，某日，当悉尼时间9:15时，小马和小杨分别乘机从悉尼和北京同时出发去对方所在地，小马于北京时间19:33分到达北京。
小马和小杨路途上时间之比为7:6，那么小杨到达悉尼时，当地时间是 。
5、将六个自然数14，20，33，117，143，175分组，如果要求每组中的任意两个数都到质，则至少需要将这些数分成 组。
6、对于大于零的分数，有如下4个结论： (1)两个真分数的和是真分数； (2)两个真分数的积是真分数；(3)一个真分数与一个假分数的和是一个假分数； (4)一个真分数与一个假分数的积是一个假分数。
其中正确结论的编号是 。
7、记A ＝21+43+87+1615+…+10241023，那么比A 小的最大自然数是 。
8、黑板上写着1至2008共2008自然数，小明每次擦去两个奇偶性相同的数，再写上它们的平均数，最后黑板上只剩下一个自然数，这个数可能的最大值和最小值的差是 。
二、解答案下列各题(每题10分，共40分，要求写出简要过程)9、10、请将四个4用四则运算符号、括号组成五个算式，使它们的结果分别等于5、6、7、8、9。
11、图2中，ABCD 和CGEF 是两个正方形，AG 和CF 相交于H ，已知CH 等于CF 的三分之一，三角形CHG 的面积等于6平方厘米，求五边形ABGEF 的面积。
华杯赛历届试题及答案
华杯赛历届试题及答案华杯赛，全称“华罗庚数学金杯赛”，是一项面向中学生的数学竞赛，旨在激发学生对数学的兴趣，提高他们的数学素养。
以下是历届华杯赛的部分试题及答案，供参考：一、选择题1. 下列哪个数是最小的正整数？- A. 0- B. 1- C. 2- D. 3答案：B2. 如果一个数除以3的余数是2，除以5的余数是1，那么这个数除以15的余数是多少？- A. 3- B. 4- C. 5- D. 6答案：A二、填空题1. 一个长方体的长、宽、高分别是8cm、6cm和5cm，其体积是________ 立方厘米。
答案：2402. 计算下列数列的第10项：1, 1, 2, 3, 5, 8, 13, 21, 34, ...答案：55三、解答题1. 一个水池有注水口和排水口，单开注水口每小时可注水20吨，单开排水口每小时可排水10吨。
如果同时打开注水口和排水口，水池每小时净增水量是多少吨？如果池中原有水100吨，需要多少时间才能将水排空？答案：同时打开注水口和排水口时，水池每小时净增水量是20吨- 10吨 = 10吨。
要将100吨水排空，需要的时间为100吨÷ 10吨/小时 = 10小时。
2. 一个班级有48名学生，其中1/3是男生，剩下是女生。
问这个班级有多少名女生？答案：班级中有48名学生，其中1/3是男生，即48 * (1/3) = 16名男生。
剩下的学生是女生，所以女生人数为48 - 16 = 32名。
四、证明题1. 证明对于任意的正整数n，n的立方与n的和不小于n的平方与n 的两倍之和。
答案：设n为任意正整数。
我们需要证明n^3 + n ≥ n^2 + 2n。
展开立方项，得到n^3 + n - n^2 - 2n = n(n^2 - n - 1) = n(n - (1 + √5)/2)(n - (1 - √5)/2)。
由于n是正整数，(n - (1 +√5)/2)和(n - (1 - √5)/2)都是负数或零，因此整个表达式是非负的，即n^3 + n ≥ n^2 + 2n。
第17届“华杯赛”网上决赛试题以及答案(小中组)
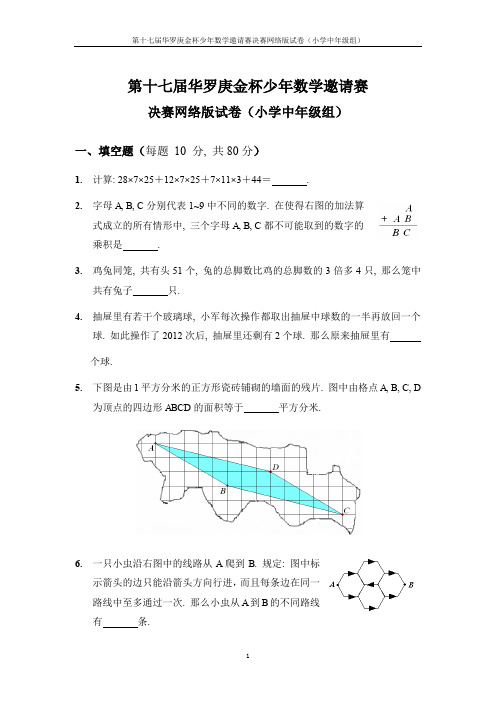
3. 鸡兔同笼, 共有头 51 个, 兔的总脚数比鸡的总脚数的 3 倍多 4 只, 那么笼中 共有兔子 只.
4. 抽屉里有若干个玻璃球, 小军每次操作都取出抽屉中球数的一半再放回一个 球. 如此操作了 2012 次后, 抽屉里还剩有 2 个球. 那么原来抽屉里有 个球. 5. 下图是由 1 平方分米的正方形瓷砖铺砌的墙面的残片. 图中由格点 A, B, C, D 为顶点的四边形 ABCD 的面积等于 平方分米.
6. 一只小虫沿右图中的线路从 A 爬到 B. 规定: 图中标 示箭头的边只能沿箭头方向行进， 而且每条边在同一 路线中至多通过一次. 那么小虫从 A 到 B 的不同路线 有 条.
1
第十七届华罗庚金杯少年数学邀请赛决赛网络版试卷（小学中年级组）
7. 有一些自然数， 它们中的每一个与 7 相乘, 其积的末尾四位数都为 2012, 那 么在这些自然数中, 最小的数是 .
8. 将棱长为 1 米的正方体木块分割成棱长为 1 厘米的小正方体积木, 设想孙悟 空施展神力将所有的小积木一个接一个地叠放起来, 成为一根长方体 “神棒”, 直指蓝天. 已知珠穆朗玛峰的海拔高度为 8844 米, 则“神棒”的高度超过珠 穆朗玛峰的海拔高度 米.
二、回答下列各题（每题 10 分, 共 40 分, 写出答案即可）
第十七届华罗庚金杯少年数学邀请赛决赛网络版试卷（小学中年级组）
第十届华罗庚金杯少年数学邀请赛
决赛网络版试卷（小学中年级组）
一、填空题（每题 10 分, 共 80 分）
1. 计算: 28× 7× 25＋12× 7× 25＋7× 11× 3＋44＝ .
2. 字母 A, B, C 分别代表 1~9 中不同的数字. 在使得右图的加法算 式成立的所有情形中, 三个字母 A, B, C 都不可能取到的数字的 乘积是 .
第十九届“华杯赛”决赛小学中年级组试题与答案
第 1 页
共 1 页
8. 将 1~6 这六个自然数分成甲、乙两组, 则甲组数的和与乙组数的和的乘积最 大是________.
第 1 页
共 2 页
二、简答题（每小题 15 分, 共 60 分, 要求写出简要过程）
9. 如下图, 将一个大三角形纸板剪成四个小三角形纸板（第一次操作）, 再将 每个小三角形纸板剪成四个更小的三角形纸板（第二次操作）. 这样继续操 作下去, 完成第 5 次操作后得到若干个小三角形纸板. 甲和乙在这些小三角 形纸板上涂色, 每人每次可以在 1 至 10 个小三角形纸板上涂色, 谁最后涂完 谁赢. 在甲先涂的情况下, 请设置一个方案使得甲赢.
10. 如右图所示, 网格中每个小正方格的面积都为 1 平方厘 米. 小明在网格纸上画了一匹红鬃烈马的剪影（马的轮 廓由小线段组成 , 小线段的端点在格子点上或在格线 上）, 则这个剪影的面积为多少平方厘米?
11. 从一块正方形土地上, 划出一块宽为 10 米的长方形土 地（如右图）, 剩下的长方形土地面积是 1575 平方米. 那么, 划出的长方形土地的面积是多少？
12. 三位数190 19 (1 9 0) , 请 写出所有这样的三位数.
第 2 页
共 2 页
第十九届华罗庚金杯少年数学邀请赛
决赛试题参考答案 （小学中年级组） 一、填空（每题 10 分, 共 80 分）
题号 答案 1 56 2 132 3 60 4 36 5 15 6 16 7 114 8 110
3. 将学生分成 35 组, 每组 3 人. 其中只有 1 个男生的有 10 组, 不少于 2 个男生 的有 19 组 , 有 3 个男生的组数是有 3 个女生的组数的 2 倍 . 则男生有 ________人. 4. 从 1~8 这八个自然数中取三个数, 其中有连续自然数的取法有________种. 5. 如右图, 三个圆交出七个部分. 将整数 0～6 分别填到七个部 分中, 使得每个圆内的四个数字的和都相等, 那么和的最大 值是________. 6. 若干自然数的乘积为 324, 则这些自然数的和最小为________. 7. 在嫦娥三号着月过程中, 从距离月面 2.4 千米到距离月面 100 米这一段称为 接近段. 下面左图和右图分别是它到距月面 2.4 千米和月面 100 米处时, 录 像画面截图. 则嫦娥三号在接近段内行驶的时间是________秒（录像时间的 表示方法：30 : 28 / 2 : 10 : 48 表示整个录像时间长为 2 小时 10 分钟 48 秒, 当 前恰好播放到第 30 分钟 28 秒处）.
华杯赛总决赛小学第三届二试(1)
C1． 写出从360到630的自然数中有奇数个约数的数。
2. 四边形ABCD 被AC 和DB 分成甲，乙，丙，丁4个三角形。
已知：BE=80cm ．CE=60cm ，DE=40cm ，AE=30cm ．问：丙、丁两个三角形面积之和是甲、乙两个三角形面积之和的多少倍？ 3. 已知：19911991199119911991a =⋅⋅⋅⋅⋅⋅个 问：a 除以13所得余数是几？4． 某班在一次数学考试中，平均成绩是78分，男、女生各自的平均成绩是75．5分、81分。
问：这个班男、女生人数的比是多少？5． 某玩具厂生产大小一样的正方体形状的积木，每个面分别涂上红、黄、蓝3种颜色中的1种，每色各涂2个面。
当两个积木经过适当的翻动以后，能使各种颜色的面所在位置相同时，它们就被看作是同一种积木块。
试说明：最多能涂成多少种不同的积木块？6． 一条双向铁路上有11个车站，相邻两站都相距7公里。
从早晨7点开始，有18列货车由第十一站顺次发出，每隔5分钟发出一列，都驶向第一站，速度都是每小时60公里。
早晨8点，由第一站发出一列客车，向第十一站驶去，时速是100公里。
在到达终点站前，货车与客车都不停靠任何一站。
问：在哪两个相邻站之间，客车能与3列货车先后相遇？C1． 写出从360到630的自然数中有奇数个约数的数。
2. 四边形ABCD 被AC 和DB 分成甲，乙，丙，丁4个三角形。
已知：BE=80cm ．CE=60cm ，DE=40cm ，AE=30cm ．问：丙、丁两个三角形面积之和是甲、乙两个三角形面积之和的多少倍？ 3. 已知：19911991199119911991a =⋅⋅⋅⋅⋅⋅个 问：a 除以13所得余数是几？4． 某班在一次数学考试中，平均成绩是78分，男、女生各自的平均成绩是75．5分、81分。
问：这个班男、女生人数的比是多少？5． 某玩具厂生产大小一样的正方体形状的积木，每个面分别涂上红、黄、蓝3种颜色中的1种，每色各涂2个面。
第三届华杯赛全套试题
第三届华罗庚金杯赛少年数学邀请赛初赛试题（小学组）1．光的速度是每秒30万千米，太阳离地球1亿5千万千米．问：光从太阳到地球要用几分钟（得数保留一位小数）？ 2．计算?712631351301=⨯⎪⎭⎫⎝⎛++3．有3个箱子，如果两箱两箱地称它们的重量，分别是83千克、85千克和86千克．问：其中最轻的箱子重多少千克？4．请将算式100.010.01.0 ++的结果写成最简分数．5．（如右图）将高都是1米，底面半径分别为1.5米、1米和0.5米的三个圆柱组成一个物体．求这个物体的表面积（取π＝3）．6．一位少年短跑选手，顺风跑90米用了10秒钟．在同样的风速下，逆风跑70米，也用了10秒钟．问：在无风的时候，他跑100米要用多少秒？7．一个矩形分成4个不同的三角形（如右图），绿色三角形面积占矩形面积的15％，黄色三角形的面积是21平方厘米．问：矩形的面积是多少平方厘米？8．有一对紧贴的传动胶轮，每个轮子上都画有一条通过轴心的标志线（如下图）．主动轮的半径是105 厘米，从动轮的半径是90厘米．开始转动时，两个轮子上的标志线在一条直线上．问：主动轮至少转了几转后，两轮的标志线又在一条直线上？9．小明参加了四次语文测验，平均成绩是68分．他想在下一次语文测验后，将五次的平均成绩提高到70分以上，那么，在下次测验中，他至少要得多少分？10．如下图中共有7层小三角形，求白色小三角形的个数与黑色小三角形的个数之比．11．下面的算式里，每个方框代表一个数字．问：这6个方框中的数字的总和是多少？12．在所有的两位数中，十位数字比个位数字大的两位数有多少个？13．有甲、乙两个同样的杯子，甲杯中有半杯清水，乙杯中盛满了含50％酒精的溶液．先将乙杯中酒精溶液的一半倒入甲杯，搅匀后，再将甲杯中酒精溶液的一半倒入乙杯．问这时乙杯中的酒精是溶液的几分之几？14．射箭运动的箭靶是由10个同心圆组成，两个相邻的同心圆半径之差等于最里面的小圆半径．最里面的小圆叫做10环（如右图所示），最外面的圆环叫做1环．问：10环的面积是1环面积的几分之几？15．王师傅在某个特殊岗位上工作、他每上8天班后，就连续休息2天．如果这个星期六和星期天他休息，那么，至少再过几个星期后他才能又在星期天休息？第三届华罗庚金杯赛少年数学邀请复赛赛试题（小学组）1．计算：9819375.4121314532852÷⎪⎭⎫⎝⎛+⨯-2．某年的10月里有5个星期六，4个星期日．问：这年的10月1日是星期几？3． 电子跳蚤每跳一步，可从一个圆圈跳到相邻的圆圈．现在，一只红跳蚤从标有数字“0”的圆圈按顺时针方向跳了1991步，落在一个圆圈里．一只黑跳蚤也从标 有数字“0”的圆圈起跳，但它是沿着逆时针方向跳了1949步，落在另一个圆圈里．问：这两个圆圈里数字的乘积是多少？4．173□是个四位数字．数学老师说：“我在这个□中先后填入3个数字，所得到的3个四位数，依次可被9、11、6整除．”问：数学老师先后填入的3个数字的和是多少？5．我们知道：339⨯=，4416⨯=，这里，9、16叫做“完全平方数”，在前300个自然数中，去掉所有的“完全平方数”，剩下的自然数的和是多少？6．如图，从长为13厘米，宽为9厘米的长方形硬纸板的四角去掉边长2厘米的正方形，然后，沿虚线折叠成长方体容器．这个容器的体积是多少立方厘米？7．在射箭运动中，每射一箭得到的环数或者是“0”（脱靶），或者是不超过10的自然数．甲、乙两名运动员各射了5箭，每人5箭得到的环数的积都是1764，但是甲的总环数比乙少4环．求甲、乙的总环数．8．下图中有6个点，9条线段．一只甲虫从A 点出发，要沿着某几条线段爬到F 点．行进中，同一个点或同一条线段只能经过1次．这只甲虫最多有多少种不同的走法？9．下图中的正方形被分成9个相同的小正方形，它们一共有16个顶点（共同的顶点算一个），以其中不在一条直线上的3个点为顶点，可以构成三角形．在这些三角形中，与阴影三角形有同样大小面积的有多少个？10．已知：199111982119811198011++++=S ，求：S 的整数部分．11．今年，祖父的年龄是小明的年龄的6倍．几年后，祖父的年龄将是小明的年龄的5倍．又过几年以后，祖父的年龄将是小明的年龄的4倍．求：祖父今年是多少岁？12．某个班的全体学生进行了短跑、游泳、篮球三个项目的测试，有4名学生在这三个项目上都没有达到优秀，其余每人至少有一个项目达到优秀，这部分学生达到优秀的项目、人数如下表： 求这个班的学生数．13．恰好能被6、7、8、9整除的五位数有多少个？14．计算：200119991197531+--+-+-15．五环图由内圆直径为8，外圆直径为10的五个圆环组成，其中两两相交的小曲边四边形（阴影部分）的面积都相等．已知五个圆环盖住的总面积是112.5，求每个小曲边四边形的面积（圆周率π取3.14）．16．下图中8个顶点处标注的数字：a 、b 、c 、d 、e 、f 、g 、h ，其中的每一个数都等于相邻三个顶点处数的和的31，求：()()h g f e d c b a +++-+++的值．第三届华罗庚金杯赛少年数学邀请赛决赛一试试题（小学组）1.计算：99163135115131++++2．说明：360这个数的约数有多少个？这些约数的和是多少？3．观察下面数表（横排为行）：根据前5行数所表达的规律，说明19491991这个数位于由上而下的第几行？在这一行中，它位于由左向右的第几个？4．将一个圆形纸片用直线划分成大小不限的若干小纸片，如果要分成不少于50个小纸片，至少要画多少条直线？请说明．5．某校和某工厂之间有一条公路，该校下午2点钟派车去该厂接某劳模来校作报告，往返需用1小时．这位劳模在下午1点钟便离厂步行向学校走来，途中遇到接他的汽车，更立刻上车驶向学校，在下午2点40分到达．问：汽车速度是劳模步行速度的几倍？6．在一个圆周上放了1枚黑色的和1990枚白色的围棋子(如右图)．一个同学进行这样的操作：从黑子开始，按顺时针方向，每隔一枚，取走一枚．当他取到黑子时，圆周上还剩下多少枚白子？第三届华罗庚金杯赛少年数学邀请赛二试试题（小学组）1．写出从360到630的自然数中有奇数个约数的数．2，四边形ABCD被AC和DB分成甲，乙，丙，丁4个三角形（如右图）．已知：BE=80cm．CE=60cm，DE=40cm，AE=30cm．问：丙、丁两个三角形面积之和是甲、乙两个三角形面积之和的多少倍？3．已知：,问：a除以13所得余数是几？4．某班在一次数学考试中，平均成绩是78分，男、女生各自的平均成绩是75.5分、81分．问：这个班男、女生人数的比是多少？5．某玩具厂生产大小一样的正方体形状的积木，每个面分别涂上红、黄、蓝3种颜色中的1种，每色各涂2个面．当两个积木经过适当的翻动以后，能使各种颜色的面所在位置相同时，它们就被看作是同一种积木块．试说明：最多能涂成多少种不同的积木块？6．一条双向铁路上有11个车站，相邻两站都相距7千米．从早晨7点开始，有18列货车由第十一站顺次发出，每隔5分钟发出一列，都驶向第一站，速度都是每小时60千米．早晨8点，由第一站发出一列客车，向第十一站驶去，时速是100千米．在到达终点站前，货车与客车都不停靠任何一站．问：在哪两个相邻站之间，客车能与3列货车先后相遇？11。
历届华杯赛初赛、复赛真题及答案
华罗庚金杯少年数学邀请赛（简称“华杯赛”）是为了纪念我国杰出数学家华罗庚教授，于1986年始创的全国性大型少年数学竞赛活动，由中国少年报社（现为中国少年儿童新闻出版社）、中国优选法、统筹法与经济数学研究会、中央电视台青少中心等单位联合发起主办的。
华杯赛堪称国内小学阶段规模最大、最正式也是难度最高的比赛。
对一个对于学校课堂内容学有余力的学生来讲，适当学习小学奥数能够有以下方面的好处
1、促进在校成绩的全面提高，培养良好的思维习惯；
2、使学生获得心理上的优势，培养自信；
3、有利于学生智力的开发；
4、数学是理科的基础，学习奥数对于这个学生进入初中后的学习物理化学都非常有好处（很多重点中学就是因为这个原因招奥数好的学生）。
5、很多重点中学招生要看学生的奥数成绩是否优秀。
您可能还感兴趣的有：。
小学数学竞赛题循环小数互化与错位相减技巧真题
【例1】计算：1.1.19
27。
(结果用小数表示)
【例2】(2005年第10届华杯赛总决赛二试10分第2题)将1
2
化成小数等于0.5，是个有限小数；将
1
11
化
成小数等于0.090…，简记为0.，是纯循环小数；将1
6
化成小数等于0.1666……，简记为0.1，
是混循环小数。
现在将2004个分数1
2
，
1
3
，
1
4
，…，
1
2005
化成小数，问：其中纯循环小数有多
少个？
【例3】写出一个最大的分数，它的分子是1并且它所化成的小数是：
⑴循环节里最少的位数是4的纯循环小数。
⑵不循环部分有两个数字，循环节里最少的位数是3的混循环小数。
循环小数互化与错位相减技巧
〖答案〗【例 1】2.2【例 2】801
【例 3】⑴分母只能取101；⑵
1 108。
华杯赛第届总决赛一试二试教师版
6. 将 1, 2, 3, 4, 5, 6, 7, 8, 9 填入图 A-60 的圆圈中, 每个圆圈恰填一 个数, 满足下列条件:
1) 正三角形各边上的数之和相等; 2) 正三角形各边上的数之平方和除以3的余数相等. 问: 有多少种不同的填入方法？ （注意, 经过旋转和轴对称反射, 排列一致的, 视为同一种填法）
所以
图 A-59
-1-
[ABF] 6 [CDF] 5. 3. 某地区的气象记录表明, 在一段时间内, 全天下雨共 1 天; 白天雨夜间晴或白天晴
夜间雨共 9 天; 6 个夜间和 7 个白天晴朗. 则这段时间有_________天, 其中全天天晴 有_________天. 【答案】12, 2. 【解答】全天晴被包含在 6 个夜间和 7 个白天晴朗之中, 并且一天记数 2 次. 而白晴夜 雨和白雨夜晴的日子也被包含在这 13 天中, 全天下雨的日子不被包含在这 13 天之中. 所以,
-2-
9 y 2z 0 , y 2z 是 11 的倍数, 所以 y 2z 0 . 注意
99z 11x2 0 , 9z x2 , 对于 z 4 , 只能有 z 1 或 4, 相应地 x 3 或 6, y 2 或 8.
综上所述, 所有满足条件的 (a, b, c)为
(33, 22, 1111), (66, 88, 444), (88, 33, 7777). 5. 纸板上写着 100、200、400 三个自然数, 再写上两个自然数, 然后从这五个数中
【答案】75.
图 A-62
【解答】设三角形 BCO 的面积为 x, 则 45 x . 解得 x 172 1 .
18 69
2
所以
-6-
四边形 ABCD 的面积 18 45 69 172 1 304 1 .
华杯赛历届试题
第一届华杯赛决赛一试试题1. 计算：2．975×935×972×〔〕,要使这个连乘积的最后四个数字都是“0〞，在括号内最小应填什么数？3．把＋、－、×、÷分别填在适当的圆圈中，并在长方形中填上适当的整数，可以使下面的两个等式都成立，这时，长方形中的数是几？9○13○7=100 14○2○5=□4．一条1米长的纸条，在间隔一端0.618米的地方有一个红点，把纸条对折起来，在对准红点的地方涂上一个黄点然后翻开纸条从红点的地方把纸条剪断，再把有黄点的一段对折起来，在对准黄点的地方剪一刀，使纸条断成三段，问四段纸条中最短的一段长度是多少米？5．从一个正方形木板锯下宽为米的一个木条以后，剩下的面积是平方米，问锯下的木条面积是多少平方米？6．一个数是5个2，3个3，2个5，1个7的连乘积。
这个数当然有许多约数是两位数，这些两位的约数中，最大的是几？7．修改31743的某一个数字，可以得到823的倍数，问修改后的这个数是几？8．蓄水池有甲、丙两条进水管，和乙、丁两条排水管，要灌满一池水，单开甲管需3小时，单开丙管需要5小时，要排光一池水，单开乙管需要4小时，单开丁管需要6小时，如今池内有池水，假如按甲、乙、丙、丁的顺序，循环各开水管，每天每管开一小时，问多少时间后水清苦始溢出水池？9．一小和二小有同样多的同学参加金杯赛，学校用汽车把学生送往考场，一小用的汽车，每车坐15人，二小用的汽车，每车坐13人，结果二小比一小要多派一辆汽车，后来每校各增加一个人参加竞赛，这样两校需要的汽车就一样多了，最后又决定每校再各增加一个人参加竞赛，二小又要比一小多派一辆汽车，问最后两校共有多少人参加竞赛？10．如以下图，四个小三角形的顶点处有六个圆圈。
假如在这些圆圈中分别填上六个质数，它们的和是20，而且每个小三角形三个顶点上的数之和相等。
问这六个质数的积是多少？11．假设干个同样的盒子排成一排，小明把五十多个同样的棋子分装在盒中，其中只有一个盒子没有装棋子，然后他外出了，小光从每个有棋子的盒子里各拿一个棋子放在空盒内，再把盒子重新排了一下，小明回来仔细查看了一番，没有发现有人动过这些盒子和棋子，问共有多少个盒子？12．如右图，把1.2，3.7, 6.5, 2.9, 4.6，分别填在五个○内，再在每个□中填上和它相连的三个○中的数的平均值，再把三个□中的数的平均值填在△中，找出一个填法，使△中的数尽可能小，那么△中填的数是多少？13．如以下图，甲、乙、丙是三个站，乙站到甲、丙两站的间隔相等。
第十届“华杯赛”小学组总决赛二试题
699 第十届 “华杯赛”总决赛小学组二试试题
l.如下页图，四边形ABCD 中，对角线AC 和BD 交于O 点。
已知：AO ＝l ，并且5
3CBD ABD =的面积三角形的面积三角形，那么OC 的长是多少？
2.将1/2化成小数等于0.5，是个有限小数；将1/11化成小数等于
0.0909……，简记为90
.0 ，是纯循环小数；将1/6化成小数等于0.l666……，简记为6
01.0 ，是混循环小数。
现在将2004个分数,2005
1,41,31,21 化成小数，问：其中纯循环小数有多少个？ 3.计算：2005
200320011975175315311⨯⨯++⨯⨯+⨯⨯+⨯⨯ 4.abc 表示一个十进制的三位数，若abc 等于由a ，b ，c 三个数码所组成的全体两位数的和，写出所有满足上述条件的三位数。
5.由26＝12＋52＝12＋32 ＋42，可以断定26最多能表示为3个互不相等的非零自然数的平方和，请你判定360最多能表示为多少个互不相等的非零自然数的平方之和？
6.有若干名小朋友，第一名小朋友的糖果比第二名小朋友的糖果多2块，第二名小朋友的糖果比第三名小朋友的糖果多2块……即前一名小朋友总比后一名小朋友多二块糖果。
他们按次序围成圆圈做游戏，从第一名小朋友开始给第二名小朋友2块糖果，第二名小朋友给第三名小朋友4块糖果……即每一名小朋友总是将前面传来的糖果再加上自己的2块传给下一名小朋友。
当游戏进行到某一名小朋友收到上一名小朋友传来的糖果但无法按规定给出糖果时，有两名相邻小朋友的糖果数的比是13：1，问最多有多少名小朋友？。
华数杯数学竞赛试题 小学
华杯赛每周一练试题及答案第一期试题一：某公司有一项运动--爬楼上班，公司正好在18楼办公。
一天该公司的箫菲爬楼上班，她从一楼爬到六楼用了90秒，由于爬楼很累每爬一层都要比上一层多用2秒时间，那么她到18楼共需要多少分钟？答案：爬到六楼每一层平均用时间：90÷（6－1）＝18（秒）。
爬第一层用时间：18－2×2＝14（秒）；到18楼共爬楼：18－1＝17（层）；爬最后一层用时间：14＋2×（17－1）＝46（秒）；总共爬楼用时：（14＋46）×17÷2÷60＝8.5（分钟）。
华杯赛每周一练试题及答案第二期试题一某公司有一项运动——爬楼上班，该公司正好在xx大厦18楼办公。
一天编辑箫菲爬楼上班，她数了一下楼梯，每段有14级台阶，每层有2段。
她想我每一步走一级或二级。
那么我到公司走楼梯共有多少种走法呢？亲爱的小朋友你能帮萧菲解决这个难题吗？解析：如果用n表示台阶的级数，an表示某人走到第n级台阶时，所有可能不同的走法，容易得到：①当n＝1时，显然只要1种走法，即a1＝1。
②当n＝2时，可以一步一级走，也可以一步走二级上楼，因此，共有2种不同的走法，即a2＝2。
③当n＝3时，如果第一步走一级台阶，那么还剩下二级台阶，由②可知有a2＝2（种）走法。
如果第一步走二级台阶，那么还剩下一级台阶，由①可知有a1＝1（种）走法。
根据加法原理，有a3＝a1＋a2＝1＋2＝3（种）类推，有：a4＝a2＋a3＝2＋3＝5（种）a5＝a3＋a4＝3＋5＝8（种）a6＝a4＋a5＝5＋8＝13（种）a7＝a5＋a6＝8＋13＝21（种）a8＝a6＋a7＝13＋21＝34（种）a9＝a7＋a8＝21＋34＝55（种）a10＝a8＋a9＝34＋55＝89（种）a11＝a9＋a10＝55＋89＝144（种）a12＝a10＋a11＝89＋144＝233（种）a13＝a11＋a12＝144＋233＝377（种）a14＝a12＋a13＝233＋377＝610（种）一般地，有an＝an－1＋an－2走一段共有610种走法。
第七届华杯赛全套试题及解答
第七届华杯赛初赛试题及解答1．将l999表示为两年质数之和：l999=口+口，在口中填入质数。
共有多少种表示法2．澳门是世界上人口密度最大的地区之一，它由一个半岛和两个小岛组成，已知澳门的人口为43万人，其中90％居住在半岛上，半岛的面积为7平方千米。
问：半岛上平均每平方千米有多少万人(取两位小数)3．某人年初买了一种股票，该股票当年下跌了20％，第二年应上涨多少才能保持原值4．某个月里有三个星期日的日期为偶数，请你推算出这个月的15日是星期几。
5．“火树银花楼七层，层层红灯倍加增，共有红灯三八一，试问四层几红灯”6．下图是由9个等边三角形拼成的六边形，已知中间最小的等边三角形的边长是1，问：这个六边形的周长是多少7． 一个正六边形的苗圃，用平行干苗圃边缘的直线把它分成许多相等的正三角形，在三角形的顶点上都栽种树苗，已知苗圃的最外面一圈栽有90棵。
问：苗圃中共栽树苗多少棵8． 甲、乙、丙三所小学学生人数的总和为l999，已知甲校学生人数的2倍，乙校学生人数减3、丙校学生人数加4都是相等的。
问：甲、乙、丙各校学生人数是多少9． 小明爷爷的年龄是一个二位数，将此二位数的数字交换得到的数就是小明爸爸的年龄，又知道他们年龄之差是小明年龄的4倍，求小明的年龄。
10． 用l0块长7厘米、宽5厘米、高3厘米的长方体积木堆拼成一个长方体，这个长方体的表面积最小是多少11． 时钟的时针和分针在6点钟反向成一直线，问：它们下—次反向成—直线是在什么时间(准确到秒)12． 1998年夏天长江洪水居高下不，8月22日武汉关水位高达2932米，已知武汉离长江入海口1125千米，而九江离武汉关269千米。
假设从武汉到入海口的长江江面搬相同，请计算当天九江的水位是多少米。
(取二位小数)第七届华杯赛复赛试题1. (错误!－＋错误!)÷错误!＋错误!×错误!2. 1999年2月份，我国城乡居民储蓄存款月末佘额是56767亿元，比月初佘额增长l8％.请问：我国城乡居民储蓄存款2月初余额是多少亿元(精确到时亿元)3. 环形跑道周长400米，甲、乙两名运动员同时顺时针自起点出发，甲每分钟跑400米，乙每分钟跑375米.问：多少时间后甲、乙再次相遇4. 两个整数的最小公倍数是1925，这两个整数分别除以它们的最大公约数，得到两个商的和是16，写出这两个整数。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
知识改变命运百度提升自我
本文为自本人珍藏版权所有仅供参考
第九届华杯赛总决赛小学组第二试试题
1．一正方形苗圃，栽种桃树和李树，一圈一圈地相间种植，即最外一圈种的是桃树，往内
一圈种的是李树，然后是桃树，…，最内一圈种了4棵桃树。
已知树苗的行距和列距都相等，桃树比李树多40棵。
问：桃树和李树一共有多少棵？
2．如下图，在以AB为直径的半圆上取一点C，分别以AC和BC为直径在ΔABC外作半圆AEC 和BFC，当C点在什么位置时图中两个弯月形（阴影部分）AEC和BFC的面积和最大？
3．甲乙两家医院同时接受同样数量的病人，每个病人患x病或y病中的一种，
经过几天治疗，甲医院治好的病人多于乙医院治好的病人。
问：经过这几天治疗，是否可能甲医院对x病的治愈率和对y病的治愈率均低于乙医院的？举例说明。
（x病的治愈率=(x病治好人数／患x病人数)×100%）
4．完成某项工程，甲单独工作需要18小时，乙需要24小时，丙需要30小时。
现甲，乙，丙按如下顺序工作：甲，乙，丙，乙，丙，甲，丙，甲，乙，…，每人工作一小时换班，问：
当工程完成时甲，乙，丙各干了多少小时？
5．求同时满足下列三个条件的自然数a,b:
(1) a>b; (2)ab
a+b
=169; (3)a+b是平方数。
6．如图，正方形跑道ABCD。
甲，乙，丙三人同时从A点出发同向跑步，他们的速度分别为
每秒5米，4米，3米。
若干时间后，甲首先看到乙和丙都与自己在正方形的同一条边上，
且他们在自己的前方。
从此时刻算起，又经过21秒，甲乙丙三人处在跑道的同一位置上，这是出发后三人第一次处在同一位置。
请计算出正方形周长的所有可能值。
用心爱心专心 1。