电磁场边界条件ppt课件
(完整版)电磁场的边界条件

电磁场的边界条件姓名:学号:专业:班级:提交日期:桑薇薇0990*******通信工程电工 1401 2016.5.28成绩:电磁场的边界条件1.引言2.边界条件分类3.边界条件的作用4.结束语5.参考文献1. 引言在两种不同媒质的分界面上,场矢量E,D,B,H 各自满足的关系,称为电磁场的边界条件。
在实际的电磁场问题中, 总会遇到两种不同媒质的分界面 (例如: 空气与玻璃的分界面、导体与空气的分界面等) ,边界条件在处理电磁场问题中占据十分重要的地位。
2. 边界条件分类1、电场法向分量的边界条件如图 3.9 所示的两种媒质的分界面, 第一种媒质的介电常数、磁导率和电导率分别为1,1和1,第二种媒质的介电常数、磁导率和电导率分别为2,2和 2 。
在这两种媒质分界面上取一个小的柱形闭合面,图 3.9 电场法向分量的边界条件如图 3.9 所示,其高h 为无限小量,上下底面与分界面平行,并分别在分界面两侧, 且底面积 S 非常小,可以认为在 S 上的电位vv v移矢量 D和面电荷密度S是均匀的。
n 1 n 2分别为上下底面的外法线单位矢量, , 在柱形闭合面上应用电场的高斯定律? v vv v S v vSSD gdS n 1 gD 1 n 2 gD 2 SS故v v v vn 1gD 1 n 2 gD 2S(3.48a)vv vvv若规定 n 为从媒质Ⅱ指向媒质Ⅰ为正方向,则 n 1 n ,n2n,式 (3.48a) 可写为v vvng(D 1D 2 )S(3.48b)或D1nD2nS(3.48c)式 (3.48 ) 称为电场法向分量的边界条件。
vvv 因为 DE ,所以式 (3.48) 可以用 E 的法向分量表示v v v v1n 1gE 12 n 2 gE 2S(3.49a)或1E 1n2 E 2nS(3.49b)若两种媒质均为理想介质时, 除非特意放置, 一般在分界面上不存在自由面电荷,即S,所以电场法向分量的边界条件变为D1nD2n(3.50a)或1E1n 2E2 n(3.50b)若媒质Ⅰ为理想介质,媒质Ⅱ为理想导体时, 导体内部电场为零,即E2,D2,在导体表面存在自由面电荷密度,则式(3.48) 变为v vn 1 gD 1 D 1nS(3.51a)或1E1ns(3.51b)2 、电场切向分量的边界条件在两种媒质分界面上取一小的矩形闭合回路 abcd ,如图 3.10 所示,该回路短边 h 为无限小量,其两个长边为l ,且平行于分界面,并分别在分界面两侧。
电磁场课件--第一章电磁场的媒质边界条

汇报人:
01
02
03
04
05
06
电磁场与媒质的相互作用是电 磁场理论的重要内容
媒质边界条件是描述电磁场与 媒质相互作用的重要工具
媒质边界条件包括电边界条件 和磁边界条件
媒质边界条件在电磁场计算和 工程应用中具有重要意义
理想边界条件:假设边界上不存在任何电磁场
非理想边界条件:假设边界上存在电磁场,但场强和场矢量满 足一定的条件
电场强度:在媒质分界面上,电场 强度必须连续
电荷密度:在媒质分界面上,电荷 密度必须连续
添加标题添加标题来自添加标题添加标题磁场强度:在媒质分界面上,磁场 强度必须连续
电流密度:在媒质分界面上,电流 密度必须连续
电场强度:在媒质分界面上,电场强度必须连续 磁场强度:在媒质分界面上,磁场强度必须连续 电荷密度:在媒质分界面上,电荷密度必须连续 电流密度:在媒质分界面上,电流密度必须连续
边界条件:描述媒质分界面上的电磁场性质 连续性条件:描述媒质分界面上电磁场的连续性 数学表达形式:通过数学公式表示边界条件 应用实例:在电磁场课件中,通过实例讲解边界条件的数学表达形式
理想导体:电场 强度为零,电流 密度无穷大
绝缘体:电场强 度不为零,电流 密度为零
边界条件:理想 导体与绝缘体之 间的边界上,电 场强度和电流密 度必须满足连续 性条件
数据采集:记录实验过程中的 数据,包括电磁场强度、温度、 湿度等
实验设计:选择合适的实验 设备,设计实验方案
数据分析:对采集到的数据进 行处理和分析,验证边界条件
的准确性
应用实例:介绍边界条件在实 际应用中的案例,如电磁屏蔽、
电磁兼容等
边界条件是电 磁场理论中的 重要概念,用 于描述电磁场 在媒质边界上
电磁场理论课件-5.6磁介质分界面上的边界条件

I
b
O 321 a
Jm
M
1
(M 2 )ez
( 0
1)
I (b2
a
2
)
e
z
在ρ=a和ρ=b处的磁化面电流为
在垂直于Jzm轴s |J平bms面|M内a2的Me磁2化[((电e0)流1为0) 2I b]ez
I 2m0:54:44 S J m d S
2 b
J ms
dl
(
0
1)I
(
0
1)I
0
2
2
三、导体边界条件
B2 H2
在理想导体内部,磁场为0。
若媒质2为导体,则由边界条件一般形式推得:
B1 n B2 n n (H1 H2 )
0
J
S
H
2
,
B2
0
B1 n 0
n
H1
JS
说明20::48:0可3 以应用边界条件计算导体边界上电流分布。6
5.6 磁介质分界面上的边界条件
四、矢量磁位的边界条件
B1
n
B2 B
n 0 A
(
A1
A2
)
n
0
A1 A2
n (H1
B H
H2)
Js A
n( 1
1
A1
1
1
A2 )
Js
1
1
(
A1 )t
1
2
(
A2 )t
Js
20:49:58
7
5.6 磁介质分界面上的边界条件
例1:铁质的无限长圆管中通过电流I,管的内、外半
B2 n
2
或: n (B1 B2 ) 0
电磁场边界条件ppt课件
lim
h0
D t
e hl
0
如果分界面的薄层内有自由电流, 则在回路所围的面积上,
lim J ds s
J e hl
h0
Js e l
e en (H1 H2 ) Js e
2
en (H1 H2 ) Js
D1n D2n 0
电位移矢量的法向分量 在边界面上才是连续的。
9
电磁场的边界条件
en
(H1
H
2
)
Js
en (B1 B2 ) 0
en
(
E1
en (D1
E2
)
D2 )
0
s
相应的标量形式为
H1t H2t B1n B2n
en
(E1
E2
)
0
en (D1 D2 ) 0
相应的标量形式为
H1t H2t B1n B2n
E1t E2t D1n D2n
12
3、漏电媒质:
Biblioteka en (H1H
2
)
Js
en (B1 B2 ) 0
en
(
E1
将积分形式的磁通连续性原理即如果分界面的薄层内有自由电荷则圆柱面内包围的总电荷为得电位移矢量的法向分量边界条件的矢量形式为limlim电位移矢量的法向分量在边界面上是不连续的
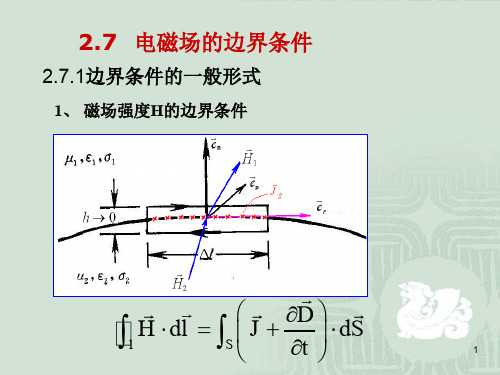
2.7 电磁场的边界条件
2.7.1边界条件的一般形式
1、 磁场强度H的边界条件
《电磁场》课件—第三章 静电场2(导体和介质中的静电场理论-边界条件).ppt

∫ ∫ ∫ ( ) ∫ qp
=
V' ρ pdV
=
V ρ pdV
=−
P⋅ d S
S
= − ∇ ⋅ P dV V
• 整块介质的极化总电荷:qp=0
复习
div P =
lim
∫S
P⋅ d S
∆V →0 ∆V
• 分界面上极化电荷面密度:作高斯面,可证
qp = −∫S P ⋅ dS
σ p = P1⋅ nˆ − P2 ⋅ nˆ
电子热运动
E 0
无电流
有表面电荷
3) 静电平衡状态的特性
E 0
• 导体是等位体,表面是等位面。 因为:电场为零,则任意两点无电位差。
• 内部无净电荷,只能分布在表面。 因为:绕任意宏观点作高斯面,根据高斯定理,又因 电场为零,则内部无净电荷。(表面?)
• 导体外、紧靠导体表面的场强为 E = σ nˆ ε0
ε1 ε2
如果介质2是真空, 或空气则 σ p= P ⋅ nˆ P1
dS
• 极化电荷体密度
ρ p = −∇ ⋅ P
和高斯定理比较 : ρ = ε0∇ ⋅ E
ε1 ε2
P2 nˆ
均匀极化, ∇ ⋅ P = 0 , 则极化体电荷为零。
4) 电位移矢量
为什么要引入 新物理量?
=D ε0 E + P
定义式
必要条件:导体内部各点—宏观点—场强为零。
E内 = 0
E 0
静电平衡时内部有无电子?
不动的正电荷晶核到哪里去了?简Leabharlann 图—— ——
—
—
—
—
—
—
— —
—
——
+29
电磁场的边界条件

也可以表示为标量形式:
可见, 的切向分量在不同的媒质分界面上不连续, H 与分界面上的传导电流面密度有关。
②、E 的边界条件
en
(E1 E2 ) 0 E E 1t 2t
结论: E 切向连续。
③ D 的边界条件
1
dv
n
D2
D1 h 0
D dS
s
2
电磁场的边界条件
1 什么是边界条件?
2 为什么要研究边界条件? 3 如何讨论边界条件?
在两种不同媒质的分界面上,场矢量E, D, B, H
各自满足的关系,称为电磁场的边界条件。
在实际的电磁场问题中,总会遇到两种不
同媒质的分界面(例如:空气与玻璃的分界面、 导体与空气的分界面等),边界条件在处理电 磁场问题中占据着十分重要的地位。
或
B 1n B 2n D 1n D 2n
2.理想导体与介质的分界面,电导率 , 假设I为介质,II为理想导体。 此时
E 2 0 , B 2 0, D 2 0, H 2 0
en en en en
H1 Js E1 0 B1 0 D 1 ρ s
dS )
由于
D t
有限,故 lim S
h 0
D t
dS 0
而 lim
h 0
J dS
s
h 0
lim
(J S )
h 0
lim
( J e p l h ) J s e p l
en ( H 1
H2) Js
H 1t H 2t J s
数
, ,
2.1_恒定磁场的边界条件__矢量磁位ppt课件
是回路包围的曲
l1 sˆnˆl
,
面ΔS的单位法线矢量,所以上式可以写为
l H d l H 1 H 2 ( s ˆ n ˆ ) l n ˆ H 1 H 2 s ˆ l 3 . 4 1
Hdl l
I0 i
3.40
(3.40〕式的右边i 可以写为
i I0iJSsˆl沿 sˆ 3方.42 向的分量
H2,
图3.17 H切向分量的边界条件
与分界面法线的夹角分别是θ1, θ2,
单位法线矢量 由介nˆ 质2指向介质
1。在两种磁介质的分界面上作一 个极窄的跨过分界面两侧的矩形 回路ABCDA,这个小矩形回路的 两边平行于分界面,且分居于分 界面两侧,另外两边h垂直穿过分 界面,且h→0。 AB=CD= l, BDC=DCA 0 ,如图3.17中所示。 利用安培环路定理
L
Id l'
a
y
Idl
d
x
A
4
l
Idl r
dA Idl 4 r
3.62 3.63
所以导线圆环在P点产生矢量磁位为
A 其 中A 2 0 d A c o s 2 0 I0 d lc R o s 3 .6 8
dlad
3.69
z
R r2a22racos 3.70
L
dA
(3.70〕式中
41Vd rV 3.57
Ay ,
1 ,
Jy
Az ,
1 ,
Jz
A e x A x + e y A y+ e zA z 4
J d V Vr
3 .5 8
体电流元产生的矢量磁位为
dA4Jd rV
3.59
2.9 电磁场的边界条件
2.9 电磁场的边界条件自强●弘毅●求是●拓新实际电磁场问题都是在一定的空间和时间范围内发 生的,它有起始状态(静态电磁场例外)和边界状 态。
即使是无界空间中的电磁场问题,该无界空间也可 能是由多种不同介质组成的,不同介质的交界面和 无穷远界面上电磁场构成了边界条件。
边界条件: 即电磁场在不同介质的边界面上服从的条件,也可 以理解为界面两侧相邻点在无限趋近时所要满足的 约束条件。
边界条件是完整的表示需要导出界面两 侧相邻点电磁场矢量所满足的约束关系。
由于在分界面两侧介质的特性参数发生突变,场在界 面两侧也发生突变。
所以Maxwell方程组的微分形式 在分界面两侧失去意义(因为微分方程要求场量连续 可微)。
而积分方程则不要求电磁场量连续,从积分 形式的麦克斯韦方程组出发,导出电磁场的边界条件把积分Maxwell方程组应用到图所表示的两媒质交界 面的扁平圆盘。
根据Gauss定理,让h→0,场在扁平 圆盘壁上的通量为零,得到: n ˆ ˆ D ds D ( n ) S D ( n S ) D 1 2 S 2 ( D2 n D1n )S s Sˆ s (D2 D1 ) n ˆ 0 (B 2 B1 ) nhr2D1 r1在介质分界面两侧,选取如图所示的积环路,应用安培环路积 分公式: D H dl H l H ( l ) ( H H ) t l ( J ) ds 1 2 1 2 l S t t N n ( H 2 H1 ) t ( H 2 H1 ) ( N n ) ˆ J N ˆ ˆ (H H ) N n2 1 sˆ ( H 2 H1 ) J s nˆ ( E 2 E1 ) 0 nD 0 E P, B 0 H Mn ( P 2 P1 ) f n (M 2 M 1 ) J mˆ s (D 2 D1 ) nn ( H 2 H1 ) J s n (B 2 B1 ) 0 ( J f J m )n ( E2 E1 ) ( f p ) / 0①任何分界面上E的切向分量是连续的 ②在分界面上有面电荷(在理想导体表面上)时,D的法向分量不 连续,其差等于面电荷密度;否则,D的法向分量是连续的 ③在分界面上若存在面电流(仅在理想导体表面上存在),H的切 向分量 不连续 ,其差等于面电流密度;否则,H的切向分量是 连续的 ④任何分界面上B的法向分量是连续的理想介质理想介质是指 0,即无欧姆损耗的简单媒质。
第3讲 电磁场的边界条件
质相对介电常数应为多少?
【解】由边界条件,若 E3平行于x轴,则 E2也必平行于x轴。 在左侧圆柱面分界面上,由电场边界条件:
E1t E2t E1 E2 E2 3
D1n D2n 1E1 2E2 E2
要使合成波E2 平行于x轴,则必有
E1z
z0
D1z
1
z0
3 0 5 0
3 5
最后得到
3
E1 ( x,
y,0)
ex 2 y
ey
5x
ez
5
D1(x, y,0) ex100 y ey x ez 30
第三讲 电磁场的边界条件
【例4】在两导体平板(z = 0 和 z = d)之间的空气中,已知电
场强度
E
ey E0
sin( π
媒质1
en 1
E1
1
媒质2 E2
2
2
en (E1 E2 ) 0
• 导体与电介质分界面
en (D1 D2 ) 0
• 场矢量的折射关系
tan1 E1t / E1n 1 / D1n 1 tan2 E2t / E2n 2 / D2n 2
en E1 0
en D1 S
第三讲 电磁场的边界条件
理想导体表面上的电荷密度等于D的法向分量 磁感应强度平行于导体表面 电场强度垂直于理想导体表面 理想导体表面上的电流密度等于H的切向分量
第三讲 电磁场的边界条件
三、几种常见边界条件
1、静电场的边界条件
• 一般形式
en (E1 E2 ) 0
en (D1 D2 ) S
• 两种电介质分界面
电磁场与电磁波第15讲边界条件电感磁能
2. Magnetization and Equivalent Current Densities
v
nv mvk
M lim k1
(A/m)
v0 v
v
v
vv
Jm M (A/m2 ) Jms M aˆn
A/m
2
3. Magnetic Field Intensity and Relative Permeability
Field and Wave Electromagnetic 电磁场与电磁波
2015. 11.10
Review
1. The Magnetic Dipole
mv
v IS
(A m2 )
v A
aˆ
0I b2 4 R2
sin
0mv aˆR 4 R2
v B
0m 4 R3
(aˆR
2 cos
aˆ
sin
)
aˆn2 (D1 D2 )S (D1n D2n S sS
vv aˆn2 ( rE1 Er2 ) 0
aˆn2 ( D1 D2 ) s
or E1t=E2t
or D1n D2n s
6
(a) 在分界面处B的法向分量是连续的.
B1n B2n
v v
aˆn2 B1 B2 0
0 I 2 2 r
aˆ
aˆ (b d r) tan 600 dr
30I2
2
d b
ln
1
b d
b
0 I 2
tan
2
600
bd
d
(b
d r
r)
dr
L12
21 I2
30 I 2 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
.
第五章 时 变 电 磁 场
例1、在两导体平板(z=0和z=d)之间的空气中传播的
电磁波,已知其电场强度为
E re ryE0sin(dz)cos(tkx)
第五章 时 变 电 磁 场
2.7 电磁场的边界条件
2.7.1边界条件的一般形式
1、 磁场强度H的边界条件
rr
r
r D
r
Ñ l
Hdl
SJ. t
dS
Ñ
r H
l
( er
d
r第五r章
l H1
r en
)
(
r H
1
时ert 变l 电Hr
磁场
2
r et
l
r
H 2)l
r r rr
h
(H1 H 2 ) (e en )l
(1)如果分界面处不存在自由电荷,即ρS = 0时,由电
位移法向分量和场强的切向分量的边界条件有:
分界面处的折射定理
tan1 1 tan2 2
折射定理表明,电场线在分界面上通常要改变方向。
.
第五章 时 变 电 磁 场 (2)若两种介质分界面不存在面电流,则在分界面 处的边界条件为
ee n n ((B H 1 1 B H 2 )2 ) 00
式中k为常数,求:(1)磁场强度;(2)两导体表面的面电流 密度和面电荷密度。
解:(1)磁场强度
r
Q
r
E0
H t
e x E zye z E xy0 H t
.
第五章 时 变 电 磁 场
可求得
r
H t E 0 0 [ e r x d c o s ( d z ) c o s (t k x ) e r z k s i n ( d z ) s i n (t k x ) ]
电场强度的切向分量 在边界面上是连续的。
第五章 时 变 电 磁 场
3、磁感应强度B边界条件
图 3-17 B的边界条件
.
第五章 时 变 电 磁 场 设底面和顶面的面积均等于ΔS。将积分形式的磁通连续性
原理(即∮S B·dS=0)应用到此闭合面上,假设圆柱体的高度h趋
于零, 得 B 1 e n S B 2 e n S 0
e n ( H 1 H 2) 0 e n ( E 1 E 2) 0
e n(B 1 B 2) 0 e n(D 1 D 2) 0
相应的标量形式为
H1t H2t B1n B2n
E1t E2t D1n D2n
.
第五章 时 变 电 磁 场 3、漏电媒质:
e e n n (( B H 1 1 B H 2 )2 ) 0J s e n e n ( D ( 1 E 1D 2 E )2 ) s 0
相应的标量形式为 H 1 t H 2 t B 1 n B 2 n
分界面处的折射定理 tan 1 1 tan 2 2
.
第五章 时 变 电 磁 场
tan 1 1 tan 2 2
折射定理表明,磁感应线在分界面上通常要改变方向。 若介质2为铁磁材料,介质1为空气,此时μ1 «μ2, 有 θ1 « θ2,及 B1 « B2 假如μ2=1000μ0, μ1=μ0,在这种情况下,当θ2=87°时,
e n ( B 1 B 2 ) 0B 1 n B 2 n
磁感应强度的法向分量在边界面上是连续的。
.
第五章 时 变 电 磁 场
4、 电位移矢量的边界条件
rr
Ñ SDdSq s D d s D 1 e n s D 2 e n s e n ( D 1 D 2 ) s
D1nD2n s
电位移矢量的法向分量 在边界面上是不连续的。
.
第五章 时 变 电 磁 场
如果分界面的薄层内没有自由面电荷时:
en(D 1D 2)0
D D 0 1n
2n
电位移矢量的法向分量 在边界面上才是连续的。
.
第五章 时 变 电 磁 场
电磁场的边界条件
e n ( H 1 H 2) Js e n (E 1 E 2 ) 0
rr r r
e [en (H1 H 2 )]l
因为 D/tm 0 D te r h l0
如果分界面的薄层内有自由电流, 则在回路所围的面积上,
rr rr
rr
sJ rd s r l i h m r0 J r e h r l r J se l
e e n (H 1 . H 2 ) J se
第五章 时 变 电 磁 场
e n (H 1 H 2) Js
H1t H2t Js
磁场强度在穿过存在面电流的分界面 时,其切向分量是不连续的。
如果分界面处没有自由面电流,则
en (H 1 H 2)0
H1t H2t
磁场强度在穿过不存在面电流的分界面 时,其切向分量是连续的。
B1t B2t
1 2
注意:磁感应强度在分界面处,其切向 分量是不连续的。
.
第五章 时 变 电 磁 场
2、 电场强度的边界条件
lE d l E 1 e t l E 2 e t l 0
上式变为
(E 1E 2)et 0
故有
en (E1 E2) 0 E1t E2t
.
图 2 - 10 切向边界条件
.
第五章 时 变 电 磁 场
如果分界面的薄层内有自由电荷,则圆柱面内包围的总 电荷为
q li m h s lis m s s s
h 0
h 0
s D d s e n ( D 1 D 2 ) S s s
得电位移矢量的法向分量边界条件的矢量形式为
e n(D 1 D 2 )s
E、H、D、B为理想导体外部附近的电磁场,那么理想导
体表面的边界条件为
e e n n B H 1 1 0Js
e e n n D E 11 0s
.
第五章 时 变 电 磁 场
2、两种理想介质分界面。理想介质是指σ = 0,所以在理想
介质分界面无自由电荷分布,不存在面电流,则在分界面处的边
界条件为
e n(B 1 B 2 ) 0 e n(D 1 D 2)s
相应的标量形式为
H1t H2t B1n B2n
E1t E2t D1n D2n
.
第五章 时 变 电 磁 场
2.7.2 两种特殊情况的边界条件
1、理想导体表面上的边界条件
理想导体是指σ→∞,所以在理想导体内部不存在电场。
此外,理想导体内部也不存在磁场。理想导体内部不存在 电磁场,即所有场量为零。设 是e理n 想导体的外法向矢量,
