金融时间序列实验报告
金融时序数据分析报告(3篇)

第1篇一、引言随着金融市场的快速发展,数据已成为金融行业的重要资产。
时序数据分析作为金融数据分析的核心方法之一,通过对金融时间序列数据的分析,可以帮助我们理解市场趋势、预测未来走势,从而为投资决策提供科学依据。
本报告旨在通过对某金融时间序列数据的分析,揭示市场规律,为投资者提供参考。
二、数据来源与处理1. 数据来源本报告所使用的数据来源于某金融交易所,包括股票、债券、期货等金融产品的历史价格、成交量、市场指数等数据。
数据时间跨度为过去五年,数据频率为每日。
2. 数据处理(1)数据清洗:对数据进行初步清洗,剔除异常值和缺失值。
(2)数据转换:将原始数据转换为适合时序分析的形式,如对数变换、标准化等。
(3)数据分割:将数据分为训练集和测试集,用于模型训练和验证。
三、时序分析方法本报告主要采用以下时序分析方法:1. 时间序列描述性分析通过对时间序列数据进行描述性统计分析,如均值、标准差、自相关系数等,了解数据的整体特征。
2. 时间序列平稳性检验使用ADF(Augmented Dickey-Fuller)检验等方法,判断时间序列是否平稳,为后续建模提供基础。
3. 时间序列建模(1)ARIMA模型:根据时间序列的自相关性,构建ARIMA模型,对数据进行拟合和预测。
(2)SARIMA模型:在ARIMA模型的基础上,考虑季节性因素,构建SARIMA模型。
(3)LSTM模型:利用深度学习技术,构建LSTM模型,对时间序列数据进行预测。
四、结果与分析1. 时间序列描述性分析通过对股票价格、成交量等数据的描述性分析,我们发现:(1)股票价格波动较大,存在明显的周期性波动。
(2)成交量与价格波动存在正相关关系。
(3)市场指数波动相对平稳。
2. 时间序列平稳性检验通过ADF检验,我们发现股票价格、成交量等时间序列均为非平稳时间序列,需要进行差分处理。
3. 时间序列建模(1)ARIMA模型:根据自相关图和偏自相关图,确定ARIMA模型参数,对数据进行拟合和预测。
金融建模实验报告书(3篇)

第1篇一、实验背景与目的随着金融市场的不断发展,金融建模在风险管理、投资决策和资产定价等方面发挥着越来越重要的作用。
为了提高对金融模型的理解和运用能力,本次实验旨在通过构建一个简单的金融模型,对金融市场中的某一具体问题进行分析和预测。
二、实验内容与方法1. 实验内容本次实验以股票市场为例,构建一个简单的股票价格预测模型。
模型将包括以下步骤:(1)数据收集:收集某只股票的历史交易数据,包括开盘价、收盘价、最高价、最低价和成交量等。
(2)数据预处理:对收集到的数据进行清洗、处理和转换,为模型构建提供高质量的数据。
(3)特征工程:根据业务需求,提取股票价格的相关特征,如均线、相对强弱指数(RSI)、移动平均线(MA)等。
(4)模型构建:选择合适的机器学习算法,如线性回归、支持向量机(SVM)等,对股票价格进行预测。
(5)模型评估:使用交叉验证等方法评估模型的预测性能。
2. 实验方法本次实验采用以下方法:(1)Python编程语言:使用Python进行数据处理、特征工程和模型构建。
(2)机器学习库:利用Scikit-learn、TensorFlow等机器学习库实现模型构建和评估。
(3)数据处理库:使用Pandas、NumPy等数据处理库进行数据预处理。
三、实验过程与结果1. 数据收集本次实验选取了某只股票的历史交易数据,数据时间跨度为一年,包含每天的开盘价、收盘价、最高价、最低价和成交量等。
2. 数据预处理对收集到的数据进行以下处理:(1)去除异常值:删除异常交易数据,如成交量异常大的交易。
(2)数据转换:将日期转换为数值型,便于后续处理。
3. 特征工程根据业务需求,提取以下特征:(1)开盘价、收盘价、最高价、最低价(2)移动平均线(MA):计算不同时间窗口内的移动平均线(3)相对强弱指数(RSI):计算股票价格变动的速度和变化幅度4. 模型构建选择线性回归算法构建股票价格预测模型。
具体步骤如下:(1)划分数据集:将数据集划分为训练集和测试集。
金融时间序列分析—总结

• 单位根检验是检验时间序列是否平稳,协整是在时间序列平
稳性的基础上做长期趋势的分析,而格兰杰检验一般是在建
立误差修正模型的后,所建立的短期的因果关系。故顺序自
然是先做单位根检验,再过协整检验,最后是格兰杰因果检
验。
h
7
建模注意要点-6
• 11、VAR建模时lag intervals for endogenous要填滞后期,但 是此时你并不能判断哪个滞后时最优的,因此要试,选择不 同的滞后期,至AIC或SC最小时,所对应着的滞后为最优 滞后,此时做出来的VAR模型才较为可靠。
• 如果变量之间不仅存在滞后影响,而且存在同期影响关系, 则适合建立SVAR模型。
• 如果非平稳(有单位根)时间序列具有协整关系,则建立协 整方程描述变量之间的长期均衡关系,建立向量误差修正模 型(VEC)描述其短期动态关系。
h
2
建模注意要点-1
• 1、单位根检验是序列的平稳性检验,如果不检验序列的平 稳性直接OLS容易导致伪回归。
h
5
建模注意要点-4
• 先做单位根检验,看变量序列是否平稳序列,若平稳,可构 造回归模型等经典计量经济学模型;
• 若非平稳,进行差分,当进行到第i次差分时序列平稳,则 服从i阶单整(注意趋势、截距不同情况选择,根据P值和原 假设判定)。若所有检验序列均服从同阶单整,可构造VAR 模型,做协整检验(注意滞后期的选择),判断模型内部变 量间是否存在协整关系,即是否存在长期均衡关系。如果有, 则可以构造VEC模型或者进行Granger因果检验,检验变量 之间“谁引起谁变化”,即因果关系。
• 6、非平稳序列很可能出现伪回归,协整的意义就是检验它
们的回归方程所描述的因果关系是否是伪回归,即检验变量
金融时间序列分析-ARIMA模型建模实验报告
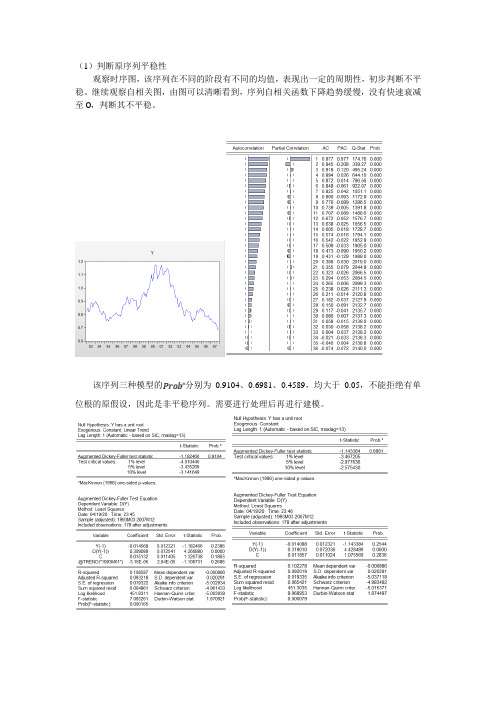
(1)判断原序列平稳性观察时序图,该序列在不同的阶段有不同的均值,表现出一定的周期性,初步判断不平稳。
继续观察自相关图,由图可以清晰看到,序列自相关函数下降趋势缓慢,没有快速衰减至0,判断其不平稳。
该序列三种模型的分别为0.9104、0.6981、0.4589,均大于0.05,不能拒绝有单位根的原假设,因此是非平稳序列。
需要进行处理后再进行建模。
(2)差分序列平稳性检验对原序列进行一次差分,再对其进行平稳性检验。
观察其时序图,该序列的时序图都表现出围绕其水平均值不断波动的过程,没有明显的趋势或周期性,粗略估计是平稳时间序列。
再观察其自相关函数图。
自相关系数快速衰减到0,在虚线范围内波动,没有明显的波动、发散,判断为平稳序列。
模型3与模型2的伴随概率为0,拒绝有单位根的原假设,说明序列是平稳的。
但模型3的时间趋势项的伴随概率为0.1789,常数项的伴随概率0.3504,在显著性水平0.05情况下不显著,故不选用。
而模型2的常数项的伴随概率为0.6608,也不显著,不选用。
因此模型1是最合适的模型,不含有常数项和时间趋势项。
(3)模型的参数估计及模型的诊断检验观察自相关图最后两列可以看到,Q检验的伴随概率均小于0.05,拒绝没有自相关性的原假设,因此该序列不是白噪声序列,没有把信息都提取出来。
接下来将尝试使用AR(1)、AR(2)、AR(3)、MA(1)、ARMA(1,1)、ARMA(2,1)模型进行拟合。
(1)AR(1):该模型各项显著,故对其进行残差项白噪声检验,观察Q检验及其伴随概率,在显著性水平为0.05时,拒绝没有自相关性的原假设,不是白噪声序列,不选用。
(2)AR(2):。
该模型各项显著,故对其进行残差项白噪声检验,观察Q检验及其伴随概率,在显著性水平为0.05时,接受没有自相关性的原假设,是白噪声序列,可以选用。
(3)AR(3):该模型各项不显著,不选用。
(4)MA(1):该模型各项显著,故对其进行残差项白噪声检验,观察Q检验及其伴随概率,在显著性水平为0.05时,接受没有自相关性的原假设,是白噪声序列,可以选用。
金融时间序列分析报告报告材料第三次作业

3.4模型为AR(1)-GARCH(1,1),假定εt服从自由度为v的标准化的t分布,导出数据的条件对数似然函数。
数据为r=[r1, r2, ……r n]模型为r t=u+φ1r t-1+a ta t=σtεtσt2=α0+α1a t-12+β1σt-12由于εt服从自由度为v的标准化的t分布,所以有εt的概率密度函数为f(εt)=Г-(v+1)/2其中Г(x)为Gamma函数(Г)由于at=σtεt,a t的条件似然函数为f(am+1,……,at)=Г-(v+1)/2所以对数条件似然函数为L=T{ln(Г)-ln(Г)-ln[(v-2)n]}-ln(σt2)+(1+v)ln(1+ )]带入实际的数据T=t,a t=r t-u-φ1r t-1,同时又有σt2=α0+α1a t-12+β1σt-12,所以有了第一个σ1后就可以递推出其余的σt。
3.5对Intel股票的对数收益率建立GARCH模型,并进行向前1到5步的波动率预测。
数据的图形如下:同时ACF和PACF如下:可知模型的基本形式应该为MA(1)。
尝试对残差建立ARMA(0,1)~Garch(1,1)模型,结果为*-----------------------------------------------------** GARCH Model Fit **-----------------------------------------------------*Conditional Variance Dynamics-----------------------------------GARCH Model : sGARCH(1,1)Mean Model : ARFIMA(1,0,0)Distribution : normOptimal Parameters------------------------------------Estimate Std. Error t value Pr(>|t|)mu 0.025807 0.006441 4.00645 0.000062 ar1 0.027009 0.054726 0.49353 0.621640 omega 0.001235 0.000615 2.00819 0.044624 alpha1 0.089186 0.033309 2.67753 0.007417 beta1 0.836646 0.055546 15.06232 0.000000LogLikelihood : 238.1461检验残差的ACF发现模型可以满足要求。
金融时间序列分析-总结

2023 WORK SUMMARY
金融时间序列分析-总 结
REPORTING
目录
• 引言 • 金融时间序列基本概念 • 数据获取与预处理 • 统计分析方法 • 模型构建与评估 • 实证分析与案例研究 • 总结与展望
https://
数据来源
公开数据源
包括证券交易所、政府统计机构、 国际经济组织等提供的公开数据。
商业数据源
如专业金融数据服务商提供的收费 数据服务,通常数据更全面、质量 更高。
学术研究数据源
学术研究机构或学者共享的数据集, 常用于特定金融问题的研究。
数据清洗
01
02
03
缺失值处理
根据数据缺失的程度和性 质,采用插值、删除或基 于模型的方法进行处理。
分布形态度量
通过偏度、峰度等指标 描述数据分布的形状。
推断性统计
参数估计
利用样本数据对总体参数进行 估计,如点估计和区间估计。
假设检验
提出原假设和备择假设,通过 构造检验统计量并计算p值,判 断原假设是否成立。
方差分析
研究不同因素对因变量的影响 程度,以及因素之间的交互作 用。
回归分析
探究自变量和因变量之间的线 性或非线性关系,建立回归模
结论与启示
总结股票价格预测的方法和效果,并探讨其在实际应用 中的局限性和改进方向。
案例二:汇率波动分析
01
02
03
04
数据来源与预处理
收集某货币对的汇率历 史数据,并进行清洗和 整理。
实证分析过程
采用GARCH模型对汇率 波动进行建模和分析, 通过极大似然估计等方 法确定模型参数。
结果分析
对模型的拟合效果和波 动率预测进行评估,包 括模型的残差分析、波 动率预测精度等。
金融实验报告(格式模板)

证券实验一、绘制K线图格式范本实验人:邓伏虎学号:2202301001时间:2005年11月9日地点:电子科技大学金融证券实验室一、实验目的1、学习股票K线图的画法。
2、了解如何通过K线图来推测股票的走势。
3、通过将股票和上证指数的K线图的对比,了解股票的基本属性。
二、模型和原理1)自己任选一只股票,自己收集交易数据,自任意时间开始,以每20日为一个周期,在坐标图纸上,连续绘制10个周期的K线图,同时标明成交量。
2) 连续10天绘制上海或深圳大盘指数的K线图三、原始数据记录1、ST大江股票2004.5.31-2004.7.20以20天为周期的原始价格记录时间ⅩⅩ股票开盘价格单(元)ⅩⅩ股票收盘价格(元)ⅩⅩ股票最高价(元)ⅩⅩ股票最低价(元)成交量(手)2004.5.31 5.09 4.24 5.18 4.13 18167 2004.6.20 4.17 3.74 4.33 3.70 17626 2004.7.10 3.81 4.39. 4.63 3.42 66911 2004.7.30 4.22 3.75 4.61 3.64 27800 2004.8.20 3.68 3.65 3.97 3.57 13245 2004.9.10 3.60 3.88 4.20 3.53 34113 2004.9.30 3.98 3.86 4.36 3.78 24282 2004.10.20 3.90 3.85 3.95 3.49 16182 2004.11.10 3.73 3.97 4.54 3.71 39469 2004.11.30 3.99 3.68 4.14 3.61 14227 2、上证指数2005.5.16-5.26以日为周期的原始价格记录时间上证指数开盘价格上证指数收盘价格上证指数最高价上证指数最低价成交量(万手)2005.5.16 1105 1095 1105 1082 1241 2005.5.17 1090 1099 1108 1083 1320 2005.5.18 1099 1102. 1108. 1090 1223 2005.5.19 1101 1103 1107 1083 1252 2005.5.20 1100 1099 1109 1095 1140 2005.5.23 1095 1070 1095 1069 1229 2005.5.24 1066 1073 1078 1057 1406 2005.5.25 1072 1072 1082 1064 1186 2005.5.26 1071 1058 1077 1055 1132 2005.5.27 1056 1051 1068 1050 1285四、K线图1、ST大江股票2004.5.31-2004.7.20以20天为周期的K线图2、上证指数2005.5.16-5.26以日为周期的K线图五、对结果的说明:通过观察ST大江和上证指数的K线图,我们可以看出一支股票的基本走势,,对其中的数据进行分析以后,我们可以很轻松地把握一支股票的历史数据,并由此来推测这支股票的走势。
金融时间序列分析2篇

金融时间序列分析2篇金融时间序列分析(一)时间序列是指一组按时间顺序排列的数据。
在金融领域,时间序列分析常用于分析股票、货币、债券、商品等资产价格的变化规律。
本文将介绍金融时间序列分析的方法和应用。
一、时间序列分析的方法时间序列分析方法包括时间序列模型、时间序列分解、时间序列平稳性检验、时间序列预测等。
其中,时间序列模型是时间序列分析的核心部分,常用的模型包括ARMA、ARIMA、GARCH等。
ARMA模型是一种自回归移动平均模型,包括自回归项和移动平均项两部分。
ARIMA模型是在ARMA模型的基础上增加了差分项,可以处理非平稳时间序列。
GARCH模型是一种波动率模型,可以处理金融资产价格的波动性。
时间序列分解可以将时间序列分解成趋势、季节性和随机性三个部分,可以更好地理解时间序列的特点。
时间序列平稳性检验可以检验时间序列的平稳性,平稳性是很多时间序列模型的前提条件。
时间序列预测可以预测未来的时间序列值,是金融时间序列分析的一个重要应用。
二、时间序列分析的应用时间序列分析在金融领域有广泛应用,例如股票价格预测、外汇汇率波动分析、资产组合优化等。
下面以股票价格预测为例介绍时间序列分析在股票市场的应用。
股票价格是众多金融时间序列中最重要的一个。
时间序列分析对于股票价格预测有重要作用。
预测股票价格涨跌的方向可以帮助投资者制定合理的投资策略。
一种基本的股票价格预测方法是使用ARIMA模型。
ARIMA模型可以处理非平稳时间序列,更好地适用于股票价格预测。
通过建立ARIMA模型,可以对未来的股票价格进行预测。
同时,还可以使用时间序列分解方法,将股票价格分解成趋势、季节性和随机性三个部分,更好地理解和预测未来的股票价格变化趋势。
三、总结时间序列分析是金融领域中重要的一种分析方法。
时间序列模型、时间序列分解、时间序列平稳性检验、时间序列预测等是时间序列分析的基本方法。
时间序列分析在股票价格预测、外汇汇率波动分析、资产组合优化等方面有广泛应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
·
《金融时间序列分析》
综合实验二
金融系金融工程专业2014 级姓名山洪国
学号20141206031048 实验地点:实训楼B305 实验日期:2017.04,21
实验题目:ARIMA模型应用
实验类型:基本操作训练
实验目的:
利用美元对欧元汇率1993年1月到2007年12月的月均价数据,进行ARIMA模型的识别、估计、检验及预测。
实验容:
1、创建Eviews文件,录入数据,对序列进行初步分析。
绘制美元对欧元汇率月均价数据折线图,分析序列的基本趋势,初步判断序列的平稳性。
2、识别ARIMA(p,d,q)模型中的阶数p,d,q。
运用单位根检验(ADF检验)确定单整阶数d;利用相关分析图确定自回归阶数p和移动平均阶数q。
初步选择几个合适的备选模型。
3、ARIMA(p,d,q)模型的估计和检验。
对备选模型进行估计和检验,并进行比较,
从中选择最优模型。
4、利用最优模型对2008年1月美元对欧元汇率的月均价进行外推预测。
评分标准:操作步骤正确,结果正确,分析符合实际,实验体会真切。
实验步骤:
1、根据所给的Excel 表格的数据,将表格的美元对欧元的汇率情况录入到EViews9中,并对所录入数据进行图形化的处理,所得到的图形结果如下图所示。
(时间段:1993.01至2007.12)
0.6
0.7
0.8
0.9
1.0
1.1
1.2
EUR/USD
分析图形数据可得,欧元对美元的汇率波动情况较为明显,其中在1999年至2003年期间欧元和美元的比值一度在1.0以上。
但近些年以来,欧元的汇率一度持续下滑,到了2007年底的时候和和美元的比值在0.7左右。
如上图所示,对前一图的折线数据进行了相关性分析,由图中的Autocorrelation可知此数据为拖尾情况,说明它是非平稳的。
再对此数据进行单位根检验,所得结果如上图所示。
其中单位根检验所对应的P值为0.6981,远大于0.05的显著性水平,因此可以说该序列是一个非平稳序列。
2、根据ARIMA模型,对该序列进行一阶的单位根检验,如下图
由该图可知,对比前面的未一阶差分的单位根检验,此一阶差分的单位根检验P值为0小于显著性水平0.05,因此拒绝原假设,证明在一阶差分下的序列数据才是平稳的。
因此该序列的单整阶数d为1
如上图所示,因为该序列的一阶为平稳的,所以作其一阶相关性分析。
从图中可看出:
自相关序列经过1期收敛于0.05区间,所以其移动平均阶数q的值为1,偏相关序列经过2阶才变为0,则可知其自回归阶数p的值为2.
综上所述,可得:p=2;d=1;q=1
初步适合EURO的模型有:ARIMA(1,1,0)、ARIMA(2,1,0)、ARIMA(0,1,1)、ARIMA (1,1,1)、ARIMA(2,1,1)
3、对模型ARIMA(p,d,q)的估计与检验
如上图所示,因为其中的截距项所对应的t统计量的Prob值为0.6606>0.05的显著性水平,因此要剔除截距项c。
将截距项c去掉之后,在进行回归可得上图所示的容。
因此,根据图的数据可知:Wt=0.309522W(t-1)
t=4.343228
单从P值来看的话,系数是显著的。
不过还要对残差进行白噪声检验
如上图所示,在对残差项进行Q检验的时候,选择K=13,得到的Q检验结果如如所示。
在第13行数据中找到Q统计量为13.406,其所对应的相伴概率(Prob)为0.340>0.05,因此接受序列不相关的假设,即可认为该残差序列是白噪声。
然后,可用类似的方法对对之前所得到的其他四个模型ARIMA(2,1,0)、ARIMA(0,1,1)、ARIMA(1,1,1)、ARIMA(2,1,1)进行与之对应的估计与检验。
经过了一系列的检验之后,ARIMA(1,1,0)、ARIMA(2,1,0)、ARIMA(0,1,1)三个检验都通过参数显著性检验、模型平稳性、可逆性检验、残差序列白噪声检验。
剩下的两个模型ARIMA(1,1,1)、ARIMA(2,1,1)则并没有通过检验。
因为R^2越大越好,说明模型的拟合程度越好。
从可决系数可看出来,ARIMA(1,1,0)模型不好。
在排除之后剩下的两个模型ARIMA(2,1,0)和ARIMA(0,1,1)中,用自回归信息Forecast预测可知,在预测方面ARIMA(2,1,0)相对较好。
因此,最终决定选择模型ARIMA(2,1,0)。
则Wt=0.354W(t-1)-0.206W(t-2)
因为Wt=ΔXt=(1-L)Xt
即(1-L)Xt=0.354(1-L)X(t-1)-0.206(1-L)X(t-2)
可得到:Xt=1.373X(t-1)-0.568X(t-2)+0.202X(t-3)
4、利用最优模型对2008年1月美元对欧元汇率的月均价进行外推预测
以下利用步骤3中得出来的最优化模型ARIMA(2,1,0)来对2006年1月的美元对欧元汇率的月均价进行推测。
根据所给的Excel数据可得,2007年12月是0.68686;2007年11月是0.68111;2007年10月是0.70249.将所选择的数据带入到公式Xt=1.373X(t-1)-0.568X(t-2)+0.202X(t-3)中,经计算可知:
Xt=1.373*0.68686-0.568*0.68111+0.202*0.70249
=0.9431-0.3869+0.1419
=0.6981
即,对2008年一月份的汇率预测为0.6981.
实验感悟:
评阅人:成绩:。
