平面应力状态下的应力研究
材料学 平面应变状态分析

3 2
首先研究与其中一个主平
面 (例如主应力3 所在的平
面)垂直的斜截面上的应力
用截面法,沿求应力的
截面将单元体截为两部分,
取左下部分为研究对象
1
2 1
1
2
3
2
主应力 3 所在的两平面上是一
对自相平衡的力,因而该斜面上的应
力 , 与3 无关, 只由主应力1 , 2
决定
3
与3 垂直的斜截面上的应力可
最大切应力所在的
截面与 2 所在的主平面 O C
B
A
垂直,并与1和3所在的
主平面成45°角.
3
2
1
例题9 单元体的应力如图所示,作应力圆, 并求出主应力和最大 切应力值及其作用面方位.
解: 该单元体有一个已知主应力
y 20MPa
因此与该主平面正交的各截
面上的应力与主应力z 无关, 依据
x截面和y 截面上的应力画出应力
假设:
O
(1)O点处沿任意方向的微段内, 应变是均匀的;
x'
x
(2)变形在线弹性范围内都是微小的, 叠加原理成立;
分别计算 x ,y ,xy单独存在时的线应变 和切应变,然后 叠加得这些应变分量同时存在时的和 .
1.推导线应变 ( Derive the linear strain)
从O点沿 x′方向取出一微段 OP = dx′, 并以它作为矩形 OAPB
的对角线.
y y'
该矩形的两边长分别为 dx 和 dy
x'
B
P
dy dx'
O
dx A
x
(1)只有正值x 存在
工程力学-应力状态与应力状态分析

8 应力状态与应变状态分析1、应力状态的概念,2、平面应力状态下的应力分析,3、主平面是切应力为零的平面,主应力是作用于主平面上的正应力。
(1)过一点总存在三对相互垂直的主平面,对应三个主应力,主应力排列规定按代数值由大到小为:321σσσ≥≥最大切应力为132max σστ-=(2)任斜截面上的应力ατασσσσσα2sin 2cos 22xy yx yx --++=ατασστα2cos 2sin 2xy yx +-=(3) 主应力的大小22minmax )2(2xyyx yx τσσσσσ+-±+=主平面的方位y x xytg σστα--=2204、主应变122122x y x y xy xyx y()()tg εεεεεεγγϕεε⎡=+±-+⎣=-5、广义胡克定律)]([1z y x x E σσμσε+-=)]([1x z y y E σσμσε+-=)]([1y x z z E σσμσε+-=G zxzx τγ=G yzyz τγ=,G xyxy τγ=6、应力圆与单元体之间的对应关系可总结为“点面对应、转向相同、夹角两倍。
”8.1 试画出下图8.1(a)所示简支梁A 点处的原始单元体。
图8.1[解](1)原始单元体要求其六个截面上的应力应已知或可利用公式直接计算,因此应选取如下三对平面:A 点左右侧的横截面,此对截面上的应力可直接计算得到;与梁xy 平面平行的一对平面,其中靠前的平面是自由表面,所以该对平面应力均为零。
再取A 点偏上和偏下的一对与xz 平行的平面。
截取出的单元体如图8.1(d)所示。
(2)分析单元体各面上的应力:A 点偏右横截面的正应力和切应力如图8.1(b)、(c)所示,将A 点的坐标x 、y 代入正应力和切应力公式得A 点单元体左右侧面的应力为:z M y I σ=bI QS z z*=τ由切应力互等定律知,单元体的上下面有切应力τ ;前后边面为自由表面,应力为零。
材料力学:第八章-应力应变状态分析

正负符号规定:
切应力 t - 使微体沿顺时针 旋转为正 方位角 a - 以 x 轴为始边、逆时针旋转 为正
斜截面应力公式推导 设α斜截面面积为dA, 则eb侧面和bf 底面面积分别为dAcosα, dAsinα
由于tx 与 ty 数值相等,同时
sa+90 ,ta+90
E
sa+90 ,ta+90
结论: 所画圆确为所求应力圆
应力圆的绘制与应用3
应力圆的绘制
已知 sx , tx , sy ,
画相应应力圆
t
先确定D, E两点位置, 过此二点画圆即为应力圆
Ds x ,t x , E s y ,t y
t
C OE
s 2 , 0
s 1 , 0
应力圆绘制 作D, E连线中垂线,与x轴相交即为应力圆圆心
tb sb
t
sa
O
C
ta
D
sa ,ta
t
s
E
sb ,tb
O
D
sa ,ta
C
s
E
sb ,tb
由|DC|=|CE|,可得sC值:
sC
s
2 β
+
t
2 β
s
2 α
+
t
2 α
2 sα sβ
点、面对应关系
转向相同, 转角加倍 互垂截面, 对应同一直径两端
应变状态
构件内一点处沿所有方位的应变总况或集合, 称为该点处的 应变状态
研究方法
环绕研究点切取微体, 因微体边长趋于零, 微体趋于所研究 的点, 故通常通过微体, 研究一点处的应力与应变状态
平面应力状态理论分析
称此圆为应力圆。
R x y xy 2 2
2
由于应力圆最早由德 国工程师莫尔 (otto.mohr,18351918)提出,故又称 为莫尔圆。
R
B
O
x y
2
A
O1
工程力学系
二、应力圆作法 (1)在坐标系内画出A1( x , xy) (2)在坐标系内画出B1( y , yx)
2 0 21
2
即:剪应力极值平面和主平面夹角为45°
工程力学系
第九章 应力状态分析
§9-3 平面应力状态分析的图解法
一、应力圆方程
x y x y cos 2 xy sin 2 2 2 斜截面应力解析表达式 x y sin 2 xy cos 2 2
y yx
zx
yz
xz
z
zy
xy
x
工程力学系
三、应力状态分类
第九章 应力状态分析
三向应力状态(空间应力状态):三个方向的主应力 都不等于0;
二向应力状态(平面应力状态):两个方向的主应力 都不等于0;
单向应力状态:只有一个方向的主应力都不等于0
y yx
zx
y yx
o
25
30
30
o
30 40
o
x y
2
x y
2
cos 60o xy sin 60o 49.7MPa
30
o
x y
2
cos 60o xy sin 60o 13.1 MPa
max
平面应力状态分析-应力圆法

应力圆法
1. 任一斜截面上的应力
2. 求主平面、主应力
应力圆最早由德国工程师莫尔在
应力圆(莫尔圆) 1882年首次提出,故又称为莫尔圆。
R
x 2
y
2
x2
R
C
O
x y
2
应力圆的绘制方法
O
C
D2(y ,y) R
xC
D1(x ,x)
单元体与相应应力圆 之间的对应关系
(1)点面对应
xC
x y
2
R
x
2
y
2
2 x
(2)二倍角转向相同
应力圆的应用1 求单元体任意斜截面上的应力
D ( , )
2
D1( x , x ) D2 ( y , y )
【例题】用应力圆法求30°斜截面上的应力
x 100 MPa y 40 MPa
x 20 MPa y 20 MPa
D1(100, 20) D2 (40, 20)
20
100 40 20
30 67 MPa
30 36 MPa
练习1 求60°斜截面上的应力
x 70MPa y 50 MPa x 0 MPa y 0 MPa
D60 (20, 50)
D2 (50, 0)
120
C(10,0) D1(70, 0)
练习2
求45°斜截面上的应力
D1(0, 80)
90
D45 (80, 0)
D2 (0, -80)
应力圆的应用2 求单元体的主平面和主应力
max
min
x
y
2
x
2
y2Leabharlann 2 x【例题】应力圆法求三个主应力
应力与应力状态分析

应力与应力状态分析拉伸模量拉伸模量是指材料在拉伸时的弹性,其计算公式如下:拉伸模量(㎏/c ㎡)=△f/△h(㎏/c ㎡)其中,△f 表示单位面积两点之间的力变化,△h 表示以上两点之间的应变化。
更具体地说,△h =(L-L0)/L0,其中L0表示拉伸长前的长度,L 表示拉伸长后的长度。
§4-1 几组基本术语与概念一、变形固体的基本假设1、均匀连续性假设:假设在变形固体的整个体积内均匀地、毫无空隙地充满着物质,并且各点处的力学性质完全相同。
根据这一假设,可从变形固体内任意一点取出微小单元体进行研究,且各点处的力学性质完全相同,因而固体内部各质点的位移、各点处的内力都将是连续分布的,可以表示为各点坐标的连续函数。
2、各向同性假设:假设变形固体在所有方向上均具有相同的力学性质。
3、小变形假设:认为构件的变形与构件的原始尺寸相比及其微小。
根据小变形假设,在研究构件上力系的简化、研究构件及其局部的平衡时,均可忽略构件的变形而按构件的原始形状、尺寸进行计算。
二、应力的概念1、正应力的概念分布内力的大小(或称分布集度),用单位面积上的内力大小来度量,称为应力。
由于内力是矢量,因而应力也是矢量,其方向就是分布内力的方向。
沿截面法线方向的应力称为正应力,用希腊字母σ表示。
应力的常用单位有牛/米2 (2/m N ,12/m N 称为1帕,代号a P )、千米/米2(2/m KN ,12/m KN 称为1千帕,代号Ka P ),此外还有更大的单位兆帕(M a P )、吉帕(G a P )。
几种单位的换算关系为:1 K a P =310a P 1 M a P =310K a P 1 G a P =310M a P =610K a P =910a P2、切应力与全应力的概念与截面相切的应力分量称为切应力,用希腊字母τ表示。
K 点处某截面上的全应力K p 等于该点处同一截面上的正应力K σ与切应力K τ的矢量和。
材料力学之应力与应变分析
3.截取原始单元体的方法、原则
①用三个坐标轴(笛卡尔坐标和极坐标,依问题和构件形状 而定)在一点截取,因其微小,统一看成微小正六面体
②单元体各个面上的应力已知或可求; ③几种受力情况下截取单元体方法:
P
P
Me B
Me
A
s A s=P/A
B t=Me/Wn
Байду номын сангаасa) 一对横截面,两对纵截面 P
⑥
ss"'
a0 *
ttxyxy a0 *
ss"'
4.极值切应力:
应力与应变分析
①令:
,可求出两个相差90o 的
a1,代表两个相互垂直的极值切应力方位。
②极值切应力:
③
(极值切应力平面与主平面成45o)
例一 图示单元体,试求:①a=30o斜
截面上的应力; ②主应力并画出主单元
体;③极值切应力。
s" 40
txy
ssxtxxy
sα
a
a
dA
tα
x
tyx sy
sy tyx
得
符号规定:
应力与应变分析
a角—以x轴正向为起线,逆时针旋转为正,反之为负
s拉为正,压为负
t—使微元产生顺时针转动趋势者为正,反之为负
3.主应力及其方位:
①由主平面定义,令t =0,得:
可求出两个相差90o的a0值,对应两个互相垂直主平面。
④单向应力状态又称简单应力状态,平面和空间应 力状态又称复杂应力状态。
第二节 平面应力状态下的 应力研究、应力圆
一、平面应力分析的解析法
1.平面应力状态图示:
弹性力学平面应力问题和平面应变问题
有限差分法的精度取决于差分格式的选择和网格的划分,同时需要注意数 值稳定性和计算精度的问题。
边界元法
边界元法是一种基于边界积 分方程的数值分析方法,通 过将微分方程转化为边界积
分方程来求解。
变形特点
应用领域
在平面应力问题中,变形主要发生在作用 面上,而在平面应变问题中,变形可以发 生在整个结构中。
平面应力问题在桥梁、建筑和机械等领域 有广泛应用,而平面应变问题在岩土、地 质和材料等领域有广泛应用。
06
结论与展望
结论总结
平面应力问题和平面应变问题在弹性力学中具有重要地位,它们是描述物体在应力作用下的变形和应 力分布的基础。
弹性模量表示材料在受力作用下的刚度,是衡量材料抵 抗弹性变形能力的重要参数。
剪切模量表示材料在剪切力作用下的刚度,与弹性模量 和泊松比有关。
03
平面应变问题
应变状态分析
平面应变条件
应变分量中,只有$varepsilon_{x}$ 、$varepsilon_{y}$和 $gamma_{xy}$不为零,其余分量为 零。
有限元法在弹性力学平面应力问题和平面应变问题中广泛 应用,因为它能够处理复杂的几何形状和边界条件,且计 算精度高。
有限元法的实现需要建立离散化的模型、选择合适的单元 类型和求解算法,并进行数值稳定性和误差分析。
有限差分法
有限差分法是一种基于差分原理的数值分析方法,通过将微分方程转化为 差分方程来求解。
薄板弯曲问题
考虑一个矩形薄板,受到一对相距较远的集中力作用,使板发生弯曲。根据平面应力问题,可以分析 板的应力分布、中性面位置以及挠度等。
材料力学:第九章 应力状态分析
τx
C
F
Me
d
C
(a)
·
σx
(b)
C
T
F
解:C点所在横截面上的正应力和切应力的分布规律如图 所示, 点所在横截面上的正应力和切应力的分布规律如图b所示 点所在横截面上的正应力和切应力的分布规律如图 所示, 其值为
FN 500 × 103 N σx = = = 63.7 × 106 Pa=63.7MPa π 2 A 0.1m ) ( 4
经整理后得到 )、(2) )、( (1) 由(1)、( )式,可以求出单 ) 元体各个截面上的应力。( 。(即 点 元体各个截面上的应力。(即a点 (2) 处各个方向上的应力) ) 处各个方向上的应力)
∑F = 0
t
τ =τ′
σ α = −τ sin 2α
τ α = τ cos 2α
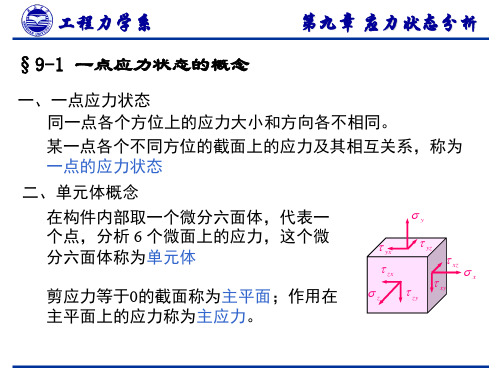
定义:构件内一点处各个方向上的应力集合, 定义:构件内一点处各个方向上的应力集合,称为该点处的 应力状态。 应力状态。
F F
横截面上只有正应力,且 横截面上只有正应力, 均匀分布 计算公式: 计算公式:
m
σ
F
FN
FN σ= A
等直圆杆扭转时横截面上的应力: 等直圆杆扭转时横截面上的应力:
Me m Me
m
横截面上只有切应力,呈 横截面上只有切应力, 线性分布
T
o
τρ
τmax
T⋅ρ 计算公式: 计算公式: τρ = Ip
R
τ
T 16 M e τ= = WP πd3
为了研究a点处各个方向的应力,围绕a点取一个各边长均为无 为了研究 点处各个方向的应力,围绕 点取一个各边长均为无 点处各个方向的应力 限小的六面体(称为单元体)。 限小的六面体(称为单元体)。 径向截面
平面应变的应力状态
平面应变的应力状态
平面应变的应力状态
平面应变是指在二维平面内,物体的形变只发生在该平面内,不发生在垂直于该平面的方向上。
在平面应变的情况下,物体可能会受到不同的应力状态。
以下是平面应变的应力状态及其特点:
1. 纯剪应力状态
在纯剪应力状态下,物体受到一个剪切力,该力沿着平面的一条方向施加,并呈45度角延伸至物体的各个点。
特点:物体的形状和大小保持不变,但体积会随之改变。
2. 平衡应力状态
在平衡应力状态下,物体受到的应力会平衡,即所有方向的应力大小和方向均相等。
特点:物体的形状和大小保持不变,没有形变。
3. 压缩应力状态
在压缩应力状态下,物体受到的应力为向内的压缩力,该力会使物体缩小。
特点:物体会变形,形变的大小取决于物体的材料和尺寸。
4. 拉伸应力状态
在拉伸应力状态下,物体受到的应力为拉伸力,该力会使物体产生延伸。
特点:物体会变形,形变的大小取决于物体的材料和尺寸。
5. 剪压应力状态
在剪压应力状态下,物体受到剪切力和压缩力的作用,这两种力有不同的方向和大小。
特点:物体会变形,形变的大小取决于物体的材料和尺寸。
剪切力的大小决定了物体的形状变化程度,压缩力的大小决定了物体的缩小程度。
6. 弯曲应力状态
在弯曲应力状态下,物体受到弯曲力的作用,其中一个面受到压缩力,另一个面受到拉伸力。
特点:物体会变形,形变的大小取决于物体的材料、尺寸和弯曲力的
大小。
弯曲力的作用方向决定了物体的形状变化程度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
D1
B1
τx
f
τx
τy
σy
C
y
D2
x
图 9-4
(4)利用应力圆求主应力
σ2
数值和主平面位置
主应力数值
o
A2 B2
C
A1和 A2两点为与主平面 对应的点,其横坐标
y
D2
σx
σ1
为主应力 1 ,2
D1
B1 A1
OA1 OC CA1 OA2 OC CA1
圆周上 E 点的 ¸ 坐标 就依次为 ¸ 。( 证明略 )
说明
点面之间的对应关系:单元体某一面上的应力,必对 应于应力圆上某一点的坐标。
夹角关系:圆周上任意两点所引半径的夹角等于单 元体上对应两截面夹角的两倍。两者的转向一致。
B1
2
A1
A
B
o
c
σy τy
σx e
σα
(b)
E
σx
o τα
B2
2
一、斜截面上的应力 1、 截面法: 假想地沿斜截面 ef 将单元体截分为二(图9-2b) , 留下左边部分的单体元 ebf 作为研究对象(图9-2c)。
e
x
x
y
y
y
n
x
x
x
e
x x
b
f
y
y
图9-2
b
f
y
y
e
x
x
y
y
y
n
x
x
x
b
f
y
y
图9-2
e
x x
b
f
y
y
:从x 轴到外法线 n 逆时针转向为正,反之为负。 正应力 :拉应力为正,压应力为负。 剪应力 :对单元体任一点的矩顺时针转为正,反之为负。
2
(
x
2
y
)2
2 x
当斜截面随方位角 变化时, 其上的应力 σα , τ α 在
- 直角坐标系内的轨迹是一个圆 ,圆心位于横坐标轴
(
轴
)上,离原点的距离为
x
y
2
半径为
此圆习惯上称为应力圆 , 或称为莫尔圆。
(
x
2
y
)2
2 x
(
x
2
y
)2
2
(
x
2
y
)2
2 x
o
C
(σ
x σ 2
y
2
)
τ
2 x
{ σ max =
σ min
26
MPa -96
A
x
3
1
σ1 26MPa σ 2 0 σ 3 96MPa
四、平面应力状态分析——应力圆
x
2
y
x
2
y
cos 2
x
sin
2
x
2
y
sin
2
x
cos 2
(1) 应力圆的概念
(9 -1) (9 - 2)
(
x
y )2
2
2
(
x
2
y )2
2 x
(
x
2
y
)2
(b)
D1
B1
连接D1D2两点的直线与 轴相交于C 点, 以C为 圆心, CD1或CD2为半径 作圆
σy τy
σx
σx
τx
τx
τy
σy
(b)
D1
o
B2
B1
C
y
D2
x
图 9-4
该圆的圆心 C 点到 坐标
原点的 距离为 x y
2
o
B2
(b)
D1
B1
半径为
(
x
2
y
)2
2 x
C
y
D2
该圆就是相应于该单元体
由公式
tg
2α
0
σ
2τ xy
x σ
y
求出0就可确定主平面的位置。
(1)主应力 将0代入公式
σα
σx
σy 2
σx
σy 2
cos 2α
τ
xy sin 2α
得到 max 和 min(主应力)
} σ max
σ min
σx σy 2
(σ
x σ 2
y
2
)
τ
2 xy
(2)主平面的位置
tg
2α
0
σ
2τ xy
x σ
,则 α1
450 450
(τ x 0) (τ x 0)
例8-4 简支梁如图所示。已知m-n截面上A点的弯曲
正应力和剪应力分别为 = -70MPa, = 50MPa 。 确定A点的主应力及主平面的方位。。
m
n a
l
A
A
解: x 70 y 0 x 50
解:
σ x 70 σ y 0 τ xy 50
x
2
y
x
2
y
cos 2
x
sin
2
x
y
2
sin 2
x
cos 2
(9 -1) (9 - 2)
二、主应力和主平面
主平面: 一点处剪应力等于零的平面称为主平面 主应力: 主平面上的正应力称为主应力
说明: 一点处必定存在这样的一个单元体, 三个相互垂直
的面均为主平面, 三个互相垂直的主应力分别记为 1 ,2 , 3
σ x σ y
2
图 9-3
(2)应力圆作法
在 - 坐标系内 ,
选定比例尺 o
量取 OB1 = x , B1D1 = x
, 得 D1点
x
σy τy
σx
σx
τx
τx
τy
σy
(b)
D1
B1
量取 OB2=y , B2D2= y ,
得D2 点
o
B2
σy τy
σx
σx
τx
τx
τy
σy
y
D2
x
图 9-4
x σ
y
α1 α 2 α1 900
α1 和 α 2 确定两个互相垂直的平面,一个是最大正应力
所在的平面,另一个是最小正应力所在的平面。
x
y
2
x
y
2
cos 2
x sin 2
x
y
2
sin 2
x
cos 2
d d
2[
x
2
y
sin
2
x
cos 2 ]
0
当即正应力达到极值的面上,剪应力必等于零。 此平面为主平面。正应力的极值为主应力。
x
应力状态的应力圆
D1 点的坐标为 ( x , x ) 因而 D1 点代表单元体 x 平面上的应力 。
σα
σy τy
e
σx
σx
E
o τα
B2
2
D1B1 CΒιβλιοθήκη xτxf τx
τy
σy
y
D2
x
(3)利用应力圆求单元体上任一 截面上的应力 从应力圆的半径 CD 1 按方位角 的转向转动 2 , 得到半径 CE ,
且规定按代数值大小的顺序来排列, 即
2 1
1 2 3
3
三、平面应力状态分析——解析法
x
y
2
x
y
2
cos 2
x
sin 2
x
y
2
sin 2
x
cos 2
令
dσ α
dα
2[σ
x
σy 2
sin 2α
τ
xy cos 2α
]
0
得到
tg
2α 0
σ
2τ xy
x σy
α1 α 2 α1 900
tg
2α
0
σ
2τ xy
y
α1 α 2 α1 900
} σ max
σ min
σx σy 2
(σ
x
σ 2
y
2
)
τ
2 xy
以1代表max作用面的方位角, 2代表min作用面的方位角。
σ x σ y ,则 α1 450 (α1在 900 范围内取值)
若 σ x σ y ,则 α1 450
{ 若 σ x σ y
tg
2α
0
σ
2τ xy
x σ
y
2 50 1.429 (70) 0
x A
62.50
27.5 0 α 0 62.50
因为 σ x σ y
-62.50 与max对应
} { σ max
σ min
σx σy 2
(σ
x σ 2
2
y)
τ
2 xy
26 MPa
-96
27.5 0 α 0 62.50
设斜截面的面积为 dA , eb 的面积为 dAcos , bf 的面积为dAsin 研究对象的受力如图 9-2d 所示
e
x x
b
f
y
y
e
τ x dAcosα
σ x dAcosα
σα dA
τ α dA
b
f
τ y dAsinα
(d)
σ y dAsinα
2、平面应力状态下, 任一斜截面 ( 截面 ) 上的应力 ¸ 的 计算公式
