四川大学信号与系统实验报告
信号与系统实验四实验报告

实验四 时域抽样与频域抽样一、实验目的加深理解连续时间信号的离散化过程中的数学概念和物理概念,掌握时域抽样定理的基本内容。
掌握由抽样序列重建原连续信号的基本原理与实现方法,理解其工程概念。
加深理解频谱离散化过程中的数学概念和物理概念,掌握频域抽样定理的基本内容。
二、 实验原理时域抽样定理给出了连续信号抽样过程中信号不失真的约束条件:对于基带信号,信号抽样频率sam f 大于等于2倍的信号最高频率m f ,即m sam f f 2≥。
时域抽样是把连续信号x (t )变成适于数字系统处理的离散信号x [k ] ;信号重建是将离散信号x [k ]转换为连续时间信号x (t )。
非周期离散信号的频谱是连续的周期谱。
计算机在分析离散信号的频谱时,必须将其连续频谱离散化。
频域抽样定理给出了连续频谱抽样过程中信号不失真的约束条件。
三.实验内容1. 为了观察连续信号时域抽样时抽样频率对抽样过程的影响,在[0,0.1]区间上以50Hz 的抽样频率对下列3个信号分别进行抽样,试画出抽样后序列的波形,并分析产生不同波形的原因,提出改进措施。
)102cos()(1t t x ⨯=π答: 函数代码为: t0 = 0:0.001:0.1;x0 =cos(2*pi*10*t0);plot(t0,x0,'r')hold onFs =50;t=0:1/Fs:0.1;x=cos(2*pi*10*t); stem(t,x); hold offtitle('连续信号及其抽样信号')函数图像为:)502cos()(2t t x ⨯=π同理,函数图像为:)0102cos()(3t t x ⨯=π同理,函数图像为:由以上的三图可知,第一个图的离散序列,基本可以显示出原来信号,可以通过低通滤波恢复,因为信号的频率为20HZ,而采样频率为50>2*20,故可以恢复,但是第二个和第三个信号的评论分别为50和100HZ,因此理论上是不能够恢复的,需要增大采样频率,解决的方案为,第二个信号的采样频率改为400HZ,而第三个的采样频率改为1000HZ,这样可以很好的采样,如下图所示:2. 产生幅度调制信号)200cos()2cos()(t t t x ππ=,推导其频率特性,确定抽样频率,并绘制波形。
信号与系统实验报告总结
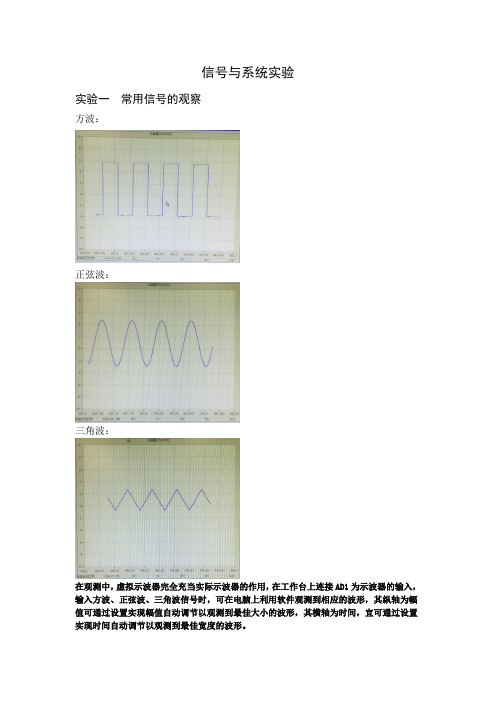
信号与系统实验实验一常用信号的观察方波:正弦波:三角波:在观测中,虚拟示波器完全充当实际示波器的作用,在工作台上连接AD1为示波器的输入,输入方波、正弦波、三角波信号时,可在电脑上利用软件观测到相应的波形,其纵轴为幅值可通过设置实现幅值自动调节以观测到最佳大小的波形,其横轴为时间,宜可通过设置实现时间自动调节以观测到最佳宽度的波形。
实验四非正弦周期信号的分解与合成方波DC信号:DC信号几乎没有,与理论相符合,原信号没有添加偏移。
方波基波信号:基波信号为与原方波50Hz信号相对应的频率为50Hz的正弦波信号,是方波分解的一次谐波信号。
方波二次谐波信号:二次谐波信号频率为100Hz为原方波信号频率的两倍,幅值较一次谐波较为减少。
方波三次谐波信号:三次谐波信号频率为150Hz为原方波信号的三倍。
幅值较一二次谐波大为减少。
方波四次谐波信号:四次谐波信号的频率为200Hz为原方波信号的四倍。
幅值较三次谐波再次减小。
方波五次谐波信号:五次谐波频率为250Hz为原方波信号的五倍。
幅值减少到0.3以内,几乎可以忽略。
综上可知:50Hz方波可以分解为DC信号、基波信号、二次、三次、四次、五次谐波信号…,无偏移时即无DC信号,DC信号幅值为0。
分解出来的基波信号即一次谐波信号频率与原方波信号频率相同,幅值接近方波信号的幅值。
二次谐波、三次谐波、四次谐波、五次谐波依次频率分别为原方波信号的二、三、四、五倍,且幅值依次衰减,直至五次谐波信号时几乎可以忽略。
可知,方波信号可分解为多个谐波。
方波基波加三次谐波信号:基波叠加上三次谐波信号时,幅值与方波信号接近,形状还有一定差异,但已基本可以看出叠加后逼近了方波信号。
方波基波加三次谐波信号加五次谐波信号:基波信号、三次谐波信号、五次谐波信号叠加以后,比基波信号、三次谐波信号叠加后的波形更加接近方波信号。
综上所述:方波分解出来的各次谐波以及DC信号,叠加起来以后会逼近方波信号,且叠加的信号越多,越是接近方波信号。
《信号与系统》课程实验报告

《信号与系统》课程实验报告《信号与系统》课程实验报告一图1-1 向量表示法仿真图形2.符号运算表示法若一个连续时间信号可用一个符号表达式来表示,则可用ezplot命令来画出该信号的时域波形。
上例可用下面的命令来实现(在命令窗口中输入,每行结束按回车键)。
t=-10:0.5:10;f=sym('sin((pi/4)*t)');ezplot(f,[-16,16]);仿真图形如下:图1-2 符号运算表示法仿真图形三、实验内容利用MATLAB实现信号的时域表示。
三、实验步骤该仿真提供了7种典型连续时间信号。
用鼠标点击图0-3目录界面中的“仿真一”按钮,进入图1-3。
图1-3 “信号的时域表示”仿真界面图1-3所示的是“信号的时域表示”仿真界面。
界面的主体分为两部分:1) 两个轴组成的坐标平面(横轴是时间,纵轴是信号值);2) 界面右侧的控制框。
控制框里主要有波形选择按钮和“返回目录”按钮,点击各波形选择按钮可选择波形,点击“返回目录”按钮可直接回到目录界面。
图1-4 峰值为8V,频率为0.5Hz,相位为180°的正弦信号图1-4所示的是正弦波的参数设置及显示界面。
在这个界面内提供了三个滑动条,改变滑块的位置,滑块上方实时显示滑块位置代表的数值,对应正弦波的三个参数:幅度、频率、相位;坐标平面内实时地显示随参数变化后的波形。
在七种信号中,除抽样函数信号外,对其它六种波形均提供了参数设置。
矩形波信号、指数函数信号、斜坡信号、阶跃信号、锯齿波信号和抽样函数信号的波形分别如图1-5~图1-10所示。
图1-5 峰值为8V,频率为1Hz,占空比为50%的矩形波信号图1-6 衰减指数为2的指数函数信号图1-7 斜率=1的斜坡信号图1-8 幅度为5V,滞后时间为5秒的阶跃信号图1-9 峰值为8V,频率为0.5Hz的锯齿波信号图1-10 抽样函数信号仿真途中,通过对滑动块的控制修改信号的幅度、频率、相位,观察波形的变化。
信号与系统实验实验报告

信号与系统实验实验报告一、实验目的本次信号与系统实验的主要目的是通过实际操作和观察,深入理解信号与系统的基本概念、原理和分析方法。
具体而言,包括以下几个方面:1、掌握常见信号的产生和表示方法,如正弦信号、方波信号、脉冲信号等。
2、熟悉线性时不变系统的特性,如叠加性、时不变性等,并通过实验进行验证。
3、学会使用基本的信号处理工具和仪器,如示波器、信号发生器等,进行信号的观测和分析。
4、理解卷积运算在信号处理中的作用,并通过实验计算和观察卷积结果。
二、实验设备1、信号发生器:用于产生各种类型的信号,如正弦波、方波、脉冲等。
2、示波器:用于观测输入和输出信号的波形、幅度、频率等参数。
3、计算机及相关软件:用于进行数据处理和分析。
三、实验原理1、信号的分类信号可以分为连续时间信号和离散时间信号。
连续时间信号在时间上是连续的,其数学表示通常为函数形式;离散时间信号在时间上是离散的,通常用序列来表示。
常见的信号类型包括正弦信号、方波信号、脉冲信号等。
2、线性时不变系统线性时不变系统具有叠加性和时不变性。
叠加性意味着多个输入信号的线性组合产生的输出等于各个输入单独作用产生的输出的线性组合;时不变性表示系统的特性不随时间变化,即输入信号的时移对应输出信号的相同时移。
3、卷积运算卷积是信号处理中一种重要的运算,用于描述线性时不变系统对输入信号的作用。
对于两个信号 f(t) 和 g(t),它们的卷积定义为:\(f g)(t) =\int_{\infty}^{\infty} f(\tau) g(t \tau) d\tau \在离散时间情况下,卷积运算为:\(f g)n =\sum_{m =\infty}^{\infty} fm gn m \四、实验内容及步骤实验一:常见信号的产生与观测1、连接信号发生器和示波器。
2、设置信号发生器分别产生正弦波、方波和脉冲信号,调整频率、幅度和占空比等参数。
3、在示波器上观察并记录不同信号的波形、频率和幅度。
信号与系统实验报告最新版

实验一信号与系统的时域分析一、实验目的1、熟悉和掌握常用的用于信号与系统时域仿真分析的MATLAB函数;2、掌握连续时间和离散时间信号的MATLAB产生,掌握用周期延拓的方法将一个非周期信号进行周期信号延拓形成一个周期信号的MATLAB编程;3、牢固掌握系统的单位冲激响应的概念,掌握LTI系统的卷积表达式及其物理意义,掌握卷积的计算方法、卷积的基本性质;4、掌握利用MATLAB计算卷积的编程方法,并利用所编写的MATLAB程序验证卷积的常用基本性质;掌握MATLAB描述LTI系统的常用方法及有关函数,并学会利用MATLAB求解LTI系统响应,绘制相应曲线。
基本要求:掌握用MATLAB描述连续时间信号和离散时间信号的方法,能够编写MATLAB程序,实现各种信号的时域变换和运算,并且以图形的方式再现各种信号的波形。
掌握线性时不变连续系统的时域数学模型用MATLAB描述的方法,掌握卷积运算、线性常系数微分方程的求解编程。
二、实验原理1. 信号的时域表示方法1.1将信号表示成独立时间变量的函数1.2用信号的波形图来描述信号1.3将信号用一个数据序列来表示2 用MATLAB仿真连续时间信号和离散时间信号2.1连续时间信号的仿真程序Program1_1是用MATLAB对一个正弦信号进行仿真的程序,请仔细阅读该程序,并在计算机上运行,观察所得图形。
% Program1_1% This program is used to generate a sinusoidal signal and draw its plotclear, % Clear all variablesclose all, % Close all figure windowsdt = 0.01; % Specify the step of time variablet = -2:dt:2; % Specify the interval of timex = sin(2*pi*t); % Generate the signalplot(t,x) % Open a figure window and draw the plotof x(t)title('Sinusoidal signal x(t)') xlabel('Time t (sec)')常用的图形控制函数在《信号与系统》课程中,单位阶跃信号u(t) 和单位冲激信号δ(t) 是二个非常有用的信号。
四川大学信号与系统实验报告

实验报告课程名称信号与系统实验名称信号与LTI系统的时频域分析实验时间2017 年 6 月15 日学院电子信息学院指导教师周新志学生姓名班级学号学院(系) 电子信息学院专业信息安全实验报告x3=x1+x2;subplot(2,2,3),stem(n,x3),grid on;title('余弦相加信号x3[n]')xlabel('Time index n');(2)a.clear;h1=[0.0031,0.0044,-0.0031,-0.0272,-0.0346,0.0374,0.1921,0.3279,0.3279,0.1921,0.0374,-0.0346,-0. 0272,-0.0031,0.0044,0.0031];k1=0:15;n=-4:4;ylabel('y3[k]');b.clear;h2=[-0.0238,0.0562,-0.0575,-0.1302,0.5252, -0.6842,-0.3129,5.6197,5.6197, -0.3129,-0.6842,0.5252,-0.1302,-0.0575,0.0562,-0.0238];k1=0:15;n=-4:4;x1=cos(0.25*pi*n);y1=conv(h2,x1);%计算序列f1与f2的卷积和fk0=k1(1)+n(1); %计算序列f非零样值的起点位置k3=length(x1)+length(h2)-2; %计算卷积和f的非零样值的宽度k=k0:k0+k3; %确定卷积和f非零样值的序号向量subplot(2,2,1);stem(k,y1);title('x1[n]与h2[n]的卷积和y1[n]');3.(a)fs=128;t=1/fs;L=256;n=0:1:L-1;x1=cos(0.25*pi*n); x2=cos(1.25*pi*n); x3=x2+x1;N = 2^nextpow2(L); X1=fft(x1,N)/N*2; X2=fft(x2,N)/N*2; X3=fft(x3,N)/N*2; f=fs/N*(0:1:N-1); figure;plot(f,abs(X3)); title('幅值频谱'); xlabel('频率(HZ)'); ylabel('幅值'); subplot(2,1,2); plot(f,angle(X3)); title('相位频谱'); xlabel('频率(HZ)'); ylabel('相位');(b)fs=128;t=1/fs;L1=256;n=0:1:L1-1;h1=[0.0031,0.0044,-0.0031,-0.0272,-0.0346,0.0374,0.1921,0.3279,0.3279,0.1921,0.0374,-0.0346,-0. 0272,-0.0031,0.0044,0.0031];x1=cos(0.25*pi*n);subplot(2,1,1); plot(f,abs(Y13)); title('幅值频谱'); xlabel('频率(HZ)'); ylabel('幅值'); subplot(2,1,2); plot(f,angle(Y13)); title('相位频谱'); xlabel('频率(HZ)'); ylabel('相位');实验报告4)从3)(b )(c )h1的频谱图可知在大约40-90的范围h1幅度几乎为零,左右两边迅速升起,最后在10和120处达到最大值后趋于平缓,h1的频谱图可知在大约60-70的范围h1幅度几乎为零,左右两边迅速升起,最后在35和100处达到最大值后趋于平缓,又由(a )中x1,x2,x3的频谱图可以看到x1,x3有两个冲击在15,110处,x2,x3有两个冲击在40-90范围内,输出信号的频谱图如(b )(c )发现其 幅值满足(e )(e )(e )j j j Y X H ωωω= 的模值相乘,如此比较它们的相位图,发现也存在这种关系,故可知验证输出信号的频谱与输入信号、h [n]的频谱关系(或卷积性质),即是否满足(e )(e )(e )j j j Y X H ωωω=5)输出信号及频谱不同的原因是:由4)我们知道它们满足(e )(e )(e )j j j Y X H ωωω=,故是因为在输入信号一定时,由系统冲击函数的不同造成的,它们趋于零的范围不同,达到的最大值不同,相位也不同,同理系统冲击函数一定时,由输入信号不同造成,所以输出信号及频谱不同。
信号与系统实验报告

一、实验目的1.熟悉常见信号的傅里叶变换,了解傅里叶变换的MATLAB 实现方法;2.理解调制定理,理解傅里叶变换的频移特性;3. 理解频分多路复用的原理;三、实验内容1.给定调制信号f (t) = Sa(pt) ,载波为cos(10πt),用matlab 画出调制信号和已调信号在时域和频域的图形,(提示:用直接调用专用函数法如例1,保存两张实验波形图。
采用同步解调方法解调,既用已调信号和相干载波相乘,实现解调,如图3.1.3。
再通过低通滤波器取出有用的低频分量,如图3.1.4所示。
程序:t=-10:0.01:10;f=sin(pi*t)./(pi*t);subplot(2,1,1);plot(t,f);grid;axis([-10 10 -0.5 1.5])title('f(t)=sin(πt)/πt');syms t w;f=sin(pi*t)./(pi*t);Fw=fourier(f,t,w);FFP=abs(Fw);subplot(2,1,2)ezplot(FFP,[-30*pi 30*pi]);grid;axis([-30*pi 30*pi 0 1.5]);figure(2);t=-10:0.1:10;y=(sin(pi*t)./(pi*t)).*cos(10*pi*t);subplot(2,1,1);plot(t,y);grid;axis([-10 10 -1 1]);title('y(t)=sin(πt)/(πt)*cos(10*π*t)');syms t wy=(sin(pi*t)./(pi*t)).*cos(10*pi*t);Fw=fourier(y,t,w);FFP=abs(Fw);subplot(2,1,2);ezplot(FFP,[-30*pi 30*pi]);grid;axis([-30*pi 30*pi 0 1])figure(3);t=-10:0.1:10;y1=(sin(pi*t)./(pi*t)).*cos(10*pi*t).*cos(10*pi*t); subplot(2,1,1);plot(t,y1);grid;axis([-10 10 -1 1]);title('y1(t)=sin(πt)/(πt)*cos(10*π*t)*cos(10*π*t)'); syms t wy1=(sin(pi*t)./(pi*t)).*cos(10*pi*t).*cos(10*pi*t); Fw=fourier(y1,t,w);FFP=abs(Fw);subplot(2,1,2);ezplot(FFP,[-30*pi 30*pi]);grid;axis([-30*pi 30*pi 0 1])figure(4);t=-10:0.01:10;f1=sin(pi*t)./(pi*t);subplot(2,1,1);plot(t,f1);grid;axis([-10 10 -1 1])title('f(t)=sin(πt)/πt');syms t w;f=sin(pi*t)./(pi*t);Fw=fourier(f,t,w);FFP=abs(Fw);subplot(2,1,2);ezplot(FFP,[-30*pi 30*pi]);grid;axis([-30*pi 30*pi 0 1.5])运行结果:2.给定调制信号 f 1 (t) = Sa 2 (pt) ,载波为cos(20πt),用matlab 画出调制信号和已调信号在时域和频域的图形,保存两张实验波形图。
《信号与系统》实验报告材料

信号与系统实验报告班级:姓名:信息与通信工程学院实验一 系统的卷积响应实验性质:提高性 实验级别:必做 开课单位:信息与通信工程学院 学 时:2一、实验目的:深刻理解卷积运算,利用离散卷积实现连续卷积运算;深刻理解信号与系统的关系,学习MATLAB 语言实现信号通过系统的仿真方法。
二、实验设备: 计算机,MATLAB 软件 三、实验原理: 1、 离散卷积和: 调用函数:conv ()∑∞-∞=-==i i k f i f f f conv S )()(1)2,1(为离散卷积和,其中,f1(k), f2 (k) 为离散序列,K=…-2, -1, 0 , 1, 2, …。
但是,conv 函数只给出纵轴的序列值的大小,而不能给出卷积的X 轴序号。
为得到该值,进行以下分析: 对任意输入:设)(1k f 非零区间n1~n2,长度L1=n2-n1+1;)(2k f 非零区间m1~m2,长度L2=m2-m1+1。
则:)(*)()(21k f k f k s =非零区间从n1+m1开始,长度为L=L1+L2-1,所以S (K )的非零区间为:n1+m1~ n1+m1+L-1。
2、 连续卷积和离散卷积的关系:计算机本身不能直接处理连续信号,只能由离散信号进行近似: 设一系统(LTI )输入为)(t P ∆,输出为)(t h ∆,如图所示。
)(t h)()(t h t P ∆∆→)()(lim )(lim )(0t h t h t P t =→=∆→∆∆→∆δ若输入为f(t):∆∆-∆=≈∑∞-∞=∆∆)()()()(k t P k f t f t f k得输出:∆∆-∆=∑∞-∞=∆∆)()()(k t hk f t y k当0→∆时:⎰∑∞∞-∞-∞=∆→∆∆→∆-=∆∆-∆==ττδτd t f k t P k f t f t f k )()()()(lim)(lim )(0⎰∑∞∞-∞-∞=∆→∆∆→∆-=∆∆-∆==τττd t h f k t hk f t y t y k )()()()(lim)(lim )(0所以:∆∆-∆=-==∑⎰→∆)()(lim)()()(*)()(212121k t f k fd t f f t f t f t s τττ如果只求离散点上的f 值)(n f ∆])[()()()()(2121∑∑∞-∞=∞-∞=∆-∆∆=∆∆-∆∆=∆k k k n f k f k n f k fn f所以,可以用离散卷积和CONV ()求连续卷积,只需∆足够小以及在卷积和的基础上乘以∆。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验报告
课程名称信号与系统
实验名称信号与LTI系统的时频域分析
实验时间2017 年 6 月15 日学院电子信息学院
指导教师周新志
学生姓名班级学号
学院(系) 电子信息学院专业信息安全
实验报告
和输出信号的频谱图;
c 、冲激响应h [n]= h 2 [n]时h [n 的频谱,三种输入信号下输出y[n]的频谱,并画出h [n]和输出信号的频谱图。
4)根据输入信号、h [n]和输出信号的频谱,验证输出信号的频谱与输入信号、h [n]的频谱关系(或卷积性质),即是否满足(e )(e )(e )j j j Y X H ωωω= 。
5)分析以上各种情况下,输出信号及频谱不同原因 (1) clear; n=-4:4;
x1=cos(0.25*pi*n);
subplot(2,2,1),stem(n,x1),grid on; title('余弦信号 x1[n]') xlabel('Time index n'); x2=cos(1.25*pi*n);
subplot(2,2,2),stem(n,x2),grid on; title('余弦信号 x2[n]') xlabel('Time index n'); x3=x1+x2;
subplot(2,2,3),stem(n,x3),grid on; title('余弦相加信号 x3[n]') xlabel('Time index n');
clear;
h1=[0.0031,0.0044,-0.0031,-0.0272,-0.0346,0.0374,0.1921,0.3279,0.3279,0.192 1,0.0374,-0.0346,-0.0272,-0.0031,0.0044,0.0031];
k1=0:15;
n=-4:4;
x1=cos(0.25*pi*n);
y1=conv(h1,x1);%计算序列f1与f2的卷积和f
k0=k1(1)+n(1);%计算序列f非零样值的起点位置
k3=length(x1)+length(h1)-2;%计算卷积和f的非零样值的宽度
k=k0:k0+k3;%确定卷积和f非零样值的序号向量
subplot(2,2,1);
stem(k,y1);
title('x1[n]与h1[n]的卷积和y1[n]');
xlabel('k');
ylabel('y1[k]');
x2=cos(1.25*pi*n);
y2=conv(h1,x2);
subplot(2,2,2);
stem(k,y2);
title('x2[n]与h1[n]的卷积和y2[n]');
xlabel('k');
ylabel('y2[k]');
x3=x1+x2;
y3=conv(h1,x3);
subplot(2,2,3);
stem(k,y3);
title('x3[n]与h1[n]的卷积和y3[n]');
xlabel('k');
ylabel('y3[k]');
b.
h2=[-0.0238,0.0562,-0.0575,-0.1302,0.5252, -0.6842,-0.3129,5.6197,5.6197, -0.3129,-0.6842,0.5252,-0.1302,-0.0575,0.0562,-0.0238];
k1=0:15;
n=-4:4;
x1=cos(0.25*pi*n);
y1=conv(h2,x1);%计算序列f1与f2的卷积和f
k0=k1(1)+n(1); %计算序列f非零样值的起点位置
k3=length(x1)+length(h2)-2; %计算卷积和f的非零样值的宽度
k=k0:k0+k3; %确定卷积和f非零样值的序号向量
subplot(2,2,1);
stem(k,y1);
title('x1[n]与h2[n]的卷积和y1[n]');
xlabel('k');
ylabel('y1[k]');
x2=cos(1.25*pi*n);
y2=conv(h2,x2);
subplot(2,2,2);
stem(k,y2);
title('x2[n]与h2[n]的卷积和y2[n]');
xlabel('k');
ylabel('y2[k]');
x3=x1+x2;
y3=conv(h2,x3);
subplot(2,2,3);
stem(k,y3);
title('x3[n]与h2[n]的卷积和y3[n]');
xlabel('k');
ylabel('y3[k]');
xlabel('频率(HZ)'); ylabel('相位');
title('幅值频谱'); xlabel('频率(HZ)'); ylabel('幅值'); subplot(2,1,2);
plot(f,angle(Y12)); title('相位频谱'); xlabel('频率(HZ)'); ylabel('相位'); figure;
subplot(2,1,1);
plot(f,abs(Y13)); title('幅值频谱'); xlabel('频率(HZ)'); ylabel('幅值'); subplot(2,1,2);
plot(f,angle(Y13)); title('相位频谱'); xlabel('频率(HZ)'); ylabel('相位');
subplot(2,1,2);
plot(f,angle(Y22)); title('相位频谱'); xlabel('频率(HZ)'); ylabel('相位'); figure;
subplot(2,1,1);
plot(f,abs(Y23)); title('幅值频谱'); xlabel('频率(HZ)'); ylabel('幅值'); subplot(2,1,2);
plot(f,angle(Y23)); title('相位频谱'); xlabel('频率(HZ)'); ylabel('相位');
4)从3)(b )(c )h1的频谱图可知在大约40-90的范围h1幅度几乎为零,左右两边迅速升起,最后在10和120处达到最大值后趋于平缓,h1的频谱图可知在大约60-70的范围h1幅度几乎为零,左右两边迅速升起,最后在35和100处达到最大值后趋于平缓,又由(a )中x1,x2,x3的频谱图可以看到x1,x3有两个冲击在15,110处,x2,x3有两个冲击在40-90范围内,输出信号的频谱图如(b )(c )发现其 幅值满足(e )(e )(e )j j j Y X H ωωω
= 的模值相乘,如此比较它们的相位图,发现也存在这种关系,故可知验证输出信号的频谱与输入信号、h [n]的频谱关系(或卷积性质),即是否满足(e )(e )(e )j j j Y X H ωωω=
5)输出信号及频谱不同的原因是:由4)我们知道它们满足(e )(e )(e )j j j Y X H ωωω=,故是因为在输入信号一定时,由系统冲击函数的不同造成的,它们趋于零的范围不同,达到的最大值不同,相位也不同,同理系统冲击函数一定时,由输入信号不同造成,所以输出信号及频谱不同。
