误差修正模型案例
计量经济学第五章协整与误差修正模型
根据需要对数据进行变换，如对数变换、差 分变换等，以满足模型对数据的要求。
模型参数估计方法选择
01
最小二乘法（OLS ）
适用于满足经典假设的线性回归 模型，通过最小化残差平方和来 估计模型参数。
02
广义最小二乘法（ GLS）
适用于存在异方差性的模型，通 过加权最小二乘法进行参数估计 ，以消除异方差性的影响。
误差修正模型定义
误差修正模型（Error Correction Model，简称ECM）是一种具有特定形式的计 量经济学模型，用于描述变量之间的长期均衡关系和短期动态调整过程。
该模型通过引入误差修正项，将变量的短期波动和长期均衡关系结合起来，从而 更准确地刻画经济现象。
误差修正项解释
误差修正项（Error Correction Term，简称ECT）是误差修正模型中的核 心部分，表示变量之间的长期均衡误差。
长期均衡
协整关系反映了时间序列之间的长期均衡，即使短期内有所偏离，长期内也会恢复到均 衡状态。
线性组合平稳
协整序列的线性组合可以消除非平稳性，得到平稳序列。
协整检验方法
EG两步法
首先通过OLS回归得到残差序列，然 后对残差序列进行单位根检验（如 ADF检验），判断其是否平稳。
Johansen检验
适用于多变量协整关系的检验，通过 构建似然比统计量来判断协整向量的 个数。
计量经济学第五章协 整与误差修正模型
汇报人：XX
目 录
• 协整理论概述 • 误差修正模型介绍 • 协整与误差修正模型关系 • 协整检验方法及应用举例 • 误差修正模型建立与评估 • 案例研究：金融市场波动性分析
01
协整理论概述
协整定义及性质
协整与误差修正模型的研究
协整与误差修正模型的研究第一部分协整理论概述 (2)第二部分误差修正模型介绍 (4)第三部分协整与误差修正关系 (7)第四部分模型构建与检验方法 (9)第五部分实证分析应用案例 (13)第六部分结果解释与经济含义 (16)第七部分模型局限性与改进方向 (18)第八部分研究展望与未来趋势 (22)第一部分协整理论概述协整理论概述在经济学和金融学中，我们常常遇到时间序列数据之间的长期均衡关系。
然而，在实际经济活动中，这种均衡关系并不总是能够得到严格的保持，而是存在着一定程度的波动和偏差。
为了解决这一问题，经济学家们提出了协整理论。
协整理论是指两个或多个非平稳的时间序列之间存在一种长期稳定的关系。
换言之，即使各时间序列本身是随机游走的过程，它们之间也可能存在一个稳定的线性组合，使得这个组合呈现出平稳性质。
协整理论的发展为研究经济变量之间的长期动态关系提供了一个强有力的工具。
协整理论的核心思想是由 Engle 和Granger 于1987 年提出的。
他们认为，如果两个非平稳的时间序列之间存在协整关系，则这两个时间序列可以通过一个线性组合达到长期均衡状态，且这个线性组合具有零均值、有限方差和恒定自相关等特性。
在这个意义上，我们可以将协整关系看作是一种长期均衡关系的表现形式。
为了检验两个时间序列之间是否存在协整关系，Engle 和 Granger 提出了一种两步法：首先检验每个时间序列是否为非平稳过程；然后，如果这两个时间序列都是非平稳过程，再通过回归分析来检验它们之间是否存在协整关系。
这种方法被称为 Engle-Granger 两步协整检验。
除了 Engle-Granger 两步协整检验之外，还有许多其他的方法可以用来检验协整关系，例如 Johansen 检验和 Pedroni 检验等。
这些方法都可以有效地帮助我们确定不同时间序列之间的协整关系。
协整理论不仅用于检验不同时间序列之间的长期均衡关系，还可以用于构建误差修正模型。
误差修正模型ECM
Error Correction Model 用EVIEWS怎么做一、利用EG两步法做协整检验。
在两个变量情况下（设为Y、X），包括两序列单整检验、两变量最小二乘法回归并得到残差序列并命名为e、对e作单位根检验。
二、在证明Y、X两序列间存在协整后，才可以建立ECM。
其中，误差修正项ecm的值就是之前的回归模型的残差序列e。
三、直接输入以下命令：ls y c y(-1) x x(-1)得到的估计结果在实际预测时比较方便，不过需要计算得到ecm项的系数。
四、也可以直接输入以下命令：ls y c x e(-1)其中，e(-1)项的系数就是ecm项的系数。
这个模型的优点是直观，但是不便于预测。
五、两种估计是等价的。
六、建议参考阅读易丹辉：《数据分析与EViews应用》，中国统计出版社2002年版。
（也许有新版也不一定）对于误差修正模型，需要先建立一个模型，然后进行回归分析，分析它的短期均衡关系。
操作：举个例子说，比如试图建立y对y(-1)和x的误差修正模型。
STEP1 建立长期关系ls y c y(-1) xSTEP2 对残差进行单位根检验来检验协整关系ecm=residuroot(10,h) ecmSTEP3 建立误差修正模型ls d(y) c d(y(-1)) d(x) ecm(-1)教程：案例1上面的分析可以证明序列lconsume、lincome及lconsme(-1)之间存在协整关系，故可以建立ecm（误差修正模型）。
先分别对序列lconsume、lincome及lconsme(-1)进行一阶差分,然后对误差修正模型进行估计。
在主窗口命令行中输入：ls d(lconsume) c d(lincome) d(lconsume(-1)) ecm(-1)此时的常数项系数不明显，我们去掉常数项后再进行回归，结果如下图8.6所示图8.6从上式可以看出上式中的T检验值均显著，误差修正项的系数为-0.252,这说明长期均衡对短期波动的影响不大。
向量误差修正模型
1）两个变量的VAR（1）模型的VECM
y1t y2t
0.4 0.2
1.5 1.5
y1,t 1 y2,t 1
1t 2t
在这个例子中，
0.6 1.5 0.2 0.5 使y1t的系数为1。这样，就可以定义 Zt y1t 2.5 y2t 为平稳的协整变量。
以写成：
y1t
Zt Byt 1
b2
b3
Hale Waihona Puke y2t y1t
b2
y2t
b3
y3t
y3t
（10.51）
根据定义，Z t 就是一个一维的随机
变量，协整向量 B 1 b2 b3(标准化了
的形式)。
调整系数矩阵A就是一个 31的向 量，从而对应的VECM形式可以写成：
增加或者减小的变化，实际上是一种
调整，所以称为误差修正。因为这里
我们研究的对象是VAR模型，所以VECM
的名字由此而来。
根据定义，矩阵A衡量了 Yt中每个 变量是如何调整，从而回复到长期的
均衡关系的水平上。所以，矩阵A经常
被称为调整系数。另外，在实践中，
经常对协整向量B进行标准化。
10.4.2 VECM模型的演示
从长期来看，即所谓的均衡状态或 者静止状态，这样的关系精确地存在， 所以在长期，我们有：
Zt BYt 0
然而，从短期来看，例如对于每个 确定的时刻t，都存在偏离协整关系 BYt 的成分。这种偏离代表了这些长期关系 在短期内的一定程度的非均衡状态，所 以偏离成分一般被称为误差。
因此，AZt1 ABYt1 促使Yt 增加或者 减少，从而使得 BYt朝着它的长期均值 移动(长期均值为0，为什么?)。这种
实验报告二——误差修正模型的建立与分析
实验报告（二）——误差修正模型(ECM)的建立与分析一、单位根检验：1、绘制cons与GDP的时间序列图：从时间序列图中可以看出，cons与GDP随时间增加都呈上升趋势，表现出非平稳性。
2、对cons进行单位根检验：先选择对原序列（level）进行单位根检验，根据cons与GDP的时间序列图的走势，选择trend and intercept的检验方法，在maximum lags中填写ADF 检验方法的滞后期为0，从上表中可以看出，P值为0.9888，大于0.05的显著性水平，说明原序列是非平稳的。
选择cons的一阶差分（1st）和trend and intercept,从上表中可以看出，经过一阶差分后，P值（=0.5099）仍然没有通过0.05的置信水平检验，说明是不平稳的，需要继续改进。
再试用ADF检验，在滞后期（maximum lags）中填入8，选择一阶差分和trend and intercept，得出上表，可以看出P值=0.0801，大于0.05，没有通过0.05的置信水平检验，说明是不平稳的，需要继续改进。
再试用ADF检验，在滞后期（maximum lags）中填入6，选择二阶差分和trend and intercept，得出上表，可以看出P值=0.0137，小于0.05，通过0.05的置信水平检验，说明是平稳的。
3、对GDP进行单位根检验：先选择对原序列（level）进行单位根检验，根据cons与GDP的时间序列图的走势，选择trend and intercept的检验方法，在maximum lags中填写ADF 检验方法的滞后期为0，从上表中可以看出，P值为1.0000，大于0.05的显著性水平，说明原序列是非平稳的。
选择GDP的一阶差分（1st）和trend and intercept,从上表中可以看出，经过一阶差分后，P值（=0.5574）仍然没有通过0.05的置信水平检验，说明是不平稳的，需要继续改进。
第六章 动态回归与误差修正模型
第6章 动态回归与误差修正模型本章假定时间序列是平稳的。
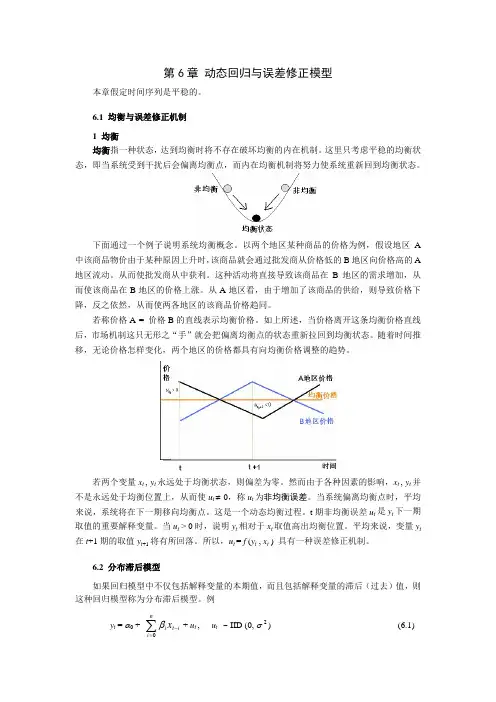
6.1 均衡与误差修正机制1 均衡均衡指一种状态，达到均衡时将不存在破坏均衡的内在机制。
这里只考虑平稳的均衡状态，即当系统受到干扰后会偏离均衡点，而内在均衡机制将努力使系统重新回到均衡状态。
下面通过一个例子说明系统均衡概念。
以两个地区某种商品的价格为例，假设地区A 中该商品物价由于某种原因上升时，该商品就会通过批发商从价格低的B地区向价格高的A 地区流动。
从而使批发商从中获利。
这种活动将直接导致该商品在B地区的需求增加，从而使该商品在B地区的价格上涨。
从A地区看，由于增加了该商品的供给，则导致价格下降，反之依然，从而使两各地区的该商品价格趋同。
若称价格A = 价格B的直线表示均衡价格。
如上所述，当价格离开这条均衡价格直线后，市场机制这只无形之“手”就会把偏离均衡点的状态重新拉回到均衡状态。
随着时间推移，无论价格怎样变化，两个地区的价格都具有向均衡价格调整的趋势。
若两个变量x t , y t永远处于均衡状态，则偏差为零。
然而由于各种因素的影响，x t , y t并不是永远处于均衡位置上，从而使u t≠ 0，称u t为非均衡误差。
当系统偏离均衡点时，平均来说，系统将在下一期移向均衡点。
这是一个动态均衡过程。
t期非均衡误差u t是y t下一期取值的重要解释变量。
当u t > 0时，说明y t相对于x t取值高出均衡位置。
平均来说，变量y t 在t+1期的取值y t+1将有所回落。
所以，u t= f (y t , x t) 具有一种误差修正机制。
6.2 分布滞后模型如果回归模型中不仅包括解释变量的本期值，而且包括解释变量的滞后（过去）值，则这种回归模型称为分布滞后模型。
例y t = α0 + ∑=−niitixβ+ u t,u t∼ IID (0, σ2 ) (6.1)上述模型的一个明显问题是x t 与x t -1 , x t -2, …, x t - n 高度相关，从而使 βj 的OLS 估计值存在严重偏倚。
误差修正模型课件
单方程误差修正模型是针对单个经济变量进行建模的方法，主要目的是检验和估计长期均衡关系及其短期调整机 制。
详细描述
单方程误差修正模型基于经济理论，通过一个经济变量对它的长期均衡关系及其短期调整机制进行建模。它通常 采用一阶差分法或协整法来处理非平稳时间序列数据，以识别和估计变量的长期均衡关系及其短期调整机制。
通常用长期均衡方程来描述。
在长期均衡方程中，变量的系数 映了其在长期均衡关系中的贡
献程度。
长期均衡关系通常是在市场机制 的作用下，通过供求关系自发调
节而形成的。
短期调整机制
短期调整机制是指当经济变量受到外 部冲击或其他因素的影响，导致其偏 离长期均衡状态时，系统会自动调整 以重新回到均衡状态的过程。
与
06
误差修正模型在经济学中的地位与作用
经济学的核心工具
误差修正模型（ECM）是现代经 济学中用于研究长期均衡关系和 短期调整机制的重要工具，尤其 在宏观和微观经济学中占据核心 地位。
揭示经济规律
通过ECM，研究者可以深入探究 经济变量之间的内在关系，揭示 其背后的经济规律和动态机制， 为政策制定提供科学依据。
外汇市场汇率调整的误差修正模型
总结词
该模型用于研究外汇市场汇率的调整机制， 通过分析汇率的短期波动和长期均衡趋势来 预测汇率变化。
详细描述
外汇市场汇率调整的误差修正模型关注汇率 的动态变化，并考虑国内外经济基本面的差 异对汇率的影响。它利用误差项来衡量短期 非均衡程度，并通过调整机制预测长期均衡 汇率的回归，有助于分析汇率的稳定性和波 动性。
短期调整机制通常是通过误差修正机 制来实现的，即系统会根据误差的大 小和方向，自动调整变量的取值，以 使其重新回到长期均衡状态。
误差修正模型
第二节 误差修正模型（Error Correction Model ，ECM ） 一、误差修正模型的构造 对于y t 的(1，1)阶自回归分布滞后模型：t t t t t y x x y εβββα++++=--12110在模型两端同时减y t-1，在模型右端10-±t x β，得：tt t t t t t t tt t t t x y x x y x y x x y εααγβεββββαββεββββα+--+∆=+---+--+∆=+-+++∆+=∆------)(])1()1()[1()1()(1101012120120121100其中，12-=βγ，)1/()(200ββαα-+=，)1/(211ββα-=。
记 11011-----=t t t x y ecm αα （5-5）则 t t t t ecm x y εγβ++∆=∆-10 （5-6） 称模型（5-6）为“误差修正模型”，简称ECM 。
二、误差修正模型的含义如果y t ~ I(1)，x t ~ I(1)，则模型（5-6）左端)0(~I y t ∆，右端)0(~I x t ∆，所以只有当y t 和x t 协整、即y t 和x t 之间存在长期均衡关系时，式（5-5）中的ecm~I(0)，模型（5-6）两端的平稳性才会相同。
当y t 和x t 协整时，设协整回归方程为：t t t x y εαα++=10它反映了y t 与x t 的长期均衡关系，所以称式（5-5）中的ecm t -1是前一期的“非均衡误差”，称误差修正模型（5-6）中的1-t ecm γ是误差修正项，12-=βγ是修正系数，由于通常1||2<β，这样0<γ；当ecm t -1 >0时（即出现正误差），误差修正项1-t ecm γ< 0，而ecm t -1 < 0时（即出现负误差），1-t ecm γ> 0，两者的方向恰好相反，所以，误差修正是一个反向调整过程（负反馈机制）。
单整,协整,误差修正模型
单整玉米价格指数x 淀粉价格指数y对玉米价格指数x做ADF检验Trend and intercept因为有趋势和截距的ADF的统计量的p值=0.7748>0.05,接受原假设，有单位根存在InterceptNone有截距和无截距，也无趋势的ADF统计量值的p值都大于0.05，接受原假设，存在单位根，原有时间序列非平稳。
一阶差分Trend and intercept一阶差分既有趋势又有截距的ADF统计量的p值<0.05，拒绝原假设，一阶差分是平稳的，即玉米价格指数x是一阶单整。
对淀粉价格指数y做ADF检验Trend and intercept因为有趋势和截距的ADF的统计量的p值=0.7817>0.05,接受原假设，有单位根存在interceptNone有截距和无截距，也无趋势的ADF统计量值的p值都大于0.05，接受原假设，存在单位根。
原有时间序列非平稳。
一阶差分Trend and intercept一阶差分既有趋势又有截距的ADF统计量的p值<0.05，拒绝原假设，一阶差分是平稳的，即淀粉价格指数y是一阶单整。
由于，玉米价格指数x，淀粉价格指数y都是一阶单整，所以可能存在协整关系协整检验首先将玉米价格指数x对淀粉价格指数y做回归从图中可知，玉米价格指数x对淀粉价格指数有显著的解释意义，两者之间是正相关关系。
玉米价格指数每增加一个单位，导致淀粉价格指数增加1.438个单位。
AEG检验对得到的残差进行单位根检验Trend and intercept残差的有趋势和截距的ADF的统计量为-2.568>-2.87,有单位根存在，非平稳。
intercept截距的ADF的统计量的p值为0.1362>0.05,接受原假设，有单位根存在，非平稳。
.None’无截距，无趋势的ADF的统计量的p值为0.015<0.05,拒绝原假设，序列平稳。
说明残差序列是I（0），平稳的。
第5章 动态回归与误差修正模型(案例)
例：（file: break2）东北、华北、华东、华中21省市1993和1998年耕地面积（land ,百万公顷）和农业产值（Y , 百亿元）数据见图（已取对数）。
用圆圈表示的观测点为1993年数据，用三角表示的观测点为1998年数据。
大体看各省市1998年耕地面积比1993年耕地面积略有减少，产值却都有增加。
以1993和1998年数据为两个子样本，以42个数据为总样本，求得残差平方和见下表-10123-2-1123LOG(LAND)LOG(Y 93)LOG(Y 98)-10123-2-1123LOG(LAND)LOG(Y 93)LOG(Y 98)样本容量 残差平方和相应自由度回归系数 1 T = 42 SSE T = 14.26 T - k = 402 n 1= 21 SSE 1 = 4.37 n 1 - k = 19 α1 3n 2= 21SSE 2 = 3.76n 2 - k = 19β1注：三次回归的模型形式Lnout t = β0 +β1 Lnland t + u t 。
因为，F =)2/()(/)]([2121k T SSE SSE k SSE SSE SSE T -++-=38/)76.337.4(2/)]76.337.4(26.14[++-= 14.33 > F (1, 40) = 7.31所以两个年度21省市的农业生产发生了很大变化。
案例1：开滦煤矿利润影响因素的实证分析（1903-1940，动态分布滞后模型，file:LH1）（发表在《学术论坛》，2003.1, p. 88-90）1000200030004000500060000510152025303540销煤量 x1图 1 开滦煤矿销煤量变化曲线（x 1, 1903-1940）2468101214160510152025303540吨煤售价 X2图2 开滦煤矿吨煤售价变化曲线（x 2, 1903-1940）100002000030000400000510152025303540利润 Y图3 开滦煤矿利润变化曲线（1903-1940）78910116.57.07.58.08.59.0LNX 1LNY图4 开滦煤矿利润对销煤量散点图78910111.01.52.02.53.0LN X 2LN Y图5 开滦煤矿利润对吨煤售价散点图1）建立ADL(2,2,2)Y t =0.2937Y t -1+0.2038 Y t -2+4.2469 X 1t –3.5106 X 1t -1（2.5） （2.4） （7.3） （-5.5）+2964.25 X 2t –1390.66 X 2t –1-1433.01 X 2t –2 (1) （7.3） （-1.7） （-2.3）R 2 = 0.96, s.e.=1504.7, LM (2) = 4.10, DW=2.16, F=128.7, Q (15) = 8.1 (1905-1940)用上式求长期关系，Y t = 1.4653 X 1t + 278.6X 2t (2)*()()j jjj s X s Y ββ=, j = 1, 2β1* = 1.4653 (1453.8 / 7134.1) = 0.2986 β2* = 278.6 (2.2067 / 7134.1) = 0.0862无量纲长期参数估计结果是Y = 0.2986 X 1 + 0.0862X 2 (3)这说明实际上X 1 对Y 的影响大于X 2对Y 的影响。
stata误差修正模型命令
stata误差修正模型命令摘要：1.Stata误差修正模型简介2.误差修正模型基本原理3.常用误差修正模型命令介绍4.实例演示5.总结与建议正文：随着计量经济学的发展，误差修正模型（Error Correction Model，简称ECM）在实证研究中得到了广泛应用。
Stata作为强大的统计分析软件，为用户提供了丰富的误差修正模型命令。
本文将介绍Stata中的误差修正模型命令，帮助读者更好地运用这些工具进行实证研究。
1.Stata误差修正模型简介误差修正模型是一种具有时间序列特征的回归模型，它将变量的当前值与过去值相结合，以预测未来趋势。
误差修正模型主要分为两类：一类是单方程误差修正模型，另一类是多元误差修正模型。
在Stata中，我们可以使用以下命令构建误差修正模型。
2.误差修正模型基本原理误差修正模型的基本原理是，将变量的当前值与过去值进行回归，得到一个方程。
然后，将这个方程的残差（即预测值与实际值之差）作为解释变量，再次进行回归，得到另一个方程。
这两个方程组成一个误差修正模型。
在Stata中，我们可以使用以下命令构建误差修正模型。
3.常用误差修正模型命令介绍（1）命令：xtserialxtserial命令用于构建单方程误差修正模型。
例如，以下命令构建了一个关于变量y的误差修正模型：```xtserial y x1 x2, ecm(1)```（2）命令：xtareasxtareas命令用于构建多元误差修正模型。
例如，以下命令构建了一个关于变量y、x1和x2的误差修正模型：```xtareas y x1 x2, ecm(1)```4.实例演示以下是一个关于我国居民消费的实例，我们使用xtserial命令构建误差修正模型：```* 导入数据use "居民消费.dta", clear* 构建误差修正模型xtserial consumption expenditure, ecm(1)```5.总结与建议本文对Stata中的误差修正模型命令进行了简要介绍。
ECM误差修正模型
协整与误差修正模型在处理时间序列数据时，我们还得考虑序列的平稳性。
如果一个时间序列的均值或自协方差函数随时间而改变，那么该序列就是非平稳的。
对于非平稳的数据，采用传统的估计方法，可能会导致错误的推断，即伪回归。
若非平稳序列经过一阶差分变为平稳序列，那么该序列就为一阶单整序列。
对一组非平稳但具有同阶的序列而言，若它们的线性组合为平稳序列，则称该组合序列具有协整关系。
对具有协整关系的序列，我们算出误差修正项，并将误差修正项的滞后一期看做一个解释变量，连同其他反映短期波动关系的变量一起。
建立误差修正模型。
建立误差修正模型的步骤如下：首先，对单个序列进行单根检验，进行单根检验有两种：ADF （Augument Dickey-Fuller ）和DF(Dickey-Fuller)检验法。
若序列都是同阶单整，我们就可以对其进行协整分析。
在此我们只介绍单个方程的检验方法。
对于多向量的检验参见Johensen 协整检验。
我们可以先求出误差项，再建立误差修正模型，也可以先求出向量误差修正模型，然后算出误差修正项。
补充一点的是，误差修正模型反映的是变量短期的相互关系，而误差修正项反映出变量长期的关系。
下面我们给出案例分析。
案例分析在此，我们考虑从1978年到2002年城镇居民的人均可支配收入income 与人均消费水平consume 的关系，数据来自于《中国统计年鉴》，如表8.1所示。
根据相对收入假设理论，在一定时期，人们的当期的消费水平不仅与当期的可支配收入、而且受前期的消费水平的影响，具有一定的消费惯性，这就是消费的棘轮效应。
从这个理论出发，我们可以建立如下（8.1）式的模型。
同时根据生命周期假设理论，消费者的消费不仅与当期收入有关，同时也受过去各项的收入以及对将来预期收入的限制和影响。
从我们下面的数据分析中，我们可以把相对收入假设理论与生命周期假设理论联系起来，推出如下的结果：当期的消费水平不仅与当期的可支配收入有关，而且还与前期的可支配收入、前两期的消费水平有关。
固定资产投资与经济增长的误差修正模型分析——以重庆市为例
个 百分点，Ｄ Ｇ Ｐ平均增加约 ０ ７ 个 百分 点，从 回归系数来看 Ｇ Ｐ的长期均衡关系、 ．２ Ｄ 格兰杰 因果和误差修正分析 ， 证明了固定
从而增强数据的平稳性 ， 使结论更准确 真实 。同时为 了大家 直 检验值 在显著性 水平 下都是稳定的 ， 明和两个序 列都是一阶 说
观 了解 Ｆ Ｉ对 Ｇ Ｐ的作用 以及两者的相关性 ， Ａ Ｄ 我们在样本 区间 单整 的， 满足 协整 关系 的前提 。 对两者数据 做了散点图， 如图 １ 所示 。
Ｌ Ｆ Ｉ —＿ ４６ Ｎ Ａ ｌ ２ ０ ０ △Ｕ Ｄ ２ ７ １ Ｇ Ｐ ．． ０ ７ ７
△Ｕ删
＿．ｌ７ ４６ １７
（，，） ｃ０ ３
．． ６Байду номын сангаас＊ 平稳 ３８ ７ ０
、
重庆固定资产投资与经济增长的实证分析
注 ：１ 表示一阶差分 ， （） 检验形式中的 Ｃ ｔ ｋ分别表示 带有 ，，
图 １ ＧＰ Ｆ Ｉ Ｄ 和 Ａ 的对数化散点图
ｌ ％ Ｃ ｉ ｃ ｌ ｌ ｅ ． ．４ ７ ０ ｒ ｉａ ｕ ２ ６ １ ｔ Ｖａ
２ 企业 导报 ２ １ 年第 １ 期 ６ ０２ １
财经纵横
检验结果表 明拟合优 度为 ０ ９ ，可 见回归方 程拟合 度优‘ 间存在 明显 的动态均衡调节机制。 ．８
（） １
对方程 产生的残 差进行平稳性检验， 如下表 ２示。
Ｔｅ ｔ ｓ
．
２７ ８ ３ １ Ｃｒ ｉａ ｌ ｅ ．３ ８ ９ ％ ｉｃ ｌ ｕ ＊ ｔ ａ
． ．６ ７ ３７ ６
ａｉｉ ｔｔ ｓｃ ５ Ｃｒ ｃ ｌ ｌ ｅ ． ．０ ８ ％ ｉ ａ ｕ ３ ０ ３ ｉ ｔ Ｖａ
财经纵横
演示文稿第三讲误差修正模型
第26页，共88页。
第27页，共88页。
1.单位根检验的方法
单位根检验有众多的模型可供选择，常 用的ADF（Augmented Dickey Fuller）检 验和P-P（Phillips-Perron）检验
推荐使用：ADF检验
第69页，共88页。
结果输出
第70页，共88页。
第71页，共88页。
结论： 协整检验说明在95%的置信区间存在2个
协整方程 协整关系写成代数表达式： lnGDP=-73.75119lnGINI+e 协整方程表达式代表两变量之间长期稳
定的关系
第72页，共88页。
方法3：检验残差
协整存在的一个重要条件就是估计协整回归方 程的残值应是平稳的。
第4页，共88页。
建立误差修正模型的步骤
数据类型：时间序列 0.数据录入 1.统计性检验 2.检验数据的平稳性 3.协整检验 4.短期误差修正
第5页，共88页。
数据的描述性检验
1. 可以直观的看出数据的变化趋势 2.可以有效的避免异常值对回归系数的
影响，剔除异常值 3.提供数据的简单统计性描述
AIC最小原则是判定模型好坏标准之一， 犹如R2（R平方）一样。 AIC和SC(舒瓦茨 信息）常常一并作为判断模型拟合程度的 标准之一，特别是在滞后阶数的选择上。
比如，一个VAR（向量自回归模型），经 济理论往往无法确定滞后阶数，这时往往 采用AIC或者SC最小原则，即观察不同的 阶数的VAR模型，哪个模型的AIC或者SC 值最小就选用哪个模型进行分析。 AIC、 SC都会在模型参数中给出。
第30页，共88页。
SC信息准则
误差修正模型实例
一、误差修正模型的构造对于y t 的(1，1)阶自回归分布滞后模型：t t t t t y x x y εβββα++++=--12110在模型两端同时减y t-1，在模型右端10-±t x β，得：tt t t t t t t tt t t t x y x x y x y x x y εααγβεββββαββεββββα+--+∆=+---+--+∆=+-+++∆+=∆------)(])1()1()[1()1()(1101012120120121100其中，12-=βγ，)1/()(200ββαα-+=，)1/(211ββα-=。
记 11011-----=t t t x y ecm αα （5-5） 则 t t t t ecm x y εγβ++∆=∆-10 （5-6） 称模型（5-6）为“误差修正模型”，简称ECM 。
二、误差修正模型的含义如果y t ~ I(1)，x t ~ I(1)，则模型（5-6）左端)0(~I y t ∆，右端)0(~I x t ∆，所以只有当y t 和x t 协整、即y t 和x t 之间存在长期均衡关系时，式（5-5）中的ecm~I(0)，模型（5-6）两端的平稳性才会相同。
当y t 和x t 协整时，设协整回归方程为：t t t x y εαα++=10它反映了y t 与x t 的长期均衡关系，所以称式（5-5）中的ecm t -1是前一期的“非均衡误差”，称误差修正模型（5-6）中的1-t ecm γ是误差修正项，12-=βγ是修正系数，由于通常1||2<β，这样0<γ；当ecm t -1 >0时（即出现正误差），误差修正项1-t ecm γ< 0，而ecm t -1 < 0时（即出现负误差），1-t ecm γ> 0，两者的方向恰好相反，所以，误差修正是一个反向调整过程（负反馈机制）。
误差修正模型有以下几个明确的含义：1．均衡的偏差调整机制2．协整与长期均衡的关系3．经济变量的长期与短期变化模型长期趋势模型：t t t x y εαα++=10 短期波动模型： t t t t ecm x y εγβ++∆=∆-10三、误差修正模型的估计建立ECM 的具体步骤为：1．检验被解释变量y 与解释变量x （可以是多个变量）之间的协整性；2．如果y 与x 存在协整关系，估计协整回归方程，计算残差序列e t ：t t t x y εβα++=0 tt t x y e 0ˆˆβα--= 3．将e t-1作为一个解释变量，估计误差修正模型： t t t t v e x y ++∆=∆-10γβ说明：（1）第1步协整检验中，如果残差是确定趋势过程，可以在第2步的协整回归方程中加入趋势变量；（2）第2步可以估计动态自回归分布滞后模型：t i t i i t i t y x y εβαα∑∑+++=--此时，长期参数为：∑∑-=)1(i i βαθ协整回归方程和残差也相应取成：t t x y θ=， tt t x y e θˆ-= （3）第2步估计出ECM 之后，可以检验模型的残差是否存在长期趋势和自相关性。
第四章误差修正原理与方法
第四章误差修正原理与方法本章主要内容⏹静态误差建模方法⏹动态误差建模方法⏹误差补偿⏹三坐标测量机的误差修正；⏹部分误差修正实例4.1 静态误差建模最小二乘法分段直线拟合三次样条拟合圆弧样条拟合需要注意的是：该模型中的数据是误差样本，并不是含误差的样本数据，即已经分离出来的误差数据。
对实际使用过程中，对光栅整个测量范围的误差分离，首先要用数学模型来表示，然后才能编制误差修正软件。
如果没有误差模型，就没有办法通过计算机实现自动修正；静态误差模型主要修正的是系统误差，采用事先分离，就是把这些离散的误差点使用一个数学模型来表示。
如何建立数学模型呢?可以使用线性回归、非线性回归；4.1.1最小二乘法特点：适合简单规律误差曲线拟合，拟合曲线不完全通过标准误差点(?)示例：一元线性回归；适合已知的数学模型；最小二乘方法适用于线性模型和非线性模型，但拟合出来的曲线不经过所有点，只是曲线与点之间的距离平方和最小。
误差信息没有充分的利用。
对准时，使用的是最小二乘方法进行拟合的，是否存在更有效的误差分离方法，更有利于对准精度的提高呢？4.1.2分段直线拟合特点：一元一次函数拟合曲线通过标准误差点，但拟合曲线不光滑。
保证曲线经过所有的标准误差点。
拟合的精度不高？如果分端间比较小的话，精度相对较低；4.1.3三次样条拟合特点：一元三次函数。
通过标准误差点，拟合曲线光滑、精度高；插值计算较繁，不具有几何不变性；对于构建误差较小的几何图形有利，但每个样点都包括了随机误差，而我们如果希望通过多个样本点相互抵消随机误差时，三次样条函数拟合是高误差的拟合方法。
例如在做使用相机进行采样，求解Krisch方法的自动聚焦模型时，明显的结果是三次样条插值的求解结果远不如最小二乘的结果。
所以在选取拟合方法时，需要考虑适应性。
样条中如果某个点的位置变化时，三次样条的曲线将发生较大的变化。
不仅影响点两侧的曲线，还间接影响到次邻近曲线段。
三次样条：在photoshop中有使用，在机械件加工时使用；4.1.4圆弧样条拟合特点：（二次函数）拟合曲线通过标准误差点，拟合曲线较光滑，分段函数为圆弧，采用局部坐标系，具有几何不变性，建模工作量大。
二阶误差修正模型的推导
二阶误差修正模型的推导误差修正模型（Error Correction Model, ECM）协整（cointegration）反映的是序列中变量之间的长期均衡关系，用网上的一个例子来描述协整就是一个醉汉牵着一只狗，他们之间的距离虽然会时远时近，但是由于绳子的存在，当达到绳子的长度时，他们的距离又会拉近，这样他们之间就存在着协整关系。
通过协整建立的模型是静态模型，而误差修正模型的使用就是为了建立短期的动态模型来弥补长期静态模型的不足，通过误差修正模型，可以判断出变量在短期波动中偏离其长期均衡关系的程度。
假设序列 X t X_{t} Xt和 Y t Y_{t} Yt存在这种长期的均衡关系，也就是协整关系，表现形式就是： Y t = a 0 + a 1 X t + u t Y_{t} = a_{0} + a_{1}X_{t} + u_{t} Yt=a0+a1 Xt+ut由于他们之间存在着长期的均衡关系，那就是说当 Y t Y_{t} Yt出现偏离均衡点时，这种现象只是暂时的。
而这种均衡关系建立的前提就是随机项 u t u_{t} ut是平稳的，这也是检验两个序列之间协整关系的一种方法，就是通过检验随机项的平稳性来判断是否存在协整关系。
试想一下，如果随机项不是平稳的，也就是它具有上升或者下降的趋势，那么 Y t Y_{t} Yt的偏离就会被长期累积下来而不能被消除。
因此，随机项也称作长期均衡误差，或者非均衡误差项，它将在误差修正模型中作为自变量。
误差修正模型的建立通过上面的分析，我们知道，如果要建立一个误差修正模型，首先要做的就是对序列进行检验，找出它们之间的协整关系，然后根据这种关系建立误差修正项，再将误差修正项作为解释变量，与其他反映短期波动的解释变量一起，建立一个短期模型，也就是误差修正模型。
从上面的例子知道长期均衡 Y t = a 0 + a 1 X t + u tY_{t} = a_{0} + a_{1}X_{t} + u_{t} Yt=a0+a1Xt+ut，而误差修正模型的具体形式是：Δ Y t = b 0 + b 1 Δ X t + γ e c m t − 1 + u t \Delta Y_{t} = b_{0} +b_{1}\Delta X_{t} + \gamma ecm_{t-1} + u_{t} ΔYt=b0+b1ΔXt+γecm t−1+ut Δ X t \Delta X_{t} ΔXt 和Δ Y t \Delta Y_{t} ΔYt 分别是一阶差分后的结果，除此之外，其中γ < 0 \gamma < 0 γ<0， e c m t − 1ecm_{t-1} ecmt−1表示误差修正项，可以表示为 e c m t − 1 = Y t − 1 − a 0 − a 1 X t − 1 ecm_{t-1} =Y_{t-1} - a_{0} - a_{1}X_{t-1} ecmt−1=Yt−1−a0−a1Xt−1，这也是为什么上面提到的随机项将在误差修正模型中作为自变量的解释。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
模型二：LnYt=0.055959+0.863243 LnGDPt-0.734005LnGDPt-1+0.850682LnYt-1
说明人均消费与人均 GDP 存在长期均衡，虽然两个序列非平稳，但两者具有 协整关系，他们之间并不是伪回归，所以依旧可以进行误差修正模型的建立 （4）误差修正模型
构建如下 ECM 模型：用两种方法：
第一种：
构建如下 ECM 模型：
⊿LnY=β0LnGDP+β1ECMT-1 +εt
ECMT-1= LnYt-1-0.865996LnGDP t-1-0.055728 对 LnY 和 LnGDP 做差分 DLnY=⊿LnY= LnYt -LnYt-1 DLnGDP=⊿LnGDP= LnGDP t -LnGDP t-1 将 DlnY、 DLnGDP 和 ECMT-1 做回归，得到结果如下： ECMT-1 为 EVIEWS 计算的前期误差项
（2） 单位根检验 1.对人均消费（LNY）序列进行单位根（ADF）检验。提出假设 H0：γ=1 存在单 位根；H1 ：γ≠1 存在单位根。
①对对数序列的原水平进行 ADF 检验，（下面实验中滞后阶数均 1），选取模 型为带截距项的检验结果如下：
从检验结果看，在 1％、5％、10％三个显著性水平下，单位根检验的 Mackinnon 临界值分别为-3.653730、-2.957110、-2.617434，t 检验统计量值 -0.528634 大于相应临界值，则接受原假设说明序列存在单位根，序列非平稳。
LnY=0.913331LnGDP-0.073751+εt
在得到残差序列后，对残差序列进行 ADF 检验，同样提出假设 H0：γ=1 存 在单位根；H1 ：γ≠1 存在单位根。
根据结果显示，回归结果存在自相关，且为正相关 接着对模型进行广义差分修正。
求的相关系数:0.848359 Yt 0.8483Yt1 0 (1 0.8483) 1 ( X t 0.8483X t1 ) t
②选择模型为有截距项和时间趋势项的模型进行对对数序列的原水平进行 ADF 检验。
从检验结果看，在 1％、5％、10％三个显著性水平下，单位根检验的 Mackinnon 临界值分别为-4.273277、-3.557759、-3.212361，t 检验统计量值 -2.435240 大于相应临界值，则接受原假设说明序列存在单位根，序列非平稳。
由于人均消费和人均 GDP 的对数都为非平稳数列，但两者都是一阶单整序 列，且从时序图中来看，两者其有可能存在协整关系。倘若两者存在协整关系， 我们就可以做出一个平稳序列来描述原变量之间的均衡关系。
（3）协整检验 采用 EG 两步法检验进行协整检验
对 LnY 和 LnGDP,用最小二乘法做回归，得到回归方程的估计结果：
3、根据实验数据的关系，建立误差修正模型，估计并进行解释。 三、实验步骤
（1） 收集数据
数据均来自于国家统计局的《统计年鉴》，1978-2011 年全体居民人均消费 取的是绝对数（实验过程中设为变量 Y，而人均国内生产总值（GDP）则是名义 值。实验过程中为了减少误差，我们将两个变量取对数，即得到 LNY 和 LNGDP。
工作态度 30%，分 4 个等级： 1、很好，积极参与，答疑及出勤情况很好 16－20 2、良好，比较能积极参与，答疑情况良好但有少量缺勤记录，或答疑情况 一般但出勤情况良好 11－15 3、一般，积极性不是很高，基本没有答疑记录，出勤情况较差 6－10 4、欠佳，不认真投入，且缺勤很多，也没有任何答疑记录 0－5
第 一 种 方 法 ： ⊿ LnY=β0 ⊿ LnGDP+β1ECMT-1 +ε1 （ ECM 模 型 的 估 计 方 法 Engle-Granger 的两步法）
我们用 ECMT-1 来纠正短期失衡。 第二种方法：LnYt=β0+β1 LnGDPt+β2LnGDPt-1+β3LnYt-1+εt 进行 OLS 估计可得出结果。 根据上述两个模型可以看出，第一种模型，AIC 和 SC 检验的参数值更小， 且该方法使用相对广泛；第二种方法建立的模型拟合优度更好，并且第二个模型 更加便于预测。
进行回归，得到结果
进行 LM 检验
结果显示修正后的回归方程不存在自相关，
修正后模型： LnYˆt* 0.055728 0.865996LnGDP * +εt，对该模型进行协正
检验，结果如下。
在 1％的显著性水平下，单位根检验的 Mackinnon 临界值分别为-2.641672、 t 检验统计量值-3.604026 小于相应临界值，则拒绝原假设说明序列不存在单位 根，序列平稳。说明残差平稳，又因为 LnY 和 LnGDP 都是 1 阶单整序列，所以 二者具有协整关系。
④.根据前三个检验数据显示，AIC 参数值分别为-3.119969，-3.369226， -3.138693.所以参数显示含有截距项和时间趋势项的模型 AIC 参数值最小，模 型越好。
所以接着以含有截距项和时间趋势项模型，对对数序列进行一阶差分。 得到结果
在 10％的显著性水平下，单位根检验的 Mackinnon 临界值分别为-3.215267、 t 检验统计量值-3.253823 小于相应临界值，则拒绝原假设说明序列不存在单位 根，序列平稳。说明⊿LnGDP 序列在ɑ=0.1 下平稳，LnGDP 是一阶单整序列
而最后的检验结果也证明了，经过一阶差分后，含截距项和时间趋势项的模 型可以使得 LnY 和 LnGDP 两个序列在 10%置信水平下趋于平稳。
2 误差修正模型的建立
第一步：建立长期关系模型
用最小二乘法建立 y 关于 x 协整回归方程，并且检验其残差序列的平稳性。 若残差是平稳的，说明这些变量之间存在相互协整关系，因此长期关系模型的变 量选择是合理的，回归是有意义的。 第二步：建立短期动态关系，即建立误差修正模型
模型一：⊿LnY=0.8630⊿LnGDP-0.15015ECMT-1+0.047297
T
(14.19696) (-3.708852) (3.36166)
回归的 t 检验结果显示人均国民生产总值当期波动对人均消费支出的当期波 动有显著性影响，上期误差对当期波动的影响也同样显著；同时，从回归系数的 绝对值大小可以看出人均国民生产总值的当期波动对人均消费支出的当期波动 调整幅度很大，每相对增加 1%的人均国民生产总值便会相对增加 0.8630%元的人 均消费支出，上期误差对当期人均消费支出的当期的单位调整比例为-0.15015。
3.误差修正模型的经济意义；
短期均衡模型： LnYˆt* 0.055728 0.865996LnGDP *
t:
(2.47)
(53.20)
短期均衡模型显示，人均国民生产总值对人居消费影响显著。当人均国内生
产总值相对增加 1%会引起居民人均消费 0.865996%的相对增长
长期均衡模型:误差修正模型：
③选择模型为不带截距项和趋势项的模型进行对对数序列的原水平进行 ADF 检验。
从检验结果看，在 1％、5％、10％三个显著性水平下，单位根检验的 Mackinnon 临界值分别为-2.639210、-1.951687、-1.610579，t 检验统计量值 2.157310 大于相应临界值，则接受原假设说明序列存在单位根，序列非平稳。
④采用 AIC 指的是赤池信息准则，参数的数值越小，就代表你所做的模型越 好 . 根 据前三个 检 验数据显 示 ，AIC 参数 值分别为 -3.102971， -3.225597， -3.101471.所以参数显示含有截距项和时间趋势项的模型 AIC 参数值最小，模型 越好。
所以接着以含有截距项和时间趋势项模型，对对数序列进行一阶差分。 得到结果
四、实验结果
1.单位根检验的三个模型
p
不含截距项和时间趋势项：Yt Yt-1 iYt-i t i 1 p
含截距项: Yt Yt -1 iYt -i t i 1 p
含截距项和时间趋势项:Yt t Yt -1 iYt -i t i 1
大型作业报告
课程名称 课程代码 题目 专业 班级 成员
计量经济学 142102601
误差修正模型 经济学
2010271 陈晓燕
上海电力学院 经济与管理学院
计量经济学大型作业评分表
序号
学号
姓名
工作 态度
课程设计报 告的质量
质量 70%，分 4 个等级： 1、按要求格式书写，计算正确，方案合理，内容完整，绘图规范整洁，符 合任务书的要求 35－40 2、按要求格式书写，计算较正确，有少量错误，方案较合理，内容完整， 绘图较规范整洁，基本符合任务书的要求 26－34 3、基本按要求格式书写，计算较正确，有部分错误，方案较合理，内容基 本完整，绘图不规范整洁，基本符合任务书的要求 15－25 4、基本按要求格式书写，计算错误较多，方案不合理，内容不完整，绘图 不规范整洁，不符合任务书的要求 0－14
做时序图
从时序图可以看出，两个序列都不平稳，并且随时间增长，序列可能存在 时间趋势项。此外，两个序列都具有几乎相同的变化趋势，所以，两者可能存在 协整关系。
根据图中显示的信息存在截距项和趋势项，所以单位根检验模型选择含截 距项和时间趋势项。此外在实验过程中，AIC 以及 SC 准则的参数都显示检验模 型选择含截距项和时间趋势项的值最小，模型最好。
实验报告
一、实验目的与要求 1、掌握时间序列的 ADF 平稳性检验； 2、掌握双变量的 Engel-Granger 检验； 3、掌握双变量的误差修正模型； 4、熟练使用 Eviews 软件建立误差修正模型。 二、实验内容
依据 1978-2010 年我国人均消费和人均 GDP 的数据，完成以下内容。 1、对实验数据进行单位根检验； 2、利用 E-G 两步法对实验数据进行协整检验；