(完整版)基本平面图形——练习题
(完整版)六年级几何图形练习题
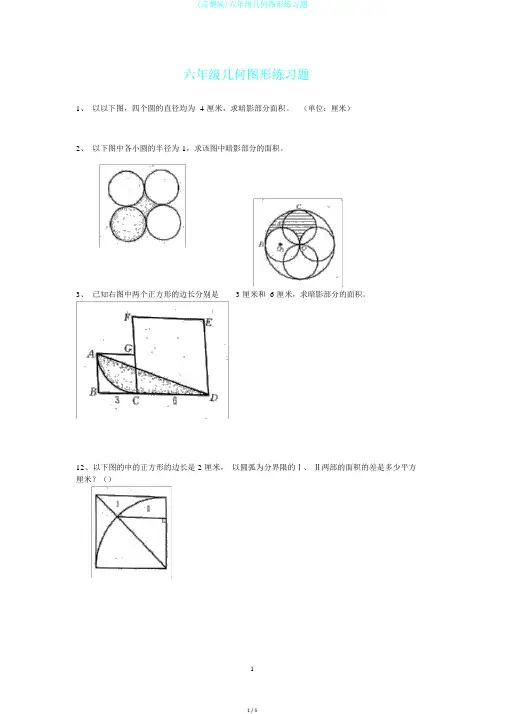
六年级几何图形练习题1、以以下图，四个圆的直径均为 4 厘米，求暗影部分面积。
（单位：厘米）2、以下图中各小圆的半径为1，求该图中暗影部分的面积。
3、已知右图中两个正方形的边长分别是 3 厘米和 6 厘米，求暗影部分的面积。
12、以下图的中的正方形的边长是 2 厘米，以圆弧为分界限的Ⅰ、Ⅱ两部的面积的差是多少平方厘米？（）4、以以下图，已知直角三角形的面积是12 平方厘米，求暗影部分的面积。
5、以以下图， O 为圆心 CO 垂直于 AB ，三角形ABC 的面积是 45 平方厘米，以 C 为圆心， CA为半径画弧将圆分红两部分，求暗影部分的面积。
6、以以下图扇形的半径OA=OB=6 厘米。
角AOB 等于 45°， AC垂直 OB于 C 点，那么图中暗影部分面积是多少平方厘米？（）7、求以下图形的暗影部分。
8、以下图中长方形的面积是18、把一块 1.35 公顷的长方形田地区分红两部分（以以下图），此中三角形田地比梯形田地少0.81 公顷，三角形的底是60 米。
这块长方形地的长和宽各是多少米？19、以以下图，半圆的直径是 10 厘米，暗影部分甲比乙的面积少 1.25 平方厘米，求三角形△ABC 的边 OA 的长。
20、以以下图，已知直角三角形ABC 中， AB 边上的高是 4.8 厘米，求暗影部分的面积。
21、以以下图，把一个圆剪成一个近似的长方形，已知长方形的周长是33.12 厘米，求暗影部分面积。
22、以以下图，求暗影部分面积。
（单位：厘米）23、以下图长方形 ABCD 中， AB=4 厘米， BC=8 厘米， M ，N 分别为两弧中点，求暗影部分的面积。
26、以下图正方形A BCD 的面积是30 厘米，求暗影部分的面积。
28、以以下图所示，两圆半径都是 1 厘米，且图中两个暗影部分部分的面积相等。
求长方形ABO 1 O 的面积。
29、求以下图的面积。
（单位：厘米）30、以下图，四边形 ABCD 是正方形，三角形 ABF 的面积比正方形 ABCD 的面积大 12 厘米，线段 BC 的长为 8 厘米。
小学数学青岛版(五四)一年级下册第三单元 牧童——认识图形认识平面图形-章节测试习题
章节测试题1.【答题】哪个物体能画出下面的图形？（）A. B. C.【答案】A【分析】此题考查的是认识平面图形.【解答】根据题意，要画正方形，利用选项A中的正方体任何一个面都可以画出正方形；选项B的各个面都是长方形，不能画出正方形；选项C的上下两个面都是圆，也不能画出正方形.选A.2.【答题】下面是长方形的是（）.A. B. C.【答案】C【分析】此题考查的是认识平面图形. 长方形的形状是长长方方的，有4条边，两长两短，且对边相等.【解答】根据题意可知，选项A是正方形，选项B是平行四边形，选项C是长方形.选C.3.【答题】下面物体不能画出三角形的是（）.A. B. C.【答案】A【分析】此题考查的是认识平面图形.【解答】根据题意，选项A是正方体只能画出正方形；选项B和C都能画出三角形，选A.4.【答题】选一选.长方形正方形三角形圆平行四边形【答案】长方形有⑻、⑼；正方形有⑷、⑸、⑺；三角形有⑵、⑾；圆有⑽；平行四边形有⑿.【分析】此题考查的是认识平面图形.【解答】根据题意，长方形有⑻、⑼；正方形有⑷、⑸、⑺；三角形有⑵、⑾；圆有⑽；平行四边形有⑿.5.【答题】至少____(3根 4根)同样长的小棒可以拼成一个正方形，4根同样长的小棒还能拼成____(长方形平行四边形).【答案】4根，平行四边形【分析】此题考查的是认识平面图形.【解答】因为正方形有4条相等的边，所以至少4根同样长的小棒可以拼成一个正方形；又因为平行四边形有4条边，且对边相等，所以4根同样长的小棒还能拼成平行四边形.6.【答题】至少______根同样长的小棒可以拼成三角形.【答案】3【分析】此题考查的是认识平面图形.【解答】因为三角形有3条边，所以至少3根同样长的小棒可以拼成三角形.7.【答题】选词填空.圆三角形长方形平行四边形红领巾是，数学书的封面是 .【答案】三角形，长方形【分析】此题考查的是认识平面图形.【解答】根据生活常识可知，红领巾是三角形，数学书的封面是长方形.8.【答题】七巧板里有______个正方形，______三角形，______个平行四边形.（填阿拉伯数字）【答案】1,5,1【分析】此题考查的是图形的认识.正方形的形状是四四方方的，有4条边，且都相等；三角形有3条边；平行四边形有4条边，且对边相等.【解答】由图可知，4是正方形，1、2、3、5、7是三角形，6是平行四边形，故七巧板里有1个正方形，有5个三角形，有1个平行四边形.9.【答题】想一想，填一填.图中有______个长方形，有______个正方形，有______个三角形，有______个圆.【答案】2,3,3,3【分析】此题考查的是图形的认识.长方形的形状是长长方方的，有4条边，两长两短，且对边相等；正方形的形状是四四方方的，有4条边，且都相等；三角形有3条边；圆由一条曲线围成.【解答】根据图形的特点可知，图中有2个长方形，有3个正方形，有3个三角形，有3个圆.10.【答题】想一想，填一填.图中有______个长方形，有______个三角形，有______个圆，有______个平行四边形.【答案】5,3,5,4【分析】此题考查的是图形的认识.长方形的形状是长长方方的，有4条边，两长两短，且对边相等；三角形有3条边；圆由一条曲线围成；平行四边形有4条边，且对边相等.【解答】根据图形的特点可知，图中有5个长方形，有3个三角形，有5个圆，有4个平行四边形.11.【答题】用下面的（）物体能够画出长方形.A. B. C.【答案】C【分析】此题考查的是图形的认识.【解答】根据生活规律可知，选项C可以画出长方形.选C.12.【答题】如图，是一个圆.（）【答案】×【分析】此题考查的是图形的认识.圆是由一条曲线围成的，是圆圆的.【解答】是椭圆，不是圆，所以此题是错误的.13.【答题】长方形、正方形、三角形、圆都是（）图形.A.平面B.立体【答案】A【分析】此题考查的是认识平面图形.【解答】长方形、正方形、三角形、圆都是平面图形.选A.14.【答题】这个墙面有一个破洞，需要用一些长方形的砖块补上，下面（）可以补好墙.A. B. C.【答案】C【分析】此题考查的是观察图形.【解答】由图可知，选项C正好可以补好空白的地方.选C.15.【综合题文】想一想，填一填.16.【答题】两个完全一样的长方形可以拼成一个（）.A. 圆B. 长方形或正方形C. 三角形【答案】B【分析】此题考查的是图形的拼组.【解答】两个完全一样的长方形可以拼成一个长方形或正方形.选B. 17.【答题】用2个相同的三角形不可能拼成的图形是（）.A. B. C.【答案】C【分析】此题考查的是图形的拼组.【解答】如图，选项A、B都可以用2个相同的三角形拼成，选项C不能用相同的三角形拼成，选C.18.【答题】是由4个（）拼成的一个（）.A. 正方形，正方形B. 三角形，正方形C. 三角形，长方形【答案】B【分析】此题考查的是用同样的图形进行简单的拼组.【解答】这个图形的总体是个正方形，是由4个小三角形拼成的，选B.19.【答题】这辆汽车中有2个三角形，有1个长方形.（）【答案】×【分析】此题考查的是图形的认识. 三角形有3条边；长方形的形状是长长方方的，有4条边，两长两短，且对边相等.【解答】由图可知，这辆汽车中，有2个三角形，有2个长方形.故此题是错误的.20.【答题】至少需要______个完全一样的正方形才能拼成一个大正方形.【答案】4【分析】此题考查的是图形的拼组.【解答】如下图所示，4个完全一样的正方形可以拼成一个大正方形.故此题的答案是4.。
(完整版)平面构成习题库及答案
平面构成习题库及答案1、什么是平面构成？平面构成的任务和研究对象是什么？2、平面构成的应用范围在哪些方面？学习平面构成有何意义？3、平面构成的造型要素有哪些？简述各自的特点。
4、什么是基本形？基本形产生的方法有哪些？5、什么是骨格？骨格有哪几种类型？6、平面构成的形式要素有哪些？7、什么是群化构成？群化构成的原则和要求是什么？8、群化构成有哪些方法？试举例说明群化构成在实际中的应用。
9、什么是重复构成？它有什么特点？重复构成有哪些类型？10、什么是近似构成？它有什么特点？近似构成有哪些类型？11、渐变构成的概念和特点是什么？渐变构成有哪些形式？12、发射构成的概念和特点是什么？发射构成的形式有哪些13、什么是对比构成？其构成形式有哪些？14、简述特异构成的概念。
特异构成的表现形式有哪几种？15、密集构成的概念、特点是什么？密集有哪些形式？16、什么是肌理？肌理可分为哪两类？常见的肌理的表现形式有哪些？习题答案１、平面构成：是将点、线、面等视觉语言元素（包含具象形态和抽象形态），在二维平面内按照一定的构成美学原理对它们进行合理的分解、组合、重构、变化，创造出新的形态，理想的组合方式，以及新的视觉形象，培养设计者的创新思维能力。
平面构成任务：平面构成是为平面设计进行创造形象的基本练习，它是设计家从事设计之前，首先要掌握和运用视觉语言的一种基本功，通过构成艺术的学习，可为我们提供更丰富的思维技巧，开阔视野，使头脑更加灵活多变，开发智能，发挥创造能力，从而为设计创造出更宽的新路。
2、研究对象：主要是在平面设计中，如何创造形象，怎样处理形象与形象之间的联系，如何掌握美的形式规律，并按照美的形式法则，构成设计所需要的图形。
应用领域：环境设计、视觉传达设计、平面设计等３、点、线、面是平面构成最基本的造型要素（形象单位）。
点是造型要素中最小、最简洁的形态，能创造出丰富的新形态，具有简洁、生动、有趣的特点。
点具有相对性特征。
小学数学青岛版(五四)一年级下册第三单元 牧童——认识图形认识平面图形-章节测试习题(2)
章节测试题1.【答题】下面的奖状是______形.【答案】长方【分析】此题考查的是认识长方形、正方形、三角形和圆.【解答】图中的奖状是长方形的.2.【答题】数一数.三角形有______个，长方形有______个，正方形有______个，圆有______个.【答案】1,3,1,4【分析】此题考查的是认识长方形、正方形、三角形和圆.【解答】三角形有1个，长方形有3个，正方形有1个，圆有4个.3.【答题】下面的墙壁缺少了______块砖.【答案】14【分析】此题考查的是图形的拼组.【解答】如下图，这面墙壁缺少了14块砖.4.【答题】选一选，填一填.长方形正方形圆三角形【答案】【分析】此题考查的是长方形、正方形、三角形和圆的认识.【解答】5.【答题】选词填空.（1）硬币是 (圆形圆柱)；（2）数学书封面是 (长方形长方体).【答案】圆柱，长方形【分析】此题考查的是平面图形和立体图形的认识.【解答】硬币是圆柱形，数学书的封面是长方形.6.【答题】三角形有______条边，长方形有______条边，正方形有______条边.【答案】3,4,4【分析】此题考查的是长方形、正方形、三角形的认识.【解答】三角形有3条边，长方形有4条边，正方形有4条边.7.【答题】拼一个三角形至少需要______根小棒，拼两个三角形至少需要______根小棒.【答案】3,5【分析】此题考查的是三角形的认识.【解答】如图，拼一个三角形至少需要3根小棒，拼两个三角形至少需要5根小棒.8.【答题】数一数，填一填.长方形有______个，正方形有______个，三角形有______个，圆有______个.【答案】4,2,7,5【分析】此题考查的是长方形、正方形、三角形和圆的认识.【解答】长方形有4个，正方形有2个，三角形有7个，圆有5个.9.【答题】摆一个长方形至少需要8根同样长的小棒.（）【答案】×【分析】此题考查的是长方形、正方形、三角形和圆的认识.【解答】如图，摆一个长方形至少需要6根同样长的小棒，故此题是错误的.10.【答题】用（）可以画出圆.A. B. C.【答案】B【分析】此题考查的是长方形、正方形、三角形和圆的认识.【解答】选项A是个球，不能画出圆；选项B是个圆柱形的茶叶罐，它上下两个底面是圆，可以画出圆；选项C是个正方体魔方，它6个面都是正方形的，不能画出圆，故选B.11.【答题】正方形不能用（）画出来.A.B.C.D.【答案】D【分析】此题考查的是长方形、正方形、三角形和圆的认识.【解答】选项A是个正方体，6个面都是正方形；选项B的底面是正方形；选项C 是特殊的长方体，它左右两个侧面是正方形；选项D的4个面都是三角形，故选D.12.【答题】右边（）能组成左边的图形.A.③和④B.②和④C.②和③D.②和⑤【答案】D【分析】此题考查的是长方形、正方形、三角形和圆的认识.【解答】仔细观察可知，②和⑤可以组成左边的图形，故选D.13.【答题】选一选，缺少的砖是（）.A. B.C. D.【答案】A【分析】此题考查的是长方形、正方形、三角形和圆的认识.【解答】通过观察可知，缺少的砖是，拼完后如下图，故选A.14.【答题】长方形的______边相等，正方形的______条边都相等.【答案】对,4【分析】此题考查的是长方形和正方形的认识.【解答】长方形的对边相等，正方形的4条边都相等.15.【答题】拼一个正方形至少需要______根小棒，拼两个正方形至少需要______根小棒.【答案】4,7【分析】此题考查的是正方形的认识.【解答】如图，拼一个正方形至少需要4根小棒，拼两个正方形至少需要7根小棒.16.【答题】______根同样长的小棒才可以摆成一个长方形.【答案】6【分析】此题考查的是长方形、正方形、三角形和圆的认识.【解答】如图，6根同样长的小棒才可以摆成一个长方形.17.【答题】数一数，填一填.【答案】6,8,7【分析】此题考查的是长方形、正方形、三角形和圆的认识.【解答】18.【答题】下图中一共有4个长方形.（）【答案】×【分析】此题考查的是长方形、正方形、三角形和圆的认识.【解答】如图，一共有5个长方形.19.【答题】右边（）能组成左边的图形.A.①和⑤B.②和③C.①和②D.①和④【答案】B【分析】此题考查的是图形的拼组.【解答】仔细观察可知，②和③可以组成左边的图形，故选B.20.【答题】选一选，缺少的砖是（）.A. B.C. D.【答案】B【分析】此题考查的是图形的拼组.【解答】通过观察可知，缺少的砖是，拼完后如下图，故选B.。
北师大版初一(上)数学配套习题第四章：基本平面图形
第四章：基本平面图形◆4.1 线段、射线、直线■课后作业 家长签字：1、数轴上表示整数的点称为整点，某数轴的单位长度是1厘米，若在这个数轴上随意画一条长15厘米的线段AB ，则AB 盖住的整数点的个数共有（ ）个A ．13或14个 B.14或15个 C.15或16个 D.16或17个2、如下图是某风景区的旅游路线示意图，其中,,B C D 为风景点，E 为两条路的交叉点，图中数据为相应两点的路程（单位：千米）．一学生从A 处出发，以2千米／时的速度步行观览景色，每个景点的逗留时间约为0.5小时．（1）当他沿着路线A B C E A ----游览回到A 处时，共用了3小时，求CE 的长；（2）若此学生打算从A 处出发，步行速度与在景点的逗留时间保持不变，且在最短时间内游览完三个景点返回A 处，请你为他设计一条步行路线，并说明这样设计的理由.（不考虑其他因素）3、如图，从A 到B 最短的路线是（ ）A. A —G —E —BB. A —C —E —BC. A —D —G —E —BD. A —F —E —B4、已知线段AB=10cm ，直线AB 上有点C ，且BC=4cm ，M 是线段AC 的中点，则AM = cm 。
5、平面内有三个点,过任意两点画一条直线,则可以画直线的条数是( )A.2条B.3条C.4条D.1条或3条6、在直线l 上顺次取A 、B 、C 三点，使得AB=5㎝，BC=3㎝，如果O 是线段AC 的中点，那么线段OB的长度是（ ）A 、0.5㎝ B 、1㎝ C 、1.5㎝ D 、2㎝7、点P 是直线l 外一点，,,A B C 为直线l 上三点，4,5,2PA cm PB cm PC cm ===,则点P 到直线l 的距离是（ ）A 、2cm B 、小于2cm C 、不大于2cm D 、4cm8、如图所示, 把一根绳子对折成线段AB , 从P 处把绳子剪断, 已知12AP PB =, 若剪断后的各段绳子中最长的一段为40cm, 则绳子的原长为（ ）A. 30 cmB. 60 cmC. 120 cmD. 60 cm 或120 cm9、下列说法不正确的是（ ）Ａ．若点C 在线段BA 的延长线上，则BA AC BC =-Ｂ．若点C 在线段AB 上，则AB AC BC =+Ｃ．若AC BC AB +>，则点C 一定在线段AB 外Ｄ．若,,A B C 三点不在一直线上，则AB AC BC <+二、填空题10、若线段AB=10㎝，在直线AB 上有一点C ，且BC=4㎝，M 是线段AC 的中点，则AM= ㎝．11、在边长都是1的正方形方格纸上画有如图所示的折线，它们的各段依次标着①，②，③，④，…的序号.那么序号为24的线段长度是 .12、在直线上取A 、B 、C 三点，使得AB = 9 厘米，BC = 4 厘米，如果O 是线段AC 的中点，则线段OA的长为 厘米.13、往返于甲、乙两地的火车中途要停靠三个站，则有 种不同的票价（来回票价一样），需准备 种车票．14、如图，从学校A 到书店B 最近的路线是①号路线，其道理用几何知识解释应是________________。
(精心整理)基本平面图形——练习题
CDB EAOCA DBC N M BA 21EOD CBA图（6）D 'B 'AOCGDB第五章基本平面图形一、1. 1.46°= ° ′ ″. 28°7′12″= °.2. 如图，已知OE 平分∠AOB ，OD 平分∠BOC ，∠AOB 为直角， ∠EOD=70°，则∠BOC 的度数为 .3. 如图,直线上四点A 、B 、C 、D,看图填空:①AC=______+BC;②CD=AD —_______;③AC+BD —BC=_______.4、如图，由泰山到青岛的某一次列车，运行途中停靠的车站依次是：泰山—济南—淄博—潍坊—青岛，那么要为这次列车制作的火车票有______．5.用一个钉子把一根细木条钉在墙上，木条就可能绕着钉子 ，原因是 ；当用两个钉子把木条钉在墙上时，木条就被固定住，其依据是 . 6.如图，AB 的长为m ，BC 的长为n ，M 、N 分别是AB 、BC 的中点，则MN=7、如图（6），把一张长方形的纸按图那样折叠后，B 、D 两点落在B ′、D ′点处， 若得∠AOB ′=700, 则∠B ′OG 的度数为 。
8、如上右图，是一副三角板重叠而成的图形，则∠AOD+∠BOC=_____________. 9.如图，直线AB 、CD 相交于O ，∠COE 是直角，∠1=57°，则∠2=10. 一个人从A 点出发向北偏东65°的方向走到B 点，再从B 点出发向南偏西15°方向走到C 点，那么∠ABC 的度数是 二、10、下列说法中，正确的是（ ）A ．直线a 、b 经过点M B. 直线A 、B 相交于点C C. 直线A 、B 相交于点m D. 直线AB,CD 相交于点m11. 一轮船航行到B 处测得的小岛A 的方向为北偏东30°，那么从A 处观测此时B 处的方向为（ ）A.北偏东30°B.北偏东60°C.南偏西30°D.南偏西60°12、在时刻8:32时，时钟上的时针与分针之间的所成的夹角是（）A.70°B.64°C.76°D.80°13.如图，圆的半径为4，阴影部分扇形的面积是（）A. πB. 2πC. 3πD. 4π14. 同一平面内有四点，每过两点画一条直线，则直线的条数是（）A．1条 B．4条 C．6条 D．1条或4条或6条15、已知A、B两点之间的距离是10 cm，C是线段AB上的任意一点，则AC中点与BC中点间的距离是（）A.3 cmB.4 cmC.5 cmD.不能计算16、平面上有四点，经过其中的两点画直线最多可画出( )．A．三条B．四条C．五条D．六条17、如图，O为直线AB上一点，∠COB＝26°30′，则∠1＝( )．A．153°30′B．163°30′C．173°30′D．183°30′18、如图6，∠AOB为平角，且∠AOC=21∠BOC ，则∠BOC的度数是（）19、如图7，军舰从港口沿OB方向航行，它的方向是（）A.东偏南30°B.南偏东60°C.南偏西30°D.北偏东30°20、下列说法中正确的是( )A、8时45分，时针与分针的夹角是30°B、6时30分，时针与分针重合C、3时30分，时针与分针的夹角是90°D、3时整，时针与分针的夹角是90°21、如果线段AB=5cm,线段BC=4cm,那么A,C两点之间的距离是（）A. 9cmB.1cmC.1cm或9cmD.以上答案都不对22、如图,下列表示角的方法,错误的是( )A.∠1与∠AOB表示同一个角;B.∠AOC也可用∠O来表示C.图中共有三个角:∠AOB、∠AOC、∠BOC;D.∠β表示的是∠BOC23、已知OA⊥OC，∠AOB：∠AOC=2：3，则∠BOC的度数为（）A.30B.150C.30或150D.以上都不对24、如图，四条表示方向的射线中，表示北偏东60°的是( )(1)ba(3)a(2)BBDCBA25.下列各角中，不能用一副三角板拼出的角度为（）A. 60°B.75°C. 135°D. 140°26.关于中点的说法正确的是（）A.若AB=BC,则点B是线段AC的中点B.若AB=21AC，则点B是线段AC的中点C. 若BC=21AC，则点B是线段AC的中点D. 若AB=BC =21AC，则点B是线段AC的中点27.在下列时刻，钟面上时针与分针成直角的情况（）A.12时15分B.9时C.3时30分D.6时45分28.直线l上顺次三点A、B、C，M是AB中点，N是AC若AB=12cm，BC=8cm,则MN=（）A.2 cmB.4 cmC.8 cmD.10 cm29.如图，下列说法错误的是（）A. A点在O点的北偏东60°方向B. B点在O点的西偏北30°方向C.C点在O点的正南方向D. D点在O点的东南方向30.下面四个选项中，能用∠1，∠AOB，∠O三种方法表示同一个角的是（）A B C D31. 一根绳子弯曲成如图（1）所示的形状，当剪刀像图（2）那样沿虚线a把绳子剪断时，绳子被剪为5段；当剪刀像图（3）那样沿虚线b(b∥a)把绳子再剪一次时，绳子被剪为9段.若剪刀在虚线a,b之间再剪（n-1）次（剪刀的方向与a平行），这样一共剪n次时（不含沿虚线a剪的一次）绳子的段数为（）A.4n+1B.4n+2C.4n+3D.4n+533、如图，在公路l的两旁有两个工厂A、B，要在公路上搭建一个货场让A、B两厂使用，要使货场到A、B两厂的距离之和最小，问货场应建在什么位置？为什么？34.你能在图中找出一点P，使点P到点A、B、C、D四个点的距离之和最小吗？东四、35如图，A 、B 、C 、D 在同一条直线上，已知AC=BD=18cm ，且AB:AD=2:11，求AB,BC 的长度。
(完整版)一年级数学下册图形练习题(2)
一、填一填。
1. 我来选一选①②③④⑤⑥⑦⑧⑨⑩⑾⑿是长方形，是正方形，是圆，是三角形，是平行四边形。
2. 我来涂一涂。
（给正方形涂上你喜欢的颜色）3.我来数一数。
长方形有( )个正方形有( )个三角形有( )个圆形有( )个二、连一连。
（用左边的哪个物体可以画出右边的图形，请你连一连。
）w W w .x K b 1.c o M三、圈一圈。
（请你找出用右侧哪一个物体可以画出左侧的图形，用笔圈出来。
）1.请你运用我们学过的平面图形画画一幅简单的图画。
2.请你运用我们学过的组成三角形，可以选择其中的一种或者几种图形组合，图形个数不限。
看看哪个小朋友画出的最多。
四、聪明屋。
X k B 1 . c o m1. 数一数下图有（）个三角形。
2. 还缺（）块砖。
1、缺了（）块2、缺了（）块3、缺了（）块4、缺了（）块1、用做成一个，数字“6”的对面是数字“（）”；数字“1”的对面是数字“（）”；数字“（）”的对面是数字“4”。
2、用做成一个，图形“△”的对面是图形“（）”；图形“○”的对面是图形“（）”；图形“（）”的对面是图形“●”。
3、用做成一个，数字“5”的对面是数字“（）”；数字“6”的对面是数字“（）”；数字“4”的对面是数字“（）”。
4、我会算：20―7―4＋3－8＋5＋2－5＋3―2―6＋13－9＋4＋4－6＋3＝64 3 2 15 ★☆△●▲○9 5 6 7 8 4一、画一画1、使正方形变成两个形状、大小一样的图形。
2、用四个三角形能拼出哪些你认识的图形?(挑战题)用画虚线的方法找出下面哪些图形是用四个相同的三角形拼成的?二、数一数，下面物体由多少个小正方体组成?三、试一试，用6个完全相同的小长方形拼成三种不同形状的大长方形。
．(挑战题)用四个完全相同的长方形可以拼成两个正方形吗?四、观察图形，填空。
1、沿虚线折一折，它变成( )体。
其中②号面与( )号面相对。
(拓展题)下面三个长方体中哪个是由下面图形折叠而成的?用线连一连。
(七年级)初一基本平面图形专项练习试题_附答案_北师大,人教版等通用版本
初一基本平面图形一、单选题1．如图，在直角坐标系xOy 中，点P 的坐标为（4，3），PQ ⊥x 轴于Q ，M ，N 分别为OQ ，OP 上的动点，则QN ＋MN 的最小值为（ ）A ．7225B ．245C ．125D ．9625 2．已知，点C 在直线 AB 上， AC =a ， BC =b ，且 a ≠b ，点 M 是线段 AB 的中点，则线段 MC 的长为（ ）A ．2a b +B ．2a b -C ．2a b +或2a b -D ．+2a b 或||2a b - 3．如图，C 、D 是线段AB 上两点，M 、N 分别是线段AD 、BC 的中点，下列结论：①若AD=BM ，则AB=3BD ；②若AC=BD ，则AM=BN ；③AC-BD=2（MC-DN ）；④2MN=AB-CD ．其中正确的结论是（ ）A ．①②③B ．③④C ．①②④D ．①②③④ 4．把 8.32°用度、分、秒表示正确的是（ ）A ．8°3′2″B ．8°30′20″C ．8°18′12″D ．8°19′12″ 5．经过平面上的四个点，可以画出来的直线条数为（ ）A ．1B ．4C ．6D ．前三项都有可能6．如图，点M 在线段AN 的延长线上，且线段MN=20，第一次操作：分别取线段AM 和AN 的中点11M N ，；第二次操作：分别取线段1AM 和1AN 的中点22,M N ；第三次操作：分别取线段2AM 和2AN 的中点33,M N ；……连续这样操作10次，则每次的两个中点所形成的所有线段之和11221010M N M N M N +++=L ( )A ．910202-B ．910202+C ．1010202-D ．1010202+ 7．已知线段AC 和BC 在同一直线上，AC ＝8cm ，BC ＝3cm ，则线段AC 的中点和BC 中点之间的距离是（ ）A ．5.5cmB ．2.5cmC ．4cmD ．5.5cm 或2.5cm8．如图，将一副三角板的直角顶点重合摆放在在桌面上，下列各组角一定能互补的是（ ）A ．∠BCD 和∠ACFB ．∠ACD 和∠ACFC ．∠ACB 和∠DCBD ．∠BCF 和∠ACF9．如图,在公路 MN 两侧分别有 A 1, A 2......A 7,七个工厂,各工厂与公路 MN(图中粗线)之间有小公路连接.现在需要在公路 MN 上设置一个车站,选择站址的标准是“使各工厂到车站的距离之和越小越好”.则下面结论中正确的是（ ）.①车站的位置设在 C 点好于 B 点;②车站的位置设在 B 点与 C 点之问公路上任何一点效果一样;③车站位置的设置与各段小公路的长度无关.A ．①B ．②C ．①③D ．②③ 10．如图，某公司有三个住宅区，A ，B ，C 各区分别住有职工10人，15人，45人，且这三个区在一条大道上(A ，B ，C 三点共线)，已知AB ＝150m ，BC ＝90m ．为了方便职工上下班，该公司的接送车打算在此间只设一个停靠点，为使所有的人步行到停靠点的路程之和最小，那么该停靠点的位置应设在( )A ．点AB ．点BC ．点A ，B 之间D ．点C 11．观察下列图形,并阅读图形下面的相关文字,如图所示:两条直线相交,三条直线相交,四条直线相交,最多有一个交点,最多有三个交点;最多有6个交点,像这样,10条直线相交,最多交点的个数是( )A．40个B．45个C．50个D．55个二、填空题12．已知点A，B，C都在直线l上，点P是线段AC的中点.设AB a=，PB b，则线段BC的长为________（用含a，b的代数式表示）13．已知点A，B，C在同一条直线上，若线段AB＝3，BC＝2，则AC＝_____．14．已知点A在数轴上对应的数为a，点B对应的数为b，且|a+2|+（b﹣1）2=0，A、B 之间的距离记作|AB|，定义：|AB|=|a﹣b|．①线段AB的长|AB|=3；②设点P在数轴上对应的数为x，当|PA|﹣|PB|=2时，x=0.5；③若点P在A的左侧，M、N分别是PA、PB的中点，当P在A的左侧移动时|PM|+|PN|的值不变；④在③的条件下，|PN|﹣|PM|的值不变．以上①②③④结论中正确的是_______（填上所有正确结论的序号）15．已知∠AOB＝90°，射线OC在∠AOB内部，且∠AOC＝20°，∠COD＝50°，射线OE、OF分别平分∠BOC、∠COD，则∠EOF的度数是_____．16．把一根绳子对折成一条线段AB，在线段AB取一点P，使AP＝13PB，从P处把绳子剪断，若剪断后的三段．．绳子中最长的一段为30cm，则绳子的原长为______cm．17．钟表4点30分时，时针与分针所成的角的度数是___________ 。
小升初——平面图形易错专项(试题)-六年级下册数学人教版
人教版数学六年级下册小升初——平面图形易错专项一、填空题（共15分，每题3分）1.将一张长方形纸按右图所示的方法折叠，∠1是（）°。
2.在周长为16 cm的正方形内作一个最大的圆，这个圆的周长是（）cm，面积是（）cm2。
3.一个梯形，上下底之和是12 cm，是高的3倍，它的面积是（）cm2。
4.一个圆柱的侧面展开是一个正方形。
如果圆柱的高增加2cm，侧面积就增加12.56cm2。
原来这个圆柱的表面积是（）平方厘米。
5.钟面上，3时整时，时针和分针成（）角；6时整时，时针和分针成（）角。
二、几何题（共35分，每题7分）1.为方便销售，售货员把啤酒瓶捆成如下图（从瓶底方向看）的形状，如果每组分别捆5圈绳子（接头处不计），每组至少需要多长的绳子？你发现了什么？2.如图，中间是边长为2cm的正方形，与这个正方形每一条边相连的都是圆心角为90的扇形，整个图形的面积是多少？3.下图中，AB＝20厘米，阴影甲的面积比乙的面积大57平方厘米，求BC长。
4.菲菲同学在学完了圆的知识后，想到了苏州的小桥流水，创作了下面一幅画。
这幅画由5个完全相同的半圆组合而成。
如果菲菲从桥上的A点走到B点，走过了多少路? 单位 (cm)5.请用直尺和圆规画一个与如图一模一样的图形。
（保留作图痕迹，不用涂改），并计算这个图形的周长。
三、解决问题（共50分，每题10分）1.一个圆形牛栏的半径是15 m，要用多长的粗铁丝才能把牛栏围上3圈？（接头处忽略不计。
）如果每隔2 m打一根木桩，大约要打多少根木桩？2.正方形ABCD的边AB、AD分别在三角形AFE的AF、AE边上，点C在EF边上，FC=10cm，CE=8cm，求两个阴影三角形的面积和。
3.一个正方形羊圈，边长是6m（如图）。
羊的主人准备了两根6m长的绳子，分别将两根绳子一端系在A或B处，一端系在羊身上。
（1）请在图中画出这两只可以吃到的草的公共区域，并用阴影表示出来。
(完整word版)基本平面图形练习题.docx
基本平面图形一．选择题1．手电筒射出去的光线,给我们的形象是()A. 直线B.射线C.线段D.折线2．下列各直线的表示法中，正确的是()A ．直线 A B．直线 AB C．直线 ab D．直线 Ab3．下列说法正确的是()A. 画射线 OA=3cm;B. 线段 AB 和线段 BA 不是同一条线段C.点 A 和直线 L 的位置关系有两种 ;D.三条直线相交有 3 个交点4．下列说法中正确的有（）①过两点有且只有一条直线；② 连接两点的线段叫两点的距离；③两点之间线段最短；④若 AC=BC ，则点 C 是线段 AB 的中点．A ． 1 个B． 2 个C． 3 个D． 4 个5．下列说法中，正确的是（）A ．两条射线组成的图形叫做角B．若 AB=BC ，则点B 是 AC 的中点C．两点之间直线最短 D ．两点确定一条直线6．下列现象中，可用基本事实“两点之间，线段最短”来解释的现象是（）A ．把弯曲的公路改直，就能缩短路程B．用两个钉子就可以把木条固定在墙上C．利用圆规可以比较两条线段的大小关系D．植树时，只要定出两棵树的位置，就能确定同一行树所在的直线7．已知点 A 、 B 、C 都是直线 l 上的点，且 AB=5cm ， BC=3cm ，那么点 A 与点 C 之间的距离是（）A ． 8cmB ．2cm C． 8cm 或 2cm D ．4cm8．如图， C 是 AB 的中点， D 是 BC 的中点．下列等式不正确的是（）A ． CD=AC ﹣ BDB ． CD=AD ﹣ BC C． CD=AB ﹣ BD D ．CD=AB ﹣ AD9．下列四种说法：①因为 AM=MB ，所以 M 是 AB 中点；②在线段 AM 的延长线上取一点 B ，如果 AB=2AM ，那么 M 是 AB 的中点；③因为 M 是 AB 的中点，所以AM=MB=AB ；④因为 A 、 M 、B 在同一条直线上，且 AM=BM ，所以 M 是 AB 中点．其中正确的是（）A ．①③④B．④C．②③④D．③④10．如图，从点 O 出发的五条射线，可以组成（）个角．A ． 4B ． 6C． 8 D ．1011．下列各式中，正确的角度互化是（）A ． 63.5 ° =63 ° 50′B ． 23° 12′ 36″ =25.48 ° C． 18° 18′ 18″ =3.33 ° D． 22.25 ° =22 ° 15′ 12、角是指 ( )A. 由两条线段组成的图形;B.由两条射线组成的图形C.由两条直线组成的图形;D.有公共端点的两条射线组成的图形C13、如图 ,下列表示角的方法,错误的是 ()B1AO(3)A. ∠ 1 与∠ AOB 表示同一个角 ;B. ∠ AOC 也可用∠ O 来表示C.图中共有三个角 :∠ AOB 、∠ AOC 、∠ BOC;D.∠ β表示的是∠ BOC14、由河源到广州的某一次列车，运行途中停靠的车站依次是：河源﹣惠州﹣东莞﹣广州，那么要为这次列车制作的 火车票有（ ）A ． 3 种B ． 4 种C ． 6 种D ． 12 种15、 下列说法中正确的个数有（ ）① 经过一点有且只有一条直线；② 连接两点的线段叫做两点之间的距离；③ 射线比直线短；④ ABC 三点在同一直线上且 AB=BC ，则 B 是线段 AC 的中点；⑤ 在同一平面内，两条直线的位置关系有两种：平行与相交；⑥ 在 8：30 时，时钟上时针和分针的夹角是 75°．A ． 1 个B ．2 个C ． 3 个D ．4 个16、根据直线、射线、线段各自的性质，下图中能相交的是（ ）A ．B ．C ．D ． 17、如图， A,B 在直线 l 上，下列说法错误的是 （）Ａ．线段 AB 和线段 BA 同一条线段 Ｂ．直线 AB 和直线 BA 同一条直线Ｃ．射线 AB 和射线 BA 同一条射线Ｄ．图中以点 A 为端点的射线有两条。
(完整版)第七章平面图形的认识(二)知识点归纳+典型例题,推荐文档
第七章 平面图形的认识（二）一、知识梳理1、在同一平面上，两条直线的位置关系有 或者 .练习：平面内三条直线的交点个数可能有 ( )A. 1个或3个B.2个或3个C.1个或2个或3个D.0个或1个或2个或3个2、判定与性质：什么叫做平行线？在同一平面内， 的两直线叫平行线。
的两直线平行。
判 定性 质（1） ，两直线平行。
（2） ，两直线平行。
（3） ，两直线平行。
（1）两直线平行， 。
（2）两直线平行， 。
（3）两直线平行，互补。
如果两条直线互相平行，那么其中一条直线上任意两点到另一条直线的距离相等,这个距离称为平行线之间的距离。
（等积变形）（2）如图，长方形ABCD 的面积为16，四边形BCFE 为梯形，BC 与DE 交于点G,则阴）如图，对面积为，使得记其面积为S 1；第二次操作，分别延长A 1B 1，B 1C 1，C 1A 1至点A 2，B 2，C 2，使得A 2B 1=2A 1B 1，B 2C 1=2B 1C 1，C 2A 1=2C 1A 1，顺次连接A 2，B 2，C 2，得到△A 2B 2C 2，记其面积为S 2；…；按此规律继续下去，可得到△A 5B 5C 5，则其面积S 5= ．（4）已知方格纸中的每个小方格是边长为1的正方形，A ，B 两点在小方格的顶点上，位置如图所示，在小方格的顶点上确定一点C ，连接AB ，AC ，BC ，使△ABC 的面积为3个平方单位．则这样的点C 共有 个．（1）如图，边长为3cm ，与5cm 的两个正方形并排放在一起，在大正方形中画一段以它的一个顶点为圆心，边长为半径的圆弧，则阴影部分的面积是______cm 2（π取3）．F3、图形的平移 在平面内，将一个图形沿着________________移动____________，这样的____________叫做图形的平移。
4、平移的性质(1)平移不改变图形的_______、________，只改变图形的_________。
2020—2021学年苏科版七年级数学下册第7章《平面图形的认识(二 )》解答题常考题(二)
苏科版七年级数学下册第7章《平面图形的认识（二 )》解答题常考题（二）1．一零件形状如图，按规定∠A应等于75°，∠B和∠C应分别是18°和22°，某质检员量得∠BDC＝114°，就断定这个零件不合格，请你运用三角形的有关知识说明零件不合格的理由．2．如图，△ABC中，∠B＝2∠C，AE平分∠BAC．（1）若AD⊥BC于D，∠C＝35°，求∠DAE的大小；（2）若EF⊥AE交AC于F，求证：∠C＝2∠FEC．3．完成下列推理结论及推理说明：如图，已知∠B+∠BCD＝180°，∠B＝∠D．求证：∠E＝∠DFE．证明：∵∠B+∠BCD＝180°（已知AB∥CD（）∠B＝（）又∵∠B＝∠D（已知）＝（等量代换）∴AD∥BE（）∠E＝∠DFE（）4．如图，AB∥CD，∠FGB＝154°，FG平分∠EFD，求∠AEF的度数．5．如图，已知在△ABC中，∠C＝90°，BE平分∠ABC，且BE∥AD，∠BAD＝20°，求∠AEB 的度数．6．如图，已知∠AGF＝∠ABC，∠1+∠2＝180°．（1）试判断BF与DE的位置关系，并说明理由；（2）若BF⊥AC，∠2＝140°，求∠AFG的度数．7．感知：如图①，∠ACD为△ABC的外角，易得∠ACD＝∠A+∠B（不需证明）；探究：如图②，在四边形ABDC中，试探究∠BDC与∠A、∠B．、∠C之间的关系，并说明理由；应用：如图③，把一块三角尺XYZ放置在△ABC上，使三角尺的两条直角边XY、XZ恰好经过点B、C，若∠A＝50°，则∠ABX+∠ACX＝度；拓展：如图④，BE平分∠ABD，CE平分∠ACD，若∠BAC＝100°，∠BDC＝150°，则∠BEC ＝度．8．如图，已知∠A＝90°+x°，∠B＝90°﹣x°，∠CED＝90°，4∠C﹣∠D＝30°，射线EF∥AC．（1）判断射线EF与BD的位置关系，并说明理由；（2）求∠C，∠D的度数．9．如图，AD为△ABC的高，BE为△ABC的角平分线，若∠EBA＝34°，∠AEB＝80°，求∠CAD的度数．10．将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起（其中，∠A＝60°，∠D＝30°；∠E＝∠B＝45°）．（1）如图1，①若∠DCE＝40°，求∠ACB的度数；②若∠ACB＝150°，直接写出∠DCE的度数是度．（2）由（1）猜想∠ACB与∠DCE满足的数量关系是．（3）若固定△ACD，将△BCE绕点C旋转，①当旋转至BE∥AC（如图2）时，直接写出∠ACE的度数是度．②继续旋转至BC∥DA（如图3）时，求∠ACE的度数．11．如图，已知AB∥CD，直线分别交AB、CD于点E，F，∠EFB＝∠B，FH⊥FB．（1）已知∠B＝20°，求∠DFH；（2）求证：FH平分∠GFD；（3）若∠CFE：∠B＝4：1，则∠GFH的度数．12．如图，AB∥CD，点E在线段AB上，连接EC、ED、AD，且AD⊥CE于F，ED平分∠CEB，若∠ADC＝40°，∠A﹣∠B＝10°，求∠BDE的度数．13．如图，∠ABC＝180°﹣∠A，EF∥BD，∠1+∠2＝96°，DO⊥AD交EF于点O．求∠BDO 的度数．14．如图，已知：AB∥CD，DB⊥BC，∠1＝40°，求∠2的度数．完成下面的证明过程：证明：∵AB∥CD（），∴∠1＝∠BCD＝40°（）．∵BD⊥BC，∴∠CBD＝．∵∠2+∠CBD+∠BCD＝（），∴∠2＝．15．已知：如图所示，AB∥CD，AE交CD于点C，DE⊥AE，垂足为E，∠A+∠1＝60°，求：∠D的度数．参考答案1．解：如图，延长BD与AC相交于点E，∵∠1是△ABE的外角，∠A＝75°，∠B＝18°，∴∠1＝∠B+∠A＝75°+18°＝93°，同理，∠BDC＝∠1+∠C＝93°+22°＝115°，∵李师傅量得∠BCD＝114°，不是115°，∴这个零件不合格．2．（1）解：∵∠C＝35°，∠B＝2∠C，∴∠B＝70°，∴∠BAC＝75°，∵AE平分∠BAC，∴∠EAC＝37.5°，∵AD⊥BC，∴∠ADC＝90°，∴∠DAC＝55°，∴∠DAE＝55°﹣37.5°＝17.5°；（2）证明：∵EF⊥AE，∴∠AEF＝90°，∴∠AED+∠FEC＝90°，∵∠DAE+∠AED＝90°，∴∠DAE＝∠FEC，∵AE平分∠BAC，∴∠EAC＝∠BAC＝（180°﹣∠B﹣∠C）＝（180°﹣3∠C）＝90°﹣∠C，∵∠DAE＝∠DAC﹣∠EAC，∴∠DAE＝∠DAC﹣（90°﹣∠C）＝90°﹣∠C﹣90°+∠C＝∠C，∴∠FEC＝C，∴∠C＝2∠FEC．3．证明：∵∠B+∠BCD＝180°（已知），∴AB∥CD（同旁内角互补，两直线平行），∴∠B＝∠DCE（两直线平行，同位角相等），∵∠B＝∠D（已知），∴∠DCE＝∠D（等量代换），∴AD∥BE（内错角相等，两直线平行），∴∠E＝∠DFE（两直线平行，内错角相等），故答案为：同旁内角互补，两直线平行，∠DCE，两直线平行，同位角相等；∴∠DCE；∠D；内错角相等，两直线平行；两直线平行，内错角相等．4．解：∵AB∥CD，∠FGB＝154°，∴∠GFD＝180°﹣∠FGB＝180°﹣154°＝26°，∵FG平分∠EFD，∴∠EFD＝2∠GFD＝2×26°＝52°，∵AB∥CD，∴∠AEF＝∠EFD＝52°．5．解：∵BE∥AD，∴∠ABE＝∠BAD＝20°，∵BE平分∠ABC，∴∠EBC＝∠ABE＝20°，∵∠C＝90°，∴∠AEB＝∠C+∠CBE＝90°+20°＝110°．6．解：（1）BF∥DE，理由如下：∵∠AGF＝∠ABC，∴GF∥BC，∴∠1＝∠3，∵∠1+∠2＝180°，∴∠3+∠2＝180°，∴BF∥DE；（2）∵BF∥DE，BF⊥AC，∴DE⊥AC，∵∠1+∠2＝180°，∠2＝140°，∴∠1＝40°，∴∠AFG＝90°﹣40°＝50°．7．解：探究：连接AD并延长至点F，由外角定理可得∠BDF＝∠BAD+∠B，∠CDF＝∠C+∠CAD；且∠BDC＝∠BDF+∠CDF及∠BAC＝∠BAD+∠CAD；相加可得∠BDC＝∠A+∠B+∠C；应用：由探究的结论易得：∠ABX+∠ACX+∠A＝∠BXC，又因为∠A＝50°，∠BXC＝90°，所以∠ABX+∠ACX＝90°﹣50°＝40°；故答案为：40；拓展：由探究的结论易得∠BDC＝∠BAC+∠ABC+∠ACB，易得∠ABC+∠ACB＝50°；而∠BEC＝（∠ABC+∠ACB）+∠A，代入∠BAC＝100°，∠BDC＝150°，易得∠BEC＝125°故答案为：1258．解：（1）EF∥BD，∵∠A+∠B＝（90+x）°+（90﹣x）°＝180°，∴AC∥BD，∵EF∥AC，∴EF∥BD；（2）∵AC∥EF∥BD，∴∠CEF＝∠C，∠DEF＝∠D，∵∠CED＝90°，∴∠C+∠D＝90°，联立，解得．9．解：∵BE为△ABC的角平分线，∴∠CBE＝∠EBA＝34°，∵∠AEB＝∠CBE+∠C，∴∠C＝80°﹣34°＝46°，∵AD为△ABC的高，∴∠ADC＝90°，∴∠CAD＝90°﹣∠C＝44°．10．解：（1）①∵∠DCE＝40°，∴∠ACE＝∠ACD﹣∠DCE＝50°，∴∠ACB＝∠ACE+∠ECB＝50°+90°＝140°；②∵∠ACB＝150°，∠ACD＝90°，∴∠ACE＝150°﹣90°＝60°，∴∠DCE＝∠ACD﹣∠ACE＝90°﹣60°＝30°，故答案为：30；（2）∵∠ACB＝∠ACD+∠BCE﹣∠DCE＝90°+90°﹣∠DCE，故答案为：∠ACB+∠DCE＝180°；（3）①∵BE∥AC，∴∠ACE＝∠E＝45°，故答案为：45°；②∵BC∥DA，∴∠A+∠ACB＝180°，又∵∠A＝60°，∴∠ACB＝180°﹣60°＝120°，∵∠BCE＝90°，∴∠BCD＝∠ACB﹣∠ECB＝120°﹣90°＝30°．11．解：（1）∵AB∥CD，∠B＝20°，∴∠DFB＝20°，∵FH⊥FB，∴∠BFH＝90°，∴∠DFH＝90°﹣∠DFB＝70°；（2）证明：∵AB∥CD，∴∠DFB＝∠B，∵∠EFB＝∠DFB，∵∠DFB+∠DFH＝90°，∴∠EFB+∠GFH＝90°，∴∠GFH＝∠DFH，∴FH平分∠GFD；（3）∵AB∥CD，∴∠CFB+∠B＝180°，∵∠EFB＝∠B，∠CFE：∠B＝4：1，∴∠EFB＝30°，∴∠GFH＝90°﹣30°＝60°．故答案为：60°．12．解：∵AB∥CD，∵∠A﹣∠B＝10°，∴∠B＝30°，∵AD⊥EF，∴∠AFE＝90°，∴∠AEF＝50°，∴∠BEC＝130°，∵DE平分∠BEC，∴∠BED＝∠BEC＝65°，∴∠BDE＝180°﹣30°﹣65°＝85°．13．解：∵∠ABC＝180°﹣∠A，即∠ABC+∠A＝180°，∴AD∥BC，∴∠1＝∠3，又∵EF∥BD，∴∠2＝∠3，∴∠1＝∠2，又∵∠1+∠2＝96°，∴2∠1＝96°，∠1＝48°，又∵DO⊥AD，∴∠ADO＝90°，∴∠BDO＝90°﹣∠1＝42°．答：∠BDO的度数为42°．14．证明：∵AB∥CD（已知），∴∠1＝∠BCD＝40°（两直线平行，同位角相等）．∵BD⊥BC，∴∠CBD＝90°．∵∠2+∠CBD+∠BCD＝180°（三角形内角和定理），∴∠2＝50°．故答案为：已知，两直线平行，同位角相等，90°，180°，三角形内角和定理，50°．15．解：∵AB∥CD，∴∠A＝∠1，∵∠A+∠1＝60°，∴∠1＝∠A＝30°，∴∠ECD＝∠1＝30°，∵DE⊥AE，∴∠DEC＝90°，∴∠D＝180°﹣∠DEC﹣∠ECD＝60°．。
小升初奥数—平面图形计算练习题及解析
小升初奥数—平面图形计算（一）一、填空题1.如下图,把三角形ABC 的一条边AB 延长1倍到D ,把它的另一边AC 延长2倍到E ,得到一个较大的三角形ADE ,三角形ADE 的面积是三角形ABC 面积的______倍.2.如下图,在三角形ABC 中,BC =8厘米,AD =6厘米,E 、F 分别为AB 和AC 的中点.那么三角形EBF 的面积是______平方厘米.3.如下图,,41,31AC CD BC BE ==那么,三角形AED 的面积是三角形ABC 面积的______.4.下图中,三角形ABC 的面积是30平方厘米,D 是BC 的中点,AE 的长是ED 的长的2倍,那么三角形CDE 的面积是______平方厘米.5.现有一个5×5的方格表(如下图)每个小方格的边长都是1,那么图中阴影部分的面积总和等于______.6.下图正方形ABCD 边长是10厘米,长方形EFGH 的长为8厘米,宽为5厘米.阴影部分甲与阴影部分乙的面积差是______平方厘米.7.如图所示,一个矩形被分成A 、B 、C 、D 四个矩形.现知A 的面积是2cm 2,B 的面积是4cm 2,C 的面积是6cm 2.那么原矩形的面积是______平方厘米.8.有一个等腰梯形,底角为450,上底为8厘米,下底为12厘米,这个梯形的面积应是______平方厘米.9.已知三角形ABC的面积为56平方厘米、是平行四边形DEFC的2倍,那么阴影部分的面积是______平方厘米.10.下图中,在长方形内画了一些直线,已知边上有三块面积分别是13,35,49.那么图中阴影部分的面积是______.二、解答题11.已知正方形的面积是50平方厘米,三角形ABC两条直角边中,长边是短边的2.5倍,求三角形ABC的面积.12.如图,长方形ABCD中,AB=24cm,BC=26cm,E是BC的中点,F、G分别是AB、CD的四等分点, H为AD上任意一点,求阴影部分面积.13.有两张正方形纸,它们的边长都是整厘米数,大的一张的面积比小的一张多44平方厘米.大、小正方形纸的边长分别是多少?14.用面积为1,2,3,4的四张长方形纸片拼成如图所示的一个长方形.问:图中阴影部分面积是多少?平面图形计算（一）习题答案1. 6.如下图,连接BE ,因为AC CE 2=,所以,ABC BCE S S ∆∆=2,即ABC ABE S S ∆∆=3.又因为BD AB =,所以,BDE ABE S S ∆∆=,这样以来,ABC ADE S S ∆∆=6.2. 6.已知E 、F 分别是AB 和AC 的中点,因此ABF ∆的面积是ABC ∆的面积的21,EBF ∆的面积又是ABF ∆的面积的21.又因为24682121=⨯⨯=⨯=∆AD BC S ABC (平方厘米),所以6242121=⨯⨯=∆EBF S (平方厘米).3.21.由,41,31AC CD BC BE ==可知AC AD BC EC 4,332==.因为ABC ∆与AEC ∆是同一个顶点,底边在同一条线段,所以这两个三角形等高,则三角形面积与底边成正比例关系,因此ABC AEC S S ∆∆=32.同理可知AEC AED S S ∆∆=43.这样以来,AED ∆的面积是ABC ∆的32的43,即是ABC ∆的面积的21.所以,AED ∆的面积是ABC ∆的21.4. 5.因为D 是BC 的中点,所以三角形ADC 和三角形ABD 面积相等(等底、等高的三角形等积),从而三角形ADC 的面积等于三角形ABC 面积的一半,即30÷2=15(平方厘米).在CDE ∆与ADC ∆中,DA DE 31=,高相等,所以CDE ∆的面积是ADC ∆面积的31.即CDE ∆的面积是51531=⨯(平方厘米)5.10三个阴影三角形的高分别为3,2,2,底依次为2,4,3,所以阴影部分面积总和等于10322142212321=⨯⨯+⨯⨯+⨯⨯.6.60设正方形ABCD 的面积为a ,长方形EFGH 的面积为b ,重叠部分EFNM 的面积为c ,则阴影部分的面积差是:b a c b c a -=---)()(.即阴影部分的面积差与重叠部分的面积大小无关,应等于正方形ABCD 的面积与长方形EFGH 的面积之差.所求答案:10×10-8×5=60(平方厘米).7.24图中的四个矩形是大矩形被两条直线分割后得到的,矩形的面积等于一组邻边的乘积.从横的方向看,两个相邻矩形的倍比关系是一致的,B 是A 的2倍,那么D 也应是C 的2倍,所以D 的面积是2×6=122cm ,从而原矩形的面积是2+4+6+12=242cm .8.20如下图,从上底的两个端点分别作底边的垂线,则BCFE 是矩形,22)812(=÷-==CD AB (厘米).因为045=∠A ,所以ABE ∆是等腰直角三角形,则2==AB BE (厘米).根据梯形的求积公式得:()2022128=⨯+=梯形S (平方厘米).9.14由已知条件,平行四边形DEFC 的面积是:56÷2=28(平方厘米)如下图,连接EC ,EC 为平行四行形DEFC 的对角线,由平行四边形的性质如,S S DEC 21=∆DEFC2821⨯=14=(平方厘米).在AED ∆与CED ∆中,ED 为公共底边,DE 平行于AC ,从而ED 边上的高相等,所以,CED AED S S ∆∆=14=(平方厘米).10.97因为长方形的面积等于ABC ∆与ECD ∆的面积和,所以ABC ∆与ECD ∆重叠部分的面积等于长方形未被这两个三角形盖住部分的面积和,即97133549=++=影阴S .11.画两条辅助线如下图,根据条件可知,正方形面积是长方形ABCD 面积的2.5倍.从而ABCD 的面积是50÷2.5=20(平方厘米).所以ABC ∆的面积是20÷2=10(平方厘米).12.连结BH ,BEH ∆的面积为)(21624)236(212cm =⨯÷⨯.把BHF ∆和DHG ∆结合起来考虑,这两个三角形的底BF 、DG 相等,且都等于长方形宽的41,它们的高AH 与DH 之和正好是长方形的长,所以这两个三角形的面积之和是:)(212112DH AH BF DH DG AH BF +⨯⨯=⨯⨯+⨯⨯)(10836244121212cm AD BF =⨯⨯⨯=⨯⨯=.于是,图中阴影部分的面积为216+108=324)(2cm .13.把两张正方形纸重叠在一起,且把右边多出的一块拼到上面,成为一个长方形,如图:这个长方形的面积是44平方厘米,它的长正好是两个正方形的边长的和,它的宽正好是两个正方形的边长的差.因为两个整数的和与它们的差是同奇或同偶,而44又只能分解成下面的三种形式:44=1×44=2×22=4×11.所以,两个正方形的边长的厘米数的和与差只能是22与2.于是,两个正方形的边长是(22+2)÷2=12(厘米),12-2=10(厘米).14.如图大长方形面积为1+2+3+4=10.延长RA 交底边于Q ,延长SB 交底边于P .矩形ABPR 面积是上部阴影三角形面积的2倍.矩形ABSQ 是下部阴影三角形面积的2倍.所以矩形RQSP 的面积是阴影部分面积的两倍.知CD CA 31=,CD CB 73=CD CD CD CA CB AB 2123173=-=-=∴因此矩形RQSP 的面积是大矩形面积的212,阴影部分面积是大矩形面积的211.阴影部分面积=211×10=2110.小升初奥数—平面图形计算（二）一、填空题1.下图是由16个同样大小的正方形组成的,如果这个图形的面积是400平方厘米,那么它的周长是______厘米.2.第一届保良局亚洲区城市小学数学邀请赛在7月21日开幕,下面的图形中,每一小方格的面积是1.那么7,2,1三个数字所占的面积之和是______.3.下图中每一小方格的面积都是1平方厘米,那么用粗线围成的图形面积是______平方厘米.4.下图的两个正方形,边长分别为8厘米和4厘米,那么阴影部分的面积是______平方厘米.5.在ABC ∆中,DC BD 2=,BE AE =,已知ABC ∆的面积是18平方厘米,则四边形AEDC 的面积等于______平方厘米.6.下图是边长为4厘米的正方形,AE =5厘米、OB 是______厘米.7.如图正方形ABCD 的边长是4厘米,CG 是3厘米,长方形DEFG 的长DG 是5厘米,那么它的宽DE是______厘米.8.如图,一个矩形被分成10个小矩形,其中有6个小矩形的面积如图所示,那么这个大矩形的面积是______.9.如下图,正方形ABCD 的边长为12,P 是边AB 上的任意一点,M 、N 、I 、H 分别是边BC 、AD 上的三等分点,E 、F 、G 是边CD 上的四等分点,图中阴影部分的面积是______.10.下图中的长方形的长和宽分别是6厘米和4厘米,阴影部分的总面积是10平方厘米,四边形ABCD 的面积是______平方厘米.二、解答题11.图中正六边形ABCDEF 的面积是54.PF AP 2=,BQ CQ 2=,求阴影四边形CEPQ 的面积.12.如图,涂阴影部分的小正六角星形面积是16平方厘米.问:大正六角星形面积是多少平方厘米.13.一个周长是56厘米的大长方形,按下图中(1)与(2)所示意那样,划分为四个小长方形.在(1)中小长方形面积的比是:2:1:=B A ,2:1:=C B .而在(2)中相应的比例是3:1:=''B A ,3:1:=''C B .又知,长方形D '的宽减去D 的宽所得到的差,与D '的长减去在D 的长所得到的差之比为1:3.求大长方形的面积.25203036161214.如图,已知5=CD ,7=DE ,15=EF ,6=FG .直线AB 将图形分成两部分,左边部分面积是38,右边部分面积是65.那么三角形ADG 面积是______.平面图形计算（二）习题答案1.170.每个小正方形的面积为400÷16=25平方厘米,所以每个小正方形的边长为5cm,因此它的周长是34×5=170厘米.2.25.7,2,1所占面积分别为7.5,10和7.5.3. 6.5.直接计算粗线围成的面积是困难的,我们通过扣除周围的正方形和直角三角形来计算.周围有正方形3个,面积为1的三角形5个,面积为1.5的三角形一个,因此围成面积是4×4-3-5-1.5=6.5(平方厘米).4.24仿上题,大、小两个正方形面积之和减去两只空白三角形的面积和,所得的差就是阴影部分的面积.]2)84(4288[8422+⨯+⨯-+=16+64-(32+24)=80-56=24(平方厘米)5.12如下图,连接AD ,因为DC BD 2=,所以ADC ABD S S ∆∆=2;又18==+∆∆∆ABC ADC ABD S S S ,所以12=∆ABD S .因为BE AE =,所以621===∆∆∆ABD ADE BDE S S S ;因此12618=-=-=∆∆BDE ABC AEDC S S S (平方厘米).6.3.2如下图,连接BE ,则8442121=⨯⨯==∆正方形S S ABE (平方厘米).从另一角度看,OB S ABE ⨯⨯=∆521,于是8521=⨯⨯OB .528÷⨯=∴OB =3.2(厘米)7. 3.2如下图,连接AG ,则AGD ∆的面积是正方形ABCD 面积的21,也是长方形DEFG 的面积的21,于是长方形DEFG 的面积等于正方形ABCD 的面积4×4=16(平方厘米).2.3516=÷=∴DE (厘米).8.243我们用A ,B ,C ,D 分别表示待计算的小矩形面积上、下两个矩形,长是相同的.A252030D 36B 16C12因此它们的面积之比,就是宽之比,反之,宽之比,就是面积之比.这样就有:20:16=A :36,45163620=⨯=A ;20:16=25:B ,20202516=⨯=B ;20:16=30:C ,24203016=⨯=C ;20:16=D :12,AC A 'C 'BD B 'D '15161220=⨯=D .因此,大矩形的面积是:45+36+25+20+20+16+30+24+15+12=2439.60如下图,连接PD ,则阴影部分就是由四个三角形:PDH ∆,PGD ∆,PEF ∆和PMN ∆组成.PGD ∆和PEF ∆的底都有3,高为12,所以1812321=⨯⨯==∆∆PEF PGD S S .PDH ∆和PMN ∆的底都是4,两条高分别为P A 和PB 则:PB P A S S PMN PDH ⨯⨯+⨯⨯=+∆∆421421=2(P A +PB )=2×12=24所以,阴影部分的面积是:++∆∆PEF PGD S S PMN PDH S S ∆∆+=18+18+24=6010.4长方形EFGH 的面积是6×4=24(平方厘米)1221==+∴∆∆EFGH AHG AEF S S S (平方厘米)阴影总面积S S S S S AHG AEF ADH EBA -+=+∴∆∆∆∆=12-10=2(平方厘米)又6244141=⨯==∆EFGH ECH S S (平方厘米)所以,四边形ABCD 的面积等于:)(ADH EBA ECH S S S ∆∆∆+-=6-2=4(平方厘米)11.如图,将正六边形ABCDEF 等分为54个小正三角形.根据平行四边形对角线平分平行四边形面积.采用数小三角形的办法来计算面积.PEF ∆面积=3;CDE ∆面积=9;四边形ABQP 面积=11.上述三块面积之和为3+9+11=23,因此,阴影四边形CEPQ 面积为54-23=31.12.如图,涂阴影部分小正六角星形可分成12个与三角形OPN 全等(能完全重叠地放在一起)的小三角形.三形OPN 的面积是341216=平方厘米.正三角形OPM 面积是由三个与三角形OPN 全等的三角形组成.所以正三角形OPM 的面积等于4334=⨯(平方厘米).由于大正方六角星形由12个与正三角形OPM 全等的三角形组成,所以大正六角星形的面积是4×12=48(平方厘米)13.设大长方形的宽为x ,则长为28-x .因为,x D 32=宽,x D 43='宽,所以,12x D D =-'宽宽.()x D -=2854长,()x D -='28109长,()x D D -=-'28101长长.由题设可知,12x :11028=-x :3或41028x x =-,于是2071028x =,8=x .大长方形的长=28-8=20,从而大长方形的面积为8×20=160平方厘米.14.三角形AEG 面积是三角形AED 面积的(15+6)÷7=3(倍),三角形BEF 面积是三角形BEC 面积的15÷(5+7)=45(倍).所以65-38×45等于三角形AEG 面积与三角形AED 面积的45之差,因此三角形AED 的面积是(65-38×45)÷(3-45)=10.三角形ADG 面积是10×(3+1)=40.。
2022年鲁教版(五四)六年级数学下册第五章基本平面图形专项练习试题(含详解)
六年级数学下册第五章基本平面图形专项练习考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。
第I卷（选择题 30分）一、单选题（10小题，每小题3分，共计30分）1、延长线段AB到C，使得BC＝3AB，取线段AC的中点D，则下列结论：①点B是线段AD的中点．②BD＝12CD，③AB＝CD，④BC﹣AD＝AB．其中正确的是（）A．①②③B．①②④C．①③④D．②③④2、如图，射线OA所表示的方向是（）A．西偏南30°B．西偏南60°C．南偏西30°D．南偏西60°3、如图，∠AOB，以OA为边作∠AOC，使∠BOC=12∠AOB，则下列结论成立的是（）A ．AOC BOC ∠=∠B ．AOC AOB ∠<∠ C ．AOC BOC ∠=∠或2AOC BOC ∠=∠D ．AOC BOC ∠=∠或3AOC BOC ∠=∠4、①直线AB 和直线BA 是同一条直线；②平角等于180°；③一个角是70°39'，它的补角是19°21'；④两点之间线段最短；以上说法正确的有（ ）A ．②③④B ．①②④C ．③④D ．①5、如图，OM 平分AOB ∠，2MON BON ∠=∠，72AON BON ∠-∠=︒，则AOB ∠=（ ）A ．96°B ．108°C ．120°D ．144°6、平面上有三个点A ，B ，C ，如果8AB =，5AC =，3BC =，则（ ）A ．点C 在线段AB 的延长线上B ．点C 在线段AB 上 C ．点C 在直线AB 外D ．不能确定7、如图，已知线段n 与挡板另一侧的四条线段a ，b ，c ，d 中的一条在同一条直线上，请借助直尺判断该线段是（ ）A．a B．b C．c D．d8、把弯曲的河道改直，就能缩短河道长度．可以解释这一做法的数学原理是（）A．两点确定一条直线B．两点之间，线段最短C．两点之间，直线最短D．线段比直线短9、下列各角中，为锐角的是（）A．12平角B．15周角C．32直角D．12周角10、下列说法正确的是（）A．正数与负数互为相反数B．如果x2＝y2，那么x＝yC．过两点有且只有一条直线D．射线比直线小一半第Ⅱ卷（非选择题 70分）二、填空题（5小题，每小题4分，共计20分）1、一个角比它的补角的3倍多40°，则这个角的度数为______．2、若一个角的补角是其余角的3倍，则这个角的度数为___．3、已知点C是线段AB的三等分点，点D是线段AC的中点．若线段2AD=，则AB=______．4、某人下午6点多钟外出购物，表上时针和分针的夹角恰好是110°，将近7点钟回到家，此时，表上时针和分针的夹角又恰好是110°，则此人外出购物所用时间是______分钟．5、把一个直径是10厘米的圆分成若干等份，然后把它剪开，照如图的样子拼起来，拼成的图形的周长比原来圆的周长增加_______厘米．三、解答题（5小题，每小题10分，共计50分）1、如图，已知平面内有四个点A，B，C，D．根据下列语句按要求画图．(1)连接AB；作直线AD．(2)作射线BC与直线AD交于点F．观察图形发现，线段AF+BF＞AB，得出这个结论的依据是：．2、已知线段a，b，点A，P位置如图所示．(1)画射线AP，请用圆规在射线AP上截取AB=a，BC=b；（保留作图痕迹，不写作法）(2)在（1）所作图形中，若M，N分别为AB，BC的中点，在图形中标出点M，N的位置，再求出当a=4，b=2时，线段MN的长．3、（1）如图l，点D是线段AC的中点，且AB＝23BC，BC=6，求线段BD的长；（2）如图2，已知OB平分∠AOD，∠BOC=23∠AOC，若∠AOD=100°，求∠BOC的度数．4、如图是燕山前进片区的学校分布示意图，请你认真观察并回答问题．(1)燕山前进二小在燕山前进中学的方向，距离大约是 m．(2)燕化附中在燕山向阳小学的方向．(3)小辰从燕山向阳小学出发，沿正东方向走200m，右转进入岗南路，沿岗南路向南走150m，左转进入迎风南路，沿迎风南路向正东方向走450m到达燕化附中．请在图中画出小辰行走的路线，并标出岗南路和迎风南路的位置．5、已知O是直线MN上一点，∠MOA＝40°，∠AOB＝90°，∠COD与∠AOB都在直线MN的上方，且射线OC在射线OD的左侧．(1)如图1，射线OC在∠AOB的内部，如果∠COD＝90°，那么图中与∠AOC相等的角是，其依据是：．(2)如图2，用直尺和圆规作∠AOB的平分线OP，如果∠COD＝60°，且OC平分∠AOP，那么∠DON ＝°；（保留作图痕迹，不要求写出作法和结论）(3)如果∠COD＝60°，设∠AOC＝m°（0＜m＜80，且m≠30），用含m的式子表示∠BOD的度数．（直接写出结论）-参考答案-一、单选题1、B【解析】【分析】先根据题意，画出图形，设AB a ，则3,4BC a AC a == ，根据点D 是线段AC 的中点，可得122AD CD AC a === ，从而得到BD a = ，BD ＝12CD ，AB ＝12CD ，BC AD a -= ，即可求解． 【详解】解：根据题意，画出图形，如图所示：设AB a ，则3,4BC a AC a == ，∵点D 是线段AC 的中点， ∴122AD CD AC a === ， ∴BD AD AB a =-= ，∴AB =BD ，即点B 是线段AD 的中点，故①正确；∴BD ＝12CD ，故②正确；∴AB ＝12CD ，故③错误；∴32BC AD a a a -=-= ，∴BC ﹣AD ＝AB ，故④正确；∴正确的有①②④．故选：B【点睛】本题主要考查了考查了线段的和与差，有关中点的计算，能够用几何式子正确表示相关线段间的关系，利用数形结合思想解答是解题的关键．2、D【解析】【详解】︒-︒=︒，解：903060根据方位角的概念，射线OA表示的方向是南偏西60度．故选：D．【点睛】本题主要考查了方向角．解题的关键是弄清楚描述方向角时，一般先叙述北或南，再叙述偏东或偏西．3、D【解析】【分析】分OC在∠AOB内部和OC在∠AOB外部两种情况讨论，画出图形即可得出结论．【详解】解：当OC在∠AOB内部时，∵∠BOC=12∠AOB，即∠AOB=2∠BOC，∴∠AOC=∠BOC；当OC在∠AOB外部时，∵∠BOC=12∠AOB，即∠AOB=2∠BOC，∴∠AOC=3∠BOC；综上，∠AOC=∠BOC或∠AOC=3∠BOC；故选：D．【点睛】本题考查了角平分线的定义，熟练掌握角平分线的定义，数形结合解题是关键．4、B【解析】【分析】根据直线的表示方法，平角，补角，线段的性质逐个判断即可．【详解】①直线AB和直线BA是同一条直线，正确②平角等于180°，正确③一个角是70°39'，它的补角应为：1807039'10921'︒-︒=︒，所以错误④两点之间线段最短，正确故选B【点睛】本题考查直线的表示方法，平角，补角，线段的性质等知识点，熟练掌握以上知识点是解题的关键．5、B【解析】【分析】设BON x ∠=，利用关系式2MON BON ∠=∠，72AON BON ∠-∠=︒，以及图中角的和差关系，得到3MOB x ∠=、722AOB x ∠=︒+，再利用OM 平分AOB ∠，列方程得到18x =︒，即可求出AOB ∠的值．【详解】解：设BON x ∠=，∵2MON BON ∠=∠，∴2MON x ∠=，∴23MOB MON BON x x x ∠=∠+∠=+=．∵72AON BON ∠-∠=︒，∴72AON x ∠=︒+，∴72722AOB AON BON x x x ∠=∠+∠=︒++=︒+．∵OM 平分AOB ∠， ∴12MOB AOB ∠=∠， ∴()137222x x =︒+，解得18x =︒． 72272218108AOB x ∠=︒+=︒+⨯︒=︒．故选：B ．【点睛】本题通过图形中的角的和差关系，利用方程的思想求解角的度数．其中涉及角的平分线的理解：一般地，从一个角的顶点出发，把这个角分成两个相等的角的射线，叫做这个角的平分线．6、B【解析】【分析】本题没有给出图形，在画图时，应考虑到A、B、C三点之间的位置关系，再根据正确画出的图形解题．【详解】解：如图：∵AB=8，AC=5，BC=3，从图中我们可以发现AC+BC=AB，所以点C在线段AB上．故选：B．【点睛】本题考查了直线、射线、线段，在此类问题中，正确画图很重要，所以能画图的一定要画图这样才直观形象，便于思维．7、B【解析】【分析】利用直尺画出遮挡的部分即可得出结论．解：利用直尺画出图形如下：可以看出线段b与n在一条直线上．故选：B．【点睛】本题主要考查了线段，射线，直线，利用直尺动手画出图形是解题的关键.8、B【解析】【分析】由把弯曲的河道改直，就缩短了河道的长度，涉及的知识点与距离相关，从而可以两点之间，线段最短来解析.【详解】解：把弯曲的河道改直，就能缩短河道长度．可以解释这一做法的数学原理是两点之间，线段最短.故选：B【点睛】本题考查的是两点之间，线段最短，掌握“利用两点之间线段最短解析生活现象”是解本题的关键.9、B【分析】求出各个选项的角的度数，再判断即可．【详解】解：A. 12平角=90°，不符合题意； B. 15周角=72°，符合题意； C. 32直角=135°，不符合题意； D. 12周角=180°，不符合题意；故选：B ．【点睛】本题考查了角的度量，解题关键是明确周角、平角、直角的度数．10、C【解析】【分析】A 中互为相反数的两个数为一正一负；B 中两个数的平方相等，这两个数可以相等也可以互为相反数；C 中过两点有且只有一条直线；D 中射线与直线无法比较长度．【详解】解：A 中正数负数分别为12-，，()1210+-=-≠，错误，不符合要求； B 中22x y =,可得x y =或x y =-，错误，不符合要求；C 中过两点有且只有一条直线 ，正确，符合要求；D 中射线与直线都可以无限延伸，无法比较长度，错误，不符合要求；故选C ．【点睛】本题考查了相反数，直线与射线．解题的关键在于熟练掌握相反数，直线与射线等的定义．二、填空题1、145︒##145度【解析】【分析】设这个角的补角的度数为x ，则这个角的度数为180x ︒- ，根据“一个角比它的补角的3倍多40°，”列出方程，即可求解．【详解】解：设这个角的补角的度数为x ，则这个角的度数为180x ︒- ，根据题意得：180340x x ︒--=︒ ，解得：35x =︒ ，∴这个角的度数为180145x ︒-=︒．故答案为：145︒【点睛】本题主要考查了补角的性质，一元一次方程的应用，利用方程思想解答是解题的关键．2、45°##45度【解析】【分析】根据补角和余角的定义，利用“一个角的补角是它的余角的度数的3倍”作为相等关系列方程求解即可得出结果．【详解】解：设这个角的度数是x，则180°-x=3（90°-x），解得x=45°．答：这个角的度数是45°．故答案为：45°．【点睛】本题考查了余角和补角的知识，设出未知数是解决本题的关键，要掌握解答此类问题的方法．3、12或6##6或12【解析】【分析】根据点C是线段AB上的三等分点，分两种情况画图进行计算即可．【详解】解：如图，∵点C是线段AB上的三等分点，∴AB=3AC，∵D是线段AC的中点，∴AC=2AD=4，∴AB=3×4=12；如图，∵D是线段AC的中点，∴AC=2AD=4，∵点C是线段AB上的三等分点，AC=2，AB=3BC，∴BC=12∴AB=3AC=6，则AB的长为12或6．故答案为：12或6．【点睛】本题考查了两点间的距离，解决本题的关键是分两种情况画图计算．4、40【解析】【分析】解设共用了x分，列方程6x-0.5x=110+110，求解即可．【详解】解：分针速度：6度/分，时针速度是：0.5度/分，设共用了x分，6x-0.5x=110+110，解得x=40，答：共外出40分钟，故答案为：40．【点睛】此题考查了一元一次方程的实际应用，正确理解题意是解题的关键．5、10【解析】【分析】由圆的面积推导过程可知：将圆拼成近似的长方形后，长方形的长就等于圆的周长的一半，宽就等于圆的半径，从而可知，这个长方形的周长比原来圆的周长多出了两个半径的长度，据此即可求解．【详解】解：因为将圆拼成近似的长方形后，长方形的长就等于圆的周长的一半，宽就等于圆的半径，所以这个长方形的周长比原来圆的周长多出了两个半径的长度，即多出了一个直径的长度，也就是10厘米．故答案为：10．【点睛】本题考查认识平面图形，理解图形周长的意义和拼图前后之间的关系是解决问题的关键．三、解答题1、 (1)见解析；(2)见解析，两点之间线段最短【解析】【分析】（1）根据线段、直线的定义即可画出图形；（2）根据射线的定义，可画出射线BC，再根据两点之间线段最短解决问题．(1)如图所示，线段AB与直线AD即为所求；(2)如上图所示，射线BC 即为所求，根据两点之间线段最短得AF +BF ＞AB ，故答案为：两点之间线段最短．【点睛】本题考查了画线段、直线、射线；两点之间线段最短，掌握线段、射线、直线的特点是解题的关键．2、 (1)见解析(2)3或1【解析】【分析】先根据射线的定义，画出射线AP ，然后分两种情况：当点C 位于点B 右侧时，当点C 位于点B 左侧时，即可求解；（2）根据M ，N 分别为AB ，BC 的中点，可得2,1BM BN == ，即可求解．(1)解：根据题意画出图形，当点C 位于点B 右侧时，如下图：射线AP 、线段AB 、线段BC 即为所求；当点C 位于点B 左侧时，如下图：(2)解： ∵M ，N 分别为AB ，BC 的中点， ∴11,22BM AB BN BC == ， ∵a =4，b =2，∴2,1BM BN == ，当点C 位于点B 右侧时，MN =BM +BN =3；当点C 位于点B 左侧时，MN =BM -BN =1；综上所述，线段MN 的长为3或1．【点睛】本题主要考查了射线的定义，尺规作图——作一条线段等于已知线段，有关中点的计算，熟练掌握射线是只有一个端点，它从一个端点向另一边无限延长不可测量长度的线；作一条线段等于已知线段的作法是解题的关键．3、（1）BD =1；（2）∠COB =20°【解析】【分析】（1）根据AB＝23BC，BC=6求出AB的值，再根据线段的中点求出AD的值，然后可求BD的长；（2）先根据角平分线的定义求出∠AOB，再根据∠BOC=23∠AOC，求解即可．【详解】解：（1）∵AB＝23BC，BC=6，∴AB＝23×6=4，∴AC=AB+BC=10，∵点D是线段AC的中点，∴AD=12AC=5，∴BD=AD-AB=5-4=1；（2）∵OB平分∠AOD，∠AOD=100°，∴∠AOB=12∠AOD=50°，∵∠BOC+∠AOC=∠AOB，∠BOC=23∠AOC，∴23∠AOC+∠AOC=50°，∴∠AOC=30°，∴∠BOC=23∠AOC=20°．【点睛】本题考查了线段的中点，线段的和差，角的平分线，角的和差，数形结合是解答本题的关键．4、 (1)正西，100(2)南偏东77°(3)见解析【解析】【分析】（1）根据图中位置解决问题即可．（2）根据图中位置解决问题即可．（3）根据题意画出路线即可．(1)燕山前进二小在燕山前进中学的正西方向，距离大约是100m．故答案为：正西，100．(2)燕化附中在燕山向阳小学的南偏东77︒方向故答案为：南偏东77︒．(3)小辰行走的路线如图：【点睛】本题考查作图-应用与设计，方向角等知识，解题的关键是熟练掌握基本知识．5、 (1)BOD ∠，等角的余角相等(2)图见解析，57.5︒(3)70m ︒-︒或30m ︒-︒【解析】【分析】（1）根据等角的余角相等解决问题即可．（2）根据DON BON DOB ∠=∠+∠，求出BON ∠，DOB ∠即可．（3）分两种情形：当030m <<时，根据BOD AOM AOB AOC COD ∠=∠+∠-∠-∠求解，如图32-中，当3080m <<时，根据BOD AOC COD AOB ∠=∠+∠-∠，求解即可．(1)解：如图1中，90AOB COD ∠=∠=︒，90AOC COB COB BOD ∴∠+∠=∠+∠=︒，AOC BOD ∴∠=∠（等角的余角相等），故答案为：等角的余角相等．(2)解：如图2中，如图，射线OP 即为所求．40AOM ∠=︒，90AOB ∠=︒，180409050NOB ∴∠=︒-︒-︒=︒， OP 平分AOB ∠，190452AOP ∴∠=⨯︒=︒， OC 平分AOP ∠，122.52AOC AOP ∴∠=∠=︒， 9022.5607.5BOD ∴∠=︒-︒-︒=︒，57.5DON BON DOB ∴∠=∠+∠=︒．(3)解：如图31-中，当030m <<时，40906070BOD AOM AOB AOC COD m m ∠=∠+∠-∠-∠=︒+︒-︒-︒=︒-︒．如图32-中，当3080m <<时，609030BOD AOC COD AOB m m ∠=∠+∠-∠=︒+︒-︒=︒-︒．综上所述，满足条件的m 的值为70m ︒-︒或30m ︒-︒．【点睛】本题考查作图-复杂作图，角平分线的定义等知识，解题的关键是学会用分类讨论的思想思考问题，属于中考压轴题．。
(完整版)小升初数学平面图形与立体图形综合练习
圆的应用题。
1、一座大钟的时针长30厘米，分针长40厘米。
一昼夜时针和分针的针尖经过的路程是多少厘米？2、一个半圆的周长是15.42分米,这个半圆的面积是多少平方分米?3、一个半圆的弧长为31.4cm，与这个半圆半径相等的圆的面积是多少？4、一个半圆的周长是51.4cm，与这个半圆半径相等的圆的面积是多少？5、一个边长是31.4cm的正方形内可容下多少个半径为5cm的圆？6、在一个边长是12cm的正方形内放入4个尽量大且相等的圆形，每个圆的面积是多少？7、一种压路机的前轮直径15分米，宽是2米。
如果每分钟滚动5圈，它每分钟前进多少米？每分钟压路面积是多少平方米？8、一个养鱼池周长是100.48米，中间有一个圆形小岛，半径是6米，这个养鱼池的水域面积是多少平方米？9、如果大圆半径是小圆半径的2倍，那么大圆的周长是小圆周长的（）倍；面积比是（）。
10、一根长31.4米的绳子，用它先围成正方形，再围成圆形，面积相差多少平方米？11、一个圆的直径是4厘米，增加到6厘米后，面积增加了多少平方厘米？12、猫和老鼠在一个半径是50米的圆周上的同一点向相反方向运动，猫每分钟走18.84米，老鼠每分钟走12.56米，当猫和老鼠相遇时，猫比老鼠多走了多少米？多边形的面积应用题1、一个梯形，下底长14厘米，高12厘米，如果下底减少6厘米，它就成为一个平行四边形。
梯形的面积是多少？2、有一块平行四边形的麦田，底275米，高60米，共收小麦19.8吨。
这块麦田有多少公顷？平均每公顷收小麦多少吨？3、一堆水泥电线杆堆成一个梯形，最上层有4根，最下层有12根，一共有5层，2堆这样的电线杆一共有多少根？4、刘店乡有一块长方形的牧地，长是宽的2倍，一辆汽车以每小时36千米的速度绕牧场一周需要0.5小时，这个牧场的面积是多少平方千米？5、一个三角形的底长3米，如果底延长1米，那么三角形的面积就增加1.2平方米，原来三角形的面积是多少平方米？6、用篱笆围成一个梯形养鸡场（如图），其中一边利用房屋墙壁。
七年级上册数学第四章基本平面图形
O C A D B OC A E DB 第四章 基本平面图形3【知识点】【知识点】角的平分线: 从一个角的顶点引出的一条射线，把这个角分成两个相等的角，这条射线叫做这个角的平分线。
从一个角的顶点引出的一条射线，把这个角分成两个相等的角，这条射线叫做这个角的平分线。
14、多边形: 由一些不在同一条直线上的线段依次首尾相连组成的封闭平面图形，叫做多边形。
由一些不在同一条直线上的线段依次首尾相连组成的封闭平面图形，叫做多边形。
从一个n 边形的同一个顶点出发，分别连接这个顶点与其余各顶点，可以把这个n 边形分割成（n-2）个三角形。
n 边形内角和等于（n-2）×1800，正多边形（每条边都相等，每个内角都相等的多边形）的每个内角都等于（n-2）×1800 / n 过n 边形一个顶点有（n-3）条对角线，n 边形共（n-3）×n / 2条对角线. 圆、弧、扇形圆、弧、扇形 圆：平面上一条线段绕着固定的一个端点旋转一周，另一个端点形成的图形叫做圆。
固定的端点称为圆心固定的端点称为圆心 弧：圆上A 、B 两点之间的部分叫做圆弧，简称弧。
两点之间的部分叫做圆弧，简称弧。
扇形：由一条弧和经过这条弧的端点的两条半径所组成的图形叫做扇形。
扇形：由一条弧和经过这条弧的端点的两条半径所组成的图形叫做扇形。
圆心角：顶点在圆心的角叫圆心角。
圆心角：顶点在圆心的角叫圆心角。
4.4 角的比较※课时达标 1.1.若若OC 是∠是∠AOB AOB 的平分线的平分线,,则∠则∠AOC=_____;AOC=_____;AOC=_____;∠∠AOC=12______; ______; ∠∠AOB=2_______. 2.12平角平角=_____=_____=_____直角直角直角, , 14周角周角=______=______=______平角平角平角=_____=_____=_____直角直角直角,135,135,135°角°角°角=______=______=______平角平角平角. . 3.3.如图如图如图,(1),(1),(1)∠∠AOC=_____ +_____ = ____ -____ ;(2) (2)∠∠AOB=______-______ =______-_____.第第3题图题图 第第4题图题图4.4.如图如图如图,O ,O 是直线AB 上一点上一点,,∠AOC=90AOC=90°°,∠DOE=90DOE=90°°,则图中相等的角有则图中相等的角有_________对对( ( 小于直角的角小于直角的角小于直角的角))分别是______.5.5.下列说法正确的是下列说法正确的是下列说法正确的是( ). ( ).A. A.两条相交直线组成的图形叫做角两条相交直线组成的图形叫做角两条相交直线组成的图形叫做角B. B.有一个公共端点的两条线段组成的图形叫做角有一个公共端点的两条线段组成的图形叫做角有一个公共端点的两条线段组成的图形叫做角C. C.一条射线绕着端点从一个位置旋转到另一个位置所成的图形叫做角一条射线绕着端点从一个位置旋转到另一个位置所成的图形叫做角一条射线绕着端点从一个位置旋转到另一个位置所成的图形叫做角D. D.角是从同一点引出的两条射线角是从同一点引出的两条射线角是从同一点引出的两条射线★基础巩固1.1.已知已知O 是直线AB 上一点上一点,OC ,OC 是一条射线是一条射线, ,则∠则∠则∠AOC AOC 与∠与∠BOC BOC 的关系是的关系是( ). ( ).A. A.∠∠AOC 一定大于∠一定大于∠BOCB.BOC B.BOC B.∠∠AOC 一定小于∠一定小于∠BOC BOCC. C.∠∠AOC 一定等于∠一定等于∠BOCD.BOC D.BOC D.∠∠AOC 可能大于可能大于,,等于或小于∠等于或小于∠BOC BOC2.2.已知∠已知∠已知∠AOB=3AOB=3AOB=3∠∠BOC,BOC,若∠若∠若∠BOC=30BOC=30BOC=30°°,则∠则∠AOC AOC 等于等于( ) ( )A.120 A.120°°B.120 B.120°或°或6060°°C.30 C.30°°D.30 D.30°或°或9090°°3.3. a Ð和b Ð的顶点和一边都重合的顶点和一边都重合,,另一边都在公共边的同侧另一边都在公共边的同侧,,且a b Ð>Ð,那么a Ð的另一半落在另一半落在b Ð的( ).A. A.另一边上另一边上另一边上B. B. B.内部内部内部;C.; C.; C.外部外部外部D. D. D.以上结论都不对以上结论都不对以上结论都不对4.2704.270°°=_______=_______直角直角直角_____________________平角平角平角________________________周角周角周角. .5.5.已知一条射线已知一条射线OA,OA,如果从点如果从点O 再引两条射线OB 和OC,OC,使∠使∠使∠AOB=60AOB=60AOB=60°°, , ∠∠BOC=20BOC=20°°,求∠求∠求∠AOC AOC 的度数的度数. .6.6.如图如图如图,,如果∠如果∠1=651=651=65°°1515′′,∠2=782=78°°3030′′,求∠求∠33是多少度是多少度? ?312☆能力提高7.7.如图（如图（如图（11）,OD,OE 分别是∠分别是∠AOC AOC 和∠和∠BOC BOC 的平分线的平分线,,∠AOD=40AOD=40°°,∠BOE=25BOE=25°°,求∠求∠AOB AOB 的度数的度数. . 解解:∵OD 平分∠平分∠AOC,OE•AOC,OE•AOC,OE•平分∠平分∠平分∠BOC(•BOC(•BOC(•已知已知已知)•,• )•,•∴∠∴∠∴∠AOC=•2•AOC=•2•AOC=•2•∠∠AOD,•∠∠BOC=•2•BOC=•2•∠∠_____( ),∵∠∵∠AOD=40AOD=40AOD=40°°,∠_______=25_______=25°°(已知已知), ),∴∠∴∠AOC=2AOC=2AOC=2××4040°°=80=80°°(•(•等量代换等量代换等量代换). ).∠BOC=2BOC=2××( )( )°°=( ),∴∠∴∠∴∠AOB=________. AOB=________.8.8.如图（如图（如图（22）,若∠若∠AOC=AOC=AOC=∠∠DOB,DOB,则∠则∠则∠AOB= AOB= AOB= ∠∠COD;•COD;•若∠若∠若∠AOB=•AOB=•AOB=•∠∠COD,•COD,•则∠则∠则∠AOC___AOC___AOC___∠∠DOB.9.9.已知∠已知∠已知∠AOB AOB 和∠和∠BOC BOC 之和为180180°°,这两个角的平分线所成的角是这两个角的平分线所成的角是_______. _______.10.10.如图（如图（如图（33）,∠AOB 是直角是直角,,∠AOC=38AOC=38°°,∠COD=COD=∠∠COB=1:2,COB=1:2,则∠则∠则∠BOD=( ). BOD=( ).A.38 A.38°°B.52 B.52°°C.26 C.26°°D.64 D.64°° E C B B A D OCB A DO (1) (2)CB AD OE C BA DO(3) (4)11.11.如图（如图（如图（44）所示）所示,OE ,OE 平分∠平分∠BOC,OD BOC,OD 平分∠平分∠AOC,AOC,AOC,∠∠BOE=20BOE=20°°,∠AOD=40•AOD=40•°°,•,•求∠求∠求∠DOE DOE 的度数的度数. .●中考在线12.12.用一副三角尺用一副三角尺用一副三角尺,,可以拼出小于180180°的角有°的角有n 个,则n 等于等于( ). A.4 B.6 C.11 D.13 ( ). A.4 B.6 C.11 D.13 13.13.已知已知α、β都是钝角都是钝角,,甲、乙、丙、丁四人计算16(α+β)的结果依次是5050°°,26,26°°,72•,72•°°,90,90°°,那么结果正确的可能是果正确的可能是( ). A.( ). A.( ). A.甲甲 B. B.乙乙 C. C.丙丙 D. D.丁丁14.14.点点P 在∠在∠MAN MAN 内部内部,,现在四个等式现在四个等式::①∠①∠PAM=PAM=PAM=∠∠MAP;MAP;②∠②∠②∠PAN=PAN=12∠A;•A;•③∠③∠③∠MAP=MAP=12∠MAN,MAN,④∠④∠④∠MAN=2MAN=2MAN=2∠∠MAP,其中能表示AP 是角平分线的等式有是角平分线的等式有( ). A.1( ). A.1个 B.2个 C.3个 D.4个15.15.如图如图如图,,∠AOD=AOD=∠∠BOC=90BOC=90°°,∠COD=42COD=42°°,求∠求∠AOC AOC AOC、∠、∠、∠AOB AOB 的度数的度数. .O C ADB16.16.如图如图如图,OA ,OA ,OA⊥⊥OB OB、、OC OC⊥⊥OD,OE 是OD 的反向延长线的反向延长线. .(1) (1)试说明∠试说明∠试说明∠AOC=AOC=AOC=∠∠BOD.(2) (2)若∠若∠若∠BOD=50BOD=50BOD=50°°,求∠求∠AOE. AOE.O CAE DB17.17.如图如图如图,AO ,AO ,AO⊥⊥CO,BO CO,BO⊥⊥DO,DO,∠∠BOC=30BOC=30°°,求∠求∠AOD AOD 的度数的度数..O CADB18.18.如图所示如图所示如图所示,OE ,OE 平分∠平分∠BOC,OD BOC,OD 平分∠平分∠AOC,AOC,AOC,∠∠BOE=20BOE=20°°,∠AOD=40•AOD=40•°°,•,•求∠求∠求∠DOE DOE 的度数的度数..E CB ADO19.19.如图如图如图,AO ,AO ,AO⊥⊥CO,BO CO,BO⊥⊥DO,DO,∠∠BOC=30BOC=30°°,求∠求∠AOD AOD 的度数的度数..OCA DB4.5 多边形和圆的初步认识※课时达标1.________1.________，，__________________，，__________________，，__________________等都是多边形等都是多边形等都是多边形. .2.2.各边相等，各角也相等的多边形叫做各边相等，各角也相等的多边形叫做各边相等，各角也相等的多边形叫做____________. ____________.3.3.下列说法中正确的是下列说法中正确的是下列说法中正确的是( ( ).A.A.圆上任意两点间的部分叫做圆弧圆上任意两点间的部分叫做圆弧圆上任意两点间的部分叫做圆弧B. B. B.圆上任意两点间的线段叫做弧圆上任意两点间的线段叫做弧圆上任意两点间的线段叫做弧C. C.圆上任意两点间的线段长度叫做弧圆上任意两点间的线段长度叫做弧圆上任意两点间的线段长度叫做弧D. D. D.任意两点间的部分叫做弧任意两点间的部分叫做弧任意两点间的部分叫做弧4.4.将一个圆分割成三个扇形，它们的圆心角的度数比为将一个圆分割成三个扇形，它们的圆心角的度数比为1：2：3，则这三个扇形的圆心，则这三个扇形的圆心角的度数分别是角的度数分别是角的度数分别是( ( ).A.30 A.30°，°，°，606060°，°，°，909090°°B.60 B.60°，°，°，120120120°，°，°，180180180°°C.40 C.40°，°，°，808080°，°，°，120120120°°D.50 D.50°，°，°，100100100°，°，°，150150150°°5.5.如图如图如图,,从四边形ABCD 的顶点A 出发，可以画出出发，可以画出__________________对角线对角线对角线,,是线段是线段____. ____.6.6.将一个圆分成三个大小相同扇形，则它们的圆心角是将一个圆分成三个大小相同扇形，则它们的圆心角是将一个圆分成三个大小相同扇形，则它们的圆心角是__________________°。
(完整版)北师版七年级上数学第四章基本平面图形知识点及练习题
4.1 线段、射线、直线1、线段、射线、直线 线段：绷紧的琴弦，人行横道线都可以近似的看做线段。
线段有两个端点。
射线：将线段向一个方向无限延长就形成了射线。
射线有一个端点。
直线：将线段向两个方向无限延长就形成了直线。
直线没有端点。
2、名称 图形 表示方法 端点 长度直线 直线AB (或BA )直线l 无端点 无法度量 射线射线OM 1个 无法度量 线段线段AB (或BA ) 线段l2个可度量长度3、直线的性质（1）直线公理：经过两个点有且只有一条直线。
（两点确定一条直线。
） （2）过一点的直线有无数条。
（3）直线是是向两方面无限延伸的，无端点，不可度量，不能比较大小。
4、点和直线的位置关系有两种：①点在直线上，或者说直线经过这个点。
②点在直线外，或者说直线不经过这个点。
※课时达标 1.填写下表:2.如图，共有 条线段.3.用两个钉子就可以把木条钉在墙上，其依据是_________ .4.平面上有五条直线，则这五条直线最多有_____交点，最少有_____个交点．5.平面上两条直线的位置关系只有两种，即__________和_________________.6.平面上有四个点，无三点共线，以其中一点为端点，并且经过另一点的射线共有_______条．※课后作业 ★基础巩固1.下列各直线的表示法中，正确的是（ ）.l BAMOlBA 名称 图例 端点数 延伸方向 有无长度 线段射线直线 A B C DA.直线AB.直线AB C直线ab D.直线Ab2.下列说法不正确的是( ) .A.直线AB与直线BA是同一条直线B.射线AB与射线BA是同一条射线C.线段AB与线段BA是同一条线段D.线段有两个端点,射线有一个端点,直线没有端点3.下列说法正确的是（）.A.射线比直线短B.两点确定一条直线C.经过三点只能作一条直线D.两条射线的长度的和等于直线的长度4.下列说法正确的是( ).A.过一点P只能作一条直线B.射线AB和射线BA表示同一条射线C.直线AB和直线BA表示同一条直线D.射线a比直线b短5.下列说法正确的是（）.A.延长射线OAB.延长直线lC.延长线段CDD.反向延长直线l6.平面内的三点可确定直线的条数是（）.A.3B.1或3C.0或1D.07.已知C,D在直线AB上，那么直线AB上的射线共有（）.A.6条B.7条C.8条D.9条8.下列说法中，错误的有（）.①射线是直线的一部分；②画一条射线，使它的长度为5厘米；③线段AB和线段BA是同一条线段；④射线AB和射线BA是同一条射线；⑤直线AB和直线BA是同一条直线.A.1个B.2个C.3个D.4个9.在一条笔直的校园大道两旁种树时，先定下两棵树的位置，然后其它树的位置也就确定下来了，这说明了直线的基本性质：________________________. 10.已知平面内的四个点A,B,C,D,过其中的两个点画直线：(1)若A,B,C,D四个点在同一条直线上，可以画出______条直线；(2)若A,B,C,D四个点有三个在同一条直线上，可以画出______条直线；(3)若A,B,C,D四个点中的任意三个都不在同一条直线上，可以画出_______条直线.11.读下列语句，并画出相应图形.(1)经过点M,N画一条直线；(2)直线ba,相交于点P，点A在直线a上，但不在直线b上；(3)三条直线cb,两两相交于点A,B,C.a,☆能力提高12.读句画图:如图所示，已知平面上四个点（1）画直线AB；（2）画线段AC；（3）画射线AD、DC、CB；（4）如图，指出图中有_____条线段，有___ 条射线并写出其中能用图中字母表示的线段和射线 .13.已知直线l上有n个点，试问：（1）此图形上有多少条射线？（2）此图形上有多少条线段？14.如图，线段AB上的点数与线段的总数有如下关系：如果线段AB上有三个点时，线段总共有3条，如果线段AB上有4个点时，线段总数有6条，如果线段AB上有5个点时，线段总数共有10条，……A C B3=2+1A C D B6=3+2+1A C D E B10=4+3+2+1(1)当线段AB上有6个点时，线段总数共有__________条.(2)当线段AB上有100个点时，线段总数共有多少条？●中考在线15.平面上不重合的两点确定一条直线，不同三点最多可确定3条，若平面上不同的n个点最多可确定21条直线，则n的值为（）.A.5B.6C.7D.816.同一平面内互不重合的三条直线的公共点的个数是( ).A.可能是0个，1个，2个B.可能是0个，2个，3个C.可能是0个，1个，2个或3个D.可能是1个或3个4.2 比较线段的长短1、线段的性质（1）线段公理：两点之间的所有连线中，线段最短。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
C
D
B E
A
O
C
A D
B
C N M B
A 21
E O
D C
B
A
图（6）D '
B '
A
O
C
G
D
B
第五章基本平面图形
一、1. 1.46°= ° ′ ″. 28°7′12″= °.
2. 如图，已知OE 平分∠AOB ，OD 平分∠BOC ，∠AOB 为直角， ∠EOD=70°，则∠BOC 的度数为 .
3. 如图,直线上四点A 、B 、C 、D,看图填空:
①AC=______+BC;②CD=AD —_______;③AC+BD —BC=_______.
4、如图，由泰山到青岛的某一次列车，运行途中停靠的车站依次是：泰山—济南—淄博—潍坊—青岛，那么要为这次列车制作的火车票有______．
5.用一个钉子把一根细木条钉在墙上，木条就可能绕着钉子 ，原因是 ；
当用两个钉子把木条钉在墙上时，木条就被固定住，其依据是 . 6.如图，AB 的长为m ，BC 的长为n ，M 、N 分别是AB 、BC 的中点，则MN=
7、如图（6），把一张长方形的纸按图那样折叠后，B 、D 两点落在B ′、D ′点处， 若得∠AOB ′=700, 则∠B ′OG 的度数为 。
8、如上右图，是一副三角板重叠而成的图形，则∠AOD+∠BOC=_____________. 9.如图，直线AB 、CD 相交于O ，∠COE 是直角，∠1=57°，则∠2=
10. 一个人从A 点出发向北偏东65°的方向走到B 点，再从B 点出发向南偏西15°方向走到C 点，那么∠ABC 的度数是 二、10、下列说法中，正确的是（ ）
A ．直线a 、b 经过点M B. 直线A 、
B 相交于点
C C. 直线A 、B 相交于点m D. 直线AB,C
D 相交于点m
11. 一轮船航行到B 处测得的小岛A 的方向为北偏东30°，那么从A 处观测此时B 处的方向
为（ ）
A.北偏东30°
B.北偏东60°
C.南偏西30°
D.南偏西60° 12、在时刻8:32时，时钟上的时针与分针之间的所成的夹角是（ ）
A.70°
B.64°
C.76°
D.80°
13.如图，圆的半径为4，阴影部分扇形的面积是（）
A. π
B. 2π
C. 3π
D. 4π
14. 同一平面内有四点，每过两点画一条直线，则直线的条数是（）
A．1条 B．4条 C．6条 D．1条或4条或6条
15、已知A、B两点之间的距离是10 cm，C是线段AB上的任意一点，则AC中点与BC中点间的距离是（）
A.3 cm
B.4 cm
C.5 cm
D.不能计算
16、平面上有四点，经过其中的两点画直线最多可画出( )．
A．三条B．四条C．五条D．六条
17、如图，O为直线AB上一点，∠COB＝26°30′，则∠1＝( )．
A．153°30′B．163°30′C．173°30′
D．183°30′
18、如图6，∠AOB为平角，且∠AOC=
2
1
∠BOC，则∠BOC的度数是（）
19、如图7，军舰从港口沿OB方向航行，它的方向是（）
A.东偏南30°
B.南偏东60°
C.南偏西30°
D.北偏东30°
20、下列说法中正确的是( )
A、8时45分，时针与分针的夹角是30°
B、6时30分，时针与分针重合
C、3时30分，时针与分针的夹角是90°
D、3时整，时针与分针的夹角是90°
21、如果线段AB=5cm,线段BC=4cm,那么A,C两点之间的距离是（）
A. 9cm
B.1cm
C.1cm或9cm
D.以上答案都不对
22、如图,下列表示角的方法,错误的是( )
A.∠1与∠AOB表示同一个角;
B.∠AOC也可用∠O来表示
C.图中共有三个角:∠AOB、∠AOC、∠BOC;
D.∠β表示的是∠BOC
23、已知OA⊥OC，∠AOB：∠AOC=2：3，则∠BOC的度数为（）
A.30
B.150
C.30或150
D.以上都不对
24、如图，四条表示方向的射线中，表示北偏东60°的是( )
25.下列各角中，不能用一副三角板拼出的角度为（）
A. 60°
B.75°
C. 135°
D. 140°
(1)
b
a
(3)
a
(2)
B
D
C
B
A
26.关于中点的说法正确的是（）
A.若AB=BC,则点B是线段AC的中点
B.若AB=
2
1
AC，则点B是线段AC的中点
C. 若BC=
2
1
AC，则点B是线段AC的中点D. 若AB=BC =
2
1
AC，则点B是线段AC的中点
27.在下列时刻，钟面上时针与分针成直角的情况（）
A.12时15分
B.9时
C.3时30分
D.6时45分
28.直线l上顺次三点A、B、C，M是AB中点，N是AC
若AB=12cm，BC=8cm,则MN=（）
A.2 cm
B.4 cm
C.8 cm
D.10 cm
29.如图，下列说法错误的是（）
A. A点在O点的北偏东60°方向
B. B点在O点的西偏北30°方向
C.C点在O点的正南方向
D. D点在O点的东南方向
30.下面四个选项中，能用∠1，∠AOB，∠O三种方法表示同一个角的是（）
A B C D
31. 一根绳子弯曲成如图（1）所示的形状，当剪刀像图（2）那样沿虚线a把绳子剪断时，
绳子被剪为5段；当剪刀像图（3）那样沿虚线b(b∥a)把绳子再剪一次时，绳子被剪为9段.
若剪刀在虚线a,b之间再剪（n-1）次（剪刀的方向与a平行），这样一共剪n次时（不含沿
虚线a剪的一次）绳子的段数为（）
A.4n+1
B.4n+2
C.4n+3
D.4n+5
33、如图，在公路l的两旁有两个工厂A、B，要在公路上搭建一个货场让A、B两厂使用，
要使货场到A、B两厂的距离之和最小，问货场应建在什么位置？为什么？
34.你能在图中找出一点P，使点P到点A、B、C、D四个点的距离之和最小吗？
四、35如图，A、B、C、D在同一条直线上，已知AC=BD=18cm，且AB:AD=2:11，求AB,BC
的长度。
东
35题图
A B C D
36.已知：如图，∠AOB 是直角，∠AOC =30°，ON 是∠AOC 的平分线，OM 是∠BOC 的平分线．求∠MON 的大小.
37、如图，将一张长方形纸斜折过去，使顶点A 落在A ′处，BC 为折痕，然后把BE 折过去，使之与A ′B 重合，折痕为BD ，那么两折痕BC 、BD 间的夹角是多少度？ 38、把一副三角尺如图所示拼在一起，求∠A 、∠B 、∠AEB 、∠ACD 的度数
39、如图8，已知∠1∶∠3∶∠4=1∶2∶4,∠2=80°，求∠1、∠3、∠4的度数
.
40、在直线l 上任取一点A ，截取AB =16 cm ，再截取AC =40 cm ，求AB 的中点D 与AC 的中点E 之间的距离.
A
B
C A ′
D
E
A E
B C D
第20题图
B
C D E C
O E D B A
41、已知线段AB=12cm ，在直线AB 上有一点C ，且BC=4cm ，M 是线段AC 的中点，求线
段AM 的长.
42、如图已知点C 为AB 上一点，AC ＝12cm, CB ＝
3
2
AC ，D 、E 分别为AC 、AB 的中点求DE 的长。
43. 如图，DO 平分∠AOC 、OE 平分∠BOC ，若O A ⊥OB ，
(1)当∠BOC=30°，∠DOE= ；
当∠BOC=60°，∠DOE= .
（2）通过上面的计算，猜想∠DOE 的度数与∠AOB 有什么关系， 并说明理由.
44.如图，线段AB 上的点数与线段的总数有如下关系：如果线段AB 上有三个点时，线段总共有3条，如果线段AB 上有4个点时，线段总数有6条，如果线段AB 上有5个点时，线段总数共有10条，……
3=2+1 6=3+2+1 10=4+3+2+1 (1)、当线段AB 上有6个点时，线段总数共有 条。
(2)、当线段AB 上有n 个点时，线段总数共有 条。
A C
B A
C
D B A C D
E B。