本福特定律和万物之源
神秘的本福特定律范文

神秘的本福特定律physixfan 2010-10-31 21:25统计一下世界上237个国家的人口数量,你觉得其中以1开头的数会占多大比例,而以9开头的数又占多大比例呢?如果你的回答是都为1/9,恭喜你你是正常人,但是事实却不是如此:以1开头的数惊人的占到了27%,而以9开头的数却只占5%。
下图可以很形象的展示出在各国人口数量问题上,以各个数字开头的数占了多大的比例(图片来自维基百科)。
为什么会相差这么大呢?这正是神秘的本福特定律在起作用。
本福特定律,也称为本福德法则,说明一堆从实际生活得出的数据中,以1为首位数字的数的出现机率约为总数的三成,接近期望值1/9的3倍,推广来说,越大的数字,以它为首几位的数出现的机率就越低;精确地数学表述为:在b进位制中,以数n起头的数出现的机率为logb(n + 1) − logb(n)。
在十进制中,首位数字出现的概率为:这个定律的发现,据说是因为本福特在翻对数表的时候发现前面几页被翻得很黑很破烂,越往后越颜色越浅。
由此他想到会不会是1开头的数字就是比其他数多,他统计了一下发现果然如此。
其实这个对数表的事情真假难辨了,就像是牛顿说自己是被苹果砸到了头才发现的万有引力定律一样,只要最后的定律有用就可以了。
首先说明一下本福特定律的适用范围这个定律是一个非常神奇的定律,它的适用范围异常的广泛,几乎所有日常生活中没有人为规则的统计数据都满足这个定律。
比如说世界各国人口数量、各国国土面积、账本、物理化学常数、数学物理课本后面的答案、放射性半衰期等等数据居然都符合本福特定律。
值得一提的是,科学家还发现,统计物理的三个重要分布,Boltzmann-Gibbs分布,Bose-Einstein分布,Fermi-Dirac分布,也基本上满足Benford定律!(来源:李淼的博客)其次这个定律毕竟还是有适用范围的第一,这些数据必须跨度足够大,必须横跨好几个数量级才能产生这个结果。
第二,有人为规则的数据就不满足次定律,比如说手机号码、身份证号、发票编号等数据,明显不满足这种对数分布律。
本福特定律

1881年,天文学家西蒙·纽康伯发现对数表包含以1起首的数那首几页较其他页破烂。
可是,亦可以以任何书起首数页也会较破烂这个观点解释。
这个故事可能是虚构的。
1938年,物理学家法兰克·本福特重新发现这个现象,还通过了检查许多数据来证实这点。
2009年,西班牙数学家在素数中发现了一种新模式,并且惊讶于为何那时才为人发现。
虽然素数一般被认为是随机分布的,但西班牙数学家发现素数数列中每个素数的首位数字有明显的分布规律,它可以被描述了素数的本福德法则。
这项新发现除了提供对素数属性的新洞见之外,还能应用于欺骗检测和股票市场分析等领域。
数字统计的一种内在规律,指所有自然随机变量,只要样本空间足够大,每一样本首位数字为1至9各数字的概率在一定范围内具有稳定性。
见右图。
即以1开首的样本占样本空间的0.3,以2开首的样本占样本空间0.17-0.19,而以9或8开首的样本始终只占0.05左右。
世界上千千万万的数据的开头数字是1到9中的任何一个数字,而且每个数字打头的概率本应该差不多,但如果你统计的数据足够多,就会惊讶地发现,打头数字是1的数据最多。
1935年,美国的一位叫做本福特的物理学家在图书馆翻阅对数表时发现,对数表的头几页比后面的页更脏一些,这说明头几页在平时被更多的人翻阅。
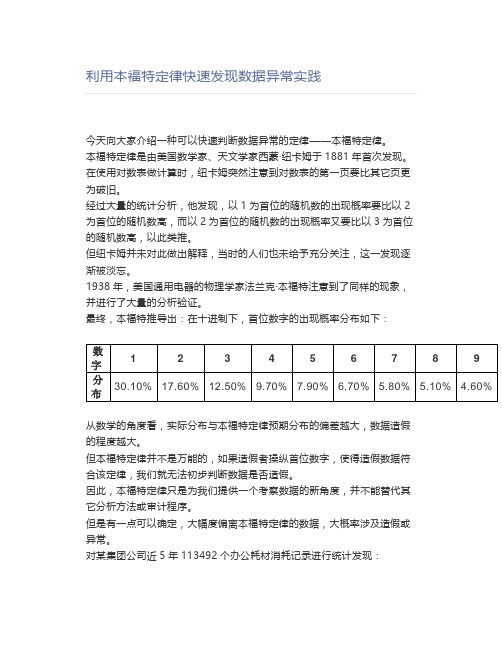
本福特再进一步研究后发现,只要数据的样本足够多,数据中以1为开头的数字出现的频率并不是1/9,而是30.1%。
而以2为首的数字出现的频率是17.6%,往后出现频率依次减少,9的出现频率最低,只有4.6%。
本福特开始对其它数字进行调查,发现各种完全不相同的数据,比如人口、物理和化学常数、棒球统计表以及斐波纳契数列数字中,均有这个定律的身影。
1961年,一位美国科学家提出,本福特定律其实是数字累加造成的现象,即使没有单位的数字。
比如,假设股票市场上的指数一开始是1000点,并以每年10%的程度上升,那么要用7年多时间,这个指数才能从1000点上升到2000点的水平;而由2000点上升到 3000点只需要4年多时间;但是,如果要让指数从10000点上升到20000点,还需要等7年多的时间。
利用本福特定律快速发现数据异常实践
利用本福特定律快速发现数据异常实践
今天向大家介绍一种可以快速判断数据异常的定律——本福特定律。
本福特定律是由美国数学家、天文学家西蒙·纽卡姆于1881年首次发现。
在使用对数表做计算时,纽卡姆突然注意到对数表的第一页要比其它页更为破旧。
经过大量的统计分析,他发现,以1为首位的随机数的出现概率要比以2为首位的随机数高,而以2为首位的随机数的出现概率又要比以3为首位的随机数高,以此类推。
但纽卡姆并未对此做出解释,当时的人们也未给予充分关注,这一发现逐渐被淡忘。
1938年,美国通用电器的物理学家法兰克·本福特注意到了同样的现象,并进行了大量的分析验证。
最终,本福特推导出:在十进制下,首位数字的出现概率分布如下:
从数学的角度看,实际分布与本福特定律预期分布的偏差越大,数据造假的程度越大。
但本福特定律并不是万能的,如果造假者操纵首位数字,使得造假数据符合该定律,我们就无法初步判断数据是否造假。
因此,本福特定律只是为我们提供一个考察数据的新角度,并不能替代其它分析方法或审计程序。
但是有一点可以确定,大幅度偏离本福特定律的数据,大概率涉及造假或异常。
对某集团公司近5年113492个办公耗材消耗记录进行统计发现:
能看出明显异常吗?
异常即为妖!审计人员带着怀疑对异常的数据5开头的数据进行分析发现:硒鼓与打印纸之间存在相关性。
按照单位对硒鼓与打印纸的数据进行对比发现下图异常的数据在红色方框之外。
沿着数据异常这个思路进一步分析发现了虚假冒用以物易物的现象,提出加强管理建议后效果显著。
2017年该方面的费用支出同比节约了近50%。
对本福特定律的感受和理解

本福特定律的感受和理解1. 引言在现代社会,我们常常会听到“本福特定律”这个词,它是由美国工程师亨利·福特所提出的经济学定律。
本福特定律指出,随着生产数量的增加,单位成本会逐渐下降,从而带来更高的效率和更低的价格。
在这篇文章中,我将分享对本福特定律的感受和理解,并探讨其在现实生活中的应用。
2. 感受与体会2.1 效率改善本福特定律的核心观点是,随着生产数量的增加,单位成本会下降。
这意味着企业可以通过规模化生产来降低成本,提高产品的生产效率。
在我个人的观察和体验中,这一观点得到了充分的验证。
举个例子,汽车制造业是本福特定律应用得非常成功的行业之一。
当汽车生产规模不断扩大时,企业可以利用大规模生产带来的规模经济,降低材料采购成本和生产设备成本,从而降低单位成本。
这使得汽车在过去几十年中价格不断下降,使得更多人能够负担得起汽车。
2.2 价格竞争因为单位成本的下降,企业有更多的空间来降低产品价格,以吸引更多的消费者。
这就引发了激烈的价格竞争,从而推动了市场的发展。
以电子产品为例,比如手机。
随着技术的进步和生产能力的提高,手机的价格逐渐下降,同时功能和性能也得到了大幅度的提升。
这使得越来越多的消费者能够购买到价格合理且功能强大的手机。
这种价格竞争不仅满足了消费者的需求,也推动了全球电子产品市场的繁荣。
2.3 产品多样性本福特定律还促进了产品多样化的发展。
当规模生产降低了单位成本之后,企业可以更容易地推出多个产品系列,满足不同消费者的需求。
通过适应不同的市场细分,企业能够生产出更多样化、更专门化的产品。
例如,汽车制造商可以根据不同国家和地区的需求,设计和生产不同尺寸、不同燃料类型、不同配置的汽车。
因此,消费者能够根据自己的喜好和需求选择适合自己的产品。
3. 应用与实践3.1 制造业在制造业领域,本福特定律的应用非常普遍。
通过扩大生产规模,企业可以降低成本,提高生产效率并降低产品价格。
这使得制造业具备了更强的竞争力。
本福特定律的应用案例

本福特定律的应用案例本福特定律的应用案例1. 引言本福特定律源自于美国制造业巨头亨利·福特的观察和实践,它是关于生产效率和资源利用的经验法则。
福特定律认为,在生产过程中,只有通过标准化和专业化的流程,才能实现最高效率和资源利用率。
本福特定律的应用案例可以在各个行业中找到,旨在帮助企业提升生产效率、降低成本,从而取得更大的竞争优势。
2. 应用案例一:汽车制造业汽车制造业是福特定律的经典应用领域之一。
福特公司在20世纪初就开始采用装配线生产方式,通过将汽车生产过程分解为一系列标准化的步骤,大幅提升了生产效率。
福特公司通过将汽车组装过程分为多个工位,每个工位专门负责一个环节,工人只需专注于自己负责的工作,大大提高了生产效率。
这种流水线生产模式不仅大幅降低了生产成本,也加速了汽车的生产速度,使得福特汽车在20世纪初成为了当时最畅销的汽车品牌之一。
3. 应用案例二:电子产品制造业电子产品制造业也是福特定律的典型应用领域之一。
随着电子产品的日益普及和更新换代的速度加快,如何提高生产效率成为了电子企业的关键挑战。
借鉴福特定律的理念,电子企业可以通过优化生产流程、采用自动化生产设备和机器人等方式来提高生产效率和资源利用率。
将电子产品的制造过程分解为多个标准化的工序,通过自动化设备来完成生产任务,既可以提高生产效率,又能提升产品质量和降低人力成本。
4. 应用案例三:餐饮行业福特定律的应用不仅限于制造业,餐饮行业也可以从中受益。
餐饮企业可以通过标准化的菜品制作流程和供应链管理,提高餐厅的营运效率和服务质量。
将菜品的制作过程细化为多个标准化的步骤,根据每个步骤的要求安排专业化的工作人员,确保每道菜品的制作效率和质量。
建立高效的供应链管理系统,减少菜品原材料和食材的浪费,提高资源利用率,对餐饮企业的经营效益和可持续发展具有重要意义。
5. 应用案例四:物流行业物流行业也是福特定律的受益者之一。
物流企业可以通过标准化的运输方式和仓储管理来提高运营效率和资源利用率。
本福特定律的原理概述

本福特定律的原理概述The principle of the Ford Duality Law is a fundamental concept in mathematics and physics. It deals with the relationship between primal and dual feasible solutions in linear programming. The law states that if a primal linear program has an optimal solution, then its dual linear program will also have an optimal solution, and the optimal values of the two solutions will be equal.福特定律的原理对数学和物理学都有重要影响。
它涉及线性规划中原问题和对偶问题之间的关系。
定律表明,如果原线性规划有最优解,则其对偶线性规划也将有最优解,并且两个最优解的值将相等。
The duality principle serves as a powerful tool in optimization theory and is crucial for understanding the underlying structure of linear programming problems. By relating the primal and dual problems, it allows us to make inferences about one problem based on the solutions of the other. This duality relationship provides insight into the nature of constraints and objectives in a linear programming model.对偶原理是优化理论中的重要工具,对于理解线性规划问题的基本结构至关重要。
神奇的本福特定律

神奇的本福特定律从常理上说,世界上千千万万的数据(非开0头)的开头数字是1到9的任何一个数字,而且每个数字开头的概率应该差不多。
现在,请你随便找本书,统计一下上面的各种开头数据的开头数字,看看是否符合我们的设想。
如果你统计的数据足够多,你就会惊讶的发现,开头数字是1的数据最多,大约占了所有数据的1/3左右,打头是2的数据其次,往后依此减少。
难道是人们对1情有独钟,把它时常写在数据的最前面吗?肮脏的对数表书页首先要恭喜你,你发现了数学上的一个有趣的定律,这就是本福特定律。
据说这个定律在1881年首先被一位天文学家在分析数据的时候发现,但是当时科学家们并没有把这个发现当回事。
直到1935年,美国的一个叫本福特的物理学家从新发现了这个定律。
当时,他在图书馆翻阅对数表时发现,对数表的头几页比后面几页更脏一些,这说明头几页在平时被更多的人翻阅。
这并不奇怪,因为许多读书的人都先看看书的开头,不喜欢就不再读下去。
但是,对数表却是一种数学工具,只有需要查数据的人才会去碰它。
因此,头几页如果比较脏,这就说明人们查阅的数据大多在头几页里,也反映出人们所使用的数据并不是散乱的,而是有些数据使用的频率比较高。
本福特再进一步研究后发现,只要数据的样本足够多,同时数据没有特定的上限和下限,则数据中以1为开头的数字出现的频率并不是人们想当然认为的1/9,而是0.301,这说明30%的数字都以1开头。
而2为首的数字出现的频率是0.176,3开头的数字出现的频率为0.125,往后出现频率依此减少,9打头的数字出现的频率最低,只有0.046。
这个规律甚至能用一个数学方程来表示。
除了对数表,其他类型的数据是否也有这样的现象呢?本福特开始对其他数字进行调查,发现各种完全不同的数据,比如人口,死亡率,物理和化学常数,棒球统计表,半衰期放射性同位素,物理书中的答案,素数数字中均有这个定律的身影。
定律成因之迷本福特定律在生活中很常见,但是为什么人们使用的数据会有这样的现象呢?几十年来,人们提出了一些猜想来解释这个现象。
万物原理简介

万物原理简介万物原理是一种哲学概念,指的是万物宇宙中的一种本质规律或原则,无论是物理、化学、生物还是哲学等各个领域都能体现其存在。
它是人类对自然界的认识和理解的总结,探索了世界的本源和本质,并试图揭示宇宙中的种种规律和现象。
万物原理的出现可以追溯到古希腊哲学和自然科学,例如亚里士多德、柏拉图和皮尔士等人,他们最早提出了万物的本源和原则,试图用自己的知识和思想来解释自然界。
在古代,万物原理通常与宇宙创造或神创说联系在一起,认为世界万物都是神创造的。
随着时代的变迁和人类知识的不断积累,万物原理的概念也逐渐演变和丰富。
在近代科学发展的背景下,有许多重要的学者和科学家探索和研究了万物原理的本质,例如牛顿、达尔文、爱因斯坦等人,他们的研究成果对于现代科学理论和技术的发展起到了极其重要的作用。
万物原理的本质是宇宙万物间的联系和律动,试图从整体上理解宇宙的运行和演化,揭示自然界的本质规律和奥秘。
从宏观到微观,从可见到不可见,万物原理无处不在,方圆天地间,无穷无尽,是我们认识和探索自然界的基石。
万物原理涵盖了世界和人类生命的本质和意义。
它不仅是自然科学的基础,也是人文思想的起点。
在现代社会,我们需要更加深入的了解和认识万物原理,以便更好地理解和应对我们所面临的各种复杂情况。
万物原理在物理学中的表现万物原理在物理学中的表现可以用几个基本原则来概括,它们是:能量守恒原理、热力学第二定律、相对论原理和量子力学基本原理。
能量守恒原理是万物运行的核心原则,它指的是能量在宇宙间的传递和转化是不断变化但总量不变,能量转化的各种过程必须满足物理学中的各种法则和规律。
热力学第二定律是指热量无法从低温物体自发地传递到高温物体,热量只能从高温物体向低温物体传递,这个定律规定了所有物质的基本运动方向。
相对论原理是爱因斯坦的理论,它是现代物理学中的核心原则,指出时间和空间是相对的,光速是宇宙中唯一不变的物理常数,它改变了我们对时间和空间的常规认识。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
本福特定律和万物之源
北京大学的研究人员发现,本福特定律与物理学中广泛使用的统计分布规律存在联系,这项发现暗示本福特定律可能是宇宙的基本规律之一。
物理学家法兰克·本福特于1938年发现了以他姓命名的本福特定律(Benford's law),这一规律描述了常用数字集和数据序列中数的首位数字分布。
比如在实际生活中,以1为首位数字的数的出现机率约为总数的三成,接近期望值1/9的3倍。
总体上说,1出现的几率是30.1%,2是17.6%,3是12.5%...9是4.6%。
推广来说,越大的数,以它为首位的数出现的机率就越低。
不过,并不是所有的数据集都符合本福特定律,比如彩票和电话号码就不遵守这一定律。
但是现在北京大学物理系马伯强教授和研究生邵立晶的新发现为本福特定律的性质提供了新的见解。
他们发现,物理学的三大统计学方法:Boltzmann-Gibbs分布、费米-狄拉克分布和玻色一爱因斯坦分布都符合本福特定律。
研究人员认为,本福特定律可能是自然复杂性背后的一项基本原则。
论文发表在预印本网站arxiv。
