统计计算题
统计学计算题整理

:典型计算题一1、某地区销售某种商品的价格和销售量资料如下:根据资料计算三种规格商品的平均销售价格。
解:36==∑∑ffxx (元)点评: 第一,此题给出销售单价和销售量资料,即给出了计算平均指标的分母资料,所以需采用算术平均数计算平均价格。
第二,所给资料是组距数列,因此需计算出组中值。
采用加权算术平均数计算平均价格。
第三,此题所给的是比重权数,因此需采用以比重形式表示的加权算术平均数公式计算。
2、某企业1992年产值计划是1991年的105%,1992年实际产值是1991的的116%,问1992年产值计划完成程度是多少解:%110%105%116===计划相对数实际相对数计划完成程度。
即1992年计划完成程度为110%,超额完成计划10%。
点评:此题中的计划任务和实际完成都是“含基数”百分数,所以可以直接代入基本公式计算。
3、某企业1992年单位成本计划是1991年的95%,实际单位成本是1991年的90%,问1992年单位成本计划完成程度是多少解: 计划完成程度%74.94%95%90==计划相对数实际相对数。
即92年单位成本计划完成程度是%,超额完成计划%。
点评:本题是“含基数”的相对数,直接套用公式计算计划完成程度。
4、某企业1992年产值计划比91年增长5%,实际增长16%,问1992年产值计划完成程度是多少解:计划完成程度%110%51%161=++=点评:这是“不含基数”的相对数计算计划完成程度,应先将“不含基数”的相对数还原成“含基数”的相对数,才能进行计算。
5、某企业1992年单位成本计划比1991年降低5%,实际降低10%,问1992年单位成本降低计划完成程度是多少解:计划完成程度%74.94%51%101=--=点评:这是“不含基数”的相对数计算计划完成程度,应先将“不含基数”的相对数还原成“含基数”的相对数,才能进行计算。
6、某企业产值计划完成103%,比上期增长5%,问产值计划规定比上期增加多少 解:103%=105%÷(1+x )x=%即产值计划规定比上期增加%.点评:计划完成程度=103%,实际完成相对数=105%,设产值计划规定比上期增加x,则计划任务相对数=1+x,根据基本关系推算出x.7、某煤矿某月计划任务为5400吨,各旬计划任务是均衡安排的,根据资料分析本月生产情况.=104%),但在节奏性方面把握不解:从资料看,尽管超额完成了全期计划(5400好。
统计学计算题整理

:典型计算题一1、某地区销售某种商品的价格和销售量资料如下:根据资料计算三种规格商品的平均销售价格。
解:36==∑∑ffxx (元)点评: 第一,此题给出销售单价和销售量资料,即给出了计算平均指标的分母资料,所以需采用算术平均数计算平均价格。
第二,所给资料是组距数列,因此需计算出组中值。
采用加权算术平均数计算平均价格。
第三,此题所给的是比重权数,因此需采用以比重形式表示的加权算术平均数公式计算。
2、某企业1992年产值计划是1991年的105%,1992年实际产值是1991的的116%,问1992年产值计划完成程度是多少?解:%110%105%116===计划相对数实际相对数计划完成程度。
即1992年计划完成程度为110%,超额完成计划10%。
点评:此题中的计划任务和实际完成都是“含基数”百分数,所以可以直接代入基本公式计算。
3、某企业1992年单位成本计划是1991年的95%,实际单位成本是1991年的90%,问1992年单位成本计划完成程度是多少?解: 计划完成程度%74.94%95%90==计划相对数实际相对数。
即92年单位成本计划完成程度是94.74%,超额完成计划5.26%。
点评:本题是“含基数”的相对数,直接套用公式计算计划完成程度。
4、某企业1992年产值计划比91年增长5%,实际增长16%,问1992年产值计划完成程度是多少?解:计划完成程度%110%51%161=++=点评:这是“不含基数”的相对数计算计划完成程度,应先将“不含基数”的相对数还原成“含基数”的相对数,才能进行计算。
5、某企业1992年单位成本计划比1991年降低5%,实际降低10%,问1992年单位成本降低计划完成程度是多少?解:计划完成程度%74.94%51%101=--=点评:这是“不含基数”的相对数计算计划完成程度,应先将“不含基数”的相对数还原成“含基数”的相对数,才能进行计算。
6、某企业产值计划完成103%,比上期增长5%,问产值计划规定比上期增加多少? 解:103%=105%÷(1+x ) x=1.9%即产值计划规定比上期增加1.9%.点评:计划完成程度=103%,实际完成相对数=105%,设产值计划规定比上期增加x ,则计划任务相对数=1+x ,根据基本关系推算出x.7、某煤矿某月计划任务为5400吨,各旬计划任务是均衡安排的,根据资料分析本月生产情况.解:从资料看,尽管超额完成了全期计划(5400=104%),但在节奏 性方面把握不好。
统计计算题

第四章五、计算要求:(1)分别计算两个车间工人的平均日产量;(2)乙车间工人平均日产量的标准差及标准差系数,并比较平均数的代表性。
2要求:(1)计算售货员日平均销售额;(2)计算日销售额的众数和中位数,并分析销售额的分布状况。
3又知乙企业的平均工资为653元,工资标准差为127.50元,试分析比较哪个企业的平均工资更具代表性。
456试分别计算2008年和2009年两个车间的平均一级品率。
7计算:(1)产量计划平均完成百分比;(2)平均一级品率。
第五章五、计算2计算:(1)一季度月平均商品流转次数;(提示:商品流转次数=商品销售额÷平均库存额)(2)一季度的商品流转次数。
3试计算:(1)该企业第二季度的平均月劳动生产率;(2)该企业上半年的劳动生产率。
5试计算:(1)各车间12月份的劳动生产率;(2)整个企业12月份的劳动生产率。
6计算:(1)第四季度平均每月的商品流转次数(提示:商品流转次数=商品销售额÷平均库存额);(2)第四季度的商品流转次数7计算:(1)分别计算甲、乙两省产量的平均发展速度;(2)按这几年的平均发展速度再有多少年甲省可以赶上乙省2007年的水平;(3)假设甲省的产量变化为直线趋势,使用最小平方法配合趋势方程,并预测2009年喝2010年的产量。
8.某地区2002年GDP为50亿元,计划2003年至2007年5年中增长60%,求年平均增长速度。
如果该地区GDP2003年比2002年增长7.1%,2004年比2003年增长7.8%,问该地区2005年至2007年的GDP年平均增长速度达到多少才能完成预定的计划?第六章五、计算1计算:(1)销售额总指数;(2)从相对数和绝对数两个方面对销售额的变动进行因素分析。
2试从相对数和绝对数两个方面对该厂生产费用总额(总成本)进行因素分析。
3.某厂三种产品的总成本2007年为129万元,比2006年多9万元,三种产品单位成本平均比2006年降低3%。
(完整word版)统计计算题(word文档良心出品)
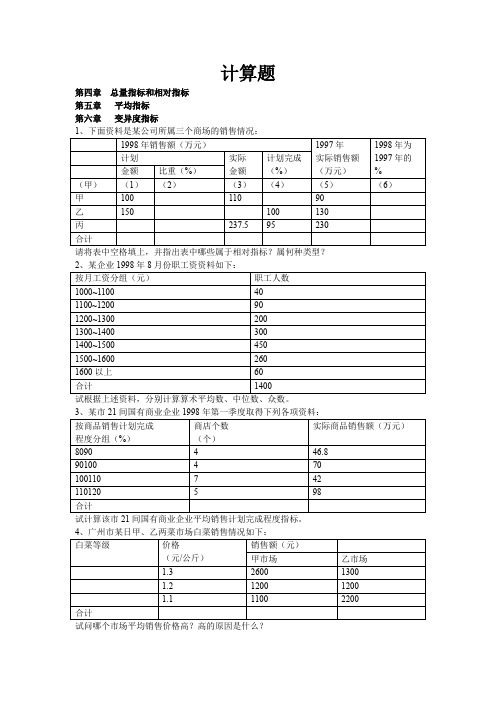
计算题第四章总量指标和相对指标第五章平均指标第六章变异度指标请将表中空格填上,并指出表中哪些属于相对指标?属何种类型?试根据上述资料,分别计算算术平均数、中位数、众数。
试计算该市21间国有商业企业平均销售计划完成程度指标。
试问哪个市场平均销售价格高?高的原因是什么?试计算:(1)两个车间计划和实际的平均一级品率;(2)一级品产值、全部产值的计划完成百分比。
试研究两个品种的平均亩产量,确定哪一品种具有较好的稳定性?第七章统计指数(2)从相对数和绝对数两方面简要分析销售量和价格变动对销售变动的影响。
试运用指数体系对核企业三种产品的总成本变动进行因素分析。
3、某商店三种商品的销售资料如下:(12分)⑴试计算销售量指数。
⑵试计算销售额指数和价格指数。
⑶试从相对数和绝对数两方面简要分析销售额变动的影响因素。
4(1)试计算出厂价格指数和由于价格变化而增加的总产值。
(2)试计算总产值指数和产品产量指数。
(3)试从相对数和绝对数两方面简要分析总产值变动的影响因素。
5、某公司2001年商品零售额为46万元,2002年比2001年增加40万元,零售物价指数上涨8%,试计算该公司商品零售额变动中由于零售价格和零售量变动的影响程度和绝对额。
第八章抽样调查1、某地外贸公司对进口的一种物品(2000件)的重量进行抽样检验,按不重复抽样的方法试以0.9545的概率估计该种物品(2000件)的平均重量的区间范围。
2、某电子元件厂随机抽选100个元件检验,其中有4个元件为废品,又知抽样数量产品总数的千分之一,若以95.45%的概率保证,试估计该厂生产的电子元件的废品率范围。
若极限误差减少一半,其他条件不变,在重复抽样的情况下,需抽多少个元件检验?在不重复抽样的情况下又如何?3、某年某月糖烟酒公司库存一批水果罐头100000罐,按纯随机抽样取1000罐进行质检,发现有20罐已变质,当概率为0.9545条件下,估计这批罐头中有多少变质?4、对某地区15000户职工进行家庭收入情况的调查,现已知职工家庭收入标准差为0.401元,在给定的极限抽样误差不超过0.05元的情况下,试问要求把握程度不低于99.73%,按纯随机不重复抽样应当调查多少户?第十章相关与回归1、某企业产品产量与单位成本的资料如下:(1)确定直线回归方程,指出产量每增加1000件时,单位成本平均下降多少元?(2)假定产量为6000件时,单位成本为多少元?(3)单位成本为70元,产量应为多少件?(1)相关系数。
统计学计算题(54学时)【精选文档】

统计学习题集第三章数据分布特征的描述五、计算题1。
某企业两个车间的工人生产定额完成情况如下表:技术水平A车间B车间工人数完成定额工时人均完成工时工人数完成工时定额人均完成工时高50 14000 280 20 6000 300中30 7500 250 40 10400 260低20 4000 200 40 8200 205合计100 25500 255 100 24600 246从表中看,各个技术级别的工人劳动生产率(人均完成工时定额)都是A车间低于B车间,试问:为什么A车间的平均劳动生产率又会高于B车间呢?3. 根据某城市500户居民家计调查结果,将居民户按其食品开支占全部消费开支的比重(即恩格尔系数)分组后,得到如下的频数分布资料:恩格尔系数(%) 居民户数20以下620~30 3830~40 10740~50 13750~60 11460~70 7470以上24合计500要求:(1)据资料估计该城市恩格尔系数的中位数和众数,并说明这两个平均数的具体分析意义。
(2)利用上表资料,按居民户数加权计算该城市恩格尔系数的算术平均数.(3)试考虑,上面计算的算术平均数能否说明该城市恩格尔系数的一般水平?为什么?恩格尔系数(%) 居民户数(户)f 组中值x 向上累积频数20以下 6 15 620~30 38 25 4430~40 107 35 15140~50 137 45 28850~60 114 55 40260~70 74 65 47670以上24 75 500合计500 --答:(1)Me=47.226%,指处于中间位置的居民家庭恩格尔系数水平;Mo=45。
661%,指居民家庭中出现最多的恩格尔系数水平;(2)均值=47.660%;4. 某学院二年级两个班的学生英语统考成绩如下表。
要求:(1)分别计算两个班的平均成绩;(2)试比较说明,哪个班的平均成绩更有代表性?哪个班的学生英语水平差距更大?你是用什么指标来说明这些问题的;为什么?英语统考成绩学生人数A班B班60以下4 660~70 12 1370~80 24 2880~90 6 890以上4 5合计50 605. 利用上题资料,试计算A班成绩分布的极差与平均差,并与标准差的计算结果进行比较,看看三者之间是何种数量关系。
统计学计算题

第三章统计整理例 1、某厂工人日产量资料如下:(单位:公斤)162 158 158 163 156 157 160 162 168 160164 152 159 159 168 159 154 157 160 159163 160 158 154 156 156 156 169 163 167试根据上述资料,编制组距式变量数列,并计算出频率。
解:将原始资料按其数值大小重新排列。
152158 159154 154 156 156 156 156 157 157 158 158 159 159 159 159 160 160 160 162 162 163 163 163 164 167168 168 169最大数=169,最小数=152,全距=169-152=17n=30, 分为 6 组例 2、某企业 50 个职工的月工资资料如下:113 125 78 115 84 135 97 105 110 130105 85 88 102 101 103 107 118 103 87116 67 106 63 115 85 121 97 117 10794 115 105 145 103 97 120 130 125 127122 88 98 131 112 94 96 115 145 143试根据上述资料,将50 个职工的工资编制成等距数列,列出累计频数和累计频率。
解:将原始资料按其数值大小重新排列。
63 97 117 118工人按日产量分组(公斤)152-154155-157158-160161-163164-166 工人数(人)361151比率(频率)(%)10.0020.0036.6016.7067 78 84 85 85 87 88 88 94 94 96 97 97 98 101 102 103 103 103 105 105 105 107 110 112 113 115 115 115 115 116 118 120 121 122 125 125 127 130 130 131 135 143 145 145按工资额分组(元)60-70 70-80 80-90频数216工人数频率( %)4212频数239向上累计频率( %)4618频数504847向下累计频率(%)1009694例 3、有 27 个工人看管机器台数如下:5 4 2 4 3 4 3 4 4 2 4 3 4 3 26 4 4 2 2 3 4 5 3 2 4 3试编制分布数列。
统计学计算题例题
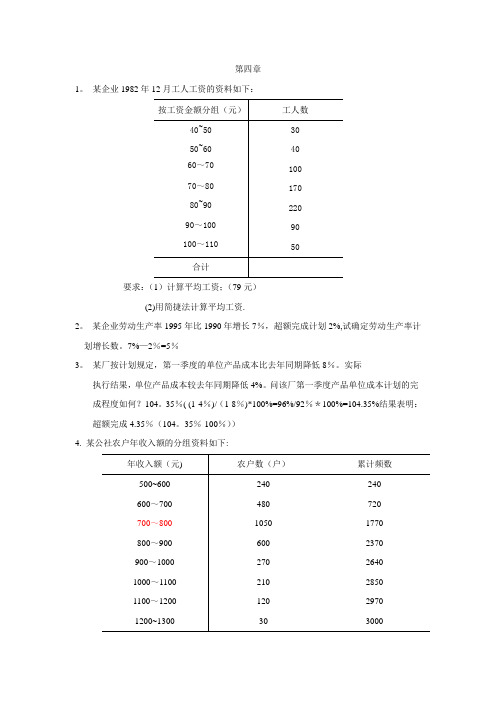
第四章1。
某企业1982年12月工人工资的资料如下:要求:(1)计算平均工资;(79元)(2)用简捷法计算平均工资.2。
某企业劳动生产率1995年比1990年增长7%,超额完成计划2%,试确定劳动生产率计划增长数。
7%—2%=5%3。
某厂按计划规定,第一季度的单位产品成本比去年同期降低8%。
实际执行结果,单位产品成本较去年同期降低4%。
问该厂第一季度产品单位成本计划的完成程度如何?104。
35%( (1-4%)/(1-8%)*100%=96%/92%*100%=104.35%结果表明:超额完成4.35%(104。
35%-100%))4. 某公社农户年收入额的分组资料如下:要求:试确定其中位数及众数。
中位数为774.3(元)众数为755。
9(元)求中位数:先求比例: (1500—720)/(1770-720)=0。
74286分割中位数组的组距:(800-700)*0。
74286=74.286加下限700+74。
286=774。
286求众数:D1=1050—480=570D2=1050-600=450求比例:d1/(d1+d2)=570/(570+450)=0。
55882分割众数组的组距:0。
55882*(800-700)=55。
882加下限:700+55.882=755。
8825.1996年某月份某企业按工人劳动生产率高底分组的生产班组数和产量资料如下:.64。
43(件/*140+85*60)/)6。
根据表中资料计算中位数和众数。
中位数为733.33(元)众数为711。
11(元)求中位数:先求比例:(50-20)/(65-20)=0。
6667分割中位数组的组距:(800—600)*0。
6667=66。
67 加下限:600+66.67=666。
677。
某企业产值计划完成103%,比去年增长5%.试问计划规定比去年增长 多少?1。
94%(上年实际完成1。
03/1.05=0。
981 本年实际计划比上年增长(1-0。
统计学计算题例题(含答案)
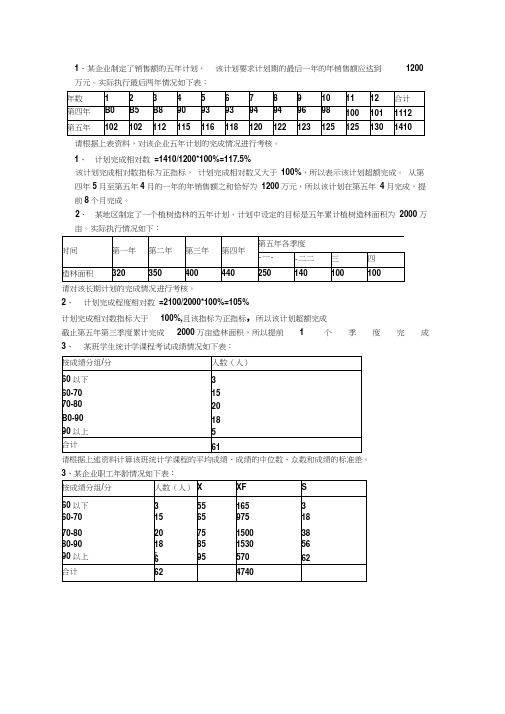
1、某企业制定了销售额的五年计划,该计划要求计划期的最后一年的年销售额应达到1200万元。
实际执行最后两年情况如下表:请根据上表资料,对该企业五年计划的完成情况进行考核。
1、计划完成相对数=1410/1200*100%=117.5%该计划完成相对数指标为正指标,计划完成相对数又大于100%,所以表示该计划超额完成。
从第四年5月至第五年4月的一年的年销售额之和恰好为1200万元,所以该计划在第五年4月完成,提前8个月完成。
2、某地区制定了一个植树造林的五年计划,计划中设定的目标是五年累计植树造林面积为2000万亩。
实际执行情况如下:请对该长期计划的完成情况进行考核。
2、计划完成程度相对数=2100/2000*100%=105%计划完成相对数指标大于100%,且该指标为正指标,所以该计划超额完成截止第五年第三季度累计完成2000万亩造林面积,所以提前1个季度完成3、某班学生统计学课程考试成绩情况如下表:请根据上述资料计算该班统计学课程的平均成绩、成绩的中位数、众数和成绩的标准差。
4、某学校有5000名学生,现从中按重复抽样方法抽取250名同学,调查其每周观看电视的小时数的情4> 样本平均数X= Sxf/Sf-l250/250-5样 ________ __________二>/刀(好予f/(工f—1)二V 1136/249二2. 14抽样平均误差U二s/ Vn=0.14因为F (t) =95%,所以日.96抽样极限误差△二t U 二 1. 96*0. 14=0. 27 区间下限=5-0. 27=4. 73 区间上限二5+0. 27-5. 27全校学生每周平均收看电视的吋间在(4.73,5.27)小时之间,概率保证程度为95%5、某企业对全自动生产线上的产品随机抽取1000件进行检验,发现有45件是不合格的,设定允许的极限误差为 1.32%。
请对全部产品的合格率进行区间估计。
5、样本合格率p=955/1000=95.5% 抽样平均误差u二V pChp)/n= 0.66%因为△=1.32%,所以t= A/ u =2所以F.(.t)-95. 45%区间下限二95. 5%-l. 32%=94. 18%区间上限二95. 5%+l. 32%二96. 82%所以我们以95. 45%的概率估计全部产品和合格率是在(94.18%, 96. 82%)之间。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一部分 随机事件及其概率例 1 设A B C 、、为三个随机事件,试用A B C 、、表示下列事件。
1)“A B 与发生,而C 不发生”(表示为ABC ); 2)“三个事件都发生”(表示为ABC );3)“三个事件至少有一个发生”(表示为A B C ⋃⋃); 4)“三个事件恰好有一个发生”(表示为ABC ABC ABC ++);5)“三个事件至少有两个发生”(表示为AB BC AC ⋃⋃或ABC ABC ABC ABC +++)6)“三个事件至多有两个发生”(表示为ABC 或A B C ⋃⋃)。
例2 将n 只球随机地放入N (N ≥n )个盒子中去,假定盒子装球容量不限, 试求1)每个盒子至多装一只球的概率,2)指定其中一个盒子装一只球的概率。
解: 设事件A =“N 个盒子中,每个盒子至多装一只球”,事件B =“指定其中一个盒子装一只球”。
1)一个球放入N 个盒子中的放法有N 种,n 个球放入N 个盒子中的放法有nN 种。
假设固定前n 个盒子各装一球,其分配方法有!n 种,从N 个盒子中任取n 个盒子各装一球,取法有nN C 种,所以,事件A 的样本点数为nN C !n ,即事件A 的概率为 n nN N n C A P !)(=2)若指定一个盒子里装一只球,首先考虑球的取法有1n C 种,其次,剩余的1N -个盒子中,1n -只球的放法有1(1)n N --种,所以事件B 的样本点数为1n C 1(1)n N --,即事件B 的概率为11(1)()n n n C N P B N --=注:还可以将模型推广,如生日问题,求事件“n 个人中至少有两人的生日相同”的概率。
设想一年有365天,将“天”看成‘盒子’,n 个人好比‘n 只球’,考虑事件A 的对立事件A =“n 个人在一年中生日全不相同”,它等价于“n 个球装入365个盒子中各装一球”,由前面的计算知:n nn C A P 365!)(365=,所以n nn C A P 365!1)(365-=。
类似的问题还有:将3封信随机投入4个邮筒,计算第2号邮筒恰好投入1封信的概率,请读者思考。
例3(匹配问题)某班n 个战士各有1支枪归个人保管使用的枪,这些枪外形完全一样,在一次紧急集合中,每人随机地取了1支枪,求至少有1人拿到自己的枪的概率。
解:设i A =“第i 个战士拿到自己的枪”,1,2,...,i n =(1)!1()!i n P A n n -==2(2)!11(),()!(1)i j nn P A A i j n n n P -===≠- 3(3)!1(),()!i j k nn P A A A i j k n P -==≠≠……121(...)!n P A A A n =1121()112121()()()......(1)(...)111...(1)1111...(1)2!3!!nnn nn i i i j n i ij i j i n n nn n n n n n P A P A P A A P A A A C C C n P P n -=≠=--=-++-=-++-=-+-+-∑∑∑U注:类似的问题还有:n 个同学聚会各带一件礼物,用抽签的方法分配礼物,求至少有一人抽到自己的礼品的概率。
第二部分 条件概率、独立性、全概率公式例1 某城市的一项调查表明:该市有30%的中学生视力有缺陷,7%的中学生听力有缺陷,2%的中学生视力和听力都有缺陷,问1)如果已知一个中学生的视力有缺陷,那么他听力也有缺陷的概率是多少? 2)如果已知一个中学生的听力有缺陷,那么他视力也有缺陷的概率是多少? 解:记A =“中学生视力有缺陷”, B =“中学生听力有缺陷”则()0.02(|)0.0667()0.3P AB P B A P A ==≈, ()0.02(|)0.2857()0.07P AB P A B P B ==≈例 2 设某人忘了某电话号码的最后一位数字,因而随意拨码,求他拨码不超过3次接通他所需要的电话的概率。
解: 设A =“拨码不超过3次而接通”,i A =“第i 次拨码接通”,1,2,3i =。
则112123A A A A A A A =++112123()()()()P A P A P A A P A A A =++1121121312()()(|)()(|)(|)P A P A P A A P A P A A P A A A =++191981310109109810=+⋅+⋅⋅=该问题与摸奖问题是关联的,设想10个人依次摸10张券,其中只有一张奖券,无放回摸取,第一、第二、…第十人摸到奖券的概率都是110。
这充分说明抓阄的合理性。
例3 假设某产品成箱包装,每箱产品有10件,其次品数从0到2是等可能的。
开箱检验时,从中任取一件,如果检验为次品,则认为该箱产品不合格而拒收。
由于检验误差,假设一件正品被误判为次品的概率为2%,一件次品被漏查误判为正品的概率为10%。
求: 1)检验一箱产品能通过验收的概率;2)已知取到的一箱产品通过了验收,抽检到一件次品的概率; 3)检验10箱产品通过率不低于90%的概率。
解:1)设i A =“一箱内有i 件次品”,0,1,2i =,显然事件012,,A A A 互斥,构成一个完备事件组。
设事件B =“一箱产品通过验收”,C ==“抽到一件正品”。
欲求()P B依题意,110(),(|) 0,1,2310i i iP A P C A i -===(|)0.98,(|)0.10P B C P B C ==运用全概率公式,得2200110()()(|)0.9310()1()10.90.1.i i i i iP C P A P C A P C P C ==-====-=-=∑∑再次运用全概率公式()()(|)()(|)0.90.980.10.10.892P B P C P B C P C P B C =+=⨯+⨯=2)()()(|)0.01(|)0.0112()()0.892P CB P C P B C P C B P B P B ===≈这说明通过了验收而抽查到次品的可能性只有约1.12%。
3)由于各箱产品是否通过验收互不影响,则设10箱产品中通过验收的箱数为,(0,2,,10)k k =L ,并且通过验收的概率为()0.892P B =,10箱产品的通过率为10k,根据二项概率公式,得到因为检验10箱产品通过率不低于90%,等价于90%910kk ≥⇔≥,即9,10k =。
所求概率为1019101010(9)(10)0.892(0.892)0.1080.705P P C +=+⋅=该题目体现了全概率公式、贝叶斯公式和二项公式的综合应用。
第三部分 一维随机变量及其分布例1. (电力供应问题)有9台设备,间歇地使用电力。
设在任一时刻每台设备都以同样的概率0.3需要一个单位的电力,且各设备是否需要电力相互独立,求有3台设备同时需要供应一个单位电力的概率。
解: 设X 表示任一时刻同时需要(一个单位的电力供应)的设备数,则),(~p n B X ,其中9=n ,3.0=p ,于是有3台设备同时需要供应电力的概率为2668.0)3.01()3.0(}3{6339≈-==C X P例2 某商店根据过去的销售记录知道某种商品每月的销售量可用参数为9=λ的泊松分布来描述。
为了以95%以上的概率保证不脱销,问商店在月底应存多少件该种商品(设只在月底进货)?解: 设该商品每月销售该商品X 件,月底存货为a 件,那么当a X ≤时就不会脱销。
现要求a ,使95.0}{≥≤a X P ,又因)9(~P X ,即使得∑∑==-≥==ak ak k e k k X P 00995.0!9}{经计算可知:∑=-<≈130995.09231.0!9k k e k ,∑=->≈140995.09554.0!9k k e k故只要保证存货不低于14件就能以95%以上的概率保证不脱销。
例3 设一大型设备上某元件在任何长为x 的时间内损坏(立即替换新的)数N (x )服从参数为x λ的泊松分布,(1)求该种元件使用寿命X 的密度函数。
(2)求使用寿命超过a (小时)的概率。
解 (1)先求X 的分布函数F (x )。
对任意实数x ,因为0≥X ,所以,当0<x 时,{}X x ≤=∅,从而0}{)(=≤=x X P x F 。
当0≥x 时,由于}1)({}{≥=≤x N x X ,故xxe x ex N P x N P x X P x F λλλ---=-==-=≥=≤=1!0)(1}0)({1}1)({}{)(0综上所述,得⎩⎨⎧≥-<=-0,10,0)(x e x x F xλ从而X 的密度函数为⎩⎨⎧≤>=-.000,)(x x e x f x λλ 可见,元件使用寿命X 服从参数为λ的指数分布。
(2)使用寿命超过a (小时)的概率为aaxx ae ae dx e dx xf a X P λλλλ-∞+--∞+=∞+-===>⎰⎰)(}{例4 设2~(,)X N μσ,求{}P X k μσ-<,k =1,2,……。
解 以k = 3为例,其它可类似计算。
{3}{33}(3)(3)33()()(3)(3)2(3)120.998610.997299.72%P X P X F F μσμσμσμσμσμσμμσμσσ-<=-<<+=+--+---=Φ-Φ=Φ-Φ-=Φ-=⨯-==同理{}68.3%{2}95.4%P X P X μσμσ-<=-<=此例说明若2~(,)X N μσ,则X 的取值落入μ附近σ3范围内的概率相当大,几乎为1,这称为正态分布的“σ3原则”。
(现在有σ6原则)例5 设甲、乙两人独立地各进行两次射击,他们每次的命中率分别为0.4和0.5,以X 和Y 分别表示甲、乙命中次数,求(,)X Y 的分布律。
解. 由题意可知,~(2,0.4),~(2,0.5)X B Y B又因为X 和Y 相互独立,于是X 和Y 的分布律为{0,0}{0}{0}0.160.250.04P X Y P X P Y ====⋅==⨯= {0,1}{0}{1}0.160.50.08P X Y P X P Y ====⋅==⨯={0,2}{0}{2}0.160.250.04P X Y P X P Y ====⋅==⨯= {1,0}{1}{0}0.480.250.12P X Y P X P Y ====⋅==⨯={1,1}{1}{1}0.480.50.24P X Y P X P Y ====⋅==⨯= {1,2}{1}{2}0.480.250.12P X Y P X P Y ====⋅==⨯={2,0}{2}{0}0.360.250.09P X Y P X P Y ====⋅==⨯= {2,1}{2}{1}0.360.50.18P X Y P X P Y ====⋅==⨯={2,2}{2}{2}0.360.250.09P X Y P X P Y ====⋅==⨯=第四部分 随机变量的数字特征例1一口袋中有i (n i ,...,2,1=)号球i 只,从中任意摸出一只球,求所得号码的数学期望。
