2017七年级数学数据的收集3.doc
七年级下册数学数据的收集整理与描述

七年级下册数学数据的收集整理与描述数据的收集、整理与描述数据的收集、整理、描述和分析是统计学中的基本过程。
数据的收集是指从总体中获取数据的过程。
数据的整理是将收集到的数据进行分类、排序和编码等操作。
数据的描述是将整理好的数据以表格、图表等形式呈现出来。
数据的分析是对数据进行统计学分析,得出结论。
知识结构统计调查有两种方式:全面调查和抽样调查。
全面调查是对总体进行调查,抽样调查是从总体中抽取一部分个体进行调查。
全面调查的优点是可靠、真实,抽样调查的优点是省时、省力,减少破坏性。
在进行数据处理时,基本过程是收集数据、整理数据、描述数据、分析数据、得出结论。
数据的表示有两种基本方法,一是统计表,二是统计图。
常见的统计图有条形统计图、扇形统计图和折线统计图。
全面调查全面调查是指对总体进行调查的方式。
在数据处理的基本过程中,全面调查包括收集数据、整理数据、描述数据、分析数据和得出结论。
其中,数据的整理和描述可以使用统计表和统计图的方式进行。
统计表可以清楚地找出数据分布的规律,统计图则可以更直观地反映数据的规律。
常见的统计图有条形统计图、扇形统计图和折线统计图。
抽样调查抽样调查是指从总体中抽取一部分个体进行调查的方式。
抽样调查只考察总体中的一部分个体,因此它的优点是调查范围小,节省人力、物力和财力。
但是,抽样调查得到的结果往往不如全面调查得到的结果准确。
为了获得较为准确的调查结果,抽样时要注意样本的代表性和广泛性。
在统计中,需要考察对象的全体叫做总体,其中从总体中抽取的部分个体叫做总体的一个样本,样本中个体的数目叫做样本容量。
表示数据的两种基本方法表示数据的两种基本方法是统计表和统计图。
统计表可以清楚地找出数据分布的规律,统计图则可以更直观地反映数据的规律。
常见的统计图有条形统计图、扇形统计图和折线统计图。
扇形统计图用圆代表总体,圆中的各个扇形分别代表总体中的不同部分,扇形的大小反映部分占总体的百分比的大小。
初一数学数据的收集与整理(精华版)

七年级数学第17 讲:数据的收集与整理成果姓名1,普查与抽样调查为了特定目的对全部考察对象进行的全面调查叫做普查;其中被考察对象的全体叫做总体,组成总体的每一个被考察对象称为个体;从总体中抽取部分个体进行调查,这种调查称为抽样调查,其中从总体抽取的一部分个体叫做总体的一个2,扇形统计图样本;抽样时要留意样本的代表性和广泛性;扇形统计图:利用圆与扇形来表示总体与部分的关系,扇形的大小反映部分占总体的百分比的大小,这样的统计图叫做扇形统计图;(各个扇形所占的百分比之和为1)圆心角度数=360°×该项所占的百分比;(各个部分的圆心角度数之和为360°)该部分所对应的圆心角360 ;在扇形统计图中,每部分占总体的百分比3,频数直方图是一种特别的条形统计图,它将统计对象的数据进行了分组(每组的最大值与最小值的差叫做组距),画在横轴上,纵轴表示各组数据的频数(数据显现的次数);当样本中的数据较多时,用频数直方图能更清晰,更直观地反映数据的整体状况;4,各种统计图的特点条形统计图:能清晰地表示出每个项目的详细数目;折线统计图:能清晰地反映事物的变化情形;扇形统计图:能清晰地表示出各部分在总体中所占的百分比;典型例题:例1,以下调查中,适合用普查方式的是()A. 明白一批炮弹的杀伤半径明白扬州电视台《关注》栏目的收视率B.C. 明白长江中鱼的种类明白某班同学对“小强热线”的知晓率D.例2,要明白全校同学的课外作业情形,你认为以下抽样方法中比较合理的是()A. 调查全体女生B. 调查全体男生C. 调查九年级全体同学调查七,八,九年级各100 名同学D.例3,为了明白一批电视机的寿命,从中抽取100 台电视机进行试验,这个问题的样本是()A. 这批电视机这批电视机的寿命B.C. 所抽取的100 台电视机的寿命D. 100例4,为了检查一批皮鞋的质量, 从中抽取了50 双作质量检查, 此问题中数目50 是( )A. 样本样本容量总体个体B. C. D.例5,为了考查某校初三年级800 名同学期末数学测试成果, 从中抽取了100.名同学的试卷进行统计分析, 这100 名同学的数学成果是()A. 个体B. 样本C. 总体D. 样本容量例6,为了明白某校八年级500 名同学的睡眠时间, 从中抽调了50 名同学进行明白. 就这个问题来说, 下面说法正确选项()A.500 名同学是总体名同学睡眠时间是样本; ;C. 每名同学是个体这种调查方式是普查; D.例7,在2021 年的世界无烟日( 5 月31 日),小明学习小组为明白本地区大约有多少成年人吸烟,随机调查了100 个成年人,结果其中有个成年人吸烟. 对于这个数据收集与处理15的问题,以下说法正确选项(A. 调查的方式是普查)本地区只有85 个成年人不吸烟B.C. 样本是15 个吸烟的成年人本地区约有15℅的成年人吸烟D.例8,如下列图的两个统计图,女生人数多的学校是()A. 甲校C. 甲,乙两校女生人数一样多B. 乙校D.无法确定例9,某校七(1)班的全体同学喜爱的球类运动用如下列图的统计图来表示,下面说法正确选项()A. 从图中可以直接看出喜爱各种球类的详细人数;B. 从图中可以直接看出全班的总人数;C. 从图中可以直接看出全班同学中学三年来喜爱各种球类的变化情况;D,从图中可以直接看出全班同学现在喜爱各种球类的人数的大小关系;例10,在扇形统计图中,其中一个扇形的圆心角为72°,就这个扇形所表示的占总体的百分数是;例11,为明白某中学男生的身高情形,随机抽取如干名男生进行身高测量,将所得到的数据整理后,画出频数直方图(如图),图中从左到右依次为第1,2,3,4,5 组.(1) 求抽取了多少名男生测量身高.(2) 身高在哪个范畴内的男生人数最多?(答出是第几个小组即可)(3) 如该中学有人数.300 名男生,请估量身高为170 cm 及170 cm 以上的例12,某省为进一步扩大内需,积极响应国务院的“家电下乡”政策.第一批列入家电下乡的产品为彩电,冰箱,洗衣机和手机四种产品.今年一季度对以上四种产品的销售情形进行了统计,绘制了如下的统计图,请你依据图中信息解答(1)该家电销售公司一季度四种电器销售的总数量是台.(2)请补全条形统计图和扇形统计图.例13,为了进一步明白七年级同学的身体素养情形,体育老师对七(1)班50 位同学进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图.如下所示:频数(人数)组别次数第1 组第2 组第3 组第4 组第5 组请结合图表完成以下问题:(1)补全表格中的数据;(2)把频数分布直方图补充完整;例14,小强就本班同学“自己选测的体育项目”进行了一次调查统计,下面是他通过收集数据后,答以下问题:人数1614121086420绘制的两幅不完整的统计图.请你依据图中供应的信息,解跳绳30%跳远18%其他排球跳绳跳远排球其他项目(1)该班共有(2)补全条形统计图;名同学;(3)在扇形统计图中,“排球”部分所对应的圆心角度数为(4)如全校有1080 名同学,请运算出全校“其他”部分的同学人数.°;课内练习:1. 为了明白七年级同学的数学成果,在全校七年级同学中抽取了50 名同学进行检测,在这个问题中,总体是,样本是__.2. 在进行数据描述时,要显示每组中的详细数据,应采纳统计图;要显示部分在总体中所占的百分比,应采纳统计图;要显示数据的变化趋势,应采纳统计图;要显示数据的分布情形,应采纳 图 .3. 为了明白某商品促销广告中所称中奖率的真实性,某人买了 100 件该商品调查其中奖率,那么他采纳的调查方式是4. 依据猜测, 21 世纪中叶我国劳动者构成比例绘制成扇形统计图如下列图, 就第一,二,三产业劳动者的构成比例是∶∶;5. 完成以下表格:小明一周内总共花了 24 元钱,各项消费金额及其所占百分比如下表所示:消费项目 消费金额 / 元 交通 文具 4 1 6午餐 105 12消遣 4 合计 24 百分比6. 小刚在学校组织的社会调查活动中负责明白他所居住的小区450 户居民的家 庭收入情形 . 他从中随机调查了 40 户居民家庭收入情形(收入取整数,单 位:元),并绘制了如下的频数分布表和频数分布直方图 户数 .分组 频数(人数)百分比 20 16600≤ x < 800 800≤ x < 1000 1000≤ x < 1200 1200≤ x < 14005% 2 12 15% 68445%600 800 1000 1200 1400 1600 1800元%依据以上供应的信息,解答以下问题:(1)补全频数分布表;(2) 9补全频数分布直方图 . ( 3)绘制 1600≤ x < 1800合计5% 2 相应的频数分布折线图 . (4)请 你估量该居民小区家庭属于中等 100%40收入(大于 1000 不足 1600 元)的大约有多少户?7.某市“每天锤炼一小时,幸福生活一辈子”活动已开展了一年,为明白该市此项活动的 开展情形,某调查统计公司预备采纳以下调查方式中的 一种进行调查:①从一个社区随机选取 200 名居民; ②从一个城镇的不同住宅楼中随机选取 ③从该市公安局户籍治理处随机抽取200 名居民;200 名城乡居民作为调查对象,然后进行调查. (1)在上述调查方式中,你认为比较合理的一种是 ( 填序号 ).(2) 由一种比较合理的调查方式所得到的数据制成了如下列图的频数直方图,在这个调 查中,这 200 名居民每天锤炼 2 小时的人数是多少?(3)如该市有 100 万人,请你利用 (2)中的调查结果, 估量该市每天锻 炼 2 小时及以上的人数是多少?(4) 你认为这个调查活动的设计有没有不合理的地方?谈谈你的理 由.。
初一数学专题三.数据的收集整理与描述讲课教案

初一数学专题三.数据的收集整理与描述仅供学习与交流,如有侵权请联系网站删除 谢谢2初一数学专题三: 数据的收集整理与描述一、本章知识网络数据处理的一般过程得出结论直方图折线图扇形图条形图据收集数据抽样调查全面调查二、知识要点归纳1、统计图 扇形统计图 容易表示出一个对象在总体中所占的百分比。
条形统计图 可以表示出各种情况下各个项目的具体数目。
折线统计图 可以表现出同一对象的发展变化情况2、全面调查 为一特定目的而对所有考察对象作的全面调查 抽样调查 为一特定目的而对部分考察对象作的调查 抽样调差中的总体 所要考察的对象的全体个体 其中每一个考察对象样本 从总体中取出的一部分个体样本容量 样本中个体的数目3、直方图画频数分布直方图的一般步骤 (1)计算最大值与最小值的差 (2)决定组距与组数(3)列频数分布表(4)画频数分布直方图 三、例题例1、右图和下图是根据某中学为地震灾区捐款情况而制作的统计图,已知该校在校学生2000人,请你根据统计图计算该校七年级有学生_____ 人, 七年级共捐款_____ __元,该校三个年级共捐款_____ ___元。
例2:某校七年级学生进行体育测试,七年级(2)班男生的立定跳远成绩制成频数分布直方图,图中从左到右各矩形的高之比是2:3:7:5:3,最后一组的频数是6,根据直方图所表达的信息,解答下列问题。
(1)该班有多少名男生? (2)若立定跳远的成绩在2.0米以上(包括2.0米)为合格率是多少练习 一、选择人均捐款数(元)0246810121416七年级八年级九年级年级仅供学习与交流,如有侵权请联系网站删除谢谢31.下列调查适合作全面调查的是 ( )A.了解在校大学生的主要娱乐方式B.了解我市居民对废电池的处理情况C.日光灯管长要检测一批灯管的使用寿命D.对甲型HINI流感患者的同一车厢乘客进行医学检查2.要了解全校学生的课外作业负担情况,你认为作抽样方法比较合适的是()A.调查全校女生B.调查全校男生C.调查九年级全体学生D.调查七、八、九年级各100人3.要反映某市一周内每天的最高气温的变化情况,宜采用()A.条形统计图B.扇形统计图C.折线统计图D.频数分布直方图4.小明在选举班委时得了28票,下列说法错误的是 ( )A.不管小明所在的班级有多少学生,所有选票中选小明的选票频率不变B. 不管小明所在的班级有多少学生,所有选票中选小明的选票频数不变C.小明所在班级的学生人数不少于28人D.小明的选票的频率不能大于15.一个班有40名学生,在期末体育考试中,优秀的有18人,在扇形统计图中,代表体育优秀扇形的圆心角度数是 ( )A.144B.162C.216D.250二、耐心填一填,你一定很棒的!6.为了考察某校七年级男生的身高情况,调查了60名男生的身高,那么它的总体是____________, 个体是_________________, 样本是________________.7.是150元,那么他家用于教育支出是____________元。
七年级数学期末复习之数据的收集与整理

如图1,在平面直角坐标系中,点A (a ,0),B (0,b )其中实数a 、b 满足b a 2+2b -=0,将线段AB 向右平移至线段CD 。
(1)如图2,若点Q 为直线AB 上的动点,连接QC 、QD ,作QF 平分∠CQD ,过Q 作QE ∥BC ,设∠BCQ =α,∠ADQ =β.当点Q 在直线AB 上运动时,∠EQF 与α、β之间有怎样的数量关系,请说明理由;(2)如图3,若点D 在x 轴正半轴上,点C 在第一象限,且S △COD =5,点E 为线段BC 的中点,点P (m ,n )为射线BA 上的动点。
若S △PDE ≥31S 四边形ABCD ,求n 的取值范围。
知识点 数据的收集、整理与描述 【知识梳理】知识点一 数据的收集、整理1.数据收集的方式:实地调查、试验、问卷调查、查阅资料、电话调查等。
2.数据收集、整理的步骤(1)明确调查目的和问题; (2)确定调查对象; (3)选择调查方法,设计调查问题; (4)展开(实施)调查; (5)记录调查结果,收集、整理数据; (6)分析数据,得出结论。
知识点二 描述数据——条形图、扇形图A.了解全校同学对动画电视节目的喜爱情况,上学时在学校门口随机调查100名同学B.了解某小区居民防火意识,对你们班同学进行调查C.了解全校同学喜欢课程的情况,对某班男同学进行调查D.了解某商场的平均日营业额,选在周末进行调查5、一组数据的最大值与最小值的差为20,若确定组距为3,则分成的组数是。
6、如图,在频率分布直方图中,各小长方形的高之比AE∶BF∶CG∶DH=2∶4∶3∶1,则第3组的频率为___________。
(第6题)(第7题)7、下面的频数分布折线图分别表示我国A市与B市在2016年元月份的日平均气温的情况,记该月A市和B市日平均气温是8℃的天数分别为a天和b天,则a+b=_________。
8、某校举行“汉字听写”比赛,每位学生听写汉字39个,比赛结束后,随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分。
(完整)关于初一数学—数据的收集与整理

初一年级数学——数据的收集与整理一、考点、热点数据的收集过程:①明确调查问题;②确定调查对象;③选择调查方式;④展开调查;⑤记录结果;⑥得出结论。
数据的整理:一般用表格整理数据,也可用画记法记录数据。
收集数据的方法:收集数据常用统计调查,分为全面调查(普查)和抽样调查;考察全体对象....的调查叫做全面调查,全面调查也称作普查,调查的方法有问卷调查、访问调查、电话调查等;只抽取一部分对象....进行调查,然后根据调查数据推断全体对象的情况,这种方法是抽样调查。
(注意:全面调查收集到的数据全面、准确,但一般花费多、耗时长,而且某些具有破坏性的调查不宜用全面调查,因此,常常用抽样调查的方式来收集数据。
)几个相关概念:要考察的全体对象称为总体;组成总体的每一个考察对象称为个体;被抽取的那些个体组成一个样本;样本中个体的数目叫做样本容量。
数据的表示:(统计图,统计表)1.扇形统计图:用圆代表总体,圆中的各个扇形分别代表总体中的不同部分,扇形的大小反映部分占总体的百分比的大小,这样的统计图叫做扇形统计图。
扇形统计图的特点:①用扇形面积表示部分占总体的百分比;②易于显示每组数据相对于总体的百分比;③扇形统计图的各部分占总体的百分比之和为100%或1. 在检查一张扇形统计图是否合格时,只要用各部分分量占总量的百分比之和是否为100%进行检查即可。
2. 条形统计图:用一个单位长度表示一定的数量关系,根据数量的多少画成长短不同的条形,条形的宽度必须保持一致,然后把这些条形排列起来,这样的统计图叫做条形统计图。
条形统计图的特点:①能够显示每组中的具体数据;②易于比较数据之间的差别。
注意:条形统计图的纵轴一般从0开始,但为了突出数据之间的差别也可以不从0开始,这样既节省篇幅,又能形成鲜明对比。
3. 一般我们称落在不同小组中的数据个数为该组的频数,频数与数据总数的比为频率。
频率反映了各组频数的大小在总数中所占的分量。
公式:频率=。
初一数学专题三数据的收集整理与描述
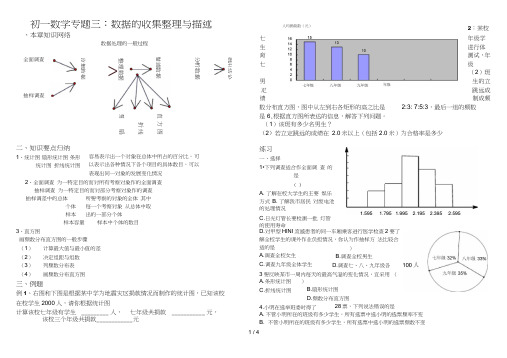
初一数学专题三:数据的收集整理与描述、本章知识网络数据处理的一般过程全面调查2:某校抽样调查收集数据整理数据>描述数据分析数据得出结论七 生 育 七 男 疋 绩人均捐款数(元)年级学进行体 测试, 年级(2)班 生的立 跳远成 制成频直方图折线图 扇数分布直方图,图中从左到右各矩形的高之比是 是6,根据直方图所表达的信息,解答下列问题。
(1)该班有多少名男生?2:3: 7:5:3,最后一组的频数(2)若立定跳远的成绩在 2.0米以上(包括2.0米)为合格率是多少二、知识要点归纳 1、统计图 扇形统计图 条形统计图 折线统计图 容易表示出一个对象在总体中所占的百分比。
可以表示出各种情况下各个项目的具体数目。
可以表现出同一对象的发展变化情况2、全面调查 为一特定目的而对所有考察对象作的全面调查 抽样调查 为一特定目的而对部分考察对象作的调查 抽样调差中的总体 个体 样本 所要考察的对象的全体 其中每一个考察对象 从总体中取出的一部分个体样本容量 样本中个体的数目3、直方图画频数分布直方图的一般步骤(1) 计算最大值与最小值的差 (2)决定组距与组数 (3)列频数分布表 (4) 画频数分布直方图 三、例题 例1、右图和下图是根据某中学为地震灾区捐款情况而制作的统计图,已知该校 在校学生2000人,请你根据统计图 计算该校七年级有学生 _________ 人, 七年级共捐款 ___________ 元, 练习一、选择1•下列调查适合作全面调 查 的是( )A. 了解在校大学生的主要 娱乐方式 B. 了解我市居民 对废电池的处理情况C.日光灯管长要检测一批 灯管的使用寿命D.对甲型HINI 流感患者的同一车厢乘客进行医学检查 2要了解全校学生的课外作业负担情况,你认为作抽样方 法比较合适的是A.调查全校女生 C.调查九年级全体学生)B.调查全校男生 D.调查七、八、九年级各3要反映某市一周内每天的最高气温的变化情况,宜采用 ( A.条形统计图 C.折线统计图4.小明在选举班委时得了)B.扇形统计图 D.频数分布直方图28票,下列说法错误的是 该校三个年级共捐款 ____________ 元A. 不管小明所在的班级有多少学生,所有选票中选小明的选票频率不变B. 不管小明所在的班级有多少学生,所有选票中选小明的选票频数不变C. 小明所在班级的学生人数不少于28人D. 小明的选票的频率不能大于15•—个班有40名学生,在期末体育考试中,优秀的有18人,在扇形统计图中,代表体育优秀扇形的圆心角度数是A.144B.162C.216D. 250;( )二、耐心填一填,你一定很棒的!6•为了考察某校七年级男生的身高情况,调查了60名男生的身高,那么它的总体是,个体是,样本是7•小明家本月的开支情况如图所示,如果用于其它方面的支出是150元,那么他家用于教育支出是 _________________ 元。
初中数学最新-七年级数学数据的收集3 精品
布置作业
课后练习(P183)第2题写在书上,第1、3题做在作业本上.
学习收集数据的方法,以及收集哪些数据.
活动5回顾与反思
这一节课我们体会了数据收的意义,体会了怎样收集数据?收集哪些数据?
我们还学习了收集数据的方法,学习了哪些收集数据的方法呢?
学生总结收集数据的方法,教师点评、鼓励.
总结本节课的学习内容.
请看课后练习(P183).我们能完成测脉搏的实验吗?
学生先设计实验方案,然后进行实验.
1.了解全班男生立定跳远的成绩.有多少人优秀?有多少人达标?有多少人不达标?
2.了解我们班的全体同学,星期日收看电视的时间.收看时间在两个小时以内的有多少人,超过两个小时的有多少人?
3.2000年11月1日,我国进行了第五次人口普查.了解各省、直辖市、自治区的人口分布情况?
学生讨论,教师指导.
达成共识后,填写P183的表格.
240
百分比
学生填表.
感受统计数据.
我们已经调查过了中巴车能乘坐的人数、一辆自行车的占地面积,下面我们估算:
⑴需要开几辆中巴车?
⑵需要修建多大面积的自行车棚?教师指导Leabharlann 生解答.体会数据对决策的作用.
活动4解决其他问题
我们圆满地解决了班车和自行车棚的问题.接着再看下面几个问题,需要哪些数据?用什么方式得到数据?
我们通过上一节课的学习,已经知道数据在决策过程中的作用,今天我们继续学习数据收集方面的问题.请看下面问题:
一所新建的中学,首次招收七年级新生6个班共240人.学校准备开通固定线路班车,并修建一个自行车棚.学校要开几辆中巴车才能满足乘车需要?需要修建多大面积的自行车棚?
学生阅读问题.
初一数学下数据的收集整理与描述
数据的收集、整理与描述知识点回忆1、统计调查的一般过程:收集数据—整理数据-描述数据-分析数据。
2、统计调查的方式:全面调查和抽样调查。
考察全体对象....的调查叫做全面调查。
只抽取一局部对象....进行调查,然后根据调查数据推断全体对象的情况,这种方法是抽样调查。
注意:全面调查收集到的数据全面、准确,但一般花费多、耗时长,而且某些具有破坏性的调查不宜用全面调查,因此,常常用抽样调查的方式来收集数据。
例1、下面的调查适合用全面调查方式的是.①调查七年级十班学生的视力情况;②调查全国农民的年收入状况;③调查一批刚出厂的灯泡的寿命;④调查各省市感染禽流感的病例。
3、总体与个体、样本与样本容量要考察的全体对象称为总体;组成总体的每一个考察对象称为个体;被抽取的那些个体组成一个样本;样本中个体的数目叫做样本容量。
例〔2〕、为了了解某七年级2000名学生的身高,从中抽取500名学生进行测量,对这个问题,下面的说法正确的选项是〔 〕A 、2000名学生是总体B 、每个学生是个体C 、抽取的500名学生是样本D 、样本容量是5004、抽样调查的特点和要求特点:花费少、时间短,破坏性小;结果往往不如全面调查准确。
要求:抽样时个体被抽到的时机均等,样本容量适当,即样本具有代表性和广泛性。
例〔3〕、请指出以下哪些抽查的样本缺少代表性:①在大学生中调查我国青年的上网情况;②从具有不同文化层次的市民中,调查市民的法治意识;③抽查电信部门的家属,了解市民对电信效劳的满意程度。
5、各个小组内的数据的个数〔叫做频数〕。
用表格整理可得频数分布表:画频数分布直方图步骤:①计算最大值与最小值的差;②决定组距和组数;③列频数分布表;④画频数分布直方图。
首先取直方图中每一个长方形上边的中点,然后在横轴上直方图的左右取两个频数为0的点,它们分别与直方图左右相距半个组距,将所取的这些点用线段依次连接起来,就得到频数折线图。
例如,在上面的直方图的左边取点〔147.5,0〕,在直方图右边取点〔174.5,0〕,将所取的这些点用线段依次连接起来,就得到频数分布折线图。
七年级数学数据的收集与整理人教实验版知识精讲
七年级数学数据的收集与整理人教实验版【本讲教育信息】一. 教学内容:数据的收集与整理二. 教学重点知识讲解:1. 体会数据在现实生活的作用,能根据简单的问题,使用适当的方法收集数据;2. 会利用统计表格,条形图对收集的数据进行整理。
3. 能根据统计结果回答一些简单的问题4. 从事收集数据,整理数据和分析数据的过程,进一步学习描述数据的方法。
5. 学习抽样调查的方法,体会运用样本估计总体的思想。
6. 体会全面调查和抽样调查各自的优点和缺点,理解在统计活动中选择不同的数据收集方法的依据。
7. 在统计活动中,总体是考察对象的全体,总体中的每一个考察对象叫做个体,从总体抽取的一部分个体叫做总体的一个样本。
8. 抽样调查是从总体中抽取样本进行调查,根据样本来估计总体的一种调查。
9. 抽样调查省时,省力,同时也能基本反映被考察的情况。
是实际中应用非常广泛的一种调查方式。
但也要注意选取有代表性的样本,因为不同的样本得到的结果可能不一样。
10. 全面调查是指考察全体对象的调查,全面调查涉及面广,工作量大,结果较为准确。
注意:1. 统计的思想方法在社会生产部门,商业,财贸和生活实际中应用十分广泛,有关统计方面的实际应用问题是中考命题中经常出现的决策性的问题,应该引起同学们的足够重视。
2. 统计表格通常由行和列组成,表格上方一般要有表头,统计表格可以设计成不同的样式,但要简单,清楚,有利于突出数据的分布规律。
【典型例题】例1. 某班班委集体讨论研究班级开展球类活动的情况,决定调查收集数据第一步:明确调查问题——你最喜欢的球类活动第二步:确定调查对象——全班每位同学第三步:选择调查方法——问卷调查第四步:展开调查——每位同学将自己心中最喜爱的球类运动项目填写在问卷上,交给体育委员;第五步:记录结果——由体育委员组织三位体育爱好者分别进行唱票、计票、检票工作,得出50个数据,用表格进行整理。
(1)请你把统计的人数与百分比填入表格内(2)请你根据表中的信息,画出条形图和扇形图描述数据人数乒乓球排球足球篮球其他(3答:最喜欢的是足球和乒乓球,它们的百分比和是70%。
七年级数学数据的收集、整理与描述
七年级数学数据的收集、整理与描述第十章数据的收集、整理与描述(小结)(第1课时)一、背景与意义分析统计主要研究现实生活中的数据,它通过收集、整理、描述和分析数据来帮助人们对事物的发展作出合理的判断,能够利用数据信息和对数据进行处理已成为信息时代每一位公民必备的素质。
通过对本章全面调查和抽样调查的学习,学生可基本掌握收集和整理数据的方法。
二、学习与导学目标1.知识积累与疏导:通过复习小结,进一步领悟到现实生活中通过数据处理,对未知的事情作出合理的推断的事实。
2.技能掌握与指导:通过复习,进一步明确数据处理的一般过程。
3.智能提高与训导:在与他人交流合作的过程中学会设计调查问卷。
4.情感修炼与提高:积极创设情境,参与调查、整理数据,体会社会调查的艰辛与乐趣。
5.观念确认与引导:体会从实践中来到实践中去的辨证思想。
三、障碍与生成关注调查问卷的设计及根据调查总结的报告给出合理的预测。
四、学程与导程活动活动一回顾本章内容,绘制知识结构图数据处理的一般过程制表绘图————活动二例题:调查中学生课外阅读情况(时间)同学小组讨论,设计调查问卷。
(抽样调查) 活动三调查观河中学初一学生最喜爱的球类活动设计问卷(全面调查) 小组讨论,完善问卷。
活动四小结:设计问卷的一般注意点。
习题:P172 1、2、3五、笔记与板书提纲课题例1 小结数据处理的一般过程例2 习题六、练习与拓展选题统计校工会服务部一天内几种商品的销售情况,设计问卷。
七、个别与重点辅导学生姓名略八、反思:数据的收集与整理(小结)(第2课时)一、背景与意义分析通过上一课的复习,学生对数据处理的基本过程与方法得以进一步巩固,对调查问卷的设计方法得到进一步加强,本课将对统计图表的选择以及自主完成整个调查过程加以训练。
二、学习与导学目标1.知识积累与疏导:通过复习,体会不同统计图表的区别,会正确绘制统计图表2.技能掌握与指导:通过实际操作,亲身体会统计调查,并以此决策的过程3.智能提高与训导:学会与他人合作交流,并在交流过程中清晰表达自己的思维过程4.情感修炼与开导:创设情景,体会数据收集与整理的艰辛与乐趣。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
活动5回顾与反思
这一节课我们体会了数据收的意义,体会了怎样收集数据?收集哪些数据?
我们还学习了收集数据的方法,学习了哪些收集数据的方法呢?
学生总结收集数据的方法,教师点评、鼓励.
总结本节课的学习内容.
请看课后练习(P183).我们能完成测脉搏的实验吗?
学生先设计实验方案,然后进行实验.
感知问题情境.
活动2设计方案.
设计解决问题的方案.
活动3解决问题.
体会整理数据做出决策的过程.
活动4解决其他问题.
学习调查的方法.
活动5回顾与反思.
总结本节课的收获.
课前准备
教具
学具
补充材料
电脑、投影仪
中巴车能乘坐的人数、存放一辆自行车的占的面积
教学过程设计
问题与情景
师生行为
设计意图
活动1问题的提出
12.1数据的收集(第2课时)
教学任务分析
教学
目标
知识与技能
1.知道数据对决策的作用;
2.知道实验、调查、查阅资料等收集数据的方法.
过程与方法
经历设计调查方案、整理数据、做出决策的过程,会用适当的方法收集数据.
情感态度与
价值观
在收集数的过程中培养学生的合作意识.
教学流Байду номын сангаас安排
活动说明
活动目的
活动1问题的提出.
训练学生收集数据的能力.
布置作业
课后练习(P183)第2题写在书上,第1、3题做在作业本上.
1.为做出科学的决策,应该搜集哪些数据?
2.应该采用什么方式进行调查获得数据呢?
学生讨论,教师指导.
设计调查方案.
活动3解决问题
下表是几位同学对全校学生进行问卷调查,获得的数据,请你完成表格中的空缺内容:
某校240名学生到校方式统计表
到校方式
步行
骑自行车
乘坐班车
其他方式
合计
人数/名
48
120
60
12
我们通过上一节课的学习,已经知道数据在决策过程中的作用,今天我们继续学习数据收集方面的问题.请看下面问题:
一所新建的中学,首次招收七年级新生6个班共240人.学校准备开通固定线路班车,并修建一个自行车棚.学校要开几辆中巴车才能满足乘车需要?需要修建多大面积的自行车棚?
学生阅读问题.
提出问题.
活动2设计方案
1.了解全班男生立定跳远的成绩.有多少人优秀?有多少人达标?有多少人不达标?
2.了解我们班的全体同学,星期日收看电视的时间.收看时间在两个小时以内的有多少人,超过两个小时的有多少人?
3.2000年11月1日,我国进行了第五次人口普查.了解各省、直辖市、自治区的人口分布情况?
学生讨论,教师指导.
达成共识后,填写P183的表格.
240
百分比
学生填表.
感受统计数据.
我们已经调查过了中巴车能乘坐的人数、一辆自行车的占地面积,下面我们估算:
⑴需要开几辆中巴车?
⑵需要修建多大面积的自行车棚?
教师指导学生解答.
体会数据对决策的作用.
活动4解决其他问题
我们圆满地解决了班车和自行车棚的问题.接着再看下面几个问题,需要哪些数据?用什么方式得到数据?
