根据逻辑函数求真值表
组合逻辑电路习题解答

自我检测题1.组合逻辑电路任何时刻的输出信号,与该时刻的输入信号 有关 ,与以前的输入信号 无关 。
2.在组合逻辑电路中,当输入信号改变状态时,输出端可能出现瞬间干扰窄脉冲的现象称为 竞争冒险 。
3.8线—3线优先编码器74LS148的优先编码顺序是7I 、6I 、5I 、…、0I ,输出为2Y 1Y 0Y 。
输入输出均为低电平有效。
当输入7I 6I 5I …0I 为时,输出2Y 1Y 0Y 为 010 。
4.3线—8线译码器74HC138处于译码状态时,当输入A 2A 1A 0=001时,输出07Y ~Y = 。
5.实现将公共数据上的数字信号按要求分配到不同电路中去的电路叫 数据分配器 。
6.根据需要选择一路信号送到公共数据线上的电路叫 数据选择器 。
7.一位数值比较器,输入信号为两个要比较的一位二进制数,用A 、B 表示,输出信号为比较结果:Y (A >B ) 、Y (A =B )和Y (A <B ),则Y (A >B )的逻辑表达式为B A 。
8.能完成两个一位二进制数相加,并考虑到低位进位的器件称为 全加器 。
9.多位加法器采用超前进位的目的是简化电路结构 × 。
(√,× ) 10.组合逻辑电路中的冒险是由于 引起的。
A .电路未达到最简 B .电路有多个输出C .电路中的时延D .逻辑门类型不同11.用取样法消除两级与非门电路中可能出现的冒险,以下说法哪一种是正确并优先考虑的A .在输出级加正取样脉冲B .在输入级加正取样脉冲C .在输出级加负取样脉冲D .在输入级加负取样脉冲12.当二输入与非门输入为 变化时,输出可能有竞争冒险。
A .01→10B .00→10C .10→11D .11→0113.译码器74HC138的使能端321E E E 取值为 时,处于允许译码状态。
A .011 B .100 C .101 D .01014.数据分配器和 有着相同的基本电路结构形式。
四川大学数字逻辑期末考题精选答案

数字逻辑考试题答案及评分标准数字逻辑考试题答案及评分标准(一)一、填空(共20分,每空1分)1. 11.75 B.C2. 000101103. 高电平 低电平 高阻状态 6. AB+AC 7. 2n 10. 0100 11. JK12. S=2N13. 原函数 反函数二、选择题(共10分,每题1分) 1. B 3. C 4. A 5. A 6. B 9. D 10. C三、简答题(共15分)1. n 位无符号二进制数的取值最小可以是全为0,最大是全为1,对应的十进制数的范围是0~2n-1。
最大的2位十进制数为99,由于27>99>26,所以表示一个最大2位十进制数至少需要7位二进制数。
3.(1)0110010100100001 (2)010*********.00000011 四、计算(共20分)1. (1)AB AB ABC A BC AB =+=+)( (3分) (2)B A B A B A =+))(( (3分)2.(3分)∑=++++++++=++++=+++++)14,12,11,9,6,5,4,1()()()(5414614129111__________m m m m m m m m m m C B A D BC D AB D C B CD B A C B A D B C A D C B D CD B A (1分)D B A D C A D B Y ++= (1分)3. (5分)CA D C D ABC B B C A B AD C D A C B B A B A C B D B C A ABBC BD AC AB BC BD AC +++=+++++++=+++++=⋅+⋅=⋅⋅⋅))(())((__________________________________________________________________________________________4. 模为6(4分) 五、1.当没有车辆行驶时,道路的状态设为0,有车辆行驶时,道路的状态为1;通道允许行驶时的状态设为1,不允许行驶时的状态设为0。
三输入变量判奇电路的真值表及表达式

三输入变量判奇电路的真值表及表达式摘要:以三输入判奇为例,通过对其输出函数表达式的形式变换,分别采用多种门电路及译码器、数据选择器等74 系列器件进行电路设计,给出了7 种电路实现形式,并分析了各种电路实现的优缺点。
此例说明了组合逻辑电路设计的灵活性及电路实现的多样性,所采用的设计方法对其他组合逻辑电路设计具有一定的启发与指导意义。
目前数字基础课程的实验内容包括验证性实验、综合性实验、设计性实验三部分,每一部分实验内容安排的侧重点不同。
比如设计性实验的关键是设计,要求学生依据设计要求,设计合理的实验电路,并选择器件、安装调试完成实验内容。
从教学实践来看,多数学生能够顺利完成实验要求,但解决问题的思路单一,设计过程灵活性差,不注意创新思维能力的锻炼。
这就要求教师在合理安排实验内容的同时,不断通过各种途径,引导学生拓宽知识面,创新思维方式,对待同一问题,积极探索多种解决问题的路径。
组合逻辑电路的设计多种多样,笔者选择一种奇偶校验电路实现进行详细阐述。
奇偶校验电路在组合逻辑电路的分析与设计中具有一定的典型性和实用性,熟悉判奇电路的逻辑功能及电路实现,有助于加深对组合逻辑电路的理解与掌握。
以判奇电路实现为例,分别讨论了用门电路、译码器、数据选择器的多种实现方案,用实例说明了组合逻辑电路设计的灵活性与多样性。
1 三输入变量判奇电路的真值表及表达式对于三输入变量的判奇问题,设其输入变量分别用A、B、C 表示,输出函数用F 表示。
当输入变量的取值组合中有奇数个1 时,输出函数值为1;当输入变量的取值组合中1 的个数为偶数时,输出函数值为0,依据这种逻辑关系可列写出三输入变量判奇电路的真值表如表1 所示。
表1 三输入判奇电路的真值表由真值表1 可见,有4 组输入变量取值组合使输出函数值为1,即分别为。
所以,三输入变量判奇逻辑问题的输出函数表达式为:2 采用门电路实现三输入变量判奇电路门电路实现三输入变量判奇电路的方法有很多,文中列举如下。
《数字电路-分析与设计》第二章习题及解答 北京理工大学出版社

5. A ⊕ B = A ⊕ B = A ⊕ B ⊕1
证明: 左边=AB+AB 中间= AB+AB=(A+B)(A+B)=AB+AB=左边 右边= (AB+AB)1+(AB+AB)1= AB+AB=中间 或者:根据 1⊕A=A,右边=中间
F1=(A+B)(B+C)(C+A)=ABC+ABC F2=(A+B)(B+C)(C+A)=ABC+ABC=F1 所以 F1=F2
习题
2. F1 = ABC + A B C , F2 = AB + BC + CA
由 1.知:F1=F2
3. F1 = C D + A B + BC , F2 = ABC + AB D + BC D
= AB + AC + BC
F = ( A + B) ⋅ ( A + C) ⋅ (B + C) = ( A + AB + AC + BC) ⋅ (B + C) = AB + ABC + BC + AC + ABC + AC + BC = AB + AC + BC
2-12 证明下列等式。
1. A ⊕ 0 = A
9. A( A + B ) = A
证明:左边=A+AB=A=右边,得证。 用真值表法略。 2-10 用逻辑代数演算证明下列等式。
2.3-2.5 逻辑代数的公式、定理、表示方法

0 1 2 3 4 5 6 7
m0 m1 m2 m3 m4 m5 m6 m7
④ 具有相邻性的两个最小项之和可以合 ① 在输入变量的任何取值下有一个最小 ③ 任意两个最小项的乘积为0。 ② 全体最小项和为1。 并成一项并消去一对因子。 项,而且仅有一个最小项的值为1。
二、最大项
在n变量逻辑函数中,若M为n个变量之 和,而且这n个变量均以原变量或反变 量的形式在M中出现一次,则称M为该 组变量的最大项。
?
思考: 2 个。 n个变量的最小项有多少个?
n
三变量(A、B、C)最小项的编号表:
相 邻
A' B ' C ' A' B ' C A' BC ' A' BC AB' C ' AB' C ABC' ABC
相 邻
0 0 0 0 1 1 1 1
0 0 1 1 0 0 1 1
0 1 0 1 0 1 0 1
证明: A A' B ( A A' )( A B)
A B
两个乘积项相加时,如果一项取反后是另一 项的因子,则此因子是多余的,可以消去。
(23) AB AB' A
当两个乘积项相加时,若它们分别包含B和B’ 两个因子而其他因子相同,则两项定能合并,且 可将B和B’消去。
(24) A( A B) A
小结: 掌握逻辑代数的基本公式和常用公式。
§ 2.4 逻辑代数的基本定理
2.4.1 代入定理
在任何一个包含A的逻辑等式中,若以另外
一个逻辑式代入式中A的位置,则等式依然成 立。
例如,已知 ( A B) A B (反演律),若用B+C代替 等式中的B,则可以得到适用于多变量的反演律, 即
逻辑函数的五种描述方法

逻辑函数的五种描述方法
逻辑函数的五种描述方法包括:
1.真值表:逻辑函数的真值表是一种描述逻辑函数的方法,它列出逻辑函数的输入和
输出变量的所有可能组合,以及对应的函数值。
2.表达式:逻辑函数可以用布尔代数表达式来描述,例如和、差、积、商、最大项、
最小项等。
这些表达式可以用来表示逻辑函数,并且可以方便地用于逻辑函数的计算和化简。
3.逻辑图:逻辑图是一种描述逻辑函数的方法,它用电路元件和连线来表示逻辑函数。
在逻辑图中,每个电路元件代表一个逻辑运算,每个连线代表一个逻辑变量。
4.卡诺图:卡诺图是一种描述逻辑函数的方法,它用方格来表示逻辑函数。
在卡诺图
中,每个方格代表一个逻辑函数,每个方格中的涂色表示逻辑函数的取值。
5.表格:逻辑函数也可以用表格来描述,表格列出逻辑函数的输入和输出变量的所有
可能组合,以及对应的函数值。
这些描述方法可以互相转换,并且在实际应用中根据需要选择合适的方法。
《数字逻辑基础》-第02章(2)

险象的分类 按险象脉冲的极性分: 若险象脉冲为负极性脉冲,则称为“0”型险象; 若险象脉冲为正极性脉冲,则称为“1”型险象。 按输入变化前后,“正常的输出”是否应该变化分: 若输出本应静止不变,但险象使输出发生了不应有的短暂变化,则 称为静态险象; 在输出应该变化的情况下出现了险象,则称为动态险象。 四种组合险象示意:
静态“0”型险象 输出波形 静态“1”型险象 动态“0”型险象 动态“1”型险象 输入信号变化的时刻
2.5.2
险象的判断与消除
1. 用代数法判断及消除险象 继续考察函数 F AB A C 令B=1、C=1保持不变,令A变化,有:
F A 1 A 1 A A
再看,对F 作变换:
0101 0011 1 1001 „„ X „„ Y „„ C-1 „„ S
S≤ 9
结果 Z = S, W = 0
1 (2) 设 C1 , X 5 Y 9 , ,则 S X Y C1。因S >9,故S不是所求的Z, 15 须对S进行加6修正,而W应为1。
0101 1001 1 1111 „„ X „„ Y „„ C-1 „„ S 1 1 1 1 „„ S 的低4位 0 1 1 0 „„ 6 Z = 0101 结果 W = 1 1 0 1 0 1 „„ Z 丢弃
F A A A A
?
因 A 多经过非门,比 A 的变化有延时,故出现险象。
?
上式中出现
或 形式的项,这样的项会产生险象。
险象判断法: 对于逻辑表达式 F ( xn , xi , x1 ) ,考察 xi (i n 1) 变化、其他量不 变时是否产生险象,则将其他量的固定值代入式中。若得到的表达式 含有形如i xi 或i xi 形式的项,则该逻辑表达式可能产生险象。 x x
第四章:逻辑代数及其化简(2)
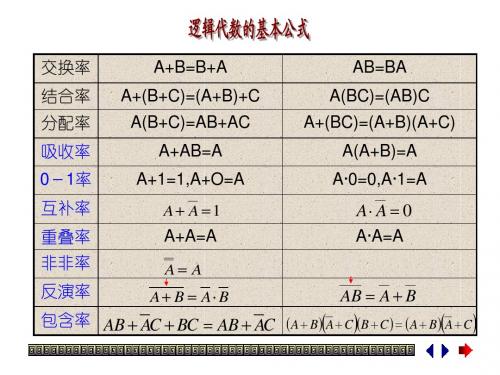
包含律:AB AC BC AB AC 证:AB AC BC AB AC A ABC
AB AC ABC ABC
AB1 C AC 1 B
若两个乘积项中分别 包含A和A两个因子, 而这两个乘积项的其 余因子组成第三个乘 积项,则第三个乘积 项是多余的。可消去
定理:任何逻辑函数 F 都可以用最小项之和的形式表示。 而且这种形式是唯一的。 1、 真值表法: 将逻辑函数先用真值表表示,然后再根据真值表写出最 小项之和。 例:将 F ABC BC AC 表示为最小项之和的形式。 解:由最小项特点知:n 个变量都出现,BC 缺变量 A ,
AC缺变量B, BC和AC不是最小项。 所以 F 是一般与-或式,不是最小项之和的标准形式。
例:已知一个奇偶判别函数的真值表(偶 ③ n个输入变量就有2n个 为1,奇为0),试写出它的逻辑函数式。
A 0 0 0
B 0 0 1
C 0 1 0
Y
0
1 1
1
0 0
1
0 1
1
1
0
解: 当ABC=011时, 使乘积项 ABC 1 1 1 1 不同的取值组合。 当ABC=101时, 使乘积项ABC 1 当ABC=110时, 使乘积项ABC 1 因此,Y的逻辑函数应当等于这三个乘积项之和。 Y ABC ABC ABC
二、从逻辑表达式列出真值表 将输入变量的所有状态组合 逐一代入逻辑式,求出函数值, 列成表,即可得到真值表。 例:已知函数 Y A BC ABC 求其对应真值表。 解:将三变量所有取值组合代 入Y式中,将计算结果列表。
A B C 0 0 0 0 0 1
BC
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
根据逻辑函数求真值表
**真值表**
| A | B | C | Z |
|--:|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
在逻辑中,一个真值表是用来表示一组逻辑变量(A,B,C)之间的联系并阐明了它们之间各种不同可能输入和输出值的情况下即关系的表示法。
上述真值表指出,在三个输入变量(A,B,C)条件下,有八种可能输入值组合,其输出Z的真值情
况如上表格所示。
从上表可以看出,在不同的输入变量处理下,Z的输出值基本
为两种情况:Z=1和Z=0,这对建立起相应的逻辑函数很有帮助。
我们还可以从表格中比较其他输入变量之间的联系,通常情况下,当A为1,B为0,C为1时,Z=1,而当A为0,B为
1,C为1时,Z=0。
真值表可以帮助我们现实生活中的决策过程,使决策变得更加客观和精确。
例如,当一个商家有以下三个因素可供选择:时间,质量和价格,以最优的方式决定哪些因素更重要,而哪些是可以忽略的可以使用真值表帮助我们实现。
总的来说,真值表是一种有效的分析工具,可以用来全面分析和识别问题。
它可以帮助我们准确判断问题,消除它们之间的不确定性,并有助于实现最优决策。
