基于MATLAB的各类混沌系统的计算机模拟(教学版)
matlab 混沌 分叉 程序

一、概述Matlab是一种用于数学计算、数据分析和图形可视化的高级编程语言和工具,混沌理论是一种描述动态系统非线性行为的数学理论,而混沌分叉是混沌系统中特有的一种现象。
编写Matlab程序对混沌分叉进行研究即是将这两种领域结合起来,本文将介绍如何使用Matlab 编写混沌分叉程序。
二、混沌分叉理论简介混沌分叉理论是描述混沌系统行为的一个重要方面,其基本原理可简要描述如下:1. 系统的参数变化:在混沌系统中,当改变系统的某些参数时,系统的行为会发生变化,这种变化可能是渐变的,也可能是突然的。
2. 分岔现象:当系统的参数发生变化时,系统的稳定点可能会出现分叉现象,即稳定点从一个点分裂成多个点,这种分叉现象是混沌系统中一个显著的特征。
3. 分形结构:在混沌分叉中,分岔现象可能形成分形结构,这种结构在混沌系统中具有重要的理论和实际意义。
三、Matlab基础知识使用Matlab编写混沌分叉程序需要具备一定的Matlab基础知识,包括但不限于以下内容:1. Matlab基本语法:了解Matlab的基本语法规则,包括变量定义、数组操作、逻辑运算等。
2. Matlab图形绘制:掌握Matlab绘制图形的基本方法,包括绘制曲线、散点图等。
3. Matlab函数编写:了解如何在Matlab中编写自定义函数,并且能够熟练运用函数调用和参数传递。
四、混沌分叉程序的编写编写混沌分叉程序的基本步骤如下:1. 设定系统参数:首先需要定义混沌系统的参数,包括系统的微分方程、初始条件以及需要变化的参数。
2. 编写微分方程:根据所研究的具体混沌系统,编写系统的微分方程,通常为非线性微分方程。
3. 参数变化循环:对系统的某些参数进行变化,并且循环计算系统的轨迹,观察混沌分叉现象。
4. 图形绘制:绘制分叉图、分岔图等用于展示混沌分叉现象的图形。
五、程序示例下面为一个简单的混沌分叉程序示例,以具体的混沌系统为 Logistic映射为例,程序演示了 Logistic 映射参数 r 变化时轨迹的分叉现象。
【matlab代做hslogic】混沌调制解调课案
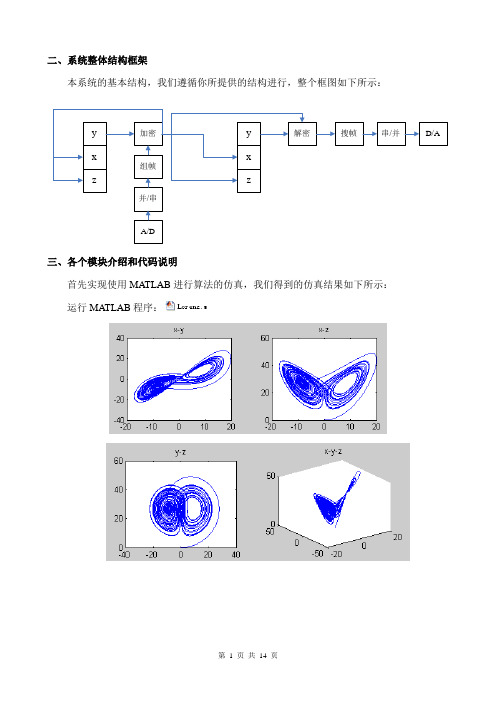
二、系统整体结构框架本系统的基本结构,我们遵循你所提供的结构进行,整个框图如下所示:三、各个模块介绍和代码说明首先实现使用MATLAB 进行算法的仿真,我们得到的仿真结果如下所示: 运行MATLAB 程序:这个是混沌模型的基本仿真,说明公式以及初始值选取的正确性。
运行MATLAB程序:这个程序是混沌加密调制解调系统的MATLAB浮点仿真结果图,说明上面的结果是正确的。
运行MATLAB程序:从上面的仿真结果可知,以定点进行仿真,只要量化宽度满足一定要求之后,其完全不影响系统的精度。
根据上面的介绍,我们可以编写了如下的程序:自上而下,依次为:系统顶层文件——加密调制模块————加密子模块,lorenz混沌序列产生模块,组帧模块,并串模块。
——解密解调模块————解密子模块,Lorenz混沌序列产生模块,搜帧模块,串并模块。
下面对各个模块进行介绍。
接口含义分别为:系统时钟系统复位测试并行信号的产生使能信号测试并行信号加密模块的使能信号串行输出串行信号组帧输出加密输出解密输出解密输出信号的符号判决搜帧模块的相关峰输出搜帧模块的使能输出搜帧模块的数据输出最后串并转化的使能最后串并转化的数据输出顶层模块,主要功能就是产生测试数据,16位宽的并行数据:然后是分别调用加密调制模块和解密解调模块:具体的接口含义,我们在介绍这些子模块的时候进行说明。
加密模块的接口含义是时钟,复位,输入并行信号的使能信号,输入并行信号,串行输出,组帧后的输出,加密信号:其中:加密输出信号o_T_signal反馈给lorenz混沌模块进行迭代,迭代后的yn输出进行加密。
分别为系统时钟,复位,数据输入,混沌y输出,加密信号输出。
其基本原理,是通过信号和混沌信号的叠加来实现的。
其接口是系统时钟,复位,加密反馈信号,混沌xyz输出。
注意,这里我们采用的是基于浮点原理的定点计算方法,由于在FPGA中直接采用浮点计算算法比较复杂,而且比较耗资源,而传统的定点计算精度不够,因此,这里我们采用的是基于浮点的定点计算,即进行位宽扩展,相乘之后进行截位的方法。
各类混沌的matlab程序实现

常微分方程及常微分方程组地求解
( )
转载▼
分类:编程之
标签:
杂谈
最近参加了数学建模,对于老师说地算法地不同步长地精度不一样,编写了一个函数文件来实现这个精度地比较,把函数附上:文档收集自网络,仅用于个人学习
[] ()
这里使用可变输出输入函数地
{}为求解常微分方程地表达式
{}为求解常微分方程地定解条件
需要给出地变量有常微分方程地范围,({}{})
为对这个区间地分割({})文档收集自网络,仅用于个人学习
写于月日
取得算法需要地变量,并附上容易理解地含义变量
{};
{}自变量地范围
{}区间地分割次数
( )步长
{}; 常微分方程地表达式
{}; 常微分方程地定解条件表达式文档收集自网络,仅用于个人学习
首先求出所给常微分方程问题地精确解
();
();
; ;
(,'');
() ;
() (,{},{()});
:()
() () ;
() ((,{},{()}));
文档收集自网络,仅用于个人学习
利用方法求解近似数值微分解
();
();
;
() ;
() (,{},{})获得原方程地初解
:()
() () ;
() () .* (((),{},{()()}))特别记录中地字符串操作,提取子字符串即(:)...
文档收集自网络,仅用于个人学习
返回经过算法算出与地值
;
;
画图进行误差比较
(,'');
;
(,'');文档收集自网络,仅用于个人学习特此记录,以后写了新地算法再分享。
基于MATLAB的各类混沌系统的计算机模拟(教学版)

z
20 0 20
50 40 30
z
20 10 0 -20 -10 x 0 10
z
20 10 0 -20 -10 0 y 10 20
4.初值敏感性: 保持初值 x0 和 y0 不变,即 x0=y0=1,改变 z0 为 1.001,千分之一的变化会引起系统 行为的显著改变,如下图所示:
y
Rossler 方 程 X-Z平 面 相 图 (较 短 时 间 后 ) 50 40 30
6. 吸引子: 指相空间的这样的一个点集 s (或一个子空间) , 对 s 邻域的几乎任意一 点, 当 t 时所有轨迹线均趋于 s, 吸引子是稳定的不动点。 7. 奇异吸引子: 又称混沌吸引子, 指相空间中具有分数维的吸引子的集合。 该吸引集 由永不重复自身的一系列点组成, 并且无论如何也不表现出任何周期性。 混沌轨道就运行在 其吸引子集中。 8. 分叉和分叉点: 又称分岔或分支。 指在某个或者某组参数发生变化时, 长时间动力 学运动的类型也发生变化。 这个参数值(或这组参数值)称为分叉点, 在分叉点处参数的微小 变化会产生不同性质的动力学特性, 故系统在分叉点处是结构不稳定的。 9. 周期解: 对于系统 xn 1 f ( xn ) , 当 n 时,若存在 xn i xn , 则称该系 统有周期 i 解 。不动点可以看作是周期为 1 的解, 因为它满足 xn 1 xn 。 10. 初值敏感性: 对初始条件的敏感依赖是混沌的基本特征, 也有人用它来定义混沌: 混沌系统是其终极状态极端敏感地依赖于系统的初始状态的系统。 敏感依赖性的一个严重后 果就在于,使得系统的长期行为变得不可预见。
引言. 混沌探秘
混沌是非线性系统所独有且广泛存在的一种非周期运动形式, 其覆盖面涉及到自然科 学和社会科学的几乎每一个分支。1972 年 12 月 29 日,美国麻省理工学院教授、混沌学开 创人之一 E.N.洛伦兹在美国科学发展学会第 139 次会议上发表了题为《蝴蝶效应》的论文, 提出一个貌似荒谬的论断:在巴西一只蝴蝶翅膀的拍打能在美国得克萨斯州产生一个龙卷 风,并由此提出了天气的不可准确预报性。为什么会出现这种情况呢?这是混沌在作怪! “混沌”译自英语中“chaos”一词,原意是混乱、无序,在现代非线性理论中,混沌 则是泛指在确定体系中出现的貌似无规则的、类随机的运动。 混沌现象是普遍的,就在我们身边,是与我们关系最密切的现象,我们就生活在混沌的 海洋中。一支燃着的香烟,在平稳的气流中缓缓升起一缕青烟,突然卷成一团团剧烈搅动的 烟雾,向四方飘散;打开水龙头,先是平稳的层流,然后水花四溅,流动变的不规则,这就 是湍流;一个风和日丽的夏天,突然风起云涌,来了一场暴风雨。一面旗帜在风中飘扬, 一 片秋叶从树上落下,它们都在做混沌运动。可见混沌始终围绕在我们的周围,一直与人类为 伴。
基于matlab对混沌掩盖通信的仿真研究

科技信息计算机与网络基于matIab对混沌掩盖通信帕仿真硼究北京邮电大学信息与通信工程学院尉志青[摘要】本文利用mad曲软件对混沌掩盖通信进行了仿真研究,具体研究了一维信号以及二维信号(数字图像)的混沌掩盖通信问题。
讨论了压缩系教对传输质量的影响。
并且对数字图像传输中的混沌加密进行了一些修正,使之加密效果更好。
[关键词】混沌加密(方法)混沌掩盖L0画如c混沌序列、.混沌掩盖也称混沌遮掩或混沌隐藏。
混沌掩盖通信的基本原理是利用具有逼近丁|高斯噪声统计特性的混沌信号对有用的信息进行混沌掩盖,接收端利用同步后的混沌信号进行解调,从而恢复出混沌掩盖之前的信号,接收有用信息。
实现通信的系统框图如图l所示:图1混沌通信系统框图映射的混沌掩盖通信系统框图本文中所用的混沌掩盖方式为相加。
在接收端用同步后的混沌信号进行与之相廊的逆运算即可恢复出有用的信息。
下面针对基于L—gi8t记映射的混沌掩盖通信系统进行仿真,研究混沌掩盖通信的一些特性。
kIgistic混沌序列的迭代式为:x(x+1)=II《n)·(1一x(n))。
其中0≤《n)≤l,O≤u≤4。
当u取值在3.58和4之间时是混沌的。
通信系统框图如图2图2基于I埘觚c映射的混沌掩盖通信系统框图以上框图中s(n)为输入的信息序列,e(n)为已调序列,s(n)为解调输出序列。
令e(n)=x‘(n+1):x(n+1)+k×s(n)x(n+1):x’(n+1)M0d(1)k为压缩系数,一般取k<1/50。
我们知道,混沌掩盖的加法方式使消息信号浮于混沌载体之上,这就决定了只能采用很小的信号,而加性的小信号极易受到同样是加性的信道噪声的干扰,稍大的噪声会使接收端的误码率大大升高;如果用大的消息信号,该信号就会从掩盖的混沌码中浮出『fIi在公开的信道上被窃取.所以k不宜太大,也不宜太小。
x(n+1)取x’(n+1)对l的模是为了使得调制输出的序列幅度不大于l,可以保证k画stic混沌序列不脱离混沌状态,可以抵御攻击者的破译。
离散混沌系统的Matlab仿真

在 35 <4的参数区域 内, .7< 系统存在混沌吸引子 , 任意取一个初值 , 得到 的一个轨道最终被吸引到 这个 吸引轨道上来 , 将不同初值所得的结果作 图, 将呈现一条复杂的曲线.
用 ei命令建立 自 d t 定义函数名为 Lg t . 然后利用 dbg o ii m, sc eu 命令直接运行 , 混沌图形如图 1 所示.
本文在基于 M t b aa 环境 , l 研究了离散混沌系统的数值解法和图形仿 真, 同时针对离散时滞 混沌 系统
给出了数值仿真的 M f b aa 程序. l 从数值仿真角度来说 , 本文所得方法对 于离散混沌系统 的混沌同步和控
制器仿真及误差描述都有积极的意义.
1 离散 混沌 系统 的数 值仿真
收稿 日期 :06一 6— 8 20 O 2 修 回 日期 :0 6— 9— 0 20 0 3
基金项 目: 安徽省教育厅 自然科学基金项 目(0 6 J4 B)安徽省 教育厅青年教师科研基金项 目(20 J l 3 资 助 20 K 29 、 0 5Q 5 ) 1 1 作者 简介 : 明(9 O ) 女 , 朱夜 17 一 , 安徽庐江人 , 安徽 大学 学报 编辑部 副编审 , 理学硕士 .
不便 .
M fb aa 是由 M t Wo l a r h k公司推 出的一种面向科学与工程计算的高级语言, 它集科学计算、 自动控制信
号处理、 神经 网络 、 图像处理等 于一体 , 具有极 高的编程效 率.M tb提供 的 S un 是一个 基于 aa l i lk m i Wi o s n w 环境下 的以图形进行编程的软件, d 可用来对动态系统建模、 仿真 和分析. 同时 M t b aa 语言编程直 l 观易懂 , a a M tb在数值计算及动态仿真等方面 , l 研究人员不但工作量小 , 编程也很容易 , 开发周期也大大缩 短, 数据也更加直观 , 因此在混沌学领域中将发挥其重大作用.
基于Matlab的混沌特性分析

基于Matlab的混沌特性分析1. 引言1.1 研究背景混沌理论起源于1960年代,是一种描述复杂系统行为的新理论,揭示了非线性系统中存在的一种无序、不可预测的动态行为。
混沌系统具有高度敏感性和非周期性,表现出随机性和确定性的结合,对于许多领域的研究具有重要的理论和实际意义。
在现代科学和工程领域,混沌系统的分析和控制已经成为一个热门的研究方向。
随着计算机技术的发展,基于Matlab的混沌特性分析方法成为研究混沌系统的有力工具。
Matlab提供了丰富的算法和库函数,可以方便地进行混沌系统建模、仿真和分析。
利用Matlab进行混沌特性分析,可以更深入地理解混沌系统的动力学行为,为系统的控制与优化提供理论支持。
1.2 研究目的研究目的的主要目标是通过基于Matlab的混沌特性分析,探讨混沌系统的特征和建模方法,并利用Matlab提供的分析工具对混沌系统进行详细分析。
通过深入研究混沌系统的特性和行为,可以更好地理解和预测混沌系统的运动规律和特点,为相关领域的研究和应用提供理论支持和参考依据。
本研究旨在探讨基于Matlab的混沌特性分析方法的有效性和可行性,为混沌系统的研究和应用提供一种新的分析途径和工具。
通过对混沌系统的特性进行深入分析和实验研究,可以揭示混沌系统背后的规律和内在机制,为相关领域的发展和应用提供新的思路和方法。
本研究的目的在于通过基于Matlab的混沌特性分析,深入探讨混沌系统的特性和行为,为相关领域的研究和应用提供新的视角和研究方法。
1.3 研究意义混沌系统在现代科学和工程中具有广泛的应用,例如在通信、控制、密码学等领域都有重要的作用。
对混沌系统进行特性分析,能够帮助我们更好地理解和掌握系统的行为规律,为系统的设计和优化提供重要的参考。
混沌系统的特性分析不仅可以帮助我们更好地理解系统的动态行为,还可以为混沌系统的控制和应用提供理论基础。
通过本文基于Matlab的混沌特性分析,我们可以更深入地探索混沌系统的特性和规律,为未来混沌系统的应用和发展提供重要参考。
各类混沌的matlab程序实现

混沌同步模型驱动系统和响应系统都是Lorenz System,只不过初值不同。
驱动系统: dx/dt=a*(y-x)dy/dt=r*x-y-xzdz/dt=x*y-b*z初值(0.1,0.1,0.1)输出信号令S(t)=x(t)响应系统:将S(t)代替x(t)作为激励信号dx/dt=a*(y-x)dy/dt=r*x-y-xzdz/dt=x*y-b*z初值(0.1,0.1,1)最后求响应系统的输出x(t),y(t),z(t)程序:function [Y1] = Lorenz_response(tspan);%%计算处于响应地位的Lorenz系统的数值解,并由此画出其相图yinit = [0.1,0.1,1];% 初始化输入y(1:3) = yinit;tstart = 0; % 时间初始值tstep = 1e-1; % 时间步长wholetimes = 1e2; % 总的循环次数steps = 1; % 每次演化的步数iteratetimes = wholetimes/steps; % 演化的次数S=output;for i=1:iteratetimes;tspan = tstart:tstep:(tstart + tstep*steps);[T,Y1] = ode45(@Lorenz_driven, tspan, y);y = Y1(size(Y1,1),:);y(1)=S(i,1);% 重新定义起始时刻tstart = tstart + tstep*steps;endfigure(1)plot3(Y1(:,1),Y1(:,2),Y1(:,3))function s=output;tstart = 0; % 时间初始值tstep = 1e-1; % 时间步长wholetimes = 1e2; % 总的循环次数% options = odeset('RelTol',1e-4,'AbsTol',[1e-4 1e-4 1e-5]);tspan=tstart:tstep:wholetimes*tstep[T,Y] = ode45(@Lorenz_driven,tspan,[0.1 0.1 0.1]);s=Yfigure(3)plot3(Y(:,1),Y(:,2),Y(:,3))function dY=Lorenz_driven(t,Y);a=10;b=8/3;r=60;dY=zeros(3,1);dY=[a*(Y(2)-Y(1));-Y(1)*Y(3)+r*Y(1)-Y(2);Y(1)*Y(2)-b*Y(3)]MatLab常微分方程及常微分方程组的求解(2011-07-08 23:01:48)转载▼分类:编程之Matlab标签:杂谈最近参加了数学建模,对于老师说的Euler算法的不同步长的精度不一样,编写了一个M 函数文件来实现这个精度的比较,把函数附上:function [x,y]= Euler(varargin)%这里使用可变输出输入函数的%varargin{1}为求解常微分方程的表达式%varargin{2}为求解常微分方程的定解条件%需要给出的变量有常微分方程的范围a,b(varargin{3},varargin{4})%n为对这个区间的分割(varargin{5})%xlt写于7月8日%取得算法需要的变量,并附上容易理解的含义变量a = varargin{3};b = varargin{4};%自变量的范围n = varargin{5};%区间的分割次数h = (b - a)/n;%步长Dy = varargin{1}; %常微分方程的表达式y0 = varargin{2}; %常微分方程的定解条件表达式%首先求出所给常微分方程问题的精确解x1 = zeros(n+1,1);y1 = zeros(n+1,1);syms f1; syms x;f1 = dsolve(Dy,y0,'x');x1(1) = a;y1(1) = subs(f1,{x},{x1(1)});for i = 2:(n+1)x1(i) = x1(i-1) + h;y1(i) = double(subs(f1,{x},{x1(i)}));end%利用Euler方法求解近似数值微分解x2 = zeros(n+1,1);y2 = zeros(n+1,1);syms y;x2(1) = a;y2(1) = subs(f1,{x},{a});%获得原方程的初解for i = 2:(n+1)x2(i) = x2(i-1) + h;y2(i) = y2(i-1) + h .* double(subs(Dy(5:end),{x,y},{x2(i-1),y2(i-1)}));%特别记录Matlab中的字符串操作,提取子字符串即A(3:6)...end%返回经过Euler算法算出x与y的值x = x2;y = y2;%画图进行误差比较plot(x1,y1,'r');hold on;plot(x2,y2,'b');特此记录,以后写了新的算法再分享文 - 汉语汉字编辑词条文,wen,从玄从爻。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基于MATLAB 的各类混沌系统的计算机模拟―――《混沌实验教学平台的设计与实现》初期报告物电05级1A 班 张丹伟 20050003101摘要:本文利用数学软件MATLAB 对Lorenz 系统等六个重要的混沌模型进行数值计算,同时模拟出各类混沌系统的独特性质,如混沌吸引子,倍周期,初值敏感性,相图,分岔图等。
通过观察和分析上述特性,加深了我们对混沌现象的理解。
关键词:混沌; 微分方程; MA TLAB ;引言. 混沌探秘混沌是非线性系统所独有且广泛存在的一种非周期运动形式, 其覆盖面涉及到自然科学和社会科学的几乎每一个分支。
1972年12月29日,美国麻省理工学院教授、混沌学开创人之一E.N.洛伦兹在美国科学发展学会第139次会议上发表了题为《蝴蝶效应》的论文,提出一个貌似荒谬的论断:在巴西一只蝴蝶翅膀的拍打能在美国得克萨斯州产生一个龙卷风,并由此提出了天气的不可准确预报性。
为什么会出现这种情况呢?这是混沌在作怪!“混沌”译自英语中“chaos”一词,原意是混乱、无序,在现代非线性理论中,混沌则是泛指在确定体系中出现的貌似无规则的、类随机的运动。
混沌现象是普遍的,就在我们身边,是与我们关系最密切的现象,我们就生活在混沌的海洋中。
一支燃着的香烟,在平稳的气流中缓缓升起一缕青烟,突然卷成一团团剧烈搅动的烟雾,向四方飘散;打开水龙头,先是平稳的层流,然后水花四溅,流动变的不规则,这就是湍流;一个风和日丽的夏天,突然风起云涌,来了一场暴风雨。
一面旗帜在风中飘扬,一片秋叶从树上落下,它们都在做混沌运动。
可见混沌始终围绕在我们的周围,一直与人类为伴。
一. 混沌的基本概念1. 混沌: 目前尚无通用的严格的定义, 一般认为,将不是由随机性外因引起的, 而是由确定性方程(内因)直接得到的具有随机性的运动状态称为混沌。
2. 相空间: 在连续动力系统中, 用一组一阶微分方程描述运动, 以状态变量(或状态向量)为坐标轴的空间构成系统的相空间。
系统的一个状态用相空间的一个点表示, 通过该点有唯一的一条积分曲线。
3. 混沌运动: 是确定性系统中局限于有限相空间的高度不稳定的运动。
所谓轨道高度不稳定, 是指近邻的轨道随时间的发展会指数地分离。
由于这种不稳定性, 系统的长时间行为会显示出某种混乱性。
4. 分形和分维: 分形是 n 维空间一个点集的一种几何性质, 该点集具有无限精细的结构, 在任何尺度下都有自相似部分和整体相似性质, 具有小于所在空间维数 n 的非整数维数。
分维就是用非整数维——分数维来定量地描述分形的基本性质。
5. 不动点: 又称平衡点、定态。
不动点是系统状态变量所取的一组值, 对于这些值系统不随时间变化。
在连续动力学系统中, 相空间中有一个点0x , 若满足当 t →∞时, 轨迹0()x t x →, 则称0x 为不动点。
6. 吸引子: 指相空间的这样的一个点集 s (或一个子空间) , 对s 邻域的几乎任意一点, 当t →∞时所有轨迹线均趋于s, 吸引子是稳定的不动点。
7. 奇异吸引子: 又称混沌吸引子, 指相空间中具有分数维的吸引子的集合。
该吸引集由永不重复自身的一系列点组成, 并且无论如何也不表现出任何周期性。
混沌轨道就运行在其吸引子集中。
8. 分叉和分叉点: 又称分岔或分支。
指在某个或者某组参数发生变化时, 长时间动力学运动的类型也发生变化。
这个参数值(或这组参数值)称为分叉点, 在分叉点处参数的微小变化会产生不同性质的动力学特性, 故系统在分叉点处是结构不稳定的。
9. 周期解: 对于系统1()n n x f x += , 当n →∞时,若存在n i n x x ξ+== , 则称该系统有周期i 解ξ 。
不动点可以看作是周期为1的解, 因为它满足1n n x x +=。
10. 初值敏感性:对初始条件的敏感依赖是混沌的基本特征,也有人用它来定义混沌:混沌系统是其终极状态极端敏感地依赖于系统的初始状态的系统。
敏感依赖性的一个严重后果就在于,使得系统的长期行为变得不可预见。
二. MATLAB 中的龙格—库塔(Runge-Kutta )实现MATLAB (Matrix Laboratory )是MathWorks 公司开发的,目前国际上最流行应用最广的科学与工程计算机软件之一。
MA TLAB 软件以矩阵运算为基础,把计算,可视化,程序设计等有机的融合在一起,具有出色的数值计算能力和强大的图形处理功能。
基于Runge —Kutta 法,MA TLAB 提供了求解微分方程数值解的函数,一般调用格式是:[,]23(@,,0)[,]45(@,,0)t y ode fname tspan y t y ode fname tspan y ==其中fname 是定义的函数文件名,该函数文件必须返回一个列向量。
Tspan 形式是[t0,tf],表示求解区间,y0是初始状态向量。
这两个函数分别采用“二阶,三阶Runge —Kutta 法”和“四阶,五阶Runge —Kutta 法”,并采用自适应的求解方法,即当解的变化较慢时采用较大的步长,从而使计算速度很快,当解的变化较快时步长会自动变小长,从而使计算精度很高。
在MA TLAB 中,一般选取四阶的龙格库塔方法。
三. Lorenz 混沌系统美国气象学家洛伦兹(E.N.Lorenz )于1963年在大气科学杂志上提出第一个表现奇异吸引子的动力学系统。
该混沌系统模型可以用下列微分方程组描述:)()(z xy b dtdzxz y ax dt dyy x c dt dx-=--=--=利用MA TLAB 数学软件对上面微分方程求解,进行数值模拟。
首先建立M -文件 Lorenz.m 定义脚本函数,然后编程调用,其中x (1)表示x ,x (2)表示y ,x (3)表示z ,程序如下:function r=lorenz(t,x) global a; global b; global c;r=[-c*(x(1)-x(2));a*x(1)-x(2)-x(1)*x(3);b*(x(1)*x(2)-x(3))];clear;global a;global b;global c;b=8/3;c=10;t0=[0,100];f0=[1,1,1];for a=10:30[t,x]=ode45(@lorenz,t0,f0);asubplot(3,1,1);plot(t,x(:,1),'r',t,x(:,2),'g',t,x(:,3),'b');title('Lorenz 模型变量时域响应');legend('x','y','z'); xlabel('t');subplot(3,1,2);plot3(x(:,1),x(:,2),x(:,3));title('Lorenz模型相图');xlabel('x');ylabel('y');zlabel('z');grid on;subplot(3,1,3);plot(x(:,1),x(:,3));title('Lorenz模型X—Z平面相图'); xlabel('x');ylabel('z');grid on;pause;end1. 固定参数b和c,设置初始值f0 和计算时间t0,通过改变参数a 可以发现系统逐步进入混沌状态的过程。
2. Lorenz 吸引子当a=28时,系统已经完全进入混沌状态,此时出现双涡旋吸引子,如下所示:3. 倍周期:通过系数的调试可以得到Lorenz混沌的一个单倍周期和两个多倍周期,如下:4.初值敏感性:保持初值x0和y0不变,即x0=y0=1,改变z0为1.001,千分之一的变化会引起系统行为的显著改变,如下图所示:四. Rossler 混沌系统Rossler 系统是化学反应系统的简化模型,是非线性动力学中非常著名的方程,该混沌系统模型可以用下列微分方程组描述)(a x z c dtdzxby dt dyz y dt dx-+=-=-= 同样地,利用MATLAB 编程求解(程序见附录),可以对该模型进行分析。
1. 逐步改变参数,观察其进入混沌状态。
2.Rossler吸引子:3.倍周期:通过调整参数和初始值,可以得到单倍周期和2倍周期,如下图:初值敏感性:五. 蔡氏电路混沌系统1983年美国电学专家蔡少棠 (L. O. Chua)首次提出了著名的蔡氏电路 (Chua ‘s circuit) ,它是混沌发展史上的一个重要里程碑. 它使人们从被动的研究混沌现象向主动的设计和控制混沌迈出了关键的一步.蔡氏电路是目前众多混沌电路中最具典型代表性的一种。
对于单涡旋的变形蔡氏电路的微分方程组为:.312..()x y k x k x y x y xz z yαβ=--=--=-当α=5.5,β=-7.4,其初值敏感性如下所示:对于多涡旋的情况,例如可以用多项式 3ax bx x cx ++产生三涡卷蔡氏混沌吸引子,其无量纲归一化状态方程可以写为:...(())x y h x y x y z z yαβ=-=-+=-其中3()h x ax bx x cx =++,参数α=12.8,β=19.1,实验中固定b =-1.1,c =0.45。
1. 改变参数a ,观察该电路模型的进入混沌状态的过程当a=0.6时,呈现三涡旋吸引子如下:其初值敏感性:六. Duffing 方程杜芬(Duffing )方程指的是非线性振子的间谐受迫振动方程:232cos()d x dx b x x a ct dt dt+-+= 该写为自洽的微分方程组为:3c o s ()dx y dtdya ct by x x dt==-+-选取参数 a =2.09, b =0.1,c =0.5,可以得到该混沌模型的相图:七. Logistic 方程Logistic 方程是离散映射方程:)1(1n n n x ax x -=+,n=0,1,2,…;其相图如下:其分岔图如下:八. Henon 方程nn n n n x y by ax x =+-=++1211其中,n=0, 1, 2, …; a=1..28, b=-0.3.其相图如下:九.总结与感想在这次科技制作中,我主要的工作是对在已有的混沌系统方程基础上,利用MATLAB 进行编程,模拟混沌系统。
由于混沌对初值和参数的依赖性很大,所以我尽可能地通过网上或者书籍寻找这些参数,减少调试时间;当然,这样不能很好地探究整个混沌系统的特性,只能停留在理论的层面上。
