第四章 主应力法 计算题
计算题1、已知应力状态如图所示,求主应力及最大切应力(图示单位为

计算题:1、已知应力状态如图所示,求主应力及最大切应力(图示单位为MPa)。
(10分)2、已知应力状态如图所示,求主应力及最大切应力。
(10分)3、已知应力状态如图所示,求主应力及最大切应力(图示单位为MPa)。
(10分)4、已知应力状态如图所示,求主应力及最大切应力(图示单位为MPa)。
(10分)5、已知应力状态如图示,图中应力单位皆为MPa,试求:(1)主应力的大小,主平面的方位;(2)最大切应力;(10分)6、已知应力状态如图示,图中应力单位皆为MPa ,试求:(3) 主应力的大小,主平面的位置; (4) 最大切应力。
(10分)7、(10分)已知三向应力状态如图所示(图中应力单位:MPa ), 试求: 1) 主应力;2)主切应力;3)形变应变能密度f e 。
8、(14分)已知K 点处为二向应力状态,过K 点两个截面上的应力如图所示(应力单位为MPa )。
试用解析法(用图解法无效)确定该点的三个主应力。
9、(8分)图示为某构件内危险点的应力状态(图中应力单位为MPa ),试分别求其第二、第四强度理论的相当应力2r σ、4r σ(3.0=μ)。
10、(8分)图示为某构件内危险点的应力状态(图中应力单位为MPa ),试分别求其第二、第四强度理论的相当应力2r σ、4r σ(3.0=μ)。
11、(4分)矩形截面细长悬臂梁如图所示。
试求A 、B 、C 三点的应力,并 用单元体分别表示这三点的应力状态。
12、(4分)已知构件内某点处的应力状态为两种应力状态的叠加结果,试求叠加后该点该平面内的(1)主应力与主应变; (2)主切应力;(3)该点的形变应变能密度fe 。
(已知材料的弹性模量GPa 200=E ,横向变形系数3.0=ν)13、图示板件,微体处于纯剪切应力状态,试计算沿对角线AC 与BD 方位的正应力,以及所对应力正应变045ε与045-ε,沿板厚方向的正应变z ε。
材料的弹性常数E 与μ均为已知。
材料力学典型例题及解析7.应力应变状态典型习题解析

应力、应变状态分析典型习题解析1 已知矩形截面梁,某截面上的剪力F S =120 kN 及弯矩m kN 10⋅=M 。
绘出表示1、2、3及4点应力状态的微体,并求出各点的主应力。
b = 60 mm ,h = 100 mm 。
解题分析:从图中可分析1、4点是单向应力状态,2点在中性轴上为纯剪切应力状态,31取平行和垂直与梁横截面的六个平面,构成微体。
则各点处的应力状态如图示。
2、梁截面惯性矩为点微体上既有正应力又有切应力。
解:、画各点处微体的应力状态图计算各点处主应力4843333m 1050012m 10100(106012−−−×=×××==)bh I z 1点处弯曲正应力(压应力)MPa 100Pa 10100m10500m 1050m N 101064833−=×=×××⋅×==−−z I My σ1点为单向压缩受力状态,所以021==σσ,MPa 1003−=σ2点为纯剪切应力状态,MPa 30Pa 1030m10100602N1012036263=×=×××××=−τ(向下)容易得到,MPa 301=σ,02=σ,MPa303−=σ3点为一般平面应力状态弯曲正应力MPa50Pa 1050m 10500m 1025m N 101064833=×=×××⋅×==−−z I My σ弯曲切应力σ14τ2F S =120 kN题图1中性轴324hστ25 mm 31b M =10 kN·mσ3150 mm 1MPa 5.22Pa 1050.22m10500m 1060m 105.372560N 101206483393*S =×=××××××××==−−−zz bI S F τMPa6.8MPa6.58Pa)10522()2Pa 1050(2Pa 1050)2(22626622minmax −=×+×±×=+−±+=x y x yx τσσσσσσ所以 MPa 6.581=σ,02=σ,MPa 6.83−=σ4点为单向拉伸应力状态,拉伸正应力的大小与1点相等。
材料力学习题

材料力学习题第2章2-1 试求出图示各杆件中Ⅰ—Ⅰ截面上的力。
2-2图示矩形截面杆,横截面上正应力沿截面高度线性分布,截面顶边各点处的正应力均为MPa100max=σ,底边各点处的正应力均为零。
杆件横截面上存在何种力分量,并确定其大小〔C 点为截面形心〕。
2-3 试指出图示各单元体表示哪种应力状态。
2-4 应力状态如下图〔应力单位为MPa〕,试用解析法计算图中指定截面的应力。
2-5 试作应力圆来确定习题2-4图中指定截面的应力。
2-6应力状态如下图〔应力单位为MPa 〕,试用解析法求:〔1〕主应力及主方向;〔2〕主切应力及主切平面;〔3〕最大切应力。
2-7 应力状态如习题2-6图所示,试作应力圆来确定:〔1〕主应力及主方向; 〔2〕主切应力及主切平面;〔3〕最大切应力。
2-8构件某点处的应力状态为两种应力状态的叠加结果,试求叠加后所得 应力状态的主应力、主切应力。
2-9图示双向拉应力状态,σσσ==y x 。
试证明任一斜截面上的正应力均等于σ,而切应力为零。
2-10K 点处为二向应力状态,过K 点两个截面上的应力如下图〔应力单位为MPa 〕。
试分别用解析法与图解法确定该点的主应力。
2-11 一点处的应力状态在两种坐标系中的表示方法分别如图 a)和b)所示。
试确定未知的应力分量y y x xy '''σττ、、的大小与方向。
2-12 图示受力板件,试证明尖角A 处各截面的正应力与切应力均为零。
2-13应力状态如下图〔单位为MPa 〕,试求其主应力及第一、第二、第三不变量321I I I 、、。
2-14应力状态如下图〔单位为MPa 〕,试画三向应力圆,并求主应力、最大正应力与最大切应力。
第3章3-1某点的位移分量u = A , v = Bx +Cy +Dz , w = Ex 2+Fy 2+Gz 2+Ixy +Jyz +Kzx 。
A 、B 、C 、D 、E 、F 、G 、I 、J 、K 均为常数,求该点处的应变分量。
工程力学材料力学第四完整版本习题答案解析
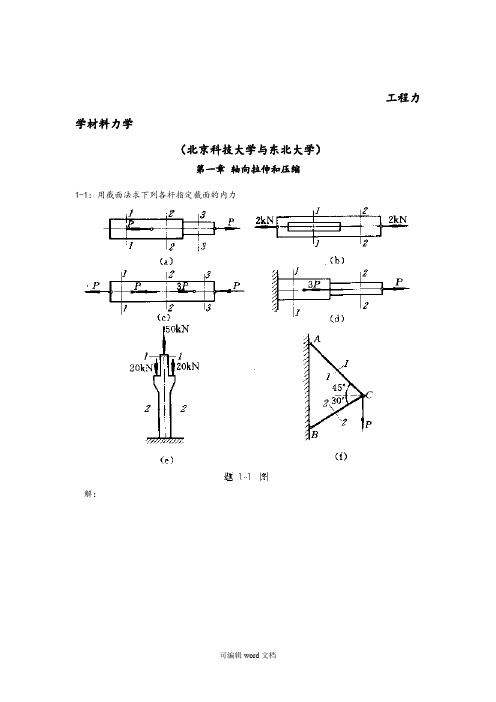
工程力学材料力学(北京科技大学与东北大学)第一章轴向拉伸和压缩1-1:用截面法求下列各杆指定截面的内力解:(a):N1=0,N2=N3=P(b):N1=N2=2kN(c):N1=P,N2=2P,N3= -P(d):N1=-2P,N2=P(e):N1= -50N,N2= -90N(f):N1=0.896P,N2=-0.732P注(轴向拉伸为正,压缩为负)1-2:高炉装料器中的大钟拉杆如图a所示,拉杆下端以连接楔与大钟连接,连接处拉杆的横截面如图b所示;拉杆上端螺纹的内径d=175mm。
以知作用于拉杆上的静拉力P=850kN,试计算大钟拉杆的最大静应力。
解:σ1=2118504P kNS dπ==35.3Mpaσ2=2228504P kNS dπ==30.4MPa∴σmax=35.3Mpa1-3:试计算图a所示钢水包吊杆的最大应力。
以知钢水包及其所盛钢水共重90kN,吊杆的尺寸如图b所示。
解:下端螺孔截面:σ1=19020.065*0.045P S=15.4Mpa上端单螺孔截面:σ2=2P S =8.72MPa上端双螺孔截面:σ3= 3P S =9.15Mpa∴σmax =15.4Mpa1-4:一桅杆起重机如图所示,起重杆AB为一钢管,其外径D=20mm,内径d=18mm;钢绳CB 的横截面面积为0.1cm2。
已知起重量P=2000N,试计算起重机杆和钢丝绳的应力。
解:受力分析得:F1*sin15=F2*sin45F1*cos15=P+F2*sin45∴σAB=11FS=-47.7MPaσBC=22FS=103.5 MPa1-5:图a所示为一斗式提升机.斗与斗之间用链条连接,链条的计算简图如图b 所示,每个料斗连同物料的总重量P=2000N.钢链又两层钢板构成,如c所示.每个链板厚t=4.5mm,宽h=40mm,H=65mm,钉孔直径d=30mm.试求链板的最大应力.解:F=6PS 1=h*t=40*4.5=180mm 2S2=(H-d)*t=(65-30)*4.5=157.5mm 2∴σmax=2F S =38.1MPa1-6:一长为30cm 的钢杆,其受力情况如图所示.已知杆截面面积A=10cm2,材料的弹性模量E=200Gpa,试求;(1) AC. CD DB 各段的应力和变形.(2) AB 杆的总变形.解: (1)σAC =-20MPa,σCD =0,σDB =-20MPa;△ l AC =NL EA =AC LEA σ=-0.01mm△l CD =CD LEA σ=0△L DB =DB LEA σ=-0.01mm(2) ∴ABl ∆=-0.02mm1-7:一圆截面阶梯杆受力如图所示,已知 材料的弹性模量E=200Gpa,试求各段的应力和应变. 解:31.8127AC ACCB CBPMPa S PMPa S σσ====AC AC AC LNL EA EA σε===1.59*104,CB CB CB LNL EA EA σε===6.36*1041-8:为测定轧钢机的轧制力,在压下螺旋与上轧辊轴承之间装置一测压用的压头.压头是一个钢制的圆筒,其外径D=50mm,内径d=40mm,在压头的外表面上沿纵向贴有测变形的电阻丝片.若测得轧辊两端两个压头的纵向应变均为ε=0.9*10-2,试求轧机的总轧制压力.压头材料的弹性模量E=200Gpa. 解:NllEAllε∆=∆=∴NEAε=62.54*10N EA Nε∴==1-9:用一板状试样进行拉伸试验,在试样表面贴上纵向和横向的电阻丝来测定试样的改变。
岩石力学第四章计算题

岩石力学第四章计算题精炼1、已知σ1=50MPa,σ=10MPa。
3及剪应力τn。
(1)求与X轴夹角40°的EF斜面上的法向应力σn(2)作出相应的莫尔应力圆,并写出莫尔应力圆的方程。
2、将一个岩石试件置于压力机上施加压力,直到1MPa时发生破坏。
已知破坏面与最大主应力所在的平面成60°,并假定抗剪强度随正应力呈线性变化。
试求:(1)在正应力为零的那个面上的抗剪强度等于多少?(2)破坏面上的正应力和剪应力。
3、某岩石的室内剪切试验成果如下,当正应力分别为6MPa和10MPa 时,剪切强度分别为19.2MPa和22MPa,假设该岩石强度服从莫尔斜直线理论,试求:(1)该岩石的剪切强度参数;(2)当侧限压力σ3=10MPa时该岩石的三轴压缩强度。
4、若σ1为最大主应力,σ3为最小主应力,C为粘聚力,φ为岩石的内摩擦角,导出以极限主应力表达的岩石强度方程。
6、已知岩块C=10MPa,φ=60°,用库仑—莫尔准则计算当围压为0和5MPa时试件破坏时的轴压。
12、有一个花岗岩岩柱,该花岗岩抗剪强度指标:凝聚力C=20MPa,φ=30°。
岩柱的横截面积A=5000cm2,柱顶承受荷载p=30MN,自重忽略不计。
(1)试问:是否会发生剪切破坏?(2)若岩柱中有一软弱结构面,其法线与轴线成75°角,试问:是否会沿此面发生破坏?7、某矿石灰岩试验成果如下:其单向抗压强度σc=10MPa;当侧压力σ1=σ2=30MPa,其破坏时σ1=210MPa;当侧压力σ2=σ3=60MPa时,其破坏时σ1=320MPa。
试问,当侧压力σ2=σ3=50MPa时,其破坏时的最大主应力σ1应等于多少?8、某岩石室内抗剪试验成果为当正应力分别为6MPa和10MPa时,剪切强度为19.2MPa和22MPa。
设岩石强度服从直线型莫尔强度判据:①求该岩石的抗剪强度参数(C、φ值);②当侧限压力σ3为5MPa时,求该岩石的三轴压缩强度(σ1m)。
应力状态和强度理论 习题及答案

应力状态和强度理论一、判断题1.若单元体某一截面上的剪应力为零,则该截面称为主平面。
()2.主平面上的剪应力称为主应力。
()3.当单元体上只有一个主应力不为零时,称作二向应力状态。
()5.图2所示单元体最大剪应力为25Mpa。
()6.图3所示单元体为单向应力状态。
()图2图3图47. 向应力状态如图4所示,其最大主应力σ1=3σ()。
8. 任一单元体,在最大正应力作用面上,剪应力为零。
()9. 主应力是指剪力为零的截面上的正应力。
()10.力圆上任一点的横坐标值对应单元体某一截面上的正应力。
()二、选择题1.图1所示应力圆对应的单元体为图()。
图 5三、选择题1.若一点的应力状态为平面应力状态,那么该点的主应力不可能为:()。
A 、σ1> 0 σ2=σ3=0 B、σ1> 0 σ2 =0 σ3 < 0C、σ1>σ2>0 σ3=0D、σ1>σ2>σ3>02.已知单元体各面上的应力如图,则其主平面方位为()。
A、B、C、D、四、填空题1.图示为一平面应力状态的单元体及其应力圆,试在应力圆上表示0-1,0-2,0-3平面的位置。
图 62.试验表明,材料受力后的破坏主要有两种形式,一种是,是由于或所引起;另一种是,是由于所引起的。
3.一单元体如图所示,则单元体的主应力为__________ ,为__________ ,为__________ ,最大主应力与x 轴的夹角为__________ 。
五、简单计算1.单元体上的应力如图7所示,试求其它应力和最大剪应力。
2.图8所示单元体,试求图示斜截面上的正应力和剪应力。
图7图8 3.试求图示单元体o斜截面应力。
已知:。
图 9。
土力学习题(按新教材)

《土质土力学》复习思考题第一章土的物理性质及工程分类一.思考题3.土的结构通常分为哪几种它和矿物成分及成因条件有何关系4.在土的三相比例指标中,哪些指标是直接测定的7.地基土分几大类各类土的划分依据是什么10.土的压实性与哪些因素有关何谓土的最大干密度和最优含水率二.填空题1.确定各粒组相对含量的方法称为颗粒分析试验,分为法和法。
2.砂粒与粉粒的分界粒径是mm。
3.当砾类土或砂类土同时满足C u≥C c = 两个条件时,视为良好级配。
4.土的结构可分为、和三种基本类型。
5.粘性土随着含水量的增加而分别处于、、及流动状态。
6.土粒的矿物成分取决于母岩的矿物成分及风化作用,可分为矿物和矿物。
7.土的物理性质指标中有三个基本指标可直接通过土工试验测定,它们分别是、和。
8.土的物理性质指标中可描述土体中孔隙被水充满的程度。
9.土中孔隙体积与土的总体积之比称为。
10.土中孔隙体积与土的土粒体积之比称为。
11.依相对密度的公式D r =(e max-e)/(e max-e min)可知,当D r = 时,表示土处于最疏松状态。
12.依相对密度的公式D r =(e max-e)/( e max-e min)可知,当D r = 时,表示土处于最密实状态。
三.单项选择题1.某土的液限为40%,塑限为20%,则该土为()。
A.砂土B.粉土C.粉质粘土D.粘土2.某土的液性指数为2,则该土处于()状态。
A.坚硬B.可塑C.流动3.对粘性土的性质影响最大的水是()。
A.强结合水B.弱结合水C.气态水4.对土体性质影响较大的气体是()A.非封闭气体B.封闭气体5.砂土和碎石土的主要结构形式是()A.单粒结构B.蜂窝结构C.絮状结构6.下列哪个物理性质指标可直接通过土工试验测定()。
A.孔隙比e B.孔隙率n C.饱和度S r D.土粒比重d s7.常用来控制填土工程施工质量的指标是:()A.孔隙比e B.孔隙率n C.饱和度S r D.干密度d8.在土工试验室中,通常用()测定土的密度A.联合测定法B.环刀法C.比重计法D.击实仪9.若某砂土的天然孔隙比与其能达到的最大孔隙比相等,则该土()A.处于最疏松状态B.处于中等密实状态C.处于最密实状态D.无法确定其状态10.对粘性土进行分类定名的依据是()A.液限B.塑性指数C.液性指数D.塑限四.判断题1.砾与砂的分界粒径是1mm。
材料力学典型例题及解析 7.应力应变状态典型习题解析

应力、应变状态分析典型习题解析1 已知矩形截面梁,某截面上的剪力F S =120 kN 及弯矩m kN 10⋅=M 。
绘出表示1、2、3及4点应力状态的微体,并求出各点的主应力。
b = 60 mm ,h = 100 mm 。
解题分析: 从图中可分析1、4点是单向应力状态,2点在中性轴上为纯剪切应力状态,31取平行和垂直与梁横截面的六个平面,构成微体。
则各点处的应力状态如图示。
2、 梁截面惯性矩为 点微体上既有正应力又有切应力。
解:、画各点处微体的应力状态图计算各点处主应力4843333m 1050012m 10100(106012−−−×=×××==)bh I z1点处弯曲正应力(压应力)MPa 100Pa 10100m 10500m1050m N 101064833−=×=×××⋅×==−−zI My σ 1点为单向压缩受力状态,所以 021==σσ,MPa 1003−=σ 2点为纯剪切应力状态, MPa 30Pa 1030m10100602N 1012036263=×=×××××=−τ(向下)容易得到,MPa 301=σ,02=σ,MPa 303−=σ 3点为一般平面应力状态弯曲正应力MPa 50Pa 1050m 10500m 1025m N 101064833=×=×××⋅×==−−zI My σ 弯曲切应力F S =120 kN题图1MPa 5.22Pa 1050.22m10500m 1060m 105.372560N 101206483393*S =×=××××××××==−−−z z bI S F τ MPa 6.8MPa 6.58Pa)105.22()2Pa 1050(2Pa 1050)2(22626622min max −=×+×±×=+−±+=xy x y x τσσσσσσ所以 MPa 6.581=σ,02=σ,MPa 6.83−=σ4点为单向拉伸应力状态,拉伸正应力的大小与1点相等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
y y
w
z z
xy
yx
1 2
u
y
v
x
yz
zy
1 2
v
z
w
y
zx
xz
1 2
w
x
u
z
x
x
1 2
y z
y
y
1 2
z
x
z
z
1 2
x y
xy
3 2
xy
yz
3 2
yz
zx
3 2
zx
x
(u) x
y
(v) y
xy
yx
1 2
P
R
p2 rdr
0
R 0
Y
Y h
R
r
2
rdr
Y
R2
1
1 3
R h
将镦粗力除以接触面面积,即得平均单位压力公式:
(u)
y
(v) x
x
x
1 2
y z
y
y
1 2
z
x
xy
3 2
xy
金属塑性成形的力学解析方法
第四章 主应力法 第五章 滑移线解法 第六章 上限法、有限元法等
第四章 金属塑性成形基本工序 的力学分析及主应力法
4.1 主应力法基本原理 4.2 圆柱体镦粗 4.3 平面压缩矩形件 4.4 平辊轧制 4.5 挤压 4.6 拉拔
r h 设σr仅随r轴变化而与z轴无关,即:
r 0, r d r
z
r dr
d r Y 0
dr h r z Y
d z Y 0
dr h
d r d z
z P
σz τf=K=0.5Y
h
τzr
σr
σr +dσr
r
d z
Y h
dr
z
Y h
r C
D=2R P
στfz=K=0.5Y
代入边界条件,求得积分常数
4.2 圆柱体镦粗
1 全滑动摩擦条件下的镦粗力计算 2 全粘着摩擦条件下的镦粗力计算 3 混合摩擦条件下的镦粗力计算
1 全滑动摩擦条件下的镦粗力计算
全滑动即假设在整个接触表面上有相对滑动,其摩擦符合 库仑摩擦条件。
r 1 r zr r 0
r r z
r
r z 0
塑性力学问题——一般三维问题
x
x
yx
y
zx
z
0
xy
x
y
y
zy
z
0
xz
yz
z
0
x y z
u
x x
y
v
y
w
z z
xy
yx
1 2
u
y
v
x
yz
zy
1 2
v
z
w
y
zx
xz
1 2
w
x
u
z
x
x
1 2
y z
y
y
1 2
z
x
z
Y h
r
C
r z Y
在r =R处,有σr =0,代入屈服条件,则:
z Y
解得
z
P
σz
C Y Y R h
z
Y
Y h
R r
τf=K=0.5Y
h
τzr
σr
σr +dσr
r
p
z
Y
Y h
R r
D=2R P
στfz=K=0.5Y
镦粗力及平均单位压力公式
p
z
Y
Y h
R r
将单位压力在接触面上积分,即得镦粗力公式:
h
τzr
σr
σr +dσr
r
d z 2 z 0
dr h
D=2R P
σz τf=μσz
d z 2 z 0
dr h
ln z
2
h
r
ln C
d z 2 dr
z
h
2 r
z Ce h
r |rR 0
2 R
C Ye h
r z Y
z Y
z P
σz τf=μσz
h
τzr
σr
σr +dσr
r
塑性成形理论的根本任务
研究不同形状和性能的坯料,在不同形状的工模具和不同外 力作用下发生塑性变形时的应力、应变和流动状态。 知道坯料塑性变形时的应力状态,即可计算出其变形力和 功能消耗,为合理选择成形设备和合理设计模具提供依据; 根据变形体的应力状态,可分析变形过程中材料产生裂纹 的可能性,为防止开裂提供解决思路; 知道坯料塑性变形时的应变和流动状态,可预测变形体的 形状尺寸变化和模腔内金属的充填情况,从而为合理确定原 毛坯或预成形坯形状、工模具形状和优化工艺过程提供科学 依据。
2 全粘着摩擦条件下的镦粗力计算
全粘着即假设在整个接触表面上没有相对滑动,其摩擦符 合最大摩擦条件。
r zr 0
r z
f K 0.5Y
设切应力在z向线性分布
zr
2K h
z
Y h
z
r Y 0
r h
z P
σz τf=K=0.5Y
h
τzr
r
D=2R P
τf=K=0.5Y σz
r Y 0
ห้องสมุดไป่ตู้
r
r zr 0
r z
f z
设切应力在z向线性分布
zr
2 z
h
z
h
r 2 z 0
r h
z P
σz τf=μσz
τzr
r
D=2R P
σz τf=μσz
r 2 z 0
r h
设σr 仅随r轴变化而与z轴无关,即:
r 0, r d r
z
r dr
d r 2 z 0
z
z
1 2
x y
xy
3 2
xy
yz
3 2
yz
zx
3 2
zx
应力边界条件 位移边界条件
塑性力学问题——平面问题
x x
yx y
zx z
0
xy x
y y
zy z
0
xz
yz
z
0
x y z
x
x
yx
y
0
xy
x
y
y
0
u
x x
z
Y
exp
2
h
R r
D=2R P
σz τf=μσz
单位压力分布公式
z
Y
exp
2
h
R r
此即接触面正应力分布公式,该应力为压应力,故写为:
p
z
Y
exp
2
h
R r
称接触面单位压力分布公式。
p
z
P τf
另外可得接触面摩擦应力分布为:
f
z
Y
exp
2
h
R
r
h
r
D=2R P
镦粗力及平均单位压力公式
dr h
z P
σz τf=μσz
h
τzr
σr
σr +dσr
r
D=2R P
σz τf=μσz
简化屈服条件
对σr =σθ的轴对称问题,其屈服准则为
r z 2 3 zr2 Y 2
为简化求解,在应用屈服准则时不考虑切应力影响,即认
为坐标方向即为主方向:
r z Y
z P
σz τf=μσz
d r d z
4.1 主应力法的基本原理
主应力法的实质是将应力平衡微分方程和塑性条件 联立求解。又叫工程法、切块法、初等解析法。
为使问题简化,采用下列基本假设:工件均质、各 向同性、初应力为零、体积力为零、体积不变。
把问题简化成平面问题或轴对称问题。 简化塑性条件。 简化平衡方程。 简化接触摩擦条件。 简化变形区几何形状。
p
z
Y
exp
2
h
R r
将单位压力在接触面上积分,即得镦粗力P:
P
R
0
p2
rdr
R
0 Y
exp
2
h
R
r
2
rdr
2 Y
h
2
2
2R e h
2R
h
1
R2Y
1
3
2R h
平均单位压力公式:
p
P
R2
Y
1
3
d h
ex 1 x 1 x2 1 x3 2! 3!
p d
n Y 1 3 h
