期权的波动率微笑策略
金融衍生工具_课程习题答案(2)
资料范本本资料为word版本，可以直接编辑和打印，感谢您的下载金融衍生工具_课程习题答案(2)地点：__________________时间：__________________说明：本资料适用于约定双方经过谈判，协商而共同承认，共同遵守的责任与义务，仅供参考，文档可直接下载或修改，不需要的部分可直接删除，使用时请详细阅读内容第一章1、衍生工具包含几个重要类型？他们之间有何共性和差异？2、请详细解释对冲、投机和套利交易之间的区别，并举例说明。
3、衍生工具市场的主要经济功能是什么？4、“期货和期权是零和游戏。
”你如何理解这句话？习题答案1、期货合约：：也是指交易双方按约定价格在未来某一期间完成特定资产交易行为的一种方式。
期货合同是标准化的在交易所交易，远期一般是OTC市场非标准化合同，且合同中也不注明保证金。
主要区别是场内和场外；保证金交易。
二者的定价原理和公式也有所不同。
交易所充当中间人角色，即买入和卖出的人都是和交易所做交易。
特点：T＋0交易；标准化合约；保证金制度（杠杆效应）；每日无负债结算制度；可卖空；强行平仓制度。
1）确定了标准化的数量和数量单位、2）制定标准化的商品质量等级、（3）规定标准化的交割地点、4）规定标准化的交割月份互换合约：是指交易双方约定在合约有效期内，以事先确定的名义本金额为依据，按约定的支付率（利率、股票指数收益率）相互交换支付的约定。
例如，债务人根据国际资本市场利率走势，将其自身的浮动利率债务转换成固定利率债务，或将固定利率债务转换成浮动利率债务的操作。
这又称为利率互换。
互换在场外交易、几乎没有政府监管、互换合约不容易达成、互换合约流动性差、互换合约存在较大的信用风险期权合约：指期权的买方有权在约定的时间或时期内，按照约定的价格买进或卖出一定数量的相关资产，也可以根据需要放弃行使这一权利。
为了取得这一权利，期权合约的买方必须向卖方支付一定数额的费用，即期权费。
期权主要有如下几个构成因素①执行价格（又称履约价格，敲定价格〕。
带你认识Skew指数
带你认识Skew指数场内期权隐含波动率一般会呈现“平值期权IV低，两侧期权IV高”的形态，即所谓的隐含波动率微笑。
但很多时候波动率并不“微笑”，而是会出现左偏或右偏这类“假笑”的结构。
造成这一现象的原因与市场对标的资产收益分布不对称的认知有关。
如股市容易遭遇黑天鹅，短期暴跌的概率要高于暴涨的概率，因此对股价下跌保护的需求导致更多人买入虚值看跌期权推升IV，而且由于有很多专业机构会从事卖虚值看涨期权的备兑增益策略，因此虚值看涨期权的IV也会稍低一些，从而呈现出IV左边高右边低的左偏结构。
而商品市场则相反，由于更容易出现极端大幅上涨行情，因此更多时候会保持虚值看涨期权IV更高的右偏结构。
为了衡量市场风险的不对称性，推出了偏度指数Skew，又被称为黑天鹅指数，该指数通过计算虚值期权价格的偏离程度来衡量市场对意外事件的担忧程度，对危机均有非常好的预警效果。
从T期权上市至今数据统计结果来看，Skew指数有61.5%的时间里小于100，隐含波动率微笑曲线更多时候会呈现出左边低右边高的右偏结构。
通过上述观察结果发现，T期权市场Skew指数在高位时会有比较好的预警效果，这与指标度量市场尾部风险的初衷一致。
当市场对行情下跌担忧增加时，往往Skew指数会上升至高位，基于这种特征，T厂在进行风险管理时，就可以选择在Skew指数高位时，卖出期货或者买入看跌期权来锁定下行风险。
两种策略都有各自的优缺点，卖出期货胜在操作简便，对T厂而言，可以直接对冲所有下跌风险，锁定榨利；买入看跌期权最大的优势就是资金占用少，不需要缴纳保证金，也不存在追保风险，而且如果后市T价不跌反涨，最大亏损也只是权利金支出，不会像卖出期货一样出现巨额套保亏损。
可以明显看出，当Skew指数处于高位时选择做空标的会是比较不错的选择，不管持有周期多久，买入看跌期权的收益均要优于卖出期货，主要原因就在于买入期权资金占用少，能更大程度地凸显出杠杆功能。
而且由于持仓周期较短，各条件下历史最大回测均较为可控，不过，由于策略只是单纯的方向性做空，因此每日收益的年化波动率较大，均超过了30%。
【最新精选】波动率微笑成因
期权波动率“微笑曲线”成因解析“波动率微笑”即具有相同到期日和标的资产而执行价格不同的期权，其执行价格偏离标的资产现货价格越远，隐含波动率越大。
波动率通常是用来描述股票、期货等资产价格变化有多快的一个指标，而涉及到期权这一衍生工具的波动率，有两类比较重要：一是历史波动率，它是基于对标的资产在过去历史行情中价格变化的统计分析得出的，也就是对其标准差的计算；二是隐含波动率，它是期权市场对标的资产在期权存续期内波动率的预测，由于在期权交易中受市场买卖力量的影响，隐含波动率与历史波动率必然会有所差异。
比如，某一月份期权只有一个历史波动率，但其隐含波动率却很多，而不同执行价格的看涨期权、看跌期权的隐含波动率也不尽相同。
期权定价模型中唯一的真正变量就是波动率，其他所有参量，包括标的资产的价格、期权的执行价格、期权到期剩余天数、现有的利率水平，在计算某一只期权合约的理论价值时都是固定的。
从这个角度讲，抛开定价模型本身的优劣程度，计算出的理论价格准确性取决于所有输入参量的精确程度。
甚至可以说，做期权就是做预期的波动率。
虽然历史波动率和隐含波动率都可以用来帮助交易者预测未来的波动率，但在实际交易中，隐含波动率更受交易者重视。
在实证研究中，通过传统BS期权定价模型计算出来的隐含波动率呈现出一种被称为“波动率微笑”的现象，即具有相同到期日和标的资产而执行价格不同的期权，这些期权的执行价格偏离标的资产现货价格越远，其隐含波动率越大。
Rubinstein（1985年）在综合了BS期权定价模型的各种异常情况下，提出了波动率“微笑”具有期限结构，即波动率“微笑效应”以某种系统的方式依赖于期权的到期期限，且这种“微笑效应”在短期期权中比长期期权更加明显。
对于这种隐含波动率的“微笑“曲线特质，研究上给出了很多种解释，大体可以分为两类：一类是从传统BS期权定价公式基本前提假设条件中的设定与现实相比的不合理之处进行的解释；另一类则是从市场交易机制层面进行的解释。
赫尔《期权、期货及其他衍生产品》（第9版）笔记和课后习题详解答案
赫尔《期权、期货及其他衍生产品》（第9版）笔记和课后习题详解答案赫尔《期权、期货及其他衍生产品》（第9版）笔记和课后习题详解完整版>精研学习?>无偿试用20％资料全国547所院校视频及题库全收集考研全套>视频资料>课后答案>往年真题>职称考试第1章引言1.1复习笔记1.2课后习题详解第2章期货市场的运作机制2.1复习笔记2.2课后习题详解第3章利用期货的对冲策略3.1复习笔记3.2课后习题详解第4章利率4.1复习笔记4.2课后习题详解第5章如何确定远期和期货价格5.1复习笔记5.2课后习题详解第6章利率期货6.1复习笔记6.2课后习题详解第7章互换7.1复习笔记7.2课后习题详解第8章证券化与2007年信用危机8.1复习笔记第9章OIS贴现、信用以及资金费用9.1复习笔记9.2课后习题详解第10章期权市场机制10.1复习笔记10.2课后习题详解第11章股票期权的性质11.1复习笔记11.2课后习题详解第12章期权交易策略12.1复习笔记12.2课后习题详解第13章二叉树13.1复习笔记13.2课后习题详解第14章维纳过程和伊藤引理14.1复习笔记14.2课后习题详解第15章布莱克-斯科尔斯-默顿模型15.1复习笔记15.2课后习题详解第16章雇员股票期权16.1复习笔记16.2课后习题详解第17章股指期权与货币期权17.1复习笔记17.2课后习题详解第18章期货期权18.1复习笔记18.2课后习题详解第19章希腊值19.1复习笔记第20章波动率微笑20.1复习笔记20.2课后习题详解第21章基本数值方法21.1复习笔记21.2课后习题详解第22章风险价值度22.1复习笔记22.2课后习题详解第23章估计波动率和相关系数23.1复习笔记23.2课后习题详解第24章信用风险24.1复习笔记24.2课后习题详解第25章信用衍生产品25.1复习笔记25.2课后习题详解第26章特种期权26.1复习笔记26.2课后习题详解第27章再谈模型和数值算法27.1复习笔记27.2课后习题详解第28章鞅与测度28.1复习笔记28.2课后习题详解第29章利率衍生产品：标准市场模型29.1复习笔记29.2课后习题详解第30章曲率、时间与Quanto调整30.1复习笔记30.2课后习题详解第31章利率衍生产品：短期利率模型31.1复习笔记31.2课后习题详解第32章HJM，LMM模型以及多种零息曲线32.1复习笔记32.2课后习题详解第33章再谈互换33.1复习笔记33.2课后习题详解第34章能源与商品衍生产品34.1复习笔记34.2课后习题详解第35章章实物期权35.1复习笔记35.2课后习题详解第36章重大金融损失与借鉴36.1复习笔记36.2课后习题详解。
重磅观点：波动率微笑是任何模型都解决不了的现象
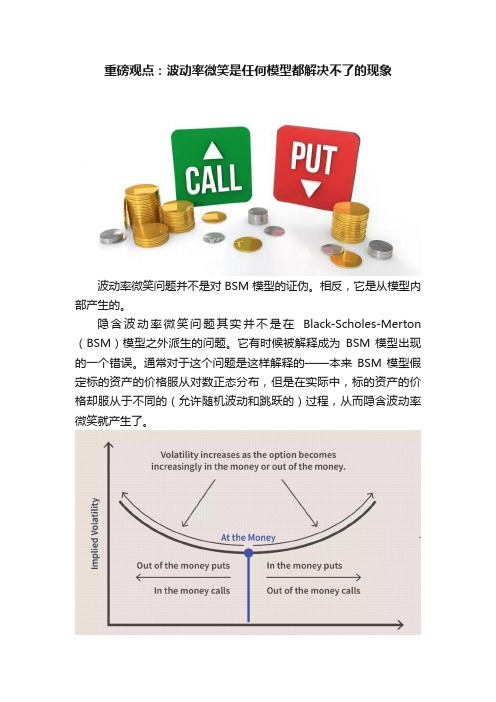
重磅观点：波动率微笑是任何模型都解决不了的现象波动率微笑问题并不是对BSM模型的证伪。
相反，它是从模型内部产生的。
隐含波动率微笑问题其实并不是在Black-Scholes-Merton （BSM）模型之外派生的问题。
它有时候被解释成为BSM 模型出现的一个错误。
通常对于这个问题是这样解释的——本来BSM 模型假定标的资产的价格服从对数正态分布，但是在实际中，标的资产的价格却服从于不同的（允许随机波动和跳跃的）过程，从而隐含波动率微笑就产生了。
图片来源：Investopedia我认为，波动率微笑的问题是从内部天生的。
这里我们考虑波动率微笑问题的另一种观点，虽然可能乍看起来有些难。
传统观点是说，BSM模型认为衍生品的交易是冗余的，即便放开对数正态分布的条件，衍生品的价格也是可以被完全复制和对冲的。
所以衍生品不需要有自己独立的交易市场。
第二种观点是说衍生品的交易在实际中是存在的，而且和标的资产的交易是密切相关的。
在展开上述论证之前，我们首先要注意不要混淆标的资产的交易与衍生品交易。
在之前的观点中并未提及衍生品的交易。
在那个观点下面，我们的证券的状态是给定的，那就是标的资产当前的价格，以及在一定的概率测度下面未来标的资产的价格分布。
至于衍生品，就是在这个假设下面的一个资产价值的评估。
事实上，第二种观点不同于传统观点的原因在于，我们从一开始就应该将衍生品视为可交易的，哪怕这个交易以后被认定是冗余的。
但如果衍生品是可交易的，那么我们也可以从一开始就给出它自己的价格变化的随机过程，就像标的资产的随机过程一样。
BSM模型为了得出衍生品可被标的资产完美动态复制这个结论，所以就假设衍生品的价值只是时间和标的资产价格的函数。
为什么衍生品的价值不是另一个关于波动率市场的交易变量的函数，或者简单地，就是它自己的函数？实际上，我认为一旦将衍生品市场的交易本质考虑进来，整个语境就会与标的资产价格的时间序列和相应的计量经济学概念不相容了。
股指期权波动率指标的含义及用途
今日话题：
• 怎么看波动率指数？ • 怎么看波动率微笑曲线？ • 怎么看波动率偏斜状况？ • 怎么看波动率锥和理论价格分布图？
今日话题：
• 怎么看波动率指数？ • 怎么看波动率微笑曲线？ • 怎么看波动率偏斜状况？ • 怎么看波动率锥和理论价格分布图？
汇点交易软件里的波动率指数
看波动率微笑曲线的注意事项
• 不同标的物的期权合约，波动率微笑曲线是不一样的 • 看波动率微笑的时候主要关注的是曲线的曲度 • 波动率微笑曲线形态的变化也可能是有意义的 • 要先确定自己看到的曲线靠谱，然后再想它的市场含义是什么
Байду номын сангаас日话题：
• 怎么看波动率指数？ • 怎么看波动率微笑曲线？ • 怎么看波动率偏斜状况？ • 怎么看波动率锥和理论价格分布图？
标的价格走势与交易者情绪对比
今日话题：
• 怎么看波动率指数？ • 怎么看波动率微笑曲线？ • 怎么看波动率偏斜状况？ • 怎么看波动率锥和理论价格分布图？
感谢聆听☺
• 汇点交易软件里面有等权和加权两个波指，加权波指正常情况下 要比等权的更能体现市场状况。
波动率指数不是恐慌指数 波动率指数不是恐慌指数 波动率指数不是恐慌指数
今日话题：
• 怎么看波动率指数？ • 怎么看波动率微笑曲线？ • 怎么看波动率偏斜状况？ • 怎么看波动率锥和理论价格分布图？
布莱克-斯科尔斯期权
『交易所期权不需要用现金股息来调节。』
购买看涨期权的人不希望股价下跌，然而股息的支付将必 然引起价格下跌。股息越高，价格下跌越多。交易所期权不 需要用现金股息支付来调节。在其它条件都相同的情况下， 支付高额股息的公司的期权费要比支付低额股息的公司的期 权费更低。这是容易理解的，让我们来考虑一个极端的例子， 一个公司宣布支付清算股息并停止经营活动的意图。在支付 股息后，公司的股份就没有价值了，与之相应的看涨期权也 就没有价值了。任何拥有这些看涨期权并在上一个除息日之 前没有执行该期权的人将损失其所有的投资。期权持有者关 注公司股息公告，并且在某些情况下会发现在除息日之前行 执行期作西格玛 (sigma)。』
表现出价格波动的资产适合于进行期权交易。资产的价格波 动性越大，它的期权费就越高。在布莱克－斯科尔斯模型中， 波动率是在期权剩余期间里基础资产预计收益的年标准差。 如同金融学的其他方面，过去发生的不像预计未来将要发生 的那样重要。可以测量出过去的波动率，但对未来的波动率 就只能进行估计。估计的波动率叫做西格玛（sigma），它 是一个不能被直接观察到的变量。
布莱克－ 布莱克－斯科尔斯期权定价模型
模 型 在第五章中我们简要地了解了这个著名 的模型。表6－1又重复列出了该模型。这是 以不支付股息的股票为基础的欧式看涨期权 的基本估价模型。
表6-1
C=SN(d1)-ke-RTN(d2)
布莱克—斯科尔斯权定价模型 布莱克 斯科尔斯权定价模型
（６－１）
其中：d1= In
布莱克－ 布莱克－斯科尔斯模型的假设
我们已经回顾了影响期权费的因素，现在让我们 着眼于模型的假设并看看它们构成了多少与现实的 背离。 1、在期权有效期内股票不支付股息。布莱克 －斯科尔斯模型假设在期权有效期内基础证券不支 付股息。如果你试图建立两个证券的模型，一个不 支付股息而另一个有3%的股息收益，通过模型会预 测到同样的看涨期权期权费，而这结果并没有反应 实际情况。股息越高，看涨期权的期权费就越低， 金融版面上反映出来的关于这两个期权的期权费很 可能也不相同。
3.3.5 波动率与波动率微笑
在以后的数年中，D.B.Madan与ne又进一步将该期权定价模型扩展到更为一般的市场条件下的期权定价模型。
为了防止元素分布数量的扩大，2000年谢赤[109]用一个具有离散水平(状态)的有限马尔可夫链来代替Ritchey二项式树，这样混合体总是有k 个元素分布。
2004年Peter Carra，b与Liuren Wuc[110]为改进传统Black-Sholes模型产生的误差，提出了收益率服从时变Levy过程的期权定价模型。
由于金融市场随时间波动较大，Black-Scholes期权定价模型中的一些参数不能总得到准确的值。
因此，Hsien-Chung Wu（2004）[111]提出用模糊收益率，模糊方程和模糊股票价格对期权定价。
在这些条件下，欧式期权的价格一定为一个模糊数，对欧式期权价格的金融分析可以从置信区间中得到。
3.3.5波动率与波动率微笑3.3.5.1波动率的概念运用期权定价模型计算期权理论价格需要五个参数，其他四个参数都可以方便得到，只有波动率是未知的。
从这个角度讲，做期权就是做预期的波动率。
而历史波动率和隐含波动率可以用来帮助交易者来预测未来的波动率。
一、历史波动率(History Volatility，HV)历史波动率是以标的期货的历史价格数据为基础计算的收益率年度化的标准差，是对历史价格波动情况的反映。
期货价格波动率越大，期货价格突破执行价格进入实值状态的可能性就越大。
因此，权利金也就越高。
相反，期货价格波动率越小，期货价格使执行期权具有收益的可能性就越小。
因此，权利金也就越低。
二、隐含波动率(Implied Volatility，IV)隐含波动率是指市场中权利金蕴含的波动率，是将某一期权合约的成交价及其他几个参数输入期权定价模型，通过试错法计算而来。
反映的是市场对波动率的看法。
当隐含波动率上升，代表投资者预期期货价格波动将扩大，因此权利金也会上涨；反之权利金则会下跌。
隐含波动率受市场买卖力量的影响，与历史波动率未必相同。
中金所杯全国大学生金融知识大赛题库及答案(判断题第601-742题)
中金所杯全国大学生金融知识大赛题库及答案（判断题第601-742题）601.2012年9月17日，美元兑离岸人民币期货在香港交易所上市交易。
根据香港交易所在官方网站上公布的人民币合约相关细贝IL合约的保证金、结算和交易费用均以人民币计价。
A.正确B.错误正确答案：B602.外汇即期价格的波动率越大，外汇期权的价格越高。
A.正确B.错误正确答案：A603.央行与商业银行开展外汇掉期交易可以调整外汇储备结构。
A.正确正确答案：A604.外汇期货做市商的主要义务为向外汇期货市场提供流动性,需要提供外汇期货交易的买价及卖价。
A.正确B.错误正确答案：A605.外汇期货跨市场套利可以分为熊市套利和牛市套利。
A.正确B.错误正确答案：B606.在实务交易中，根据起息日不同，中国外汇交易中心的外汇掉期(FXswap)交易形式包括即期对远期、远期对远期、隔夜掉期三种形式。
A.正确B.错误607.国内商品期权设有做市商制度，金融期权未设有做市商制度QA.正确B.错误正确答案：A608.近月平值期权的Delta等于0.5。
A.正确B.错误正确答案：A609.中金所沪深300股指期权的标的为中金所沪深300股指期货。
A.正确B.错误正确答案：B610.当金融市场处于持续的利率下跌过程中，逆向浮动利率票据的投资收益将增加。
A.正确正确答案：A611.在沪深300股指期权中，中金所在期权到期时会对未申请放弃行权的实值期权消除，持有者不用担忧忘记行权的问题。
A.正确B.错误正确答案：A612.信用曲线是不同主体同一期限债券的信用价差。
A.正确B.错误正确答案：B613.其他条件相同时，看涨期权的执行价格越高，期权价值越大。
A.正确B.错误正确答案：B614.2012年9月17日，人民币期货在香港交易所上市交易，根据香港交易所在官方网站公布的细则，合约的保证金、结算和交易费用均以人民币计价。
A.正确B.错误正确答案：B615.使用股指期货可降低所持有的股票组合的系统性风险.A.正确B.错误正确答案：A616.下列行情报价表明存在无风险套利机会。
随机波动率微笑模型及套利-20180504财通证券
随机波动率微笑模型及套利-20180504财通证券投资要点：金融市场的波动率金融市场波动率具有尖峰肥尾、波动率群集、具有杠杆效应等特点。
本文将简单地分析金融市场波动率重要的几个特性，并介绍50ETF相关波动率的度量方法。
波动率微笑与BS模型假设不同，隐含波动率ω (t，t + h) 在很大程度上取决于日历时间t 、到期期限h 和期权的货币性，隐含波动率曲面呈现明显的微笑或倾斜的特征。
本文将简单地介绍隐含波动率微笑的基本特性。
利用随机波动率模型进行套利Vanna-Volga模型，SVI模型，SABR模型都可以用来拟合隐含波动率微笑。
通过模型刻画的隐含波动率与通过BS公式反算的隐含波动率进行对比，找到每日最被低估和高估的期权合约，分别买入和卖出。
通过合约的持仓数量，形成delta 中性，从而赚取波动率估值回归的收益。
结果显示，在看涨期权季月合约上进行波动率套利有不错效果，三种模型年化收益率都超过20%。
风险提示：未来市场变幻莫测，模型有失效的可能。
正文1、波动率的分类在期权世界中，波动率可以简单的分为历史波动率、隐含波动率、已实现波动率三大类，分别对应着过去的波动率、隐含在期权价格中的波动率(也被称之为预期波动率)以及实际的波动率。
对于这三种波动率的理解对于期权交易来说是至关重要的，这不仅可以用于期权的定价，还可以用于直接的波动率交易，包含波动率的方向性交易及波动率的套利交易。
1.1、历史波动率 (HV)历史波动率是基于过去的统计分析得出的，假定未来是过去的延伸，利用历史方法估计波动率类似于估计标的资产收益系列的标准差。
1.1.1、标准差标准差是衡量风险的常用标准，是与时间期限相关的概念，例如日标准差、周标准差、月标准差、年标准差等等。
在风险评价中，常用的是年标准差。
计算方法(以标的证券过去30个交易日的历史波动率为例)；1。
根据计算周期(交易周期；周、月、季度、年均指日历周期) 在所选时间段内拆分出N个区间(头尾包含的不完整日历周期舍去)。
波动率微笑
执行价格
两分布具有相同期望和标准差 标的资产价格分布比BS分布尖峰胖尾
考虑
一个深度虚值的货币看涨期权，执行价 格是很高的X2 一个深度虚值的货币看跌期权，执行价 格是很低的X1
波动率微笑
外汇期权波动率微笑存在的原因
9
1. 现实情况表明：汇率的极端变化要比对数正态分布所 描绘的更经常出现
2. 资产价格为对数正态分布需两个条件：
11
分析：这些期权相对较便宜，且成为实值期权的可能性比对 数正态分布模型预测的要多一些，你的期权平均收益要远 远大于期权成本
实际情况： 20世纪80年代中期，对汇率分布有正确认识的交易员采用 上述策略获得巨大盈利。 到80年代后期，几乎所有人都认识到了虚值期权隐含波动 率要高，套利机会消失。
波动率微笑
二、股票期权的波动率微笑（偏斜）
12
隐含波动率
向右下 方偏斜
两分布具 有相同期 望和方差
执行价格
偏斜波动率微笑原因：一个可能解释 与股市“崩盘”有关 偶发的崩盘事件深刻影响了投资者的心理，因此市场对价 格变化的概率估计是不对称的 价格显著下跌的可能性远远大于显著上升的可能性
波动率微笑
练习
13
1. 在下列情形所观察到的波动率微笑是什么形式？
从长期看，隐含波动率大多呈现均值回归现象（Meanreverting）。即到期日接近时，隐含波动率的变化较剧烈， 随着到期时间的延长，隐含波动率逐渐向历史波动率的平均 值靠近
波动率微笑
3 波动率矩阵
15
把波动率微笑和波动率期限结构结合在一张表里，可得 任何执行价格和任何到期时间的期权所对应的隐含波动 率，就形成了波动率矩阵。
波动率微笑
1 波动率微笑
[考研专业课课件] 赫尔《期货、期权及其他衍生产品》 课件 第19章 波动率微笑
![[考研专业课课件] 赫尔《期货、期权及其他衍生产品》 课件 第19章 波动率微笑](https://img.taocdn.com/s3/m/7b721531a5e9856a56126066.png)
隐含概率分布（implied distribution）：
由在某一时间到期的期权波动率微笑确定的在一 定时间资产价格的风险中性概率分布。 图19-1所示的波动率微笑对应于图19-2中由 实线表达的概率分布。图19-2中的虚线代表一个 与隐含分布有同样的期望值及标准差的对数正态 分布,隐含分布比对数正态分布更具有肥尾特征。
权。
【例19-1】澳元的价格为0.60美元。美国的无
风险利率为每年5％，澳大利亚的无风险利率为每年 10％。一个澳元1年期限、执行价格为0.59美元的期
权价格为0.0236。DerivaGem所示的隐含波动率为
14.5％。为了保证无套利，式（19-1）所示的看跌看涨平价关系式必须成立，其中q为外国（澳洲）无
表19-3所对应的波动率微笑
表19-3 隐含波动率 （单位：美元）
注：这里的真实分布为二项分布。
本章小结
1．布莱克-斯科尔斯-默顿模型及其推广均假
定资产价格在将来时刻的概率分布服从对数正态
分布。这一假设与交易员的假设是不一样的。他 们一般假定股票价格的分布相对于对数正态分布 来讲有较肥的左端尾部与较度的右端尾部，还假 定兑换率的概率分布相对于对数正态分布来讲有 较肥的左端尾部与较肥的右端尾部。
－默顿模型对具有相同期限与执行价格的看跌及 看涨期权定价时,公式所产生的误差应完全相同。 假定，欧式看跌期权的隐含波动率为22％。 这意味当布莱克-斯科尔斯-默顿模型中的波动率 为22％时，pBS=pmkt。由式（19-2）得出，当采用 同一波动率时，cBS=cmkt，因此看涨期权的隐含波 动率也是22％。
图19-1与图l9-2具有一致性
考虑一个执行价格为K2的深度虚值（deepout-of-money）看涨期权。这一期权只有在兑换 率高于K2时才会产生收益，图19-2说明这一期权 在隐含概率分布下产生收益的概率比在对数正态 分布下要大。因此期望对于这一期权，隐含概率 分布所产生的价格会偏高。较高的价格对应于较 高的波动率，这刚好是在图19-1中所观察到的。
第12讲：波动率的微笑曲线
13
Implied Distribution for Foreign Currency Options
Implied distribution and lognormal distribution for foreign currency options
The volatility is lowest for ATM options, and becomes progressively higher as an option moves either in the money or out of money.
波动率在两平期权时最小，并随实值或者虚值的程度 增大而增大。 The volatility used to price a low strike option (deep OTM put or ITM call) or a high strike option (deep OTM call or ITM put) is higher than that used to price an ATM option. This pattern is observed in all currency options, on average.
12: Volatility Smiles
8
Implied Volatilities: An Example（隐含波动率的 一个例子） On 21 March 2001, the AU$ is at 0.60. r and rf = 5% and 10% in the US and Australia respectively. A European call on AU$ with maturity of 1 year and strike of $0.59 is 0.0236. What is the price and implied volatility of a European put on AU$ with the same strike and maturity. The implied volatility from the call is 14.5% per annum. Based on put-call parity, we have p + 0.60e0.10*1 = 0.0236 + 0.59e-0.05*1, and p = 0.0419. If p = 0.0419, what is the implied volatility for the put?
金融衍生工具 名词解释2
期权的时间价值:p232 是指期权购买者为购买期权而支付的费用超过该期权内在价值的部分，这部分价值源于期权到期前标的资产价格波动可能给投资者带来的收益，即期权购买者希望在期权到期前，标的股票的市场价格会向有利的方向变动，执行期权将获得更好的收益.期权的内在价值:p232是指期权购买者立即执行该期权能够获得的收益。
如果立即执行期权不能产生正的期权价值，则内在价值为零。
因此，期权的内在价值就是下列两者中较大的一个：(1)期权处于实值状态的量，(2)零。
期权的内在价值由标的股票的现价和期权的执行价格决定.逆日历价差期权:是指投资者购买期限短的期权，同时出售期限长的期权。
展期：指的是将证券的到期期限向前延展。
展期包括两个交易：在期权到期前买入同样的一份先前出售的期权将空头平仓，再出售一份标的物和执行价格相同但到期期限更晚的期权。
无套利原理P42：套利是这样一个投资策略，即保证在某些偶然情况下获取正报酬而没有负报酬的可能性，也无需有净投资。
换句话讲，套利是一个可以以零成本建立投资组合并能够保证组合的价值增加或者保持为零的一个机会。
无风险套利有如下几点前提：1）无卖空限制2）无交易成本3）无买入价和卖出价之间的差别4）收益和损失的税率相同5）借款利率等于贷款利率。
套利有两个核心特征：第一，存在一个无风险的收益，即所谓“保证获取正报酬而没有负报酬”，我们以V(t)表示投资组合在时点的t价值，P表示事件出现概率，P[V(t)]=0+P[V(t)]>0=1；第二，存在一个自融资策略，即所谓的“无需有净投资”V(0)=0，或者如美国著名金融工程学家约翰•马歇尔所言，是指“头寸”完全可以用贷款来融资（即无资本）。
无套利原理是指具有相同价值的金融产品在同一个竞争的市场应当具有相同的价格。
欧式期权的put-call关系:P263（1）无股利情况下的欧式期权Put-Call等式:欧式看涨期权和看跌期权之间的平价关系（Put-Call Parity）：c+Xe－rT=p+S（2）有股利支付情况下的欧式Put-Call等式：在期权到期日前如果会派发红利，则欧式看涨期权和看跌期权之间的平价关系需要作相应的调整为：c+D+Xe－rT=p+S美式期权的put-call关系: P263（1）无股利条件下，美式期权Put－Call关系：C+X＞P+S＞C+Xe－rT（2）有股利条件下，美式期权Put－Call关系：C+D+X＞P+S＞C+Xe－rTP328布莱克-斯科尔斯-默顿微分方程：Black-Scholes-Merton微分方程：隐含波动率：隐性波动率，又叫隐含波动率，是将市场上的期权交易价格代入布莱克-斯科尔斯期权定价公式中，反推出来的波动率数值。
期权成交量、交易价差对波动率微笑的影响：基于GARCH期权定价模型的实证研究
.POFZOFTT
7PMVNF
注：样本时间跨度为：1999 年 10 月 30 日至 2001 年 10 月 30 日。
隐含波动率与波动率微笑数值实验
附件4 实验项目编写范例隐含波动率与波动率微笑数值实验实验项目开发背景：随着全球经济一体化和金融市场的不断深化，金融学科的实验教学发展面临巨大的挑战，一方面要求真实金融市场数据全面进课堂，另一方面要求在传统专业课基础上紧跟市场发展趋势开设前沿性的实验课，致力于培养能与业界无缝对接的金融投资人才。
其中，《期货与期权》实验课成为金融工程专业、投资专业、数理金融等专业的核心课程。
在《期货与期权》实验课中，期权定价是重点实验内容，要求学生通过实验全面掌握期权定价离散模型及连续时间模型及其相关数值方法核心内容和算法实现。
全部实验均要求学生使用万得数据终端和彭博数据终端获取公司和金融市场的真实数据，同时，考虑到学生的背景和未来的职业选择差异，设计了三种编程的算法实现手段，即轻量级的解决方案——Excel 及其VBA，中量级的解决方案——Matlab及其图形用户界面，重量级的解决方案——C++及其Excel加载宏。
既训练了不同知识背景和技能的学生的定价模型编程实现技巧，又考虑到面向用户展示和使用时的友好性和直观性。
“隐含波动率与波动率微笑数值实验”是《期货与期权》实验课中一个代表性实验项目。
一、实验目的要求学生使用EXCEL和MATLAB计算隐含波动率并利用苹果公司股票期权真实交易数据绘制波动率微笑。
通过该实验实现以下目的：1．使学生掌握隐含波动率计算方法的原理，并在具有隐含波动率和期权执行价格数据的条件下，通过绘制波动率微笑，使学生更为感性地认知波动率微笑现象的真实存在。
2．促使学生发现B-S-M定价模型的历史局限性，从而为定价模型的扩展提供思路和线索，启发学生探索更为先进的定价模型。
3．由于这两种方法均采用相同的真实数据，学生可以比较数值计算结果，从而验证实验结果的正确性。
二、实验准备（简单列示开展该实验项目需要的知识点以及需掌握的软件或数据终端）1．回顾波动率微笑的概念、内涵以及产生的原因。
2．掌握隐含波动率的理论计算方法。
人民币对美元外汇期权波动率微笑与偏斜研究
贸易与流通经济与社会发展研究人民币对美元外汇期权波动率微笑与偏斜研究上海大学 李术维摘要：2019年8月5日，离岸人民币兑美元跌破7关口，人民币兑美元中间价跌破6.90关口，我国进出口企业面临着较大的外汇风险，避险需求增加。
外汇期权作为一种避险工具，具有互换和远期所不具备的灵活性和波动率交易特征，因此本文聚焦于人民币对外汇期权的波动率研究。
通过构建单变量回归方程研究各个期限人民币对美元外汇期权隐含波动率与历史波动率之间的关系，研究结果显示人民币对美元外汇期权隐含波动率曲线存在微笑和偏斜效应。
同时，本文构建了隐含波动率偏斜指标用于衡量隐含波动率曲线的偏斜程度，结果显示受中美贸易战的影响，贸易时隐含偏度的波幅放宽，呈现更明显的右偏，市场看空情绪高涨。
关键词：人民币对美元外汇期权；隐含波动率；波动率微笑与偏斜人民币对美元外汇期权是一种选择权，外汇期权的买方支付一笔期权费后拥有到期买卖一定数量美元的权力，外汇期权卖方收取期权费后具有在按合约规定和买方要求履约的义务。
期权隐含波动率代表期权的价格，令横轴为期权行权价，纵轴为期权隐含波动率，可得到不同行权价下的隐含波动率分布曲线，根据曲线的形状，被称为波动率微笑或波动率假笑。
不同波动率曲线形状的出现部分源于市场多空双方的交易行为。
因外汇期权独特的报价机制，人民币对外汇期权隐含波动率曲线以delta值代表行权价，左侧为不同delta值下看跌期权隐含波动率分布，曲线右侧为不同delta值下看涨期权隐含波动率分布。
一、隐含波动率微笑与偏斜相关理论（一）隐含波动率微笑传统的B-S期权定价模型假设同一到期日的所有期权合约不论行权价是否相同，波动率都是一致的，即隐含波动率曲线为一条水平线（零峰度）。
然而，在期权实际交易中人们发现不同行权价下的隐含波动率是存在差异的，具有平值期权隐含波动率较低，实值和虚值期权的隐含波动率较高的特征，并且距离平值期权越近，隐含波动率越低。
隐含波动率曲线呈现出中间低两边高的“微笑”形态，即隐含波动率微笑。
波动率微笑曲线与外汇期权定价模型
波动率微笑曲线与外汇期权定价模型
周臻
【期刊名称】《中国货币市场》
【年(卷),期】2016(000)004
【摘要】在市场业务发展对期权定价提出更高要求的背景下，就常用的期权定价模型，包括无风险利率与波动率为常数假设下的Black—Scholes模型、随机波动率假设下的Vanna—Volga模型和SABR模型，文章简要介绍了其模型特征、模型隐含的市场策略构建和模型的现实适用情况。
【总页数】3页(P28-30)
【作者】周臻
【作者单位】交通银行金融市场业务中心
【正文语种】中文
【中图分类】F830.91
【相关文献】
1.波动率微笑曲线与外汇期权定价模型 [J], 周臻
2.基于随机波动率的LNG远期定价模型 [J], 李亚君; 王中兴
3.人民币外汇期权隐含波动率和实际波动率的比较研究——兼论对交易和汇兑层面宏观审慎管理的启示 [J], 张雪鹿
4.人民币外汇期权隐含波动率的各期限因子:形成机制和定价能力 [J], 张雪鹿
5.波动率不确定模型在外汇期权定价中的应用 [J], 徐静;任庆忠
因版权原因，仅展示原文概要，查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
期权的波动率微笑策略
期权有一个重要的指标叫隐含波动率（IV），是根据将期权的市场价格代入标准BS
期权定价模型计算出来的。
由于BS模型假定标的资产价格服从对数正态分布，收益率服
从正态分布，所以期权的波动率是一个常数。
然而，用实际市场数据计算隐含波动率时，具有相同到期日和标的资产的期权，各个
行权价的隐含波动率会呈现高低差异。
在大部分情况下，行权价格距离标的资产现货价格
越远的期权，其隐含波动率越大，使得期权的波动率曲线产生偏移，呈现两端翘起、中间
凹陷的“微笑”形态，这种现象被称为波动率微笑。
波动率微笑产生的原因，在研究上有多种解释，其中一种解释是从模型假设角度给出的。
由于BS模型假定标的资产价格和收益率都服从对数正态分布，但大量实证检验发现，在现实市场中，金融资产的收益率分布更加显示出“尖峰肥尾”的特征。
在这种分布下，收
益率出现极端值的概率高于正态分布。
因此，期权价值在到期时变为深度实值与深度虚值
的概率要比模型假设的概率更大，相应的深度实值和深度虚值期权的价格和波动率也会更高。
回归假设
虽然大部分情况下，隐含波动率曲线都呈现两端翘起、中间凹陷的“微笑”（Smile）形态，但有时候也会出现其他形态，例如，两端塌陷、中间凸起的“皱眉”形态（Frown），
一边高一边低的“假笑”形态（Smirk），以及其他的不规则形态。
由于隐含波动率曲线呈现“微笑”形态是最普遍的，所以本文假设当出现波动率“皱眉”
或其他形态时，曲线都会往“微笑”形态回归。
图为波动率曲线的“微笑”形态图为波
动率曲线的“皱眉”形态
由于Delta绝对值为0.25的期权虚值程度比Delta绝对值为0.3的期权更深，根据假设，波动率曲线呈现“微笑”形态时，越虚值的期权隐含波动率越大，此时IV0.25>IV0.3>IV
平值，其中IV0.25表示Delta绝对值为0.25期权的隐含波动率，IV0.3表示Delta绝对值
为0.3期权隐含波动率，IV平值表示平值期权的隐含波动率。
策略构建
根据假设，波动率曲线会回归到“微笑”形态，那么由此推断IV0.25将会上升或IV0.3
将会下降。
因此，投资者可以考虑构建买入Delta绝对值为0.25的虚值期权，卖出Delta
绝对值0.3的虚值期权，持有至IV0.25>IV0.3时平仓。
入场时机：IV0.25<IV0.3。
出场时机：IV0.25>IV0.3。
看涨期权策略：买入Delta为0.25位置高一档行权价的看涨期权；卖出Delta为0.3
位置低一档行权价的看涨期权。
看跌期权策略：买入Delta为-0.25位置低一档行权价的看跌期权；卖出Delta为-0.3
位置高一档行权价的看跌期权。
实盘追踪
根据以上策略构造情况，对上证50ETF期权进行分钟级别的策略追踪（2018年10月8日—2019年3月19日），策略初始资金为10万元，每次交易20组，资金占用约50%，不考虑滑点和手续费，对看涨期权策略和看跌期权策略进行分开回测。
回测结果显示，看涨期权回归策略的收益率达到76.6%，策略的持仓时间占全部交易时间的比例约38%，最长一次非“微笑”形态出现在2019年1月23日9：31至2019年1月31日15：00。
看跌期权回归策略的收益率达到72.4%，策略的持仓时间占全部交易时间的比例约32%，最长一次非“微笑”形态出现在2018年11月9日9：31至2018年11月13日13：01。
策略损益情况如下图所示：
图为看涨期权收益曲线
图为看跌期权收益曲线。