第12章 动载荷与动应力-2013
工程力学动载荷

y
x
A
B
工程力学动载荷
例:重为P的重物从h处自由落下,冲击梁上的D点. 梁的EI及W均为已知.求:梁内max及梁中点处的挠度
h
A
CD B
P
A
CD B
yD=Pbx(l2-x2-b2)/6lEI
A
CD B
工程力学动载荷
h
A
CD B
P
A
CD B
1
A
B
工程力学动载荷
例 已知:重为G的重物以水平速度v冲击到圆形截面AB 梁的C点,EI已知. 求:σd max
解:水平冲击问题 ※确定动荷系数
静载时σmax出现于固定端A处
工程力学动载荷
图示钢杆的下端有一固定圆盘,盘上放置弹簧.弹簧在1kN 的静载荷作用下缩短0.0625cm.钢杆的直径d=4cm,l=4m许 用应力 =120Mpa,E=200GPa.若重为15kN的重物自由落下, 求其许可高度H.又若没有弹簧,许可高度H将等于多大?
注意:上面的论述是对等截面杆而言的,不能用于变截面杆的 情况。
工程力学动载荷
三、变截面杆同等截面杆的比较:
如图所示:一变截面杆,一等截面杆,同样受到重量 为Q,速度为v的重物的冲击,试比较它们的动应力。
根据机械能守恒定律,可求得两杆的冲击载荷分别为:
工程力学动载荷
于是两杆的冲击应力分别为: (a)
上升。若只考虑工字钢的重量而不计吊索自重,试求吊索的
动应力,以及工字钢在危险点的动应力d,max 欲使工字钢中的 d,max 减至最小,吊索位置应如何安置?
2m 4m 4m 2m
ACB a
(a)
z y
动载荷

动荷系数 K d
v2 g st
P d K d P st d K d st
d K d st
三、冲击响应计算
例 直径0.3m的木桩受自由落锤冲击,落锤重5kN,
求:桩的最大动应力。E=10GPa
解:①求静变形 stP E stLAW EA L 42m 5m ②动荷系数
Wv h=1m
K d11 2h st112 4 12 05 0201 .97
1
一、动载荷:
§10-1 基本概念
载荷不随时间变化(或变化极其平稳缓慢),构件各部
件加速度保持为零(或可忽略不计),此类载荷为静载荷。
载荷随时间急剧变化,构件的速度有显著变化,此类载
荷为动载荷。
二、动响应:
构件在动载荷作用下产生的各种响应(如应力、应变、位
移等),称为动响应。
实验表明:只要应力不超过比例极限 ,在动载荷下胡克定
1、起重机丝绳的有效横截面面积为A , [] =300MPa ,物体单位体 积重为 , 以加速度a上升,试校核钢丝绳的强度(不计绳重)。
解:①受力分析如图:
x
aa
L
Nd
mn
qst
x
qG
惯性力q:GgAa
Nd(qstqG)xA(x 1g a)
②动应力
d
Nd A
x(1a)
g
最大动应力
dmax L(1g a)Kdstmax
1.假设: ①冲击物为刚体; ②冲击物不反弹; ③不计冲击过程中的声、光、热等能量损耗(能量守恒); ④冲击过程为线弹性变形过程。(保守计算)
2.动能 T ,势能 V ,变形能 U,冲击前、后,能量守恒: (冲击 )T 1V 前 1U 1T2V2U2(冲击 ) 后
工程力学第12章答案
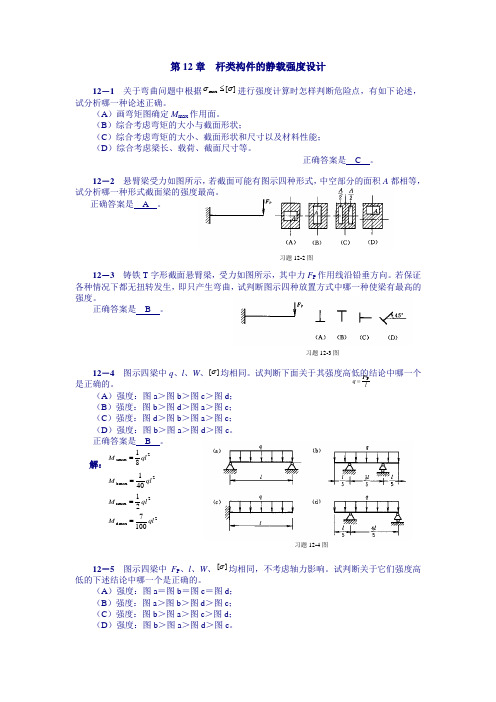
习题12-3图 习题12-2图习题12-4图 第12章 杆类构件的静载强度设计12-1 关于弯曲问题中根据][max σσ≤进行强度计算时怎样判断危险点,有如下论述,试分析哪一种论述正确。
(A )画弯矩图确定M max 作用面。
(B )综合考虑弯矩的大小与截面形状;(C )综合考虑弯矩的大小、截面形状和尺寸以及材料性能; (D )综合考虑梁长、载荷、截面尺寸等。
正确答案是 C 。
12-2 悬臂梁受力如图所示,若截面可能有图示四种形式,中空部分的面积A 都相等,试分析哪一种形式截面梁的强度最高。
正确答案是 A 。
12-3 铸铁T 字形截面悬臂梁,受力如图所示,其中力F P 作用线沿铅垂方向。
若保证各种情况下都无扭转发生,即只产生弯曲,试判断图示四种放置方式中哪一种使梁有最高的强度。
正确答案是 B 。
12-4 图示四梁中q 、l 、W 、][σ均相同。
试判断下面关于其强度高低的结论中哪一个是正确的。
(A )强度:图a >图b >图c >图d ; (B )强度:图b >图d >图a >图c ; (C )强度:图d >图b >图a >图c ; (D )强度:图b >图a >图d >图c 。
正确答案是 B 。
解:2amax 81ql M =2bmax 401ql M =2cmax 21ql M = 2dmax 1007ql M =12-5 图示四梁中F P 、l 、W 、][σ均相同,不考虑轴力影响。
试判断关于它们强度高低的下述结论中哪一个是正确的。
(A )强度:图a =图b =图c =图d ; (B )强度:图a >图b >图d >图c ; (C )强度:图b >图a >图c >图d ; (D )强度:图b >图a >图d >图c 。
l q PF=3231ABM )(o M(a)习题12-5题习题12-6题32l M P /F 31(d-1)lM P /F 21AB(c-1)lM P /F 10351BA 10351 (b-1) l M P /F 41AB 41 (a-1) 正确答案是 B 。
综合篇 单元十二 动载荷与疲劳破坏

解得
FN
G
G g
a
G 1
a g
40 1
5 9.8
kN
60.4kN
(2)计算钢索的横截面面积A 由强度条件σd=FN/A≤[σ]得钢索的横截面面积为
A
FN
60.4 103 80
755mm2
单元十二 动载荷与疲劳破坏 课题二 加速度引起的动载荷问题
解 (1)计算静挠度Δj和最大 静应力σjmax。查型钢表得22a工
字钢的截面轴惯性矩Iz、抗弯截
面系数Wz为
Iz=3400cm4
Wz=309cm3
简支梁的梁中点受集中力作用时的挠度为
j
Gl 3 48EI z
1103 (3103)3 48 200103 3400104
mm 8.28102 mm
解 (1)应用截面法计算动内力FN,沿 m—m截面将钢索截开,取下半部分为研
究对象,画出受力图并加上重物的惯性
力 ,如图b所示。研究对象被假想成平
衡状态,建立平衡方程
Fy 0
FN
G
G g
a
0
单元十二 动载荷与疲劳破坏 课题二 加速度引起的动载荷问题
• 一、构件在等加速直线运动时的动载荷问题
a g
)
j
(1
a) g
式中,σj=G/A是静载荷G在钢索中产生的应力,称为静应力。
单元十二 动载荷与疲劳破坏 课题二 加速度引起的动载荷问题
• 一、构件在等加速直线运动时的动载荷问题
引入系数 则
Kd
1
动载荷的概念及其分类

第12章 动载荷§12-1 动载荷的概念及其分类1.动载荷的概念前面各章讨论的都是构件在静载荷作用下的应力、应变及位移计算。
静载荷是指构件上的载荷从零开始平稳地增加到最终值。
因加载缓慢,加载过程中构件上各点的加速度很小,可认为构件始终处于平衡状态,加速度影响可略去不计。
动载荷是指随时间作明显变化的载荷,即具有较大加载速率的载荷。
一般可用构件中材料质点的应力速率( dt d σσ=•)来表示载荷施加于构件的速度。
实验表明,只要应力在比例极限之内,应变与应力关系仍服从胡克定律,因而,通常也用应变速率( dt d εε=•)来表示载荷随时间变化的速度。
一般认为标准静荷的 ,随着动载荷 的增加,它对材料力学性能的影响越趋明显。
对金属材料,静荷范围约在 ,如果 ,即认为是动载荷。
min /)~.(3010=•ε•ε/2−s ~41010−•=εs /210−•≥ε2.加速运动构件中的动应力分析三类动载荷问题:根据加载的速度与性质,有三类动荷问题。
(1)一般加速度运动(包括线加速与角加速)构件问题,此时还不会引起材料力学性能的改变,该类问题的处理方法是动静法。
•ε(2) 冲击问题,构件受剧烈变化的冲击载荷作用。
大约在 ,它将引起材料力学性能的很大变化,由于问题的复杂性,工程上采用能量法进行简化分析计算。
•εs /~101(3)振动与疲劳问题,构件内各材料质点的应力作用周期性变化。
由于构件的疲劳问题涉及材料力学性能的改变和工程上的重要性,一般振动问题不作重点介绍,而将专章介绍疲劳问题。
§12-2 构件作等加速运动时的应力计算1.动应力分析中的动静法度为 a 的质点,惯性力为其质量 m 与 a 的乘积,方向与a 相反。
达朗贝尔原理指出,对作加速度运动的质点系,如假想地在每一质点上加上惯性力,则质点系上的原力系与惯性力系组成平衡力系。
这样,可把动力学问题在形式上作为静力学问题处理,这就是动静法。
动载荷

材料力学
§2
惯性力问题
动载荷
2、等角速度旋转的构件
•旋转圆环的应力计算 一平均直径为D的薄壁圆环绕通过其圆心且垂直于圆环平面 的轴作等角速度转动。已知转速为,截面积为A,比重为,壁 厚为t。 解:等角速度转动时,环内各
qd
an
D o
t
o
点具有向心加速度,且D>>t 可近似地认为环内各点向心 an 2 D / 2 。 加速度相同, 沿圆环轴线均匀分布的惯性 力集度 q d 为:
圆环横截面上的应力:
式中 v D 是圆环轴线上各点的线速度。强度条件为:
2
d
材料力学
v 2
g
[ ]
§2
惯性力问题
动载荷
•旋转圆环的变形计算
D , 在惯性力集度的作用下,圆环将胀大。令变形后的直径为 则其直径变化 D D D ,径向应变为
t D ( D D) r t D D E d v 2 D
式中 k d 为冲击时的动荷系数,
2
kd st
2H kd 1 1 st
其中 st 是结构中冲击受力点在静载荷(大小为冲击物重量) 作用下的垂直位移。
材料力学
§3
冲击问题
动载荷
因为
Pd d d kd Q st st
所以冲击应力为
d k d st
2H 当 110 时,可近似取 k d st
2 H ,误差<5%。 st 2 H ,误差<10%。 st
4、 k d 不仅与冲击物的动能有关,与载荷、构件截面尺寸有关, 更与 st 有关。这也是与静应力的根本不同点。构件越易变 形,刚度越小,即“柔能克刚”。
材料力学习题(7)第十二章 哈工业大材料力学本科生试卷和课后题目

材料力学习题(7)第十二章哈工业大材料力学本科生试卷和课后题目材料力学习题第12章12-1 一桅杆起重机,起重杆AB的横截面积如图所示。
钢丝绳的横截面面积为10mm2。
起重杆与钢丝的许用力均为[?]?120MPa,试校核二者的强度。
习题2-1图习题12-2图12-2 重物F=130kN悬挂在由两根圆杆组成的吊架上。
AC是钢杆,直径d1=30mm,许用应力[?]st=160MPa。
BC是铝杆,直径d2= 40mm, 许用应力[?]al= 60MPa。
已知ABC为正三角形,试校核吊架的强度。
12-3 图示结构中,钢索BC由一组直径d =2mm的钢丝组成。
若钢丝的许用应力[?]=160MPa,横梁AC单位长度上受均匀分布载荷q =30kN/m作用,试求所需钢丝的根数n。
若将AC改用由两根等边角钢形成的组合杆,角钢的许用应力为[?] =160MPa,试选定所需角钢的型号。
12-4 图示结构中AC为钢杆,横截面面积A1=2cm2;BC杆为铜杆,横截面面积A2=3cm2。
[?]st = 160MPa,[?]cop = 100MPa,试求许用载荷[F]。
习题12-3图习题12-4图12-5 图示结构,杆AB为5号槽钢,许用应力[?] = 160MPa,杆BC为hb= 2的矩形截面木杆,其截面尺寸为b = 5cm, h = 10cm,许用应力[?] = 8MPa,承受载荷F = 128kN,试求:(1)校核结构强度;(2)若要求两杆的应力同时达到各自的许用应力,两杆的截面应取多大?习题12-5图习题12-6图12-6 图示螺栓,拧紧时产生?l = 0.10mm的轴向变形,试求预紧力F,并校核螺栓强度。
已知d1=8mm, d2=6.8mm, d3=7mm, l1=6mm, l2=29mm, l3=8mm; E=210GPa,[?]=500MPa。
12-7 图示传动轴的转速为n=500r/min,主动轮1输入功率P1=368kW,从动轮2和3分别输出功率P2=147kW和P3=221kW。
动载荷与交变应力

则 Fd K d Fst
Fd Fst 钢索中的动应力为 d K d K d st A A
st 为静载荷下钢索中的静应力
此时的强度条 件为
Fst m m
A
Fd
m m x
A
A
g a
d K d st [ ]
结论
x
G
G
G a g
只要将静载荷下的应力、变形,乘以动荷 因数Kd即得动载荷下的应力与变形。
例:一重量为 P的重物由高度为 h 的位置自由下落,与 一块和直杆AB 相连的平板发生冲击。杆的横截面面积 为A。求杆中的冲击应力。
解:重物是冲击物, 杆 AB(包括圆盘) 是被冲击物。
冲击物减少的势能:
A
A
P
B
V P(h d )
动能无变化:T 0
B
d
假使Δd为冲击发生后重物与平 板一起下降的最大位移, Pd为 重物与平板之间的相互作用力
惯性力:大小等于质点的质量 m 与加速度 a 的乘积, 方向与 a 的方向相反。
FIR ma
构件上除外加载荷外,再在构件的各点上加上 惯性力,则可按求静载荷应力和变形的方法, 求得构件的动应力和动变形。
例1:一起重机钢索以加速度 a 提升一重为 G 的物体,设钢索的横截面面积为 A ,钢索单位 体积的重量为 ,求距钢索下端为 x 处的 m-m A 截面上的应力。 Fst a g m m 解: 钢索的重力集度为 : A 物体的惯性力为:
(1) 不计冲击物的变形,且冲击物与被冲击物接触 后无反弹,成为一个运动系统。
(2)被冲击物的质量很小可略去不计,材料服 从胡克定律。
(3) 过程中只有势能、动能与应变能的转化, 略去其它能量的损失。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
12.2.1. 自由落体冲击应力和变形
EI
h
P
d
初
末
Pd
初时刻:T1 = 0, V1 = P(h+d), U1 = 0
末时刻:T2 = 0, V2 = 0, U2 = Pdd /2
2014-7-3
材料力学
19
12.2.1. 自由落体冲击应力和变形
T1 + V1 + U1 = T2 + V2 + U2
A
强度条件: d
D 2 2
4
4
v 2
v
动应变:周向线应变
πD1 πD D d D 2 2 v 2 d πD D E 4E E
极限速度(转速)
直径改变量:D
2014-7-3
D3 2
4E
Dv 2
E
ma
大小:ma
a
○m
F R F
v
v2 m R
m
方向:与加速度a相反
惯性力 Fg= -ma
圆周运动
2014-7-3 材料力学 9
3. 达朗伯原理
在运动物体上假想地加上惯性力,则惯性力与主动力、 约束力在形式上组成平衡力系。
a
○m
4. 动静法
F
ma
○m
F
运用达朗伯原理,将动力学问题在形式上转化为静力学问题。
k 2st kd 2h 0
2 st d
其解为: k 1 1 2h d
st
2h 取正号: kd 1 1 st
自由落体冲击 动荷系数
h: 冲击高度 st:将冲击物重量按静载方式加到冲击点 引起该点相应位移。
2014-7-3
材料力学
21
三. 自由落体冲击应力和变形 EI h P
kd 1 1
2014-7-3
2T W st
材料力学 24
例2 钢制圆截面杆上端固定,下端固连一无重刚性托盘以承
接落下的环形重物。已知杆的长度 l=2m ,直径 d=30mm , 弹性模量E=200GPa。若环形重物的重力P= 500N,自高 度 h=50mm 处自由落下,使杆受到冲击。求下列两种情 况下,杆的动应力: (1) 重物直接落在刚性托盘上; (2) 托盘上放一刚度系数k=1MN/m的弹簧,环形重物落在弹 簧上。 解:(1) 环形重物直接落在刚性 托盘上 冲击点沿冲击方向的静荷位移
d
st
P 2 初:T1 v V1= 0, U1= 0 2g
末: T2=0, V2=0, U2= Pdd/2 能量守恒:T1+V1+U1 = T2+V2+U2
记 Pd=kdP
初 末
d=kdst
P 2 1 2 v kd Pst 2g 2
kd v2 g st
30
2014-7-3
Pl st1 EA
2014-7-3
500 2 6 7.074 10 m 2 π 0.03 200 109 4
材料力学 25
例2
动荷系数:
kd1 1 1
2h
st
2 0.05 1 1 120 6 7.074 10
P 500 静荷应力: st1 0.7074 MPa 2 A π 0.03 4
d
原冲击问题 等效静荷问题
EI
d
EI P
st
Pd = kdP
Pd
研究最大动应力和最大动变形时,可转化为等效静荷问 题求解。关键:求kd。
2014-7-3 材料力学 22
三. 自由落体冲击应力和变形
类似问题
2014-7-3
材料力学
23
12.2.1. 自由落体冲击应力和变形 讨论:
2h 自由落体冲击 kd 1 1 动荷系数
解:(1) 确定动荷系数 横梁作匀加速提升,动荷系数:
a kd 1 g
(2) 计算起吊力 静荷起吊力等于梁的自重,即 Fst Al g
a 所以,动荷起吊力 F kd Fst (1 ) Al g g
2014-7-3 材料力学 13
例1
(3) 计算最大弯矩 梁单位长度重力
q A g
作出弯矩图,得最大静荷弯矩
M st max
ql 2 A gl 2 40 40
a A gl 2 (1 ) g 40
最大动荷弯矩
M d max kd M st max
2014-7-3
材料力学
14
12.2.2等速转动构件的动应力
单位体积质量: 横截面面积:A 单位长度质量:A
2014-7-3
材料力学
2
2. 动载荷: 引起构件产生明显加速度的荷载。
直线变速提升重物:
>P FN = P!
2014-7-3
材料力学
3
2. 动载荷:
匀速转动圆环: FNd
飞轮的制动:
FNd
2014-7-3
材料力学
4
2. 动载荷:
绕轴匀速转动的直杆:
FNd
自由落体冲击梁:
2014-7-3
不 平 衡
2014-7-3
加惯性力
平 衡
10
材料力学
12.1.1直线变速运动构件的动应力
轴力:
P Fy 0, FN P a 0 g a FN (1 ) P g a 记 kd 1 动荷系数 g
则 FN = kdP
2014-7-3
材料力学
11
12.1.1直线变速运动构件的动应力
P(h+d)=Pdd/2
令 则
Pd kd P
冲击动荷系数
st:将冲击物重量当作 静载加到冲击点引 P(h+kdst) = kdPkdst/2 起的冲击点位移
Pd kd P d kd st
k 2st kd 2h 0
2 st d
2014-7-3
材料力学
20
三. 自由落体冲击应力和变形
第12章 动载荷与动应力
12.1 惯性载荷作用下的动应力
12.2 冲击应力
12.3 振动应力
2014-7-3
材料力学
1
12.1 惯性载荷作用下的动应力
一. 静载荷与动载荷
1. 静载荷:
载荷值由零开始,缓慢增加,到一定数值后不再 变化或变化很小。
特点:加载过程中结构内任意点加速度近似为零, 即结构时刻保持平衡。 在此之前所研究的载荷都是静载荷。
例3
A
(3) 求kd
2h kd 1 1 st
Pa st EI
3
P
B C
2a M Pa
st max
M max Pa W W
a
2hEI 1 1 Pa3
(4) 求stmax (5) 求dmax
2014-7-3
d max
(2) 冲击载荷:构件受剧烈变化力的作用
加速度不易求,材料的力学性质变化较大; 用能量法简化求解。
(3) 振动载荷: (4) 交变载荷:(下一章讨论) 应力作周期变化。
2014-7-3
材料力学
8
12.1 惯性载荷作用下的动应力
1. 特点:加速度可求
形式:直线变速运动构件,等速转动构件。
2. 惯性力
与 (或v)有关
16
材料力学
12.2 冲击应力
一、冲击现象
冲击物
P
冲击物
P
被冲击物 冲击物
P
冲击作用时间很短10-6~10-3秒。 由于冲击载荷的变化规律难以精确掌握,因此常采用能 量转化及守恒定律求近似解。
2014-7-3
材料力学
17
二、假设:
1. 冲击物的变形很小,可以忽略不计,即视为刚体,并且 从冲击开始到产生最大位移的整个过程中,冲击物与被 冲击物一起运动,不发生分离。 不吸收变形能 2. 忽略被冲击物的质量,认为冲击载荷引起的应力和变形, 在冲击瞬时遍及被冲击物,被冲击物仍处于线弹性范围 内,并且无反弹。 不计被冲击物的动能和势能 3. 忽略其它能量损失,如接触区局部塑性变形的能量损失、 发热、发声等,只有位能、动能和应变能的转化。 机械能守恒定律仍然成立 动能T, 势能V, 变形能U 任意时刻有:T + V + U = 常数
材料力学
5
3. 动荷响应的特点 (1) 构件各部分有明显的加速度; 不平衡,内力难以用静力平衡方程计算。 (2) 材料的力学性质与静荷载作用不同。 一般可用应变率来区分静荷载与动荷载: 静荷载: 105 ~ 101 1/ s
1 8 动荷载: 10 ~ 10 1/ s
2014-7-3
动应力: d1 kd1 st1 120 0.7074= 84.9MPa
2014-7-3
材料力学
26
例2
(2) 环形重物落在弹簧上
此时,冲击点沿冲击方向的静荷 位移为杆的静荷轴向伸长与弹簧 静荷变形之和,有
500 2 500 st2 2 π 0.03 1 106 9 200 10 4 7.074 106 + 500 106 = 507.074 106 m Pl P EA k
A B
P
C
2a M
A B
a 1
C
Pa
M
2014-7-3 材料力学
a
33
例3
A
P
B
C
2ቤተ መጻሕፍቲ ባይዱ M Pa M
