高一数学复数的乘除法运算
7.2.2复数的乘、除运算+教学设计2023-2024学年高一下学期数学人教A版(2019)必修二

§7.2.2复数的乘、除运算——乘除运算片段教学(偏讲解)一、教材分析本节为人教A版必修第二册第七章第二节的内容,主要内容是代数形式的复数乘、除法运算法则。
两个复数的乘法可以类似于两个多项式的乘法运算来进行,两个复数的除法可以通过共轭复数转化为乘法运算。
本节的内容较为基础,主要考察学生的数学运算的能力,复数的乘除运算结合是常考的内容。
二、学情分析在学习本节内容前,学生已经在初中学习了多项式的乘法运算,前面又学习了复数的加减运算,为本节内容的学习奠定良好的,基础学生在学习复数的乘除运算时能够更好地进入状态,更加理解本节课的内容。
三、教学目标1.掌握复数代数形式的乘法和除法运算;2.理解复数乘法的交换律、结合律和乘法对加法的分配律;3.理解复数除法运算的实质,会利用复数四则运算求解相关问题数学学科素养1.数学抽象:复数乘法、除法运算法则;2.逻辑推理:复数乘法运算律的推导;3.数学运算:复数四则运算;4.数学建模:结合复数四则运算,解决复数范围内的问题四、教学重难点重点:复数代数形式的乘、除运算法则难点:灵活运用复数的乘、除运算法则求解相关问题五、教学方法讲解法,提问法,讨论法六、教学过程教学环节教师活动学生活动设计意图复习回顾【教师提问】1.已知复数z1=a+bi,复数z2=c+di(a,b,c,d∈R),则z1+z2,z1−z2如何表示?2.设a,b,c,d∈R,则(a+b)(c+d)怎样展开?【教师引导】上述式子是我们初中所学习的多项式乘法,如何展开?【教师进一步提问】复数z1=a+bi,复数z2=c+di,(a,b,c,d∈R),则z1⋅z2=(a+bi)(c+di),按照上述运算法则将其展开,则z1⋅z2等于什么?【教师总结】两个复数相乘,类似于两个多项式相乘,只要在所得的结果中把i2换成−1,并且把实部与虚部分别合并即可【学生回答】学生思考并回答:z1+z2=(a+c)+(b+d)iz1−z2=(a−c)+(b−d)i(a+b)(c+d)=ac+ad+bc+bd【学生思考】同桌之间讨论,需要将复数的乘积按照多项式展开z1⋅z2=(a+bi)(c+di)=ac+adi+bci+bdi2=ac+adi+bci−bd=(ac−bd)+(ad+bc)i通过复习,为引入本节新课做好铺垫。
9.4三角形式下复数的乘除、乘方、开方运算(第2课时)高一数学(沪教版2020必修第二册)

3 cos + sin
⋅ 2 cos + sin
12
12
4
4
1
+ sin
⋅ 2 cos + sin
12
12
4
4
= 3 × 2 cos
+
+ sin
+
12 4
12 4
= 6 cos + sin
3
3
1
3
= 6
+
2
2
解 1
3 cos
6 3 2
=
+
2
2
4
4
4 cos 3 + sin 3
2
+
3
2
3
+
= 2 × 3
=
5
6(
6
2
3
+
= −3 3 + 3
+
3
2
3
6
5
)
6
6
+
6
6
6
3 +
+
2
3
+
6
两个复数三角形式相乘,把
模相乘作为积的模,把辐角相加
作为积的辐角,若遇到复数的代
= 2(150° + 150°)
=− 3+
除,则商还是一个复数,它
的模等于被除数的模除以除
120° + 120°
复数的乘、除法运算及几何意义 课件-高一下学期数学人教A版(2019)必修第二册

课堂练习 教材P80练习
1. 计算: (1)(7 6i)(3i);(2)(3 4i)(2 3i);(3)(1 2i)(3 4i)(2 i). 2. 计算:
(1)( 3 2 i) ( 3 2 i) ;(2)(1 i)2;(3)i(2 i)(1 2i).
化简后就可得到上面的结果.这与作根式除法时的处理是很类似的.
2
PART TWO
例题精讲
例3: 计算(1-2i)(3+4i)(-2+i). 解析: (1-2i)(3+4i)(-2+i)=(11-2i)(-2+i)=-20+15i. 例4:计算(1) (2+3i)(2-3i); (2) (1+i)2. 解析: (1)(2+3i)(2-3i)=22-(3i)=4-(-9)=13.
= (ac-bd)+(ad+bc)i. 即 (a+bi)(c+di)= (ac-bd)+(ad+bc)i 注意:两个复数的积是一个确定的复数.
知识点一 复数的乘法运算
问题1 规定了复数乘法运算法则,请回答下列问题? (1)两个复数的积是个什么数?它的值唯一确定吗? (2)当 z1 ,z2 都是实数时,与实数乘法法则一致吗? (3)运算中的实质是什么?类似于实数的哪种运算方法?
通过以上探究,我们知道,两个复数的积仍然是一个复数,且唯一确定, 运算中与实数的乘法法则保持一致,类似于两个多项式相乘
知识点一 复数的乘法运算
问题2 复数的加法满足实数运算中的运算律,那么,复数的乘法是 否满足实数乘法的交换律、结合律、分配律呢?
复数的知识点总结高一数学

复数的知识点总结高一数学高一数学复数的知识点总结复数在数学中扮演着重要的角色,它是由实数部分和虚数部分组成的。
接下来,我将对高一数学中与复数相关的知识点进行总结和概述。
1. 复数的定义和表示复数是由实数部分和虚数部分组成的数。
一般地,表示为z=a+bi,其中a是实数部分,b是虚数部分,i是虚数单位,满足i^2=-1。
2. 复数的运算复数的运算包括加减乘除四则运算。
对于两个复数z1=a+bi和z2=c+di,它们的加法、减法、乘法和除法分别为:- 加法:z1+z2=(a+c)+(b+d)i- 减法:z1-z2=(a-c)+(b-d)i- 乘法:z1*z2=(ac-bd)+(ad+bc)i- 除法:z1/z2=(ac+bd)/(c^2+d^2)+((bc-ad)/(c^2+d^2))i3. 共轭复数对于一个复数z=a+bi,它的共轭复数记作z*=a-bi。
共轭复数与原复数的实部相同,虚部的符号相反。
4. 模和参数表示对于一个复数z=a+bi,它的模记作|z|=√(a^2+b^2),表示复数到原点的距离。
复数还可以使用模和参数来表示,其中参数θ满足tanθ=b/a。
5. 纯虚数如果一个复数z=a+bi的实部a为0,即a=0,那么它就是一个纯虚数。
纯虚数可以表示为z=bi。
6. 复数的平方根对于一个复数z=a+bi,它的平方根记作√z。
复数的平方根存在两个值,分别表示为√z=√(r(cosθ+i*sinθ)),其中r=|z|,θ=arg(z),n为整数。
7. 欧拉公式欧拉公式是一种重要的数学公式,它将复数与三角函数之间建立了联系。
欧拉公式表示为e^(ix)=cosx+isinx,其中e是自然对数的底数。
8. 复数的应用领域复数在数学中有着广泛的应用,例如在电路分析、信号处理、量子力学等领域中都得到了广泛的应用。
复数的运算规律和性质也使得它成为处理波动、振荡、相位等问题的有力工具。
经过以上的总结,我们对于高一数学中的复数知识点有了更加清晰的认识。
高一下学期数学人教A课件:复数的四则运算
+ ( + )( − )
+ + −
=
=
=
+ ( + )( − )
+
例4.计算: + ÷ − .
新课讲解
例3.计算:
①
+ −
=
;
② | + | =
;
③ | − + + | =
;
观察各复数与它们乘积的模,你有什么发现?
你能证明它们吗?
= + , = ( + )
新课讲解
复数的乘除运算:
结合复数乘法模的计算特征,
你觉得复数除法的模也有类似特征吗?
例5.化简 =
−+ +
+
,并计算 .
1
|1 |
=
2
|2 |
新课讲解
例6.在复数范围内解下列方程:
① + + =
② =
课堂小结
若 = + , = +
则 + =
复习引入
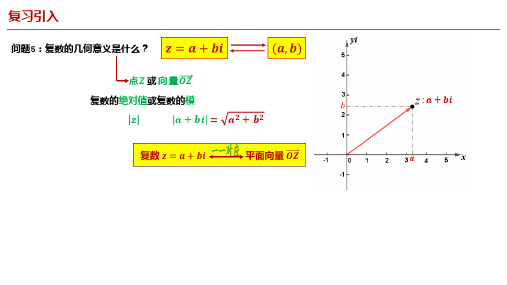
问题5:复数的几何意义是什么?
点 或 向 量
复数的绝对值或复数的模
| + | =
: +
+
新课讲解
复数的加减运算:
问题:若 = + , = + ,你认为应该如何定义 + ?为什么?
问题:若 = + , = + ,则 − =
复数的乘、除运算课件-2022-2023学年高一下学期数学人教A版(2019)必修第二册

(z1·z2)·z3= z1·(z2·z3) (结合律)z1(z2+z3)=z1·z2+z1·z3 (分配律)
同理易得:
复数乘法的运算律:
∴
ca+dbi2+bci+adi =
(ac-bd)+(ad+bc)i
当堂练习
则对应的点的坐标为(2,4)
1.
2.
例题讲解
02
【例2】计算
例题讲解
03
复数的除法
03
【例5】在复数范围内解下列方程:;;;
①二次项系数化为1
用配方法解方程:
P65
例题讲解
03
【例5】在复数范围内解下列方程:;
解:①二次项系数化为1:::
03
【例5】在复数范围内解下列方程:;;;
①二次项系数化为1
1、用配方法解方程:
2、用求根公式解方程:
03
【例5】在复数范围内解下列方程:(4);
解:①二次项系数化为1,得: 得:, ,所以
,
课堂小结
04
ONE
课标小结
3、复数的除法:4、在复数范围内解方程:
1、复数的乘法: 2、乘法运算律:
①写成分式的形式
②分母实数化,同时乘以分母的 共轭复数
③化简结果成代数形式
(1)配方法: ①二次项系数化为1::
(2)求根公式法:
7.2.2复数的乘除运算
温故
温故知新
01
探新
问题1:多项式与多项式相乘等于什么? .
试试自己猜测,复数的乘法法则:
问题2:
=
1、复数的乘法
探究新知
02
我们规定,复数的乘法如下:是任意的两个复数,
复数乘除运算的三角表示式及其几何意义高一数学系列

.
7.设复数 z 满足 z-3z 的辐角的主值为5π4 ,z+1 的模为 10 , 求复数 z.
解:设 z=x+yi(x,y∈R).
由|z+1|= 10 ,得|(x+1)+yi|= 10 ,
所以 (x+1)2+y2=10.
又 z-3z=(x+yi)-3(x-yi)=-2x+4yi,
由 arg(z-3z)=5π4
[cos(1
2
)
i
sin(1
2 )]
r1 (cos 1
i sin1),
所以根据复数除法的定义,有
r1 (cos 1 r2 (cos2
i sin1) i sin2 )
r1 r2
[cos(1
2)
i sin(1
2 )]
这就是说,两个复数相除, 商的模等于被除数模除以除数的模所得的 商, 商的辐角等于被除数的辐角减去除数的辐角所得的差.
r
r
0 arg z 2
复数的三角形式和代数形式可以根据需要进行互化.
复数的代数形式的乘除运算法则
(1) (a bi)(c di)
(2) (a bi) (c di)
ac adi bci bd (ac bd) (ad bc)i
a bi (a bi) (c di) c di (c di) (c di)
学习目标
1.了解复数乘、除运算的三角表示(重点) 2.了解复数乘、除运算的几何意义 3.会利用复数三角形式进行复数乘、除运算 (重点、难点)
复数的两种形式
代数形式
三角形式
z a bi
z =r cos i sin
实部 a 虚部 b
辐角
联系
辐角主值
r a2 b2 ,cos a ,sin b
7.2.2+复数的乘、除运算课件-2024-2025学年高一下学期数学人教A版(2019)必修第二册

2-i
3.[苏教版教材例题]计算 .
3-4i
解 (方法
2-i
1)设 =x+yi(x,y∈R),则(3-4i)(x+yi)=2-i,
3-4i
=
3 + 4 = 2,
即(3x+4y)+(3y-4x)i=2-i,所以
解得
3-4 = -1,
=
2-i
因此
3-4i
(方法
=
2
1
+
i.
5
5
2-i
2)
3-4i
(1+i)(4+3i)
(2)计算:
(2-i)(1-i)
-2+i
=
4+3i+4i+3i2
解析 原式=
2-2i-i+i
=
22+11i+14i+7i2
2
=
1+7i
1-3i
4-i
2
=
15+25i
=3+5i.
5
.
=
(1+7i)(1+3i)
(1-3i)(1+3i)
=
1+3i+7i+21i2
1-9i
2
=
-20+10i
1-3i
∵z=
1+i
=
(1-3i)(1-i)
(1+i)(1-i)
∴复数z的虚部是-2.
故选D.
1 2 3 4 5 6
D.-2
=
-2-4i
=-1-2i,
2
2.m∈R,i为虚数单位,若(m+i)(2-3i)=5-i,则m的值为( A )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(ac bd) (ad bc)i
显然,两个复数的乘积仍为复数
2.复数运算满足交换律、结合律、分配 律。
• •
1
2
2
1
( • )• •( • )
1
2
3
1
2
3
•( ) • •
1
2
3
1
2
13
三、【例题讲解】
例1
已知1 1 2i, 2 3 4i
理解复数乘法的运算律
会在复数范围内解方程
核心素养 数学运算
逻辑推理 数学运算
一、【回顾旧知】
复数加减法的运算法则:
运算法则: 设复数z1=a+bi,z2=c+di,那么:
z1+z2=(a+c)+(b+d)i; z1-z2=(a-c)+(b-d)i.
即:两个复数相加(减)就是实部与实部,虚部与虚部分 别相加(减).
(ac
bd ) c2
(bc d2
ad )i
分母实数化
例5.计算 (1 2i) (3 4i)
解:
练习
求
已知 z1
z1 z2 ,
3 2i
z1 z2
,
,
z2
z1
•
1
z2
4i
, z1 z2
5.在复数范围内解下列方程. 例 6. (1)x2+5=0; (2)x2+4x+6=0.
【解】 (1)因为 x2+5=0,所以 x2=-5, 又因为( 5i)2=(- 5i)2=-5, 所以 x=± 5i, 所以方程 x2+5=0 的根为± 5i. (2)法一:因为 x2+4x+6=0, 所以(x+2)2=-2, 因为( 2i)2=(- 2i)2=-2, 所以 x+2= 2i 或 x+2=- 2i, 即 x=-2+ 2i 或 x=-2- 2i, 所以方程 x2+4x+6=0 的根为 x=-2± 2i.
所以方程
2x2 + 3x + 4 = 0
的根为
x = -3±
-(-23)i 2×2
=
-3± 23i 4.
练习 2.已知 3+2i 是关于 x 的方程 2x2+px+q=0 的一个根, 求实数 p,q 的值. 解:因为 3+2i 是方程 2x2+px+q=0 的根, 所以 2(3+2i)2+p(3+2i)+q=0,即 2(9+12i-4)+(3p+2pi)+q =0, 整理得(10+3p+q)+(24+2p)i=0, 所以1204+ +32pp+ =q0= ,0,解得pq= =- 26.12,
又因为 b≠0, 所以a22a-+b42=+04,a+6=0, 解得 a=-2,b=± 2. 所以 x=-2± 2i, 即方程 x2+4x+6=0 的根为 x=-2± 2i.
在复数范围内,实系数一元二次方程 ax2+bx+c=00
时,x=-b±
b2-4ac
书少成天才功山小就=有艰是不欢苦百路分学的勤迎之劳习一为动光,的径+老灵正,临感确学来!,的欢百海徒方分无迎法之伤+崖九指少悲十苦谈导九空作!的话汗舟水!
7.2.2 复数的乘除运算
2020年4月25日星期六
考点 复数的 乘除运算 复数乘法 的运算律 解方程
学习目标 掌握复数乘除运算的运算法 则,能够进行复数的乘除运算
A.5-4i
B.5+4i
C.3-4i
D.3+4i
(2)把复数 z 的共轭复数记作-z ,已知(1+2i) -z =4+3i,求 z.
(1)选 D.因为 a-i 与 2+bi 互为共轭复数, 所以 a=2,b=1,所以(a+bi)2=(2+i)2=3+4i. (2)设 z=a+bi(a,b∈R),则-z =a-bi, 由已知得,(1+2i)(a-bi)=(a+2b)+(2a-b)i=4+3i,由复数相等 的条件知,a2+ a-2bb= =43, ,解得 a=2,b=1, 所以 z=2+i.
2a
.
②当 Δ<0 时,x=-b±
-(b2-4ac)i
2a
.
(2)利用复数相等的定义求解
设方程的根为 x=m+ni(m,n∈R),将此代入方程 ax2+bx+c
=0(a≠0),化简后利用复数相等的定义求解.
练习 1. (1)在复数范围内解方程 2x2+3x+4=0.
解:因为 b2-4ac=32-4×2×4=9-32=-23<0,
两个互为共轭的复数的乘积等于这个复数 (或其共轭复数)模的平方
结论: •
2
2
4.复数的除法法则
先把除式写成分式的形式,再把分子
与分母都乘以分母的共轭复数,化简后
写成代数形式(分母实数化).即
(a bi) (c di) a bi c di
(a bi)(c di) (c di)(c di)
计算1 • 2。
解:
1 • 2 (1 2i)(3 4i)
3 4i 6i 8i2
11 2i
例2 : (1 2i)(3 4i)(2 i)
解:
例3 计算:
(3+4i)(3-4i) = 9-16i2
=9+16=25
练习:计算 (1)(a bi)(a bi)
a2 abi abi b2i2
法二:由 x2+4x+6=0 知 Δ=42-4×6=-8<0, 所以方程 x2+4x+6=0 无实数根. 在复数范围内,设方程 x2+4x+6=0 的根为 x=a+bi(a,b∈R 且 b≠0), 则(a+bi)2+4(a+bi)+6=0, 所以 a2+2abi-b2+4a+4bi+6=0, 整理得(a2-b2+4a+6)+(2ab+4b)i=0, 所以a22a-b+b24+b=4a0+,6=0,
探究:i 的运算性质
例 7.(1)复数 z=11+-ii,则 ω=z2+z4+z6+z8+z10 的值为(
二、【新课探究】
1.复数的乘法法则
两个复数的乘法可以按照多 项式的乘法运算来进行,只
是在遇到 i2 时,要把 i2 换
成-1,并把最后的结果写成
a bi(a,b R) 的形式。
设 z1 a bi , z2 c di
(a,b,c,d R)
则 z1 • z2 (a bi)(c di)
a2 b2
3、共轭复数的定义
当两个复数的实部相等,虚部互为相反数时, 这两个复数叫做互为共轭复数。虚部不等于0的 两个共轭复数也叫做共轭虚数。
特别地,实数的共轭复数是实数本身。
Z的共轭复数记作Z
例 4.(1)已知 a,b∈R,i 是虚数单位,若 a-i 与 2+bi 互为共轭
复数,则(a+bi)2=( )
