K-均值聚类分析
有关k-均值聚类算法的理解

有关k-均值聚类算法的理解1.K-均值聚类算法的历史:聚类分析作为一种非监督学习方法,是机器学习领域中的一个重要的研究方向,同时,聚类技术也是数据挖掘中进行数据处理的重要分析工具和方法。
1967 年MacQueen 首次提出了K 均值聚类算法(K-means算法)。
到目前为止用于科学和工业应用的诸多聚类算法中一种极有影响的技术。
它是聚类方法中一个基本的划分方法,常常采用误差平方和准则函数作为聚类准则函数迄今为止,很多聚类任务都选择该经典算法,K-means算法虽然有能对大型数据集进行高效分类的优点,但K-means算法必须事先确定类的数目k,而实际应用过程中,k 值是很难确定的,并且初始聚类中心选择得不恰当会使算法迭代次数增加,并在获得一个局部最优值时终止,因此在实际应用中有一定的局限性。
半监督学习是近年来机器学习领域的一个研究热点,已经出现了很多半监督学习算法,在很多实际应用中,获取大量的无标号样本非常容易,而获取有标签的样本通常需要出较大的代价。
因而,相对大量的无标签样本,有标签的样本通常会很少。
传统的监督学习只能利用少量的有标签样本学习,而无监督学习只利用无标签样本学习。
半监督学习的优越性则体现在能同时利用有标签样本和无标签样本学习。
针对这种情况,引入半监督学习的思想,对部分已知分类样本运用图论知识迭代确定K-means 算法的K值和初始聚类中心,然后在全体样本集上进行K-均值聚类算法。
2. K-算法在遥感多光谱分类中的应用基于K-均值聚类的多光谱分类算法近年来对高光谱与多光谱进行分类去混的研究方法很多,K-均值聚类算法与光谱相似度计算算法都属于成熟的分类算法.这类算法的聚类原则是以数据的均值作为对象集的聚类中心。
均值体现的是数据集的整体特征,而掩盖了数据本身的特性。
无论是对高光谱还是对多光谱进行分类的方法很多,K-均值算法属于聚类方法中一种成熟的方法。
使用ENVI将多光谱图像合成一幅伪彩色图像见图1,图中可以看出它由标有数字1 的背景与标有数字2 和3的两种不同的气泡及标有数字4的两个气泡重叠处构成。
K-均值聚类

一种改进的K-均值聚类算法摘要:在K-均值聚类算法中,K值需事先确定且在整个聚类过程中不能改变其大小,而按照经验K值划分所得的最终聚类结果一般并非最佳结果。
本文将最大最小距离算法与K-均值算法结合,通过最大最小距离算法估算出K值,再用K-均值算法改进聚类精度。
1. 概述聚类(cluster)做为数据挖掘技术的主要研究领域之一,近年来被广泛应用于各行各业。
聚类分析方法做为一种无监督的学习方法,采用“物以类聚”的思想,将数据对象按某些属性分组成为多个类或簇,并且使得同类或簇中数据对象相似度尽可能大,而不同类或簇之间的差异尽可能大。
K- 均值聚类算法是聚类分析中一种基本的划分方法,因其思想可靠,算法简洁,而且能有效的应用于大数据集而被广泛使用。
但是传统的K 均值聚类算法往往受初始中心点选取的影响并且常常终止于局部最优。
因此初始中心点的选择在K-均值聚类算法中非常重要,通常希望找到散布较大的点作为初始中心点。
但是在传统的K-均值聚类算法中初始中心点选择的随机性较强,导致聚类结果的随机性。
而且在传统的K-均值聚类算法中K的值需要给定,如果K值给定的不合理也将影响聚类的效果。
针对以上缺点本文将最大最小距离聚类算法和传统的K-均值聚类算法结合。
形成一种初始中心点的距离最大,中心点数自动调整的K-均值算法。
以达到更高的聚类精度。
2.K-均值聚类算法基本思想K 均值聚类算法是一种基于划分方法的经典聚类算法之一,该算法的核心思想如下:首先从所给n 个数据对象中随机选取k 个对象作为初始聚类中心点,然后对于所剩下的其它对象,则根据它们与所选k 个中心点的相似度(距离)分别分配给与其最相似的聚类,然后在重新计算所获聚类的聚类中心(该聚类中所有对象的均值),不断重复这一过程直到标准测度函数开始收敛为止,其基本算法流程如下:1) 从n个数据对象中任意选择k个对象作为初始聚类中心。
2) 根据每个聚类对象的均值(中心对象),计算每个对象与这些中心对象的距离并根据最小距离对相应对象进行划分。
k均值聚类的方法原理

k均值聚类的方法原理k均值聚类是最常见的非层次聚类算法之一,它通过将数据点划分为k个聚类来对数据进行聚类分析,其中k是用户预先指定的聚类数量。
在该算法中,数据点被分配给最接近的聚类,以此来形成聚类。
1. 选择k个初始聚类中心点:在一开始,需要选择k个点作为聚类的中心点。
通常情况下,这些点被选择为随机的数据点。
2. 分配每个数据点到最近的聚类中心:每个数据点将被分配到最接近的聚类中心。
这可以通过计算数据点与每个聚类中心之间的距离来完成。
通常,欧氏距离是用于计算两点之间距离的最常用方法。
3. 更新聚类中心:在每个数据点被分配给最近的聚类中心后,需要更新聚类中心,以确保它们仍然代表该聚类中心的所有数据点。
为此,需要通过计算每个聚类中心周围所有数据点的平均值来更新该中心点。
4. 重复以上步骤:以上三个步骤需要不断重复,直到聚类中心不再发生变化,或者指定的迭代次数达到预定值。
通过以上步骤,k均值聚类可以将数据点分成k个聚类,每个聚类中心代表该聚类的中心点。
该聚类方法的优点在于它易于实现和可扩展性,而且对于大规模数据集具有较高的速度和良好的适应性。
1. 初始聚类中心的选择会影响聚类结果:如果初始聚类中心点选择的不够好,就有可能导致算法不能正确地将数据点分配到它们所属的聚类中。
3. 对于非球形分布的数据集,k均值聚类的效果会受到影响:如果数据点不是均匀分布在球形区域内,就有可能导致聚类结果不准确。
在实际使用k均值聚类算法时,需要根据具体数据集的特征选择最合适的k值和初始聚类中心点,以达到最佳的聚类效果。
需要注意算法的局限性,避免使用不适合该算法的数据集。
在进一步了解k均值聚类的方法原理之前,需要先了解什么是聚类分析。
聚类分析是一种常见的无监督学习方法,它可以将数据集中的每个数据点划分到不同的类别中,以便研究数据中的内在结构。
聚类分析可用于各种各样的应用,如市场细分、图像分割、搜索引擎、信号处理、家庭健康研究等。
实验三-K-均值聚类算法实验报告

实验三K-Means聚类算法一、实验目的1) 加深对非监督学习的理解和认识2) 掌握动态聚类方法K-Means 算法的设计方法二、实验环境1) 具有相关编程软件的PC机三、实验原理1) 非监督学习的理论基础2) 动态聚类分析的思想和理论依据3) 聚类算法的评价指标四、算法思想K-均值算法的主要思想是先在需要分类的数据中寻找K组数据作为初始聚类中心,然后计算其他数据距离这三个聚类中心的距离,将数据归入与其距离最近的聚类中心,之后再对这K个聚类的数据计算均值,作为新的聚类中心,继续以上步骤,直到新的聚类中心与上一次的聚类中心值相等时结束算法。
实验代码function km(k,A)%函数名里不要出现“-”warning off[n,p]=size(A);%输入数据有n个样本,p个属性cid=ones(k,p+1);%聚类中心组成k行p列的矩阵,k表示第几类,p是属性%A(:,p+1)=100;A(:,p+1)=0;for i=1:k%cid(i,:)=A(i,:); %直接取前三个元祖作为聚类中心m=i*floor(n/k)-floor(rand(1,1)*(n/k))cid(i,:)=A(m,:);cid;endAsum=0;Csum2=NaN;flags=1;times=1;while flagsflags=0;times=times+1;%计算每个向量到聚类中心的欧氏距离for i=1:nfor j=1:kdist(i,j)=sqrt(sum((A(i,:)-cid(j,:)).^2));%欧氏距离end%A(i,p+1)=min(dist(i,:));%与中心的最小距离[x,y]=find(dist(i,:)==min(dist(i,:)));[c,d]=size(find(y==A(i,p+1)));if c==0 %说明聚类中心变了flags=flags+1;A(i,p+1)=y(1,1);elsecontinue;endendiflagsfor j=1:kAsum=0;[r,c]=find(A(:,p+1)==j);cid(j,:)=mean(A(r,:),1);for m=1:length(r)Asum=Asum+sqrt(sum((A(r(m),:)-cid(j,:)).^2));endCsum(1,j)=Asum;endsum(Csum(1,:))%if sum(Csum(1,:))>Csum2% break;%endCsum2=sum(Csum(1,:));Csum;cid; %得到新的聚类中心endtimesdisplay('A矩阵,最后一列是所属类别'); Afor j=1:k[a,b]=size(find(A(:,p+1)==j));numK(j)=a;endnumKtimesxlswrite('data.xls',A);五、算法流程图六、实验结果>>Kmeans6 iterations, total sum of distances = 204.82110 iterations, total sum of distances = 205.88616 iterations, total sum of distances = 204.8219 iterations, total sum of distances = 205.886........9 iterations, total sum of distances = 205.8868 iterations, total sum of distances = 204.8218 iterations, total sum of distances = 204.82114 iterations, total sum of distances = 205.88614 iterations, total sum of distances = 205.8866 iterations, total sum of distances = 204.821Ctrs =1.0754 -1.06321.0482 1.3902-1.1442 -1.1121SumD =64.294463.593976.9329七、实验心得初始的聚类中心的不同,对聚类结果没有很大的影响,而对迭代次数有显著的影响。
K-均值聚类算法

4.重复分组和确定中心的步骤,直至算法收敛;
2.算法实现
输入:簇的数目k和包含n个对象的数据库。 输出:k个簇,使平方误差准则最小。
算法步骤:
1.为每个聚类确定一个初始聚类中心,这样就有K 个初始 聚类中心。
2.将样本集中的样本按照最小距离原则分配到最邻近聚类
给定数据集X,其中只包含描述属性,不包含 类别属性。假设X包含k个聚类子集X1,X2,„XK;各 个聚类子集中的样本数量分别为n1,n2,„,nk;各个 聚类子集的均值代表点(也称聚类中心)分别为m1, m2,„,mk。
3.算法实例
则误差平方和准则函数公式为:
k
2
E p mi
i 1 pX i
单个方差分别为
E1 0 2.52 2 22 2.5 52 2 22 12.5 E2 13.15
总体平均误差是: E E1 E2 12.5 13.15 25.65 由上可以看出,第一次迭代后,总体平均误差值52.25~25.65, 显著减小。由于在两次迭代中,簇中心不变,所以停止迭代过程, 算法停止。
示为三维向量(分别对应JPEG图像中的红色、绿色 和蓝色通道) ; 3. 将图片分割为合适的背景区域(三个)和前景区域 (小狗); 4. 使用K-means算法对图像进行分割。
2 015/8/8
Hale Waihona Puke 分割后的效果注:最大迭代次数为20次,需运行多次才有可能得到较好的效果。
2 015/8/8
例2:
2 015/8/8
Ox y 102 200 3 1.5 0 450 552
数据对象集合S见表1,作为一个 聚类分析的二维样本,要求的簇的数 量k=2。
K-中心点和K-均值聚类算法研究的开题报告

K-中心点和K-均值聚类算法研究的开题报告题目:K-中心点和K-均值聚类算法研究一、研究背景随着数据规模不断增大,如何高效地将数据进行分类和聚类成为了人们研究的焦点。
聚类算法是一种常用的数据挖掘技术,该技术可以将具有相似性的数据同时划分为一个组,从而帮助人们在数据中获取有用的信息。
因此,研究聚类算法具有重要的理论和应用价值。
本研究旨在对K-中心点和K-均值聚类算法进行深入研究,为实际应用提供参考。
二、研究目的本研究的主要目的如下:1.掌握K-中心点和K-均值聚类算法的原理和流程。
2.分析K-中心点和K-均值聚类算法的优缺点。
3.通过对比实验和分析,确定哪种聚类算法更适用于不同的数据集以及对应的优化方案。
三、研究内容本研究的主要内容如下:1. 对K-中心点聚类算法进行研究。
通过对K-中心点聚类算法的原理、流程和优缺点进行深入分析,探索K-中心点聚类算法在各种数据集上的聚类效果。
2. 对K-均值聚类算法进行研究。
通过对K-均值聚类算法的原理、流程和优缺点进行深入分析,探索K-均值聚类算法在各种数据集上的聚类效果。
3. 对比研究两个聚类算法。
通过对比K-中心点和K-均值聚类算法的不同之处,以及它们在不同数据集上的表现,探索哪种聚类算法更适用于不同的数据集。
四、研究方法本研究将采用实验研究、文献研究和统计分析等方法。
1.实验研究:在多个常用数据集上分别使用K-中心点和K-均值聚类算法进行实验,评估其聚类效果。
2.文献研究:通过查阅相关文献,掌握K-中心点和K-均值聚类算法的原理、应用、优缺点等方面的知识,为本研究提供参考。
3.统计分析:通过对实验数据进行统计分析,探索K-中心点和K-均值聚类算法的优劣之处。
五、研究意义本研究的意义如下:1.对K-中心点和K-均值聚类算法进行深入研究,掌握各自的特点、优缺点和应用领域。
2.通过实验研究和对比分析,为实际应用提供聚类算法的选取参考,减少聚类算法的试错成本。
3.在理论上为聚类算法的研究提供新的思路和方法,推进数据挖掘技术的发展。
基于SPSS用K-means聚类做聚类分析
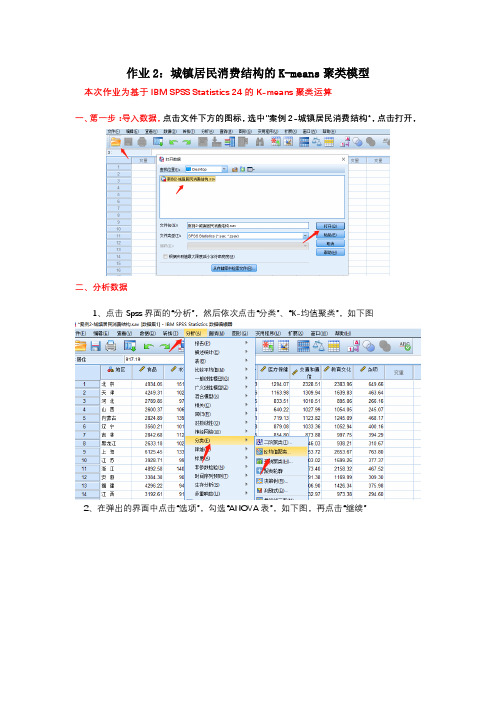
作业2:城镇居民消费结构的K-means聚类模型
本次作业为基于IBM SPSS Statistics 24的K-means聚类运算
一、第一步:导入数据,点击文件下方的图标,选中”案例2-城镇居民消费结构“,点击打开,
二、分析数据
1、点击Spss界面的“分析”,然后依次点击“分类”、“K-均值聚类”,如下图
2、在弹出的界面中点击“选项”,勾选“ANOVA表”,如下图,再点击“继续”
3、在弹出的界面中点击“保存”,勾选“聚类成员”、“与聚类中心距离”,如下图所示,点击“继续”
4、最后在弹出的界面中,把“地区”放入“个案标注依据”,其余的放入“变量”中,如下图所示,点击“确定”。
三、结果展示
ANOVA。
简述k-均值聚类的计算步骤

简述k-均值聚类的计算步骤
K-means聚类是一种基于距离计算的聚类分析方法,主要包括以下步骤:
1.确定聚类数:首先需要根据问题的需求和数据特点确定聚类数量k。
2.选择初始点:从数据集中随机选择k个点作为初始簇中心。
3.计算距离:将每个数据点分别与k个初始簇中心进行距离计算,然后将其分配至离它最近的簇中心。
4.重计算簇中心:对于每个簇,重新计算其所有成员的平均值,以得到新的簇中心,作为下一轮迭代的簇中心。
5.再度分类:根据新计算的簇中心,重新将每个数据点分配到最近的簇中心。
6.迭代:重复执行步骤4和步骤5,直到簇中心不再变化或者达到迭代次数的限制。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1案例题目:选取一组点(三维或二维),在空间内绘制出来,之后根据K均值聚类,把这组点分为n类。
此例中选取的三维空间内的点由均值分别为(0,0,0),(4,4,4),(-4,4,-4),协方差分别为300030003⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦,000030003⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦,300030003⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦的150个由mvnrnd函数随机生成。
2原理运用与解析:2.1聚类分析的基本思想聚类分析是根据“物以类聚”的道理,对样本或指标进行分类的一种多元统计分析方法,它们讨论的对象是大量的样本,要求能合理地按各自的特性进行合理的分类。
对于所选定的属性或特征,每组内的模式都是相似的,而与其他组的模式差别大。
一类主要方法是根据各个待分类模式的属性或特征相似程度进行分类,相似的归为一类,由此将待分类的模式集分成若干个互不重叠的子集,另一类主要方法是定义适当的准则函数运用有关的数学工具进行分类。
由于在分类中不需要用训练样本进行学习和训练,故此类方法称为无监督分类。
聚类的目的是使得不同类别的个体之间的差别尽可能的大,而同类别的个体之间的差别尽可能的小。
聚类又被称为非监督分类,因为和分类学习相比,分类学习的对象或例子有类别标记,而要聚类的例子没有标记,需要由聚类分析算法来自动确定,即把所有样本作为未知样本进行聚类。
因此,分类问题和聚类问题根本不同点为:在分类问题中,知道训练样本例的分类属性值,而在聚类问题中,需要在训练样例中找到这个分类属性值。
聚类分析的基本思想是认为研究的样本或变量之间存在着程度不同的相似性(亲疏关系)。
研究样本或变量的亲疏程度的数量指标有两种:一种叫相似系数,性质越接近的样本或变量,它们的相似系数越接近1或-1,而彼此无关的变量或样本它们的相似系数越接近0,相似的为一类,不相似的为不同类。
另一种叫距离,它是将每一个样本看做p维空间的一个点,并用某种度量测量点与点之间的距离,距离较近的归为一类,距离较远的点应属于不同的类。
2.2动态聚类法思想动态聚类方法、亦称逐步聚类法.一类聚类法.属于大样本聚类法。
具体作法是:先粗略地进行预分类,然后再逐步调整,直到把类分得比较合理为止。
这种分类方法较之系统聚类法,具有计算量较小、占用计算机存贮单元少、方法简单等优点,所以更适用于大样本的聚类分析,是一种普遍被采用的方法。
这种方法具有以下三个要素:(1) 选定某种距离度量作为样本间的相似性度量; (2) 确定某种可以评价聚类结果质量的准则函数;(3) 给定某个初始分类,然后用迭代算法找出使得准则函数取极值的最好聚类结果。
动态聚类法在计算迭代过程中,类心会随着迭代次数进行修正和改变。
动态聚类法的基本步骤:(1) 选取初始聚类中心及有关参数,进行初始聚类。
(2) 计算模式和聚类的距离,调整模式的类别。
(3) 计算各聚类的参数,删除,合并或分裂一些聚类。
(4) 从初始聚类开始,运用迭代算法动态地改变模式的类别和聚类的中心,使准则函数取极值或设定的参数达到设计要求时停止。
2.3K-均值聚类算法的思想K-均值算法是一种基于划分的聚类算法,它通过不断的迭代过程来进行聚类,当算法收敛到一个结束条件时就终止迭代过程,输出聚类结果。
由于其算法思想简便,又容易实现,因此K 一均值算法己成为一种目前最常用的聚类算法之一。
K-均值算法解决的是将含有n 个数据点(实体)的集合12{,,...,}n X x x x = 划分为k 个类j C 的问题,其中1,2,...,j k = ,算法首先随机选取k 个数据点作为k 个类的初始类中心,集合中每个数据点被划分到与其距离最近的类中心所在的类中,形成了k 个聚类的初始分布。
对分配完的每一个类计算新的类中心,然后继续进行数据分配的过程,这样迭代若干次之后,若类中心不再发生变化,则说明数据对象全部分配到自己所在的类中,证明函数收敛。
在每一次的迭代过程中都要对全体数据点的分配进行调整,然后重新计算类中心,进入下一次迭代过程,若在某一次迭代过程中,所有数据点的位置没有变化,相应的类中心也没有变化,此时标志着聚类准则函数已经收敛,算法结束。
通常采用的目标函数形式为平方误差准则函数:21i iKi ii x c E x c ===-∑∑其中,i x 为数据对象,i c 表示类i C 的质心,E 则表示数据集中所有对象的误差平方和。
该目标函数采用欧氏距离。
K-均值聚类算法的过程描述如下:(1) 任选k 个模式特征矢量作为初始聚类中心:(0)(0)(0)12,,...,c z z z ,令k=0.(2) 将待分类的模式识别特征矢量集{}i x u r中的模式逐个按最小距离原则分划给k 类中的某一类,即如果()()min[]k k il ij d d = ,1,2,...,i N = ,则判(1)k i l x ω+∈式中,()k ij d 表示i x 和()k j ω 的中心()k j z 的距离,上标表示迭代次数,于是产生新的聚类ω (1),1,2,...,k j j k ω+= (3) 计算重新分类后的各类心 (1)(1)(1)1,1,2,...,k i j k j i k x jz x j k nω+++∈==∑式中,(1)k j n +为(1)k jω+类中所含模式的个数。
(4) 如果(1)()(1,2,...,)k k j j z z j k +== ,则结束;否则,1k k =+ ,转至步骤(2)。
3.结果分析在二维和三维空间里,原样本点为蓝色,随机选取样本点中的四个点作为中心,用*表示,其他对象根据与这四个聚类中心(对象)的距离,根据最近距离原则,逐个分别聚类到这四个聚类中心所代表的聚类中,每完成一轮聚类,聚类的中心会发生相应的改变,之后更新这四个聚类的聚类中心,根据所获得的四个新聚类中心,以及各对象与这四个聚类中心的距离,根据最近距离原则,对所有对象进行重新归类。
再次重复上述过程就可获得聚类结果,当各聚类中的对象(归属)已不再变化,整个聚类操作结束。
经过K均值聚类计算,样本点分为红,蓝,绿,黑四个聚类,计算出新的四个聚类中心,用*表示。
该算法中,一次迭代中把每个数据对象分到离它最近的聚类中心所在类,这个过程的时间复杂度O(nkd),这里的n指的是总的数据对象个数,k是指定的聚类数,d是数据对象的位数:新的分类产生后需要计算新的聚类中心,这个过程的时间复杂度为O(nd)。
因此,这个算法一次迭代后所需要的总的时间复杂度为O(nkd).通过实验可以看出,k个初始聚类中心点的选取对聚类结果有较大的影响,因为在该算法中是随机地任意选取k个点作为初始聚类中心,分类结果受到取定的类别数目和聚类中心初始位置的影响,所以结果只是局部最优。
K-均值算法常采用误差平方和准则函数作为聚类准则函数(目标函数).目标函数在空间状态是一个非凸函数,非凸函数往往存在很多个局部极小值,只有一个是全局最小。
所以通过迭代计算,目标函数常常达到局部最小而难以得到全局最小。
聚类个数k的选定是很难估计的,很多时候我们事先并不知道给定的数据集应该分成多少类才合适。
关于K-均值聚类算法中聚类数据k值得确定,有些根据方差分析理论,应用混合F统计量来确定最佳分类树,并应用了模糊划分熵来验证最佳分类的准确性。
将类的质心(均值点)作为聚类中心进行新一轮聚类计算,将导致远离数据密集区的孤立点和噪声点会导致聚类中心偏离真正的数据密集区,所以K-均值算法对噪声点和孤立点非常敏感。
图1为未聚类前初始样本及中心,图2为聚类后的样本及中心。
图1 未聚类前初始样本及中心图1 聚类后的样本及中心4.程序:clear;clc;TH = 0.001;N = 20;n = 0;th = 1;%第一类数据mu1=[0 0 0]; % 均值S1=[3 0 0;0 3 0;0 0 3];% 协方差矩阵X1=mvnrnd(mu1,S1,50); %产生多维正态随机数,mul为期望向量,s1为协方差矩阵,50为规模%第一类数据mu2=[4 4 4];% 均值S2=[0 0 0;0 3 0;0 0 3];% 协方差矩阵X2=mvnrnd(mu2,S2,50);%第一类数据mu3=[-4 4 -4];% 均值S3=[3 0 0;0 3 0;0 0 3];% 协方差矩阵X3=mvnrnd(mu3,S3,50);X=[X1;X2;X3]; %三类数据合成一个不带标号的数据类plot3(X(:,1),X(:,2),X(:,3),'+');%显示hold ongrid ontitle('初始聚类中心');k=4;[count,d] = size(X);centers=X(round(rand(k,1)*count),:);id = zeros(count,1);%会出聚类中心plot3(centers(:,1),centers(:,2),centers(:,3),'kx',...'MarkerSize',10,'LineWidth',2)plot3(centers(:,1),centers(:,2),centers(:,3),'ko',...'MarkerSize',10,'LineWidth',2)dist = zeros(k,1);newcenters = zeros(k,d);while( n < N && th > TH)%while n<Nfor ix = 1:countfor ik = 1:kdist(ik) = sum((X(ix,:)-centers(ik,:)).^2);end[~,tmp]=sort(dist); %离哪个类最近则属于那个类id(ix) =tmp(1);endth = 0;for ik = 1:kidtmp = find(id == ik);if length(idtmp) == 0return;endnewcenters(ik,:)= sum(X(idtmp,:),1)./length(idtmp); th = th + sum((newcenters(ik,:) - centers(ik,:)).^2); endcenters = newcenters;n = n+1;endfigure(2)plot3(X(find(id==1),1),X(find(id==1),2),X(find(id==1),3), 'r*'),hold onplot3(X(find(id==2),1),X(find(id==2),2),X(find(id==2),3), 'g*'),hold onplot3(X(find(id==3),1),X(find(id==3),2),X(find(id==3),3), 'b*'),hold onplot3(X(find(id==4),1),X(find(id==4),2),X(find(id==4),3), 'k*'),hold ontitle('最终聚类中心');plot3(centers(:,1),centers(:,2),centers(:,3),'kx',...'MarkerSize',10,'LineWidth',2)plot3(centers(:,1),centers(:,2),centers(:,3),'ko',...'MarkerSize',10,'LineWidth',2)grid on。
