应用数学题库1-0-8
八年级数学专题 二元一次方程组重难点(参数问题、实际应用问题)(北师大版)
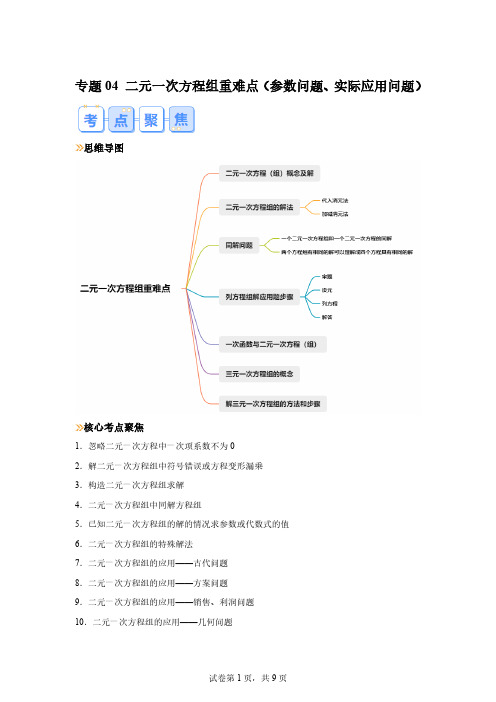
ì3x - 2 y = -1
ìx =1 ìm + 5 =1
ìm = -4
íî3x + 2 y = 7
,解得
í î
y
=
2
,即
íîn
+
3
=
2
,解得
íîn
=
-1
.
(1)学以致用,模仿乐乐同学的“整体换元”的方法,解方程组
ì ïï í ï ïî
x x
+ 3 + 3
y y
+ -
x x
5 5
y y
= =
4 .
-2
试卷第 2 页,共 9 页
义,否则,若把 y=ax+b 代入变形的原方程,必然得到一个恒等式; ③用代入法求出一个未知数的值后,再求另一个未知数时,一般代入变形后得到的方
程比较简单.
2.加减消元法
把方程组的两个方程(或先作适当变形)相加或相减,消去其中一个未知数,从而把
解二元一次方程组转化为解一元一次方程.这种解方程组的方法叫做加减消元法,简
联立成方程组,求出未知数的值,然后代入含有参数的方程即可求出参数的值.
四、列方程组解应用题步骤
1.列方程组解应用题是把“未知”转化为“已知”的重要方法,它的关键是把已知量和未 知量联系起来,找出题目中的相等关系.一般来说,有几个未知量就必须列出几个方
程,所列方程必须满足:
①方程两边表示的是同类量;②同类量的单位要统一;③方程两边的数值要相等.
y
=
与 41
íî2
x
+
3
y
=
-7
有相同的解,求
a,b
的值.
高等数学应用题.

第一章 函数 极限 连续问题1. 上岸点的问题有一个士兵P ,在一个半径为R 的圆形游泳池(图1—1)222x y R +≤内游泳,当他位于点(,02R-)时,听到紧急集 合号,于是得马上赶回位于A=(2R ,0)处的营房去,设该士 兵水中游泳的速度为1v ,陆地上跑步的速度为2v ,求赶回营房 所需的时间t 与上岸点M 位置的函数关系。
图1-1解:这里需要求的是时间t 与上岸点M 位置的函数关系,所以一定要先把上岸点M 的位置数字化,根据本题特点可设(cos ,sin )M R R θθ=其中θ为M 的周向坐标(即极坐标系中的极角),于是本题就成为了求函数关系()t f θ=的问题。
由对称性,我们可只讨论在上半圆周上岸的情况,即先确定函数()t f θ=的定义域为0θπ≤≤。
该士兵在水中游泳所花的时间为111PM t v === 而在陆地上跑步所需的时间,则要视上岸点位置的两种不同的情况要分别进行讨论:① 当03πθ≤≤时,有222M A t v '== ② 当3πθπ≤≤时,要先跑一段圆弧MB ,再跑一段且线段BA ,所以2221()(3R t MB BA v v πθ=+=-。
综上所述,可得121203(33t R v πθππθθπ≤≤=-≤≤问题2 外币兑换中的损失某人从美国到加拿大去度假,他把美元兑换成加拿大元时,币面数值增加12%,回国后他发现把加拿大元兑换成美元时,币面数值减少12%。
把这两个函数表示出来,并证明这两个函数不互为反函数,即经过这么一来一回的兑换后,他亏损了一些钱。
解:设1()f t 为将x 美元兑换成的加拿大元数,2()f t 为将x 加拿大元兑换成的美元数,则1()12% 1.12,0f t x x x x =+⋅=≥ 2()12%0.88,0f t x x x x =-⋅=≥而21(())0.880.120.9856,f f t x x x =⨯=<故1()f t ,2()f t 不互为反函数。
移动数学试题及答案

移动数学试题及答案一、选择题(每题3分,共30分)1. 一个数的平方等于其本身,这个数是()。
A. 0B. 1C. 0或1D. 以上都不是答案:C2. 以下哪个选项是无理数()。
A. 2B. πC. 0.5D. 0.333...答案:B3. 已知函数f(x) = 2x + 3,求f(-1)的值()。
A. -1B. 1C. -5D. 5答案:A4. 以下哪个选项是等差数列()。
A. 2, 4, 6, 8B. 1, 3, 5, 7C. 3, 6, 9, 12D. 以上都是答案:D5. 一个圆的半径是5,那么它的面积是多少()。
A. 25πB. 50πC. 75πD. 100π答案:B6. 以下哪个选项是二次方程的解()。
A. x^2 - 4x + 4 = 0B. x^2 - 4x + 5 = 0C. x^2 - 4x + 3 = 0D. x^2 - 4x + 6 = 0答案:A7. 以下哪个选项是反比例函数()。
A. y = 2xB. y = 2/xC. y = x^2D. y = √x答案:B8. 以下哪个选项是奇函数()。
A. f(x) = x^2B. f(x) = x^3C. f(x) = x^4D. f(x) = x答案:D9. 以下哪个选项是偶函数()。
A. f(x) = x^2B. f(x) = x^3C. f(x) = x^4D. f(x) = x答案:A10. 以下哪个选项是周期函数()。
A. f(x) = x^2B. f(x) = sin(x)C. f(x) = ln(x)D. f(x) = e^x答案:B二、填空题(每题4分,共20分)11. 一个等差数列的首项是3,公差是2,那么它的第5项是()。
答案:1112. 一个等比数列的首项是2,公比是3,那么它的第3项是()。
答案:1813. 一个函数f(x) = ax^2 + bx + c,如果a = 1,b = -3,c = 2,那么f(0)的值是()。
大学数学试题题库及答案

大学数学试题题库及答案一、选择题(每题5分,共20分)1. 下列哪个选项是微积分的基本定理?A. 牛顿-莱布尼茨公式B. 泰勒公式C. 欧拉公式D. 柯西-黎曼公式答案:A2. 矩阵的行列式表示为:A. 矩阵的对角线元素之和B. 矩阵的对角线元素之积C. 矩阵的对角线元素之差的绝对值D. 矩阵的对角线元素之和的平方答案:B3. 以下哪个函数不是周期函数?A. sin(x)B. cos(x)C. e^xD. tan(x)答案:C4. 以下哪个选项是线性代数中矩阵的特征值?A. 矩阵的行数B. 矩阵的列数C. 矩阵的迹D. 矩阵的行列式答案:C二、填空题(每题5分,共20分)1. 圆的面积公式为______。
答案:πr²2. 欧拉公式中e^(ix)等于______。
答案:cos(x) + i*sin(x)3. 线性代数中,一个矩阵是可逆的当且仅当其______不为零。
答案:行列式4. 微积分中,不定积分的基本定理表明,如果F(x)是f(x)的一个原函数,则∫f(x)dx = F(x) + C,其中C是______。
答案:常数三、解答题(每题10分,共60分)1. 计算定积分∫(0到π) sin(x)dx。
答案:-cos(x) | (0到π) = 22. 求函数f(x) = x² - 4x + 3在x=2处的切线方程。
答案:y = x - 13. 证明:如果一个数列{a_n}收敛于L,则它的子数列{a_{2n}}也收敛于L。
答案:略4. 解线性方程组:\[\begin{cases}x + 2y = 5 \\3x - y = 1\end{cases}\]答案:\[\begin{cases}x = 2 \\y = 1.5\end{cases}\]5. 计算级数∑(1到∞) (1/n²)的和。
答案:π²/66. 证明:对于任意正整数n,有1³ + 2³ + ... + n³ = (n(n+1)/2)²。
数学试题大全及答案

数学试题大全及答案一、选择题1. 下列哪个选项是整数?A. 3.14B. 5C. -2.7D. 0.5答案:B2. 圆的面积公式是什么?A. A = πr²B. A = 2πrC. A = πrD. A = r²答案:A二、填空题1. 一个数的平方根是它本身的数是______和______。
答案:0, 12. 一个直角三角形的两个直角边分别为3和4,其斜边长度为______。
答案:5三、计算题1. 计算下列表达式的值:(1) 2 + 3 × (4 - 1)(2) (-2)³答案:(1) 2 + 3 × 3 = 2 + 9 = 11(2) (-2)³ = -82. 解下列方程:(1) 2x + 5 = 13(2) 3x - 4 = 14答案:(1) 2x = 13 - 5 = 8x = 8 / 2 = 4(2) 3x = 14 + 4 = 18x = 18 / 3 = 6四、解答题1. 一个长方体的长、宽、高分别为2米、3米和4米,求其体积。
答案:长方体的体积 V = 长× 宽× 高= 2 × 3 × 4 = 24 立方米。
2. 某工厂生产一批零件,合格率为98%,如果生产了1000个零件,求不合格的零件数。
答案:不合格的零件数= 1000 × (1 - 98%) = 1000 × 0.02 = 20 个。
五、应用题1. 某商店购进一批商品,进价为每件100元,标价为每件150元。
如果商店希望获得20%的利润率,那么应该打几折销售?答案:首先计算期望的售价:100 × (1 + 20%) = 120元。
然后计算折扣:120 / 150 = 0.8,即打八折。
2. 一个水池有一个进水管和一个出水管,单独开进水管每小时可以注满水池的1/5,单独开出水管每小时可以放空水池的1/6。
数学考试题型及答案

数学考试题型及答案一、选择题(每题3分,共30分)1. 下列哪个数是最小的正整数?A. 0B. 1C. 2D. 3答案:B2. 圆的周长公式是?A. C = πdB. C = 2πrC. C = πrD. C = 2πd答案:B3. 一个数的相反数是-5,这个数是?A. 5B. -5C. 0D. 10答案:A4. 计算下列哪个表达式的结果是正数?A. (-3) × (-2)B. (-3) × 2C. (-3) × (-2) × (-1)D. (-3) × 0答案:A5. 一个等腰三角形的底角是45度,那么顶角是多少度?A. 90B. 45C. 60D. 120答案:C6. 一个数的绝对值是5,这个数可能是?A. 5B. -5C. 5或-5D. 0答案:C7. 下列哪个是二次方程?A. 2x + 3 = 0B. x^2 + 3x + 2 = 0C. 3x - 5 = 0D. x^3 - 2x + 1 = 0答案:B8. 一个数的立方是-8,这个数是?A. 2B. -2C. 8D. -8答案:B9. 计算下列哪个表达式的结果是负数?A. 5 - 3B. -5 - 3C. 5 + 3D. -5 + 3答案:B10. 一个直角三角形的两条直角边分别是3和4,斜边是多少?A. 5B. 7C. 9D. 12答案:A二、填空题(每题4分,共20分)11. 一个数的平方根是2,这个数是______。
答案:412. 一个数的立方根是-8,这个数是______。
答案:-51213. 计算 (2/3) × (3/4) 的结果是______。
答案:1/214. 一个等差数列的首项是2,公差是3,那么第5项是______。
答案:1715. 一个二次函数的顶点是(2, -1),且经过点(0, 3),这个二次函数的解析式是 y = a(x - 2)^2 - 1,其中a的值是______。
数学测试题大全及答案
数学测试题大全及答案一、选择题(每题2分,共20分)1. 下列哪个数是最小的正整数?A. 0B. 1C. 2D. 3答案:B2. 圆的周长公式是什么?A. C = πrB. C = 2πrC. C = πRD. C = 2πR答案:B3. 如果一个数的平方根是它自己,那么这个数是:A. 0B. 1C. -1D. 4答案:A4. 以下哪个是二次方程?A. x + 2 = 0B. x^2 + 2x + 1 = 0C. x^3 - 4x^2 + 4x = 0D. 2x^2 + 3x = 5答案:B5. 以下哪个是正弦函数的图像?A. 直线B. 抛物线C. 正弦曲线D. 双曲线答案:C6. 一个等腰三角形的两边相等,如果底边长度为5,那么腰的长度至少是多少?A. 2B. 3C. 4D. 5答案:D7. 以下哪个是勾股定理的表达式?A. a^2 + b^2 = c^2B. a + b = cC. a × b = cD. a / b = c答案:A8. 一个数的绝对值是它自己,这个数可能是:A. 正数B. 负数C. 零D. 所有以上答案:D9. 以下哪个是复数的表示方法?A. a + biB. a - biC. a × biD. a / bi答案:A10. 以下哪个是矩阵的行列式?A. 矩阵的对角线元素的乘积B. 矩阵的转置C. 矩阵的逆D. 矩阵的秩答案:A二、填空题(每题2分,共20分)11. 一个直角三角形的两个直角边分别是3和4,斜边的长度是________。
答案:512. 函数 y = 2x^2 + 3x - 1 的顶点坐标是________。
答案:(-3/4, -25/8)13. 集合 {1, 2, 3} 和 {2, 3, 4} 的交集是________。
答案:{2, 3}14. 圆的面积公式是________。
答案:πr^215. 一个数的对数是2,如果以10为底,那么这个数是________。
一次函数的应用同步练习 2024-2025学年北师大版八年级数学上册
一次函数的应用[时间: 60分钟分值: 100分]一、选择题(每题4分,共32分)1. 已知正比例函数的图象如图所示,则这个函数的表达式为( )A.y=−12x B. y 12C. y=-2xD. y=2x2.如图,直线y= ax+b过点A(0,2),B(-3,0),则方程ax+b=0的解是( )A. x=2B. x=0C. x=-1D. x=-33.已知方程kx+b=0的解是x=3,则函数y= kx+b的图象可能是( )4.数形结合是解决数学问题常用的思想方法.如图,一次函数y= kx+b(k,b为常数,且k<0)的图象与直线y=13x都经过点A(3,1),当kx+b<13x时,根据图象可知,x的取值范围是( )A. x>3B. x<3C. x<1D. x>15. 小聪在画一次函数的图象时,他列表后,发现题中一次函数y=◆x+◆中的k和b看不清了,根据如下表格可知( )A. k=2,b=3B.k=−23,b=2x 0 3C. k=3,b=2D. k=1,b=-1 y 2 06. 身边的数学一辆汽车油箱中剩余的油量y(L)与已行驶的路程x( km)的对应关系如图所示,如果这辆汽车每千米耗油量相同,当油箱中剩余的油量为35 L时,该汽车已行驶的路程为( )A.150 kmB.165 kmC.125 kmD.350 km7.身体中的数据大拇指与小拇指尽量张开时,两指尖的距离称为“指距”,研究表明,一般情况下,人的身高h ( cm)与指距d( cm)之间的一次函数为h=9d+b,已知当d=20时,h=160,当某人的身高为178 cm时,他的指距约为( )A.21 cmB.22 cmC.23 cmD.24 cm8.甲、乙两车沿同一路线从A城出发前往B城,在整个行程中,汽车离A 城的距离y与时刻t的对应关系如图所示,关于下列结论:①A,B两城相距300 km;②甲车的平均速度是60 km/h,乙车的平均速度是100 km/h;③乙车先出发,先到达B 城;④甲车在9:30追上乙车.正确的有( )A.①②B.①③C.②④D.①④二、填空题(每题5分,共20分)9.如图,已知函数y=2x+b和y= ax-3的图象交于点(-2,-5),根据图象可得关于x 的方程2x+b= ax-3的解是.10.如图,一次函数y= kx+b的图象与正比例函数y=2x的图象互相平行,且经过点A,则一次函数y= kx+b 的表达式为.11.如图,在平面直角坐标系中,直线y=x-6分别与x轴、y轴交于点A,B,点P的坐标为(0,8).若点M在直线AB 上,则PM长的最小值为.12.生活应用快递员经常驾车往返于公司和客户之间.在快递员完成某次投递业务时,他与客户的距离s( km)与行驶时间t(h)之间的函数关系如图所示(因其他业务,曾在途中有一次折返,且快递员始终匀速行驶),那么快递员的行驶速度是km/h.三、解答题(共48分)13.(18 分)如图,在平面直角坐标系中,直线l经过点A(0,2),B(-3,0).(1)求直线l的函数表达式;(2)若点M(3,m)在直线l上,求m的值;(3)若y=-x+n的图象过点B,交y轴于点C,求△ABC的面积.14.(16 分)已知A,B两地之间有一条长440千米的高速公路,甲、乙两车分别从A,B两地同时出发,沿此公路相向而行,甲车先以100千米/小时的速度匀速行驶200 千米后与乙车相遇,再以另一速度继续匀速行驶4小时到达B地;乙车匀速行驶至A地,两车到达各自的目的地后停止,两车距A 地的路程y(千米)与各自的行驶时间x(小时)之间的函数关系如图所示.(1) m= ,n= ;(2)求两车相遇后,甲车距A地的路程y与x之间的函数关系式;(3)当乙车到达A地时,求甲车距A 地的路程.15.(14 分) 我国航天事业发展迅速,2024年4月25 日20时59分,神舟十八号载人飞船成功发射.某玩具店抓住商机,先购进了1 000件相关航天模型玩具进行试销,进价为50元/件.(1)设玩具售价为x元/件,全部售完的利润为y元,求利润y(元)关于售价x(元/件)的函数表达式;(2)当售价定为60元/件时,该玩具销售火爆,该店继续购进一批该种航天模型玩具,并从中拿出这两批玩具销售利润的20%用于支持某航模兴趣组开展活动,在成功销售完毕后,资助经费恰好为10 000元,请问该店继续购进了多少件航天模型玩具?一、1. A 2. D 3. C 4. A5. B 【点拨】将x=0,y=2;x=3,y=0分别代入y= kx+b中,得b=2,3k+b=0,解得k=−23.故选B.6. A7. B 【点拨】把d=20,h=160代入h=9d+b,得160=9×20+b,解得b=-20.所以h=9d-20.当h=178时,178=9d-20,解得d= 22.所以他的指距约为22 cm.8. D 【点拨】由图象可知,A,B 两城相距300 km,乙车先出发,甲车先到达B城,故①符合题意,③不符合题意;甲车的平均速度是300÷3=100( km/h),乙车的平均速度是300÷5=60( km/h),故②不符合题意;由图象知,甲车在9:3 0追上乙车,故④符合题意.综上所述,正确的有①④.故选D.二、9. x=-210. y=2x-4 【点拨】由一次函数y= kx+b的图象与正比例函数y=2x的图象互相平行可得k=2,然后把点(1,-2)的坐标代入y=2x+b即可求出b的值.11.√2【点拨】如图,过P点作PQ⊥y轴交直线AB 于Q,由垂线段最短可知,当PM⊥AB时,PM的长有最小值.在y=x-6中,当x=0时,y=-6;当y=8时,x=14,所以B(0,-6), Q(14,8).因为P(0,8),所以PQ=14,PB=14.所以BQ=√BP2+PQ2=14√2.因为S PQB=12BP⋅PQ=12BQ⋅PM,即14×14=14√2PM,所以PM=7√2,所以PM长的最小值为√212.35 【点拨】因为快递员始终匀速行驶,所以快递员的行驶速度是8.750.55−2×(0.35−0.2)=35(km/ℎ).三、13.【解】(1)设直线l的函数表达式为y= kx+b.把点A(0,2),B(-3,0)的坐标分别代入,得b=2,-3k+b=0,解得k=23.所以直线l的函数表达式为y=23x+2(2)当x=3时, 23×3+2=4.所以m=4.(3)因为y=-x+n的图象过点B,所以3+n=0,所以n=-3,所以y=-x-3. 所以当x=0时,y=-3.所以C(0,-3).所以AC=5.因为B(-3,0),所以OB=3.所以S ABC=12AC⋅OB=12×5×3=152.14.【解】(1)2;6(2)两车相遇后,甲车的速度是(440-200)÷(6-2)=60(千米/小时),所以两车相遇后,甲车距A地的路程y与x 之间的函数关系式为y=200+60(x-2)=60x+80(2<x≤6).(3)乙车的速度为(440-200)÷2=120(千米/小时).所以乙车到达A地所需时间为440÷120=113(小时).当x=113时,y=60×113+80=300,所以当乙车到达A地时,甲车距A地的路程为300千米.15.【解】(1)函数表达式为y=1000(x-50)=1000x-50 000.(2)设该店继续购进了m 件航天模型玩具,根据题意,得(60-50)(1000+m)×20%=10 000,解得m=4 000.答:该店继续购进了4 000件航天模型玩具.。
考研应用数学试题及答案
考研应用数学试题及答案一、选择题(每题3分,共30分)1. 下列函数中,满足条件f(x+y)=f(x)+f(y)的函数是:A. f(x) = x^2B. f(x) = sin(x)C. f(x) = e^xD. f(x) = ln(x)答案:C2. 设随机变量X服从参数为λ的泊松分布,其概率质量函数为P(X=k)=λ^k/k!e^λ,k=0,1,2,...。
若P(X=1)=0.1,则λ的值为:A. 0.5B. 1C. 2D. 3答案:B3. 在二维空间中,若向量a=(1, 2)和向量b=(2, 1),则向量a与向量b的夹角的余弦值为:A. 1/2B. √2/2C. √3/2D. 3/4答案:D4. 对于函数f(x)=x^3-6x^2+9x+2,其在区间(2, +∞)上的最小值为:A. -2B. 2C. 5D. 8答案:C5. 设矩阵A=\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix},矩阵B=\begin{bmatrix} 5 & 6 \\ 7 & 8 \end{bmatrix},则矩阵C=2A-3B 的值为:A. \begin{bmatrix} -19 & -22 \\ -22 & -26 \end{bmatrix}B. \begin{bmatrix} -5 & -2 \\ -11 & -6 \end{bmatrix}C. \begin{bmatrix} 1 & 4 \\ 9 & 12 \end{bmatrix}D. \begin{bmatrix} 13 & 16 \\ 17 & 20 \end{bmatrix}答案:B6. 某工厂生产的产品经过三道工序,第一道工序的合格率为80%,第二道工序的合格率为85%,第三道工序的合格率为90%。
若整个产品的合格率为76.5%,则三道工序之间:A. 相互独立B. 不相互独立C. 只有第一、二道工序相互独立D. 只有第二、三道工序相互独立答案:B7. 设函数f(x)在区间[a, b]上连续,且∫[a, b]f(x)dx = 3,则函数F(x)=∫[a, x]f(t)dt在区间[a, b]上的定积分为:A. 3B. 6C. 9D. 无法确定答案:B8. 对于常微分方程y'' - 2y' + y = 0,其通解为:A. y = e^tB. y = e^(t/2)sin(t)C. y = e^t + e^(2t)D. y = e^(3t)答案:C9. 设函数g(x) = x^3 - 3x^2 + 2,若g(x) ≥ 1,则x的取值范围为:A. (-∞, 1]∪ [2, +∞)B. (-∞, 2] ∪ [1, +∞)C. (-∞, 0] ∪ [1, +∞)D. (-∞, 0] ∪ [2, +∞)答案:B10. 某投资项目,初始投资额为100万元,预计未来5年内每年末能获得的净收益为30万元。
2008—数一真题、标准答案及解析
2008年全国硕士研究生入学统一考试数学一试题一、选择题:1~8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内。
(1)设函数2()ln(2)x f x t dt =+⎰则()f x '的零点个数( )()A 0()B 1 ()C 2()D 3(2)函数(,)arctanxf x y y=在点(0,1)处的梯度等于( ) ()A i()B -i ()C j()D -j(3)在下列微分方程中,以123cos2sin 2x y C e C x C x =++(123,,C C C 为任意常数)为通解的是( )()A 440y y y y ''''''+--=.()B 440y y y y ''''''+++=.()C 440y y y y ''''''--+=.()D 440y y y y ''''''-+-=.(4)设函数()f x 在(,)-∞+∞内单调有界,{}n x 为数列,下列命题正确的是( )()A 若{}n x 收敛,则{}()n f x 收敛. ()B 若{}n x 单调,则{}()n f x 收敛.()C 若{}()n f x 收敛,则{}n x 收敛.()D 若{}()n f x 单调,则{}n x 收敛.(5)设A 为n 阶非零矩阵,E 为n 阶单位矩阵. 若30A =,则( )()A E A -不可逆,E A +不可逆.()B E A -不可逆,E A +可逆.()C E A -可逆,E A +可逆.()D E A -可逆,E A +不可逆.(6)设A 为3阶实对称矩阵,如果二次曲面方程(,,)1x x y z A y z ⎛⎫ ⎪= ⎪ ⎪⎝⎭在正交变换下的标准方程的图形如图,则A 的正特征值个数为( )()A 0.()B 1. ()C 2.()D 3.(7)设随机变量,X Y 独立同分布且X 分布函数为()F x ,则{}max ,Z X Y =分布函数为( )()A ()2F x .()B ()()F x F y .()C ()211F x --⎡⎤⎣⎦.()D ()()11F x F y --⎡⎤⎡⎤⎣⎦⎣⎦.(8)设随机变量()~0,1X N ,()~1,4Y N 且相关系数1XY ρ=,则( )()A {}211P Y X =--=. ()B {}211P Y X =-=. ()C {}211P Y X =-+=.()D {}211P Y X =+=.二、填空题:9-14小题,每小题4分,共24分,请将答案写在答题纸指定位置上. (9)微分方程0xy y '+=满足条件()11y =的解是y = . (10)曲线()()sin ln xy y x x +-=在点()0,1处的切线方程为 .(11)已知幂级数()02nn n a x ∞=+∑在0x =处收敛,在4x =-处发散,则幂级数()03nn n a x ∞=-∑的收敛域为.(12)设曲面∑是z =的上侧,则2xydydz xdzdx x dxdy ∑++=⎰⎰ .(13)设A 为2阶矩阵,12,αα为线性无关的2维列向量,12120,2A A αααα==+,则A 的非零特征值为 .(14)设随机变量X 服从参数为1的泊松分布,则{}2P X EX == .三、解答题:15-23小题,共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.(15)(本题满分10分)求极限()40sin sin sin sin lim x x x x x →-⎡⎤⎣⎦. (16)(本题满分10分) 计算曲线积分()2sin 221Lxdx xydy +-⎰,其中L 是曲线sin y x =上从点()0,0到点(),0π的一段.(17)(本题满分10分)已知曲线22220:35x y z C x y z ⎧+-=⎨++=⎩,求曲线C 距离XOY 面最远的点和最近的点.(18)(本题满分10分)设()f x 是连续函数,(1)利用定义证明函数()()0xF x f t dt =⎰可导,且()()F x f x '=;(2)当()f x 是以2为周期的周期函数时,证明函数()22()()xG x f t dt x f t dt =-⎰⎰也是以2为周期的周期函数.(19)(本题满分10分)()21(0)f x x x π=-≤≤,用余弦级数展开,并求()1211n n n-∞=-∑的和.(20)(本题满分11分)T T A ααββ=+,T α为α的转置,T β为β的转置.(1)证()2r A ≤;(2)若,αβ线性相关,则()2r A <. (21)(本题满分11分)设矩阵2221212n na a aA a a ⨯⎛⎫⎪⎪= ⎪⎪⎝⎭,现矩阵A 满足方程AX B =,其中()1,,Tn X x x =,()1,0,,0B =,(1)求证()1n A n a =+(2)a 为何值,方程组有唯一解,求1x (3)a 为何值,方程组有无穷多解,求通解(22)(本题满分11分)设随机变量X 与Y 相互独立,X 的概率分布为{}()11,0,13P X i i ===-,Y 的概率密度为()1010Y y f y ≤≤⎧=⎨⎩其它,记Z X Y =+ (1)求102P Z X ⎧⎫≤=⎨⎬⎩⎭(2)求Z 的概率密度.(23)(本题满分11分)设12,,,n X X X 是总体为2(,)N μσ11ni i X X n ==∑,2211()1n ii S X X n ==--∑,221T X S n =- (1)证 T 是2μ的无偏估计量.(2)当0,1μσ==时 ,求DT .2008年全国硕士研究生入学统一考试数学一试题解析一、选择题 (1)【答案】B【详解】2()[ln(2)]2f x x x '=+⋅,(0)0f '=,即0x =是()f x '的一个零点又2224()2ln(2)02x f x x x''=++>+,从而()f x '单调增加((,)x ∈-∞+∞) 所以()f x '只有一个零点. (2)【答案】A【详解】因为2211x y f x y '=+,2221y x y f x y -'=+,所以(0,1)1x f '=,(0,1)0y f '=所以 (0,1)10f =⋅+⋅=grad i j i (3)【答案】D【详解】由微分方程的通解中含有xe 、cos 2x 、sin 2x 知齐次线性方程所对应的特征方程有根1,2r r i ==±,所以特征方程为(1)(2)(2)0r r i r i --+=,即32440r r r -+-=. 故以已知函数为通解的微分方程是40y y y ''''''-+-= (4)【答案】B【详解】因为()f x 在(,)-∞+∞内单调有界,且{}n x 单调. 所以{()}n f x 单调且有界. 故{()}n f x 一定存在极限(5)【答案】C【详解】23()()E A E A A E A E -++=-=,23()()E A E A A E A E +-+=+= 故,E A E A -+均可逆. (6)【答案】B【详解】图示的二次曲面为双叶双曲面,其方程为2222221x y z a b c '''--=,即二次型的标准型为222222x y z f a b c'''=--,而标准型的系数即为A 的特征值.(7)【答案】A【详解】()(){}{}()()()()()2max ,Z Z Z Z F z P Z z P X Y z P X z P Y z F z F z F z =≤=≤=≤≤==(8)【答案】D【详解】 用排除法. 设Y aX b =+,由1XY ρ=,知道,X Y 正相关,得0a >,排除()A 、()C由~(0,1),~(1,4)X N Y N ,得0,1,EX EY ==所以 ()()E Y E aX b aEX b =+=+01,a b ⨯+= 所以1b =. 排除()B . 故选择()D 二、填空题 (9) 【答案】1x 【详解】由dy y dx x -=,两端积分得1ln ln y x C -=+,所以1x C y=+,又(1)1y =,所以1y x =. (10) 【答案】1y x =+【详解】设(,)sin()ln()F x y xy y x x =+--,则1cos()11cos()x y y xy F dy y x dx F x xy y x--'-=-=-'+-,将(0)1y =代入得1x dy dx==,所以切线方程为10y x -=-,即1y x =+(11)【答案】(1,5]【详解】幂级数(2)nn n a x ∞=+∑的收敛区间以2x =-为中心,因为该级数在0x =处收敛,在4x =-处发散,所以其收敛半径为2,收敛域为(4,0]-,即222x -<+≤时级数收敛,亦即nn n a t∞=∑的收敛半径为2,收敛域为(2,2]-. 则(3)nn n a x ∞=-∑的收敛半径为2,由232x -<-≤得15x <≤,即幂级数(3)nn n a x ∞=-∑的收敛域为(1,5] (12)【答案】4π【详解】加221:0(4)z x y ∑=+≤的下侧,记∑与1∑所围空间区域为Ω,则2xydydz xdzdx x dxdy ∑++⎰⎰ 1122xydydz xdzdx x dxdy xydydz xdzdx x dxdy ∑+∑∑=++-++⎰⎰⎰⎰2222222441()0()2x y x y ydxdydz x dxdy x y dxdy Ω+≤+≤=--=++⎰⎰⎰⎰⎰⎰⎰22300142d r dr πθπ==⎰⎰(13)【答案】1【详解】1212121202(,)(,)(0,2)(,)01A A A αααααααα⎛⎫==+=⎪⎝⎭记12(,)P αα=,0201B ⎛⎫= ⎪⎝⎭,则AP PB =因为12,αα线性无关,所以P 可逆. 从而1B P AP -=,即A 与B 相似. 由2||(1)001E B λλλλλ--==-=-,得0λ=及1λ=为B 的特征值.又相似矩阵有相同的特征值,故A 的非零特征值为1. (14)【答案】12e【详解】由22()DX EX EX =-,得22()EX DX EX =+,又因为X 服从参数为1的泊松分布,所以1DX EX ==,所以2112EX =+=,所以 {}21111222P X e e --===!三、解答题(15) 【详解】 方法一:4300[sin sin(sin )]sin sin sin(sin )limlim x x x x x x x x x →→--=22220001sin cos cos(sin )cos 1cos(sin )12lim lim lim 3336x x x xx x x x x x x →→→--==== 方法二:331sin ()6x x x o x =-+ 331sin(sin )sin sin (sin )6x x x o x =-+4444400[sin sin(sin )]sin sin (sin )1lim lim 66x x x x xx o x x x x →→⎡⎤-∴ =+=⎢⎥⎣⎦(16) 【详解】 方法一:(直接取x 为参数将对坐标的曲线积分化成定积分计算)2222220000sin 22(1)[sin 22(1)sin cos ]sin 21cos 2cos 2sin 2sin 222222Lxdx x ydyx x x x dx xxdxx x x x xdx x xdx ππππππππ+-=+-⋅==-+=-+-=-⎰⎰⎰⎰⎰方法二:(添加x 轴上的直线段用格林公式化成二重积分计算)取1L 为x 轴上从点(,0)π到点(0,0)的一段,D 是由L 与1L 围成的区域112220sin 2000022000sin 22(1)sin 22(1)sin 22(1)14sin 24cos 22sin 21(1cos 2)sin 2sin 22222LL L L xDxdx x ydyxdx x ydy xdx x ydyxydxdy xdx dx xydy x x xdx x x x x dx x xdx πππππππππ++-=+--+-=--=--=-=--=-+-=-⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰方法三:(将其拆成2sin 222LLxdx ydy xydy -+⎰⎰,前者与路径无关,选择沿x 轴上的直线段积分,后者化成定积分计算)2212sin 22(1)sin 222LLLxdx x ydy xdx ydy x ydy I I +-=-+=+⎰⎰⎰对于1I ,因为0P Qy x∂∂==∂∂,故曲线积分与路径无关,取(0,0)到(,0)π的直线段积分10sin 20I xdx π==⎰2222202200022122sin cos sin 2cos 221111cos 22cos 2sin 222221111sin 2cos 22222LI x ydy x x xdx x xdx x d x x x x xdx xd xx x x ππππππππππ====-=-+=-+⎡⎤=-++=-⎢⎥⎣⎦⎰⎰⎰⎰⎰⎰所以,原式212π=-(17) 【详解】点(,,)x y z 到xOy 面的距离为||z ,故求C 上距离xOy 面的最远点和最近点的坐标,等价于求函数2H z =在条件22220x y z +-=与35x y z ++=下的最大值点和最小值点.令 2222(,,,,)(2)(35)L x y z z x y z x y z λμλμ=++-+++-所以 22220(1)20(2)2430(3)20(4)35(5)xy zL x L y L z z x y z x y z λμλμλμ'=+=⎧⎪'=+=⎪⎪'=-+=⎨⎪+-=⎪++=⎪⎩ 由(1)(2)得x y =,代入(4)(5)有 220235x z x z ⎧-=⎨+=⎩,解得555x y z =-⎧⎪=-⎨⎪=⎩ 或111x y z =⎧⎪=⎨⎪=⎩(18)【详解】(I) 对任意的x ,由于f 是连续函数,所以0000()()()()limlim x xxx x f t dt f t dtF x x F x xx+→→-+-=⎰⎰0()()limlimlim ()x x xx x x f t dt f xf xxξξ+→→→===⎰ ,其中ξ介于x 与x x +之间 由于0lim ()()x f f x ξ→=,可知函数()F x 在x 处可导,且()()F x f x '=.(II)方法一:要证明()G x 以2为周期,即要证明对任意的x ,都有(2)()G x G x +=,()(2)()H x G x G x =+-,则()()()()()()()()22222()2(2)22(2)2()0x x H x f t dt x f t dt f t dt x f t dtf x f t dt f x f t dt +'''=-+--=+--+=⎰⎰⎰⎰⎰⎰又因为 ()()()22(0)(2)(0)2200H G G f t dt f t dt =-=--=⎰⎰所以 ()0H x =,即(2)()G x G x +=方法二:由于f 是以2为周期的连续函数,所以对任意的x ,有()()()()222(2)()2(2)2x x G x G x f t dt x f t dt f t dt x f t dt ++-=-+-+⎰⎰⎰⎰()()()()2222002x xf t dt f t dt f t dt f t dt +⎡⎤=+--⎢⎥⎣⎦⎰⎰⎰⎰()()()()000222[2]0x x xf t dt f u du f t f t dt ⎡⎤=-++=+-=⎢⎥⎣⎦⎰⎰⎰ 即()G x 是以2为周期的周期函数.(19)【详解】 由于 220022(1)23a xdx πππ=-=-⎰21224(1)cos (1)1,2,n n a x nxdx n n ππ+=-=- =⎰所以 210211(1)()cos 14cos 023n n n n a f x a nx nx x n ππ+∞∞==-=+=-+ ≤≤∑∑令0x =,有 2121(1)(0)143n n f n π+∞=-=-+ ∑ 又(0)1f =,所以 1221(1)12n n n π+∞=- =∑ (20)【详解】(I) ()()()()()()2T T T T r A r r r r r ααββααββαβ=+≤+≤+≤(II) 由于,αβ线性相关,不妨设k αβ=. 于是()2()()(1)()12T T T r A r r k r ααβββββ=+=+≤≤<(21)【详解】(I)证法一:2222122212132101221221122aa a a a a aa aA r ar aaa a =-=121301240134(1)2(1)3231(1)0n n n a a a n a a n ar ar a n a nnn a n--+-=⋅⋅⋅=++ 证法二:记||n D A =,下面用数学归纳法证明(1)n n D n a =+. 当1n =时,12D a =,结论成立. 当2n =时,2222132a D a a a==,结论成立. 假设结论对小于n 的情况成立.将n D 按第1行展开得2212102121212n n a a a aD aD a a-=-21221222(1)(1)n n n n n aD a D ana a n a n a ---- =-=--=+故 ||(1)n A n a =+证法三:记||n D A =,将其按第一列展开得 2122n n n D aD a D --=-, 所以 211212()n n n n n n D aD aD a D a D aD ------=-=-222321()()n n n n a D aD a D aD a ---=-==-=即 12122()2n n n n n n n n D a aD a a a aD a a D ----=+=++=++2121(2)(1)n n n n n a a D n a a D --==-+=-+1(1)2(1)n n n n a a a n a -=-+⋅=+(II)因为方程组有唯一解,所以由Ax B =知0A ≠,又(1)nA n a =+,故0a ≠.由克莱姆法则,将n D 的第1列换成b ,得行列式为2221122(1)(1)112102121221122n n n nn n a aa a a aa aD na a a a a --⨯-⨯-===所以 11(1)n n D nx D n a-==+ (III)方程组有无穷多解,由0A =,有0a =,则方程组为12101101001000n n x x x x -⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 此时方程组系数矩阵的秩和增广矩阵的秩均为1n -,所以方程组有无穷多解,其通解为 ()()10000100,T Tk k +为任意常数.(22)【详解】 (I) 1201(0,)11112(0)(0)()122(0)22P X Y P Z X P X Y X P Y dy P X =≤≤==+≤===≤===⎰ (II) (){}{}Z F z P Z z P X Y z =≤=+≤{,1}{,0}{,1}P X Y z X P X Y z X P X Y z X =+≤=-++≤=++≤= {1,1}{,0}{1,1}P Y z X P Y z X P Y z X =≤+=-+≤=+≤-={1}{1}{}{0}{1}{1}P Y z P X P Y z P X P Y z P X =≤+=-+≤=+≤-= []1{1}{}{1}3P Y z P Y z P Y z =≤++≤+≤- []1(1)()(1)3Y Y Y F z F z F z =+++- 所以 []1()(1)()(1)3Z Y Y Y f z f z f z f z =+++-1,1230,z ⎧-≤<⎪=⎨⎪⎩其它(23) 【详解】(I) 因为2(,)X N μσ,所以2(,)X N n σμ,从而2,E X DX n σμ= =. 因为 221()()E T E X S n =-221()E X E S n=- 221()()DX E X E S n =+-222211n nσμσμ=+-= 所以,T 是2μ的无偏估计(II)方法一:22()()D T ET ET =-,()0E T =,22()1E S σ==所以2()D T ET =442222()S E X X S n n =-⋅+ 4224221()()()()E X E X E S E S n n=-+ 因为(0,1)X N ,所以1(0,)X N n, 有10,E X D X n ==,()221E X DX E X n =+=所以2242222()()()()()E X D X E X D D X E X⎡⎤=+=++⎣⎦ 2221()D D X n ⎡⎤=+⎣⎦2221132n n n ⎛⎫=⋅+= ⎪⎝⎭ ()2422222()1ES E S DS ES DS ⎡⎤==+=+⎢⎥⎣⎦因为2222(1)(1)(1)n S W n S n χσ-==--,所以2(1)DW n =-,又因为22(1)DW n DS =-,所以22(1)DS n =-,所以4211(1)1n ES n n +=+=-- 所以 2223211111n ET n n n n n +=-⋅⋅+⋅-2(1)n n =-. 方法二:当0,1μσ==时221()()D T D X S n=- (注意X 和2S 独立) 222222221111(1)(1)DX DS D D n S n n n n ⎡⎤=+=+⋅-⎣⎦- 222111222(1)(1)(1)n n n n n n =⋅+⋅⋅-=--。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
应用数学题库1-0-8
问题:
[单选]在数据处理过程中,人们常用“四舍五入”法取得近似值。
对于统计大量正数的平均值而言,从
统计意义上说,“四舍五入”对于计算平均值()
A.不会产生统计偏差
B.产生略有偏高的统计偏差
C.产生略有偏低的统计偏差
D.产生忽高忽低结果,不存在统计规律
从统计意义上说,正数的分布是随机的。
而计算平均值而言,其最后的结果是“入”还是“舍”,也是随机的。
就最后取舍的某一位而言,就是0~9之间的10位数字,对于0、1、2、3、4采取“舍”,对实际的数据影响是0、-1、-2、-3、-4。
对于5、6、7、8、9采取“入”,对实际的数据影响是+5、+4、+3、+2、+1。
因为各位数字出现的情况是等概率的,因此“入”的影响要大于“舍”的影响,所以,对于计算
正数平均值而言,会产生略有偏高的统计结果。
问题:
[单选]图18-11标出了某地区的运输网。
各结点之间的运输能力如表18-6(单位:万吨小时)。
从结点
①到结点⑥的最大运输能力(流量)可以达到()万吨/小时。
A.26
B.23
C.22
D.21
问题:
[单选]某学院10名博士生(B1~B10)选修6门课程(A~F)的情况如表18-7所示(用√表示选修)。
现需要安排这6门课程的考试,要求是:
(1)每天上、下午各安排一门课程考试,计划连续3天考完。
(2)每个博士生每天只能参加一门课程考试,在这3天内考完全部选修课。
(3)在遵循上述两条的基础上,各课程的考试时间应尽量按字母升序做先后顺序安排(字母升序意味着课程难度逐步增加)。
为此,各门课程考试的安排顺序应是()
A.AE,BD,CF
B.AC,BF,DE
C.AF,BC,DE
D.AE,BC,DF
首先,我们直接从来考虑问题。
可以根据试题的限制条件:“每个博士生每天只能参加一门课程考试,在这3天内考完全部选修课”,来进行判断各选项是否满足。
如果按照A选项,第2天考BD,则因为B1同时选修了这2门课程,将违反“每个博士生每天只能参加一门课程考试”的约束。
如果按照B选项,第1天考AC,则因为B2同时选修了这2门课程,将违反“每个博士生每天只能参加一门课程考
试”的约束。
如果按照c选项,第1天考AF,则因为B3同时选修了这2门课程,将违反“每个博士生每天只能参加一门课程考试”的约束。
因此,只有选项D符合要求。
下面再介绍另外一种解法(图示法)。
将6门课程作为6个结点画出,如图18-14所示。
我们可以在两个课程结点之间画连线表示他们不可以在同一天安排考试,那么,每个博士生的各门选修课程之间都应画出连线。
例如,B1博士生选修了A、B、D三门课程,则ABD之间都应有连线,表示这三门课中的任何二门都不能安排在同一天。
从图18-14可以看出,能够安排在同一天考试的课程(结点之间没有连线)有AE、BC、DE、DF。
因此,课程A必须与课程E安排在同一天。
课程B必须与课程C安排在同一天,余下的课程D只能与课程F安排在同一天。
出处:森林舞会游戏 https://;
问题:
[单选]A、B两个独立的网站都主要靠广告收入来支撑发展,目前都采用较高的价格销售广告。
这两个网站都想通过降价争夺更多的客户和更丰厚的利润。
假设这两个网站在现有策略下各可以获得1000万元的利润。
如果一方单独降价,就能扩大市场份额,可以获得1500万元利润,此时,另一方的市场份额就会缩小,利润将下降到200万元。
如果这两个网站同时降价,则他们都将只能得到700万元利润。
这两个网站的主管各自经过独立的理性分析后决定()
A.A采取高价策略,B采取低价策略
B.A采取高价策略,B采取高价策略
C.A采取低价策略,B采取低价策略
D.A采取低价策略,B采取高价策略
这是一个简单的博弈问题,可以表示为图18-15所示的得益矩阵。
由图18-15可以看出,假设B网站采用高价策略,那么A网站采用高价策略得1000万元,采用低价策略得1500万元。
因此,A网站应该采用低价策略。
如果B网站采用低价策略,那么A网站采用高价策略得200万元,采用低价策略得700万元,因此A网站也应该采用低价策略。
采用同样的方法,也可分析B网站的情况,也就是说,不管A 网站采取什么样的策略,B网站都应该选择低价策略。
因此,这个博弈的最终结果一定是两个网站都采用低价策略,各得到700万元的利润。
这个博弈是一个非合作博弈问题,且两博弈方都肯定对方会按照个体行为理性原则决策,因此虽然双方采用低价策略的均衡对双方都不是理想的结果,但因为两博弈方都无法信任对方,都必须防备对方利用自己的信任(如果有的话)谋取利益,所以双方都会坚持采用低价,各自得到700万元的利润,各得1000万元利润的结果是无法实现的。
即使两个网站
都完全清楚上述利害关系,也无法改变这种结局。
问题:
[单选]博学公司项目经理向客户推荐了四种供应商选择方案。
每个方案损益值已标在图18-16的决策树上。
根据预期收益值,应选择设备供应商()
A.1
B.2
C.3
D.4
本题考查决策树的使用,利用决策树来进行决策的方法属于风险型决策,我们只要直接计算出各分支的预期收益值,然后选择其中一个最大的值就可以了。
设备供应商1的预期收益值:100000×60%+(-30000)×40%=60000-12000=48000。
设备供应商2的预期收益值:50000×90%+(-10000)×10%=45000-1000=44000。
设备供应商3的预期收益值:10000×99%+(-1000)×1%=9900-10=9890。
设备供应商4的预期收益值:20000×80%+(-10000)×20%=16000-2000=14000。
设备供应商1的预期收益值最大,因此应该选择设备供应商1。
问题:
[单选]如图9-7所示为某地区的运输网。
各节点之间的运输能力如表9-7所示(单位:万吨小时):从节点①到节点⑥的最大运输能力(流量)可以达到()万吨小时。
A.26
B.23
C.22
D.21
为了便于计算,我们把表9-7的数据标记到图9-7上,形成图9-8。
从图9-8中可以看出,只能从节点④和⑤到达到节点⑥,其运输能力为26。
而只能从节点②和③到达节点⑤,且能满足最大运输量
21(14+7)。
但是,到达节点③的最大数量为11(10+1),因此,节点⑤的最终输出能力为18,即从节点①到节点⑥的最大运输能力为23。
最终的运输方案如图9-9所示。
问题:
[单选]评估和选择最佳系统设计方案时,甲认为可以采用点值评估方法,即根据每一个价值因素的重要性,综合打分来选择最佳的方案。
乙根据甲的提议,对如表9-8所示的系统A和B进行评估,那么乙认为()
A.最佳方案是A
B.最佳方案是B
C.条件不足,不能得出结论
D.只能用成本效益分析方法做出判断
点值评估方法将根据每一个价值的重要性为其指定一个加权值(以百分数表示),然后用每个因素来评估每一个候选的信息系统方案,得到一个等级分,范围为0~100,其中0分表示候选方案根本没有达到价值因素的要求,100分表示该候选方案完全达到了价值因素的要求。
将每个候选系统的各个价值因素的得分累加,总分最佳的候选方案为最佳选择。
根据题目给出的表,相对于硬件(35%)和供应商支持(25%),软件这一因素被赋予最大的权重(40%),系统A的得分是82.5,系统B的得分是86.75(更接近100),所以B是最佳方案。
问题:
[单选]某企业拟进行电子商务系统的建设,有4种方式可以选择:
①企业自行从头开发;
②复用已有的构件来构造;
③购买现成的软件产品;
④承包给专业公司开发。
针对这几种方式,项目经理提供了如图9-10所示的决策树,根据此图,管理者选择建设方式的最佳决策是()
A.企业自行从头开发
B.复用已有的构件来构造
C.购买现成的软件产品
D.承包给专业公司开发
在软件应用领域,直接获取(购买)计算机软件常常比自行开发的成本要低得多。
软件工程管理者面临着做出自行开发还是购买的决策问题,而且由于存在多种可选的获取方案使得决策更加复杂。
这些决策包括:从头开始构造系统;复用已有的"具有部分经验"的构件来构造系统;购买现在的开发
软件,并进行修改已满足当前项目的需要;将软件开发承包给外面的开发商。
可以采用决策树分析来帮助管理者进行决策,题目给的图中路径上的数字是出现该情况的概率,树叶金额是出现该情况的成本,成本的期望值=∑(路径概率)×(估算的路径成本),其中i是决策树的某条路径。
经过计算可知,采用购买方式预期方式预期成本最低,因此管理者选择建设方式的最佳决策是购买现成的软件产品。
