振动与波习题课及课后作业解答
大学物理振动与波练习题与答案
【解】:(1) y 5cos(20 4x) 厘米
(2) y 5cos(3t 11) 厘米
(3) y 5cos3(t 4 x 5) , c 3 (cm/ s)
33
4
(4) y 5cos(3t 9) , yI 15 sin(3t 9) 0
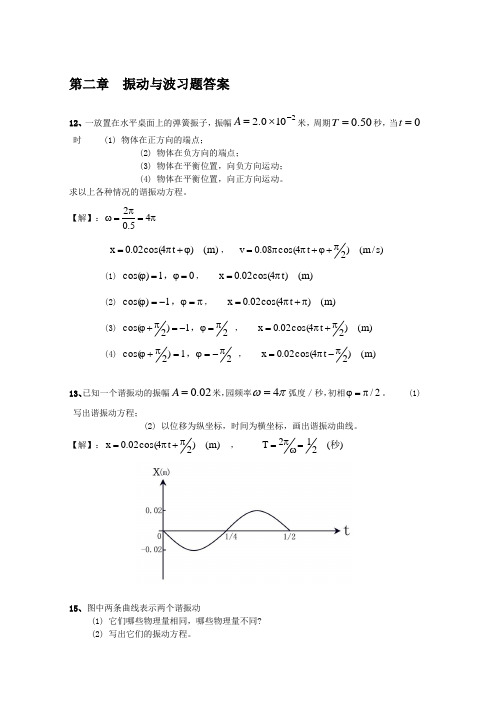
23、一平面简谐波沿 x 轴正方向传播,波速 c=8 m/s, 若 t=0 时的波形曲线如图 2-23 所示 (1)写出波动方程 (2)画出 t=1.25 s 时的波形曲线 【解】:
t=0 时,y=0, v>0 cm T=5s
所以 2 。 波长= 40
y 4.0 cos[0.4t ] (cm) 2
B 点的振动方程
yA
(t)
5 c os [10
(t
20) 300
2
]
5 c os (10t
7 6
)cm
(2)
A,B 相位相同
(3) 或 O 点的振动方程
yo
(t)
5
cos(10t
2
)
(cm)
O 点相位
o
2
OB,OA 间的相位差
oA
oB
2 3
O 比 A 超前
oA
o
A
2 3
A
7 6
同时 B 点
13、已知一个谐振动的振幅 A 0.02 米,园频率 4 弧度/秒,初相 / 2 。 (1)
写出谐振动方程; (2) 以位移为纵坐标,时间为横坐标,画出谐振动曲线。
【解】: x 0.02cos(4 t 2) (m) ,
T
2
1 2
大学物理 第5章 振动和波动习题解答

第5章 振动和波动5-1 解:(1))s rad (105.050===m kωmax 222max 100.040.4(m/s)100.044(m/s )v A a A ωω==⨯===⨯=(2) 设cos()x A t ωϕ=+,则d sin()d xv A t tωωϕ==-+ 2222d cos()d x a A t x t ωωϕω==-+=-当x=0.02m 时,cos()1/2,sin()3/2t t ωϕωϕ+=+=±,所以20.230.346(m/s)2(m/s )1(N)v a F ma =⨯==-==-(3) 作旋转矢量图,可知:π2ϕ=-π0.04c o s (10)2x t =-5 解:A=0.04(m) 0.7(rad/s)0.3(rad)10.11(Hz)8.98(s)2πT ωϕωνν==-====5-3 证明:如图所示的振动系统的振动频率为1212πk k mυ+=式中12,k k 分别为两个弹簧的劲度系数,m为物体的质量。
解: 以平衡位置为坐标原点,水平向右为x 轴正方向。
设物体处在平衡位置时,弹簧1的伸长量为10x ,弹簧2的伸长量为20x ,则应有0202101=+-x k x k当物体运动到平衡位置的位移为x 处时,弹簧1的伸长量就为x x +10,弹簧2的伸长量就为x x -20,所以物体所受的合外力为11022012()()()F k x x k x x k k x =-++-=-+由牛顿第二定律得 2122d ()d xm k k x t =-+即有 2122()d 0d k k x x t m++=上式表明此振动系统的振动为简谐振动,且振动的圆频率为12k k x mω+=振动的频率为 1212π2πk k mων+==5-4解:以平衡时右液面位置为坐标原点,向上为x 轴正方向,建立坐标系。
右液面偏离原点为至x 时,振动系统所受回复力为:22ππ242d d g F x g x ρρ=-⋅⋅=-振动角频率 2π2d gm ρω=振动周期 222ππmT d gρ=5-5解:弹簧、滑轮、物体和地球组成的系统不受外力作用,非保守内力作功之和为零,系统机习题5-4 图械能守恒,以物体的平衡位置为坐标原点向下为x 轴正方向,建立坐标系。
振动与波练习(题目与解答)
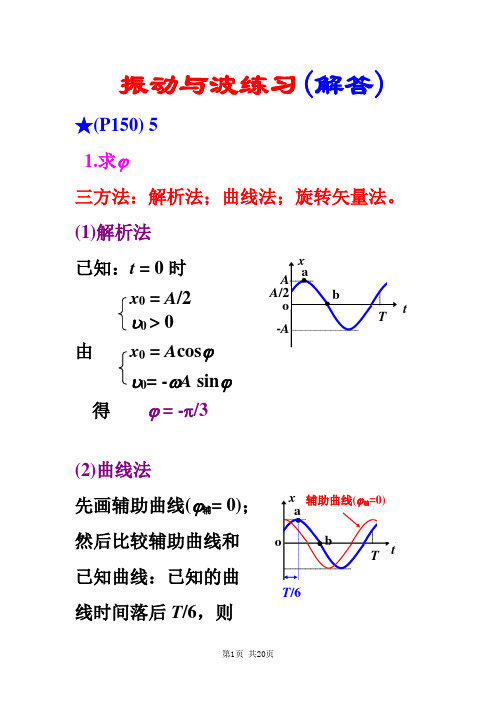
振动与波练习(解答) ★(P150) 51.求ϕ三方法:解析法;曲线法;旋转矢量法。
(1)解析法已知:t = 0时x0 = A/2υ0 > 0由x0 = A cosϕυ= -ωA sinϕ得ϕ = -π/3(2)曲线法先画辅助曲线(ϕ辅= 0)然后比较辅助曲线和已知曲线:已知的曲线时间落后T/6,则位相落后π/3,故已知振动的初相ϕ = -π/3(3)旋转矢量法由图ϕ = -π/3。
2.求a、b点的位相·a点:ξa = A;υa = 0,可得位相= 0。
·b点:ξb = 0;υb = -ωA,可得位相= π/2。
由解析法亦可。
3.求从t = 0到a、b两态的时间由旋转矢量图知,·从t = 0到a态,矢量转过π/3,故∆t a = T/6·从t = 0到b态,矢量转过π/3 + π/2,故 ∆t b = 5T /12 ★ (动力学解题两方法:受力法;能量法。
1.受力法:分析物体在任一位置时受力对m对轮 TR - fR = J β (2) 另 f = k ( y 0 + y ) f 0 = k y 0 = mg a = β Rd 2y d t 2 mg - T = m (1)可得说明振动是SHM ,其角频率为2.能量法:分析物体在任一位置时系统的能量。
·势能零点:平衡位置。
· 两边求导,并用 k y 0 = mg ;υ = ω角R , 可得d t 2 + ( ) y = 0 d 2ykR 2J + mR 2kR 2J + mR 2 ω = √m ( )2 + J ω角2 - m gy+ k (y 0+ y )2 = const.d y d t1 2 1 2 12d t 2 + ( ) y = 0 d 2y kR 2J + mR 2★(P151) 7 用能量法· 势能零点:平衡位置。
· 势能:(ρSy )gy · 系统能量:·两边求导,得 ·角频率为L 为液体总长度,m = ρSLyd y d tm ( )2+ ρS gy 2 = const. 1 2 d t 2 + ( ) y = 0d 2y 2ρSgm 2ρSg m ω = √ 2gL=√★(P160) 2已知x = 0处质元(波源)的振动曲线t(s)此曲线初相= ?1.画x = 25m处质元的振动曲线·由图T = 4 s ;知λ = uT = 20m·x = 0处质元的初相ϕo = - π/2·x = 25m处质元的初相x = 25m处质元的位相比x = 0处质元的落后多少?∆ϕ = k⋅25 = 2.5π,(波数k = 2π/λ = π/10) x = 25m处质元的初相ϕ 25 = - 3π = - π·x = 25m处质元也可先列出振动表达式再画振动曲线:·x = 0处质元(波源)的振动表达式ξ(0, t) = 2 cos(ωt - π/2) cm·x = 25m处质元的振动表达式ξ(25, t) = 2 cos(ωt - π/2- k⋅25) cm= 2 cos(ωt - 3π) cm= 2 cos(ωt - π) cm由此也可画x = 25m处质元的振动曲线。
第5章 振动和波动课后答案

第5章振动和波动5-1一个弹簧振子0.5kg m =,50N m k =,振幅0.04m A =,求 (1)振动的角频率、最大速度和最大加速度;(2)振子对平衡位置的位移为x =0.02m 时的瞬时速度、加速度和回复力; (3)以速度具有正的最大值的时刻为计时起点,写出振动方程。
解:(1))s rad (105.050===m kω(2) 设当(3) 5-2解:ν=5-3式中1,k10x ,弹簧2所受的合外力为由牛顿第二定律得2122d ()d xm k k x t =-+即有2122()d 0d k k x x t m++= 上式表明此振动系统的振动为简谐振动,且振动的圆频率为振动的频率为2πων==5-4如图所示,U 形管直径为d ,管内水银质量为m ,密度为ρ,现使水银面作无阻尼自由振动,求振动周期。
振动周期5-55-6如图所示,轻弹簧的劲度系数为k ,定滑轮的半径为R 、转动惯量为J ,物体质量为m ,将物体托起后突然放手,整个系统将进入振动状态,用能量法求其固有周期。
习题解:设任意时刻t ,物体m 离平衡位置的位移为x ,速率为v ,则振动系统的总机械能 式中于是5-7已知5-8平衡位置距O '点为:000l x l k+=+以平衡位置为坐标原点,如图建立坐标轴Ox ,当物体运动到离开平衡位置的位移为x 处时,弹簧的伸长量就是x x +0,所以物体所受的合外力为物体受力与位移成正比而反向,即可知物体做简谐振动国,此简谐振动的周期为5-9两质点分别作简谐振动,其频率、振幅均相等,振动方向平行。
在每次振动过程中,它们在经过振幅的一半的地方时相遇,而运动方向相反。
求它们相差,并用旋转矢量图表示出来。
习题5-6图解:根据题意,两质点分别在2A x =和2Ax -=处相向通过,由此可以画出相应的旋转矢量图,从旋转矢量图可得两个简谐振动的相位差为π34π或32==ϕϕ∆∆5-10一简谐振动的振幅A =24c m、周期T =3s ,以振子位移x =12cm 、并向负方向运动时为计时起点,作出振5-11(1)x (2)x当以(1)x 轴正向向上时:πϕ=-=)(01.00m x振动方程为))(1010cos(01.0m t x π+= (2)x 轴正向向下时:0)(01.00==ϕm x振动方程为))(1010cos(01.0m t x =5-12劲度系数为k 的轻弹簧,上端与质量为m 的平板相联,下端与地面相联。
大学物理习题及解答(振动与波、波动光学)

1. 有一弹簧,当其下端挂一质量为m 的物体时,伸长量为9.8 ⨯10-2 m 。
假如使物体上下振动,且规定向下为正方向。
〔1〕t =0时,物体在平衡位置上方8.0 ⨯10-2 m处,由静止开始向下运动,求运动方程。
〔2〕t = 0时,物体在平衡位置并以0.60m/s 的速度向上运动,求运动方程。
题1分析:求运动方程,也就是要确定振动的三个特征物理量A 、ω,和ϕ。
其中振动的角频率是由弹簧振子系统的固有性质〔振子质量m 与弹簧劲度系数k 〕决定的,即m k /=ω,k 可根据物体受力平衡时弹簧的伸长来计算;振幅A 和初相ϕ需要根据初始条件确定。
解:物体受力平衡时,弹性力F 与重力P 的大小相等,即F = mg 。
而此时弹簧的伸长量m l 2108.9-⨯=∆。
如此弹簧的劲度系数l mg l F k ∆=∆=//。
系统作简谐运动的角频率为1s 10//-=∆==l g m k ω〔1〕设系统平衡时,物体所在处为坐标原点,向下为x 轴正向。
由初始条件t = 0时,m x 210100.8-⨯=,010=v 可得振幅m 100.8)/(2210102-⨯=+=ωv x A ;应用旋转矢量法可确定初相πϕ=1。
如此运动方程为])s 10cos[()m 100.8(121π+⨯=--t x〔2〕t = 0时,020=x ,120s m 6.0-⋅=v ,同理可得m 100.6)/(22202022-⨯=+=ωv x A ,2/2πϕ=;如此运动方程为]5.0)s 10cos[()m 100.6(122π+⨯=--t x2.某振动质点的x -t 曲线如下列图,试求:〔1〕运动方程;〔2〕点P 对应的相位;〔3〕到达点P 相应位置所需要的时间。
题2分析:由运动方程画振动曲线和由振动曲线求运动方程是振动中常见的两类问题。
此题就是要通过x -t 图线确定振动的三个特征量量A 、ω,和0ϕ,从而写出运动方程。
曲线最大幅值即为振幅A ;而ω、0ϕ通常可通过旋转矢量法或解析法解出,一般采用旋转矢量法比拟方便。
振动和波课后习题答案

− kxc − f = mxc
(1)
fR = (1 mR2 )θ = 1 mR2 xc
2
2R
(2)
由(2)式可得
f
=
1 2 mxc
代入(1)式得:
−
kxc
−
1 2
mxc
=
mxc
推出
3 2
mxc
+
kxc
=
0
k
m
题 6.9 图
ω = 2k 3m
6.10 如题 6.10 图所示,弹簧的倔强系数为 k,定滑轮的质量为 m’,半径为 R,转动惯量为 I,物体的质量为 m。轴处摩擦不计,弹簧和绳的质量也不计,绳与滑轮间无相对滑 动。(1)试求这一振动系统的振动频率,(2)如果在弹簧处于原长时由静止释放物体 m,m 向下具有最大速度时开始计时,并令 m 向下运动为 x 的正坐标,试写出 m 的振 动表达式。
2
2
(4) < Ek
>=< E p
>=
E 2
=
1 KA2 4
=
1 mω 2A2 4
=
4 ×10−6π 2 (J )
ห้องสมุดไป่ตู้
(5) t = 0.1s 时,ϕ = 8π + π = 25 π ; 33
t = 10s 时,ϕ = 80π + π = 241π 。 33
6.14 在阻尼振动中,量τ = 1 叫做弛豫时间。(1)证明 τ 的量纲是时间;(2)经过时间 τ δ
∵ m1 x1 = m2 x2
x
=
m1 + m2 m2
x1
Δx1 + Δx2 = Δx
mm1
振动和波动课后答案

精心整理第5章 振动和波动5-1 一个弹簧振子0.5kg m =,50N m k =,振幅0.04m A =,求 (1) 振动的角频率、最大速度和最大加速度;(2) 振子对平衡位置的位移为x = 0.02m 时的瞬时速度、加速度和回复力;(2) (3) 解:式中解: 以平衡位置为坐标原点,水平向右为x 轴正方向。
设物体处在平衡位置时,弹簧1的伸长量为10x ,弹簧2的伸长量为20x ,则应有当物体运动到平衡位置的位移为x 处时,弹簧1的伸长量就为x x +10,弹簧2的伸长量就为x x -20,所以物体所受的合外力为由牛顿第二定律得 2122d ()d xm k k x t =-+即有 2122()d 0d k k x x t m++= 上式表明此振动系统的振动为简谐振动,且振动的圆频率为 振动的频率为 1212π2πk k mων+== 5-4 如图所示,U 形管直径为d ,管内水银质量为m ,密度为ρ,现使水银面作无阻尼自由振动,求振动周期。
解:以平衡时右液面位置为坐标原点,向上为x 轴正方向,建立坐标系。
右液面偏离原点为至x 时,振动系统所受回复力为:振动角频率 2π2d gmρω=振动周期 222ππmT d gρ= 5-5 如图所示,定滑轮半径为R ,转动惯量为J ,轻弹簧劲度系数为k ,物体质量为m ,现将物体从平衡位置拉下一微小距离后放手,不计一切摩擦和空气阻力。
试证明该系统作简谐振动,并求其作微小振动的周期。
习题5-4解:弹簧、滑轮、物体和地球组成的系统不受外力作用,非保守内力作功之和为零,系统机械能守恒,以物体的平衡位置为坐标原点向下为x 轴正方向,建立坐标系。
设平衡时弹簧伸长0l ,有:0kl mg = (1) 物体位于x 位置时(以原点为重力势能零点): 对上式两边求导:,物体械能于是ω=5-7如图所示,质量为10g的子弹,以01000m sv=速度射入木块并嵌在木块中,使弹簧压缩从而作简谐运动,若木块质量为4.99kg,弹簧的劲度系数为3810N m⨯,求振动的振幅。
机械振动和波习题及解答.

(1)波的波速、频率和波长; (2)绳子上各质点振动时的最大速度和最大加速度; (3)求=0.2m 处质点在=1s时的位相,它是原点在哪一时刻的位相?这一 位相所代表的运动状(SI).
(1)写出=4.2 s时各波峰位置的坐标式,并求此时离原点最近一个波峰 的位置,该波峰何时通过原点? (2)画出=4.2 s时的波形曲线.
机械振动和波习题
4-4 质量为的小球与轻弹簧组成的系统,按的规律作谐振动,求: (1)振动的周期、振幅和初位相及速度与加速度的最大值; (2)最大的回复力、振动能量、平均动能和平均势能,在哪些位置上动 能与势能相等? (3)与两个时刻的位相差; 4-7 有一轻弹簧,下面悬挂质量为的物体时,伸长为.用这个弹簧和 一个质量为的小球构成弹簧振子,将小球由平衡位置向下拉开后 ,给 予向上的初速度,求振动周期和振动表达式. 4-8 图为两个谐振动的曲线,试分别写出其谐振动方程.
(3)因任一时刻同一波线上两点之间的位相差为
将,及代入上式,即得 .
5-9 沿绳子传播的平面简谐波的波动方程为=0.05cos(10),式中,以米
计,以秒计.求: (1)波的波速、频率和波长; (2)绳子上各质点振动时的最大速度和最大加速度; (3)求=0.2m 处质点在=1s时的位相,它是原点在哪一时刻的位相?这一 位相所代表的运动状态在=1.25s时刻到达哪一点? 解: (1)将题给方程与标准式
题图
5-17 一平面余弦波,沿直径为14cm的圆柱形管传播,波的强度为
18.0×10-3J·m-2·s-1,频率为300 Hz,波速为300m·s-1,求 : (1)波的平均能量密度和最大能量密度? (2)两个相邻同相面之间有多少波的能量?
机械振动和波习题及解答
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
π
2π
λ
2OB π = 5π
2π
= 入 反 = π
λ
x (5π +
2π
λ
x) = 6π
4π
2kπ , 波腹 = (2k + 1)π , 波节
0≤x≤1.25λ ≤ ≤ λ
λ
x
3. 空气中声速为 空气中声速为340m/s, 一列车以 一列车以72km/h的速度行驶 车上旅客 的速度行驶, 的速度行驶 听到汽笛声频率为360Hz, 则目送此火车离去的站台上的旅客听到 听到汽笛声频率为 此汽笛声的频率为( 此汽笛声的频率为 B) (A) 360Hz (B) 340Hz (C) 382.5Hz (D) 405Hz 解:
t = ( / 2π )T = T / 12 6
A/2 -π/3
π
ω
x
A
2. 如图为用余弦函数表示的一质点作谐振动曲线 振动圆频率 如图为用余弦函数表示的一质点作谐振动曲线, ,从初始状态到达状态 所需时间为 2s 从初始状态到达状态a所需时间为 . 为 7π/6 π 从初始状态到达状态 分析: 分析:本题的关键是确定各时刻 X(m) 6 的位相, 的位相,在振动曲线上由位移和 3 速度方向(斜率的正负) 速度方向(斜率的正负)定 0 t=0时: -3 X0=A/2,v0<0 = π/3 t=1时: X=0,v>0 ωt+= 3π/2
u vs
s
u = 334m s 1 (3)
u v0 ( 4) λ ′ = ν′ 334 65 = = 0.190m 1418
ω
t = 0, v0 = ωA sin 0 = 10cm / s
3 ∴0 = π 2
3 ∴ x = 2 cos(5t + π )cm 2
波动三(46) 波动三 1. 某时刻驻波波形曲线如图所示 则a,b两的位相差是 ) 某时刻驻波波形曲线如图所示, 两的位相差是(A 两的位相差是 (A) π (B) π/2 (C) π/4 (D) 0 两波节之间的点同相,一个波节两侧的点反相. 两波节之间的点同相,一个波节两侧的点反相.
π
5. 劲度为 1的轻弹簧与劲度为 2的弹簧如图连接 在K2 的下端挂 劲度为K 的轻弹簧与劲度为K 的弹簧如图连接, 一质量为m的物体 的物体, 证明当m在竖直方向发生微小位移后 在竖直方向发生微小位移后, 一质量为 的物体 (1) 证明当 在竖直方向发生微小位移后 系统 作谐振动. 作谐振动. (2) 将m从静止位置向上移动 然后释放任其运动 写出振动方程 从静止位置向上移动a, 从静止位置向上移动 然后释放任其运动, (取物体开始运动为计时起点 X轴向下为正方向 取物体开始运动为计时起点, 轴向下为正方向) 取物体开始运动为计时起点 轴向下为正方向
v 0 = 65m s 1 u = 334m s 1
(1)声源运动的前方 声源运动的前方: 声源运动的前方 u vs 334 30 λ1 = = = 0.281m ν 1080 声源运动的后方: 声源运动的后方 u + vs 334 + 30 λ2 = = = 0.337 m ν 1080
334 + 65 = × 1080 = 1418 Hz 334 30
vm=0.8π=2.51m/s am=6.4π2=63.1m/s2
k = mω 2 = 0.1× (8π ) 2 = 63.1N / m
Fm=kA=6.31N
1 2 E = kA = 0.316 J 2
4. 一质点在 轴上作简谐振动 选取该质点向右运动通过 点时 一质点在X轴上作简谐振动 选取该质点向右运动通过A点时 轴上作简谐振动, 作为计时起点(t=0), 经过 秒后质点第一次经过 点, 再经过 秒 经过2秒后质点第一次经过 秒后质点第一次经过B点 再经过2秒 作为计时起点 后质点第二次经过B点 若已知该质点在A, 两点具有相同的速 后质点第二次经过 点, 若已知该质点在 ,B两点具有相同的速 率, 且AB=10cm, 求 A,B两点关于原点对称 (1) 质点的振动方程 t=4 B t=2 X A t=0 O (2) 质点在 点处的速率 质点在A点处的速率 点处的速率.
(2) 设振动方程为
x = A cos(ωt + 0 )
vm = Aω = 10cm / s
10
0
∴ v = Aω sin(ωt + 0 )
由v—t图知 图知: 图知
V(cm/s)
2π 4 T = π ∴ ω = = 5rad s 1 10 T vm A= = 2cm
1
2
3
4
t(π/10)s -10
-6
2
1
t(s) a
a点: X0=-A/2,v0<0
3 π π 2 3 = 7π ω= 1 0 6
或由曲线的 ωta+ = 2π/3+2π 对称性从初 始到1s时刻 始到 时刻 8 π 和从1s到 状 π 和从 到a状 3 = 2 s 态应经历相 ta = 3 7 同的时间 π 6
3. 质量为 质量为0.1kg的小球与轻弹簧组成的弹簧振子 按X=0.1 的小球与轻弹簧组成的弹簧振子, 的小球与轻弹簧组成的弹簧振子 cos(8πt+2π/3)的规律作谐振动 的规律作谐振动,(SI), 求: + 的规律作谐振动 (1) 振动周期,振幅,初相及速度,加速度的最大值; 振动周期,振幅,初相及速度,加速度的最大值; (2) 求最大弹性力及振动能量 求最大弹性力及振动能量. 解:由振动方程知A=0.1m, ω=8π, =2π/3 v=-0. 8πsin(8πt+2π/3) + a=-6.4π2sin(8πt+2π/3) + T=2π/ω=0.25s
( x ≥ 0)
λ
2 ; (k = 0,1, LL)
波腹
π A = 2 A cos 2λ = 2 A
∴x = k
π 波节: 波节 A = 2 A cos 2λ = 0
x = (2k + 1) λ ; (k = 0,1, LL) 4
5.一声源的频率为 一声源的频率为1080Hz,相对于地以 相对于地以30m/s的速率向右运动 在其 的速率向右运动, 一声源的频率为 相对于地以 的速率向右运动 右方有一反射面相对于地以65m/s的速率向左运动 设空气的声速为 的速率向左运动, 右方有一反射面相对于地以 的速率向左运动 334m/s, 求: (1) 声源在空气中发出声音的波长; 声源在空气中发出声音的波长 (2) 每秒钟到达反射面的波数 每秒钟到达反射面的波数; (3) 反射波的速率 反射波的速率; (4) 反射波的波长 1 u + v0 解: ν = 1080Hz v s = 30m s (2) ν ′ = ν
2 A v0 > 0 t=0: x0 = 2 = 2 π = 4 t=1: x = 0 v < 0 π 3π ωt + = ω= 2 4
X(m) 2 0 1
t(s)
3. 两个同方向同频率的谐振动 其合振幅为 两个同方向同频率的谐振动, 其合振幅为20cm, 合振动周相 与第一个振动的周相差为60° 第一个振动的振幅为 第一个振动的振幅为A 与第一个振动的周相差为 °,第一个振动的振幅为 1=10cm , 则第一振动与第二振动的周相差为(B 则第一振动与第二振动的周相差为 ) A (A) 0 (B) π/2 (C) π/3 (D) π/4 A2
Y a 9λ/8 λ/2 b X
2. 如图 在X=0处有一平面余弦波波源 其振动方程是 如图, 处有一平面余弦波波源, 处有一平面余弦波波源 Y=Acos(ωt+π), 在距 点为 在距O点为 点为1.25λ处有一波密媒质界面 处有一波密媒质界面MN, 则O, 处有一波密媒质界面 , λ 3λ 5λ B间产生的驻波波节的坐标是 间产生的驻波波节的坐标是 ; ; . 4 4 4 M ,波腹的坐标是 λ 0; ; λ . 2 反射波在O点的初相: 反射波在 点的初相: 点的初相
.
u = 340m s 1
vs = 72km / h = 20m s 1
ν = 360 Hz
∴ν ′ =
u ν = 340 Hz u + vs
4. 设入射波的波动方程为 1=Acos2π(t/T+x/λ), 在x=0处发生反射 设入射波的波动方程为Y 处发生反射, 处发生反射 反射点为一自由端,求 反射点为一自由端 求: (1) 反射波的波动方程 (2) 合成波的方程 并由合成波方程说明哪些点是波腹 哪些点 合成波的方程,并由合成波方程说明哪些点是波腹 并由合成波方程说明哪些点是波腹,哪些点 是波节. 是波节 y20 = A cos(2πt / T ) 反射波在反射点0点振动方程为 解:(1)反射波在反射点 点振动方程为 反射波在反射点 点振动方程为:
1 1 1 = + K 2 K1 K 2 2 K1 K 2 K= 2 K1 + K 2
K1 K2 m K1
平衡位置 Kx0 = mg
d 2x 任意位置 F = K ( x + x0 ) + mg = Kx = m 2#43; π )
振动习题课后作业(43) 振动习题课后作业 1. 当谐振子的振幅增大到 时, 它的周期不变 速度最大值变为 当谐振子的振幅增大到2A时 它的周期不变 速度最大值变为 不变, 原来的2倍 加速度最大值变为原来的 变为原来的2倍 填增大 减小, 原来的 倍, 加速度最大值变为原来的 倍.(填增大 ,减小,不变 或变几倍) 或变几倍 2. 如图所示质点的谐振动曲线所对应的振动方程 如图所示质点的谐振动曲线所对应的振动方程(D) (A) X=2cos(3t/4+π/4) (m) (B) X=2cos(πt/4+5π/4) (m) (C) X=2cos(πt-π/4) (m) (D) X=2cos(3πt/4-π/4) (m) - -
