材料力学 静不定结构-习题课
吉林大学考研材料力学题型六静不定

第 1 页/共 10 页(2000)八、水平曲拐ABC 为圆截面杆,在C 段上方有一铅垂杆DK ,发明时DK 杆短了△。
曲拐AB 和BC 段的抗扭刚度和抗弯刚度皆为GI P 和EI 。
且GI P =45EI 。
杆DK 抗拉刚度为EA ,且EA=225EIa 。
试求:(1)在AB 段杆的B 端加多大扭矩,才可使C 点刚好与D 点相接触? (2)若C 、D 两点相接触后,用铰链将C 、D 两点连在一起,在逐渐撤除所加扭矩,求DK 杆内的轴力和固定端处A 截面上的内力。
(15分)(2001)五、已知钢架受力如图,试求: A 处的约束反力。
(12分)(2002)七、圆截面杆AB、BC的直径、材料均相同,已知:p、a,E=2.5G,且CD杆的EA=2EI/5a2,试求:CD杆的内力。
(12分)(2003)五、圆截面平面曲拐OAB与直杆CD直径、材料均相同。
已知P、L,且=0.8EI,EA=0.4EI/L2,求O端的约束反力。
(20分)GIp第3 页/共10 页(2004)三、已知平面曲拐ABC和DF梁的抗弯刚度为EI、抗扭刚度为GI和CD杆p=2EAL2。
试求CD杆的内力。
(20分)的抗拉刚度为EA,设EI=4GIP(2023年年)二、结构受力如图所示,已知平面钢架ABCD的抗弯刚度为EI,EF 杆的抗拉刚度为EA,设3EI=EAL2。
试求E、F两点的相对位移。
(20分)第5 页/共10 页(2023年年)八、已知平面钢架EI为常数,试问:若在C处下端增强一刚度为K=3EI/A3(单位:N/M)的弹性支座后,该钢架的承载能力(强度)将提高多少倍?(20分)第 7 页/共 10 页(2023年年)七、求BC 杆的内力,设2/EA EI a 。
(20分)(08.3)(2023年年)三、平面直角曲拐ABC和CD杆均为圆截面,材料相同,已知:3EI=GIp,第9 页/共10 页3EI=EAL2,试求CD杆的内力。
工程力学(静力学与材料力学)课后习题

1-1试画出以下各题中圆柱或圆盘的受力图。
与其它物体接触处的摩擦力均略去。
1-2试画出以下各题中AB 杆的受力图。
1-3试画出以下各题中AB 梁的受力图。
(d)A(F(((d)A(e)(c)(a)(a)(c)F (b)1-4 试画出以下各题中指定物体的受力图。
(a) 拱ABCD ;(b) 半拱AB 部分;(c) 踏板AB ;(d) 杠杆AB ;(e) 方板ABCD ;(f) 节点B 。
1-5 试画出以下各题中指定物体的受力图。
(a) 结点A ,结点B ;(b) 圆柱A 和B 及整体;(c) 半拱AB ,半拱BC 及整体;(d) 杠杆AB ,切刀CEF 及整体;(e) 秤杆AB ,秤盘架BCD 及整体。
2-2 杆AC 、BC 在C 处铰接,另一端均与墙面铰接,如图所示,F 1和F 2作用在销钉C 上,F 1=445N ,F 2=535N ,不计杆重,试求两杆所受的力。
(a)(b)(c)(d)(e)W(f)(c)(d)(b)(e)F 12-3 水平力F 作用在刚架的B 点,如图所示。
如不计刚架重量,试求支座A 和D 处的约束力。
2-4 在简支梁AB 的中点C 作用一个倾斜45o 的力F ,力的大小等于20KN , 如图所示。
若梁的自重不计,试求两支座的约束力。
2-6 如图所示结构由两弯杆ABC 和DE 构成。
构件重量不计,图中的 长度单位为cm 。
已知F =200N ,试求支座A 和E 的约束力。
2-7 在四连杆机构ABCD 的铰链B 和C 上分别作用有力F 1和 F 2,机构在图示位置平衡。
试求平衡时力F 1和F 2的大小之间 的关系。
2-9 三根不计重量的杆AB ,AC ,AD 在A 点用铰链连接,各杆与水平面的夹角分别为450,,450和600,如图所示。
试求在与 O D 平行的力F 作用下,各杆所受的力。
已知F =0.6kN 。
3-1已知梁AB 上作用一力偶,力偶矩为M ,梁长为l ,梁重不计。
材料力学2-2拉压静不定

ቤተ መጻሕፍቲ ባይዱ
7)组合体伸长: 6)应力: (压) (拉)
作业: P73
P81
2.43
2.47
P81
2.48
九、应力集中的概念
P
P 0 A
P
max
P
P
P
P
理论应力集中系数:k
max 0
习 题 课
例题1:图示构架,两杆的材料相同,其横截面面积之 比为A1:A2=2:3,承受载荷为P,试求: 1)为使两杆内的应力相等,夹角应为多大? 2)若P=10kN,A1=100mm2,则杆内的应力为多大?
0.06 10 3 L1 0 .1 L2 0 .3
作业:
P82 2.51
P84 2.53
soc
1
L
1L 3L soc , 3L
)2 ( 0 soc 1 N 2 3 N,0 Y )1(
2
已知三杆的EA相同,3杆制造短了长度, 若将三杆用铰A装配,试求装配后各杆的受力。
解: 1)平衡方程
2)装配后的变形几何关系(变形图)
3
L N L 1N soc 3 A 3E soc 1A 1E
3
L N 3L 3 N , 1 1 1L 3L A A 3E 1 1E
3
soc 3L 2L 1L
2)变形几何关系、变形图:
3)物理关系:
5)联立求解:
4)补充方程:
3. 静不定问题特征: 1)各杆的受力与刚度有关; 2)静不定问题可能产生初应力或温度应力。
tAE R tE B t A A
例1: D1=45mm,t = 3mm,d2=30mm,E1=210GPa, 1=1210 -61/oC, E2=110GPa, 2=16 10 - 61/oC, t从30o升高至180o(30o为装配时温度),求钢管和铜 杆内的应力以及组合体的伸长。 解:1)
材料力学课件:静不定问题分析-1

是否是原结构静力 许可场?
Page20
例2:图示桁架,各杆EA相同,求各杆轴力
a
a
4
2
a 57
8 3
1
6
解: 判断静不定度: P 存在1个多余内部约束
内力静不定度: 8 - 25 + 3 = 1
4
m
5 N7m’N7 8 3
2 1
6
1、 去除多余约束,建立相当系统
P
2、 建立补充方程(找变形协调条件)
内力静定
5度
5度
4度
Page6
➢ 混合(一般)静不定
2度
6度
➢ 组合梁或梁杆结构的静不定度分析
Page7
➢ 组合梁或梁杆结构的静不定度分析
安装法 2度
拆卸法
2度
Page8
拆卸法
1度
安装法 两杆多余,2度内力静不定
Page9
➢ 静不定问题的分析方法: 力法: 以多余未知力为待定量,利用变形 协调条件列方程。 位移法: 以位移为待定量,利用平衡条件求解。
4 - 24 + 3 = -1
5 - 24 + 3 = 0
6 - 24 + 3 = 1
Page4
平面刚架: 三度内力静不定
断开:内力静定
刚性连接:多了三 个约束
两度内力静不定
六度内力静不定
四度内力静不定
封闭框架三内,加一铰减一,加一刚接杆加三,加一铰支杆加一
Page5
平面曲杆:
三度内力静不定 两度内力静不定 ➢ 例:判断内力静不定度
l
B
l
B
l
l
A RC
l
C
HC
材料力学(15)第十四章 静不定问题分析

静不定问题分析
F
1(内)+1(外)= 2 度
3(内)+3(外)= 6 度
F
梁:外3 环:内3 圆环
梁环接触:1
3+3+1=7 度
Page 9
第十四章
静不定问题分析
梁杆结构的静不定问题
(b) (a) (a): 1度 (b): 2度 (c) (c): 2度
Page10
第十四章
静不定问题分析
§14-2
8
静不定问题分析
a 4 a 5 7 6 8 3
a 2
1
N i N i li m / m EA i 1 a [(2 2) N 7 (2 2) P] 0 P EA
2 N7 P 2
1 1
思考:若求加载点的水平位移,如何选择单位载荷状态
4 5
6 8 3
2 1
4 5
q
FS
M
FN
断开:内力静定
刚性连接:多了三个约束
F F
单闭口的平面刚架或曲杆 内3度静不定
内6度
Page 7
第十四章 F F
静不定问题分析
6度内力静不定
F
F
5度内力静不定 加一中间铰减 少一度静不定
F F
F F
2度内力静不定
4度内力静不定,加一根二力 杆增加一度静不定
Page 8
第十四章 混合静不定
H
利用单位载荷法建立补充方程
Page20
P
第十四章
x2
B
RB N
静不定问题分析
x1 C
N
D
真实载荷状态(相当系统):
RB RD N 2
习题课-静力学

习题课-静力学
3.图示力偶中等效的是(B)
NEFU- Junkai Lu
(A) a和c (B) a和b (C) b和c (D) b和d
36Fd顺
36Fd顺
36Fd逆
48Fd顺
4.关于力对点之矩的说法,下列哪个是错误的(B)
(A) 互相平衡的两个力,对同一点之矩的代数和等于零。
(B) 力对点之矩与力的大小和方向有关,而与矩心位置无关。
4.关于力对点之矩的说法,下列哪个是错误的( ) (A) 互相平衡的两个力,对同一点之矩的代数和等于零。 (B) 力对点之矩与力的大小和方向有关,而与矩心位置无关。 (C) 力的数值为零、或力的作用线通过矩心时,力矩均为零。 (D) 力对点之矩不会因为力矢沿其作用线移动而改变。
10
School of Civil Engineering
习题课-静力学
NEFU- Junkai Lu
10. 力系的平衡
平面任意力系
Fx 0
Fy 0
M o 0
Fx 0
M A 0
M B 0
A、B两点 连线不得 与投影轴 x轴垂直
空间任意力系
Fix 0 Fiy 0 Fiz 0
(C) 力的数值为零、或力的作用线通过矩心时,力矩均为零。
(D) 力对点之矩不会因为力矢沿其作用线移动而改变。
力有关,力偶无关
11
School of Civil Engineering
习题课-静力学
NEFU- Junkai Lu
5.图示正方体顶角上作用着六个大小相等的力,此力系向任一点简化的结 果是( )
D
F3
材料力学:ch14 静不定问题分析
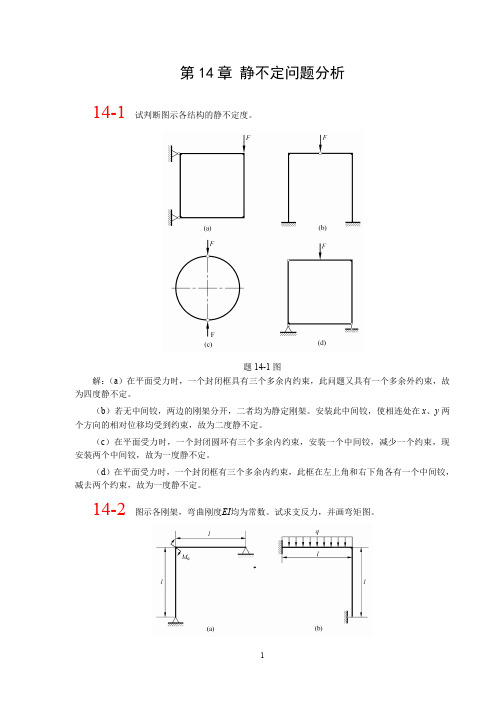
图 14-9(a) 根据对称条件,截面 C 的水平位移 ΔCx 为零,即
由此得到
ΔCx 0
FNC
3F 8
(→)
12
弯矩图如图(2)所示,最大弯矩为
|
M
|max
Fl 4
(b)解:此为三度静不定问题。有反对称性可利用。
在结构对称面 C 处假想切开,由于反对称,故有
FNC 0 , M C 0
待求未知内力仅有FSC一个。 求 ΔCy 的载荷状态及单位状态如图 14-9(b)所示。
弯矩方程为
图 14-2(b)
M x1 FBx x1 ,
M
x 2
F Bx l
q 2
x
2 2
将其代入 积分后,得 代入协调条件
M x1 x1 , M x2 l
ΔBx
1 EI
lM
0
x1
M
x1
dx1
1 EI
lM
0
x2
M
x2
dx2
ΔBx
1 EI
4 3
FBxl 3
ql 4 6
ΔBx 0
弯矩方程为
将其代入 积分后,得 代入协调条件
图 14-3(a)
M
FCx Rsin
F 2
R1
cos
M Rsin
ΔCx
1 EI
π/2 M M Rd
0
ΔCx
R3 EI
π 4
FCx
F 4
ΔCx 0
4
得 进而求得
(b)解:此为一度静不定问题。
FCx
F π
(←)
FBx
F π
(→)
求 ΔAy 的载荷状态及单位状态可示如图 14-3(b)。
材料力学(单辉祖)第十四章静不定问题分析

求解上式可得
X1
=
1−
π2
π
4⋅ −1
P 2
=
4−π π2 −8
P
,8X2来自=π π−3
2
−1
⋅
PR 4
=
2(π
π2
− 3)
−8
PR
8
27
Example-7
在平面xy内,由k根等直杆组 y
成的杆系,在结点A处用铰连 接在一起,并受到水平载荷P1 和垂直载荷P2的作用。已知各 杆的材料相同,其拉压弹性模
∂X 1
∂X 2
Rϕ
25
Example-6
由对称截面处的约束条件, 可得变形相容性条件
Δ = ∂Uc = 0, θ = ∂Uc = 0
∂X 1
∂X 2
P/2 X2
X1 X3
Rϕ
即
∫ − 1
EI
π 2
0
⎜⎛ ⎝
PR 2
sin
ϕ
−
X 1R(1 −
cos ϕ )
−
X
2
⎟⎞ ⎠
⋅
R(1 −
cosϕ )Rdϕ
F
M (ϕ ) = FR (1− cosϕ ) − FByR sinϕ
π
∫ Δ By
=
∂Vε ∂FBy
=
2
[M
0
(ϕ ) ∂M (ϕ )][EI ]−1Rdϕ
∂FBy
8
Example-1
π
M (ϕ ) = FR (1− cosϕ ) − FByR sinϕ
∫ Δ By
=
∂Vε ∂FBy
=
2
[EI ]−1 ⎡⎣FR (1− cosϕ ) − FBy R sinϕ ⎤⎦ (−R sinϕ ) Rdϕ
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
dx ,
MiMF ΔiF = ∫ dx EI l
对于静不定桁架:
n
δi j =
∑
k =1
FN i , k FN j , k l k E k Ak
n
,
Δi F =
∑
k =1
FN i , k FN F,k l k E k Ak
例1:刚架的弯曲刚度为EI,承受力F后,支座C有一 下陷量Δ,试求刚架C处的反力。
∫
0
a
0
x1 dx1 +
2
∫
a
0
⎞ 4a a dx2 ⎟ = ⎠ 3EI
2
3
a A
1 ⎡ ⎢ Δ1F = EI ⎢ ⎣
∫
a⎛
3⎞ q x ⎜ − 0 1 ⎟ x1 dx1 + ⎜ 6a ⎟ ⎝ ⎠
∫
a⎛
0
2 ⎞ ⎤ q a 0 ⎜− ⎟ a dx 2 ⎥ q 0 ⎜ ⎟ 6 ⎥ ⎝ ⎠ ⎦
q0 a 4 =− 5 EI
N
= C−
P , Q 2
C−
= X1
∆v C =∆ 1=0
, ∆ 1 = ∆ 1 P + δ 11X 1= 0
1 M P = − PR (1 − cos ϕ ) M 0= R sin ϕ 2
3 1 π − 1 PR 2 2 ∆ 1P = PR (1 − cos ϕ ) sin ϕ ⋅ Rdϕ = − 0 ∫ EI 2 AEI π 1 2 2 2 πR 3 δ 11= 0 R sin ϕ ⋅ Rdϕ = ∫ EI 4 EI
δ i j 表示X i 作用点沿着X i 方向由于X j = 1单独
作用时所产生的位移
ΔiF 表示X i 作用点沿着X i 方向由于实际载荷单独
作用所产生的位移
X i = 1引起的弯矩为M i 设 ⎧ ⎪
⎨ X j = 1引起的弯矩为M j ⎪实际载荷引起的弯矩为M F ⎩
则 δi j = ∫
l
MiM j EI
⎛ π ⎞⎞ ⎛ − FR sin ⎜ ϕ − ⎟ ⎟ ( R sin ϕ ) Rdϕ ∫π 4 ⎜ 4 ⎠⎠ ⎝ ⎝
π
2
X
1
A
F
C
B
φ
A
∆1F F ∴ X1 = − = ↑) ( δ11 2 2
C
1
φ
B
A
例 8 、求图示结构 的约束反力
C EI
EA
3)对静定基进行受力分析,建立相当系统 4)研究AB梁的B点与BC杆的B点的竖直相 对线位移,建立正则方程
3 a _F __ 7
3 a _F __ 7
M图
4 a _F __ 7 4 a _F __ 7
例12:试求图示平面刚架的支座反力。已知各杆 EI=常数。
q B a a A C a D
3 ⎛ a 2 2a ⎞ 4 a ⎜ ⋅ δ 11 + a2 ⋅ a⎟ = ⎜ 2 3 ⎟ 3EI ⎝ ⎠ 3 4 ⎞ 1 ⎛ qa qa Δ1F = − ⎜ ⋅ a⎟ = − ⎟ EI ⎜ 2 2 EI ⎝ ⎠
由 δ 11 X 1 + Δ1F = − Δ
得
29 F 3EIΔ X1 = − 3 64 4a
例2:刚架的弯曲刚度为 EI ,承受力 F。 A 试求:刚架多余约束反力。
F
A B A
F
B a
X1
X1 B
a
FD
C D C
D a A a
C
F
a
F
F
a
X1
X1 B
2 ⎛ a 2 2a 5a 3 3⎞ δ11 = ⎜ × +a ⎟= EI ⎝ 2 3 ⎠ 3EI 1 ⎡ Fa 2 2a Fa 2 ⎤ 5Fa 3 Δ1F = − ⎢ × + ×a⎥ = − EI ⎣ 2 3 2 6EI ⎦
x2
⎧ M ( x1 ) = − x1 AB段: ⎨ ⎩ T ( x1 ) = a BC段: M ( x2 ) = x2
2
3
∆1F X1 = − δ11
Fa 3 − 3F 8 EI =− 3 = a 8 3EI
例11:图示刚架 EI为常量,画出 刚架的弯矩图。
F a a A B
F
解:
X1 F a/ 2
1
F
δ 11
7a 3 = 24 EI
a/ 2 A Fa
Fa 3 Δ1F = − 4 EI
6F X1 = 7
F
6_ F _ 7
M
M
2 1 1 2 1 . ( .a. a. . a ) EI 2 2 3 2 1 1 1 2 + . (a.1.1) + . ( .a.a. .a ) EI 2 EA 3 a3 a = + 1 2 EI EA
∆1 = ∆1P + δ11. X 1 = 0
B
1 P.a 2
∆1P
X1
a E
3 2 1 1 2 1 Pa = .( .a. Pa. . a ) = EI 2 2 3 2 6 EI
C
δ11 =
N
X1
M
1 a 2
P 3)对静定基进行受力分析, 建立相当系统
4)研究DE梁的C点与BC杆的C点的 竖直相对线位移,建立正则方程 5)根据相当系统图,求出其他 全部约束反力
例18:已知平面刚架的EI, GI P ,求C处约束反力. A C
2a
P
a
x1
P AB段: M ( x1 ) = Px1
∆1 = ∆1P + δ11. X 1 = 0
a A EI
l
B
−1
P 解: 1)判断静不定种类及次数 约束反力一次静不定 2)解除B点约束,建立静定基 P
Pl
M
N
1
l
M
X1
1 1 2 Pl 3 ∆1P = . ( .l.Pl. .l ) = ⎫ EI 2 3 3EI ⎬ 3 1 a ⎭ 1 1 2 l .(a.1.1) = δ11 = . ( .l.l. .l ) + + EA EI 2 3 3EI EA
A
F C
B
F
C
B
M = − FR cos (ϕ−π/4) ϕ∈[π/4,π/2] M = R sin ϕ ϕ∈[0,π/2] M2 1 π2 π R3 2 δ11 = ∫ ds = ( R sin ϕ ) Rdϕ = ∫ 0 EI EI 4 EI s
MM 1 ∆1P = ∫ ds = EI EI s π FR 3 =− 8 2 EI
1
FNA
F Fa = , MA = 2 8
A X1 F/ 2
F/ 2
例6:已知刚架的弯曲刚度为EI。 试求截面A处弯矩。 2a qa 3 解: δ 11 = , Δ1F = − EI EI
a q
a
a q q A a
由 δ 11 X 1 + ∆1F = 0 得
1 2 M A = X 1 = qa 2
1 = EI
由δ 11 X 1 + Δ1F = 0 得
3qa X1 = 8
FBx = 0, FBy FAx = 0, FAy
3qa = ↓ 8
() ()
qa (逆时针) MA = 8
2
11qa = ↑ , 8
例13:已知刚架的弯曲刚度为EI。 试求支座B处的反力。
q0 C a B
解:
δ 11
1 ⎛ = ⎜ EI ⎝
MM PR 3 FR 3π VBx = ∫ dx = − l EI 4 EI 4 EI 1 ⎡1 2 8FR 3 ⎤ ′ = (2 FR × 2 R ) × × 2 R⎥ = VBx ⎢ EI ⎣ 2 3 ⎦ 3EI
θ
B
θ
B
F
F
N=P/2
N=P/2
P/2 F F
P/2
协调条件
′ V Bx = V Bx
a D a C
∆1P F X1 = − = δ11 2
例3:刚架的弯曲刚度为 EI ,承受力 F。 试求:刚架多余约束反力。
F 1
F a a A
F
B F X1 X1 a
a F A A
2 3
1 ⎛a 2a a δ11 = + ⎜ EI ⎝ 8 3 2 4
⎞ 7a ⎟= ⎠ 24EI3a A B1 ⎡ Fa 2 a ⎤ Fa 3 Δ1F = − ⎢ × ⎥=− EI ⎣ 2 2 ⎦ 4EI
5 Fa = 作用于固定端A 6
a
a a
1 F
Fa
例5:已知结构的弯曲刚度为 EI , 试求对称轴上A截面的内力。
a
F
a a
解:δ 11
2 2a Fa , Δ1F = − = 4 EI EI
A a
由 δ 11 X 1 + ∆1F = 0 得 Fa X1 = 8 ∴ FSA = 0
F a
1 1
F a/2
F=
3P 32 + 3π
因AD与BF对称,其受力也对称, 6 PR M D = M F = Fl = F × 2 R = 32 + 3π
例16、选择题:
一、(a)图所示悬臂梁,如在自由端B上 加一个活动铰支座(b)图,则该梁的 (A) 强度提高,刚度不变 (B) 强度不变,刚度提高 (C) 强度,刚度都提高 (D) 强度,刚度都不变 答案:(C) (a)图 二、下图所示结构是 静不定机构 (A) 1次 (B) 2次 (C) 3次 (D) 4次 答案:(B) (b)图 四、下图所示结构是 三、下图所示结构是 静不定机构
∆1P P X 1= − = = 0.318 P ( ↑ ) δ11 π
