3[1]3总体方差的假设检验
假设检验-方差分析及回归分析

1.645 时,拒绝 H0。
率有显著提高,此时犯(第一类)错误的 5% 。 概率不会超过
若取 0.005 , 查表得
z 0.005 2.57 , 仍有 z 3.125 2.57 , 所以在显著性水平 0.005 下
也拒绝 H0,从而可断定犯错误的概率 不会超过 0.5% 。
( n1 1) s ( n2 1) s , n1 n2 2
2 1 2 2
若 t t ( n1 n 2 2) ,则拒绝 H0
2
右边检验
H 0 : 1 2 0 , H 1 : 1 2 0
若 t t ( n1 n 2 2 ) ,则拒绝 H0
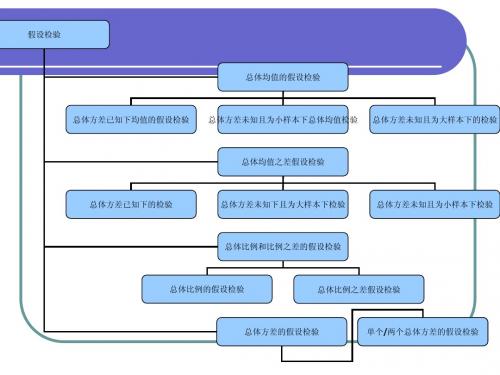
第八章 假设检验
第九章 方差分析及回归分析
第八章 假设检验
§1 假设检验
§2 正态总体均值的假设检验
§3 正态总体方差的假设检验
§5 分布拟合检验
§1 假设检验 实际推断原理 概率很小的事件在一
次试验中实际上可认为是不会发生的。本章 的内容,一是已知总体的分布类型,而对包 含的未知参数作某些假设,二是未知总体的 分布类型,而对总体的分布作出假设。 所谓假设检验就是提出假设后,根据实 际推断原理作出接受还是拒绝的判断。
2
均未知。 2 2 2 2 H0 : 1 2 , H1 : 1 2
s 检验统计量 F , s
若 F F ( n1 1, n 2 1)
2
2 1 2 2
或 F F1 ( n1 1, n 2 1) ,
2
则拒绝 H0。
若
2 2
F1 ( n1 1, n2 1) F F ( n1 1, n2 1) ,
假设检验与方差分析

三、假设检验的步骤
1、提出原假设(null hypothesis)和备择假设 (alternative hypothesis)
原假设为正待检验的假设:H0; 备择假设为可供选择的假设:H1 一般地,假设有三种形式:
(1)双侧检验:
H0 : 0; H1 :0 (2)左侧检验:
这两个例子中都是要对某种“陈述”做出判
断:
例1要判明工艺改革后零件平均 长度是否仍为4cm;
进行这种判断 的信息来自
例2要判明该批产品的次品率是 所抽取的样本
否低于3%。
所谓假设检验,就是事先对总体参数或总体分 布形式作出一个假设,然后利用样本信息来判断 原假设是否合理,即判断样本信息与原假设是否 有显著差异,从而决定是否接受或否定原假设
对比来构造检验统计量。
可以证明,若H0为真,则
2
(n 1)S 2
2 0
~
2 (n 1)
因此,可构造2 统计量进行总体方差
的假设检验。
当H0成立时,S2/02 接近于1,2的 值在一个适当的范围内,
当H0不成立时,S2/02远离1,2的值 相当大或相当小。
在例2中,由于所抽样本只为10,为小样本,因 此无法构造Z统 计量进行总体比例的假设检验。
如果总体X~N(,2),在方差已知的情况下,对总体均 值进行假设检验。
由于
因此,可通过构造Z统计量来进行假设检验:
注意: 如果总体方差未知,且总体分布未知,但如果是大样
本(n>=30),仍可通过 Z 统计量进行检验,只不过总体 方差需用样本方差 s 替代。
例3:根据以往的资料,某厂生产的产品的使用寿命服从正 态分布N(1020, 1002)。现从最近生产的一批产品中随机抽取16 件,测得样本平均寿命为1080小时。问这批产品的使用寿命 是否有显著提高(显著性水平:5%)?
假设检验
t分布与正态分布的比较
正态分布
T分布(n’=6)
T分布(n’=2)
T分布与正态分布的比较
t值表
1)表中左侧第一列的数值是自由度n ',它的值为n ' = n − 1。 随着n ' 值的不同,t分布曲线的形式也是呈现不同的态势。 每一横行的数据,属于一条t分布曲线。最下面一行n ' = ∞, t分布曲线与标准正态曲线重合,因此t分布表中这一 行的数据与标准正态分布表中的值是相同的。 2)表中顶端一行是显著性水平α的值。它的值等于分布图 α 中位于两尾部面积之和,单侧尾部面积为 。如下图 2 α 3 表中间的数值是代表t分布在图中单侧尾部面积为 时, ) 2 所对应的t临界值如下图所示。 t α=
(? 无效假设H 0:µ1 ≤ µ2的否定域为u ≥ u α。 )
(三 )总体方差σ1和σ2未知,但σ12=σ22且为小样本时,两个总体均值之差的假设检验
此时的检验统计− (µ1 − µ 2 )
)
1 2 1 SC + n 1 n2 其服从自由度为n 1 + n 2 − 2的t分布。
中心极限定理:给出一 个具有任何函数形式的 总体,其平均值为 µ,方差 σ2有限。 若从这一总体抽出容量 为 n的样本,则当样本容量 很大时,由这些样本算 出的 x 的抽样分布近似服从平 均值为 µ,方差为 σ2 / n正态分布。在实际问题 中,常需 要在总体方差未知的条 件下对总体均数进行检 验。此时,通常用 s2近似代替 σ2, 对大样本来说误差不大 ,由中心极限定理可知 x的分布近似正态分布。 此时的检 验统计量为 U= x − µ0 s/ n ~ N (0,1)
p(H 0 )0.05,接受H 0 ∴ 认为可以用49.1秒作为该运动员400米跑成绩的代表值。
假设检验的定义和步骤

假设检验的定义和步骤
假设检验是统计学中一种常用的推断方法,用于判断样本数据
是否支持对总体参数的某个假设。
通过对样本数据进行分析,假设
检验可以帮助我们判断我们所做的假设是否合理,并据此对总体参
数进行推断。
假设检验的步骤通常包括以下几个步骤:
1. 提出假设,首先,我们需要明确提出一个关于总体参数的假设,通常包括原假设(H0)和备择假设(H1)两种。
2. 选择检验统计量,根据所提出的假设,选择适当的检验统计量,该统计量应能够在原假设成立时具有已知的概率分布。
3. 确定显著性水平,确定显著性水平(α),即拒绝原假设的
概率阈值。
通常选择0.05作为显著性水平。
4. 计算统计量的值,利用样本数据计算出所选检验统计量的值。
5. 做出决策,根据检验统计量的值和显著性水平,做出决策,
即是拒绝原假设还是不拒绝原假设。
6. 得出结论,根据做出的决策,得出对原假设的结论,判断样本数据是否支持原假设。
总的来说,假设检验是一种通过对样本数据进行统计分析,以判断对总体参数的假设是否成立的方法。
通过严格的步骤和逻辑推理,假设检验可以帮助我们做出合理的推断和决策。
常用的假设检验方法(U检验、T检验、卡方检验、F检验)

常⽤的假设检验⽅法(U检验、T检验、卡⽅检验、F检验)⼀、假设检验假设检验是根据⼀定的假设条件,由样本推断总体的⼀种⽅法。
假设检验的基本思想是⼩概率反证法思想,⼩概率思想认为⼩概率事件在⼀次试验中基本上不可能发⽣,在这个⽅法下,我们⾸先对总体作出⼀个假设,这个假设⼤概率会成⽴,如果在⼀次试验中,试验结果和原假设相背离,也就是⼩概率事件竟然发⽣了,那我们就有理由怀疑原假设的真实性,从⽽拒绝这⼀假设。
⼆、假设检验的四种⽅法1、有关平均值参数u的假设检验根据是否已知⽅差,分为两类检验:U检验和T检验。
如果已知⽅差,则使⽤U检验,如果⽅差未知则采取T检验。
2、有关参数⽅差σ2的假设检验F检验是对两个正态分布的⽅差齐性检验,简单来说,就是检验两个分布的⽅差是否相等3、检验两个或多个变量之间是否关联卡⽅检验属于⾮参数检验,主要是⽐较两个及两个以上样本率(构成⽐)以及两个分类变量的关联性分析。
根本思想在于⽐较理论频数和实际频数的吻合程度或者拟合优度问题。
三、U检验(Z检验)U检验⼜称Z检验。
Z检验是⼀般⽤于⼤样本(即⼤于30)平均值差异性检验的⽅法(总体的⽅差已知)。
它是⽤标准的理论来推断差异发⽣的概率,从⽽⽐较两个的差异是否显著。
Z检验步骤:第⼀步:建⽴虚⽆假设 H0:µ1 = µ2 ,即先假定两个平均数之间没有显著差异,第⼆步:计算Z值,对于不同类型的问题选⽤不同的计算⽅法,1、如果检验⼀个样本平均数(X)与⼀个已知的总体平均数(µ0)的差异是否显著。
其Z值计算公式为:其中:X是检验样本的均值;µ0是已知总体的平均数;S是总体的标准差;n是样本容量。
2、如果检验来⾃两个的两组样本平均数的差异性,从⽽判断它们各⾃代表的总体的差异是否显著。
其Z值计算公式为:第三步:⽐较计算所得Z值与理论Z值,推断发⽣的概率,依据Z值与差异显著性关系表作出判断。
如下表所⽰:第四步:根据是以上分析,结合具体情况,作出结论。
《概率论与数理统计》第八章1假设检验的基本概念

2. 从某批矿砂中,抽取10样本,检验这批砂矿的含 铁量是否为3%?
双侧检验 H0 : 0 3%, H1 : 3%
3.某学校学生英语平均分65分, 先抽取某个班的平均 分,看该成绩是否显著高于全校整体水平?
单侧检验 H0 : 0 65, H1 : 65
0.497 0.506 0.518 0.524 0.498 0.511 0.520 0.515 0.512, 问机器是否正常?
分析 以 和 分别表示这一天袋装糖的净重
总体X 的均值和标准差,
由长期实践表明标准差比较稳定, 我们就设
0.015,于是 X ~ N(, 0.0152 ),这里 未知. 问题 问题是根据样本值判断 0.5 还是 0.5 .
所
以,原假
设H
不正确
0
。
对于这两种解释,哪种解释比较合理呢?
我们需要判断以上两种假设谁对谁错,并给出判断的理由
以上例子属于参数检验(parametric test) 的问题,(如针对总体均值,总体方差等参数的假 设检验)。
另外还有非参数检验(Nonparametric test) 的问题,如关于总体服从某种分布(如正态分布, 泊松分布)的假设检验。
4. 拒绝域与临界点
拒绝域W1: 拒绝原假设 H0 的所有样本值 (x1, x2, ···, xn)所组成的集合.
W1 W1 :拒绝原假设H0的检验统计量的取值范围.
临界点(值):拒绝域的边界点(值) (相应于检验统计量的值).
如: 在前面例4中,拒绝域 {u :| u | u / 2 }.
5. 双边备择假设与双边假设检验
之 下 做 出 的.
2. 检验统计量
统计学三大检验方法
统计学三大检验方法引言统计学三大检验方法是指假设检验、置信区间估计和方差分析。
这三种方法是统计学中非常重要的工具,用来对样本数据进行分析和推断。
本文将详细介绍这三种方法的原理、应用和步骤。
一、假设检验假设检验是一种基于样本数据对总体参数进行推断的方法。
它的目的是判断样本数据对某一假设的支持程度。
假设检验的步骤可以分为以下几个部分:1.明确研究问题和假设。
首先确定研究的目的和问题,然后提出关于总体参数的假设,包括原假设和备择假设。
2.选择合适的检验统计量。
根据问题和数据的特点,选择适合的检验统计量,如均值差检验的t统计量、比例差检验的z统计量等。
3.设定显著性水平。
显著性水平是在假设检验中用来判断是否拒绝原假设的标准,通常取0.05或0.01。
4.计算检验统计量的观察值。
根据样本数据计算出具体的检验统计量的观察值。
5.给出结论。
通过计算观察值与临界值的比较,得出对原假设的结论,并解释结果的意义。
二、置信区间估计置信区间估计是一种用来对总体参数进行估计的方法。
它通过样本数据计算出的区间,给出了总体参数的一个估计范围。
1.确定置信水平。
置信水平是在置信区间估计中用来描述区间的可靠程度,通常取0.95。
2.选择适合的估计方法。
根据总体参数的类型和样本数据的特点,选择适合的估计方法,如均值估计的t分布、比例估计的正态分布等。
3.计算置信区间。
根据样本数据和所选的估计方法,计算出具体的置信区间,通常采用公式:估计值±临界值×标准差/√n。
4.解释结果。
解释置信区间的意义,并进行合理的解释和讨论。
三、方差分析方差分析是一种用于比较两个或多个组之间差异的方法。
它是通过分解总体方差,分析组内与组间的差异,来判断组间的差异是否显著。
1.确定研究问题。
确定需要比较的组,并明确研究的目的和问题。
2.设定假设。
设定组间差异的原假设和备择假设。
3.计算方差。
计算组内方差和组间方差。
4.计算F统计量。
根据方差计算出F统计量。
正态总体均值和方差的假设检验
给定检验水平,查t(n-1)表得, t1-/2(n-1),使
得,
P{| T | t (n 1)}
即得,
1 2
P{|
x s
0
|
t 1
(n 1)}
n
2
拒绝域: 即
算出|T|与 t1比较,若 2 否则,接受H 0.
T , t1拒 绝 , H 0 2
例3 在某砖厂生产的一批砖中,随机地抽取6块进 行抗断强度试验,测得结果(单位:kg/cm2)如下: 32.56, 29.66, 31.64, 30.00, 31.87, 31.03, 设砖的抗断强度服从正态分布.问这批砖的 平均抗断强度是否为32.50 (kg/cm2)?(=0.05)。
2 0
,
H1
:
2
2 0
给定检验水平 ,查 2 n 1 分布表得
2 (n 1),
使得 P 2 2 (n 1)
根据样本值计算统计量的值.
如果 2 2 (n 1)
则拒绝 H 0 , 接受 H1.
第一类错误
弃真错误
第二类错误
取伪错误
假设检验的两类错误
所作判断 真实情况
H0 为真 H0 为假
接受 H0
拒绝 H0
正确
第二类错误 (取伪)
第一类错误 (弃真)
正确
犯第一类错误的概率通常记为 犯第二类错误的概率通常记为
P
否定H0
H
为真
0
P第一类错误
P
不否定H0
H
为假
0
P第二类错误
若 T t,1拒绝 ,H接0 受
H1
T t1 ,接受 H,0 拒绝 H。1
3,4形式的检验成为右边检验.
统计学导论 科学出版社 第五章 假设检验
右侧检验
或
H1 : µ > µ0
H1 : µ > µ0
确定适当的检验统计量
什么检验统计量? 什么检验统计量?
用于假设检验问题的统计量 选择统计量的方法与参数估计相同, 选择统计量的方法与参数估计相同,需考虑
是大样本还是小样本 总体方差已知还是未知
检验统计量的基本形式为
z= x − µ0
σ
n
选择显著性水平α,确定临界值
☺
☺ ☺ ☺ ☺ ☺ ☺ ☺ ☺
抽取随机样本
均值 ☺ ☺ X = 20
假设检验的基本思想
抽样分布
这个值不像我 们应该得到的 样本均值 ... ... 因此我们拒 绝假设 µ = 50
... 如果这是总 体的真实均值 20
µ = 50 H0
样本均值
假设检验应用举例
例1:抽样检验食品包装机工作是否正常 : 例2:由样本推断产品次品率是否超标 : 例3:研究黑人儿童是否有民族意识 : 例4:检验电池寿命波动性是否有显著变化 : 5: 例5:判断男女职工看电视时间是否有显著差异 例6:检验新工艺是否比旧工艺更好 : 例7:研究生活习惯是否影响血压 : 例8:检验两次地震间的天数是否服从指数分布 : 例9:比较两公司进货次品率,作出进货决策 :比较两公司进货次品率,
3、特点 、
采用逻辑上的反证法 依据统计上的小概率原理
第一节 假设检验的基本原理
一. 假设检验的一般思想 二. 假设检验的步骤 三. 假设检验的两类错误
假设检验的过程
(提出假设→抽取样本→作出决策) 提出假设→抽取样本→作出决策)
提出假设 作出决策
拒绝假设! 拒绝假设 别无选择. 别无选择
总体
应用统计学 经管类 第7章 假设检验
• • • • • •
二、假设检验的步骤 (一)提出原假设与备择假设 (二)构造检验统计量 (三)确定拒绝域 (四)计算检验统计量的样本观测值 (五)做出结论
1、提出原假设与备择假设
• 消费者协会实际要进行的是一项统计检验 H0 工作。检验总体平均 =250是否成立。这 就是一个原假设(null hypothesis),通常用 表示,即: H0 : =250
第三节 自由分布检验
一、自由分布检验概述 自由分布检验与限定分布检验不同, 它是指在假设检验时不对总体分布的形状和参数加 以限制的检验。与参数检验相对应,自由分布检验又称为非参数检验,但这里的非参数只是 指未对检验统计量服从的分布及其参数做出限制, 并不意味着在检验中 “不涉及参数” “不 或 对参数进行检验” 。
• 解:通过统计软件进行计算。
(二)配对样本的均值检验 设配对观察值为(x,y),其差值是 d = x-y。设 d 为差值的总体均值,要检验的是:
H 0 : d 0 , H1 : d 0
记d
d ,则其方差是: n
2
2 d d / n Sd n(n 1) n
t
X 1000 S/ n
第三步:确定显著性水平,确定拒绝域。 α=0.05,查 t-分布表(自由度为 8),得临界值是 t / 2, n 1 t0.025,8 =2.306, 拒绝域是(-,-2.306]∪[2.306,+)。在 Excel 中,可以使用函数 TINV(0.05,8) 得到临界值 t0.025,8 。 第四步:计算检验统计量的样本观测值。 将 X 986 ,n=9,S=24,代入 t 统计量得:
H1 • 与原假设对立的是备选假设(alternative hypothesis) ,备选假设是在原假设被否 定时另一种可能成立的结论。备选假设比 原假设还重要,这要由实际问题来确定, 一般把期望出现的结论作为备选假设。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§3 检验母体方差 3.1 检验正态母体的方差
——2
χ检验
母体),(~2σμN X ,2
,σμ均未知,试对
2
σ与2
0σ有无显著差异作假设检验.
①在母体上作
假设
↔=2
020:σσH 2021:σσ≠H
②检验统计量
)1( ~ )1(22
02
2
--=*n S
n H χσχ
③给定显著水平α,如图存在
)1(22
1--
n α
χ
和)1(2
2
-n αχ,使
2
)}1({)}1({2
2
222
12α
χχχ
χαα
=
->=-<-
n P n P
故取拒绝域
}
)1()1(),,,{(2
2
222
12
21->-<=-
n n x x x W n αα
χχχ
χ或
④决策:当抽样结果是
W
x x x n ∈),,,(21 时,拒绝0
H ,认为2
σ与2
0σ有
显著差异;否则接受0
H ,认为2
σ与20
σ无
显著差异.
例3.3.1 某细纱车间纺出的一种细纱支数的标准差2.10=σ,现从某日纺出的一批细纱中随机抽出16缕进行支数测
量,算得子样标准差1.2*
=s ,问:纱的均
匀度有无显著变化(取05.0=α)?假定
母体分布是正态的。
解: 设该日纺出的纱的支数
),(~2
σμN X ,2
,σμ均未知,
作假设↔=2.1:20σH 2.1:21
≠σH 检验统计量)1(~
)1(22
22
--=
*n S
n H χσ
χ
给定显著水平α,拒绝域为
}
)1()1(),,,{(2
2
222
1221->-<=-n n x x x W n ααχχχχ或
这时16=n ,2.10=σ,1.2*
=s ,从而94.452
=χ,又05.0=α,查表得
262.6)15()1(975.02
1==--
χχ
α
n ,
488.27)15()1(025.02
==-χχαn ,
可见)1(2
2
->n αχχ,故应拒绝0H ,认为
这天细纱的均匀度有显著变化。
例3.3.2
),(~2
σμN X ,
2
,σμ均未知,
当45>n ,作如下假设检验
↔=2
2
0:σσH 2021:σσ≠H
检验统计量取为2
02
2
)1(σχ
*-=
S
n ,证明:给
定显著水平α,则拒绝域为
}
)1(2)1({})1(2)1({2
22
2ααχχu n n u n n W ---≤-+-≥= .
证明:作假设↔=2020:σσH 2
021:σσ≠H ,
0H 成立时检验统计量
)1(~)1(2
20
22
--=
*n S
n H χσ
χ
而45>n ,由2
χ分布的性质知,
)
1,0()
1(2)
1(~
2
N n n U H 近似
---=
χ
给定显著水平α,拒绝域为
}
)
1(2)
1({
}{2
22
ααχu n n u U W ≥---=≥=
}
)1(2)1({})1(2)1({2
22
2ααχχu n n u n n ---≤-+-≥= 证毕.
3.2 检验两个正态母体的方差相等——F 检验
设母体),(~2
11σμN X ,母体),(~2
22σμN Y ,
且X 与Y 相互独立,
2
221σσ,未知,试对21σ与
2
2
σ有无显著差异作假设检验.
①在母体上作假设
↔=22210:σσH 2
2211:σσ≠H
②
检
验
统计量
)
1,1(~ / 212*2*22
212*2*0
--==n n F S
S S S
F H
Y
X H Y
X σσ ③给定显著水平α,如图存在
)1,1(212
1---
n n F α和)1,1(212
--n n F α,使 2
)}1,1({)}1,1({212
212
1α
αα
=
-->=--<-
n n F F P n n F
F P
故取拒绝域
()1,1(),,,;,,,{(1
2
212
1212121>--<=-
n F F n n F
F y y y x x x W n n αα
或
④决策:当抽样结果是W y y y x x x n n ∈),,,;,,,(2
1
2121 时,拒绝0
H ,认
为2
1σ与22σ有显著差异;否则接受0
H ,认为2
1σ与22σ无显著差异.
注①: 在本章检验两个正态母体的均值相等,及在上一章求两个正态母体的均值之差的置信区间时,均须假定两个正态母体的方差相等。
——实际问题中,这一假设是否合理,可以用上述方
法去检验。
例3.3.3 有两种冶金方法,所得产
品中的杂质含量(%)分别为,
),(~2
11σμN X ,),(~2
22σμN Y ,且
X 与Y 相互独立,各抽取
一个子样,杂质含量(%)如下:
问:两种方法生产的产品中所含杂质的波动性有无显著差异(取05.0=α)?
解:作假设↔=22210:σσH 2
2211:σσ≠H
检验统计量 )
1,1(~
212
*2
*0
--=n n F S S
F H Y
X
拒绝域
()1,1(),,,;,,,{(1
2
212
1212121>--<=-
n F F n n F
F y y y x x x W n n αα
或
给定显著水平05.0=α,9,1321
==n n ,
则查表可得
20.4)8,12()1,1(025.0212
==--F n n F α,
28
.051
.31
)12,8(1)8,12()1,1(025.0975.02121====---F F n n F α
接受域为)20.4,
28.0(=W
又算得862.52*=X
S
,641.12*=Y
S
,从而
W
F ∈=572.3
故接受0
H ,即认为两种方法生产的产品中所含杂质的波动性无显著差异。
注②: 注意到附表4(F 分布的上侧
分位数表)中1),(21>n n F α,故在上述F 检
§4 单侧假设检验
(1)引例及说明
P102例
①原假设
H的选取原则: 检验产
品质量是否合格时,取
H为合格;检验
技术革新后某参数值有无显著变化时,取
H为变化不大。
②检验统计量的选取:与双侧检
验的相应情形一致。
③小概率事件的选取原则:给定α,依1H 选取。
④单侧检验拒绝域中的不等号方向与备择假设1H 中的一致。
(2)作法:(仅以下述几种情形为例)
①正态母体方差未知时,对均值的左边检验
作假设↔≥00:μμH 01:μμ<H
检验统计量 )1(~/0*0
--==n t n
S X T 时
μμμ
给定显著水平α,如图知有)
1(-n t α
使αα=--<)}1({n t T P ,故取拒绝域
})1(),,,{(21--<=n t T x x x W n α .
②大子样情形,对母体均值的右边检验
作假设↔
≤00:μμH :01μμ>H (其中
0μ已知)
检验统计量 )1,0(~
/00N n
S X U 时
近似
μμμ=-=
给定显著水平α,有αu 使αα≈≥}{u U P ,故取拒绝域
}),,,{(21αu U x x x W n ≥=
③对方差相等的两个正态母体均值之差的左边检验
作假设↔≥210:μμH 211:μμ<H 检验统计量
)
2(~
1111)()(212
1*
2
121*21212121-++
-=
+---===n n t n n S X X n n S X X T 时
时μμμμμμ
其中:2
)1()1(21*2
2*1
12
*22
-+-+-=n n S
n S n S
给定显著水平α,有)
2(21-+n n t
α
使
αα=-+-<)}2({21n n t T P ,故取拒绝域
}
)2(),,,;,,,{(21212121-+-<=n n t T y y y x x x W n n α。
