第02章变压器的运行分析(2)—负载运行
合集下载
2.2变压器的负载运行
1、变压器带负载运行时，当负载增大（不考虑漏抗压降），则一次电流将，空载电流。
2、变压器带负载运行，当负载增大，则其铜损耗，铁损耗。
3、变压器由空载到满载，下列各物理量将如何变化（忽略漏抗压降），，，，。
4、变压器一次侧接额定电压，二次侧接纯电阻性负载，则从一次侧输入的功率。
（A）只含有有功功率；（B）只含有感性无功功率；（C）既含有有功功率又含有感性无功功率；（D）既含有有功功率又含有容性无功功率。
5、变压器负载时，一次磁动势为，一次漏磁通为，一次漏抗为；变压器空载时，一次磁动势为，一次漏磁通为，一次漏抗为，它们的关系是。
（A）；（B）；（C）；（D）。
6、变压器负载（）增加时，从理论上讲，其主磁通。
（A）稍增大；（B）稍减小；（C）增大很多；（D）减小很多。
7、电源电压一定时，试分析当变压器负载（）增加时，如何变化？8、电源电压降低对变压器铁心饱和程度，励磁电流，励磁阻抗，铁耗和铜耗等有何影响？9、简述变压器空载和负载时，励磁磁动势有何不同？10、画出变压器的“T”形、近似和简化等效电路。
11、画出变压器简化等效电路和简化向量图。
12、画出变压器短路时的等效电路，并画出与之对应的向量图。
1、增大不变2、增大不变3、不变不变不变增大4、（C）5、（B）6、（B）7、答：降低。
由外特性曲线知，随负载电流（）增大而下降。
增大。
负载越大，越大，由磁动势平衡方程式知，就越大。
不变。
大小与负载大小基本无关。
不变。
因电源电压不变，磁路饱和情况不变，故不变。
不变。
因漏磁路不饱和，。
8、答：铁心饱和程度降低。
，降低，减少，故饱和程度降低。
励磁电流减少。
由磁化曲线知，励磁电流随磁通减少而减少。
励磁阻抗增大。
励磁阻抗随饱和程度下降而增大。
铜耗减小。
电压降低，，减小，故铜耗减小。
铁耗减小。
，故铁耗减小。
9、答：，空载时I2=0，，所以空载时励磁磁动势仅为一次空载磁动势。
负载时，，励磁磁动势为一、二次的合成磁动势。
10、省略。
变压器的空载运行及负载运行
N1I0 N1 I0 N1 I1L N2 I2
N1 I1L - N2 I2
其中I1L远远大于I0，大部分用来抵抗副边电流引起的磁通量变化。
当负载运行时可认为I1L=I1。
I1
I2 k
或 I1 I2
1 k
N2 N1
k为变压器变比
一、二次电流比近似与匝数成反 比。可见匝数不同，不仅能改变 电压，同时也能改变电流。
产业信息
中国变压器设备-尤其是特种变压器-已 走向世界成为“中国制造” 品牌
谢谢聆听
P0 = PFe + Pcu ≈ PFe
铁损耗分量
铁损耗分量：符号为I10P，供给铁磁材料 铁损（磁滞和涡流损耗），为有功分量
Part 2 空载运行分析
思考
如果误将变压器高低压侧接反，会发生什么异常现象？
变压器低压侧如果接到高压电源上，则铁心主磁 通Φm会增加，磁路饱和程度增加，因而励磁电流I0大 大增加，有可能烧毁线圈（励磁电流随磁路饱和程度 增加而急剧增大）
单相变压器空载运行示意图
Part 2 空载运行分析
空载电流的作用与组成
I10 I10Q I10P
励磁分量
励磁分量：符号为I10Q，用来建立主磁 通，相位与主磁通相同，为无功分量
变压器空载运行时，只从电源吸收少量有功功率P0， 用来供给铁心中铁损PFe和少量绕组铜损Pcu=R1I102 （可忽略不计）。容量越大，空载功率P0越小
Part 3 变压器的负载运行
变压器作用 通过对变压器负载运行的分析，可以清楚地看出变压器具有变电压、 变电流、变阻抗的作用。
• 变换电压 U1/U2≈E1/E2=k=N1/N2
• 变换电流 I1/I2≈N2/N1=1/k
变压器的运行分析资料
1 I1 I 2 k
2. 负载时二次电压、电流的关系
A
I0
E E 1 s1
m
I 2
s 2
a
U 2
U 1
X
s1
N1
E E 2 s2
ZL
N2
x
二次回路的电压方程为
U2 E2 Es 2 I2 R2
Es 2 jI 2 X 2
U2 E2 I2 (R2 jX 2 ) E2 I 2 Z2
F0 N1I0
m
E1
E2 U 20
1.主磁通、漏磁通
U 1
A
I0
E E 1 s1
m
a
s1
N1 N2
E 2
U 20
X
x
主磁通：沿铁心闭合，同时与一、二次绕组相交链的磁通， 其幅值用m表示。
漏磁通：主要以空气或变压器油等非铁磁材料构成回路， 仅与一次绕组相交链的磁通称为一次绕组的漏磁通，其幅 值用s1 表示。 主磁通和漏磁通的区别：
N1I0
F 1F 2 F 0
或 用电流形式表示为
N1I1 N2 I2 N1I0
N2 I1 I2 I0 N1 N2 1 I1 I 0 I 2 I 0 I 2 I 0 I1L k N1
N2 1 I1 I 0 I 2 I 0 I 2 I 0 I1L k N1 N1 式中， k 为变压器变比； N2
磁化电流图解法
t
0
i0
t i0
i0
i03
i01
•当主磁通为正弦波时，由于磁路饱和， 励磁电流为尖顶波。
第二章 (2)变压器的运行分析
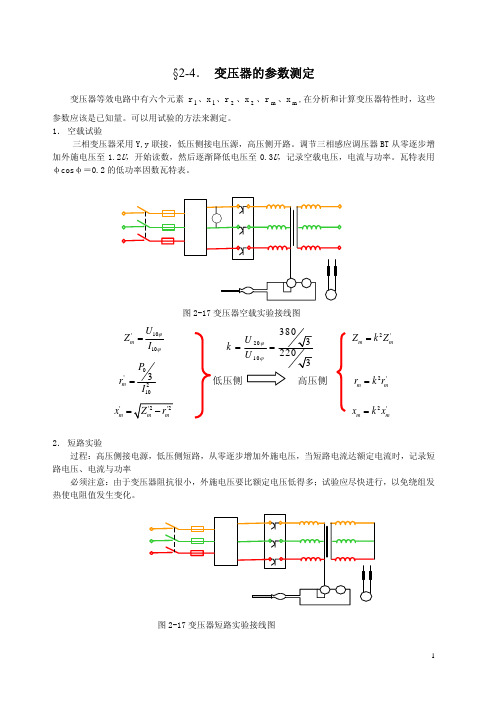
U 2Nφ I 2Nφ
* 相应的原、副绕组漏阻抗的标么值为： Z1 =
Z I ⋅Z Z1 I ⋅Z * = 1N 1 ， Z 2 = 2 = 2N 2 Z 2N U 2N Z2N U1N
3．标么值的优点 1）便于对不同容量变压器进行比较 2）采用标么值，原副边各物理量不需要进行归算了。因为归算前后，标么值相等。 3）采用标么值更能说明问题的实质 4） U K =
0.8 感性时。 Δu % ～5%（额定负载所以一般电力变压器在 5%里头以便调剂。
∗ U2
cos(-ϕ2 )=0.8
cosϕ2 = 1 cos ϕ 2 =0.8
∗ I2
3
图 2-19 电压调整曲线
2．变压器的损耗与效率
负载损耗 PCu = I 2 2 rk = (
2 2 铁耗 PFe ∝ β m ∝ U1
5
图 2-17 变压器空载实验接线图
' = Zm
U10ϕ I10ϕ
k =
U 20 ϕ U 10 ϕ
380 = 220
3 3
' Zm = k 2Zm
P0 r =
' m
3 2 I10
低压侧
高压侧
' rm = k 2 rm
' '2 '2 xm = Zm − rm
' xm = k 2 xm
2． 短路实验 过程：高压侧接电源，低压侧短路，从零逐步增加外施电压，当短路电流达额定电流时，记录短 路电压、电流与功率 必须注意：由于变压器阻抗很小，外施电压要比额定电压低得多；试验应尽快进行，以免绕组发 热使电阻值发生变化。
η max = (1 −
2P0 P0 ⋅ SN COSϕ2 + 2P0 PKN
2-变压器负载运行
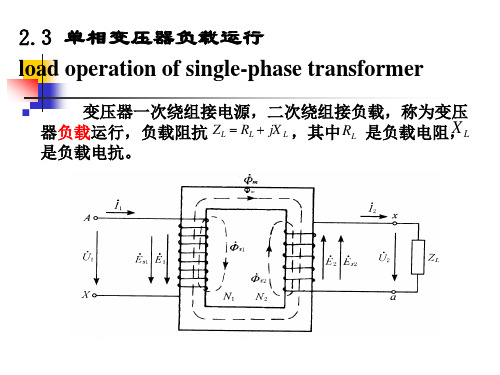
的大小
与空载运行时相比,负载时一次绕组的电流变化了,电源电压
不变,严格说来,负载时的
•
E
与空载时的不同。但在电力变压
1
器仍的然设还计是I中1N Z1I•0很U1小.仍,即存使在在U1额 E定1 由负载E1下 4运.44行fN1,I1Nm
比I0 大很多倍, 看出,空载、负
载与表运示空行。载,时其的主在磁数通值• m上的差数不值多差,仍别可很以小用,即同负一载个时符的号励I•磁0 N磁1或动势F• 0
因
，可认为 Zm
Z
' 2
Z
' L
无限Zm大而断开，于是等效电路变成了“一”型，
称为简化等效电路。如图：
单相变压器的负载运行
b.电压平衡方程式：
•
•
•
•
•
•
•
•
U1
I1
Z1
I 1 Z2'
U
' 2
I1
Z1
Z
' 2
U
' 2
I1 Zk
U
' 2
•
•
I1
I
' 2
•
•
U
' 2
Z
' L
单相变压器的负载运行
b.变压器接感性负载的相量图2-12a图：
单相变压器的负载运行
※相量图的绘制过程： 根据给定的条件不同，画法不同，但都是电压方程式 的相量图表示。
如给定U2, I2,cos2, k 及各参数，画图步骤为：
（（（（（（（1234567）））））））根画在画画画E•1 据出出出出U•2'EU超•I2•'的•20' IE••前21相和E，•1，E量•910它/加I上Z•2的' m与，上，，主I其•I•1加画磁0R夹1上出通的，I角•2'U•相R•1再m为2' I量•，0加；和再上，2为加。它j上II••超11XjI•1；2前'得X2'到得•一m 出U•个1E•。2'铁耗；角；
第2章 变压器的工作原理和运行分析
SN SN ，I 2 N 3U 1 N 3U 2 N
注意！对于三相系统，额定值都是指线间值。
第二节 变压器空载运行
空载：一次侧绕组接到电源，二次侧绕组开路。 一、电磁现象
u1
Φm
i0
Φ 1σ
e1 e1σ
N1
N2
e2
u20
i
二、参考方向的规定
e
i i
e
e
三、变压原理、电压变比
对于变压器的原边回路，根据电路理论有：
u1 i0 r1 e1 e1
空载时 i0r1 和 e1σ 都很小，如略去不 计，则 u1 = - e1 。设外加电压 u1 按 正弦规律变化，则 e1 、Φ 和e2 也都 按正弦规律变化。 设主磁通 m sin t ，则：
u1
Φm
u1
Φm
e1
e2
ωt 0 180° 360°
现在的问题是，要产生上述大小的主磁通 Φm ，需 要多大（什么样）的激磁电流 Im ？
励磁电流的大小和波形受磁路饱和、磁滞及涡 流的影响。
1、磁路饱和对励磁电流的影响
mm mm
i0 tt
00
i0i0 tt
00
i0 i0
tt
tt
磁路不饱和时，i0 ∝φ，其波形为正弦波。
磁路饱和时，i0与φ 不成线性关系，φ越大，磁路 越饱和，i0/φ比值越大，励磁电流的波形为尖顶波。
六、漏抗 漏电势的电路模型与励磁特性的电路模型类似， 只是漏磁通所经路径主要为空气，磁阻大，磁通量 小，磁路不饱和，因此可以忽略漏磁路的铁耗，即 漏电势的电路模型中的等效电阻为零，即漏电势
电机学：变压器第二章 变压器的运行分析03
m
E2 j4.44
fN2
m
E2 j4.44
fN1
由于归算前后主磁场不变，所以
E2
E2
j4.44 fN1 j4.44 fN2
E2
N1 N2
E2
kE2
即归算后的副边电动势比实际电动势放大了k倍。
变压器的运行分析
2. 副边电流的归算值
实际变压器副边磁动势 I2 N2 假想变压器副边磁动势 I2 N1
)2
X2
k2X2
U 2
E2
I2 (R2
jX 2 )
kE2
I2 k
(k 2 R2
jk 2 X 2 )
k E2 I2 (R2 jX 2 ) kU 2
即副边电压与电动势有同样的归算关系。
变压器的运行分析
6. 负载阻抗的归算值
Z L
U 2 I2
kU 2 I2 / k
k 2 U 2 I2
k 2ZL
即负载阻抗的归算值与漏阻抗有同样的归算关系。
当把副边各物理量归算到原边时，凡 是单位为伏的物理量（电动势、电压等） 的归算值等于其原来的数值乘以k；凡是 单位为欧姆的物理量（电阻、电抗、阻抗 等）的归算值等于其原来的数值乘以k2； 电流的归算值等于原来数值乘以1/k 。
折合或归算
折合算法是一种等效处理方法，并不改变 变压器的电磁关系，因此也不会改变其功 率平衡关系。
样，励磁电流I0 、电动势E1与E2、励磁电 阻Rm与励磁电抗Xm都基本不变，漏阻抗 Z1、Z2也是常数，因此，一、二次 电流的大小就取决于负载阻抗ZL 。
折合算法
E1 E 2
k
I1
I2 k
I0
一次、二次绕组的之间 存在变比；
第二章 变压器的运行分析
& Eσ 1 = − j I1 x1
A
& U1 X
& & Eσ 2 = − jI 2 x2
I&1
& & F1 = I1w1
& Φσ 2
& E2
ZL
& Φσ 1
& & Fm = I m w1
& Eσ 1
& E1
& Φm
& E2
I& 2
& & F2 = I 2 w2
& Φσ 2
& Eσ 2
A & U1
r1 & Io
jx1
rm & E1 jxm
X
16
§2-2 变压器的负载运行 一、基本方程式 & I1 1、 磁动势分析 、
A
& Φ
& Φσ 1 & I2 a & U2 x ZL
& & & F1 + F 2 = Fm
& U1 X
& E1
& Φσ 2
& & & I 1 w1 + I 2 w2 = I m w1
′ Z2 = k 2Z2
&′ & &′ ′ U 2 = E 2′ − I 2 ( r2′ + jx2 ) & I2 2 & = kE2 − ( k r2 + jk 2 x2 ) k & & & = k E2 − I 2 ( r2 + jx2 ) = kU 2
A
& U1 X
& & Eσ 2 = − jI 2 x2
I&1
& & F1 = I1w1
& Φσ 2
& E2
ZL
& Φσ 1
& & Fm = I m w1
& Eσ 1
& E1
& Φm
& E2
I& 2
& & F2 = I 2 w2
& Φσ 2
& Eσ 2
A & U1
r1 & Io
jx1
rm & E1 jxm
X
16
§2-2 变压器的负载运行 一、基本方程式 & I1 1、 磁动势分析 、
A
& Φ
& Φσ 1 & I2 a & U2 x ZL
& & & F1 + F 2 = Fm
& U1 X
& E1
& Φσ 2
& & & I 1 w1 + I 2 w2 = I m w1
′ Z2 = k 2Z2
&′ & &′ ′ U 2 = E 2′ − I 2 ( r2′ + jx2 ) & I2 2 & = kE2 − ( k r2 + jk 2 x2 ) k & & & = k E2 − I 2 ( r2 + jx2 ) = kU 2
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
压器本身要有损耗。
pcu1
pFe
pcu 2
P1
P2
P1 m1U1I1c os1 P2 P1 pcu1 pFe pcu2
P2 m2U2I2c os2
A I1
U1
E1
E s1
2. 副边电压与电流关系
U2 I2Z L I2 (RL jX L )
I1
A
I2
s2
E s 2
U1
EEs11
U2 E2 E s2 I2R2
X
Es2 jI2 X 2
U2 E2 I2 (R2 jX 2 ) E2 I2Z2
s2 N1 N2
I2
x
E2 Es2
U2
ZL
a
U1 E1 I1Z1
U2 E2 I2Z2
U 2
I2
Z
L
E1 E2 E1 I0Zm
I1 I0 I2
2）“T”型等效电 路
E1 I0Zm I0 (Rm jX m )
E1 E2'
适用于对称、稳态运行Fra bibliotekE 2'
U
' 2
I2 Z 2
U
' 2
I2( R2'
jX
' 2
)
U
2
I2
Z
L
U1 E1 I1Z1 E1 I1( R1 jX1)
由于 I0 比较小，Z1 也比较小，所以有： U1 E10
负载情况下：
A I1
U1
E1
E s1
X
m
s1 s2
N1 N2
I2 x
EEs22
U 2
a
负载时的 m ，由合成磁动势 F0 产生。
F0 F1 F2 N1I1 N2I2
F0
m
E1
负载时一次绕组：U1 E1 I1Z1
I1 I0
④ 定义：如果保持二次绕组磁动势不变，而假想
它的匝数与一次绕组匝数相同的折合算法，称为二 次向一次折合。
⑤ 折合值：二次向一次折合为例。
⑴ I2 N 2 I2 N1
I2
N2 N1
I2
1 k
I2
⑵电动势
E
2
j 4.44
fN1 m
E2 j 4.44 fN 2 m
E
2
kE 2
⑶阻抗
Z 2 k 2 Z 2
⑷负载电压 U 2 kU 2
Z L k 2 Z L
折合前后，电压、电动势、电流只变大小，相位不变 参数只变大小，阻抗角不变 功率不变 损耗不变 功率因数不变
说明：折合算法其结果不改变变压器运行的物理本质
等效电路 (Equivalent circuit )
1）折合后的六个基本方程式
U1 E1 I1Z1
Zk 短路阻抗 ， Rk 短路电阻，X k 短路电抗
★ 在没给励磁阻抗 Zm ，只给短路阻抗 Zk 的情
况下用简化等值电路。
注意：
1、等值电路中所表示的物理量及参数都是相值，用 在三相变压器时，是指对称运行时的一相的情况。
2、变压器变比 k 必须按原副边额定相电压计算。
3、对称负载时，不必考虑原副边电路接法是否相 同，只需要把所有量转换为相值。且负载接法与 副边接法应相同。
压； l 励磁电抗Xm很大； l X1和X2很小
(Conversion algorithm)
① 目的: a 、使一、二次绕组“有”电连接的 等效电路，这样就可以用电路知识来解题了。
b、画相量图方便（定量画法）。
② 定义：保持一个绕组的磁动势不变而改变其电流 和匝数的算法称为归算法（折合算法）。
③解决方法（算法根据） 保持 F2 不变，就不会影响 F1 的变化。
一次电流从空载到负载 I1 I1N 时，由于 Z1 比较小，
依然有： I1Z1 E1
所以： U1 E1
由于电源电压 U1 不变，所以一次绕组感应电动势 E1
在负载和空载情况下变化不大，因此 m 基本不变。
F0 I1N1 I2 N2 I0 N1
I1N1 I0 N1 (I2 N2 )
U2 E2 I2Z2 U2 I2ZL E1 I0Zm
A I1 *
U 1
E 1
X
I1N1 I2N2 I0N1
k
EE12
N1 N2
m s1 s 2
E s1 E s 2
N1
N2
I2
x
E 2 U 2
ZL
*
a
l 注意： l 不仅适用单相，也适用三相（指一相）； l 主磁通Φm由励磁电流I0产生，大小取决于端电
I1 I0 I2
I1
R1
. jX 1
I0
R2'
jX
' 2
I2
U1
Rm
E1 E2'
U
' 2
ZL
jX m
3）“一”字型等效电路
R1 jX1 R2'
jX
' 2
由“T”型等效电路可得:
I1
I0
I2
I1
Z1
Zm
U1
|| Z2
Z
L
I11
U1
Rm
E1
U
' 2
Z L
jX m
进而可求出 I2 I0 U2 。
F1 N1I1 由两部分组成：
1）励磁磁动势
F0 N1I0
2）与副边磁动势大小相等、方向相反的负载磁动势
F2 N2I2
I1N1 I0 N1 (I2 N2 )
改写成电流形式：
I1
I0
(
N2 N1
) I2
1）产生主磁通的励磁电流 I0 2）随副边电流增大而相应增大的负载分量
(
N2 N1
)I2
☆ “一”字型等效电
R1 jX1 R2'
jX
' 2
I1
I2
路不适用空载，适用正 U1
U
' 2
常负载运行和稳态短路。
4）简化等效电路 (Simplified equivalent circuit )
Zk Z1 Z2
Xk X1 X2
U1
Rk R1 R2
Rk
jX k
I1 I2
U
' 2
Z L
Rk
I1 I2 U1
jX
' k
jI1X K
U 2'
U1
ZL
I1RK
U
' 2
U1
U
' 2
I1 ( RK
jX K )
0
U1
U
' 2
I1 ( RK
jX K )
I1 I2'
1
2
I1 I2'
感性负载简化相量图
五、功率关系 (Power)
负载所消耗的功率是变压器从电源吸收电功率
后，经原、副边传递过来的，在能量传递过程，变
jI1 X 1
已知：U2 、I2 、cos2 、k U1
U
2
I2
Z
L
E 2'
U
' 2
I2 Z 2
I1R1
E1
I2'
1
I1
E1 E2 j4.44 f N1 m
I0
m
I0 E1 / Zm
I1 I0 I2
U1 E1 I1Z1
I2' 2
I2'
U R2'
' 2
jI2'
X
' 2
E1 E2'
定义：变压器原边接电源，副边接负载的运行状态 称为负载运行。
I1
A
*
U1
E s1 E1
m
s1 s2
I2
x
E2 E s 2 U2
ZL
X
N1
N2
*
a
一、负载时电压与电流的关系
1.原副边的电流关系(磁动势平衡关系)
空载时：
N1I0
m 0
E10
空载一次绕组电压平衡方程式：
U1 E10 I0Z1 E10 I0(R1 jX1)