1.3.1函数的单调性例题
1.3.1函数的单调性与导数

二次函数 f ( x) ax 2
2 y 3 x 3 x 的单调区间。 (1)求函数
解法一: 利用二次函数图象特征,对称轴求单调区间。 解法二: y ' 6 x 3 1 1 令y ' 0得x , 令y ' 0得x 2 1 2 2 y 3 x 3 x 的单调递增区间为 ( , ) 2 1 单调递减区间为 ( , ) 2
画出下列函数的图像,并根据图像指出每个函数的单调区间
1 y x
y
y x 2x 1
2
y 3
y
x
y
o
x
o
1
x
1 o
x
在(- ∞ ,0),(0, +∞) 在(- ∞ ,1)上是减 上是减函数。但在定义域 函数,在(1, +∞)上 是增函数。 上不是减函数。
在(- ∞,+∞)上 是增函数
判断函数单调性有哪些方法? 定义法 图象法
(1) 1 (ln x ) . x
(4).对数函数的导数:
(2)
1 (log a x) . x ln a
(5).指数函数的导数:
(1) ( 2) (e x ) e x . (a x ) a x ln a(a 0, a 1).
一、复习回顾
函数 y = f (x) 在给定区间 I上,当 x 1、x 2 ∈I 且 x 1< x 2 时
y
y f ( x)
1 2
x o
y
y f ( x)
y
o y
1
2
x
y f '( x )
1 2 x
(A)
y f ( x)
2 x o
(B) y y f ( x)
高中数学 1.3.1 单调性与最大(小)值(第2课时)复合函数的单调性及单调性的应用课件 新人教A版

第一页,共20页。
1.3 函数的基本性质
第二页,共20页。
1.3.1 单调性与最大(小)值(第2课时) 复合函数的单调性及单调性的应用
第三页,共20页。
课时学案 课时作业
第四页,共20页。
Hale Waihona Puke 课时学案第五页,共20页。
题型一 复合函数的单调性 例1 (1)已知g(x)是[m,n]上的减函数,且a≤g(x)≤b,f(x) 是[a,b]上的增函数,求证:f[g(x)]在[m,n]上也是减函数.
第十九页,共20页。
思考题3 已知函数y=f(x)在R上是增函数,且f(0)=1,求 不等式f(2x-1)-1>0的解集.
【答案】 (12,+∞)
第二十页,共20页。
第六页,共20页。
【证明】 设m≤x1<x2≤n, ∵g(x)是[m,n]上的减函数,且a≤g(x)≤b, ∴b≥g(x1)>g(x2)≥a. 又∵f(x)是[a,b]上的增函数, ∴f[g(x1)]>f[g(x2)]. 由函数的单调性定义知,f[g(x)]在[m,n]上是减函数.
第七页,共20页。
定义域.
(2)上述表格可以总结成一句话:“同增异减”.
第十一页,共20页。
思考题1 写出函数y= 3x+2的单调区间. 【答案】 单调增区间[-23,+∞)
第十二页,共20页。
题型二 单调性的应用 例2 如果函数f(x)=x2+bx+c,对任意实数t都有f(2+t)= f(2-t),比较f(1),f(2),f(4)的大小. 【思路点拨】 本题关键是弄懂f(2+t)=f(2-t)所表达的意 思.它表示数2加t或减t,函数值不变,即x=2是这个二次函数 的对称轴.
1.3.1函数的单调性与导数1-人教A版高中数学选修2-2课件

令(x
1)(x x2
1)
0,解得 1
x
0或0
x
1
y x 1 的单调减区间是(1,0)和(0,1) x
注: 如果一个函数具有相同单调性的单调区间不止 一个,这些单调区间一般不能用“∪”连接,而 只能用“逗号”或“和”分开。
四、课堂练习 1、判断下列函数的单调性, 并求出单调区间:
(1) f ( x) x 2 2x 4; (2) f ( x) e x x;
2
3
3
因 此 , 函 数f ( x)的 递 增 区 间 是(2k 2 ,2k 2 )(k Z );
3
3
递 减 区 间 是(2k 2 ,2k 4 )(k Z ).
3
3
(2) f ( x) x ln(1 x) 1 2
解:函数的定义域是(1,),f ( x) 1 1 x 1 . 2 1 x 2(1 x)
2
2
归纳: 1°什么情况下,用“导数法” 求函数单调性、单 调区间较简便?
总结: 当遇到三次或三次以上的,或图象很难画出的函数求 单调性问题时,应考虑导数法。
2°求可导函数f(x)单调区间的步骤: ①求定义域
②求f'(x)
③令f'(x)>0解不等式⇒f(x)的递增区间 f'(x)<0解不等式⇒f(x)的递减区间
(2) f ( x) x 2 2x 3;
(3) f ( x) sin x x, x (0, );
(4) f ( x) 2x 3 3x 2 24x 1.
解:
(3)因为f ( x) sin x x, x (0, ),所以f ( x) cos x 1 0.
因此,函数f ( x) sin x x在x (0, )上单调递减
《1.3.1函数的单调性(1)》同步练习2

《1.3.1函数的单调性(1)》同步练习2一、选择题1.设(a ,b ),(c ,d )都是函数f (x )的单调增区间,且x 1∈(a ,b ),x 2∈(c ,d ),x 1<x 2,则f (x 1)与f (x 2)的大小关系是( ) A .f (x 1)<f (x 2) B .f (x 1)>f (x 2) C .f (x 1)=f (x 2) D .不能确定[答案] D2.下列函数在区间[0,+∞)上是增函数的是( ) ①y =2x ②y =x 2+2x -1 ③y =|x +2| ④y =|x |+2 A .①② B .①③ C .②③④ D .①②③④[答案] D3.函数f (x )=⎩⎪⎨⎪⎧x +1,x ≥0x -1,x <0在R 上是( )A .减函数B .增函数C .先减后增D .无单调性[答案] B4.定义在R 上的函数f (x )对任意两个不相等实数a ,b ,总有f a -f b a -b>0成立,则必有( )[来源:学.科.网] A .函数f (x )是先增加后减少 B .函数f (x )是衔减少后增加 C .f (x )在R 上是增函数 D .f (x )在R 上是减函数[答案] C5.已知函数f (x )=2x 2-ax -1,在[-1,2]上单调,则实数a 的取值范围是( ) A .[-4,8] B .(-∞,-4]C .[8,+∞]D .(-∞,-4]∪[8,+∞)[答案] D[解析] 由已知得二次函数f (x )=2x 2-ax -1的对称轴为x =a4,若在[-1,2]上单调则满足:a 4≤ -1或a4≥2,∴a ≤-4或9≥8,故选D .6.(2013~2014南阳市一中月考试题)若在[1,+∞)上函数y =(a -1)x 2+1与y =ax 都单调递减,则a 的取值范围是( ) A .a >0B .a >1C .0≤a ≤1D .0<a <1[答案] D[解析] 由于两函数在(1,+∞)上递减应满足⎩⎪⎨⎪⎧a -1<0a >0∴0<a <1.故选D .二、填空题7.写出下列函数的单调区间. (1)y =|x |+1________________. (2)y =-x 2+ax ________________. (3)y =|2x -1|________________. (4)y =-1x +2________________.[答案] (1)增区间[0,+∞),减区间(-∞,0];(2)增区间(-∞,a 2],减区间[a2,+∞);(3)增区间[12,+∞),减区间(-∞,12];(4)增区间 (-∞,-2)和(-2,+∞),无减区间.8.若函数y =-2x 2+mx -3在[-1,+∞)上为减函数,则m 的取值范围是________. [答案] m ≤-4[解析] 由条件知-m2×-2≤-1,∴m ≤-4.9.已知函数f (x )是区间(0,+∞)上的减函数,那么f (a 2-a +1)与f (34)的大小关系为________.[答案] f (a 2-a +1)≤f (34)[解析] ∵a 2-a +1=(a -12)2+34≥34>0,又f (x )在(0,+∞)上为减函数,∴f (a 2-a +1)≤f(34). 三、解答题10.证明函数f (x )=x 2-4x -1在[2,+∞)上是增函数.[证明] 设x 1,x 2是区间[2,+∞)上的任意两个实数,且x 2>x 1≥2,则f (x 1)-f (x 2)=(x 21-4x 1-1)-(x 22-4x 2-1)=x 21-x 22-4x 1+4x 2=(x 1-x 2)(x 1+x 2)-4(x 1-x 2)=(x 1-x 2)(x 1+x 2-4).∵x 2>x 1≥2,∴x 1-x 2<0,x 1+x 2>4, 即x 1+x 2-4>0,∴f (x 1)-f (x 2)<0,即f (x 1)<f (x 2).∴函数f (x )=x 2-4x -1在[2,+∞)上是增函数.11.若函数f (x )=⎩⎪⎨⎪⎧2b -1x +b -1,x >0-x 2+2-b x ,x ≤0在R 上为增函数,求实数b 的取值范围.[分析] 分别考虑两个分段解析式的单调性→再根据整体的单调性求b 的取值范围 [来源:学科网][解析] 由题意得⎩⎪⎨⎪⎧2b -1>02-b ≥0b -1≥f 0,解得1≤b ≤2①[注释] ①本题在列不等式组时很容易忽略b -1≥f (0),即只考虑到了分段函数在各自定义域上的单调性,忽略了f (x )在整个定义域上的单调性.[方法探究] 解决此类问题,一般要从两个方面思考:一方面每个分段区间上函数具有相同的单调性,由此列出相关式子;另一方面要考虑端点处的衔接情况,由此列出另一部分的式子.12.(能力拔高题)(1)写出函数y =x 2-2x 的单调区间及其图象的对称轴,观察:在函数图象对称轴两侧的单调性有什么特点?(2)写出函数y =|x |的单调区间及其图象的对称轴,观察:在函数图象对称轴两侧的单调性有什么特点?(3)定义在[-4,8]上的函数y =f (x )的图象关于直线x =2对称,y =f (x )的部分图象如图所示,请补全函数y =f (x )的图象,并写出其单调区间,观察:在函数图象对称轴两侧的单调性有什么特点?(4)由以上你发现了什么结论?(不需要证明)[解析] (1)函数y =x 2-2x 的单调递减区间是(-∞,1],单调递增区间是[1,+∞);其图象的对称轴是直线x =1;区间(-∞,1]和区间[1,+∞)关于直线x =1对称,函数y =x 2-2x 在对称轴两侧的单调性相反.(2)函数y =|x |的单调减区间为(-∞,0],增区间为[0,+∞),图象关于直线x =0对称,在其两侧单调性相反..(3)函数y =f (x ),x ∈[-4,8]的图象如图所示.函数y=f(x)的单调递增区间是[-4,-1],[2,5];单调递减区间是[5,8],[-1,2];区间 [-4,-1]和区间[5,8]关于直线x=2对称.区间[-1,2]和区间[2,5]关于直线x =2对称,函数y=f(x)在对称轴两侧的对称区间内的单调性相反.(4)发现结论:如果函数y=f(x)的图象关于直线x=m对称,那么函数y=f(x)在直线x=m两侧对称区间内的单调性相反.。
1.3.1函数的单调性基础复习
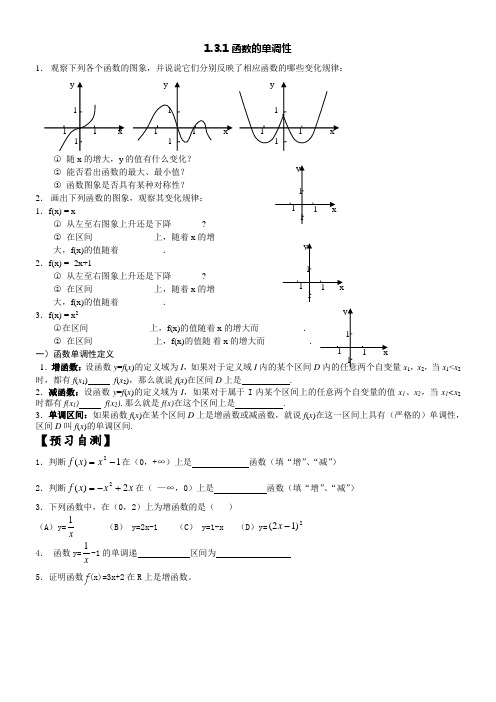
1.3.1函数的单调性1. 观察下列各个函数的图象,并说说它们分别反映了相应函数的哪些变化规律:○1 随x 的增大,y 的值有什么变化? ○2 能否看出函数的最大、最小值? ○3 函数图象是否具有某种对称性? 2. 画出下列函数的图象,观察其变化规律: 1.f(x) = x○1 从左至右图象上升还是下降 ______? ○2 在区间 ____________ 上,随着x 的增 大,f(x)的值随着 ________ .2.f(x) = -2x+1○1 从左至右图象上升还是下降 ______? ○2 在区间 ____________ 上,随着x 的增 大,f(x)的值随着 ________ .3.f(x) = x 2○1在区间 ____________ 上,f(x)的值随着x 的增大而 ________ . ○2 在区间 ____________ 上,f(x)的值随 着x 的增大而 ________ 一)函数单调性定义1.增函数:设函数y =f (x )的定义域为I ,如果对于定义域I 内的某个区间x 1,x 2,当x 1<x 2时,都有f (x 1) f (x 2),那么就说f (x )在区间D 上是 .2.减函数:设函数y =f (x )的定义域为I ,如果对于属于I 内某个区间上的任意两个自变量的值x 1、x 2,当x 1<x 2时都有f(x 1) f(x 2).那么就是f(x)在这个区间上是 .3.单调区间:如果函数f (x )在某个区间D 上是增函数或减函数,就说f (x )在这一区间上具有(严格的)单调性,区间D 叫f (x )的单调区间.【预习自测】1.判断1)(2-=x x f 在(0,+∞)上是 函数(填“增”、“减”) 2.判断x x x f 2)(2+-=在( —∞,0)上是 函数(填“增”、“减”) 3.下列函数中,在(0,2)上为增函数的是( ) (A )y=x1(B ) y=2x-1 (C ) y=1-x (D )y=2)12(-x4. 函数y=x1-1的单调递 区间为5.证明函数f (x)=3x+2在R 上是增函数。
1.3.1函数的单调性与导数

∴f’(x)=3ax2+6x-1≤0在R上恒成立,
∴a<0且△=36+12a≤0,
∴a ≤-3
玉林市一中高二数学组
练习2 已知函数f (x )= 2ax - x 3,x (0, 1],a 0, 若f (x )在(0, 1]上是增函数,求a的取值范围。
'(x)>0(或<0) 但由f(xf )在这个区间上单调递增(递减) 而仅仅得到 是不够的。还有可 能导数等于0也能使f(x)在这个区间上单调,
本题用到一个重要的转化: 所以对于能否取到等号的问题需要单独验证
m≥f(x)恒成立 m f (x)max m f (x)恒成立 m f (x)min
玉林市一中高二数学组
2.用定义证明函数的单调性的一般步骤: 取值→作差→变形→定号→下结论 3. 判断函数单调性有哪些方法? 定义法
图象法
玉林市一中高二数学组
思考:那么如何求出下列函数的单调性呢? (1)f(x)=2x3-6x2+7 (2)f(x)=ex-x+1 (3)f(x)=sinx-x 发现问题:用单调性定义讨论函数单调性虽然
分析:
当x 3或x 2时,f '( x ) 0; f ( x )在此区间递增 当x 3或x 2时,f '( x ) 0. f ( x )图象在此两处
附近几乎没有升降
试画出函数
f ( x ) 图象的大致形状。
变化,切线平行x轴
y f ( x)
y A B
1.3.1函数的单调性与最值性
显明教育学生课后作业1、函数y ==x 2-6x +10在区间(2,4)上是( )A 、递减函数B 、递增函数C 、先递减再递增D 、选递增再递减、 2、函数f (x )=-2x +2(a -1)x +2在(-∞,4)上是增函数,则a 的范围是( )A 、a ≥5B 、a ≥3C 、a ≤3D 、a ≤-53、若函数)(x f 在区间(a ,b )上为增函数,在区间(b ,c )上也是增函数,则函数)(x f 在区间(a ,c )上( )A 、必是增函数B 、必是减函数C 、是增函数或是减函数D 、无法确定增减性 4、(x)=x 2-2ax+1在(]1,∞-上是减函数,则a 的取值范围是____________________5、数y=x x 22-的单调递增区间是_______________6、||2x x y +-=,单调递减区间为 ,最大值和最小值的情为 .7、(x )是定义在R 上的增函数,f (xy )=f (x )+f (y ),f (3)=1,求解不等式f (x )+f (x -2)>1.8、()211y x x x =--≤≤的最大值,最小值.9、数()21y x x =-+的图象,并根据函数的图象找出函数的单调区间. 10、]3,1[,)2()(2-∈-=x x x f ,求函数)1(+x f 得单调递减区间.显明教育学生预习内容一、函数的奇偶性定义1.偶函数:一般地,对于函数f(x)的定义域内的任意一个x,都有,那么f(x)就叫做偶函数.2.奇函数:一般地,对于函数f(x)的定义域内的任意一个x,都有,那么f(x)就叫做奇函数.注意:○1函数是奇函数或是偶函数称为函数的奇偶性,函数的奇偶性是函数的整体性质;○2由函数的奇偶性定义可知,函数具有奇偶性的一个必要条件是,对于定义域内的任意一个x,则-x也一定是定义域内的一个自变量(即定义域关于原点对称).二、具有奇偶性的函数的图象的特征偶函数的图象关于对称;奇函数的图象关于对称。
1.3.1函数的单调性与导数(一)
1.3.1函数的单调性与导数(一)【学习目标】1. 记住函数的单调性与导数之间的关系;2. 学会用导数研究函数的单调性,会求函数的单调区间.【重点难点】重点: 函数的单调性与导数之间的关系难点: 利用函数的导数判断单调性【学习过程】【预习案】预习教材P22~26,完成以下问题1.一般地,设函数y=f(x)在某个区间内有导数,如果在这个区间内,f ′(x)>0,那么函数y=f(x)为在这个区间内的如果在这个区间内,f ′(x)<0,那么函数y=f(x)为在这个区间内的2.函数图象的变化趋势与导数值大小的关系3.用导数求函数单调区间的步骤:①优先确定函数的定义域;②求函数f(x)的导数f ′(x);③定义域内满足不等式f ′(x)>0的x的区间就是递增区间;满足不等式f ′(x)>0的x的区间就是递减区间.[预习诊断]判断(正确的打“√”,错误的打“×”)1.函数f(x)在定义域上都有f′(x)>0,则函数f(x)在定义域上单调递增.() 2.函数在某一点的导数越大,函数在该点处的切线越“陡峭”.( )3.函数在某个区间上变化越快,函数在这个区间上导数的绝对值越大.( ) 【探究案】探究一函数余导函数图象间的关系例1:设函数f(x)在定义域内可导,y=f(x)的图象如图所示,则导函数y=f ′(x)的图象可能为()【变式训练】设f ′(x)是函数f(x)的导函数,f ′(x)的图象如图所示,则f(x)的递增区间是.探究二利用导数求函数的单调区间例2:求下列函数的单调区间:(1)f(x)=x-x3;(2)f(x)=x2-ln x.【变式训练】证明:函数xxxfsin)(=在区间),2(ππ上单调递减.注意事项:①求函数的单调区间,必须在函数的定义域内进行.②如果函数的单调区间有多个时,单调区间不能用“∪”符号连接,只能用“,”或“和”隔开.③导数法求得的单调区间一般用开区间表示【检测案】1.函数f(x)=x+ln x在(0,6)上是()A.单调增函数B.单调减函数C.在⎝⎛⎭⎫0,1e上是减函数,在⎝⎛⎭⎫1e,6上是增函数D.在⎝⎛⎭⎫0,1e上是增函数,在⎝⎛⎭⎫1e,6上是减函数2.函数y=x2-4x+a的增区间为________,减区间为________.是()4.如图所示的是函数y=f(x)的导函数y=f′(x)的图象,则在[-2,5]上函数f(x)的单调递增区间为________.5.函数f(x)=(x-3)e x的单调递增区间是()A.(-∞,2) B.(0,3)C.(1,4) D.(2,+∞)6.函数y=12x2-ln x的单调递减区间为()A.(-1,1] B.(0,1]C.[1,+∞) D.(0,+∞)7.判断函数xxxfln)(=在区间(0,e)上的单调性。
2019-2020学年高中数学(苏教版 选修2-2)教师用书:第1章 1.3.1 单调性 Word版含答案
1.3 导数在研究函数中的应用1.3.1单调性1.利用导数研究函数的单调性.(重点)2.含有字母参数的函数单调性的讨论,单调区间的求解.(难点)3.由单调性求参数的取值范围.(易错点)[基础·初探]教材整理函数的单调性与其导数的关系阅读教材P28“例1”以上部分,完成下列问题.1.函数的单调性与其导数的关系(1)一般地,在某区间上函数y=f(x)的单调性与导数有如下关系:(2)2.导数与函数图象间的关系(1)导函数图象在x轴上方的区间为原函数的单调增区间,导函数图象在x轴下方的区间为原函数的单调减区间.(2)一般地,如果一个函数在某一范围内导数的绝对值较大,那么函数在这个范围内变化得快,这时,函数的图象就比较“陡峭”;反之,函数的图象就“平缓”一些.1.判断正误:(1)若函数f(x)在(a,b)上是增函数,则对任意x∈(a,b),都有f′(x)>0.( )(2)函数f(x)=1x在其定义域上是单调减函数.( )(3)函数f(x)=x3-2x在(1,+∞)上单调递增.( )(4)若存在x∈(a,b)有f′(x)=0成立,则函数f(x)为常数函数.( )【答案】(1)×(2)×(3)√(4)×2.函数f(x)=(x-3)e x的单调递增区间是________.【解析】f′(x)=(x-3)′e x+(x-3)(e x)′=(x-2)e x,令f′(x)>0,解得x>2.【答案】(2,+∞)[质疑·手记]预习完成后,请将你的疑问记录,并与“小伙伴们”探讨交流:疑问1:_______________________________________________解惑:_______________________________________________疑问2:_______________________________________________解惑:_______________________________________________疑问3:_______________________________________________解惑:_______________________________________________[小组合作型](1)0)内是减函数.(2)判断函数f(x)=ln xx在区间(0,2)上的单调性.【精彩点拨】求出导数f′(x),然后判断导数的符号即可.【自主解答】(1)证明:由于f(x)=e x-x-1,所以f′(x)=e x-1,当x∈(0,+∞)时,e x>1,即f′(x)=e x-1>0.故函数f(x)在(0,+∞)内为增函数,当x∈(-∞,0)时,e x<1,即f′(x)=e x-1<0. 故函数f(x)在(-∞,0)内为减函数.(2)由于f(x)=ln x x,所以f′(x)=1x·x-ln xx2=1-ln xx2.由于0<x<2,所以ln x<ln 2<1,x2>0.故f′(x)=1-ln xx2>0.∴函数f(x)在区间(0,2)上是单调递增函数.1.利用导数证明函数f(x)在给定区间上的单调性,实质上就是证明f′(x)>0(或f′(x)<0)在给定区间上恒成立.2.利用导数判断可导函数f(x)在(a,b)内的单调性,步骤是:(1)求f′(x);(2)确定f′(x)在( a,b)内的符号;(3)得出结论.[再练一题]1.证明:函数y=ln x+x在其定义域内为增函数.【证明】显然函数的定义域为{x|x>0},又f′(x)=(ln x+x)′=1x+1,当x>0时,f′(x)>1>0,故y=ln x+x在其定义域内为增函数.(1)f(x)=x2-ln x;(2)f(x)=exx-2;(3)f (x )=-x 3+3x 2.【精彩点拨】 首先确定函数的定义域,再求导数,进而解不等式得单调区间. 【自主解答】 (1)函数f (x )的定义域为(0,+∞). f ′(x )=2x -1x=错误!.因为x >0,所以2x +1>0,由f ′(x )>0,解得x >22,所以函数f (x )的单调递增区间为⎝ ⎛⎭⎪⎪⎫22,+∞; 由f ′(x )<0,解得x <22,又x ∈(0,+∞),所以函数f (x )的单调递减区间为⎝ ⎛⎭⎪⎪⎫0,22. (2)函数f (x )的定义域为(-∞,2)∪(2,+∞). f ′(x )=错误!=错误!.因为x ∈(-∞,2)∪(2,+∞), 所以e x >0,(x -2)2>0.由f ′(x )>0,解得x >3,所以函数f (x )的单调递增区间为(3,+∞);由f ′(x )<0,解得x <3,又x ∈(-∞,2)∪(2,+∞),所以函数f (x )的单调递减区间为(-∞,2)和(2,3).(3)函数f (x )的定义域为R . f ′(x )=-3x 2+6x =-3x (x -2).当0<x <2时,f ′(x )>0,所以函数f (x )的单调递增区间为(0,2);当x <0或x >2时,f ′(x )<0,所以函数f (x )的单调递减区间为(-∞,0)和(2,+∞).利用导数求函数单调区间的步骤: (1)确定函数f (x )的定义域; (2)求导数f ′(x );(3)由f ′(x )>0(或f ′(x )<0),解出相应的x 的范围;当f ′(x )>0时,f (x )在相应的区间上是增函数;当f ′(x )<0时,f (x )在相应区间上是减函数.(4)结合定义域写出单调区间.[再练一题]2.若函数f (x )=x 2-2x -4ln x ,则函数f (x )的单调递增区间为________.【导学号:01580011】【解析】 由已知f (x )的定义域为(0,+∞), f ′(x )=2x -2-4x =2x2-2x -4x,由f ′(x )>0得x 2-x -2>0,解得x <-1或x >2, 又x >0,所以函数f (x )的单调递增区间为(2,+∞). 【答案】 (2,+∞)[探究共研型]探究【提示】 由已知得f ′(x )=3x 2-a , 因为f (x )在(-∞,+∞)上是单调增函数, 所以f ′(x )=3x 2-a ≥0在(-∞,+∞)上恒成立, 即a ≤3x 2对x ∈R 恒成立,因为3x 2≥0,所以只需a ≤0. 又因为a =0时,f ′(x )=3x 2≥0, f (x )=x 3-1在R 上是增函数,所以a ≤0.探究2 若函数f (x )=x +ax +ln x (a ∈R )在(1,+∞)上单调递增,求a 的取值范围.【提示】 函数f (x )的定义域为(0,+∞),f ′(x )=1-ax2+1x =x2+x -ax由题意知,f ′(x )≥0在(1,+∞)上恒成立, 即x 2+x -a ≥0在(1,+∞)上恒成立, 令g (x )=x 2+x -a =⎝ ⎛⎭⎪⎪⎫x +122-14-a ,则g (x )>2-a ,从而2-a ≥0,∴a ≤2. 当a =2时,f ′(x )>0在(1,+∞)上恒成立, 因此实数a 的取值范围是(-∞,2].已知关于x 的函数y =x 3-ax +b .(1)若函数y 在(1,+∞)内是增函数,求a 的取值范围; (2)若函数y 的一个单调递增区间为(1,+∞),求a 的值.【精彩点拨】 (1)函数在区间(1,+∞)内是增函数,则必有y ′≥0在(1,+∞)上恒成立,由此即可求出a 的取值范围.(2)函数y 的一个单调递增区间为(1,+∞),即函数单调区间的端点值为1,由此可解得a 的值.【自主解答】 y ′=3x 2-a .(1)若函数y =x 3-ax +b 在(1,+∞)内是增函数. 则y ′=3x 2-a ≥0在x ∈(1,+∞)时恒成立, 即a ≤3x 2在x ∈(1,+∞)时恒成立, 则a ≤(3x 2)最小值. 因为x >1,所以3x 2>3.所以a ≤3,即a 的取值范围是(-∞,3]. (2)令y ′>0,得x 2>a3.若a ≤0,则x 2>a3恒成立,即y ′>0恒成立,此时,函数y =x 3-ax +b 在R 上是增函数,与题意不符. 若a >0,令y ′>0,得x >a 3或x <-a 3.因为(1,+∞)是函数的一个单调递增区间,所以a3=1,即a =3.1.解答本题注意:可导函数f (x )在(a ,b )上单调递增(或单调递减)的充要条件是f ′(x )≥0(或f ′(x )≤0)在(a ,b )上恒成立,且f ′(x )在(a ,b )的任何子区间内都不恒等于0.2.已知f (x )在区间(a ,b )上的单调性,求参数范围的方法(1)利用集合的包含关系处理f (x )在(a ,b )上单调递增(减)的问题,则区间(a ,b )是相应单调区间的子集;(2)利用不等式的恒成立处理f (x )在(a ,b )上单调递增(减)的问题,则f ′(x )≥0(f ′(x )≤0)在(a,b)内恒成立,注意验证等号是否成立.[再练一题]3.将上例(1)改为“若函数y在(1,+∞)上不单调”,则a的取值范围又如何?【解】y′=3x2-a,当a<0时,y′=3x2-a>0,函数在(1,+∞)上单调递增,不符合题意.当a>0时,函数y在(1,+∞)上不单调,即y′=3x2-a=0在区间(1,+∞)上有根.由3x2-a=0可得x=a3或x=-a3(舍去).依题意,有a3>1,∴a>3,所以a的取值范围是(3,+∞).[构建·体系]1.设函数f(x)在定义域内可导,y=f(x)的图象如图1-3-1所示,则导函数y=f′(x)的图象可能是( )图1-3-1【解析】当x<0时,f(x)为增函数,f′(x)>0,排除①,③;当x>0时,f(x)先增后减再增,对应f ′(x )先正后负再正.故选④.【答案】 ④2.下列函数中,在区间(-1,1)上是减函数的有________(填序号). ①y =2-3x 2;②y =ln x ;③y =1x -2;④y =sin x .【解析】 显然,函数y =2-3x 2在区间(-1,1)上是不单调的; 函数y =ln x 的定义域为(0,+∞),不满足题目要求; 对于函数y =1x -2,其导数y ′=错误!<0,且函数在区间(-1,1)上有意义,所以函数y =错误!在区间(-1,1)上是减函数;函数y =sin x 在⎝ ⎛⎭⎪⎪⎫-π2,π2上是增函数,所以函数y =sin x 在区间(-1,1)上也是增函数.【答案】 ③3.函数f (x )=2x 3-9x 2+12x +1的单调减区间是________.【解析】 f ′(x )=6x 2-18x +12,令f ′(x )<0,即6x 2-18x +12<0,解得1<x <2. 【答案】 (1,2)4.已知函数f (x )=ax +1x +2在(-2,+∞)内单调递减,则实数a 的取值范围为________.【解析】 f ′(x )=错误!,由题意得f ′(x )≤0在(-2,+∞)内恒成立,∴解不等式得a ≤12,但当a =12时,f ′(x )=0恒成立,不合题意,应舍去,所以a 的取值范围是⎝ ⎛⎭⎪⎪⎫-∞,12.【答案】 ⎝⎛⎭⎪⎪⎫-∞,125.已知函数f (x )=ln x ,g (x )=12ax 2+2x ,a ≠0.若函数h (x )=f (x )-g (x )在[1,4]上单调递减,求a 的取值范围. 【解】 h (x )=ln x -12ax 2-2x ,x ∈(0,+∞),所以h ′(x )=1x -ax -2.因为h (x )在[1,4]上单调递减,所以x ∈[1,4]时,h ′(x )=1x -ax -2≤0恒成立,即a ≥1x2-2x恒成立,所以a ≥G (x )最大值,而G (x )=⎝ ⎛⎭⎪⎪⎫1x -12-1.因为x ∈[1,4],所以1x ∈⎣⎢⎢⎡⎦⎥⎥⎤14,1,所以G (x )最大值=-716(此时x =4), 所以a ≥-716. 当a =-716时,h ′(x )=1x +716x -2=16+7x2-32x16x=错误!.因为x ∈[1,4],所以h ′(x )=错误!≤0, 即h (x )在[1,4]上为减函数. 故实数a 的取值范围是⎣⎢⎢⎡⎭⎪⎪⎫-716,+∞.我还有这些不足:(1)_______________________________________________ (2)_______________________________________________我的课下提升方案:(1)_______________________________________________(2)_______________________________________________。
人教版必修一1.3.1函数的单调性课件
2.已知
f
(x)
1,由于
x
f
(2)
f
(1) ,所以 f
( x)是增函数
。
3.因为函数
所以函数 f
f (
(x) 1 x) 1x
x
在区间 在区间
(,0)和(0, )都是减函数,
,0 0, 是减函数。
1.错
2.错
3.错
例1 下图是定义在闭区间[-5,5]上的函 y f (x) 数 y f (x)的图象,根据图象说出的单调区间,以及 在每一区间上, y f (x) 是增函数还是减函数.
4 定号(即判断差f(x1)-f(x2)的正负); 5 下结论(即指出函数f(x)在给定的区间D上的 单调性).
练习.探究一次函数y mx b(x R) 的单调性,并用 定义证明你的结论 m<0时,一次函数是减函数;m>0,一次函数是增函数。
证明:任取 x1, x2 R,且x1 x2, 则
例2 证明:根据单调函数的定义证明 f (x) 1
x
在(0,+∞)上是减函数。
证明:设x1,x2是(0,+∞)上任意两个实
取值
数,
且x1f<(xx21,) 则f (x2 )
作差
1 1 x2 x1
x1 x2 x1x2
变形
由于x1,x2 (0,) ,得x1x2>0,又由x1<x2得x2-x1>0
-2 -5 -4 -3 -1
3
2 1
O1 2 3 4 5 -1 -2
解:函数 y f (x)的单调区间有 [-5,-2), [-2,1), [1,3), [3,5],
在区间[-5,-2), [1,3)上是减函数 在区间[-2,1), [3,5)上是增函数.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.3.1函数的单调性题型一、利用函数的图象确定函数的单调区间 例1.作出下列函数的图象,并写出函数的单调区间 (1)12-=x y ; (2)322++-=x x y ; (3)2)2(1-++=x x y ; (4)969622++++-=x x x x y相应作业1:课本P32第3题. 题型二、用定义法证明函数的单调性用定义法证明函数的单调性步骤:取值 作差变形 定号 下结论✍取值,即_____________________________;✍作差变形,作差____________,变形手段有__________、_____、_____、_______等; ✍定号,即____________________________________________________________;④下结论,即______________________________________________________。
例2.用定义法证明下列函数的单调性(1)证明:1)(3+-=x x f 在()+∞∞-,上是减函数.▲定义法证明单调性的等价形式: 设[]b a x x ,21∈、,21x x ≠,那么[])(0)()(0)()()(21212121x f x x x f x f x f x f x x ⇔>--⇔>--在[]b a ,上是增函数;[])(0)()(0)()()(21212121x f x x x f x f x f x f x x ⇔<--⇔<--在[]b a ,上是减函数.(2)证明:x x x f -+=1)(2在其定义域内是减函数;(3)证明:21)(xx f =在()0,∞-上是增函数; 法一: 作差 法二:作商(4)已知函数)(x f y =在()+∞,0上为增函数,且)0(0)(><x x f ,试判断)(1)(x f x F =在()+∞,0上的单调性,并给出证明过程;▲方法技巧归纳——判断函数单调性的方法:1、直接法:熟悉的函数,如一次函数、二次函数、反比例函数等;如,练习册P27(2)P31(上5、1)2、图象法;3、定义法;4、运算性质法:①当0>a 时,函数)(x af 与)(x f 有相同的单调性; 当0<a 时,函数)(x af 与)(x f 有相反的单调性; ②当函数)(x f 恒不等于零时,)(x f 与)(1x f 单调性相反;③若0)(≥x f ,则)(x f 与)(x f 具有相同的单调性;④若)(x f 、)(x g 的单调性相同,则)()(x g x f +的单调性与之不变; ▲即:增+增=增 减+减=减⑤若)(x f 、)(x g 的单调性相反,则)()(x g x f -的单调性与)(x f 同.▲即:增-减=增 减-增=增 注意:(1)可熟记一些基本的函数的单调性,一些较复杂的函数可化为基本函数的组合形式,再利用上述结论判断; (2))()(x g x f 与)()(x g x f 的单调性不能确定.相应作业2:(1)讨论函数1)(2-=x axx f 在()1,1-上的单调性(0≠a ); ▲(2)务必记住“对勾”函数)0()(>+=k xkx x f 的单调区间(见练习册P29探究之窗.探究1)知识拓展——复合函数单调性(▲难点)一、复习回顾:复合函数的定义:如果函数)(t f y =的定义域为A ,函数)(x g t =的定义域为D ,值域为C ,则当A C ⊆时,称函数))((x g f y =为f 与g 在D 上的复合函数,其中t 叫做中间变量,)(x g t =叫内层函数,)(x f y =叫外层函数。
二、引理1 已知函数y=f [g(x)].若t=g(x)在区间(a,b)上是增函数,其值域为(c ,d),又函数y=f(t)在区间(c,d)上是增函数,那么,原复合函数y=f [g(x)]在区间(a,b)上是增函数.引理2 已知函数y=f [g(x)].若t=g(x)在区间(a,b)上是减函数,其值域为(c ,d),又函数y=f(t)在区间(c,d)上是减函数,那么,复合函数y=f [g(x)]在区间(a,b)上是增函数. 引理1的证明:▲重要结论1:复合法则规律可简记为“_____________________”(四个字)▲重要结论2:若一个函数是由多个简单函数复合而成的,则此复合函数的单调性由简单函数中减函数的个数决定:✍若减函数有偶数个,则复合函数为增函数; ✍若减函数有奇数个,则复合函数为减函数.规律可简记为“_____________________”(四个字) 题型三、求复合函数的单调区间 例3. 求下列函数的单调区间. (1)267x x y --=(2)3212--=x x y▲小结:1、注意:(1)求单调区间必先求定义域; (2)单调区间必须是定义域的子集;(3)写多个单调区间时,区间之间不能用“ ”并起来,应用“,”隔开. 2、判断复合函数单调性步骤: ✍求函数的定义域;✍将复合函数分解成基本初等函数:)(t f y =与)(x g t =; ✍确定两个函数的单调性;④由复合法则“同増异减”得出复合函数单调性. 相应作业3:求下列函数的单调区间.(1)228x x y --= (2)3212--=x x y(3)xx y 412-=单调性的应用题型四、比较函数值的大小例4.已知函数)(x f y =在[)+∞,0上是减函数,试比较)43(f 与)1(2+-a a f 的大小.题型五、已知单调性,求参数范围 例5.已知函数2)(2)(2+--=x a x x x f(1)若)(x f 的减区间是(]4,∞-,求实数a 的值; (2)若)(x f 在(]4,∞-上单调递减,求实数a 的取值范围.例6.若函数⎩⎨⎧≤-+->-+-=0,)2(0,1)12()(2x x b x x b x b x f 在R 上为增函数,求实数b 的取值范围.题型六、利用单调性,求解抽象不等式例7.已知函数)(x f y =是()1,1-上的减函数,且)1()1(2->-a f a f ,求实数a 的取值范围.例8.已知)(x f 是定义在()+∞,0上的增函数,且)()()(y f x f yx f -=,且1)2(=f ,解不等式2)31()(≤--x f x f .相应作业4:已知)(x f 是定义在()+∞,0上的增函数,且)()()(y f x f xy f +=,且1)2(=f ,解不等式3)2()(≤-+x f x f .题型七、抽象函数单调性的判断——定义法 解决此类问题有两种方法:✍“凑”,凑定义或凑已知条件,从而使用定义或已知条件得出结论; ✍赋值法,给变量赋值要根据条件与结论的关系,有时可能要进行多次尝试.例9.已知函数)(x f 对任意实数x 、y 都有)()()(y f x f y x f +=+,且当0>x 时0)(>x f ,求证:)(x f 在R 上单调递增.例10.已知定义在()+∞,0上的函数)(x f 对任意x 、y ∈()+∞,0,恒有)()()(y f x f xy f +=,且当10<<x 时0)(>x f ,判断)(x f 在()+∞,0上单调性.相应作业5:定义在()+∞,0上的函数)(x f 对任意x 、y ∈()+∞,0,满足)()()(n f m f mn f +=,且当1>x 时0)(>x f .(1)求)1(f 的值; (2)求证:)()()(n f m f nmf -=; (3)求证:)(x f 在()+∞,0上是增函数;(4)若1)2(=f ,解不等式2)2()2(>-+x f x f ;函数的最大(小)值1、函数的最大(小)值定义2、利用单调性求最值常用结论(1)若函数)(x f y =在闭区间[]b a ,上单调递增,则)(min a f y =,)(max b f y =; (2)若函数)(x f y =在闭区间[]b a ,上单调递减,则)(min b f y =,)(max a f y =; (3)若函数)(x f y =在开区间()b a ,上单调递增,则函数无最值,但值域为())(),(b f a f ; (4)若函数)(x f y =在闭区间[]b a ,上单调递增,在闭区间[]c b ,上单调递减,那么函数)(x f y =,[]c a x ,∈在b x =处有最大值,即)(max b f y =;(5)若函数)(x f y =在闭区间[]b a ,上单调递减,在闭区间[]c b ,上单调递增,那么函数)(x f y =,[]c a x ,∈在b x =处有最小值,即)(min b f y =.题型八、单调性法求函数最值(值域) 例11、(1)函数121)(-=x x f 在[]5,1上的最大值为________,最小值为________;(2)函数112++=x x y 在[]4,2上的最大值为________,最小值为________;(3)函数x x y 212--=的值域为________________;(4)函数1-+=x x y 的值域为________________;(5)函数212+--=x x y 的值域为________________;(6)函数x xy +=1的值域为________________;二次函数的区间最值的求法二次函数在给定区间[]n m ,上求最值,常见类型: (1)定轴定区间:对称轴与区间[]n m ,均是确定的; (2)动轴定区间: (3)定轴动区间: (4)动轴动区间: 1、定轴定区间可数形结合,较易解决,注意对称轴与区间位置关系。
例12.当22≤≤-x 时,求函数322--=x x y 的最值.相应作业6:求函数542++-=x x y 在[]5,1上的最值.2、动轴定区间例13.已知函数22)(2++=ax x x f ,求)(x f 在[]5,5-上的最值.▲动轴定区间问题一般解法:对对称轴在区间左侧、右侧、内部三种情况进行讨论,从而确定最值在区间端点处还是在顶点处取得.相应作业7:求函数12)(2--=ax x x f 在[]2,0上的最值.3、定轴动区间例14.已知函数22)(2+-=x x x f ,当[]1,+∈t t x 时,求)(x f 的最小值)(t g .相应作业8:已知函数34)(2-+-=x x x f ,当[]2,+∈m m x 时,求)(x f 的最大值)(m g . 4、动轴动区间解决方法:可将对称轴和区间之一看做不动,进行讨论.例15.求函数ax x y +-=2在[]a x ,1-∈上的最大值.相应作业9:求函数222--=ax x y 在[]1,a x -∈上的最值.。
