单电子辐射跃迁选择定则的讨论
原子物理学褚圣麟第四、五章复习

第四章:碱金属原子和电子自旋锂、钠、钾、铷、铯、钫化学性质相仿、都是一价、电离电势都比较小,容易被电离,具有金属的一般性质。
一、碱金属原子的光谱1、四个线系(锂为例):其他碱金属光谱系相仿,只是波长不同主线系:波长范围最广,第一条线是红色的,其余在紫外,系限2299.7埃;第一辅线系(漫线系):在可见部分;第二辅线系(锐线系):第一条线在红外,其余在可见部分;伯格漫线系(基线系):全在红外。
2、巴尔末氢原子光谱规律: ,5,4,3),1-21(1~22===n nR v H λ 碱金属原子光谱:2*∞-~~nR v v n = R 为里德伯常数,当,所以∞v ~是线系限的波数,且有效量子数*n 不是整数,Δ==-*n TR n 3、碱金属原子的光谱项:22*Δ)-(n R n R T == 4、同一线系的有效量子数与主量子数差别不大;与某一量子数对应不同线系的有效量子数差别明显,引进角量子数加以区分:5、每一线系线系限波数恰好是另一线系第二谱项值中最大的那个。
共振线:主线系第一条。
6、碱金属原子氢原子能级的比较n 很大时,碱金属原子能级 很接近氢原子能级;n 较小时,碱金属原子能级 与氢原子能级相差大; 且n 相同,l 不同的能级高低差别很大。
二、原子实极化和轨道贯穿:原子=原子实+价电子1、原子实:碱金属原子中的电子具有规则组合,共同点是在一个完整的结构之外,多余一个电子,这个完整而稳固的结构称为原子实。
由于原子实的存在,发生原子实的极化和轨道在原子实中的贯穿。
2、价电子:原子实外的那个电子称作价电子。
价电子在较大的轨道上运动,与原子实结合不是很强,容易脱离。
它决定元素的化学性质,在较大的轨道上运动。
3、原子实的极化:由于价电子的电场的作用,原子实中带正电的原子核和带负电的电子的中心发生微小相对位移,于是负电的中心不再在原子核上,形成一个电偶极子。
① 角量子数l 小:轨道偏心率大(椭圆),极化强,能量影响大;② 角量子数l 大:轨道偏心率小(接近圆),极化弱,能量影响小。
7跃迁和选择定则—电偶极跃迁.pdf

/
Ef
原子分子的低激发态的能级寿命一般在10-8 ~ 10-9 s,相 应的能级宽度为Γ = 10-8 ~ 10-7 eV。
对于稳定的基态,τ=∞,相应的 Γ = 0。
§2.7 跃迁和选择定则—原子光谱
满足电偶极跃迁的选择定则
( ) 谱线位置 =ω Ei − Ef /
谱线强度 I ∝ Niλfi
I
0
谱线宽度:(1) 自然宽度;
(2) 多普勒展宽;
I0/2
(3) …..;
(4) 光谱仪的分辨本领。
0
Ei
( ) =ω Ei − Ef /
Ef
E
E1 E0 E2
多普勒展宽
第三章 电子自旋和原子能级的精细结构
角动量空间取向量子化
=L l(l +1) Lz = ml
对于给定量子数 l,
受激辐射系数 Bfi
自发辐射的跃迁概率 Afi
自发辐射系数 Afi
在温度 T下,达到平衡,设处于上能级状态的原子数 为 Ni ,处在下能级状态的原子数为 Nf
激发的原子数 ∝ Bif I (ω)N f
退激发的原子数 ∝ ( Afi + Bfi I (ω)) Ni
A. Einstein (1879-1955)
Ef
uf
自发辐射
dNi / Ni = − Afidt
= Ni (t) Ni0 exp(− Afit)
其中 Ni0 = Ni t=0
§2.7 跃迁和选择定则—能级的平均寿命
每个原子的退激发是独立进行的,激发态存在的时间的 长短是随机的。但退激发的速率是确定的,因而大量原子的 退激发服从统计规律。 我们可以计算激发态i的平均寿命。
第5节 辐射跃迁的普用选择定则

l
不允许出现跃迁
i
1 2 3 (奇数)
同理,同一组态中不同原子组态间的跃迁也是不允许的。
除了满足奇偶性条件外,还要满足如下关系: L-S耦合选择定则: S 0、L 1、J 0, 1(0 0除外) 碱金属的只有一个电子,如果满足了 l 1 ,自然也 就满足了奇偶性的变化以及 L 1 的要求;同时S总 是1/2,所以 S 0 自然满足。 在有些较重的原子中,由于L-S 耦合遭到部分破坏,会产 生例外的跃迁。如汞原子的一个波长2537埃的强谱线,是 由6s6p3P1 6s6s1S0跃迁产生的,违反了 S 0 。 J-J耦合选择定则: J p 0 或对换 j 0, 1
J 0,பைடு நூலகம்1(0 0除外)
P165有错
§ 5.5 辐射跃迁的普用选择定则
对于多个电子的辐射跃迁,也存在着一个选择定则 原子中电子的空间分布分为偶性和奇性两类,这性质称作 “宇称”。原子中各电子的 l 量子数相加,如果得到偶数, 则原子为偶性,如果得到奇数,则原子为奇性。跃迁只发生 在不同宇称的状态之间.
偶性态( li 偶数) 奇性态( li 奇数) (必要条件)
高二物理竞赛单电子辐射跃迁的选择定则课件

•只考虑自旋轨道耦合时,
Els 0, j l 1 /2; 3p(n=3,l=1)
Els 0, j l 1 / 2; •相对论效应与自旋轨道耦合都考虑后,
Er Els 0
3p(n=3,l=1)
32P3/2 32P1/2
32P3/2 32P1/2
11
Balmer系第一条谱线Hα 7种跃迁,5条谱线
单电子辐射跃迁的选择定则
一、选择定则: 单电子,电偶极辐射跃迁(吸收或发射光子)只能在
下列条件下发生,
l 1 j 0, 1
• 主量子数n的改变不受限制; • 跃迁对角动量有选择性; •选择性既是由光谱线实验测量规律总结,在量子力学中也 有理论推导.
1
4.5 单电子辐射跃迁的选择定则
二、碱金属光谱的解释
n,j相同、l不同的能级简并
氢原子精细结构能级图 •主量子数n的改变不受限制,但是由于跃迁几率与辐射频 率立方成正比,同一n值的不同能级间跃迁的几率很小.
12
例题: 氢原子考虑精细结构之后有状态32D3/2, 32P3/2和 22P1/2, 22S1/2。试问这两组状态之间能否产生跃迁, 有几种可能,实际对应几条谱线?
A. 不能跃迁; B. 二种可能,一条谱线; C. 四种可能,四条谱线; D. 二种可能,两条谱线。
13
氢 原 子 光 谱 的 精 细 结 构
E
S L =0
p
d
L =1
L =2
f L =3
Hn
…
32
12
12
52 32
72
4
32
12
12
52 32
3
32
2
12
12
跃迁类型和选择定则
将原子和电偶极辐射场作为一个整体系统处理,用k表示 辐射的波矢,ε表示偏振态,-er是电偶极矩。 如果系统处在有nk,ε个量子的初始态(用i标记)中,则单 位时间内系统跃迁到有nk,ε+1个量子的终态(用f标记)的跃迁 速率为
λif =
( Ei − E f
3πε 0 c
)
3
4 3
∫ψ
* f
(-er )ψ i dτ (nk,ε + 1)
M ˆ M ba1E2 = ψ b (ik ⋅ r )(ε ⋅∇) ψ a M E = M ba1 + M ba2
其中
M
M1 ba
=−
ωba
2 c
ψ b ly ψ a
E M ba2
2 imωba =− ψ b xi zi ψ a 2 c
原子序数为Z的类氢离子的磁偶极跃迁的跃迁速率与电 偶极跃迁速率之比为:
三、跃迁类型和选择定则
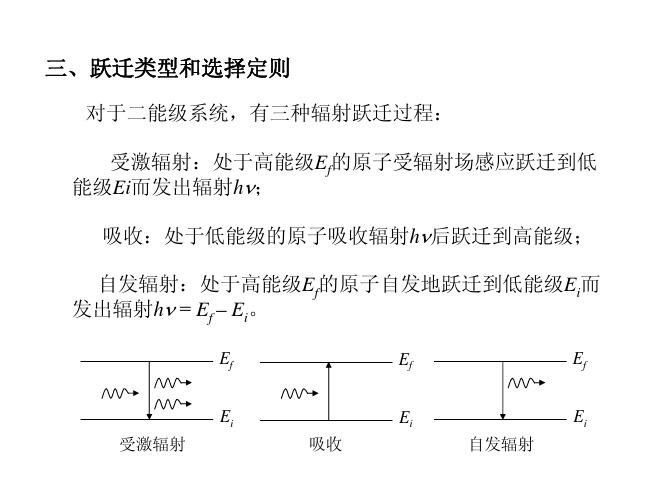
对于二能级系统,有三种辐射跃迁过程: 受激辐射:处于高能级Ef的原子受辐射场感应跃迁到低 能级Ei而发出辐射hν; 吸收:处于低能级的原子吸收辐射hν后跃迁到高能级; 自发辐射:处于高能级Ef的原子自发地跃迁到低能级Ei而 发出辐射hν = Ef – Ei。
Ef Ei 受激辐射 吸收 Ef Ei 自发辐射 Ef Ei
2
电偶极矩-er在空间反演下变号,宇称为奇,P = -1。由于 宇称守恒,初态和末态波函数的宇称必须改变。
e
− ik ⋅r
1 = 1 − (ik ⋅ r ) + (ik ⋅ r ) 2 − 2!
磁偶极和电四极辐射由展开式第二项贡献,要多乘一项 k·r。因而磁偶极和电四极辐射作用算符是偶宇称的,P = 1, 由于宇称守恒,初态和末态波函数的宇称应不变。 由此可以得到电多极辐射和磁多极辐射的宇称,以及原 子分子初态和末态宇称Pf和Pi与光子角动量有如下关系:
跃迁类型和选择定则

2 2 2
电四极跃迁的跃迁速率与电偶极跃迁速率之比为
λE2 3 ⎛ ω r ⎞ 3 ⎛ Zα ⎞ ≈ ⎜ = ⎜ ≈ 10−6 λE1 40 ⎝ c ⎟ 40 ⎝ 2 ⎟ ⎠ ⎠
λif =
( Ei − E f
3πε 0 c
)
3
4 3
∫ψ
* f
(-er )ψ i dτ (nk,ε + 1)
2
式中Ei – Ef = hν,上式已对k和ε的各个方向取了平均,相当 于原子与各向同性的非偏振辐射的相互作用。
跃迁速率包括两项: 第一项对应于受激辐射,在通常光源作用下可以忽略,只有 在较强光场中才明显出现。 第二项对应于自发辐射,即外界不存在辐射 (nk,ε= 0)时的辐 射速率。 如果存在简并态,自发辐射的速率变为
磁偶极跃迁M1
0→0
电四极跃迁E2
ΔJ = 0, ±1, ±2 0 → 0,1
1 2
0 → 0 ΔJ = 0, ±1,
→
1 2
ΔM=0,±1 宇称改变 有单电子跃迁 Δl = ±1 ΔS=0
ΔL = 0, ±1, 0→0
ΔM=0,±1 宇称不变 无单电子跃迁 Δl = 0, Δn = 0 ΔS=0 ΔL=0
j = 0 (无辐射) 的跃迁,称为单极跃迁,只能通过电子碰撞 或其他无辐射方式跃迁。
定则2同样来自角动量守恒以及原子波函数相对量子化 轴的角向对称性。 定则3来自宇称守恒。 电偶极辐射的宇称:
λif
( Ei − E f ) =
3πε 0 c
4 3
原子物理课件 第5节 辐射跃迁的普用选择定则
碱金属的只有一个电子,如果满足了 l 1 ,自然也 就满足了奇偶性的变化以及 L 1 的要求;同时S总 是1/2,所以 S 0 自然满足。
在有些较重的原子中,由于L-S 耦合遭到部分破坏,会产 生例外的跃迁。如汞原子的一个波长2537埃的强谱线,是 由6s6p3P1 6s6s1S0跃迁产生的,违反了 S 0 。
J-J耦合选择定则:J p j
0,
0 1
或对换
J 0, 1(0 0除外)
P165有错
§ 5.5 辐射跃迁的普用选择定则
对于多个电子的辐射跃迁,也存在着一个选择定则 原子中电子的空间分布分为偶性和奇性两类,这性质称作 “宇称”。原子中各电子的 l 量子数相加,如果得到偶数, 则原子为偶性,如果得到奇数,则原子为奇性。跃迁只发生 在不同宇称的状态之间.
偶性态( li 偶数) 奇性态( li 奇数) (必要条件)
例:sp ቤተ መጻሕፍቲ ባይዱ态和 pd 组态能否出现跃迁?
sp 组态: li 0 1 1 (奇数) 不允许出现跃迁 pd 组态: li 1 2 3 (奇数)
同理,同一组态中不同原子组态间的跃迁也是不允许的。
除了满足奇偶性条件外,还要满足如下关系:
L-S耦合选择定则: S 0、L 1、J 0, 1(0 0除外)
宇称—原子状态的奇偶性态
• j-j 耦合 J J P je
sP (sP 1) s(s 1)
J LS
对三个或三个以上价电子的原子,洪特定则,朗德间隔特定则仍
有效。对同科电子仍需考虑泡利原理。
同一次壳层由同科电子构成。同科 s 电子最多只能有2个,同科 p 电子最多6 个,同科 d 电子最多10个,…
➢ 多个电子同时激发到高能级 双里德伯态原子:现在应用激光技术,将两个电子同时激发到高
➢ 多价电子的原子态
任何原子的状态,都可以看作它的一次电离的离子加一个电子形成 的。而它的一次电离离子的状态同按周期表顺序前一个元素的状态 相似,所以有前一个元素的状态可推知后继元素的状态。
• L-S耦合
LP e
L LP Le S S p Se
n2 n3 n3 n4
三层能级之间的跃迁产生一组复杂结构的谱线
主线系:
~ 23S1 n3P0,1,2 , n 2
第二辅线系: 第一辅线系:
~ ~ ~
2233PP00,1,2n3Dn31S1 23P1 n3D1,2
, ,
n
3 n3
基线系:
~ ~ ~ ~
23P2
n3D1,2,3
33D1 n3F2 32D2 n3F2,3
❖ 电离电势和激 发电势较低
3P2
•存在两个亚稳态
3P1
3P0
6s6p的3P2和3P0
汞原子能级图
四. 复杂原子光谱的一般规律
➢ 位移定律
具有原子序数Z的中性原子的光谱和能级,同具有原子序数Z+1的 原子一次电离后的光谱和能级很相似 — 光谱和能级的位移定律。
➢ 多重性的交替律
元素周期表中相邻元素原子的能级多重数呈奇偶交替变化 — 原子 能级多重性的交替律。
宇称—原子状态的奇偶性态
➢ 多价电子的原子态
任何原子的状态,都可以看作它的一次电离的离子加一个电子形成 的。而它的一次电离离子的状态同按周期表顺序前一个元素的状态 相似,所以有前一个元素的状态可推知后继元素的状态。
• L-S耦合
LP lP (lP 1) Le l(l 1)
SP Se
L LP Le S S p Se
• j-j 耦合 J J P je
sP (sP 1) s(s 1)
J LS
对三个或三个以上价电子的原子,洪特定则,朗德间隔特定则仍
有效。对同科电子仍需考虑泡利原理。
同一次壳层由同科电子构成。同科 s 电子最多只能有2个,同科 p 电子最多6 个,同科 d 电子最多10个,…
➢ 多个电子同时激发到高能级 双里德伯态原子:现在应用激光技术,将两个电子同时激发到高
忽略
介质
热平衡 状态
粒子数 反转态
N2
E2 E1
e kT
1
N1
光强 I 的变化
N1 N2 I 0
N2 N1 I 0
说明
若介质处于粒子数反转态,光在其中传播时得以放大。 采用光泵浦方法。
例 He-Ne(5:1或10:1)激光器中Ne气粒子数反转态的实现
• 激活介质中光强随传播距离的变换关系 激活介质:处于粒子数反转态的介质。光传播时被放大。
末 系
的 2发
射
与
吸
收 1
• 热激发原子的能量分布
达到热平衡状态时( T ) ,各状态的原子数
E3
E2
N i e Ei / kT
若能级是 gi 重简并的
E1
Ni
g e Ei / kT i
N g e i
i ( Ei E1 ) / kT
跃迁选择定则
Ji = Jf + j, Jf + j -1, …, ⏐Jf - j⏐
对一定的多极辐射场j,原子分子初态和末态之间可能 取的角动量差为 ΔJ = ±j, ±(j-1), …, 0
由于跃迁速率随跃迁多极次 j 增加而迅速减少,一般情 况下只有最小极次j =∣Ji - Jf∣的辐射才能出现。如果它被 禁戒,则可出现下一极次的辐射。 光谱实验上能够观测到辐射除了电偶极辐射E1之外, 只有M1+E2和M2+E3的混合辐射。 由于j ≥ 1, 所以 0→0的跃迁是禁戒的。
2
式中Ei – Ef = hν,上式已对k和ε的各个方向取了平均,相当 于原子与各向同性的非偏振辐射的相互作用。
跃迁速率包括两项: 第一项对应于受激辐射,在通常光源作用下可以忽略,只有 在较强光场中才明显出现。 第二项对应于自发辐射,即外界不存在辐射 (nk,ε= 0)时的辐 射速率。 如果存在简并态,自发辐射的速率变为
. ..
5(1) 4(1) 3(1)
537.0 6675.2
. ..
5(2) 4(2) 3(2)
. ..
5(1) 4(1) 3(1)
. ..
5(2,1,0)
. ..
5(3,2,1) 4(3,2,1) 4(2,1,0) 3(3,2,1) 3(2,1,0)
5875.6
3(0)
538.9
2(0) 171129.148
λm1 1 μ ⎛ Z μ B ⎞ ⎛ Zα ⎞ −5 ≈ 2 ≈⎜ = ≈ 10 ⎟ ⎟ ⎜ λE1 c er ⎝ ea0 c ⎠ ⎝ 2 ⎠
2 2 2
电四极跃迁的跃迁速率与电偶极跃迁速率之比为
λE2 3 ⎛ ω r ⎞ 3 ⎛ Zα ⎞ −6 10 ≈ ⎜ = ≈ ⎜ ⎟ λE1 40 ⎝ c ⎟ 40 ⎝ 2 ⎠ ⎠
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
单电子辐射跃迁选择定则的讨论(理学院物理系物理学)摘要原子辐射跃迁选择定则是原子物理学中的一个重要原则。
本文主要采用两种方法对单电子辐射跃迁选择定则进行讨论。
第一种方法,利用量子方法讨论;第二种方法,利用半经典方法讨论;两种方法分别对电子的轨道和自旋有无耦合的情况下进行了推导。
用两种不同的方法,得到了一致的结果。
关键词:电偶极辐射;跃迁几率;角动量守恒;量子数;选择定则Discussion of Single Elect ron’s transition Selection Rule(Department of Physics, College of science, Physics )AbstractSelection rule of atom transition is one of the important principles in the atom physics. This paper adopts two methods to discuss the selection rule of the single electron transition.In the first method, quantum method is used to analyze the problem.In the second method, semiclassical method is used to discuss the thesis. Two cases that the electric orbit and spin have coupling and no coupling are respectively discussed in both methods. By two different methods, the same result is conclued.Keywords:Electric dipole radiation;Transition probability;Conservation of angular momentum;Quantum number;Selection rule目录1 引言 (1)2 量子方法讨论选择定则 (1)2.1 电子的轨道和自旋无耦合的情况 (1)2.2 电子的轨道和自旋有耦合的情况 (3)3 半经典方法讨论选择定则 (7)3.1 角动量的矢量合成法则 (7)3.2 电子组态变动定则 (7)3.3 L S-无耦合的跃迁选择定则 (9)3.4 L S-有耦合的跃迁选择定则 (10)4 结论 (11)参考文献 (12)致谢 (13)1引言微观粒子(分子、原子、原子核、基本粒子等)的运动规律,是本世纪二十年代在总结大量实验事实和旧量子论的基础上建立起来的。
随着它的出现,人类对于物质微观结构的认识日益深入,从而能较深刻地掌握物质的微观理论,为用于生产开辟了广阔的途径。
电子跃迁就是微观状态发生跳跃式变化的过程。
由于微观粒子的状态常常是分立的,所以从一个状态到另一个状态的变化常常是跳跃式的。
跃迁选择定则有很多种,不同跃迁遵从不同的跃迁选择定则。
从跃迁的性质来分,主要分为电性和磁性两种。
在原子物理中涉及的L-S 耦合跃迁选择定则指的是电偶极矩跃迁,原因是电偶极矩跃迁强度比磁极跃迁和多极矩跃迁强度大得多(5810~10倍)。
原子的辐射跃迁选择定则也是指电偶极辐射跃迁选择定则。
本文采用量子和半经典两种方法,分别从电子的轨道和自旋(L-S )有无耦合的情况下对电偶极辐射跃迁选择定则加以讨论。
使人们对单电子辐射跃迁选择定则有更加深入的理解。
2量子方法讨论选择定则下面分别从电子的轨道和自旋有无耦合的情况下对单电子辐射跃迁选择定则进行讨论。
2.1电子的轨道和自旋无耦合的情况原子对光的发射和吸收是原子体系与光相互作用所产生的现象。
当光照射到原子上时,光波中的电场ε和磁场B 都对原子中的电子有作用,但和电场的作用相比较,磁场对电子的作用可以忽略,所以只考虑光波中的电场对电子的作用。
对于入射光为各向同性,且偏振是无规则的,则原子体系在单位时间内由k Φ态跃迁到m Φ态的几率为:()222243s k mmk mk e w I r πω→= (1)由此可知,当且仅当mk m k r r φφ= 不为零,即其三个直角坐标系分量,mk mk z x 和mk y 不全为零时,原子光吸收的跃迁几率方不为零。
再由:22243s km mkmk e B B r π== (2)222mkkm km A B cωπ= (3)两式可知原子受激发射和自发发射的跃迁几率也不为零。
其中 km B 表示吸收系数,mk B 表示受激发射系数,km A 表示自发发射系数。
这称原子在0m E 和0k E 两能级之间的跃迁是允许的。
否则,辐射跃迁是禁戒的。
因此0mk r ≠这个条件,可以得出产生原子跃迁选择定则。
我们具体讨论氢原子、类氢离子及碱金属原子。
其哈密顿算符写成为()2ˆˆ2p H V r μ=+ 其本征矢量若用电子自旋——轨道角动量无耦合的态矢量,,,l s n l m m ,在ˆr和ˆz s 共 同表象写为:()()()(),,l slsnlm mz nl lm m z r s R r Y X s ψθϕ= (4)则mk z 的具体形式是:ˆ,,,,,,l s l s n l m m z n l m m ''''()()*cos s s n l m l lm m nlm r r r d δψθψτ''''=⎰()()()()2*3*0,cos ,s s n l l l m m nl l m lm R r R r r dr Y Y d ππδθϕθθϕ''∞'''=Ω⎰⎰⎰(5)利用球谐函数的一个递推公式:1,1,cos l ll lm l ml m Y θ+-=+ (6)及球谐函数的正交归一化表示式,可知若满足:100l l l s s s l l l m m m m m m '''∆=-=±∆=-=∆=-= (7)时,则矩阵元ˆ,,,,,,0l s l s n l m m z n l m m ''''≠ 同样,mk x 和mk y 的具体形式分别为:ˆ,,,,,,l s l s n l m m x n l m m '''' ()()*sin cos s s n l m l lm m nlm r r r d δψθϕψτ''''=⎰()()()()2*3*0,sin ,2s s n l l l i i m m nl l m lm e e R r R r r dr YY d ϕϕππδθϕθθϕ''-∞'''+=Ω⎰⎰⎰(8) ˆ,,,,,,l s l s n l m m y n l m m '''' ()()*sin sin s s n l m l lm m nlm r r r d δψθϕψτ''''=⎰()()()()2*3*,sin ,2s s n l l l i i m m nl l m lm e e R r R r r dr YY d ϕϕππδθϕθθϕ''-∞'''-=Ω⎰⎰⎰(9) 利用球谐函数的另一个递推公式:1,11,1()(1)sin (2(21)(21)l l l i l l l lm l m l m l m l m l m e Y Y l l l ϕθ±+±-±±+-=±+-+ (10)及球谐函数的正交归一化表示式可知,若110l l l s s s l l l m m m m m m '''∆=-=±∆=-=±∆=-= (11)时,则矩阵元ˆ,,,,,,0l s l s n l m m x n l m m ''''≠ ˆ,,,,,,0l s l s n l m m y n l m m ''''≠ 综合(7)(11)两式可知:100l s l m m ∆=±∆=∆=为跃迁的电偶极辐射选择定则。
原子的两个定态,,,l s n l m m ''''和,,,l s n l m m 之间如果满足上式,则在电偶极近似下光吸收和发射的跃迁几率不等于零,会有光谱线产生。
2.2电子的轨道和自旋有耦合的情况原子由一种态跃迁到另一种态有一定的几率,设电子的自旋和轨道有耦合作用下电子的本征态为j nljm ψ。
则电子由态j nljm ψ跃迁到jn l j m ψ''''电偶极自发跃迁几率为:222343n n n n e A r cω''→= (12) 其中,n n '各代表4个量子数,()nl n l E E ω''=-。
上式中2222n n n n n n n n r x y z ''''=++ (13)三个矩阵元中至少有一个不等于零,跃迁才是允许的。
j nljm ψ可以表示为:()(),,jj nljmnl ljm z R r s ψφθϕ= (14)其中()nl R r 为径向波函数,j ljm φ为()22,,z l j j 的共同本征函数,可以分成两类:,111,,22jlm A jm j l m j l m m φ+⎫⎪==+=+⎪⎭(15),111,,22jl m Bjm j l m j l m m φ''+⎛⎫'⎪==-=+⎪⎭(16) 利用式(14),矩阵元n n r '可以分离变量地表示成:3jj n n l j m ljm n l nl rr R R r dr rφφ∞''''''︒=⎰(17)其中径向积分通常与选择定则无关。
利用公式2rr rr γγγσσσσσσ⎛⎫=+=⋅ ⎪⎝⎭ (18)jjjjA B B Ajm jmjm jmγγσφφσφφ=-=-(19)即得jj j j j j B B A A A A j m jm j m jm j m jm r r r r r rγγφφφσσφφφ''''''==,()21γσ= (20) 类似地,可得jj j j B A A Bj m jm j m jm r r r rφφφφ''''=(21)再利用(18)式,可得2jj j j j j A A A B B Aj m jm j m jm j m jm r rφφφσφφσφ''''''-=+(22)'2j j j j j jB A A A B B jm j m jm j m jm j m r rφφφσφφσφ'''''-=+ (23) 利用Pauli 矩阵σ的具体形式为:0110x σ⎛⎫= ⎪⎝⎭ ,00y i iσ-⎛⎫= ⎪-⎝⎭ ,1001z σ⎛⎫= ⎪-⎝⎭以及lm Y 的正交归一性和式(15)(16)(17)三式就可算出这些矩阵元。
