多电子原子光谱--电偶极跃迁的选择定则-USTC
合集下载
多电子原子光谱-- 电偶极跃迁的选择定则
LS耦合：
0 ∆S = ∆L = 0, ±1 ∆J = 0, ±1 ( J = 0 → J = 0除外） ∆M J = 0, ±1 (当∆J = 0时，M J = 0 → M J = 0除外)
jj耦合
∆j = 0, ±1 (跃迁电子） ∆J = 0, ±1 ( J = 0 → J = 0除外） ∆M = 0, ±1 (当∆J = 0时，M = 0 → M = 0除外) J J J
X射线不带电、很强的穿透性、直 线传播、使照相底片感光、使气 体电离奇特性质等。
The Nobel Prize in Physics 1901
§4.5原子的内层能级和特征X射线—X射线的波性 X射线是电磁波
晶体衍射 1912年，劳厄建议，鉴于晶体内部原子间距与X射 线的波长数量级相同，同时规则排列，可以当作 三维光栅，做晶体衍射实验。
(波长10-3 nm~1nm)
Max von Laue (1879 -1960)
实验：W. Friedrich, P. Knipping
劳厄斑
The Nobel Prize in Physics 1914
§4.5原子的内层能级和特征X射线—X射线的能谱
晶体衍射 1912年，小布拉格提出一种更简便的晶体衍射方法。 规则排列的原子形成布拉格平面，X射线从相邻平面 散射，形成干涉。
1 1 − 2 2 2 3
0.9
0.8
Lα线
L = ν R ( Z − 7.4) 2
Kα
0.7
Lα
0.6
Cr FeCu
0.5 20
Mo
40
W
Z
60
80
K线和L线的莫塞莱图
根据实验测量的特征线波数，从莫塞莱图上就可以标识元素的种类， 所以特征谱又称为标识谱。
0 ∆S = ∆L = 0, ±1 ∆J = 0, ±1 ( J = 0 → J = 0除外） ∆M J = 0, ±1 (当∆J = 0时，M J = 0 → M J = 0除外)
jj耦合
∆j = 0, ±1 (跃迁电子） ∆J = 0, ±1 ( J = 0 → J = 0除外） ∆M = 0, ±1 (当∆J = 0时，M = 0 → M = 0除外) J J J
X射线不带电、很强的穿透性、直 线传播、使照相底片感光、使气 体电离奇特性质等。
The Nobel Prize in Physics 1901
§4.5原子的内层能级和特征X射线—X射线的波性 X射线是电磁波
晶体衍射 1912年，劳厄建议，鉴于晶体内部原子间距与X射 线的波长数量级相同，同时规则排列，可以当作 三维光栅，做晶体衍射实验。
(波长10-3 nm~1nm)
Max von Laue (1879 -1960)
实验：W. Friedrich, P. Knipping
劳厄斑
The Nobel Prize in Physics 1914
§4.5原子的内层能级和特征X射线—X射线的能谱
晶体衍射 1912年，小布拉格提出一种更简便的晶体衍射方法。 规则排列的原子形成布拉格平面，X射线从相邻平面 散射，形成干涉。
1 1 − 2 2 2 3
0.9
0.8
Lα线
L = ν R ( Z − 7.4) 2
Kα
0.7
Lα
0.6
Cr FeCu
0.5 20
Mo
40
W
Z
60
80
K线和L线的莫塞莱图
根据实验测量的特征线波数，从莫塞莱图上就可以标识元素的种类， 所以特征谱又称为标识谱。
7跃迁和选择定则—电偶极跃迁.pdf
Γ称为能级宽度。− E f
/
Ef
原子分子的低激发态的能级寿命一般在10-8 ~ 10-9 s，相 应的能级宽度为Γ = 10-8 ~ 10-7 eV。
对于稳定的基态，τ＝∞，相应的 Γ = 0。
§2.7 跃迁和选择定则—原子光谱
满足电偶极跃迁的选择定则
( ) 谱线位置 =ω Ei − Ef /
谱线强度 I ∝ Niλfi
I
0
谱线宽度：(1) 自然宽度；
(2) 多普勒展宽；
I0/2
(3) …..；
(4) 光谱仪的分辨本领。
0
Ei
( ) =ω Ei − Ef /
Ef
E
E1 E0 E2
多普勒展宽
第三章 电子自旋和原子能级的精细结构
角动量空间取向量子化
=L l(l +1) Lz = ml
对于给定量子数 l，
受激辐射系数 Bfi
自发辐射的跃迁概率 Afi
自发辐射系数 Afi
在温度 T下，达到平衡，设处于上能级状态的原子数 为 Ni ，处在下能级状态的原子数为 Nf
激发的原子数 ∝ Bif I (ω)N f
退激发的原子数 ∝ ( Afi + Bfi I (ω)) Ni
A. Einstein (1879-1955)
Ef
uf
自发辐射
dNi / Ni = − Afidt
= Ni (t) Ni0 exp(− Afit)
其中 Ni0 = Ni t=0
§2.7 跃迁和选择定则—能级的平均寿命
每个原子的退激发是独立进行的，激发态存在的时间的 长短是随机的。但退激发的速率是确定的，因而大量原子的 退激发服从统计规律。 我们可以计算激发态i的平均寿命。
/
Ef
原子分子的低激发态的能级寿命一般在10-8 ~ 10-9 s，相 应的能级宽度为Γ = 10-8 ~ 10-7 eV。
对于稳定的基态，τ＝∞，相应的 Γ = 0。
§2.7 跃迁和选择定则—原子光谱
满足电偶极跃迁的选择定则
( ) 谱线位置 =ω Ei − Ef /
谱线强度 I ∝ Niλfi
I
0
谱线宽度：(1) 自然宽度；
(2) 多普勒展宽；
I0/2
(3) …..；
(4) 光谱仪的分辨本领。
0
Ei
( ) =ω Ei − Ef /
Ef
E
E1 E0 E2
多普勒展宽
第三章 电子自旋和原子能级的精细结构
角动量空间取向量子化
=L l(l +1) Lz = ml
对于给定量子数 l，
受激辐射系数 Bfi
自发辐射的跃迁概率 Afi
自发辐射系数 Afi
在温度 T下，达到平衡，设处于上能级状态的原子数 为 Ni ，处在下能级状态的原子数为 Nf
激发的原子数 ∝ Bif I (ω)N f
退激发的原子数 ∝ ( Afi + Bfi I (ω)) Ni
A. Einstein (1879-1955)
Ef
uf
自发辐射
dNi / Ni = − Afidt
= Ni (t) Ni0 exp(− Afit)
其中 Ni0 = Ni t=0
§2.7 跃迁和选择定则—能级的平均寿命
每个原子的退激发是独立进行的，激发态存在的时间的 长短是随机的。但退激发的速率是确定的，因而大量原子的 退激发服从统计规律。 我们可以计算激发态i的平均寿命。
多电子原子光谱--电偶极跃迁的选择定则-USTC
K线系：Kα、Kβ、Kγ 等谱线； L线系：Lα、Lβ、Lγ 等谱线。
原子序数大的元素会出现更多的谱系，分别称为M系，N系。
H. Moseley (1887-1915)
§4.5原子的内层能级和特征X射线—X射线的能谱
各元素的特征线波数的平方根与原子序数(原子核电荷数)成线性关系
莫塞莱经验公式 (莫塞莱定律)
Kα线
νK
=R(Z
−
1)2
1 12
−
1 22
Lα线
νL
= R(Z
−
7.4)2
1 22
−
1 32
(1/λ)1/2 (m-1/2)
1.0
0.9
0.8
Kα
0.7
Lα
0.6
CrFeCu Mo
0.5 20
40
Z
W
60
80
K线和L线的莫塞莱图
根据实验测量的特征线波数，从莫塞莱图上就可以标识元素的种类， 所以特征谱又称为标识谱。
轫致辐射(bremsstrahlung，刹车辐射)
hν= T − T ′
hν max=
hc =
λmin
T=
eU
杜安(W. Duane)和亨特(P. Hunt)于1915年实验测定了h 值，与利用光电效应 实验测定的h值十分接近。
§4.5原子的内层能级和特征X射线—X射线的能谱 X射线特征谱
当加速电压大于一定值时，在连续谱 上出现了分立的线谱：
LS耦合：
∆S =0
∆L = 0, ±1
∆J
=
0, ±1
(J = 0 → J = 0除外）
∆M J = 0, ±1 (当∆J = 0时，M J = 0 → M J = 0除外)
原子序数大的元素会出现更多的谱系，分别称为M系，N系。
H. Moseley (1887-1915)
§4.5原子的内层能级和特征X射线—X射线的能谱
各元素的特征线波数的平方根与原子序数(原子核电荷数)成线性关系
莫塞莱经验公式 (莫塞莱定律)
Kα线
νK
=R(Z
−
1)2
1 12
−
1 22
Lα线
νL
= R(Z
−
7.4)2
1 22
−
1 32
(1/λ)1/2 (m-1/2)
1.0
0.9
0.8
Kα
0.7
Lα
0.6
CrFeCu Mo
0.5 20
40
Z
W
60
80
K线和L线的莫塞莱图
根据实验测量的特征线波数，从莫塞莱图上就可以标识元素的种类， 所以特征谱又称为标识谱。
轫致辐射(bremsstrahlung，刹车辐射)
hν= T − T ′
hν max=
hc =
λmin
T=
eU
杜安(W. Duane)和亨特(P. Hunt)于1915年实验测定了h 值，与利用光电效应 实验测定的h值十分接近。
§4.5原子的内层能级和特征X射线—X射线的能谱 X射线特征谱
当加速电压大于一定值时，在连续谱 上出现了分立的线谱：
LS耦合：
∆S =0
∆L = 0, ±1
∆J
=
0, ±1
(J = 0 → J = 0除外）
∆M J = 0, ±1 (当∆J = 0时，M J = 0 → M J = 0除外)
跃迁类型和选择定则
将原子和电偶极辐射场作为一个整体系统处理，用k表示 辐射的波矢，ε表示偏振态，-er是电偶极矩。 如果系统处在有nk,ε个量子的初始态（用i标记）中，则单 位时间内系统跃迁到有nk,ε+1个量子的终态（用f标记）的跃迁 速率为
λif =
( Ei − E f
3πε 0 c
)
3
4 3
∫ψ
* f
(-er )ψ i dτ (nk,ε + 1)
M ˆ M ba1E2 = ψ b (ik ⋅ r )(ε ⋅∇) ψ a M E = M ba1 + M ba2
其中
M
M1 ba
=−
ωba
2 c
ψ b ly ψ a
E M ba2
2 imωba =− ψ b xi zi ψ a 2 c
原子序数为Z的类氢离子的磁偶极跃迁的跃迁速率与电 偶极跃迁速率之比为：
三、跃迁类型和选择定则
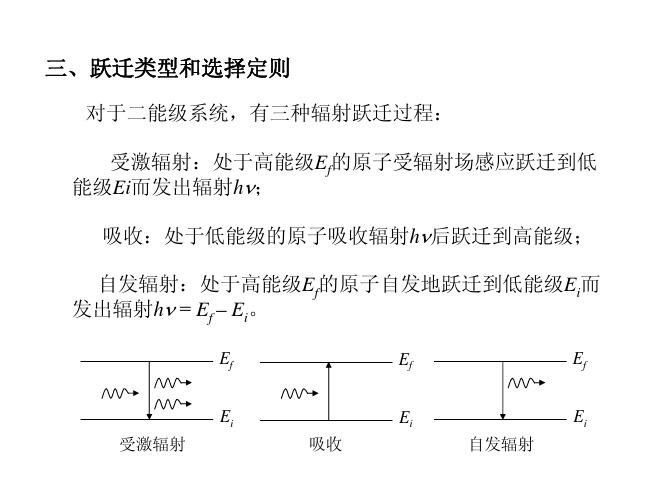
对于二能级系统，有三种辐射跃迁过程： 受激辐射：处于高能级Ef的原子受辐射场感应跃迁到低 能级Ei而发出辐射hν； 吸收：处于低能级的原子吸收辐射hν后跃迁到高能级； 自发辐射：处于高能级Ef的原子自发地跃迁到低能级Ei而 发出辐射hν = Ef – Ei。
Ef Ei 受激辐射 吸收 Ef Ei 自发辐射 Ef Ei
2
电偶极矩-er在空间反演下变号，宇称为奇，P = -1。由于 宇称守恒，初态和末态波函数的宇称必须改变。
e
− ik ⋅r
1 = 1 − (ik ⋅ r ) + (ik ⋅ r ) 2 − 2!
磁偶极和电四极辐射由展开式第二项贡献，要多乘一项 k·r。因而磁偶极和电四极辐射作用算符是偶宇称的，P = 1， 由于宇称守恒，初态和末态波函数的宇称应不变。 由此可以得到电多极辐射和磁多极辐射的宇称，以及原 子分子初态和末态宇称Pf和Pi与光子角动量有如下关系：
多电子原子的光谱项概述PPT(52张)
一原子轨道中电子的两种取向，即顺时针方向和逆时针方向。
基态原子核外电子排布的规则 LOGO
❖ 基态的原子核外电子应遵从三条原则： – 泡利不相容原理：一个原子中不可能存在两个具有相同的4个量 子数的电子，可见，一个原子轨道最多只能排两个电子，而且这 两个电子的自旋必须相反。 – 能量最低原理：为了使原子系统能量最低，在不违背泡利不相容 原理的前提下，电子尽可能地先占据能量最低的轨道。这个状态 就使原子系统的基态。 – 洪德原则：在等能量（n,l相同）的轨道上，自旋平行电子数越 多原子系统的能量则越低。即：在一组能量相同的轨道上，电子 尽可能以自旋相同的方向分占不同的轨道。 – 作为洪德规则的补充，能量兼并的轨道上全充满、半充满或全空 的状态是比较稳定的。
多电子原子的光谱项概述PPT(52张)培 训课件 培训讲 义培训 教材工 作汇报 课件PP T
LOGO
多电子原子的光谱项概述PPT(52张)培 训课件 培训讲 义培训 教材工 作汇报 课件PP T
原子光谱项的求法
多电子训 教材工 作汇报 课件PP T
第4章 多电子原子的光谱项
1
LOGO
基态原子核外电子排布的规则 单个原子的核外电子的运动状态用n、l、m、ms4个量子数来表示. 主量子数n：取值为1，2，3，…非零的正整数. 电子运动的能量主要由主量子数n来决定，在氢原子中， 电子的能量为：E=-13.6/n2eV，n值越大，电子离核平均距离越远， 电子的能量越高 轨道角动量量子数l，简称角量子数. 决定电子的原子轨道角动量的大小，描述电子云的形状. 当n值一定时，不同的l对电子的能量也稍有影响，l越大能量越高. L取值为0，1，2，3， …，（n-1）等n个从0开始的正整数 磁量子数m：描述着电子云在空间的伸展方向它的取值受角量子数l的 限制，m=0，± 1， ± 2，…， ± l 自旋磁量子数ms：描述原子中的电子的自旋运动，取值为± 1/2分别 表示同
基态原子核外电子排布的规则 LOGO
❖ 基态的原子核外电子应遵从三条原则： – 泡利不相容原理：一个原子中不可能存在两个具有相同的4个量 子数的电子，可见，一个原子轨道最多只能排两个电子，而且这 两个电子的自旋必须相反。 – 能量最低原理：为了使原子系统能量最低，在不违背泡利不相容 原理的前提下，电子尽可能地先占据能量最低的轨道。这个状态 就使原子系统的基态。 – 洪德原则：在等能量（n,l相同）的轨道上，自旋平行电子数越 多原子系统的能量则越低。即：在一组能量相同的轨道上，电子 尽可能以自旋相同的方向分占不同的轨道。 – 作为洪德规则的补充，能量兼并的轨道上全充满、半充满或全空 的状态是比较稳定的。
多电子原子的光谱项概述PPT(52张)培 训课件 培训讲 义培训 教材工 作汇报 课件PP T
LOGO
多电子原子的光谱项概述PPT(52张)培 训课件 培训讲 义培训 教材工 作汇报 课件PP T
原子光谱项的求法
多电子训 教材工 作汇报 课件PP T
第4章 多电子原子的光谱项
1
LOGO
基态原子核外电子排布的规则 单个原子的核外电子的运动状态用n、l、m、ms4个量子数来表示. 主量子数n：取值为1，2，3，…非零的正整数. 电子运动的能量主要由主量子数n来决定，在氢原子中， 电子的能量为：E=-13.6/n2eV，n值越大，电子离核平均距离越远， 电子的能量越高 轨道角动量量子数l，简称角量子数. 决定电子的原子轨道角动量的大小，描述电子云的形状. 当n值一定时，不同的l对电子的能量也稍有影响，l越大能量越高. L取值为0，1，2，3， …，（n-1）等n个从0开始的正整数 磁量子数m：描述着电子云在空间的伸展方向它的取值受角量子数l的 限制，m=0，± 1， ± 2，…， ± l 自旋磁量子数ms：描述原子中的电子的自旋运动，取值为± 1/2分别 表示同
多原子分子的电子光谱
(1a1)2(2a1)2(1b2)2(3a1)2(1b1)2(4a1)0
3. 有两个单占据轨道(都是非简并轨道)的组态 谱项的对称性由这两个单占据轨道的直积给出, S = 0 或 1, 多重度为 1 或 3。 如乙烯的激发态 (D2h) 有以下组态: ···(b3u)1(b2g)1 b3ub2g = B1u，其谱项为：1B1u，3B1u。
当Qi为非全对称的一维不可约表示，则：
Vi Vi' Vi'' 0, 2, 4,
当Qi为二重简并态，并受到多重激发，则： li 0
Vi Vi' Vi'' 0, 2, 4,
若电子和振动的相互作用很大，则由下式确定：
R e'V 'e''V '' 'eV 'e' V
电子振动态的选择定则比纯电子态的选择定则
(1a1)2(2a1)2(1b2)2(3a1)2(1b1)2(4a1)0
2. 只有一个单占据轨道的电子组态 谱项由该轨道的对称性决定， 多重度为 2S + 1 = 2。 例如若组态为：
(1a1)2(2a1)2(1b2)2(3a1)2(1b1)1 则其谱项为：2B1。
CO2电子组态: (1g)2(1u)2(2g)2(3g)2(2u)2(4g)2(3u)2 (1u)4(1g)4。 H2O (C2V) 的电子组态:
若 e 是简并态，则对操作 R 有：
Rˆl Djl (R) j
j
简并态的波函数构成一个多 维不可约表示的基函数。
§9.2 分子轨道与电子组态
一、电子组态
电子组态：将电子波函数看成单电子波函数的乘
积，考虑到自旋，每个轨道放两个电子，按分子
3. 有两个单占据轨道(都是非简并轨道)的组态 谱项的对称性由这两个单占据轨道的直积给出, S = 0 或 1, 多重度为 1 或 3。 如乙烯的激发态 (D2h) 有以下组态: ···(b3u)1(b2g)1 b3ub2g = B1u，其谱项为：1B1u，3B1u。
当Qi为非全对称的一维不可约表示，则：
Vi Vi' Vi'' 0, 2, 4,
当Qi为二重简并态，并受到多重激发，则： li 0
Vi Vi' Vi'' 0, 2, 4,
若电子和振动的相互作用很大，则由下式确定：
R e'V 'e''V '' 'eV 'e' V
电子振动态的选择定则比纯电子态的选择定则
(1a1)2(2a1)2(1b2)2(3a1)2(1b1)2(4a1)0
2. 只有一个单占据轨道的电子组态 谱项由该轨道的对称性决定， 多重度为 2S + 1 = 2。 例如若组态为：
(1a1)2(2a1)2(1b2)2(3a1)2(1b1)1 则其谱项为：2B1。
CO2电子组态: (1g)2(1u)2(2g)2(3g)2(2u)2(4g)2(3u)2 (1u)4(1g)4。 H2O (C2V) 的电子组态:
若 e 是简并态，则对操作 R 有：
Rˆl Djl (R) j
j
简并态的波函数构成一个多 维不可约表示的基函数。
§9.2 分子轨道与电子组态
一、电子组态
电子组态：将电子波函数看成单电子波函数的乘
积，考虑到自旋，每个轨道放两个电子，按分子
电偶极跃迁的选择定则
电偶极跃迁的选择定则电偶极跃迁的选择定则，听起来像个科学家开的玩笑，其实它可真是个有趣的课题。
想象一下，原子就像个跳舞的舞者，而电偶极跃迁就是它在舞台上的表演。
这个舞者可以在不同的能量状态之间切换，但并不是随便怎么跳舞都行哦。
它有一套自己的规则，就像跳舞的时候不能乱扭，得跟着节拍走。
让我们聊聊什么是电偶极跃迁。
简单来说，这就是原子或分子吸收或发射光子的时候发生的一种能量变化。
想象一下，原子像个孩子，光子就像一颗糖果。
孩子看到糖果，就会兴奋地跳起来，直接把手伸向那颗糖。
这个过程其实是能量的转移，能量高的时候就是个兴奋的小家伙，能量低的时候就是乖乖待在原地的老实人。
说到这里，有趣的事情来了。
不是所有的糖果都能吸引每个孩子，这就是选择定则的魅力所在。
电偶极跃迁的选择定则告诉我们，只有特定的能量状态才能进行跃迁。
换句话说，有些能量状态就像是孩子的“心头好”，而有些则是“看不上”的。
就像你去吃自助餐，看到那道你最爱吃的菜，立马就扑过去了，别的菜根本没在你的考虑范围内。
再来谈谈这个选择定则的具体条件。
一般来说，跃迁的起始和结束状态之间的量子数差必须符合特定的条件。
比如，主量子数、角动量量子数等的变化都有讲究。
简单点说，有点像打麻将，不能随便碰牌，要符合规则才能成牌。
如果不符合这些条件，跃迁就像是碰上了阻碍，想跳也跳不起来。
咱们再来细聊聊偶极矩的概念。
这个偶极矩就像是舞者的舞姿，能量的高低、位置的变化都会影响它的表现。
强的偶极矩意味着跃迁更容易发生，就像一位舞者跳得越好，观众自然就越喜欢。
反之，偶极矩弱，那就很可能在舞台上显得有些尴尬。
哦，大家都知道，尴尬的舞者很容易就会被观众遗忘。
有趣的是，选择定则也让我们对光谱的理解更加深入。
不同的原子和分子有不同的跃迁方式，发出的光谱线就像他们的名片，清晰地显示出它们的特性。
比如说，氢原子和氦原子虽然都是气体，但它们的光谱完全不同。
就好比两个不同风格的明星，虽然都在演戏，但一开口就能让你认出来。
多电子原子的光谱项
这些实验技术能够精确地测量超精细结构能级分裂的大小和形
03
状，从而揭示原子核和电子之间的相互作用机制。
06
总结与展望
本文主要内容和创新点回顾
介绍了多电子原子的基本概念 和理论框架，包括原子结构、
电子组态、光谱项等。
详细阐述了多电子原子光谱项 的计算方法和实验技术，包括 变分法、微扰法、组态相互作
光谱支项确定及标记规则
光谱支项确定
根据泡利原理，同一电子组态可以形成的光谱项数目由电子数n和轨道数l决定。对于给定的电子组态，可以形成 的光谱项数目为(2l+1)。
标记规则
光谱项用大写英文字母S、P、D、F等表示，分别对应于L=0、1、2、3等。对于多重态，用数字2S+1表示，其 中S为总自旋量子数。例如，对于钠原子的3s^1电子组态，可以形成的光谱项为^2S_(1/2)。
电子自旋与轨道运动耦合
多电子原子中，电子自旋与轨道运动之间存在相互作用，导致能级发生分裂， 形成精细结构。
自旋-轨道耦合强度
自旋-轨道耦合强度与原子序数的平方成正比，因此重元素中精细结构现象更为 显著。
相对论效应对精细结构影响
质量速度关系
相对论效应导致电子质量随速度增加而增大，进而影响电子 在原子中的运动状态。
谱线强度与选择定则
谱线强度
表示原子光谱中某条谱线的发光 强度或吸收强度，与跃迁几率和
原子浓度等因素有关。
选择定则
决定原子能级间跃迁是否发生的规 则，如电偶极辐射的选择定则要求 Δl=±1。
影响因素
谱线强度受温度、压力、磁场等外 部条件的影响，同时也与原子本身 的性质有关。
02
多电子原子结构特点
电子云分布与形状
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
P. V. Auger (1899-1993)
K壳层出现一个空位后，一个L壳层s支壳层上的电 子(2s电子)跃迁到K壳层填充这个空位，释放出的 能量传递给L壳层p支壳层上的一个电子(2p电子)并 使之电离，这一过程称为KLILII,III俄歇跃迁。
俄歇电子的动能
EA = EK − ELI − ELII ,III
轫致辐射(bremsstrahlung，刹车辐射)
hν= T − T ′
hν max=
hc =
λmin
T=
eU
杜安(W. Duane)和亨特(P. Hunt)于1915年实验测定了h 值，与利用光电效应 实验测定的h值十分接近。
§4.5原子的内层能级和特征X射线—X射线的能谱 X射线特征谱
当加速电压大于一定值时，在连续谱 上出现了分立的线谱：
§4.4 多电子原子—多电子原子光谱--电偶极跃迁的选择定则
+-
+-
+-
原子处在定态
激发电偶极振荡
辐射相同频率光子
跃迁速率
∫ λ=fi
ω3 6ε 0 hc3
2
p=
ห้องสมุดไป่ตู้
ω3 6ε 0 hc3
2
u
* f
(−er
)ui
dτ
≠0
§4.4 多电子原子—多电子原子光谱--电偶极跃迁的选择定则
电偶极辐射的选择定则 (多电子原子情形) 拉波特定则：跃迁只允许在宇称相反的态之间发生。
W. L. Bragg (1890-1971)
布拉格条件(相干加强) 2= d sinθ n= λ, n 1, 2,3
大布拉格的X射线分光仪
W. H. Bragg (1862 -1942)
The Nobel Prize in Physics 1915
§4.5原子的内层能级和特征X射线—X射线的能谱 X光管发射的能谱
§4.4 多电子原子—多电子原子光谱--电偶极跃迁的选择定则 单电子状态的宇称为 (-1)l
若 l 为偶数，则波函数在反演变换下不变，称该状态具有偶宇称。 若 l 为奇数，则波函数在反演变换下变号，称该状态具有奇宇称。
对于多电子原子，在中心力场近似下，原子的状态由电子组态描述，宇 称为：
(−1)∑li
K线系：Kα、Kβ、Kγ 等谱线； L线系：Lα、Lβ、Lγ 等谱线。
原子序数大的元素会出现更多的谱系，分别称为M系，N系。
H. Moseley (1887-1915)
§4.5原子的内层能级和特征X射线—X射线的能谱
各元素的特征线波数的平方根与原子序数(原子核电荷数)成线性关系
莫塞莱经验公式 (莫塞莱定律)
在中心力场下，单电子的波函数为
unlml (r) = Rnl (r)Ylml (θ ,φ )
空间反演 r → -r
在球坐标下，这种反演变换为：
r→r
θ
→
π
−θ
φ → π + φ
径向函数不变，而角向的球谐函数有
Ylml (π −θ ,π + φ ) =(−1)l Ylml (θ ,φ )
Otto Laporte
§4.5原子的内层能级和特征X射线—X射线的能谱
νK
=R(Z
− 1)2
1 12
−
1 22
νL
= R(Z − 7.4)2
1 22
−
1 32
特征X射线产生机制
§4.5原子的内层能级和特征X射线—X射线的能谱
选择定则：
跃迁电子要满足
∆l =±1
∆j = 0, ±1
§4.5原子的内层能级和特征X射线—俄歇电子能谱
Max von Laue (1879 -1960)
实验：W. Friedrich, P. Knipping
劳厄斑
The Nobel Prize in Physics 1914
§4.5原子的内层能级和特征X射线—X射线的能谱
晶体衍射 1912年，小布拉格提出一种更简便的晶体衍射方法。 规则排列的原子形成布拉格平面，X射线从相邻平面 散射，形成干涉。
LS耦合：
∆S =0
∆L = 0, ±1
∆J
=
0, ±1
(J = 0 → J = 0除外）
∆M J = 0, ±1 (当∆J = 0时，M J = 0 → M J = 0除外)
jj耦合
∆j = 0, ±1 (跃迁电子）
∆J
=
0, ±1
(J = 0 → J = 0除外）
∆M J = 0, ±1 (当∆J = 0时，M J = 0 → M J = 0除外)
在电偶极辐射中，光子带走的角动量为 ，由于宇称守恒，要求电偶极
跃迁的选择定则是
∆∑li = ±1
§4.4 多电子原子—多电子原子光谱--电偶极跃迁的选择定则
一般情况下，原子光谱只涉及到单电子的跃迁 选择定则简化为
∆l =±1
氦原子的能级和相关的光谱跃迁
§4.4 多电子原子—多电子原子光谱--电偶极跃迁的选择定则
Wilhelm Röntgen (1845-1923)
The Nobel Prize in Physics 1901
§4.5原子的内层能级和特征X射线—X射线的波性
X射线是电磁波 (波长10-3 nm~1nm)
晶体衍射 1912年，劳厄建议，鉴于晶体内部原子间距与X射 线的波长数量级相同，同时规则排列，可以当作 三维光栅，做晶体衍射实验。
Kα线
νK
=R(Z
−
1)2
1 12
−
1 22
Lα线
νL
= R(Z
−
7.4)2
1 22
−
1 32
(1/λ)1/2 (m-1/2)
1.0
0.9
0.8
Kα
0.7
Lα
0.6
CrFeCu Mo
0.5 20
40
Z
W
60
80
K线和L线的莫塞莱图
根据实验测量的特征线波数，从莫塞莱图上就可以标识元素的种类， 所以特征谱又称为标识谱。
§4.4 多电子原子—多电子原子光谱—He原子光谱
基态：1s2 1S 单电子激发态：
1sns 1S 3S 1snp 1P 3P 1snd 1D 3D 1snf 1F 3F
氦原子的能级和相关的光谱跃迁
§4.5原子的内层能级和特征X射线—X射线的发现
1895年，伦琴发现了X射线
X射线不带电、很强的穿透性、直 线传播、使照相底片感光、使气 体电离奇特性质等。
§4.5原子的内层能级和特征X射线—俄歇电子能谱
(1) 其波长与加速电压无关，只与靶 材料有关，因此称为特征谱。
(2) 不同的靶材料，除了波长不同外， X射线的特征谱具有相似的结构。
§4.5原子的内层能级和特征X射线—X射线的能谱
1913年，莫塞莱(H. G. J. Moseley)系统地测量了从铝到 金总共38种元素的特征谱。
发现特征谱包含两组谱线，按波长的次序称为：