高等数学二重积分图形
高等数学：第三讲 极坐标系下二重积分的计算
解：画出积分区域，极点 在区域 D 的外部 区域 D可表示为
D {(r, ) | 2 r 3, 0 2 }
因此Biblioteka ex2y2dxdy 2d
3 er2 rdr
D
0
2
y
2 r 3
4 x2 y2 9
O
x
0 2
例2
2 0
[
1 2
er2
] |32
d
2 ( 1 e9 1 e4 )d
D
o
i1 i
i
r ri1 r ri
x
极坐标系下计算二重积分
再由直角坐标与极坐标的关系
x r cos , y r sin
可得
D f ( x, y)dxdy D f ( x, y)d D f (r cos , r sin )rdrd
D
o
i1
i
r
ri 1
i
r ri
x
极坐标系下计算二重积分
因此
O
x
x2 y2dxdy
d
2sin
r rdr
D
0
0
例3
0
[
1 3
r
3
]
|2sin
0
d
8 sin3 d
30
32 9
y
x2 y2 2y
2 sin
•
0
O
x
谢谢
此时
D f (r cos , r sin )rdrd
r ( )
= d 0 f (r cos , r sin )rdr
r r( )
D
o x
例1
计算
D1
1 x2
高等数学--二重积分的计算
D
∫ ∫ b
d
= a ( f1( x) ⋅ c f2( y)dy )dx
∫ ⋅∫ 得 =
b
a f1( x)dx
d
c f2( y)dy
即等于两个定积分的乘积.
7
二重积分的计算法
X型区域的特点: 穿过区域且平行于y轴的直线 与区域边界相交不多于两个交点.
Y型区域的特点: 穿过区域且平行于x轴的直线 与区域边界相交不多于两个交点.
0
0
0
y
∫ ∫ =
a 0
f
( y)⋅
x
a y
dy
=
a
O
(a − y) f ( y)dy
0
•(a,a)
a
x
∫a
= (a − x) f ( x)dx 0
证毕.
21
二重积分的计算法
立体顶部 x2 + z2 = R2
例 求两个底圆半径为立R体,且底这部两x个2 圆+ 柱y2面= 的R2方程
分别为 x2 + y2 = R2及 x2 + z2 = R2 .求所围成的
x2
y +
y
2
⎟⎞ ⎠
=
f ( x, y),
∫ ∫ 故
1
f ( x, y)dy =
0
1 ∂ ⎜⎛ 0 ∂y ⎝
x2
y +
y2
⎞⎟ dy ⎠
=
x2
y +
y2
1 0
=
x
1 2+
; 1
∫ ∫ ∫ 所以 I1 =
1
1
dx f ( x, y)dy =
0
0
高等数学课件D92二重积分的计算
电磁学中电荷分布问题
电荷分布概述
在电磁学中，电荷分布是研究电场和 磁场的基础。了解电荷分布对于预测 电场强度、电势差以及电磁波的传播 等具有重要意义。
二重积分在电荷分布 中的应用
二重积分在电磁学中广泛应用于计算 电荷分布。通过将电荷区域离散化为 微小单元，对每个单元的电荷密度进 行积分，并利用二重积分对整个区域 进行积分，可以得到总电荷量和电荷 分布。
在每个子区域内分别进行积分计算，然后将结果相加得到最 终的二重积分值。这种策略可以降低计算难度，提高计算效 率。
03 典型例题分析与求解
平面区域上函数积分问题
确定积分区域
根据题目要求，确定需要积分的平面区域，通常是由 不等式组或曲线围成。
选择积分次序
根据积分区域的形状和复杂性，选择合适的积分次序， 即先对哪个变量进行积分。
图像处理算法与二重积分
在实际应用中，图像处理算法（如直方图均衡化、滤波算法）经常需要利用像素值统计来实现图像增强和特 征提取。二重积分作为计算像素值统计的重要工具，在这些算法中发挥着关键作用。
其他领域应用举例
地理学中的地形分析
在地理学中，地形分析是研究地 表形态和地貌特征的重要手段。 二重积分可以用于计算地表高程、 坡度、坡向等地形参数，进而实 现地形分类、地貌特征提取等应 用。
梯形法
将积分区域划分为若干个小梯形， 以梯形的面积近似代替被积函数 的面积，通过求和所有梯形的面 积得到二重积分的近似值。
辛普森法
在梯形法的基础上，通过采用更 精确的插值多项式来逼近被积函 数，从而提高二重积分计算的精 度。
误差估计及收敛性判断
误差估计
对于不同的数值方法，可以通过理论分析和实际计算来估计其误差的大小，以便更好地控制计算精度 。
高等数学 课件 PPT 第九章 重积分
若函数ρ(x,y)=常数，则薄片的质量可用公式 质量=面密度×面积 来计算.现在面密度ρ(x,y)是变化的，故不能用上述公式来求. 这时仍可采用处理曲顶柱体体积的方法来求薄片的质量.分为下列 几个步骤：
一、二重积分的概念
(1)分割将D分成n个小闭区域Δσ1,Δσ2,…,Δσn（小区域 的面积也用这些符号表示），第i个小块的质量记为 ΔMi(i=1,2,…,n)，则平面薄片的质量
于是
一、在直角坐标系下计算二重积分
图 9-11
一、在直角坐标系下计算二重积分
【例3】
计算
，D是由抛物线y2=2x与直线y=x－4所
围成的区域．
解 画出积分区域D的草图如图9-12所示．若先对x积分，
则有
一、在直角坐标系下计算二重积分
图 9-12
一、在直角坐标系下计算二重积分
若先对y积分，则需将D分为两个区域D1和D2， 于是
一、在直角坐标系下计算二重积分
【例1】
试将
化为两种不同次序的累次积分，其中
D是由y=x,y=2－x和x轴所围成的区域．
解 积分区域D如图9-9所示．首先说明如何用“穿线法”
确定累次积分的上、下限．如果先积x后积y，即选择Y型积
分区域，将区域D投影到y轴，得区间［0,1］，0与1就是对y
积分的下限与上限，即0≤y≤1，在［0,1］上任意取一点y，
二、二重积分的性质
二重积分与定积分有类似的性质.假设 下面所出现的积分是存在的.
二、二重积分的性质
性质1
设c1,c2为常数,则
性质2
若闭区域D分为两个闭区域D1与D2，则
二、二重积分的性质
性质3
(σ为D的面积）.
性质4
高等数学二重积分概念及性质
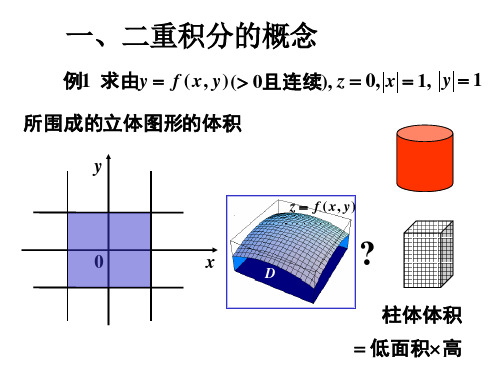
例1 求由y f ( x , y ) ( 0且连续), z 0, x 1, y 1
所围成的 立体图形的体积
y
z f ( x, y)
0
x
D
?
柱体体积 低面积 高
V lim f ( i ,i ) i
0 i 1
n
例 2 设有界闭区域D内 有一张 平面薄片 （不计厚度）
设下列函数 在D上可积 前提：
性质1：若f ( x , y ) 1, D的面积为 0 , 则 d 0
、 R 性质2 （线性性质）
D
[f ( x , y ) g( x, y )] d D
f ( x , y )d g ( x , y )d
面密度为f ( x , y )(连续)， 求其质量
y
( i ,i )
i
o
x
n
m lim f ( i ,i ) i
0 i 1
定义 设 f ( x, y ) 是定义在区域D上的二元函数
(1) 分割 D : ij
i 1,, m; j 1,n
ij ( 2 ) 取点: ( i , j )
记为
D
f ( x , y ) d 直角坐标系下，记做
D
f ( x , y ) dxdy
即
lim f ( i ,i ) i f ( x, y ) d 0 i 1
D
n
积 分 区 域
被 积 函 数
积 分 变 量
面 被 积积 积 元分 表 素和 达 式
当 f ( x , y )在闭区域上连续或分片连续时， 定义中和式的极限必存在， 即二重积分必存在.
二重积分的计算及几何意义的可视化解释-图解高等数学-下 17
二重积分的计算及几何意义的可视化解释-图解高等数学-下1712.1 二重积分将一元函数积分推广来看对于连续函数f(x,y) 如何求二重积分. 每个二重积分都可以方便地用定积分的方法分步进行计算.矩形区域上的二重积分设f(x,y) 在矩形区域R: a当网格不断进行细分使?x 和?y 都趋近零时, 则趋于R 的面积趋近于极限值, 则称该极限值为f 在R 上的二重积分, 记为:值得注意的是f 函数的连续性是二重积分存在的一个充分条件, 对于许多不连续的函数, 该极限也存在.二重积分的性质连续函数的二重积分也有一些代数性质:二重积分的几何意义当f(x,y) 为正函数时, 则可以把矩形区域R 上的f 函数二重积积分视为曲面为z=f(x,y) 的棱柱体的体积.计算二重积分的Fubini 定理现在计算xy 平面内矩形区域R ：0也就是说体积可以这样计算出来: 先固定x, 将4-xy 先关于y 从y=0 到y=1, 然后再对所得x 的表达式关于x 从x=0 到x=2 积分. 则体积可以写成表达式:上述表达式称为二重积分或累次积分(iterated integral).Guido Fubini(圭多.富比尼) 在1907年证明了矩形域上任意一个连续函数的二重积分都可以用两种累次积分的任一种次序计算.有界非矩形区域上的二重积分函数f(x,y) 在非矩形区域R 上的二重积分, 设想被网格覆盖, 不过在R 内的小块面积为红色, 如下图所示:可以看到随着网格不断细分, R内包含的小矩形方块越来越趋于零时, S 就会有极限, 则称该极限为f 在R 上的二重积分:如果f(x,y) 为正, 且在R 上连续, 则曲面z=ff(x,y) 与R 之间的立体趋于的体积为:观看下面的动画:在xy 平面内, 如果R 是一个由两条曲线g1(x) 和g2(x) 围城的区域. 则也可以用切片法来求体积. 先计算截面面积A(x):然后再对A(x) 从x=a 到x=b 作积分可以求得体积:观察下面动画A(x) 从x=a 到x=b 作积分的过程:。
中国矿业大学(北京)《高等数学》课件-第10章重积分
“分割, 近似, 求和, 取极限”
解决方法:
质量 M .
密度函数为
定义. 设
且相等,
称为体积元素,
若对 作任意分割:
任意取点
则称此极限为函数
在 上的三重积分.
在直角坐标系下常写作
三重积分的性质与二重积分相似.
性质:
例如
下列“乘
中值定理.
在有界闭域 上连续,
则存在
使得
V 为 的
体积,
其中
解: 积分域 D 的边界为圆周
它在与 x 轴的交点 (1,0) 处与直线
从而
而域 D 位于直线的上方, 故在 D 上
估计下列积分之值
解: D 的面积为
由于
积分性质5
即: 1.96 I 2
D
例2.
判断积分
的正负号.
解: 分积分域为
则
原式 =
猜想结果为负 但不好估计 .
总有：
引例1中曲顶柱体体积:
引例2中平面薄板的质量:
如果 在D上可积,
元素d也常记作
二重积分记作
这时
分区域 D ,
因此面积
可用平行坐标轴的直线来划
二重积分存在定理:
若函数
定理2.
(证明略)
定理1.
在D上可积.
限个点或有限条光滑曲线外都连续 ,
积.
在有界闭区域 D上连续,
计算该薄片的质量 M .
度为
设D 的面积为 ,
则
若
非常数 ,
仍可用
其面密
“分割, 近似, 求和, 取极限”
解决.
1)“分割”
用任意曲线网分D 为 n 个小区域
二重积分的计算方法
二重积分的计算方法在高等数学中，二重积分是一个重要的概念，它在许多领域都有着广泛的应用，比如物理学、工程学、经济学等。
理解和掌握二重积分的计算方法对于解决相关的实际问题和理论研究都至关重要。
二重积分的定义是在平面区域上对函数进行积分。
直观地说，它可以用来计算平面区域上某个量的总和，比如平面薄片的质量、平面区域的面积等。
那么，如何计算二重积分呢？常见的计算方法主要有直角坐标法和极坐标法。
直角坐标法是我们最常接触的方法之一。
当积分区域是由直线边界围成的矩形、三角形或者其他简单形状时，直角坐标法往往比较适用。
我们先来看 X 型区域。
如果积分区域可以表示为＼（a\leq x\leqb\），＼（＼varphi_1(x)＼leq y\leq ＼varphi_2(x)＼），那么二重积分可以写成：＼＼int\！＼！＼int_D f(x,y) d\sigma ＝＼int_{a}＾｛b}dx ＼int_{＼varphi_1(x)｝＾｛＼varphi_2(x)｝ f(x,y) dy＼这里要先对＼（y\）积分，再对＼（x\）积分。
再来看 Y 型区域。
如果积分区域可以表示为＼（c\leq y\leq d\），＼（＼psi_1(y)＼leq x\leq ＼psi_2(y)＼），那么二重积分可以写成：＼＼int\！＼！＼int_D f(x,y) d\sigma ＝＼int_{c}＾｛d}dy ＼int_{＼psi_1(y)｝＾｛＼psi_2(y)｝ f(x,y) dx＼在使用直角坐标法计算二重积分时，关键是要正确确定积分区域的类型，以及积分的上下限。
接下来我们说一说极坐标法。
当积分区域具有圆形、扇形或者是与圆相关的形状时，极坐标法通常会更加简便。
在极坐标系中，点用＼（（＼rho,＼theta)＼）表示，其中＼（＼rho\）表示点到原点的距离，＼（＼theta\）表示极角。
如果积分区域可以表示为＼（＼alpha\leq\theta\leq\beta\），＼（＼varphi_1(＼theta)＼leq\rho\leq\varphi_2(＼theta)＼），那么二重积分可以写成：＼＼int\！＼！＼int_D f(x,y) d\sigma ＝＼int_{＼alpha}＾｛＼beta}d\theta ＼int_{＼varphi_1(＼theta)｝＾｛＼varphi_2(＼theta)｝ f(＼rho\cos\theta,＼rho\sin\theta)＼rho d\rho＼在极坐标法中，要注意＼（＼rho\）的积分上下限以及函数在极坐标下的表达式。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
z=f (x,y)
D是矩形区域 [a,b ; c,d] Q( y ) =
d
b
a
f ( x , y )dx
I
c
Q( y )dy
b
d
c
dy f ( x , y )dx
a
0
c
y
d
y
a
. .
b
.
D
b d
x
同理，也可以先对 y 积分
I
a
dx f ( x, y )dy
c
5. 二重积分的计算（D是曲线梯形区域） z
11. 将二重积分化成二次积分 D: 由四条直线 : x=3，x=5, y 3x – 2y+4 = 0, 3x –2y+1 = 0 19 2 共同围成的区域 先对y积分
I
f ( x , y )d xdy
D
I
dx
( x ) ( x )
8
D1 D2
i 1
n
D
.
x
2. 曲顶柱体的体积 S : z = f (x,y)
元素法
1 任意分割区域 D,化整为零
2 以平代曲
z
Vi f ( x i , yi ) i
3 积零为整 V f ( x i , y i ) i
i 1 n
V
4 取极限
令分法无限变细
0 y
.
V = lim f ( x i , y i )Δ σ i
i 1
n
记
f ( x , y )d
D
x
.
3. 比较大小
比较 I ( x y ) d
D
与 I ( x y ) d 的大小,
D
其中
D由 ( x ) ( y )
y
围成
由二重积分的性质
I1 I 2
更确切的 I 1 < I2
0
D1
b
b
y
. .
a
x
a ( b y ) dy b
ab ab 2
ab （定积分三角代换） cos d
=
瓦里斯公式
10. 将二重积分化成二次积分 D: x + y =1 , x – y = 1，x = 0 所围
i 1 n
0 y
.
i
x
D
2. 曲顶柱体的体积 S : z = f (x,y)
元素法
1 任意分割区域 D,化整为零
2 以平代曲
z
Vi f ( x i , yi ) i
3 积零为整 V f ( x i , y i ) i
i 1 n
4 取极限
令分法无限变细
0 y
V = lim f ( x i , y i )Δ σ i
推广
三重积分
高斯公式
2. 曲顶柱体的体积 S : z = f (x,y)
元素法
1 任意分割区域 D,化整为零
2 以平代曲
z
S
0 y
i
x
D
2. 曲顶柱体的体积 S : z = f (x,y)
元素法
1 任意分割区域 D,化整为零
2 以平代曲
z
Vi f ( x i , yi ) i
3 积零为整 V f ( x i , y i ) i
D
先对 y 积分
x =1– y
I
dx
x
x
f ( x , y )dy
D1
0
先对 x 积分 （不分块儿行吗？）
1
x
I
D1 D2
D2 x = y +1
.
dy
y
y
f ( x, y )dx
f ( x, y )dx
–1
. .
dy
z=f (x,y)
D: (y) x (y) cyd
Q( y ) =
ψ( y )
φ( y)
f ( x, y )dx
0
c
y
x=(y)
d
y
I = c
d
Q( y )dy
d
c
dy
.
.
ψ( y )
φ ( y)
f ( x, y )dx
D
x x=(y)
6. 二重积分计算的两种积分顺序
1
y
I
f ( x , y )d xdy
D
先对 y 积分
y =1– x
I dx
x
x
f ( x, y )dy
0
1
x
y = x –1
–1
. .
10. 将二重积分化成二次积分
D: x + y =1 , x – y = 1，x = 0 所围
1
y
I
f ( x , y )d xdy
D
23 计算I f ( x,y)dxdy. D : x 2 y 2 4x , x2 y 2 8x, x y, y 2x所围 24 将积分换序
I dx
0
2a
2 ax 2 ax x 2
f ( x,y)dy
R 1 R 2
25 将积分化为极坐标形式
I
1 画出区域 D 图形
xydxdy ,
D
D: y x 与
y x 所围区域
2 先对 y 积分（从下到上）
y
xydxdy dx x xydy
x
1
D
xdx ydy
x
x
1 1 1 3 5 ( x x )dx 24 2 0
3 先对 x 积分（从左到右）
f ( x , y )dy
11 将二重积分化成二次积分 D: 由四条直线 : x =3，x = 5, 3x –2y+4 = 0, 与 3x –2y+1 = 0 共同围成的区域
12 将二重积分换序： 13 将二重积分换序：
I dy
0
1
y
y
f ( x,y)dx
I dx
0
a
2 ax x 2
x
f ( x,y)dy
I = a dxy ( x ) f ( x, y )dy
7. 计算
I
D
y dxdy x y
D:
y x y
y
I
y
3
dy
y y
y=x
y dx x y
. . .
D 1
x=y2
3 1 ln 2 12 2
0
1
3
x
8. 用两种顺序计算
I
D
f ( x , y )d xdy
z=f (x,y)
D: (y) x (y) cyd
0
c
y
x=(y)
d
y
D
x x=(y)
5. 二重积分的计算（D是曲线梯形区域） z
I
D
f ( x , y )d xdy
z f ( x, y ) y y .
z=f (x,y)
i 1
n
i
.
D
x
2. 曲顶柱体的体积 S : z = f (x,y)
元素法
1 任意分割区域 D,化整为零
2 以平代曲
z
Vi f ( x i , yi ) i
3 积零为整 V f ( x i , y i ) i
i 1 n
4 取极限
令分法无限变细
0 y
i
V = lim f ( x i , y i )Δ σ i
0
x+y>1 1
2
1
2
x + y =1
x
4.二重积分的计算 (D是矩形区域z)
复习§2：平行截面面 积为已知的立体的体积
I
D
f ( x , y )d xdy
z=f (x,y)
D是矩形区域 [a,b ; c,d]
0
c
y
d
y
a
b
x
D
4. 二重积分的计算 (D是矩形区域z)
I
D
z f ( x, y ) y y
I
f ( x , y )d xdy
D
D: x1(y) x x2(y) cyd
y
d
x1 (y) x2(y)
y
c
0
D
x
I=
x ( y )
x ( y )
f ( x , y )dx
6. 二重积分计算的两种积分顺序
I
f ( x , y )d xdy
D
D: x1(y) x x2(y) cyd
14 （练习）将二重积分化成二次积分 15 为什么引用极坐标计算二重积分 16 利用极坐标计算二重积分
17 怎样用极坐标计算二重积分
18 怎样用极坐标计算二重积分 19
(1) 极点不在区域 D 的内部
(2) 极点位于区域 D 的内部
把 I f ( x,y)dxdy 变为极坐标形式
其中 D : ( x a) 2 y 2 a 2 与 y 0 所围区域