一些经典初等数学模型
初中几何48个模型作业帮

初中几何是数学中的一个重要部分,它涉及到许多基本的几何概念和定理。
在学习初中几何时,了解和掌握一些常见的几何模型是非常有帮助的。
以下是48个初中几何模型:1. 等边三角形模型2. 等腰三角形模型3. 直角三角形模型4. 平行四边形模型5. 菱形模型6. 矩形模型7. 正方形模型8. 梯形模型9. 圆模型10. 扇形模型11. 弓形模型12. 切线模型13. 抛物线模型14. 双曲线模型15. 椭圆模型16. 角平分线定理模型17. 中线定理模型18. 弦长定理模型19. 勾股定理模型21. 外角和定理模型22. 线段比例定理模型23. 相似三角形判定定理模型24. 三角形内心定理模型25. 三角形外心定理模型26. 三角形重心定理模型27. 三角形垂心定理模型28. 四边形对角线性质定理模型29. 四边形面积公式模型30. 圆的周长公式模型31. 圆的面积公式模型32. 扇形面积公式模型33. 弓形面积公式模型34. 点到直线距离公式模型35. 两点间距离公式模型36. 角平分线性质定理模型37. 中位线定理模型38. 切线的性质定理模型39. 切线的判定定理模型40. 抛物线性质定理模型41. 双曲线性质定理模型43. 角的平分线性质定理的逆定理模型44. 三线合一的逆定理模型45. 线段垂直平分线的逆定理模型46. 余角、补角定理的逆定理模型47. 同位角、内错角、同旁内角定理的逆定理模型48. 正弦、余弦、正切的应用(三角函数的应用)这些几何模型可以帮助你更好地理解和掌握初中几何的知识点,并且能够让你更加熟练地解决各种几何问题。
希望这些信息对你有所帮助!。
初中数学八大经典模型

初中数学八大经典模型数学是人类探索宇宙奥秘的手段,在它的领域里有着深厚的文化底蕴,从古至今都有强大的科学后果,也激发了前所未有的实际活动。
初中数学是一门极其有趣的学科,它拥有独特的传统知识,拥有丰富的讲解内容。
尽管初中数学涉及的内容很多,但其八大模型却是最基本也是最重要的。
下面,就来认识下其中的八大经典模型。
第一经典模型是“极坐标函数”,该模型在数学的宇宙中扮演着重要的角色,它可以描述和表示曲线在多维空间中的分布规律。
它的坐标系定义和应用都是极其有趣的,在很多实际的例子中,它的应用非常广泛。
第二经典模型是“极限”,它是一种数学概念,表示某个变量在某一时刻改变量趋近于某一值。
它可以用来分析函数在不同情况下的变化趋势,也可以用来推导结论。
第三经典模型是“微积分”,它是数学科学的核心模型,可以解决函数变化等问题,是推动数学发展的重要力量。
微积分主要是研究函数在某一点处或某一范围内的变化情况,如果掌握了这个模型,就可以合理的解释和推导函数的弯曲程度,即变化的极限。
第四经典模型是“偏微分方程”,它具有比较强的数学思维,可以用来研究某些动态系统的变化,描述的是一类线性不变的方程组,它的求解非常复杂,要求掌握一定的知识,但是它的应用在科学界非常广泛,如运动算法,流体力学等都有它的身影。
第五经典模型是“图论”,它是一种数学模型,可以用来描述某种新的连接结构,它可以用来描述复杂的网络关系,根据顶点和边的不同来描述不同的复杂系统,它是一种抽象的数学模型,可以用来描述复杂的网络结构,也可以用来解决一系列问题。
第六经典模型是“几何变换”,它是数学上研究几何图形变换的模型,主要是探讨几何图形随着某种变换函数而发生变化的情况,其内容很好理解,学习相关概念和知识,也能够运用它来解决一系列几何问题,其实它也是几何学的基础。
第七经典模型“统计学”,它是研究数据分析方法的一种模型,它可以用来描述一组数据的特征,推断出它的规律和趋势,用来找出未知问题的答案,统计学是一种发现客观规律的重要工具,如果掌握了它,就可以更加有效的分析和挖掘隐藏在数据背后的价值。
初中数学最值问题六种模型

初中数学最值问题有六种模型,包括将军饮马模型、一箭穿心模型、费马点模型、阿氏圆模型、胡不归模型和瓜豆原理模型。
1. 将军饮马模型:当两定点A、B在直线l同侧时,在直线上找一点P,使PA+PB最小。
可以理解为两点之间线段最短。
连接AB交直线l于点P,点P即为所求作的点。
2. 一箭穿心模型:在直线l上找M、N两点(M在左),使得AM+MN+NB最小,且MN=d。
将点A向右平移d个单位到A′,作A′关于直线l的对称点A",连接A"B交直线l 于点N,将点N向左平移d个单位到M,点M、N即为所求。
3. 费马点模型:在三角形ABC中,若D、E分别是AB、AC 上的点,则DE的延长线与BC的延长线交于费马点处,此时三角形周长最小。
4. 阿氏圆模型:以给定点A为圆心,给定距离r为半径画圆,与已知直线l相交于两点B、C,连接两点B、C并延长交于D。
则D点的轨迹是以A为圆心,r为半径的圆。
这个圆被称为阿氏圆。
5. 胡不归模型:在直角三角形ABC中,AB=c,AC=b,BC=a,AD为BC边上的高。
若点P在BC边上,问是否存在点P使得DP垂直于BC边?如果存在,求出点P的位置;
如果不存在,请说明理由。
6. 瓜豆原理模型:在一条直线上有若干个点,每个点都有一个到直线的距离,问如何选择若干个点使得这些点到直线的距离之和最小?瓜豆原理告诉我们,选择任意两个相邻的点并连接它们与直线的交点,然后选择第三个点与前两个点的距离之和最小即可。
以上是初中数学最值问题的六种模型,希望对解决这类问题有所帮助。
(全)初中数学|23种模型汇总

(全)初中数学|23种模型汇总1. 数列模型数列模型是一组按照特定规律排列的数字,常见的数列有等差数列和等比数列。
在解题中,需要掌握其通项公式和求和公式。
2. 几何模型几何模型是通过图形来表示问题,需要熟练掌握各种几何图形的性质和定理,如圆、三角形、直线等。
3. 等式模型等式模型是通过等式来表示问题,需要掌握化简等式、配方、移项等技巧。
4. 方程模型方程模型是通过方程来表示问题,需要掌握解方程的方法和技巧,如消元法、相似变形法、套公式法等。
5. 数据分析模型数据分析模型需要对给定的数据进行处理和分析,如找出最大值、最小值、平均值等。
6. 概率模型概率模型需要根据事件发生的可能性来计算概率,需要掌握概率的基本原理和计算方法。
8. 百分数模型百分数模型需要将数值转化为百分数进行计算,需要掌握百分数的计算方法和应用。
9. 推理模型推理模型需要根据已知的信息推出未知的结果,需要掌握逻辑思维和推理技巧,如分类讨论法、反证法等。
10. 图表模型图表模型是通过图表来表示问题,需要掌握读图和解决图表问题的技巧。
11. 统计模型统计模型需要对给定的数据进行统计分析,如频数分布、统计量计算等。
12. 函数模型函数模型需要根据函数的定义和性质来计算未知量,需要掌握函数的基本概念和图像变化规律。
13. 同余模型同余模型需要根据同余关系来计算未知量,需要掌握同余关系的基本性质和计算方法,如模运算等。
14. 最优化模型最优化模型需要找出满足特定条件下的最优解,需要掌握最优化方法和技巧,如最大值最小值法、拉格朗日乘数法等。
16. 排列组合模型排列组合模型需要计算不同元素之间的排列和组合方式,需要掌握排列组合的基本概念和计算方法。
17. 质数模型质数模型需要计算满足质数条件的解,需要掌握质数的基本性质和计算方法,如质因数分解等。
23. 递推模型递推模型需要利用递推公式来计算未知项,需要掌握递推公式的推导方法和递推问题的解法。
中考数学十大模型

中考数学十大模型中考数学是学生的必修课程之一,对于许多学生来说,数学是一个困难的学科。
然而,在中考数学考试中,有一些常见的数学模型可以帮助学生更好地理解和掌握数学知识。
下面将介绍中考数学中的十大模型。
1.几何模型:在中考数学中,几何是一个非常重要的部分。
通过几何模型,学生可以更好地理解和运用几何知识,如三角形、四边形、圆等。
几何模型可以帮助学生更好地理解空间关系和形状属性。
2.代数模型:代数是中考数学中的另一个重要部分。
通过代数模型,学生可以更好地理解和运用代数知识,如方程、不等式、函数等。
代数模型可以帮助学生更好地解决实际问题和提高数学计算能力。
3.统计模型:统计是数学中的一个重要分支,通过统计模型,学生可以更好地理解和运用统计知识,如概率、样本调查、数据分析等。
统计模型可以帮助学生更好地理解数据和做出正确的决策。
生可以更好地理解和运用函数知识,如线性函数、二次函数、指数函数等。
函数模型可以帮助学生更好地描述和分析实际问题。
5.图形模型:在中考数学中,图形是一个常见的题型,通过图形模型,学生可以更好地理解和分析各种图形,如折线图、饼状图、柱状图等。
图形模型可以帮助学生更准确地表示和比较数据。
6.初等模型:初等数学是中考数学的基础,通过初等模型,学生可以更好地掌握基本的数学运算和基本的数学概念,如加减乘除、分数、百分数等。
初等模型可以帮助学生建立数学基础,为进一步学习数学打下坚实的基础。
7.空间模型:空间是几何的重要组成部分,通过空间模型,学生可以更好地理解和运用空间知识,如平行线、垂直线、平行四边形等。
空间模型可以帮助学生更好地理解几何问题和解决实际问题。
8.时间模型:时间是统计中的重要概念,通过时间模型,学生可以更好地理解和运用时间知识,如时间单位、时间比较、时间序列等。
时间模型可以帮助学生更好地描述和分析时间数据。
生可以更好地理解和运用测量知识,如长度、面积、体积等。
测量模型可以帮助学生更准确地测量物体的大小和形状。
初中几何十大模型-总汇
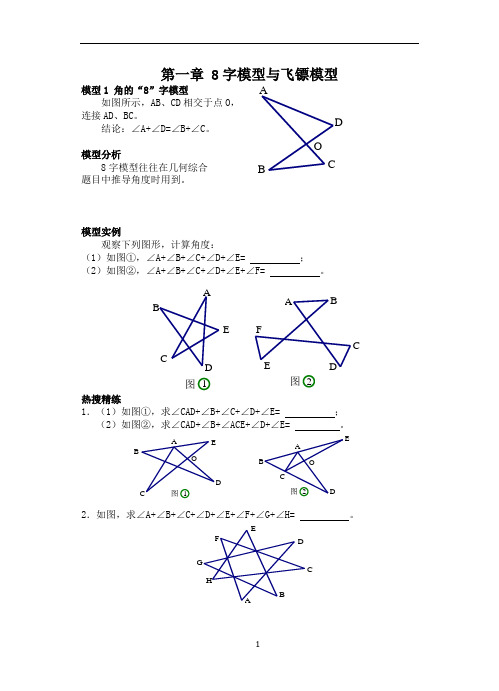
第一章 8字模型与飞镖模型模型1 角的“8”字模型 如图所示,AB 、CD 相交于点O , 连接AD 、BC 。
结论:∠A+∠D=∠B+∠C 。
模型分析8字模型往往在几何综合 题目中推导角度时用到。
模型实例观察下列图形,计算角度:(1)如图①,∠A+∠B+∠C+∠D+∠E= ; (2)如图②,∠A+∠B+∠C+∠D+∠E+∠F= 。
热搜精练1.(1)如图①,求∠CAD+∠B+∠C+∠D+∠E= ; (2)如图②,求∠CAD+∠B+∠ACE+∠D+∠E= 。
2.如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H= 。
OD C BA 图12图E AB C D E F DC B A O O 图12图E AB C D EDC B A H GE F DC BA模型2 角的飞镖模型 如图所示,有结论: ∠D=∠A+∠B+∠C 。
模型分析飞镖模型往往在几何综合 题目中推导角度时用到。
模型实例如图,在四边形ABCD 中,AM 、CM 分别平分∠DAB 和∠DCB ,AM 与CM 交于M 。
探究∠AMC 与∠B 、∠D 间的数量关系。
热搜精练 1.如图,求∠A+∠B+∠C+∠D+∠E+∠F= ;2.如图,求∠A+∠B+∠C+∠D = 。
D CB A M DC B A O135E FD C BA 105OO120D C B A模型3 边的“8”字模型 如图所示,AC 、BD 相交于点O ,连接AD 、BC 。
结论:AC+BD>AD+BC 。
模型实例如图,四边形ABCD 的对角线AC 、BD 相交于点O 。
求证:(1)AB+BC+CD+AD>AC+BD ;(2)AB+BC+CD+AD<2AC+2BD.模型4 边的飞镖模型 如图所示有结论: AB+AC>BD+CD 。
O DCBA ODCB AO C B A模型实例如图,点O 为三角形内部一点。
求证:(1)2(AO+BO+CO )>AB+BC+AC ;(2)AB+BC+AC>AO+BO+CO.热搜精练1.如图,在△ABC 中,D 、E 在BC 边上,且BD=CE 。
100个经典初等数学问题
100个经典初等数学问题第01题阿基米德分牛问题Archimedes' Problema Bovinum太阳神有一牛群,由白、黑、花、棕四种颜色的公、母牛组成. 在公牛中,白牛数多于棕牛数,多出之数相当于黑牛数的1/2+1/3;黑牛数多于棕牛数,多出之数相当于花牛数的1/4+1/5;花牛数多于棕牛数,多出之数相当于白牛数的1/6+1/7.在母牛中,白牛数是全体黑牛数的1/3+1/4;黑牛数是全体花牛数1/4+1/5;花牛数是全体棕牛数的1/5+1/6;棕牛数是全体白牛数的1/6+1/7.问这牛群是怎样组成的?第02题德•梅齐里亚克的法码问题The Weight Problem of Bachet de Meziriac一位商人有一个40磅的砝码,由于跌落在地而碎成4块.后来,称得每块碎片的重量都是整磅数,而且可以用这4块来称从1至40磅之间的任意整数磅的重物.问这4块砝码碎片各重多少?第03题牛顿的草地与母牛问题Newton's Problem of the Fields and Cowsa头母牛将b块地上的牧草在c天内吃完了;a'头母牛将b'块地上的牧草在c'天内吃完了;a"头母牛将b"块地上的牧草在c"天内吃完了;求出从a到c"9个数量之间的关系?第04题贝韦克的七个7的问题Berwick's Problem of the Seven Sevens在下面除法例题中,被除数被除数除尽:* * 7 * * * * * * * ÷ * * * * 7 * = * * 7 * ** * * * * ** * * * * 7 ** * * * * * ** 7 * * * ** 7 * * * ** * * * * * ** * * * 7 * ** * * * * ** * * * * *用星号(*)标出的那些数位上的数字偶然被擦掉了,那些不见了的是些什么数字呢?第05题柯克曼的女学生问题Kirkman's Schoolgirl Problem某寄宿学校有十五名女生,她们经常每天三人一行地散步,问要怎样安排才能使每个女生同其他每个女生同一行中散步,并恰好每周一次?第06题伯努利-欧拉关于装错信封的问题The Bernoulli-Euler Problem of the Misaddressed letters求n个元素的排列,要求在排列中没有一个元素处于它应当占有的位置.第07题欧拉关于多边形的剖分问题Euler's Problem of Polygon Division可以有多少种方法用对角线把一个n边多边形(平面凸多边形)剖分成三角形?第08题鲁卡斯的配偶夫妇问题Lucas' Problem of the Married Couplesn对夫妇围圆桌而坐,其座次是两个妇人之间坐一个男人,而没有一个男人和自己的妻子并坐,问有多少种坐法?第09题卡亚姆的二项展开式Omar Khayyam's Binomial Expansion当n是任意正整数时,求以a和b的幂表示的二项式a+b的n 次幂.第10题柯西的平均值定理Cauchy's Mean Theorem求证n个正数的几何平均值不大于这些数的算术平均值.第11题伯努利幂之和的问题Bernoulli's Power Sum Problem确定指数p为正整数时最初n个自然数的p次幂的和S=1p+2p+3p+…+np.第12题欧拉数The Euler Number求函数φ(x)=(1+1/x)x及Φ(x)=(1+1/x)x+1当x无限增大时的极限值第13题牛顿指数级数Newton's Exponential Series将指数函数ex变换成各项为x的幂的级数.第14题麦凯特尔对数级数Nicolaus Mercator's Logarithmic Series不用对数表,计算一个给定数的对数.第15题牛顿正弦及余弦级数Newton's Sine and Cosine Series不用查表计算已知角的正弦及余弦三角函数.第16题正割与正切级数的安德烈推导法Andre's Derivation of the Secant and Tangent Series在n个数1,2,3,…,n的一个排列c1,c2,…,cn中,如果没有一个元素ci的值介于两个邻近的值ci-1和ci+1之间,则称c1,c2,…,cn为1,2,3,…,n的一个屈折排列.试利用屈折排列推导正割与正切的级数.第17题格雷戈里的反正切级数Gregory's Arc Tangent Series已知三条边,不用查表求三角形的各角.第18题德布封的针问题Buffon's Needle Problem在台面上画出一组间距为d的平行线,把长度为l(小于d)的一根针任意投掷在台面上,问针触及两平行线之一的概率如何?第19题费马-欧拉素数定理The Fermat-Euler Prime Number Theorem每个可表示为4n+1形式的素数,只能用一种两数平方和的形式来表示.第20题费马方程The Fermat Equation求方程x2-dy2=1的整数解,其中d为非二次正整数.第21题费马-高斯不可能性定理The Fermat-Gauss Impossibility Theorem证明两个立方数的和不可能为一立方数.第22题二次互反律The Quadratic Reciprocity Law(欧拉-勒让德-高斯定理)奇素数p与q的勒让德互反符号取决于公式(p/q)•(q/p)=(-1)[(p-1)/2]•[(q-1)/2].第23题高斯的代数基本定理Gauss' Fundamental Theorem of Algebra每一个n次的方程zn+c1zn-1+c2zn-2+…+cn=0具有n个根.第24题斯图谟的根的个数问题Sturm's Problem of the Number of Roots求实系数代数方程在已知区间上的实根的个数.第25题阿贝尔不可能性定理Abel's Impossibility Theorem高于四次的方程一般不可能有代数解法.第26题赫米特-林德曼超越性定理The Hermite-Lindemann Transcedence Theorem系数A不等于零,指数α为互不相等的代数数的表达式A1eα1+A2eα2+A3eα3+…不可能等于零.第27题欧拉直线Euler's Straight Line在所有三角形中,外接圆的圆心,各中线的交点和各高的交点在一直线—欧拉线上,而且三点的分隔为:各高线的交点(垂心)至各中线的交点(重心)的距离两倍于外接圆的圆心至各中线的交点的距离.第28题费尔巴哈圆The Feuerbach Circle三角形中三边的三个中点、三个高的垂足和高的交点到各顶点的线段的三个中点在一个圆上.第29题卡斯蒂朗问题Castillon's Problem将各边通过三个已知点的一个三角形内接于一个已知圆.第30题马尔法蒂问题Malfatti's Problem在一个已知三角形内画三个圆,每个圆与其他两个圆以及三角形的两边相切.第31题蒙日问题Monge's Problem画一个圆,使其与三已知圆正交.第32题阿波洛尼斯相切问题The Tangency Problem of Apollonius.画一个与三个已知圆相切的圆.第33题马索若尼圆规问题Macheroni's Compass Problem.证明任何可用圆规和直尺所作的图均可只用圆规作出.第34题斯坦纳直尺问题Steiner's Straight-edge Problem证明任何一个可以用圆规和直尺作出的图,如果在平面内给出一个定圆,只用直尺便可作出.第35题德里安倍立方问题The Deliaii Cube-doubling Problem画出体积为一已知立方体两倍的立方体的一边.第36题三等分一个角Trisection of an Angle把一个角分成三个相等的角.第37题正十七边形The Regular Heptadecagon画一正十七边形.第38题阿基米德π值确定法Archimedes' Determination of the Number Pi设圆的外切和内接正2vn边形的周长分别为av和bv,便依次得到多边形周长的阿基米德数列:a0,b0,a1,b1,a2,b2,…其中av+1是av、bv的调和中项,bv+1是bv、av+1的等比中项. 假如已知初始两项,利用这个规则便能计算出数列的所有项. 这个方法叫作阿基米德算法.第39题富斯弦切四边形问题Fuss' Problem of the Chord-Tangent Quadrilateral找出半径与双心四边形的外接圆和内切圆连心线之间的关系.(注:一个双心或弦切四边形的定义是既内接于一个圆而同时又外切于另一个圆的四边形)第40题测量附题Annex to a Survey利用已知点的方位来确定地球表面未知但可到达的点的位置.第41题阿尔哈森弹子问题Alhazen's Billiard Problem在一个已知圆内,作出一个其两腰通过圆内两个已知点的等腰三角形.第42题由共轭半径作椭圆An Ellipse from Conjugate Radii已知两个共轭半径的大小和位置,作椭圆.第43题在平行四边形内作椭圆An Ellipse in a Parallelogram,在规定的平行四边形内作一内切椭圆,它与该平行四边形切于一边界点.第44题由四条切线作抛物线A Parabola from Four Tangents已知抛物线的四条切线,作抛物线.第45题由四点作抛物线A Parabola from Four Points.过四个已知点作抛物线.第46题由四点作双曲线A Hyperbola from Four Points.已知直角(等轴)双曲线上四点,作出这条双曲线.第47题范•施古登轨迹题Van Schooten's Locus Problem平面上的固定三角形的两个顶点沿平面上一个角的两个边滑动,第三个顶点的轨迹是什么?第48题卡丹旋轮问题Cardan's Spur Wheel Problem.一个圆盘沿着半径为其两倍的另一个圆盘的内缘滚动时,这个圆盘上标定的一点所描出的轨迹是什么?第49题牛顿椭圆问题Newton's Ellipse Problem.确定内切于一个已知(凸)四边形的所有椭圆的中心的轨迹.第50题彭赛列-布里昂匈双曲线问题The Poncelet-Brianchon Hyperbola Problem确定内接于直角(等边)双曲线的所有三角形的顶垂线交点的轨迹.第51题作为包络的抛物线A Parabola as Envelope从角的顶点,在角的一条边上连续n次截取任意线段e,在另一条边上连续n次截取线段f,并将线段的端点注以数字,从顶点开始,分别为0,1,2,…,n和n,n-1,…,2,1,0.求证具有相同数字的点的连线的包络为一条抛物线.第52题星形线The Astroid直线上两个标定的点沿着两条固定的互相垂直的轴滑动,求这条直线的包络.第53题斯坦纳的三点内摆线Steiner's Three-pointed Hypocycloid确定一个三角形的华莱士(Wallace)线的包络.第54题一个四边形的最接近圆的外接椭圆The Most Nearly Circular Ellipse Circumscribing a Quadrilateral一个已知四边形的所有外接椭圆中,哪一个与圆的偏差最小?第55题圆锥曲线的曲率The Curvature of Conic Sections确定一个圆锥曲线的曲率.第56题阿基米德对抛物线面积的推算Archimedes' Squaring of a Parabola确定包含在抛物线内的面积.第57题推算双曲线的面积Squaring a Hyperbola确定双曲线被截得的部分所含的面积.第58题求抛物线的长Rectification of a Parabola确定抛物线弧的长度.第59题笛沙格同调定理(同调三角形定理)Desargues' Homology Theorem (Theoremof Homologous Triangles)如果两个三角形的对应顶点连线通过一点,则这两个三角形的对应边交点位于一条直线上.反之,如果两个三角形的对应边交点位于一条直线上,则这两个三角形的对应顶点连线通过一点.第60题斯坦纳的二重元素作图法Steiner's Double Element Construction由三对对应元素所给定的重迭射影形,作出它的二重元素.第61题帕斯卡六边形定理Pascal's Hexagon Theorem求证内接于圆锥曲线的六边形中,三双对边的交点在一直线上.第62题布里昂匈六线形定理Brianchon's Hexagram Theorem求证外切于圆锥曲线的六线形中,三条对顶线通过一点.第63题笛沙格对合定理Desargues' Involution Theorem一条直线与一个完全四点形*的三双对边的交点与外接于该四点形的圆锥曲线构成一个对合的四个点偶. 一个点与一个完全四线形*的三双对顶点的连线和从该点向内切于该四线形的圆锥曲线所引的切线构成一个对合的四个射线偶. *一个完全四点形(四线形)实际上含有四点(线)1,2,3,4和它们的六条连线交点23,14,31,24,12,34;其中23与14、31与24、12与34称为对边(对顶点).第64题由五个元素得到的圆锥曲线A Conic Section from Five Elements求作一个圆锥曲线,它的五个元素——点和切线——是已知的.第65题一条圆锥曲线和一条直线A Conic Section and a Straight Line一条已知直线与一条具有五个已知元素——点和切线——的圆锥曲线相交,求作它们的交点.第66题一条圆锥曲线和一定点A Conic Section and a Point已知一点及一条具有五个已知元素——点和切线——的圆锥曲线,作出从该点列到该曲线的切线.第67题斯坦纳的用平面分割空间Steiner's Division of Space by Planesn个平面最多可将整个空间分割成多少份?第68题欧拉四面体问题Euler's Tetrahedron Problem以六条棱表示四面体的体积.第69题偏斜直线之间的最短距离The Shortest Distance Between Skew Lines计算两条已知偏斜直线之间的角和距离.第70题四面体的外接球The Sphere Circumscribing a Tetrahedron确定一个已知所有六条棱的四面体的外接球的半径.第71题五种正则体The Five Regular Solids将一个球面分成全等的球面正多边形.第72题正方形作为四边形的一个映象The Square as an Image of a Quadrilateral证明每个四边形都可以看作是一个正方形的透视映象.第73题波尔凯-许瓦尔兹定理The Pohlke-Schwartz Theorem一个平面上不全在同一条直线上的四个任意点,可认为是与一个已知四面体相似的四面体的各隅角的斜映射.第74题高斯轴测法基本定理Gauss' Fundamental Theorem of Axonometry正轴测法的高斯基本定理:如果在一个三面角的正投影中,把映象平面作为复平面,三面角顶点的投影作为零点,边的各端点的投影作为平面的复数,那么这些数的平方和等于零.第75题希帕查斯球极平面射影Hipparchus' Stereographic Projection试举出一种把地球上的圆转换为地图上圆的保形地图射影法.第76题麦卡托投影The Mercator Projection画一个保形地理地图,其坐标方格是由直角方格组成的.第77题航海斜驶线问题The Problem of the Loxodrome确定地球表面两点间斜驶线的经度.第78题海上船位置的确定Determining the Position of a Ship at Sea利用天文经线推算法确定船在海上的位置.第79题高斯双高度问题Gauss' Two-Altitude Problem根据已知两星球的高度以确定时间及位置.第80题高斯三高度问题Gauss' Three-Altitude Problem从在已知三星球获得同高度瞬间的时间间隔,确定观察瞬间,观察点的纬度及星球的高度.第81题刻卜勒方程The Kepler Equation根据行星的平均近点角,计算偏心及真近点角.第82题星落Star Setting对给定地点和日期,计算一已知星落的时间和方位角.第83题日晷问题The Problem of the Sundial制作一个日晷.第84题日影曲线The Shadow Curve当直杆置于纬度φ的地点及该日太阳的赤纬有δ值时,确定在一天过程中由杆的一点投影所描绘的曲线.第85题日食和月食Solar and Lunar Eclipses如果对于充分接近日食时间的两个瞬间太阳和月亮的赤经、赤纬以及其半径均为已知,确定日食的开始和结束,以及太阳表面被隐蔽部分的最大值.第86题恒星及会合运转周期Sidereal and Synodic Revolution Periods确定已知恒星运转周期的两共面旋转射线的会合运转周期.第87题行星的顺向和逆向运动Progressive and Retrograde Motion of Planets行星什么时候从顺向转为逆向运动(或反过来,从逆向转为顺向运动)?第88题兰伯特慧星问题Lambert's Comet Prolem借助焦半径及连接弧端点的弦,来表示慧星描绘抛物线轨道的一段弧所需的时间.第89题与欧拉数有关的斯坦纳问题Steiner's Problem Concerning the Euler Number如果x为正变数,x取何值时,x的x次方根为最大?第90题法格乃诺关于高的基点的问题Fagnano's Altitude Base Point Problem在已知锐角三角形中,作周长最小的内接三角形.第91题费马对托里拆利提出的问题Fermat's Problem for Torricelli试求一点,使它到已知三角形的三个顶点距离之和为最小.第92题逆风变换航向Tacking Under a Headwind帆船如何能顶着北风以最快的速度向正北航行?第93题蜂巢(雷阿乌姆尔问题)The Honeybee Cell (Problem by Reaumur)试采用由三个全等的菱形作成的顶盖来封闭一个正六棱柱,使所得的这一个立体有预定的容积,而其表面积为最小.第94题雷奇奥莫塔努斯的极大值问题Regiomontanus' Maximum Problem在地球表面的什么部位,一根垂直的悬杆呈现最长?(即在什么部位,可见角为最大?)第95题金星的最大亮度The Maximum Brightness of Venus在什么位置金星有最大亮度?第96题地球轨道内的慧星A Comet Inside the Earth's Orbit慧星在地球的轨道内最多能停留多少天?第97题最短晨昏蒙影问题The Problem of the Shortest Twilight在已知纬度的地方,一年之中的哪一天晨昏蒙影最短?第98题斯坦纳的椭圆问题Steiner's Ellipse Problem在所有能外接(内切)于一个已知三角形的椭圆中,哪一个椭圆有最小(最大)的面积?第99题斯坦纳的圆问题Steiner's Circle Problem在所有等周的(即有相等周长的)平面图形中,圆有最大的面积.反之:在有相等面积的所有平面图形中,圆有最小的周长.第100题斯坦纳的球问题Steiner's Sphere Problem在表面积相等的所有立体中,球具有最大体积.在体积相等的所有立体中,球具有最小的表面.。
完整版)初中数学经典几何模型
完整版)初中数学经典几何模型初中数学经典几何模型(模型即套路),是初中数学里的重要部分。
在解决几何证明问题时,我们可以运用这些模型,从而更加高效地解决问题。
人们常说几何很困难,其中一个难点就在于辅助线的运用。
为了更好地运用辅助线,我们需要把握定理和概念,并且刻苦加钻研,找出规律凭经验。
在绘制图形时,我们可以利用角平分线向两边作垂线,或者将图形对折来寻找对称关系。
利用角平分线的平行线,我们可以构造等腰三角形。
同时,我们也可以尝试将角平分线加上垂线,从而将三条线合为一条。
线段垂直平分线时,我们可以将线段向两端延长或缩短来验证线段的倍数与半数关系。
在三角形中,连接两中点可以构造出中位线,同时延长中线也可以等于中线。
对于平行四边形,我们可以找到对称中心等分点。
在梯形中,我们可以利用高线平移一腰来解决问题。
同时,平行移动对角线,补成三角形也是常见的方法。
当证明相似时,我们可以通过比线段,添加平行线来构造相似三角形。
在等积式子比例换时,寻找线段也是很关键的。
直接证明有困难时,我们可以通过等量代换来简化问题。
在计算圆的相关问题时,我们可以利用半径与弦长计算,或者利用勾股定理来计算切线长度。
同时,在判断是否为切线时,我们可以通过半径垂线来进行辨别。
在解决相交圆的问题时,我们需要注意作公共弦。
对于内外相切的两个圆,我们可以通过切点来构造公切线。
同时,我们也可以利用连心线来确定切点。
在绘制图形时,我们需要注意勿改变虚线的位置。
基本作图也是很关键的,我们需要熟练掌握。
在解题时,我们需要多动脑筋,经常总结方法。
同时,我们也需要注意方法的灵活性,不要盲目乱添线。
在选用分析综合方法时,我们需要根据具体情况进行选择。
最重要的是,我们需要虚心勤学,加以苦练,才能在数学上取得更好的成绩。
斜边上作高线,比例中项一大片。
--。
在斜边上作高线,可以得到比例中项一大片。
半径与弦长计算,弦心距来中间站。
--。
通过计算半径和弦长,可以得到弦心距。
初中数学30种模型汇总(最全几何知识点)
10.等面积模型:D是BC的中点
20.平移构造全等
30.二次函数中平行四边形存在性模型
01.三线八角
同位角:找F型
内错角:找Z型
同旁内角:找U型
02.拐角模型
一.锯齿型
1
1
3
2
2
3
4
∠1+∠3=∠2
∠1+∠2=∠3 +∠4
左和=右和
二.鹰嘴型
1
1
2
3
3
2
∠1+∠3=∠2
∠1+∠3=∠2
鹰嘴+小=大
一.大小等边三角形
虚线相等,且夹角为60°
(全等,八字形)
四.大小等腰三角形(顶角为α)
结论:虚线相等,且夹角为α
(全等,八字形)
三. 大小等腰直角三角形
结论:虚线相等,且夹角为90°
(全等,八字形)
二.大小正方形
结论:虚线相等,且夹角为90°
(全等,八字形)
15.半角模型
条件:正方形ABCD
∠EDF=45°
证:EF=AE+CF
条件:CD=AD,∠ADC=90°
∠EDF=45°
∠A+∠C=180°
证明:EF=AE+CF
条件:AB=AD
∠B+∠D=180°
∠EAF=1 ∠BAD
2
证明:EF=BE+DF
条件:AB=AC,∠BAC=90°
∠DAE=45°
证明:DE2=BD2+CE2
△CEF为直角三角形
初中数学30种模型汇总
(最全几何知识点)
01.三线八角
02.拐角模型
03.等积变换模型
一些经典初等数学模型
一些经典初等数学模型
1. 走迷宫:在一个有迷宫的场地内,从起点到终点,找到最短的路线。
2. 鸡兔同笼:已知笼子里面有若干只鸡和兔子,总共有头和只脚,求鸡和兔子的数量。
3. 填数字:在一个九宫格里填入数字1到9,每行、每列、每个宫内数字互不重复。
4. 数列求和:给定一个数列,求其中任意连续段的和,或者整个数列的和。
5. 球与盒子:有若干个不同颜色的球和盒子,球可以放入盒子中,求有多少种不同的放法。
6. 求根公式:已知二次方程的系数,求解出这个二次方程的根。
7. 绳子问题:两根不同长度的绳子分别燃烧完的时间不同,如何用这两根绳子在规定时间内测量出一个15分钟的时间。
8. 凸包问题:给定一些点的坐标,如何找到能够包住所有点的最小凸多边形。
9. 最小生成树:给定一个连通的无向图,找到一棵包含所有节点的生成树,使得边的权值之和最小。
10. 铺地砖:已知一个矩形地面,和两种不同形状的砖块,如何将这些砖块拼接在一起,使得地面完全被铺满。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初等数学模型本章重点是:雨中行走问题、动物的身长与体重、实物交换、代表名额的分配与森林救火模型的建立过程和所使用的方法复习要求1.进一步理解基本建模过程,掌握类比法、图示法以及问题分析、合理假设的内涵。
2.进一步理解数学模型的作用与特点。
类比法是建立数学模型的一个常见而有力的方法.作法是把问题归结或转化为我们熟知的模型上去给以类似的解决:这个问题与我们熟悉的什么问题类似?如果有类似的问题曾被解决过,我们的建模工作便可省去许多麻烦.实际上,许多来自不同领域的问题在数学模型上看确实具有相类似的甚至相同的结构.利用几何图示法建模.有不少实际问题的解决只要从几何上给予解释和说明就足以了,这时,我们只需建立其图模型即可,我们称这种建模方法为图示法.这种方法既简单又直观,且其应用面很宽.1.雨中行走问题雨中行走问题的结论是:(1)如果雨是迎着你前进的方向落下,即20πθ≤≤,那么全身被淋的雨水总量为⎪⎭⎫ ⎝⎛++=++=+=h v hr dr pwD v r h dr v pwD C C C θθθθcos sin )]cos (sin [21 这时的最优行走策略是以尽可能大的速度向前跑.(2)如果雨是从你的背后落下,即πθπ≤≤2. 令απθ+=2,则20πα<<. 那么全身被淋的雨水总量为 ⎪⎭⎫ ⎝⎛+-=h v rh rd Dpw v C ααθsin cos ),( 这时你应该控制在雨中行走的速度,使得它恰好等于雨滴下落速度的水平分量.从建模结果看,“为了少些淋雨,应该快跑”,这个一般的“常识”被基本上否定,那么根据何在?由此提出了建模目的:减少雨淋程度. 而为减少雨淋程度,便自然提出“被淋在身上的雨水量”这个目标函数C ,而C =C (v ),于是问题便归结为确定速度v ,使C (v )最小——本模型的关键建模步骤便得以确定。
有了确定的建模目的,自然引出与C (v )有关的量的设定与简化假设. 一般地,开始时不要面面俱到地把所有相关量都涉及到,往往只需考虑几个主要量,甚至暂时舍弃某个主要量,以求尽快建立模型.尤其对初学者,这样做有助于建模信心的增强.自不必说建模过程往往如此,更有模型尚有的进一步修改和推广的主要步骤.而一旦建立起简单模型后,其进一步的改善也相对容易多了.这就是本模型只所以建立了两个模型的原因,是符合人们的认识规律的.另外,为了检验所建模型的合理性,建模后用较为符合实际的几组数据对模型加以检验是重要的,它既是对所建模型是否基本符合实际的检测,也是进一步完善模型的需要.例1 在某海滨城市附近海面有一台风.据监测,当前台风中心位于城市O (如图2-1)的东偏南)102(cos =θθ方向300km 的海面P 处,并以20km /h 的速度向 西偏北︒45方向移动.台风侵袭的范围为圆形区域,当前半径为 60km ,并以10km /h 的速度不断增大. 问几小时后该城市开始受到台风的侵袭?问题分析与假设1. 根据问题解决目的:问几小时后该城市开始受到台风的侵袭,以及台风侵袭的范围为圆形的假设,只要求出以台风中心p (动点)为圆心的圆的半径r ,这个圆的半径划过的区域自然是侵袭范围.2. 台风中心是动的,移动方向为向西偏北︒45,速度为20km /h ,而当前半径为60km ,并以10km /h 的速度不断增大,即半径的增加速度为t t r 1060)(+=,t 为时间.于是只要6010+≤t p o ,便是城 图2-1市O 受到侵袭的开始.模型I 如图2-2建立坐标系:以O 为原点,正东方向为x 轴正向.在时刻t (h )台风中心),(y x P 的坐标为⎪⎪⎩⎪⎪⎨⎧⨯+⨯-=⨯-⨯=.22201027300,2220102300t y t x 此时台风侵袭的区域是,)]([)()(222t r y y x x ≤-+-其中r (t )=10t +60. 图2-2若在t 时刻城市O 受到台风的侵袭,则有,)6010()0()0(222+≤-+-t y x即 ,)6010()22201027300()2220102300(222+≤⨯+⨯-+⨯-⨯t t t 整理可得 ,0288362≤+-t t由此解得 12≤t ≤24,即12小时后该城市开始受到台风的侵袭.模型II 设在时刻t (h )台风中心为P (如图2-2),此时台风侵袭的圆形半径为10t +60,因此,若在时刻t 城市O 受到台风侵袭,应有6010+≤t P O由余弦定理知.cos 2222P OP PO P P PO P P P O ∠⋅⋅-+=注意到 t P P OP 20,300==,542210212210245sin sin 45cos cos )45cos(cos 2=⨯-+⨯=︒⋅+︒⋅=︒-=∠θθθP OP故 .30096002054300202300)20(222222+-=⨯⨯⨯-+=t t t t P O因此 .)6010(3009600202222+≤+-t t t即 0288362≤+-t t解得 .2412≤≤t 2.动物的身长与体重问题在生猪收购站或屠宰场工作的人们,有时希望由生猪的身长估计它的体重.试建立数学模型讨论四足动物的躯干的长度(不含头、尾)与它的体重的关系,(1)问题分析众所周知,不同种类的动物,其生理构造不尽相同,如果对此问题陷入对生物学复杂生理结构的研究,就很难得到我们所要求的具有应用价值的数学模型并导致问题的复杂化.因此,我们舍弃具体动物的生理结构讨论,仅借助力学的某些已知结果,采用类比方法建立四足动物的身长和体重关系的数学模型.类比法是依据两个对象的已知的相似性,把其中一个对象的已知的特殊性质迁移到另一对象上去,从而获得另一个对象的性质的一种方法. 它是一种寻求解题思路、猜测问题答案或结论的发现的方法,而不是一种论证的方法,它是建立数学模型的一种常见的、重要的方法.类比法的作用是启迪思维,帮助我们寻求解题的思路.,而它对建模者的要求是具有广博的知识,只有这样才能将你所研究的问题与某些已知的问题、某些已知的模型建立起联系.(2)模型假设与求解我们知道对于生猪,其体重越大、躯干越长,其脊椎下陷越大,这与弹性梁类似.为了简化问题,我们把动物的躯干看作圆柱体,设其长度为l 、直径为d 、断面面积为S (如图2—3). 将这种圆柱体的躯干类比作一根支撑在四肢上的弹性梁,这样就可以借助力学的某些结果研究动物的身长与体重的关系.设动物在自身体重(记为f )的作用下,躯干的最大下垂度为b ,即弹性梁的最大弯曲. 根据对弹性梁的研究,可以知道23Sdfl b ∝. 又由于∝f Sl (体积),于是23d l l b ∝. b 是动物躯干的绝对下垂度,b /l 是动物躯干的相对下垂度.b /l 太大,四肢将无法支撑动物的躯干,b /l 图2—3太小,四肢的材料和尺寸超过了支撑躯干的需要,无疑是一种浪费,因此,从生物学角度可以假定,经过长期进化,对于每一种动物而言,b /l 已经达到其最适宜的数值,换句话说,b /l 应视为与动物尺寸无关的常数,而只与动物的种类有关.因此23d l ∝,又由于2,d S Sl f ∝∝,故 44,kl f l f =∝从而.即四足动物的体重与躯干长度的四次方成正比.这样,对于某种四足动物(如:生猪),根据统计数据确定上述比例系数k 后,就可以依据上述模型,由躯干的长度估计出动物的体重了.(3)模型评注在上述模型中,将动物的躯干类比作弹性梁是一个大胆的假设,其假设的合理性,模型的可信度应该用实际数据进行仔细检验.但这种思考问题、建立数学模型的方法是值得借鉴的.在上述问题中,如果不熟悉弹性梁、弹性力学的有关知识,就不可能把动物躯干类比作弹性梁,就不可能想到将动物躯干长度和体重的关系这样一个看来无从下手的问题,转化为已经有明确研究成果的弹性梁在自重作用下的挠曲问题.例2 在中学数学中,通过类比推测或联想而发现新命题、新解法并不少见.诸如,由分数的性质类似地推测分式的性质;由直线与圆的位置关系推测圆与圆的位置关系;由一次函数、一次方程、一次不等式的某些性质和解法,推测二次函数、二次方程、二次不等式的某些类似的性质与解法等.情形1 已知:ABC ∆中,︒=∠90C ,AC =BC =1,BD 是AC边上的中线,E 点在AB 边上,且BD ED ⊥.求DEA ∆的面积.如图2-4,引BA CF ⊥,易证24/1=∆DEA S 类比 若去掉情形1中直角这一特性,是否会产生类似命题呢?由此想到 图2-4情形2 已知ABC ∆中(图2-5),A B C ∠=∠=∠44,BD 是AC 边上的中线,E 点在AB 上,且C AED ∠=∠,1=∆ABC S ,求AED S ∆.类似情形1的证法,易证得12/1=∆AED S ;当2/1=∆ABC S 时,24/1=∆AED S ,与情形1结果相同. 图2-5类比 若保留情形1中的直角条件,去掉等腰三角形这一特殊性,可以类似地得到.情形3 已知ABC ∆中︒=∠90C ,AC =2BC =2,BD 是AC 边上中线,AB CF ⊥交BD 于H ,求CBH S ∆.同样可证6/1=∆CBH S .这里,若在情形3中令AC =2BC =1,也有24/1=∆ADE S ,与情形1结论相同;情形3是由情形1类比而来,最自然的想法是求ADE S ∆,为了增加变换方式获得新命题,本情形求的是CBH S ∆.3.实物交换问题实物交换是人类发展史上一种重要的交换方式,在当今的社会生活中也是屡见不鲜的,这种实物交换问题可以出现在个人之间或国家之间的各种类型的贸易市场上. 例如:甲乙二人共进午餐,甲带了很多面包,乙有香肠若干,二人希望相互交换一部分,达到双方满意的结果.显然,交换的结果取决于双方对两种物品的偏爱程度和需要程度,而对于偏爱程度很难给出确切的定量关系.因此可以采用图示的方法建立实物交换的数学模型,确定实物交换的最佳交换方案.下面依据等价交换准则确定最佳交换方案. 等价交换准则是指两种物品用同一种货币衡量其价值,进行等价交换.不失一般性,设交换前甲占有数量为x 0的物品X ,乙占有数量为y 0的物品Y ;交换后甲所占有的物品X ,Y 的数量分别记为x ,y ;单位数量的物品X ,Y 的价值(价格)设为p 1,p 2.由等价交换准则,x ,y 满足方程,0,0,)(00201y y x x y p x x p ≤≤≤≤=-容易证明,在此直线上的点进行交换均满足等价交换准则。
在等价交换准则下双方均满意的交换方案必是此直线与曲线AB 的交点(如图2—6).无差别曲线概念的提出是用图形方法建立实物交换模型的基础,确定这种曲线需要收集大量的数据,还可以研究无差别曲线的解析表达式及其性质.例3 消费者的选择在本章中讨论实物交换模型时,引进了无差别曲线描述人们对两种物品的满意和偏爱程度,用图形的方法确定两个人进行实物交换时应遵循的途径. 本例要利用无差别曲线族的概念讨论,一个消费者用一定数额的钱去购买两种商品时应作怎样的选择,即他应该分别用多少钱去买这两种商品.记甲乙两种商品的数量分别是q 1和q 2,当消费者占有它们时的满意程度,或者说它们给消费者带来的效用,用q 1、q 2 的函数,记作U (q 1,q 2),经济学中称为效用函数(Utility function ). 图2-7U (q 1,q 2)=c (常数)的图形就是无差别曲线族,如图2-7是一族单调降、下凸、互不相交的曲线.在每一条曲线上,对于不同的点,效用函数U (q 1,q 2)的值不变.而随着曲线向右上方移动,U (q 1,q 2)的值增加(图中l 2上的U 值高于l 1上的U 值).曲线下凸的具体形状则反映了消费者对甲乙两种商品的偏爱情况.这里假定消费者的效用函数U (q 1,q 2),即他的无差别曲线族已经完全确定了.设甲乙两种商品的单价分别是p 1和p 2(元),消费者有s (元)钱.当消费者用这些钱买这两种商品时所作的选择,即分别用多少钱买甲和乙,应该使效用函数U (q 1,q 2)达到最大,即得到最大的满意度.经济学上称这种最优状态为消费者平衡.因为当消费者对两种商品的购买量分别为q 1和q 2时,他用的钱分别为p 1q 1和p 1q 2,于是问题归结为在条件p 1q 1+p 2q 2=s (2.1)下求比例p 1q 1/p 2q 2,使效用函数U (p 1,q 2)达到最大.这是二元函数的条件极值问题,用拉格朗日乘子法不难得到最优解应满足图2—62121p p q u q u=∂∂∂∂ (2.2) 当效用函数U (q 1,q 2)给定后,由(2.2)式即可确定最优比例p 1q 1/p 2q 2.上述问题也可用图形法求解.约束条件(2.1)在该图上是一条直线MN.MN 必与无差别曲线族U (q 1,q 2)=c 中的某一条曲线相切(图中是与l 2相切),则q 1,q 2的最优值必在切点Q 处取得.图解法的结果与(2.2)式是一致的.因为在切点Q 处直线MN 与曲线l 2的斜率相同,而MN 的斜率是K MN =- p 1/p 2,l 2的斜率是21122q U q U dq dq K l ∂∂∂∂-==,在Q 点处2l MN K K =,即给出(2.2)式. 经济学中1q U ∂∂,2q U ∂∂称为边际效用,即商品购买量增加一个单位时效用函数的增量.(2.2)式表明,消费者均衡状态在两种商品的边际效用之比恰等于它们的价格之比时达到.从以上讨论可见,建立消费者均衡模型的关键是确定效用函数U (q 1,q 2).下面列举几个常用的效用函数,并分析消费者均衡状态,即最优比例p 1q 1/p 2q 2的实际含义.(1)若效用函数为0,,),(212121>+=βαβαq q q q q q U (2.3) 根据(2.2)式可以求得最优比例p 1q 1/p 2q 2为212211αp βp q p q p = (2.4) 结果表明均衡状态下购买两种商品所用钱的比例,与商品价格比的平方根成正比.同时与效用函数U (q 1,q 2)中的参数α、β有关:α越大购买商品甲的钱越少,β越大购买商品甲的钱越多.这说明在(2.3)式给出的效用函数中,参数β和α分别表示消费者对商品甲和乙的偏爱程度.于是调整β和α可以改变消费者对两种商品的爱好倾向,或者说可以改变无差别曲线的具体形状.(2)若效用函数为1,0,),(2121<<=μλμλq q q q U (2.5)根据(2.2)式可以求得最优比例p 1q 1/p 2q 2为μλ=2211q p q p (2.6) 这表明均衡状态下购买两种商品所用钱的比例与价格无关,而参数λ和μ分别表示消费者对商品甲和乙的偏爱程度.(3)设效用函数为0,,)(),(22121>+=b a q b q a q q U (2.7)对(2.7)式的求解及结果分析留给读者.应用这个模型时,可以根据上面的分析决定选用哪一种形式的效用函数,并由经验数据确定其参数.4.代表名额的分配问题:(1)问题的提出分配问题是日常生活中经常遇到的问题,它涉及到如何将有限的人力或其他资源以“完整的部分”分配到下属部门或各项不同任务中.分配问题涉及的内容十分广泛,例如:大到召开全国人民代表大会,小到某学校召开学生代表大会,均涉及到将代表名额分配到各个下属部门的问题.代表名额的分配(亦称为席位分配问题)是数学在人类政治生活中的一个重要应用,应归属于政治模型.一个自然的问题是如何分配代表名额才是公平的呢?(2)模型的分析与建立在数学上,代表名额分配问题的一般描述是:设名额数为N ,共有s 个单位,各单位的人数分别为p i ,i =1,2,…,s .问题是如何寻找一组整数q 1,…,q s 使得q 1+q 2+…+ q s =N ,其中q i 是第i 个单位所获得的代表名额数,并且“尽可能”地接近它应得的份额p i N /(p 1+p 2+…+p s ),即所规定的按人口比例分配的原则.如果对一切的i =1,2,…,s ,严格的比值)/(1∑=si i i p N p 恰好是整数,则第i 个单位分得q i 名额,这样分配是绝对公平的,每个名额所代表的人数是相同的.但由于人数是整数,名额也是整数,q i 是整数这种理想情况是极少出现的,这样就出现了用接近于q i 的整数之代替的问题.在实际应用中,这个代替的过程会给不同的单位或团体带来不平等,这样,以一种平等、公正的方式选择q i 是非常重要的,即确定尽可能公平(不公平程度达到极小)的分配方案.设某校有3个系(s =3)共有200名学生,其中甲系100名(p 1=100),乙系60名(p 2=60),丙系40名(p 3=40).该校召开学生代表大会共有20个代表名额(N =20),公平而又简单的名额分配方案是按学生人数的比例分配,显然甲乙丙三个系分别应占有q 1=10,q 2=6,q 3=4个名额.这是一个绝对公平的分配方案.现在丙系有6名同学转入其他两系学习,这时p 1=103,p 2=63,p 3=34,按学生人数的比例分配,此时q i 不再是整数,而名额数必须是整数,一个自然的想法是:对q i 进行“四舍五入取整”或者“去掉尾数取整”,这样将导致名额多余或者名额不够分配.因此,我们必须寻求新的分配方案.Hamilton (哈密顿)方法哈密顿方法具体操作过程如下:① 先让各个单位取得份额q i 的整数部分[q i ];② 计算r i =q i -[q i ],按照从大到小的数序排列,将余下的席位依次分给各个相应的单位,即小数部分最大的单位优先获得余下席位的第一个,次大的取得余下名额的第二个,依此类推,直至席位分配完毕.上述三个系的20个名额的分配结果见表2—1.哈密顿方法看来是非常合理的,但这种方法也存在缺陷.譬如当s 和人数比例)/(1∑=si i i p N p 不变时,代表名额的增加反而导致某单位名额q i 的减少.表2—1 按哈密顿方法确定的20个代表名额的分配方案考虑上述某校学生代表大会名额分配问题.因为有20个代表参加的学生代表大会在表决某些提案时可能出现10:10的局面,会议决定下一届增加一个名额.按照哈密顿方法分配结果见表2—2.表2—2显然这个结果对丙系是极其不公平的,因为总名额增加一个,而丙系的代表名额却由4个减少为3个.由此可见,哈密顿方法存在很大缺陷,因而被放弃.20世纪20年代初期,由哈佛大学数学家Huntington (惠丁顿)提出了一个新方法,简述如下.Huntington (惠丁顿)方法众所周知,p i /n i 表示第i 个单位每个代表名额所代表的人数.很显然,当且仅当p i /n i 全相等时,名额的分配才是公平的.但是,一般来说,它们不会全相等,这就说明名额的分配是不公平的,并且p i /q i 中数值较大的一方吃亏或者说对这一方不公平.同时我们看到,在名额分配问题中要达到绝对公平是非常困难的.既然很难作到绝对公平,那么就应该使不公平程度尽可能的小,因此我们必须建立衡量不公平程度的数量指标. 不失一般性,我们考虑A ,B 双方席位分配的情形(即s =2).设A ,B 双方的人数为p 1,p 2,占有的席位分别为n 1,n 2,则A ,B 的每个席位所代表的人数分别为p 1/n 1,p 2/n 2,如果p 1/n 1=p 2/n 2,则席位分配是绝对公平的,否则就是不公平的,且对数值较大的一方不公平.为了刻划不公平程度,需要引入数量指标,一个很直接的想法就是用数值|p 1/n 1-p 2/n 2|来表示双方的不公平程度,称之为绝对不公平度,它衡量的是不公平的绝对程度.显然,其数值越小,不公平程度越小,当|p 1/n 1-p 2/n 2|=0时,分配方案是绝对公平的.用绝对不公平度可以区分两种不同分配方案的公平程度,例如: ,2.4,11,100,9,12022112211=-====n P n P n p n p ,2,10,100,10,12022112211=-====n P n P n p n p 显然第二种分配方案比第一种更公平.但是,绝对不公平度有时无法区分两种不公平程度明显不同的情况:,2,10,100,10,12022112211=-====n P n P n p n p ,2,10,10000,10,1002022112211=-====n P n P n p n p 第一种情形显然比第二种情形更不公平,但它们具有相同的不公平度,所以“绝对不公平度”不是一个好的数量指标,我们必须寻求新的数量指标.这时自然想到用相对标准,下面我们引入相对不公平的概念.如果p 1/n 1>p 2/n 2,则说明A 方是吃亏的,或者说对A 方是不公平的,称1),(122122221121-=-=n p n p n p n p n p n n r A为对A 的相对不公平度;如果p 1/n 1<p 2/n 2,则称1),(211211112221-=-=n p n p n p n p n p n n r B 为对B 的相对不公平度.相对不公平度可以解决绝对不公平度所不能解决的问题,考虑上面的例子:,10,10000,10,10020,10,100,10,12022112211========n p n p n p n p显然均有p 1/n 1>p 2/n 2,此时 002.0)10,10(,2.0)10,10(21==A A r r与前一种情形相比后一种更公平.建立了衡量分配方案的不公平程度的数量指标r A ,r B 后,制定分配方案的原则是:相对不公平度尽可能的小.首先我们作如下的假设:(1)每个单位的每个人都具有相同的选举权利;(2)每个单位至少应该分配到一个名额,如果某个单位,一个名额也不应该分到的话,则应将其剔除在分配之外;(3)在名额分配的过程中,分配是稳定的,不受任何其他因素所干扰.假设A ,B 双方已经分别占有n 1,n 2个名额,下面我们考虑这样的问题,当分配名额再增加一个时,应该给A 方还是给B 方,如果这个问题解决了,那么就可以确定整个分配方案了,因为每个单位至少应分配到一个名额,我们首先分别给每个单位一个席位,然后考虑下一个名额给哪个单位,直至分配完所有名额.不失一般性,假设p 1/n 1>p 2/n 2,这时对A 方不公平,当再增加一个名额时,就有以下三种情形: 情形1:p 1/(n 1+1)>p 2/n 2,这表明即使A 方再增加一个名额,仍然对A 方不公平,所以这个名额应当给A 方;情形2:p 1/(n 1+1)<p 2/n 2,这表明A 方增加一个名额后,就对B 方不公平,这时对B 的相对不公平度为1)1(),1(211221-+=+n p n p n n r B ; 情形3:p 1/n 1>p 2/(n 2+1),这表明B 方增加一个名额后,对A 方更加不公平,这时对A 的相对不公平度为1)1()1,(122121-+=+n p n p n n r A . 公平的名额分配方法应该是使得相对不公平度尽可能的小,所以若情形1发生,毫无疑问增加的名额应该给A 方;否则需考察r B (n 1+1,n 2)和r A (n 1,n 2+1)的大小关系,如果r B (n 1+1,n 2)<r A (n 1,n 2+1),则增加的名额应该给A 方,否则应该给B 方.注意到r B (n 1+1,n 2)<r A (n 1,n 2+1)等价于)1()1(11212222+<+n n p n n p , 而且若情形1发生,仍然有上式成立.记)1(2+=i i i i n n p Q , 则增加的名额应该给Q 的值较大的一方.上述方法可以推广到s 个单位的情形,设第i 个单价的人数为p i ,已经占有n i 个名额,i =1,2,…,s ,当总名额增加一个时,计算)1(2+=i i i i n n p Q , 则这个名额应该分给Q 值最大的那个单位.表2—3是利用惠丁顿法重新分配三个系21个名额的计算结果.丙系保住了险些丧失的一个名额. 表2—3 惠丁顿法分配21个名额的结果(3)模型评注名额(席位)分配问题应该对各方公平是理所当然的,问题的关键是在于建立衡量公平程度的即合理又简明的数量指标.惠丁顿法所提出的数量指标是相对不公平值r A ,r B ,它是确定分配方案的前提.在这个前提下导出的分配方案—分给Q 值最大的一方—无疑是公平的.但这种方法也不是尽善尽美的,这里不再探讨.5.森林救火模型森林失火了!消防站接到火警后,立即决定派消防队员前去救火.一般情况下,派往的队员越多,火被扑灭的越快,火灾所造成的损失越小,但是救援的开支就越大;相反,派往的队员越少,救援开支越少,但灭火时间越长,而且可能由于不能及时灭火而造成更大的损失,那末消防站应派出多少队员前去救火呢?(1)问题分析如题中所述,森林救火问题与派出的消防队员的人数密切相关,应综合考虑森林损失费和救援费,以总费用最小为目标来确定派出的消防队员的人数使总费用最小.救火的总费用由损失费和救援费两部分组成.损失费由森林被烧毁的面积大小决定 ,而烧毁面积与失火、灭火(指火被扑灭)的时间(即火灾持续的时间)有关,灭火时间又取决于参加灭火的队员的数目,队员越多灭火越快.救援费除与队员人数有关外,也与灭火时间长短有关.救援费可具体分为两部分:一部分是灭火器材的消耗及消防队员的薪金等,与队员人数及灭火时间均有关;另一部分是运送队员和器材等一次性支出,只与队员人数有关.设火灾发生时刻为t =0,开始救火时刻为t =t 1,灭火时刻为t =t 2,t 时刻森林烧毁面积为B (t ),则造成损失的被烧毁的森林的面积为B (t 2),而dtdB是森林被烧毁的速度,也表示了火势蔓延的程度.从火灾发生时刻开始到火被扑灭的过程中,被烧毁的森林的面积是不断扩大的,因而B (t )应是时间t 的单调非减的函数,即20,0t t dtdB≤≤≥.从火灾发生到消防队员到达并开始救火这段时间内,火势是越来越大的,即1220,0t t dtBd ≤≤≥.开始救火以后,即21t t t ≤≤时,如果队员灭火能力足够强,火势会越来越小,即2122,0t t t dt B d ≤≤≤,并且当t =t 2时,0=dtdB. 在建立数学模型之前,需要对烧毁森林的损失费、救援费及火势蔓延程度dtdB作出合理的假设.(2)模型假设① 森林中树木分布均匀,而且火灾是在无风的条件下发生的;② 损失费与森林烧毁面积B (t 2)成正比,比例系数为c 1,即烧毁单位面积的损失费为c 1;③ 从失火到开始救火这段时间内,火势蔓延程度dtdB与时间t 成正比,比例系数为β,称之为火势蔓延速度,即;0,1t t t dtdB≤≤=β ④ 派出消防队员x 名,开始救火以后(1t t ≥),火势蔓延速度降为x λβ-(线性化),其中λ可视为每个队员的平均灭火速度,且有x λβ<,因为要扑灭森林大火,灭火速度必须大于火势蔓延的速度,否则火势将难以控制;⑤ 每个消防队员单位时间费用为c 2(包括灭火器材料的消耗及消防队员的薪金等),救火时间为t 2-t 1,于是每个队员的救火费用为c 2(t 2-t 1);每个队员的一次性支出为c 3(运送队员、器材等一次性支出).对于假设3可作如下解释:由于森林中树木分布均匀,且火灾是在无风条件下发生的,因而火势可看作以失火点为中心,以均匀速度向四周呈圆形蔓延,因而蔓延半径r与时间t 成正比,又因为烧毁面积B 与r 2成正比,故B 与t 2成正比,从而dtdB与t 成正。
