相图的建立及匀晶相图分析
二元匀晶相图

一、相图分析
1、相图的坐标
纵坐标是温度坐标,横坐 标是成分坐标:左端线是表 示100%的Cu,右端线表示 100%的Ni,从左至右Ni的 含量增加(直至100%)、Cu 的含量减少(直至0%)。
2、相图中的线和区
相图中有二条曲线,将整个图形分成三个区域。
实用文档
2
上面一条曲线称为液相线(Liquid line),液相线以上的区域 称为液相区(Liquid-phase field),温度高于液相线时合金的状
也称为杠杆定律。
实用文档
5
三、典型合金冷却过程分析
各种成分的Cu-Ni合金都属于匀晶合金。下面以Cu-53%Ni 合金为例,分别对合金结晶过程中液、固二相的成分变化规律, 二相相对量的计算和微观组织的形成进行分析讨论。
1、液-固两相成分的变化
合金从液态开始缓慢冷却,当温度 降低到液相线(1点)时,结晶开始。此
设合金的平均成分为x,合金
的总量为Q,在温度T1时液、 固两相平衡,液相的成分为xL、 质量为QL,固相的成分为xS、 质量为QS。则有:
Q QxIQm LQ N LaQoSxgLeQSxS
实用文档
4
上式可变换为:
QL xS x QS x xL
还可以变换为:
或 Q L x x L Q S x S x
QL xS x Q xS xL 或 QS xL x Q xS xL
合金的平均成分点看作杠杆的支点o; T1温度水平线与液、固相线的交点a、 b为杠杆的两个端点;液、固两相的
质(重)量为作用在端点上的力。
为了计算简便,一般取合金总量Q =1。
因上述结果与物理学中的杠杆定律的表达式相似,所以这里
采用均匀化热处理(Homogenizing heat treatment)可以 消除枝晶偏析。
二元匀晶相图
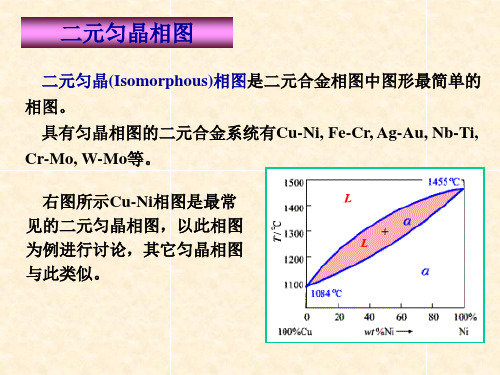
二元匀晶(Isomorphous)相图是二元合金相图中图形最简单的 相图。
具有匀晶相图的二元合金系统有Cu-Ni, Fe-Cr, Ag-Au, Nb-Ti, Cr-Mo, W-Mo等。
右图所示Cu-Ni相图是最常 见的二元匀晶相图,以此相图 为例进行讨论,其它匀晶相图 与此类似。
一、相图分析
2、相的相对量计算
1300˚C时,液相的相对量QL/Q(可以取合金总量Q =1):
QL 58 53 0.38 38% Q 58 45
固相的相对量QS /Q:
QS 53 45 0.62 62% Q 58 45
因为 QL + QS = Q,取Q =1
所以 QS =1-QL = 1-38% = 62%
金的总量为Q,在温度T1时液、 固两相平衡,液相的成分为xL、 质量为QL,固相的成分为xS、 质量为QS。则有:
Q QL QS Q x QL xL QS xS
上式可变换为:
QL xS x QS x xL
还可以变换为:
或 QL x xL QS xS x
液相的成分沿液相线变化,固相的 成分沿固相线变化。
动画
温度降低到1300℃时,液相成分为45%Ni, 固相成分为58%Ni。 当温度降低到2点,即固相线温度时,液相的成分为L2,固相的 成分为合金的平均成分(53%Ni)。此时液相实际上已经不存在了, 都已结晶成为固相。
温度继续下降,一直冷却到室温,合金在固态没有任何转变 发生。仔细观察动画。
采用均匀化热处理(Homogenizing heat treatment)可以消除枝 晶偏析。
匀晶合金的 非平衡组织
因此,能够形成匀晶合金系的两种组元必须具有相同的晶体 结构,相同的原子价,原子半径接近(相差不超过15%),相互 不形成化合物。
第十七讲三元匀晶相图

第十七讲三元匀晶相图第三节三元匀晶相图一、主要内容:相图分析三元合金的结晶过程等温界面图变温截面图投影图二、要点:三元匀晶相图的点、面、区的意义,三元匀晶相图的结晶过程的特点,与二元合金的相同点和不同点,蝴蝶形规律,等温截面图点、线、区的意义,直线法则杠杆定律在等温截面中的应用,变温截面图点、线、区的意义,变温截面图与二元合金相图的不同点,投影图的线、区的意义,三、方法说明:画三元匀晶相图的立体图形说明点、面、区的意义,从立体图形中截取等温截面图和垂直截面图进行说明,说明直线法则和杠杆定律只能在等温截面图上应用授课内容:三个组元在液态及固态均无限互相溶解的相图叫三元匀晶相图。
一、相图分析三元匀晶相图立体模型如图:三个组元的熔点:液相面,固相面。
液相区,固相区,液固两相共存区。
二、三元固溶体合金的结晶过程随着温度的不断下降液相的数量不断的减少,固相的数量不断的增多。
固相的成分沿着固相面变化,液相的成分沿着液相面变化。
由于液相面和固相面都是空间曲面,所以固相的成分变化线和液相的成分变化线,不处于同一个垂直平面上,也不处于同一个水平平面上,它们在成分三角形上的投影很像一只蝴蝶,所以,成为蝴蝶规律。
三、等温截面(水平截面)整个截面可以分为三个不同的相区:液相区(L),固相区(α),液固两相区(L+α)。
曲线L1L2为液相线,曲线S1S2为固相线。
在两相区,可以利用杠杆定律计算两平衡相的含量。
四、变温截面图(垂直截面图)变温截面图相当于在三元相图的立体模型重插入一个垂直于成分三角形的截面。
变温截面有两种:一种是平行于成分三角形的一边所做的垂直截面。
另一种是通过成分三角形的某一顶点所做的截面。
变温截面图可分为:固相区,液相区,液固两相区利用变温截面图可以分析合金的结晶过程,确定相变温度,了解合金在不同温度下所处的状态。
变温截面上的液相线和固相线,不能表示平衡相的成分,不能根据这些线应用杠杆定律计算平衡相的含量。
匀晶相图ppt

距离
中期:
L相:界面层堆积非常严重-扩
散不够快,远端保持C0 S相:保持C0
后 期:—— 终端瞬态区 L相:浓度较大--界面层扩散受阻 --浓度再次增加,且幅度很大 S 相:结晶出高浓度溶质
3. 正常凝固溶质分布综合比较
浓度
C0
快速
中速
平衡 缓慢
S/L 界面处溶质分布: k0 < 1
缓慢凝固: CS
浓度
S
L/S界面
k0C1
k0C2
S相:忽略扩散的作用 —— 溶质不混合 L相:搅拌、对流、扩散— 溶质完全混合
开始-中前期:
溶质原子富集在L相中 ——L相
L
较多—— L相浓度变化不大——
C1
S相浓度维持较低水平
距离 中期-中后期:
C2
L相富集程度加大—— L相量减
少—— L相浓度增加—— S相中
不得不结晶出较多的溶质—— S
(2) 固相扩散难度 > 液相扩散
α1 α'2 α2
L1
L'1
L2
α3
L'2
L3
α'3
α4
L'3
α'4
L'4
难度 —— 固相平均成分线 偏离固相线程度 > 液相平 均成分线偏离液相线程度
L4
(3) 固相难扩散 —— 先后结晶
部分保持各自溶质浓度 ——
Ni
Cu
偏析 —— 影响性能 ——
(解决途径)均匀化退火
第二节 二元匀晶相图
匀晶转变:
由液相直接结晶出单相固溶体的转变(相变)
匀晶相图:
体系只具有匀晶转变的
一、相图分析
培训_42匀晶相图

态过渡区宽度减小
C0
S 相:浓度增大很快,达到C0
并稳定
距离 中期:
L相:界面层堆积非常严重-
扩散不够快,远端保持C0 S相:保持C0
后 期:—— 终端瞬态区 L相:浓度较大--界面层扩散受 阻--浓度再次增加,且幅度很 大
S 相:结晶出高浓度溶质
3. 正常凝固溶质分布综合比较
浓度
C0
快速
中速
平衡 缓慢
外界条件:G↓、R↑
—— 左边值↓
2. 固溶体生长形貌
固溶体:L/S界面溶质重新分配
有偏析 有成分过冷
平面状 胞状
树枝状
α1 α2
L1
L'1
L2
α'
2
α3
α'3
L'2
α4
L'3
L3
α'4
L'4
(2) 固相扩散难度 > 液相扩
散难度 —— 固相平均成
分线偏离固相线程度 >
液相平均成分线偏离液
L4
(3)
固相相线难程扩度散
——
先后结
晶部分保持各自溶质浓
Ni
Cu
度 —— 偏析 —— 影响
性能 —— (解决途径)均
匀化退火
5. 微观偏析
-- 总质量一定
W0 x WL xL W x
--溶质量一定
WL ar W rb
xα
Ni 力1 × 力臂1 = 力2 × 力臂2
—— 杠杆定律
T (℃)
t1
Cu
L
ar
xL x
即:
b
α
二元合金的相结构与结晶相图建立与匀晶相图2258103
9
在杠杆定律中,杠杆的支点是合金的成分,杠杆的端
点是所求的两个平衡相的成分。
例(如图)
0.53 0.45 Q 100% 61.5% 0.58 0.45 0.58 0.53 QL 100% 38.5% 0.58 0.45
3
4
三、相律及杠杆定律
(一) 相律及其应用
相律:表示平衡条件下,系统的组元数、相数和自由度数之间的关系。 表达式:
F=C-P+2 (压力:不等) F=C-P+1 (压力:常数) C-组元数(component); P-相数(phase); F-自由度数(free) 平衡系统的自由度数:平衡系统的独立、可变的因素数。 (在保持合金系的相数不变的条件下,合金系中可改变的、影 响合金状态的内部因素和外部因素的数目) (成分、温度、压力)
如 Cu-Ni,Fe-Cr, Au-Ag Cu-Ni合金相图
15
一、相图分析
两个点——Cu和Ni的熔点
两条线——上面是液相线,
下面是固相线。
L
三个区——液相区L ,
固相区 ,
+
L
固液共存的两相区(L+ )。
16
二、固溶体合金的平衡结晶过程
平衡结晶——极缓慢的冷却条件下进行的结晶过程
§3-3 二元合金相图的建立
相图 (phase diagram) :表示在平衡条件下合金的状态与温度、 成分之间关系的图解,又称为平衡图或状态图。(工具)
热分析法

4、合金的不平衡结晶与树枝状偏析
由于冷却速度较快,合金在结晶过程中,无 论固相或液相中的原子都来不及充分扩散,这 种结晶过程称为不平衡结晶。
由于各层之间的原子来不及扩散,这种成分 不均匀现象可保持到结晶完毕,直至室温,这 种现象叫枝晶偏析或树枝状偏析。
2. 合金的工艺性能与相图的关系
● 铸造性能 液固相线距离愈小,结
晶温度范围愈小(如接近共 晶成分的合金),则流动性 好,不易形成分散缩孔。
● 锻造、轧制性能 单相固溶体合金,变形抗
力小,变形均匀,易开裂。
Pb
X2
Sn
冷却曲线 t
(c)2003 Brooks/Cole, a division of Thomson Learning, Inc. Thomson Learning™ is a trademark used herein under license.
(c)2003 Brooks/Cole, a division of Thomson Learning, Inc. Thomson Learning™ is a trademark used herein under license.
由于一个枝晶形成一个晶粒,也叫晶内偏析。
三、共晶相图
共晶转变:由一定成分的液相同时结晶出两个一定成分固 相的转变。
共晶相图:具有共晶转变特征的相图。(液态无限互溶、 固态有限互溶或完全不溶,且发生共晶反应。)
共晶组织:共晶转变产物(是两相混合物) 。
三、共晶相图 1.相图分析(相图三要素)
T,C
T,C
(+ )
讲座-42匀晶相图学习文档

k0C0
1
z k0 1
L
中速凝固:
CS
keC0
1
z ke1
L
快速凝固:
CL
x
C0
1
1 k0 k0
exp
Rx D
4. 区域熔炼
原理: 顺序结晶 —— 使杂质富集于终端 —— 除端部,纯度增加
应用: 感应加热 —— 局部熔化,顺序结晶 —— 反复进行,提纯
3)结晶温度
纯金属结晶:
f=c-p+1=1-2+1=0
—— 恒温结晶 二元匀晶:
f=c-p+1=2-2+1=1
—— 变温结晶
5. 杠杆定律
T (℃)
L
t1
a
r
Cu
xL x
b
α
合金总重量W0,成份x
液相重WL,液相成分xL
α相重Wα ,液相成分xα
t1时:
其中 x、xL、xα为已知
W0 WL W
影响因素: 移动速度↓—— 液相均匀性↑—— 固相均匀性↓—— 杂质端部富 集↑—— 提纯效果↑
五、成分过冷与固溶体组织形态
1. 成分过冷:
(1)成分过冷的形成:
溶
1 2
质
34
分
布
熔
点
分
34 2
布
1
T(℃)
T4 T3 T2 T1
S
L
4 3
2 1
C4 C3 C2 C1
成
温
分 过
度 分 布
冷
(2) 成分过冷临界条件
液相线斜率
温度梯度
合金成分
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
WL X 2 X ob WS X X 1 oa
WL ob 100% Wo ab Ws oa 100% Wo ab
WL a (X1)
WS b (X2)
o(X)
15
(6)二元相图中的几何规律
相图中所有的线条都代表发生相转变的温度和平衡相的 成分,所以相界线是相平衡的体现,平衡相成分必须沿着相 界线随温度而变化;
100%
2 X 0 2 l2
a1 a2 a3
0%
X 0 l2 2 l2
0%
100%
在液固两相共存区,随着温度的降低,液相的量
不断减少,固相的量不断增多,同时液相的成分 沿液相线变化,固相成分沿固相线变化。
27
固溶体结晶的特点 (1)异分结晶
固溶体合金结晶时所结晶出的固相成分与液相成分不同,
由于合金凝固时的结晶潜热较大,结晶时冷却曲
线上的转折比较明显,因此常用热分析法来测合
金的结晶温度,即测液相线、固相线。
8
热分析法
利用合金在转变时伴有热学性能变化的特性,通
过测量系统温度的变化来得到临界温度,从而建立起
相图。
9
10
热分析法建立二元合金相图的步骤
将给定两组元配制成一系列不同成分的合金;
1. 二元合金相图的坐标系为
A 压力—温度;
B 压力—成分;
C 温度—成分。
答案:C 单元系相图一般采用“压力—温度”坐标系统,二元 系相图则采用“温度—成分”坐标系统。
33
思考题
2.杠杆定律仅适用于平衡相图的二相区。
A. 是
B. 否
答案:A 杠杆定律只能在平衡相图的二相区应用。
34
思考题
3. 匀晶合金的室温组织为单相固溶体。 A. 是 B. 否 答案:A 匀晶合金的室温组织为单相固溶体,即使是非平衡凝 固的匀晶合金也是如此。
23
当合金缓慢冷却至L1
点以前时,均为单一 的液相;
冷却到L1点时,开始
从液相中析出α固溶体, 冷却到a3点时,合金 全部转变为α固溶体;
若继续从a3点冷却到
室温,为单一的α固溶 体。
24
匀晶转变过程中原子扩散示意图
25
26
温度
成分 t1 t2 t3 L1 L2 L3
L α 质量分数 变化趋势 成分 质量分数 变化趋势
6
二元相图中的成分按国家标准有两种表示法:
①质量分数(w):
RA x A RB xB wA , wB RA xA RB xB RA xA RB xB
②摩尔分数(x):
wA / RA wB / RB xA , xB wA / RA wB / RB wA / RA wB / RB
35
思考题
4. 下述哪些下列说法哪些是正确的? A 温度高于液相线的合金为液态; B 温度低于液相线的合金为固态; C 温度低于固相线的合金为固态;
D 温度高于固相线的合金为液态。
答案:AC
36
思考题
5. A-B二元匀晶合金相图如右图所示。 应用杠杆定 律计算,当成分为40%B的合金冷却到1000˚C时,结 晶出了多少固相?剩余多少液相(相对量)?
f=C-P+1
4
3.2 二元合金相图的建立
(3)二元相图表示方法
二元合金相图常 用温度、成分相图, 表示合金的状态随成 分和温度变化而发生 变化的情况。
二元Pb-Sb合金相图
5
在相图中,任意一点都 叫“表象点”。 一个表象点的坐标值反 映一个给定合金的成分 和温度。
在相图中,由表象点所在的相区可以判定在该温度下合金 由哪些相组成。 二元合金在两相共存时,两个相的成分可由过表象点的水 平线与相界线的交点确定。
中溶质浓度的比值。
K 0 CS / C L
表明k0的示意图 (a) k0<1 ; (b) k0>1
30
平衡凝固时固相的溶质分布
形核→相界平衡→扩散破坏平衡→长大→相界平衡
31
本节要点
概念:匀晶转变、平衡凝固 匀晶相图的分析 固溶体的凝固过程
下节内容:共晶相图及其合金凝固
32
思考题
示;在TaTb凹曲线以下为固相的单相区,用α表示;
α是Cu-Ni互溶形成的置换式无限固溶体。在 TaTb凸
曲线和TaTb凹曲线之间为液、固两相平衡区,用 L+α表示。
Tb
Ta
22
(2)固溶体合金的平衡凝固及组织 平衡结晶:每个时刻都能达到平衡的结晶过程。 平衡结晶过程分析
冷却曲线:温度-时间曲线;
16
两个单相区之间定有一个由该两相组成的两相区把它
们分开,而不能以一条线接界,两个两相区必须以单相区或 三相水平线隔开,也就是说,在二元相图中,相邻相区的相 数差为1(点接触情况除外),这个规则称为相区接触法则;
17
二元相图中的三相平衡必为一条水平线,表示恒温反应, 在这条水平线上存在三个表示平衡相的成分点,其中两点应 在水平线的两端,另一点在端点之间,水平线的上下方分别 与三个两相区相接;
本章知识结构
合金中的相及相结构 匀晶相图及固溶体的凝固 共晶相图及合金的凝固 相图分析 包晶相图及合金的凝固 二元相图的分析和使用
二元合金相图的建立
其他类型的二元合金相图
1
3.2 二元合金相图的建立
(1)相平衡条件
在平衡条件下,合金系中各相的成分保持着相对的稳定 性,宏观上没有组元在相间转移。 在恒温恒压下,相间成分的改变引起的体系自由能的变 化等于组元的转移量和它们在各相化学位乘积的叠加,即
式中:wA、wB分别为A、B组元的质量分数;xA、
xB分别为A、B组元的摩尔分数,RA、RB分别为A、
B组元的相对原子质量。
7
(4)二元相图的建立
建立相图的关键是要准确地测出各成分合金的相
变临界点(临界温度)。
临界点:物质结构状态发生本质变化的相变点。
测临界点的方法通常有热分析法、硬度法、金相 分析、X射线结构分析、磁性法、膨胀法、电阻 法等。
18
当两相区与单相区的分界线与三相等温线相交,
则分界线的延长线应进入另一两相区内,而不会进 入单相区内。
19
3.4 匀晶相图及固溶体的凝固
(1)相图分析
由液相结晶出单相固溶体
Tb
的过程称为匀晶转变。
L
两组元在液态无限溶解,
Ta
在固态无限固溶,并且发 生匀晶反应的相图,称为 匀晶相图。
dG i dni
式中
i 为i组元的化学位;dni为i组元在相间的转移量。
化学位差是组元在相间转移的驱动力。
2
(1)相平衡条件
如果dni的i组元从α相中转移到β相中,则体系的自由能 变化
dG i i dni
在平衡条件下dG=0,故
i i
既α、β两相平衡的条件是,两相中同一组元的化学位相等。
28
与纯金属结晶的比较
①
相同点:基本过程:形核-长大;
热力学条件:⊿T>0;
能量条件:能量起伏;
结构条件:结构起伏。 ② 不同点:合金在一个温度范围内结晶 可能性:相律分析; 必要性:成分均匀化。 合金结晶是异分结晶:需成分起伏。
29
(3)固溶体合金凝固时的溶质分布
平衡分配系数:在一定温度下,固、液两平衡相
20
点:相图中Ta,Tb点分别为纯组元Cu,Ni的熔点。
线:TaTb凸曲线为液相线。各不同成分的合金加热
到该线以上时全部转变为液相,而冷却到该线时开
始凝固出α固溶体。
Tb
TaTb凹曲线为固相
线。各不同成分的
合金加热到该线时 开始熔化,而冷却 到该线时全部转变 为α固溶体。
21
Ta
相区:在TaTb凸曲线以上为液相的单相区,用L表
若合金有n个组元,P个相,则它们的平衡条件可以写成:
1 1 ........... 1p
2 2 ........... 2p
………. p n n ........... n
3
(2)相 律
在平衡条件下,合金的组元数和相数之间存在一定的关 系,这种关系称为相律。Gibbs相律:在只受外界温度和压 力影响的平衡系统中,它的自由度数等于系统的组元数和相 数只差再加上2。
这种结晶出的晶体与母相化学成分不同的结晶称为异分结 晶,或称选择结晶。
(2)固溶体合金的结晶需要在一定的温度范围
固溶体合金的结晶需要在一定的温度范围内进行,在此温
度范围内的每一温度下,只能结晶出一定数量的固相。 随着温度的降低,固相的数量增加,同时固相和液相的成 分分别沿着固相线和液相线而连续地改变,直至固相的成 分与原合金的成分相同时,才结晶完成。
37
答案:
根据杠杆定律,固相的相对量计算如下:
液相的相对量则为,
38
f c p2
式中f为系统的自由度数;C为系统的组元数;P为相数。 所谓的系统的自由度数,就是平衡系统的独立可变因素 (如温度、压力、浓度等)的数目。这些因素可在一定范围内 任意独立地改变而不会影响到原有的共存相数和状态,即不会 影响原有的平衡状态。对于不含气相的凝聚系统,通常范围的 压力改变对平衡影响极小,一般可忽略压力的影响,则自由度 数
