二元匀晶相图
合集下载
材料科学基础-8-二元相图(2)
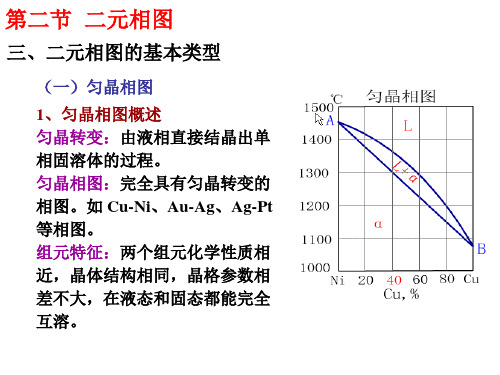
第二节 二元相图
（一）匀晶相图
2、固溶体的平衡凝固
（3）固溶体的结晶规律
c.固溶体的凝固过程与纯金
属一样，也包括形核与长大
两个阶段
e. 平衡凝固得到的固溶体显
微组织和纯金属相同，除了
晶界外，晶粒之间和晶粒内
部的成分却是相同的。
d.合金结晶形核时需要能量
起伏和成分起伏
a. 固溶体的结晶与纯金属不同，它不在
（2）压力加工性：压力加工合金通常是相图上单相固溶体
成分范围内的单相合金或含有少量第二相的合金。
——单相固溶体合金切削加工性能
不够好，而具有两相组织的合金切
削加工性一般比较好。
（4）热处理性：
相图上无固态相变或固溶度变化的
合金不能进行热处理。
孔等缺陷。
——我国20世纪60年代开始研制Pt-Ag合金，但至今无法批量
稳定发展
——国内外通过添加Pd（钯）制成Pt-Pd-Ag三元合金，虽综合
性能不如Pt-Ag合金，但加工性能得以改善。
第二节 二元相图
（三）包晶相图
2、包晶合金的凝固及其平衡组织
（1）ω (Ag)为42.4％的Pt-Ag合金（合金I）
′
% =
× %
第二节 二元相图
1186℃
A
LP+αC ↔ βD
（三）包晶相图
f=2-3+1=0
包晶点
• 1、包晶相图
• 包晶转变：由一个固相与
液相作用生成另一个固相
的过程。
• 包晶相图：两组元在液态
无限互溶，固态下有限互
溶，并发生包晶反应的二
元系相图。
第二节 二元相图
2、包晶合金的凝固及其平衡组织
材料科学基础4.3二元匀晶相图
4.4 匀晶相图
4.两平衡相的相对量
在T2温度下，合金x （成分O）由液相（成分L2） 和固相（成分α2）组成，令合金重W0，液相 重Wl ，固相重Wα,有：
W0＝ Wl + Wα 溶质含量为：
W0 × O ＝ Wl × L2 + Wα × α2 （Wl + Wα）× O ＝ Wl × L2 + Wα × α2 Wl （ O－ L2）＝ Wα （ α2 － O ）
Wl / Wα ＝ （ α2 － O ）/ （ O－ L2） 两平衡相的相对量与其在相图上平衡成分
线段长度成反比。
Wl / （W0 － Wl ）＝ （α2 － O ）/ （ O－ L2） 所以：
Wl / W0＝ （ α2 － O ）/ （α2 － L2） Wα / W0＝ 1－ Wl / W0
＝ （ O － L2）/ （α2 － L2） 上式就是二元系中的杠杆定律，杠杆的支 点是合金成分点，杠杆的两端点是两平衡相的 平衡成分点。
4.4.3 固溶体的非平衡凝固
• 偏析－合金内部成分不均匀； • 晶内偏析－晶粒内部成分不均匀； • 枝晶偏析－树枝晶内的偏析； • 枝晶偏析对铸件影响很大，可在低于固相线
温度下进行均匀化退火或进行热轧、锻造降 低枝晶偏析；
• 不平衡凝固偏离固相线、液相线，但液、固 相界面仍然符合相图的平衡关系。
4.两平衡相的相对量
在T2温度下，合金x （成分O）由液相（成分L2） 和固相（成分α2）组成，令合金重W0，液相 重Wl ，固相重Wα,有：
W0＝ Wl + Wα 溶质含量为：
W0 × O ＝ Wl × L2 + Wα × α2 （Wl + Wα）× O ＝ Wl × L2 + Wα × α2 Wl （ O－ L2）＝ Wα （ α2 － O ）
Wl / Wα ＝ （ α2 － O ）/ （ O－ L2） 两平衡相的相对量与其在相图上平衡成分
线段长度成反比。
Wl / （W0 － Wl ）＝ （α2 － O ）/ （ O－ L2） 所以：
Wl / W0＝ （ α2 － O ）/ （α2 － L2） Wα / W0＝ 1－ Wl / W0
＝ （ O － L2）/ （α2 － L2） 上式就是二元系中的杠杆定律，杠杆的支 点是合金成分点，杠杆的两端点是两平衡相的 平衡成分点。
4.4.3 固溶体的非平衡凝固
• 偏析－合金内部成分不均匀； • 晶内偏析－晶粒内部成分不均匀； • 枝晶偏析－树枝晶内的偏析； • 枝晶偏析对铸件影响很大，可在低于固相线
温度下进行均匀化退火或进行热轧、锻造降 低枝晶偏析；
• 不平衡凝固偏离固相线、液相线，但液、固 相界面仍然符合相图的平衡关系。
第四节 二元包晶相图
0E
20
F 100
Pt P57图3-20
Ag%
Ag
Pt-Ag合金相图
单相区L、 、 双相区L 、 L + 、 +
二、包晶合金的平衡结晶过程与室温组织
L L
1800
A
T/ ℃
1600
1
L
1
1400
1200 温 度 1000
C
1186
D
P
10.5
42.4
66.3
B
D
D'
+ Ⅱ
β
1200
1100
1000
1000
800
β
0
B
900
600
800
Ni
W Cu (%)
Cu
A
B%
B
400
E
20
40
60
80
F 100
Ag%
L α β α
L
β
四、相图的应用
1、识别分析相图要领 基本反应，三种线，水平线是关键； 相区有一有二没有三，三相共存水平线；
杠杆定律别小看，能定成分能把量来算。
2、分析合金结晶
本章知识回顾
一、基本概念
1、固态合金的相结构
纯 金 属 合 金 三元 合金 固溶体 二元 合金 金属间化合物 多元 合金 置换固溶体 正常价化合物
金 属 材 料
间隙固溶体
非正常价化合物
2、相图
（二元匀晶相图、二元共晶相图、二元包晶相图）
3、几种转变
（匀晶转变、共晶反应、包晶反应）
4、平衡结晶、非平衡结晶、晶内偏析、扩散退火
二元匀晶相图
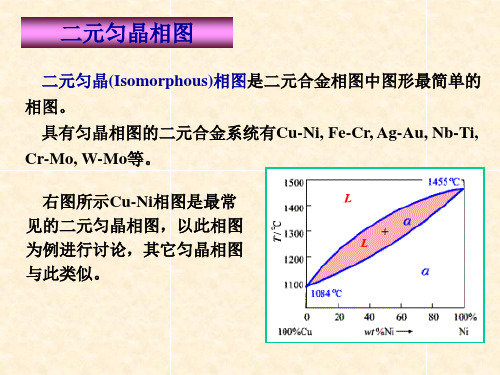
二元匀晶相图
二元匀晶(Isomorphous)相图是二元合金相图中图形最简单的 相图。
具有匀晶相图的二元合金系统有Cu-Ni, Fe-Cr, Ag-Au, Nb-Ti, Cr-Mo, W-Mo等。
右图所示Cu-Ni相图是最常 见的二元匀晶相图，以此相图 为例进行讨论，其它匀晶相图 与此类似。
一、相图分析
2、相的相对量计算
1300˚C时，液相的相对量QL/Q（可以取合金总量Q =1）：
QL 58 53 0.38 38% Q 58 45
固相的相对量QS /Q：
QS 53 45 0.62 62% Q 58 45
因为 QL + QS = Q，取Q =1
所以 QS =1-QL = 1-38% = 62%
金的总量为Q，在温度T1时液、 固两相平衡，液相的成分为xL、 质量为QL，固相的成分为xS、 质量为QS。则有：
Q QL QS Q x QL xL QS xS
上式可变换为：
QL xS x QS x xL
还可以变换为：
或 QL x xL QS xS x
液相的成分沿液相线变化，固相的 成分沿固相线变化。
动画
温度降低到1300℃时，液相成分为45%Ni, 固相成分为58%Ni。 当温度降低到2点，即固相线温度时，液相的成分为L2，固相的 成分为合金的平均成分(53%Ni)。此时液相实际上已经不存在了， 都已结晶成为固相。
温度继续下降，一直冷却到室温，合金在固态没有任何转变 发生。仔细观察动画。
采用均匀化热处理(Homogenizing heat treatment)可以消除枝 晶偏析。
匀晶合金的 非平衡组织
因此，能够形成匀晶合金系的两种组元必须具有相同的晶体 结构，相同的原子价，原子半径接近(相差不超过15％)，相互 不形成化合物。
二元匀晶(Isomorphous)相图是二元合金相图中图形最简单的 相图。
具有匀晶相图的二元合金系统有Cu-Ni, Fe-Cr, Ag-Au, Nb-Ti, Cr-Mo, W-Mo等。
右图所示Cu-Ni相图是最常 见的二元匀晶相图，以此相图 为例进行讨论，其它匀晶相图 与此类似。
一、相图分析
2、相的相对量计算
1300˚C时，液相的相对量QL/Q（可以取合金总量Q =1）：
QL 58 53 0.38 38% Q 58 45
固相的相对量QS /Q：
QS 53 45 0.62 62% Q 58 45
因为 QL + QS = Q，取Q =1
所以 QS =1-QL = 1-38% = 62%
金的总量为Q，在温度T1时液、 固两相平衡，液相的成分为xL、 质量为QL，固相的成分为xS、 质量为QS。则有：
Q QL QS Q x QL xL QS xS
上式可变换为：
QL xS x QS x xL
还可以变换为：
或 QL x xL QS xS x
液相的成分沿液相线变化，固相的 成分沿固相线变化。
动画
温度降低到1300℃时，液相成分为45%Ni, 固相成分为58%Ni。 当温度降低到2点，即固相线温度时，液相的成分为L2，固相的 成分为合金的平均成分(53%Ni)。此时液相实际上已经不存在了， 都已结晶成为固相。
温度继续下降，一直冷却到室温，合金在固态没有任何转变 发生。仔细观察动画。
采用均匀化热处理(Homogenizing heat treatment)可以消除枝 晶偏析。
匀晶合金的 非平衡组织
因此，能够形成匀晶合金系的两种组元必须具有相同的晶体 结构，相同的原子价，原子半径接近(相差不超过15％)，相互 不形成化合物。
第四章4.1二元匀晶相图
4h
第二节 二元匀晶相图
3 固溶体的不平衡结晶 （1）原因:冷速快(假设液相成分均匀、固相成分不均 匀)。 （2）结晶过程特点：固相成分按平均成； 组织多为树枝状。
第一节 相图的基本知识
2 相图的表示与建立 （1）状态与成分表示法 状态表示：温度－成分坐标系。 坐标系中的点－表象点。 成分表示：质量分数或摩尔分数。
第一节 相图的基本知识
2 相图的表示与建立 （2）相图的建立 方法：实验法和计算法。 过程：配制合金－测冷却曲线－确定转变温度 －填入坐标－绘出曲线。 相图结构(匀晶)：两点、两线、三区。
1 匀晶相同及其分析 （1）匀晶转变：由液相直接结晶出单相固溶体的转变。 （2）匀晶相图：具有匀晶转变特征的相图。 (两组元在液态和固态都无限互溶)
（3）相图分析 两点：纯组元的熔点； 两线：L, S相线； 三区：L, α, L+α。
第一节 相图的基本知识
3 杠杆定律-相含量的计算工具 （1）平衡相成分的确定（根据相律，若温度一定，则自由 度为0，平衡相成分随之确定。） （2）数值确定：直接测量计算或投影到成分轴测量计算。 （3）注意：只适用于两相区；三点(支点和端点)要选准。
第二节 二元匀晶相图
第二节 二元匀晶相图
4 稳态凝固时的溶质分布 (4) 区域熔炼（上述溶质分布规律的应用）
第二节 二元匀晶相图
5 成分过冷及其对晶体生长形态的影响 （1）成分过冷：由成分变化与实 际温度分布共同决定的过冷。 （2）形成：界面溶质浓度从高到低 →液相线温度从低到高。 （图示：溶质分布曲线→ 匀晶相图→ 液相线温度分布曲线→ 实际温度分布曲线→ 成分过冷区。）
第二节 二元匀晶相图
2 固溶体合金的平衡结晶 （1）平衡结晶：每个时刻都能达到平衡的结晶过程。 （2）平衡结晶过程分析 ① 冷却曲线：温度－时间曲线；
第二节 二元匀晶相图
3 固溶体的不平衡结晶 （1）原因:冷速快(假设液相成分均匀、固相成分不均 匀)。 （2）结晶过程特点：固相成分按平均成； 组织多为树枝状。
第一节 相图的基本知识
2 相图的表示与建立 （1）状态与成分表示法 状态表示：温度－成分坐标系。 坐标系中的点－表象点。 成分表示：质量分数或摩尔分数。
第一节 相图的基本知识
2 相图的表示与建立 （2）相图的建立 方法：实验法和计算法。 过程：配制合金－测冷却曲线－确定转变温度 －填入坐标－绘出曲线。 相图结构(匀晶)：两点、两线、三区。
1 匀晶相同及其分析 （1）匀晶转变：由液相直接结晶出单相固溶体的转变。 （2）匀晶相图：具有匀晶转变特征的相图。 (两组元在液态和固态都无限互溶)
（3）相图分析 两点：纯组元的熔点； 两线：L, S相线； 三区：L, α, L+α。
第一节 相图的基本知识
3 杠杆定律-相含量的计算工具 （1）平衡相成分的确定（根据相律，若温度一定，则自由 度为0，平衡相成分随之确定。） （2）数值确定：直接测量计算或投影到成分轴测量计算。 （3）注意：只适用于两相区；三点(支点和端点)要选准。
第二节 二元匀晶相图
第二节 二元匀晶相图
4 稳态凝固时的溶质分布 (4) 区域熔炼（上述溶质分布规律的应用）
第二节 二元匀晶相图
5 成分过冷及其对晶体生长形态的影响 （1）成分过冷：由成分变化与实 际温度分布共同决定的过冷。 （2）形成：界面溶质浓度从高到低 →液相线温度从低到高。 （图示：溶质分布曲线→ 匀晶相图→ 液相线温度分布曲线→ 实际温度分布曲线→ 成分过冷区。）
第二节 二元匀晶相图
2 固溶体合金的平衡结晶 （1）平衡结晶：每个时刻都能达到平衡的结晶过程。 （2）平衡结晶过程分析 ① 冷却曲线：温度－时间曲线；
匀晶相图ppt
距离
中期：
L相：界面层堆积非常严重－扩
散不够快，远端保持C0 S相：保持C0
后 期：—— 终端瞬态区 L相：浓度较大--界面层扩散受阻 --浓度再次增加，且幅度很大 S 相：结晶出高浓度溶质
3． 正常凝固溶质分布综合比较
浓度
C0
快速
中速
平衡 缓慢
S/L 界面处溶质分布： k0 < 1
缓慢凝固： CS
浓度
S
L/S界面
k0C1
k0C2
S相：忽略扩散的作用 —— 溶质不混合 L相：搅拌、对流、扩散— 溶质完全混合
开始－中前期：
溶质原子富集在L相中 ——L相
L
较多—— L相浓度变化不大——
C1
S相浓度维持较低水平
距离 中期－中后期：
C2
L相富集程度加大—— L相量减
少—— L相浓度增加—— S相中
不得不结晶出较多的溶质—— S
（2） 固相扩散难度 > 液相扩散
α1 α'2 α2
L1
L'1
L2
α3
L'2
L3
α'3
α4
L'3
α'4
L'4
难度 —— 固相平均成分线 偏离固相线程度 > 液相平 均成分线偏离液相线程度
L4
（3） 固相难扩散 —— 先后结晶
部分保持各自溶质浓度 ——
Ni
Cu
偏析 —— 影响性能 ——
（解决途径）均匀化退火
第二节 二元匀晶相图
匀晶转变：
由液相直接结晶出单相固溶体的转变（相变）
匀晶相图：
体系只具有匀晶转变的
一、相图分析
二元合金相图的基本类型和分析
“二元合金相图的基本类型和分析”部分结束！ 请转入：
“铁碳合金相图及应用”
LE 183。C C B
⑤ 固溶线：CF线及DG线分别为α固溶体和β固溶体的固溶线。
2．合金的结晶过程及组织 合金Ⅰ、合金Ⅱ、合金Ⅲ、合金Ⅳ的结晶过程及其组织如
图所示。
分析：
① 相组成
② 组织组成物
③ 属这类相图的合金还 有Pb-Sn、Al-Si、AlSn、Al-Cu、Pb-Sb、 Ag-Cu等。
4）在两相平衡区，可应用杠杆定律求出各相的相对量。
2．相图的应用
① 相图反映了合金的成分与组成相之间的关系，而组成相的本质 及其相对含量与合金力学性能、物理化学性能密切相关。
② 相图反映了合金的结晶特性。 ③ 在某种程度上可根据相图来判断合金力学性能、物理化学性能
及合金的铸造性能。如图所示。
④ 相图也是制定热处理和热变形工艺的重要依据。
干个简单相图所组成。
五、具有固态转变的二元合金相图
1．固态转变主要有：
① 固溶体的脱溶转变； ② 共析转变； ③ 包析转变； ④ 固溶体的同素异晶转变； ⑤ 有序—无序转变等。
2．固溶体的脱溶转变
固溶体因溶解度变化而发生的脱溶转变。如图所示。
3．共析转变
由图分析可知：
① 从固相中同时析出两种不同新相的反应称为共析反应。 ② 共析反应的产物为共析物。 ③ 由于共析反应在固态进行，所以共析组织比共晶组织要细
二、二元共晶相图
二组元在液态无限互溶，而在固态仅有限互溶且发 生共晶反应。 以Pb-Sn合金为例。
1．相图分析 ① 相及相区：有α、β、L三种相； 由三个单相区、三个双相区组成相图。 ② AEB为液相线 , ACEDB为固相线。
7.3.1二元匀晶相图
通常将固溶体中析出另一种固相的过程称 为脱溶转变，脱溶转变的产物一般称为次 生相或二次相。次生相β固溶体用βⅡ表示， 以区别从液相中直接凝固出的β固溶体。由 于次生相是从固相中析出的，而原子在固 相中的扩散速度慢，所以次生相一般都较 细小，并分布在晶界上或固溶体的晶粒内 部。由上述分析可知该合金在室温时的组 织为α+βⅡ，见图7.27。图中黑色基体为α相， 白色颗粒为βⅡ相。图7.28为该合金的平衡 凝固过程示意图。
2．共晶合金（61.9%Sn-Pb）
由相图可以看出共晶合金②从液态缓慢冷却到tE 温度时, 在恒温下从液相中同时结晶出两个成分不 同的固相,即发生共晶转变LE→αM+βN (L61.9%→α19%+β97.5% )由于发生共晶转变时是 三相平衡,所以可以用相律证明它是在恒温下进行 的。共晶转变在恒温下一直进到液相完全消失,继 续冷却αM 和βN分别析出次生相βⅡ 和αⅡ,成分分 别沿着MF和NG线变化。 由于析出的αⅡ和βⅡ与 共晶体中的α和β常常混合在一起,所以在显微镜下 很难分辨。因此该合金在室温时的组织一般认为 是由(α+β) 共晶体组成。
图7.29 铅锡共晶合金的显微组织 200×
图7.30 共晶合金凝固过程示意图
合金的显微组织： 是指在金相显微镜下能够 观察到的组成部分。 共晶合金的显微组织是由α和β两相组成,所以 它的相组成物为α和β两相。 相组成物：是指组成合金显微组织的基本相。 组织组成物： 是指合金在结晶过程中,形成的 具有特定形态特征的独立组成部分。 如共晶合金的组织组成物为100%的（ α + β ） 共晶体。 而相组成物的相对量可用杠杆定律计算 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
一、相图分析
1、相图的坐标
纵坐标是温度坐标，横坐 标是成分坐标：左端线是表 示100％的Cu，右端线表示 100％的Ni，从左至右Ni的 含量增加(直至100％)、Cu 的含量减少(直至0％)。
2、相图中的线和区
相图中有二条曲线，将整个图形分成三个区域。
实用文档
2
上面一条曲线称为液相线(Liquid line)，液相线以上的区域 称为液相区(Liquid-phase field)，温度高于液相线时合金的状
也称为杠杆定律。
实用文档
5
三、典型合金冷却过程分析
各种成分的Cu-Ni合金都属于匀晶合金。下面以Cu-53%Ni 合金为例，分别对合金结晶过程中液、固二相的成分变化规律， 二相相对量的计算和微观组织的形成进行分析讨论。
1、液-固两相成分的变化
合金从液态开始缓慢冷却，当温度 降低到液相线(1点)时，结晶开始。此
设合金的平均成分为x，合金
的总量为Q，在温度T1时液、 固两相平衡，液相的成分为xL、 质量为QL，固相的成分为xS、 质量为QS。则有：
Q QxIQm LQ N LaQoSxgLeQSxS
实用文档
4
上式可变换为：
QL xS x QS x xL
还可以变换为：
或 Q L x x L Q S x S x
QL xS x Q xS xL 或 QS xL x Q xS xL
合金的平均成分点看作杠杆的支点o； T1温度水平线与液、固相线的交点a、 b为杠杆的两个端点；液、固两相的
质(重)量为作用在端点上的力。
为了计算简便，一般取合金总量Q =1。
因上述结果与物理学中的杠杆定律的表达式相似，所以这里
采用均匀化热处理(Homogenizing heat treatment)可以 消除枝晶偏析。
匀晶合金的 非平衡组织
实用文档
9
实用文档
10
No
所以 QS =1-QL = 1-38% = 62%Image
四、匀晶合金的非平衡结晶
匀晶合金在平衡条件下结晶，冷却速度
极其缓慢，先后结晶的固相虽然成分不
同，但是有足够的时间进行均匀化扩散。
所以，室温下的组织是均匀的固溶体， 匀晶合金平衡组织示意图
在光学显微镜下观察，与纯金属十分相
似。
实用文档
8
但是，在实际生产中合金的冷却速度很快，远远达不到平衡 的条件。因此，固、液二相中的扩散来不及充分进行，先后结 晶出来的固相中较大的成分差别被保留下来。这种成分差别的 存在，还造成结晶时固相以树枝状形态生长。因此，这种成分 上的不均匀性被称为“树枝状偏析”或枝晶偏析。
温度继续下降，一直冷却到室温，合金在固态没有任何转变 发生。仔细观察动画。
2、相的相对量计算
1300˚C时，液相的相对量QL/Q（可以取合金总量Q =1）：
QL 58530.3838% Q 5845
实用文档
7
固相的相对量QQ 5845
因为 QL + QS = Q，取Q =1
二元匀晶相图
二元匀晶(Isomorphous)相图是二元合金相图中图形最简单 的相图。
具有匀晶相图的二元合金系统有Cu-Ni, Fe-Cr, Ag-Au, NbTi, Cr-Mo, W-Mo等。
右图所示Cu-Ni相图是最常 见的二元匀晶相图，以此相图 为例进行讨论，其它匀晶相图 与此类似。
实用文档
1
固相区。
因此，能够形成匀晶合金系的两种组元必须具有相同的晶体
结构，相同的原子价，原子半径接近(相差不超过15％)，相互
不形成化合物。
实用文档
3
二、杠杆定律
杠杆定律只适应于平衡相图的二相区。
二元合金在平衡状态下两相共存，如结晶时，可以利用杠杆 定律(Lever rule)计算出某一温度下两相的相对量。
态为液相(L)；
下面的一条曲线是固相线(Solid line)，固相线以下的区域为 固相区(Solid-phase field)，温度低于固相线时合金为固相(α)。
两条曲线之间的区域是液、固两相共存的二相区(L + α)。
3、匀晶相图的特点
二组元在液态和固态都能够完全相互溶解，所有成分(Ni:
0~100%)的合金在固态只有一种晶体结构，相图中只有一个
时结晶出来的极少量固相成分为S1，
液相的成分基本未变。随着温度降低， 固相逐渐增多，液相不断减少。
液相的成分沿液相线变化，固相的 成分沿固相线变化。
实用文档
动画
6
温度降低到1300℃时，液相成分为45%Ni, 固相成分为
58%Ni。当温度降低到2点，即固相线温度时，液相的成分为L2，
固相的成分为合金的平均成分(53%Ni)。此时液相实际上已经 不存在了，都已结晶成为固相。