高中一年级竞赛练习(2)
数学竞赛试题高一及答案

数学竞赛试题高一及答案一、选择题(每题5分,共20分)1. 若函数f(x) = 2x^2 + 3x + 1的图像关于直线x = -1/2对称,则下列哪个函数的图像也关于直线x = -1/2对称?A. g(x) = x^2 + 2x + 3B. h(x) = -x^2 + 2x - 3C. i(x) = x^2 - 2x + 3D. j(x) = -x^2 - 2x - 3答案:B2. 已知集合A = {1, 2, 3},集合B = {2, 3, 4},则A∪B等于:A. {1, 2, 3, 4}B. {1, 2, 3}C. {2, 3}D. {1, 3, 4}答案:A3. 若方程x^2 - 5x + 6 = 0的两个根为α和β,则α + β的值为:A. 1B. 2C. 3D. 5答案:C4. 函数y = |x - 2| + 3的图像与x轴交点的个数是:A. 0B. 1C. 2D. 3答案:B二、填空题(每题5分,共20分)1. 已知等差数列的前三项依次为2, 5, 8,则该数列的第五项为________。
答案:112. 圆的方程为x^2 + y^2 - 6x - 8y + 25 = 0,则圆心坐标为________。
答案:(3, 4)3. 函数y = sin(x)在区间[0, π]上的最大值为________。
答案:14. 已知三角形的三边长分别为3, 4, 5,则该三角形的面积为________。
答案:6三、解答题(每题15分,共30分)1. 证明:若一个三角形的两边长分别为a和b,且满足a^2 + b^2 =c^2(c为第三边长),则该三角形为直角三角形。
证明:根据勾股定理,若三角形的两边长为a和b,且满足a^2 + b^2 = c^2,则第三边c所对的角θ为直角,即θ = 90°。
因此,该三角形为直角三角形。
2. 解方程:2x^2 - 3x - 2 = 0。
解:首先,我们计算判别式Δ = b^2 - 4ac = (-3)^2 - 4*2*(-2) = 9 + 16 = 25。
高一数学竞赛试题及答案

高一数学竞赛试题及答案一、选择题(每题5分,共50分)1. 已知函数\( f(x) = x^2 - 4x + 3 \),求\( f(1) \)的值。
A. -2B. -1C. 0D. 12. 圆的半径为5,圆心到直线的距离为3,求圆与直线的位置关系。
A. 相切B. 相交C. 相离D. 内切3. 集合\( A = \{1, 2, 3\} \),\( B = \{2, 3, 4\} \),求\( A \cup B \)。
A. \( \{1, 2, 3, 4\} \)B. \( \{1, 2, 3\} \)C. \( \{2, 3, 4\} \)D. \( \{1, 4\} \)4. 已知等差数列的第1项为2,公差为3,求第5项的值。
A. 14B. 17C. 20D. 235. 已知正弦函数\( y = \sin x \)的周期为2π,求\( y = \sin 2x\)的周期。
A. πB. 2πC. 4πD. 8π6. 已知三角形ABC的三边长分别为3, 4, 5,求三角形ABC的面积。
A. 6B. 9C. 12D. 157. 函数\( g(x) = \frac{1}{x} \)在区间(1, 2)上的单调性是?A. 单调递增B. 单调递减C. 先减后增D. 先增后减8. 已知\( a^2 + b^2 = 13 \),\( a + b = 5 \),求ab的值。
A. 12B. 10C. 8D. 69. 已知\( \cos x = \frac{3}{5} \),\( \sin x \)的值在区间[-1,1]内,求\( \sin x \)的值。
A. \( -\frac{4}{5} \)B. \( \frac{4}{5} \)C. \( -\frac{3}{5} \)D. \( \frac{3}{5} \)10. 已知\( \log_2 8 = 3 \),求\( \log_{16} 8 \)的值。
A. \( \frac{3}{4} \)B. \( \frac{1}{2} \)C. \( \frac{3}{2} \)D. \( \frac{4}{3} \)二、填空题(每题5分,共30分)11. 已知函数\( h(x) = x^3 - 6x^2 + 11x - 6 \),求\( h(2) \)的值。
高中一年级 第2试

3×420+2,4×420+2,即共有5个符合题意的自然数,其中最大的自然数是4×420+2=1682.23.当b=0时,|x2-1|=110x,此时要求x≥0,去掉绝对值,解一元二次方程得x=-1±槡40120或x=1 ±槡40120,舍去两负根,因此A中只有2个元素.当b=1时,|x2-1|=110x+1,此时要求x≥-10,去掉绝对值,解一元二次方程得x=0,-110或1 ±槡80120.它们都满足x≥-10,因此A中有4个元素.24.an={2,4,8,16,32,64,128,256,512,…},若{an}中的元素在{cn}中,则必须满足减2以后能被3整除,则只有8,32,128,512,…满足条件,即23,25,27,29,…故cn=22n+1,即公比q=22(n+1)+122n+1=22n+322n+1=4,所以Sn=8(1-4n)1-4=83(4n-1).25.第n组中有2n-1个数对,则前n组共有1+3+5+…+(2n-1)=n2个数对.因为442=1936<2005<452=2025,所以2005在第45组.因为前44组共有1936个数对,且2005-1936=69,所以第2005个数对是第45组中的第69个数对.观察规律可知,由于45为奇数,所以第一个数对为(0,44),数对中的第一个数逐步增加到44,即第45个数对为(44,44),然后第二个数44逐步减去1,所以第45组中第69个数对是(44,20).高中一年级第2试一、选择题1.已知等差数列{an}中(an∈Z,n∈N*),a1=5,a2=b,则an≠0的充要条件为()(A)b≠0.(B)b≠4.(C)b≠0或b≠4.(D)b≠0且b≠4.2.对1949°,1966°,2005°,2008°依次求余弦,则余弦值最大及最小的角依次是()(A)1949°,1966°.(B)1966°,1949°.(C)2008°,1966°.(D)2005°,2008°.3.下列函数中,值域为R+的是()(A)y=2-|x-1|.(B)y=3x+1(x>0).(C)y=x2+x+2.(D)y=1x2.4.设集合M=x x=k2+14,k∈Z{},N=x x=k4+18,k∈Z{},P=x x=k8+14,k∈Z{},则下面的结论中正确的是()(A)M∪N=P.(B)M∩N=P.(C)M∩P=P.(D)M∩N=M.5.偶函数f(x)(x∈R)满足:f(-4)=f(1)=0,在区间[0,3]与[3,+∞)上分别递减和递增,则不等式x3 f(x)<0的解集为()(A)(-∞,-4)∪(4,+∞).(B)(-4,-1)∪(1,4).(C)(-∞,-4)∪(-1,0).(D)(-∞,-4)∪(-1,0)∪(1,4).·14·6.如果f(x)=max{sinx,cosx}(x∈R),则下面命题正确的是()(A)函数f(x)的值域是[-1,1].(B)当且仅当x=2kπ+π2(k∈Z)时,f(x)取得最大值.(C)函数f(x)的最小正周期是π.(D)当且仅当2kπ+π<x<2kπ+3π2(k∈Z)时,f(x)<0.7.Four people,A,B,Cand Dare accusedin a trial.It is known that(1)if Ais guilty,then Bis guilty;(2)if Bis guilty,then Cis guilty or Aisnot guilty;(3)if Dis not guilty,then Ais guilty andCis not guilty;(4)if Dis guilty,then Ais guilty.How many of the accused are guiltyAnswer:()(A)2.(B)3.(C)4.(D)Insufficient information to determine.8.已知f1(x)=x+1,f2(x)=2x,f3(x)=-3x+5,F(x)=min{f1(x),f2(x),f3(x)},则F(x)的最大值为()(A)1.(B)2.(C)4.(D)8.9.满足a2-3b-9=0(a,b∈Z),且|b|≤1000的数组(a,b)的个数是()(A)57.(B)54.(C)37.(D)109.10.有“黄河源头第一县”之称的青海省果洛藏族自治州玛多县,被称作“千湖之县”.受连续干旱影响,该县有数百个湖泊相继干涸,且鼠害十分猖獗,草原在加速退化,每年因鼠害造成的退化面积达20%.按这样的退化速度,自2005年起,经过()草原退化总面积将开始超过2005年草原总面积的一半.(A)3年.(B)4年.(C)5年.(D)6年.二、填空题11.设集合A={1,2,3,4,5,6},则从A到A的映射f有个,其中,满足f(A)≥a的映射有个.12.若f(x)=x+1,1,烅烄烆x≥0,x<0.则f(cos2)=;当x∈[0,2π)且满足cosx+f(sinx)>1的x的集合为.13.一个三位数与它的各位数字和的比值为p(例如对于三位数462,p=4624+6+2=772),若三位数的各位数字都不为0,则当p取得最小值时,此三位数是;当p取得最大值时,此三位数是.14.函数y=3x2-6x+2 2x-x槡2+4的最大值为,最小值为.15.如果△ABC边上的点的坐标(x,y)在映射f:(x,y)→(2x+2,2y-5)的作用下的像的集合所对应的图形是△A′B′C′,已知△ABC的面积为6,则△A′B′C′的面积等于.16.Let aand b be the two real roots ofthe quadratic equation x2-(k-1)x+k2+3k+4=0,where k is some real num ber.Thelargest possible value of a2+b2 is.17.某校高一新生共有784人,每班分配56人.方法是:将每人的入学成绩从高分到低分依次编号(成绩相同的学生按姓氏笔画的顺序),然后按S形顺序编班.例如:若有8个班,按编号1至8号分别编在1至8班,9至16号分别编在8至1班,17至24号分别编在1至8班…….该校高一新生中编号为300(每号只对应1人)的同学编在班.18.函数y=x2(-2≤x≤2)与函数y=x+m的图象恰有1个公共点在y轴的右侧,则·24·m的取值范围是.19.数列{an}的前三项依次为5,55,555,但第4项不是5555,请写出一个适合题意的通项公式:an=.20.集合M={x|x=9n,n=0,1,2,…,2005},已知92005是1914位数,则在M中最高位是9的数共有个.图1三、解答题21.如图1所示,在凸四边形ABCD中,AB=5,BC=CD=DA=2,∠A=θ.(1)求BD的长(用θ表示);(2)设△ABD的面积为S1,△BCD的面积为S2,f(θ)=S21+S22,求函数f(θ)的值域.22.密码员王超设计了一种给自然数编码的方法:(1)先将自然数表示成五进制数(逢五进一);(2)再将五进制中的5个数码与集合{V,W,X,Y,Z}中的元素建立一个一一对应关系.后来,他发现三个递增的相邻的十进制自然数被编成VYZ,VYX,VVW.求被编成VWXYZ的数所对应的十进制数.23.已知函数f(x)=x2+kx+1x2+x+1.(1)当k=2时,求f(x)的值域;(2)若存在实数a,b,c,使f(a)+f(b)<f(c),求实数k的取值范围.参考答案一、选择题1.等差数列公差d=b-5.如果等差数列不存在值为零的项,那么对于任意非零自然数n,不等式5+(n-1)(b-5)≠0恒成立,即n≠55-b+1 N*,所以5-b≠1且5-b≠5,即b≠4,且b≠0.反之,可证当b≠4且b≠0时,55-b+1N*,即对于任意非零自然数n,当b≠4且b≠0时,不等式5+(n-1)(b-5)≠0恒成立.所以这个数列中不存在零项的充要条件为b≠0且b≠4.故选(D).2.cos1949°=cos149°,cos1966°=cos166°,cos2005°=cos205°=cos155°,cos2008°=cos208°=cos152°,在区间(90°,180°)内,余弦函数是减函数,故cos149°>cos152°>cos155°>cos166°,故选(A).3.y=2-|x-1|的值域是(0,1];y=3x+1(x>0)的值域是(1,+∞);y=x2+x+2的值域是74,+∞[).故选(D).4.因为M=x|x=k2+14,k∈Z{}=x|x=2(2k+1)8,k∈Z{},N=x|x=k4+18,k∈Z{}=x|x=2k+18,k∈Z{},P=x|x=k8+14,k∈Z{}=x|x=k+28,k∈Z{},所以M∪N≠P,M∩N≠P,M∩N= ,·34·故排除(A),(B),(D),又M P,所以M∩P=M.故选(C).5.由偶函数性质及单调性,知图2f(-4)=f(-1)=f(1)=f(4)=0,画出f(x)对应的大致图象,如图2所示.当x<-4或-1<x<1或x>4时,f(x)>0;当-4<x<-1或1<x<4时,f(x)<0.当x<0时,x3<0;当x>0时,x3>0.所以x3 f(x)<0的解集为{x|x<-4或-1<x<0或1<x<4}.故选(D).图36.作出函数f(x)的图象,如图3所示,只有(D)是正确的.7.从D入手,分有罪和无罪两种情况讨论:假设D无罪,由(3)知,A犯罪且C无罪;由(1)知,B犯罪.由(2)知,A无罪或C犯罪,与A犯罪且C无罪矛盾,故假设D无罪不成立,即D犯罪.由(4)知,A犯罪;由(1)知,B犯罪;由(2)知,C也犯罪.因此犯罪的共有4人.故选(C).8.如图4所示,作出f1(x),f2(x),f3(x),易得F(x)的图象.由F(x)的图象,可知F(x)的最大值为2.故选(B).图49.由a2-3b-9=0,得b=a23-3.①由|b|≤1000,有-1000≤a23-3≤1000,0≤a2≤3009,所以-槡3009≤a≤槡3009.因为a是整数,所以-54≤a≤54.②因为b是整数,即a23-3是整数,所以a2是3的倍数,即a·a3是整数,所以a是3的倍数.结合②知,a的值为-54,-51,-48,…,51,54共37个.故选(C).10.设2005年的草原总面积为x,设经过m年后(即2005+m年),草原的面积退化超过x2,即15x+15×45x()+15×45()2x+…+15×45()m-1x>x2,即45()m<12.当m=3时,45()3=64125>12;·44·当m=4时,45()4=256625<12.所以最多经过4年,草原退化总面积就超过2005年草原总面积的一半.故选(B).二、填空题11.(1)如图5所示,其它元素也如此,因此,从A到A的映射f共有6×6×6×6×6×6=66(个).图5图6(2)如图6所示,其它元素也如此,因此,满足f(A)≥a的映射共有1×2×3×4×5×6=720(个).12.因为cos2<0,所以f(cos2)=1,因此,原不等式等价于sinx≥0,cosx+sinx+1>1,烅烄烆或sinx<0,cosx+1>1,烅烄烆解得0≤x<3π4或3π2<x<2π.故满足条件的x的集合为0,3π4[)∪3π2,2π().13.设此三位数为abc,则p=100a+10b+ca+b+c.(1)先固定b,c,则p=100(a+b+c)-90b-99ca+b+c=100-99b+99ca+b+c.因为b,c固定,所以a越小时,p越小.所以当a=1时,p才可能取到最小值.(2)再固定c,则p=100+10b+c1+b+c=10(b+c+1)-9c+901+b+c=10+90-9c1+b+c.因为90-9c恒大于零,所以b越大,p越小.从而知当b=9时,p才可能取到最小值.(3)p=100+90+c1+9+c=c+10+180c+10=1+180c+10.因为c越大,p越小,所以当c=9时,p才能取到最小值,故可知使p取到最小值的三位数为199.同理,使p取到最大值的三位数为911.14.令t=2x-x槡2=-(x-1)2 +槡1,0≤t≤1,则y=3(x2-2x)+2 2x-x槡2+4=-3t 2+2t+4=-3 t-13()2+133,由0≤t≤1,得3≤y≤133.故y的最大值和最小值分别为133和3.15.作图可知△ABC∽△A′B′C′,且ABA′B′=12,又由三角形相似性质,得·54·S△A′B′C′=4S△ABC=24.16.由题意知x2-(k-1)x+(k2+3k+4)=0有两实数根,所以Δ=(k-1)2-4(k2+3k+4)≥0,解得-3≤k≤-53.由韦达定理得a+b=k-1,ab=k2+3k+4,a2+b2=(a+b)2-2ab=-k2-8k-7=-(k+4)2+9,由-3≤k≤-53,得a2+b2的最大值为8.17.因为784÷56=14,所以共可分成14个班.又300÷(14×2)=10……20,20-14=6,14-6+1=9,所以编号是300号的同学应分在9班.18.当直线与抛物线相切时,即x2-x-m=0有重根,可得m=-14;当y=x+m的图象分别过点(2,4)及点(0,0)时,它与y=x2(-2≤x≤2)的图象都恰有1个在y轴右侧的交点,此时m分别为0和2;当m在区间(0,2)内变化时,也满足题意.所以m的取值范围是[0,2]∪-14{}.19.an=59(10n-1)+(n-1)(n-2)·(n-3).(答案不唯一)20.将M中元素从小到大排列,若从第m个与第m+1个数的位数没有增加,则第m+1个数的最高位必是9;反之,最高位是9的数与前一个数的位数一定相同,所以M中最高位是9的数共有2006-1914=92(个).三、解答题21.(1)作DE⊥AB于E(如图7所示),图7则DE=2sinθ,AE=2cosθ,BE=5-2cosθ,BD=DE2+EB槡2=4sin2θ+25-20cosθ+4cos2槡θ=29-20cos槡θ.(2)S1=12AB·DE=5sinθ,取BD中点M,连接CM(如图7所示),由DC=CB,得CM⊥BD,CM2=DC2-DM2=4-14(29-20cosθ)=5cosθ-134,S22=12BD·CM()2=14(29-20cosθ)5cosθ-134()=-25cos2θ+1052cosθ-37716,于是f(θ)=S21+S22=25sin2θ-25cos2θ+1052cosθ-37716=-50cos2θ+1052cosθ+2316=-50cosθ-2140()2+48732.当D,C,B共线时,由余弦定理可得cosθ=1320;当A,D,C共线时,同理可得cosθ=3740.因为ABCD是凸四边形,·64·所以cosθ的取值区间为1320,3740().令cosθ=t,则f(θ)=-50 t-2140()2+48732=g(t).因为t∈1320,3740(),所以g(t)在1320,3740()上单调递减,又g1320()=23116,g3740()=23132,所以f(θ)的值域为23132,23116().22.由题中给出的对应关系,有V,W,X,Y,Z∈{0,1,2,3,4}.由于三个递增的相邻的自然数被编成VYZ,VYX,VVW,所以25V+5Y+Z=25V+5Y+X-1,25V+5Y+X=25V+5V+W-1,烅烄烆即Z=X-1,5(V-Y)=X-W+1.烅烄烆①②因为被编成VYX,VVW的十进制的自然数是递增的,所以V>Y.由②知5|X-W+1,且X-W>0,所以X-W+1=5,V-Y=1,即X=4+W≥4,但X≤4,所以X=4,W=0,Z=3,于是V,Y∈{1,2},而V-Y=1,所以V=2,Y=1.因此,VWXYZ所对应的十进制数是2×54+0×53+4×52+1×5+3=1358.23.(1)即求y=x2+2x+1x2+x+1的值域,易得(x2+x+1)y=x2+2x+1,所以(y-1)x2+(y-2)x+(y-1)=0.当y=1时,-x=0,即x=0;当y≠1时,Δ=(y-2)2-4(y-1)2≥0,即y(3y-4)≤0,解得0≤y≤43.综上可知y=x2+2x+1x2+x+1的值域为0,43[].(2)由y=x2+kx+1x2+x+1可得(x2+x+1)y=x2+kx+1,即(y-1)x2+(y-k)x+(y-1)=0.当k=1时,y≡1,所以不存在灾数a,b,c使f(a)+f(b)<f(c);当k≠1时,若y=1,则x=0;若y≠1,则Δ=(y-k)2-4(y-1)2≥0,即3y2+(2k-8)y+(4-k2)≤0,解得4-k-2|k-1|3≤y<1或1<y≤4-k+2|k-1|3.综上可知y∈4-k-2|k-1|3,4-k+2|k-1|3[].假设对任意的实数a,b,c都有f(a)+f(b)≥f(c),则有2(4-k-2|k-1|)3≥4-k+2|k-1|3,解得k∈25,107[].所以若存在实数a,b,c使得f(a)+f(b)<f(c),则k∈-∞,25()∪107,+∞().·74·。
高一竞赛赛试题和答案

高一竞赛英语试题(满分100分)第一部分:语言知识应用(共两节,满分45分)第一节:完形填空(共15小题;每小题2分,满分30分)阅读下列短文,掌握其大意,然后从1—15各题所给的(A, B, C和D)中,选出最佳选项。
Water costs money.In some places water is hard 1 .What 2 when a townhas these problems?A small town in California found a happy 3.Very little rain ever fell there.The town had no water of its own.The water it used was 4 froma river 300 miles away.As more people 5 live in the town, 6 water was needed.Now water7 to be brought in from 600 miles away.All these cost 8 money.The town 9 a plan.It found a way to clean its “dirty” water.Once the cleaned water was reused10 many ways.Five man-made lakes were built.Here people could swim and fish and go11 .They could have picnics in their new parks.Farmers had more water 12 their crops.New factories can be built,now that they have the promise of 13 .In most places,water is used and thrown 14 .The town that saved 15 waterhas saved the town!1.A.supplying B.getting C.to get D.to supply2.A.happens B.happening C is happened D.happened3.A.key B.answer C answering D.way4.A.fetch B.take C.brought in D.guided5.A.come to B.came to C.coming to D.came for6.A.many B.plenty of C.more D.many more7.A.has B.had C.must D.needed8.A.many B.a few C.a great many D.a lot of9.A.put B.made C.supply D.noticed10.A.for B.by C.at D.in11.A.boating B.to boat C.to boating D.on boating12.A.as B.with C.for D.to13.A.water enough B.enough waterC. crops enough D.enough crops14.A.off B.of C.away D.out of15.A.it’s B.its C.one’s D.his第二节:语法填空(共10小题,每小题1.5分,满分15分)阅读下面短文,按照句子结构的语法性和上下文连贯的要求,在空格处填入一个适当的词或使用括号中词语的正确形式填空。
高一数学竞赛试题及答案

高一数学竞赛试题及答案一、选择题(每题5分,共30分)1. 若a,b,c是三角形的三边长,且满足a² + b² = c²,那么这个三角形是:A. 锐角三角形B. 直角三角形C. 钝角三角形D. 不能确定2. 函数f(x) = 2x³ - 3x² + 1在区间[-1,2]上的最大值是:A. 1B. 7C. 9D. 无法确定3. 已知集合A = {1, 2, 3},B = {2, 3, 4},求A∪B的元素个数:A. 3B. 4C. 5D. 64. 等差数列的首项a₁ = 3,公差d = 2,第10项a₁₀的值是:A. 23B. 25C. 27D. 295. 圆的方程为(x - 2)² + (y - 3)² = 9,圆心到直线x + 2y - 7= 0的距离是:A. 2B. 3C. 4D. 56. 已知函数y = |x| + 1的图像与直线y = kx平行,那么k的值是:A. 1B. -1C. 0D. 无法确定二、填空题(每题4分,共20分)7. 若二次函数y = ax² + bx + c的顶点坐标为(-1, -4),则a =_______。
8. 已知等比数列的首项为2,公比为3,第5项的值为 _______。
9. 一个正六边形的内角和为 _______。
10. 若直线y = 2x + b与曲线y = x² - 3x相切,则b = _______。
11. 圆的方程为x² + y² = 25,圆上一点P(4,3)到圆心的距离是_______。
三、解答题(每题25分,共50分)12. 已知直线l₁:2x - 3y + 6 = 0与直线l₂:x + y - 2 = 0相交于点M,求点M的坐标。
13. 已知函数f(x) = x³ - 3x + 2,求证:对于任意的x > 0,都有f(x) > x。
高一年级数学竞赛试题及答案
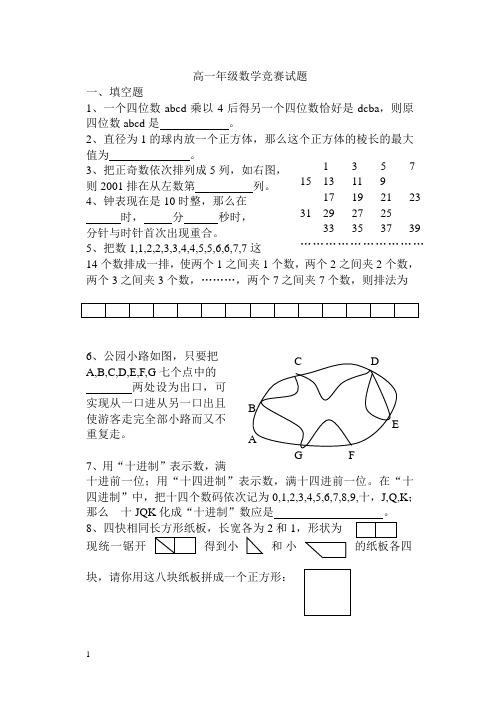
1 3 5 7 15 13 11 9 17 19 21 23 31 29 27 25 33 35 37 39 ……………………………高一年级数学竞赛试题一、填空题1、一个四位数abcd 乘以4后得另一个四位数恰好是dcba ,则原四位数abcd 是 。
2、直径为1的球内放一个正方体,那么这个正方体的棱长的最大值为 。
3、把正奇数依次排列成5列,如右图, 则2001排在从左数第 列。
4、钟表现在是10时整,那么在 时, 分 秒时, 分针与时针首次出现重合。
5、把数1,1,2,2,3,3,4,4,5,5,6,6,7,7这 14个数排成一排,使两个1之间夹1个数,两个2之间夹2个数,两个3之间夹3个数,………,两个7之间夹7个数,则排法为6、公园小路如图,只要把 A,B,C,D,E,F,G 七个点中的 两处设为出口,可实现从一口进从另一口出且使游客走完全部小路而又不重复走。
7、用“十进制”表示数,满十进前一位;用“十四进制”表示数,满十四进前一位。
在“十四进制”中,把十四个数码依次记为0,1,2,3,4,5,6,7,8,9,十,J,Q,K ;那么 十JQK 化成“十进制”数应是 。
8、四快相同长方形纸板,长宽各为2和1,形状为现统一锯开 得到小 和小块,请你用这八块纸板拼成一个正方形:班级学号姓名成绩二、解答题:9、证明:整数被表示成两个整数平方和的充要条件是该整数的2倍也能表示成两个整数的平方和。
10、用S表示原地不动,T表示向左转,R表示向右转,L表示向后转。
集合X={S,T,R,L}中的元素有一种运算“+”表示“紧接着”的意思。
(例如T+S表示向左转紧接着向后转,当然运算结果为向右转,因而有T+L=R)。
若集合X中某元素E,满足E+E=E,则E叫单位,若某两个元素A和B满足A+B=E,则A,B叫做互为逆元。
①求集合X中的单位。
②求集合X中的每个元素的逆元。
11、有2001个小球堆在一起,二人进行轮流拿球游戏,每次可以拿一个、二个或三个球,不能多拿也不能不拿,至拿完全部小球游戏结束。
寒假高中一年级竞赛班校本第二版
冬季班高一物理竞赛班专项训练(第1讲)曲线运动【知识要点】1、曲线运动中速度的方向是时刻改变的,质点在某一点(或某一时刻)的速度的方向是在曲线的这一点的切线方向.2、物体做直线运动的条件:物体所受合外力为零或所受合外力方向和物体的运动方向在同一直线上.3、物体做曲线运动的条件合外力方向与速度方向不在同一直线上.4、曲线运动的特点:曲线运动一定是变速运动;质点的路程总大于位移大小;质点作曲线运动时,受到合外力和相应的速度一定不为零,并总指向曲线侧. [注意]:①做曲线运动的物体所受合外力不一定变化。
②两个分运动是匀速直线运动,则合运动是匀速直线运动或静止. ③已知两个分运动都是匀加(互成一定角度,不共线)则合运动是:1合合与v a 共线是匀加直线运动;2合合与v a 不共线是匀变曲线运动.④一个分运动是匀速,另一个是匀加(初速度为零),则合运动:1合合与v a 共线⎪⎩⎪⎨⎧-=+=atv v at v v 00合合反向,同向, 2合合与v a 不共线:匀变速曲线运动.【例题精讲】【例1】画出图中沿曲线ABCDE 运动的物体在A 、B 、C 、D 、E 各点的速度方向.略【例2】某质点在恒力 F 作用下从A 点沿图1中曲线运动到 B 点,到达B 点后,质点受到的力大小仍为F ,但方向相反,则它从B 点开始的运动轨迹可能是图中的[ ]A.曲线aB.曲线bC.曲线CD.以上三条曲线都不可能 答案:A 【夯实双基】1.关于曲线运动,下列说法中正确的是( ).(A)物体作曲线运动时,它的速度可能保持不变(B)物体只有受到一个方向不断改变的力的作用,才可能作曲线运动(C)所有作曲线运动的物体,所受合外力方向与速度方向肯定不在一条直线上(D)所有作曲线运动的物体,加速度方向与所受合外力方向始终一致答案:CD2.物体受到几个力的作用而做匀速直线运动,如果只撤掉其中的一个力,其它力保持不变,它可能做[ ]A.匀速直线运动B.匀加速直线运动C.匀减速直线运动D.曲线运动2、BCD3.(高考科研题)一质点在某段时间做曲线运动,则在这段时间( ) A.速度一定不断改变,加速度也一定不断改变;B.速度一定不断改变,加速度可以不变;C.速度可以不变,加速度一定不断改变;D.速度可以不变,加速度也可以不变。
高一数学竞赛试题及答案
高一数学竞赛试题及答案一、选择题(每题5分,共20分)1. 下列哪个数是无理数?A. 3.1415926B. πC. √2D. 0.33333(无限循环小数)答案:B2. 已知函数f(x) = 2x^2 + 3x - 5,求f(-2)的值。
A. -15B. -7C. -3D. 1答案:B3. 一个圆的半径为r,圆心到直线的距离为d,如果d < r,那么该直线与圆的位置关系是:A. 相切B. 相交C. 相离D. 内含答案:B4. 如果一个等差数列的前三项和为9,第四项为5,求该数列的首项a1。
A. 1B. 2C. 3D. 4答案:B二、填空题(每题4分,共12分)5. 一个长方体的长、宽、高分别是a、b、c,其体积的公式是______。
答案:abc6. 若sinθ = 1/3,且θ在第一象限,求cosθ的值。
答案:2√2/37. 已知等比数列的前n项和公式为S_n = a1(1 - r^n) / (1 - r),其中a1是首项,r是公比。
如果S_5 = 31,a1 = 1,求r的值。
答案:2三、解答题(每题18分,共54分)8. 证明:对于任意正整数n,n^5 - n 能被30整除。
证明:由题意,我们需要证明n^5 - n 能被30整除。
首先,我们知道任何正整数n都能被1、2、3、5中的至少一个整除。
设n = 2a + b,其中a和b是整数,且b属于{0, 1, 2, 3, 4}。
则n^5 - n = (2a + b)^5 - (2a + b) = 32a^5 + 20a^4b + 5a^3b^2 + a^2b^3 + 2ab^4 - 2a - b。
可以看到,除了最后两项,其他项都能被2整除。
对于最后两项,我们有2a - b = 2(a - b/2),当b为偶数时,2a - b能被2整除;当b为奇数时,a - b/2为整数,所以2a - b也能被2整除。
同理,b - 1能被3整除,因为b属于{0, 1, 2, 3, 4}。
高一数学竞赛试题及答案
高一数学竞赛试题一、猜一猜:(每小题2分共16分)1.司药(打一数学名词)——配方2.招收演员(打一数学名词)——补角3.搬来数一数(打一数学名词)——运算4.你盼着我,我盼着你(打一数学名词)——相等5.北(打一数学名词)——反比6.从后面算起(打一数学名词)——倒数7.小小的房子(打一数学名词)——区间8.完全合算(打一数学名词)——绝对值二、试一试:(每小题4分共8分)1.把12、18、7、6、11分别填入下面□中,使算式成立。
□+□=□=□+□12+6=18=7+112.按规律填数1、6、7、12、13、18、( 19 )、( 24 )、( 25 )三、画一画:(6分)24个人排成6列,要求5个人为一列,你知道应该怎样来排列吗? (一个六边形)四、脑筋急转弯:(每小题4分共20分)1.桌子上原来有12支点燃的蜡烛,先被风吹灭了3根,不久又一阵风吹灭了2根,最后桌子上还剩几根蜡烛呢解答:5根2.一个人花8块钱买了一只鸡,9块钱卖掉了,然后他觉得不划算,花10块钱又买回来了,11块卖给另外一个人。
问他赚了多少?答案:2元3.一根绳子两个头,三根半绳子有几个头?解:8个头,(半根绳子也是两个头)4.一栋住宅楼,爷爷从一楼走到三楼要6分钟,现在要到6楼,要走多少分钟?答:15分钟5.如果有5只猫,同时吃5条鱼,需要5分钟时间才吃完。
按同样的速度,100只猫同时吃掉100条鱼,需要( )分钟时间。
解:5分钟6.100个包子,100个人吃,1个大人吃3个,3个小孩吃1个,多少个大人和多少小孩刚好能吃完?解答:25个大人,75个小孩五、算一算:(每小题5分共25分)1. 兄弟共有45元钱,如果老大增加2元钱,老二减少2元钱,老三增加到原来的2倍,老四减少到原来的1/2,这时候四人的钱同样多,原来各有多少钱?解:老大8 老二12 老三5 老四202. 幼儿园新买回一批小玩具。
如果按每组10个分,则少了2个;如果按每组12个分,则刚好分完,但却少分一组。
高一数学竞赛试题及答案
高一数学竞赛试题及答案题一:某数列的前n项和为Sn,已知Sn=(2n+1)(n+2),求该数列的通项表达式。
解答一:设该数列的通项为an,则该数列的前n项和可表示为Sn=∑an。
根据已知得,Sn=(2n+1)(n+2)。
我们可以尝试寻找数列项an之间的关系,进而求得通项表达式。
由于Sn是前n项和,所以我们可以利用数学归纳法得到两个基础式子:当n=1时,S1=∑a1,代入已知条件得到S1=(3)(2)=6;当n=2时,S2=∑(a1+a2),代入已知条件得到S2=(5)(4)=20。
通过观察可以发现,S2=2×S1+8,这是一个重要的线索。
我们可以推测,Sn可能与Sn-1之间存在一种类似的关系,即Sn=2×Sn-1+C,其中C为常数。
接下来,我们来进行数学归纳法的假设和证明:假设Sn=2×Sn-1+C成立,即前n项和Sn与前n-1项和Sn-1之间存在关系。
则我们可以推导得到Sn+1=2×Sn+C',其中C'为常数。
根据已知条件进行计算:Sn+1=(2(n+1)+1)(n+1+2)=(2n+3)(n+3)=2n²+9n+9;由假设得,Sn=2×Sn-1+C,带入Sn+1的计算结果,得到Sn+1=2(2×Sn-1+C)+C'=4×Sn-1+3C+C',其中3C+C'为新的常数。
比较Sn+1和Sn的关系,可得到4×Sn-1+3C+C'=2n²+9n+9,由此可以推断,3C+C'=9,即C'=9-3C。
综上所述,我们已经推导出两个重要的关系式:Sn=2×Sn-1+CC'=9-3C我们再通过计算已知条件的S1和S2进行迭代计算,得到:C=6,C'=9-3(6)=-9因此,该数列的通项表达式为an=2×an-1+6,其中a1=6。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中一年级练习(2)
一、选择题(以下每题的四个选择支中,仅有一个是正确的)
1、已知,则的值为()
(A)0 (B)1 (C)-1 (D)
2、一个半径为R的球,在一个内半径也为R的半圆柱形槽内恰好可以无滑动地滚动一周,设球的表面积为S,槽的内壁面积为S′,则S与S′的大小关系是()
(A)S=S′(B)S<S′
(C)S>S′(D)不能确定的
3、设,且,则的单调减区间是()
(A)(B)
(C)(D)
二、填空题
1、若方程的根是正数,则参数a的取值范围是()
2、正三棱锥A-BCD的侧棱长与底面边长相等,顶点A、B、C、D在同一
个球面上,和是该球的直径,则平面ABC与平面所成角的正弦值为()
3、函数对于任意的,都有,则实数a的取值范围是()
4、偶函数的定义域为R,且对于任意,都有,
又当时,,则当时,()
5、A、B、C是同一条直线上的三点,AB=BC=1千米,塔M在A的正东北方向,在B的正东方向,在C的南偏东60°,则塔与直线AC的距离等于()
6、集合,则实数m的取值范围是()
7、正三棱锥V-ABC底面边长及锥高都等于4,过AB的截面将棱锥体积二等分,则锥顶V到该截面的距离等于()
三、解答题
1、设,函数的定义域为[0,1]且,,当
时,有,求
(1);
(2)的值;
(3)函数的单调递增区间。
