2012年台湾中考数学试卷及解析
2012年中考数学典型题目组卷
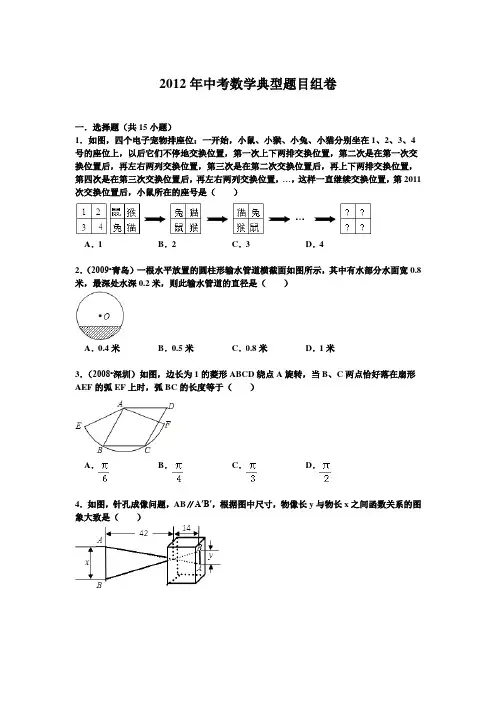
2012年中考数学典型题目组卷一．选择题（共15小题）1．如图，四个电子宠物排座位：一开始，小鼠、小猴、小兔、小猫分别坐在1、2、3、4号的座位上，以后它们不停地交换位置，第一次上下两排交换位置，第二次是在第一次交换位置后，再左右两列交换位置，第三次是在第二次交换位置后，再上下两排交换位置，第四次是在第三次交换位置后，再左右两列交换位置，…，这样一直继续交换位置，第2011次交换位置后，小鼠所在的座号是（）A．1B．2C．3D．42．（2009•青岛）一根水平放置的圆柱形输水管道横截面如图所示，其中有水部分水面宽0.8米，最深处水深0.2米，则此输水管道的直径是（）A．0.4米B．0.5米C．0.8米D．1米3．（2008•深圳）如图，边长为1的菱形ABCD绕点A旋转，当B、C两点恰好落在扇形AEF的弧EF上时，弧BC的长度等于（）A．B．C．D．4．如图，针孔成像问题，AB∥A′B′，根据图中尺寸，物像长y与物长x之间函数关系的图象大致是（）A ．B ． C． D ．5．（2008•江西）下列四个三角形中，与图中的三角形相似的是（ ）A ．B ．C ．D ．6．（2011•台湾）如图，圆O 为△ABC 的外接圆，其中D 点在上，且OD ⊥AC ．已知∠A=36°，∠C=60°，则∠BOD 的度数为何？（ ）A ． 132B ． 144C ． 156D ． 1687．如图，已知⊙O 的半径为，锐角△ABC 内接于⊙O ，BD ⊥AC 于点D ，OM ⊥AB 于点M ，则sin ∠CBD 的值等于（ ）A ． O M 的长B ． 2OM 的长C ． CD 的长 D ． 2CD 的长8．（2011•聊城）如图，用围棋子按下面的规律摆图形，则摆第n 个图形需要围棋子的枚数为（ ）A ． 5nB ． 5n ﹣1C ． 6n ﹣1D ． 2n 2+19．有三个不同的信箱，今有四封不同的信欲投其中，则不同的投法有（ ）种．A ． 81B ． 64C ． 24D ． 410．（2009•铁岭）将一等腰直角三角形纸片对折后再对折，得到如图所示的图形，然后将阴影部分剪掉，把剩余部分展开后的平面图形是（ ）A ．B ．C ．D ．11．如图，AC ，BD 是⊙O 直径，且AC ⊥BD ，动点P 从圆心O 出发，沿O→C→D→O 路线作匀速运动，设运动时间为t （秒），∠APB=y （度），则下列图象中表示y 与t 之间的函数关系最恰当的是（ ）A ．B ．C ．D ．12．（2011•兰州）如图，A 、B 、C 三点在正方形网格线的交点处，若将△ABC 绕着点A 逆时针旋转得到△AC′B′，则tanB′的值为（ ）A ．B ．C ．D ．13．（2011•河北）如图，在△ABC 中，∠C=90°，BC=6，D ，E 分别在 AB 、AC 上，将△ABC 沿DE 折叠，使点A 落在点A′处，若A′为CE 的中点，则折痕DE 的长为（ ）A ．B ． 2C ． 3D ． 414．（2005•山西）点P （a ，b ）是直线y=﹣x+5与双曲线y=的一个交点．则以a 、b 两数为根的一元二次方程是（ ） A ． x 2﹣5x+6=0 B ． x 2+5x+6=0 C ． x 2﹣5x ﹣6=0 D ． x 2+5x ﹣6=015．已知：如图，E （﹣4，2），F （﹣1，﹣1），以O 为位似中心，按比例尺 1：2，把△EFO 缩小，则点E 的对应点E′的坐标为（ ）A ． （2，﹣1）或（﹣2，1）B ． （8，﹣4）或（﹣8，4）C ． （2，﹣1）D ． （8，﹣4）二．填空题（共14小题） 16．如图，直线l 1：y=x+1与直线l 2：y=﹣x ﹣把平面直角坐标系分成四个部分，点（﹣，）在第 _________ 部分．17．（2009•嘉兴）如图，在直角坐标系中，已知点A （﹣3，0），B （0，4），对△OAB 连续作旋转变换，依次得到三角形①，②，③，④…，则三角形⑩的直角顶点的坐标为 _________ ．18．（2010•金华）已知二次函数y=﹣x2+2x+m的部分图象如图所示，则关于x的一元二次方程﹣x2+2x+m=0的解为_________．19．如图，在△ABC中，∠A=90°，AB=AC=2．以BC的中点O为圆心的圆弧分别与AB、AC相切于点D、E，则图中阴影部分的面积是_________．20．如图1是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成的．若AC=12，BC=10，将四个直角三角形中边长为12的直角边分别向外延长一倍，得到图2所示的“数学风车”，则这个风车的外围周长是_________．21．如图，矩形ABCD的对角线BD经过坐标原点，矩形的边分别平行于坐标轴，点C在反比例函数的图象上．若点A的坐标为（﹣2，﹣2），则k的值为_________．22．如图，在3×3的正方形网格中，已有两个小正方形被涂黑，再将图中剩余的编号为1﹣7的小正方形中任意一个涂黑，则所得图案是一个轴对称图形的概率是_________．23．（2008•泰州）分别以梯形ABCD的上底AD、下底BC的长为直径作⊙O1、⊙O2，若两圆的圆心距等于这个梯形的中位线长，则这两个圆的位置关系是_________．24．如图，△ABC是以AB为斜边的直角三角形，AC=4，BC=3，P为AB上一动点，且PE⊥AC于E，PF⊥BC于F，则线段EF长度的最小值是_________．25．（2009•衡阳）如图，直线AB切⊙O于C点，D是⊙O上一点，∠EDC=30°，弦EF∥AB，连接OC交EF于H点，连接CF，且CF=2，则HE的长为_________．26．（2011•宜宾）已知一元二次方程x2﹣6x﹣5=0的两根为a、b，则的值是_________．27．（2008•淮安）如图，点O（0，0）、B（0，1）是正方形OBB1C的两个顶点，以对角线OB1为一边作正方形OB1B2C1，再以正方形OB1B2C1的对角线OB2为一边作正方形OB2B3C2，…，依次下去，则点B6的坐标是_________．28．（2010•长春）如图，⊙P与x轴切于点O，点P的坐标为（0，1）．点A在⊙P上，且位于第一象限，∠APO=120°．⊙P沿x轴正方向滚动，当点A第一次落在x轴上时，点A 的横坐标为_________．（结果保留π）29．如图所示，矩形ABCG与矩形CDEF全等，点BCD在一条直线上，∠APE的顶点P 在线段BD上移动，使得∠APE为直角的点P的个数是_________个．三．解答题（共1小题）30．如图，已知二次函数y=ax2+2x+3的图象与x轴交于点A、点B，与y轴交于点C，其顶点为D，tan∠OBC=1，（1）求点B的坐标；（2）求a的值和二次函数y=ax2+2x+3的顶点坐标；（3）求直线DC的解析式；（4）在该二次函数的图象上是否存在点P（点P与点B、C不重合），使得△PBC是以BC 为一条直角边的直角三角形？若存在，求出点P的坐标，若不存在，请你说明理由．。
台湾中考数学真题与解析
台湾中考数学真题与解析部门： xxx时间： xxx整理范文，仅供参考，可下载自行编辑由图可知男生身高的中位数约165(cm>，女生身高的中位数约160(cm>设小明买了x包饼干，则剩下的钱为300－(50＋90＋120＋13x>元，整理后为(40－13x>元3，40－13x＝1故选(B>，得(A>依题意得：(A>3＝错误!＜错误!＜错误!＝4 ⇒错误!＝3.…⇒甲＝5＋错误!＝8.…p1EanqFDPw 4＝错误!＜错误!＜错误!＝5 ⇒错误!＝4.…⇒乙＝3＋错误!＝7.…DXDiTa9E3d 4＝错误!＜错误!＜错误!＝5 ⇒错误!＝4.…⇒丙＝1＋错误!＝5.…RTC rpUDGiT(A>由关系式可知2x－100 ⇒两件商品减100元0.3 ⇒打3折＜1000 ⇒不到1000元所以0.3(2x－100>＜1000即为(B>完成短除法如下8、12、18的最小公倍数为2×3×2×2×1×3＝72故选(B>(C>四千零七十亿元可写成407000000000(C>六人份需20×6＝120克砂糖，尚需120－50＝70克砂糖所求＝70×错误!＝21(小匙>故选(C>5PCzVD7HxA 的方格纸上有一平行四边形ABCD，其顶点(A> (B>(C> (D>由(A>、(B>、(C>、(D>四个图可知，(D>图上的F点到的距离＞E点到的距离jLBHrnAILg所以△FBC的面积＞△EBC的面积故选(D>(B>完成线对称图形如右则涂成灰色的小方格在第二列第一行的外接圆由∠DAE＝12°得错误!＝12°×2＝24°∵错误!＝错误!＝错误!，∴错误!＝(360°－24°>÷3＝112°xHAQX74J0X∠ABC＝错误!(错误!＋错误!>＝错误!(24°＋112°>＝68°，故选抽出红色牌机率＝＝错误!Zzz6ZB2Ltk抽出黄色牌机率＝＝错误!dvzfvkwMI1(－1000错误!>×(5－10>＝－(1000＋错误!>×(－5>EmxvxOtOco＝1000×5＋错误!×58x2－10x＋2＝2(4x2－5x＋1>＝2(4x－1>(x－1>＝(4x－1>(2x－2>故选(A>另解：分别将8x2－10x＋2除以四个选项如右图连，以A点为圆心，为半径画弧，交大圆于B1、B2两点SixE2yXPq5则B1、B2即为所求(＝＝>6ewMyirQFL∴满足条件的B点共有2个(B>如右图，延长，交于N点∵＝ △ABC为等腰三角形又M是△ABC的重心∴为中线，且⊥kavU42VRUs∴＝＝错误!＝8y6v3ALoS89＝错误!＝15＝错误!错误!＝错误!×15＝10M2ub6vSTnP(A>(B>(C>(D>(B>由数字乘以3可得3x加6可得3x＋6结果除以3可得(3x＋6>÷3＝x＋2再减去一开始写的数字可得x＋2－x＝2y＝ax2＋bx＋c－5x2－3x＋7＝(a－5>x2＋(b－3>x＋(c＋7>若此二次函数图形有最低点则图形的开口向上⇒x2项系数为正数⇒a－5＞0，a＞5｜a－c｜＝(A>｜a｜＋｜b｜＋｜c｜＝＋＋≠0YujCfmUCw(B>｜a－b｜＋｜c－b｜＝＋＝eUts8ZQVRd(C>｜a－d｜－｜d－c｜＝－＝sQsAEJkW5T(D>｜a｜＋｜d｜－｜c－d｜＝＋－＝GMsIasNXkA(A> 10 (B> 45 (C> 55 (D> 99(C>由表知36～42岁及50～56岁的职员人数共有200－6－40－42－2＝110人a%＋b%＝×100%＝55%⇒a＋b＝55如右图∵ABCDEF为正六边形∴∠ABC＝120°，∠CBG＝60°又＝1(＝＝>TIrRGchYzg∴＝错误!(＝错误!>7EqZcWLZNX四边形CDHG的周长＝(1＋错误!>×2＝2＋错误!lzq7IGf02E∵两段圆柱形树干的体积比为2：1∴两段圆柱形树干的柱高比为2：1则体积较大的树干柱高为15×错误!＝10(公尺>∵圆柱体的底面积为9π平方公尺∴圆柱体的底圆半径为3公尺所求＝(2×π×3>×10＝60π(平方公尺>原式＝(错误!>6×[(错误!>－2]2(∵错误!＝(错误!>－1∴(错误!>2＝[(错误!>－1]2＝(错误!>－2>zvpgeqJ1hk＝(错误!>6×(错误!>－4NrpoJac3v1＝(错误!>6－4＝(错误!>21nowfTG4KI由题意知红豆汤圆每杯错误!元，豆花每杯错误!元fjnFLDa5Zo又豆花每杯比红豆汤圆便宜10元即错误!＝错误!－10 ⇒错误!＝错误!＋10tfnNhnE6e5由L：3x－y＝－3可知，L交y轴于(0 , 3>，由图可知当0＜a＜3时L'与L的交点会在第二象限，故选(A>。
(中考数学真题复习)第7讲 一元一次方程及分式方程基础例题 附答案解析
中考数学复习一元一次方程及分式方程【基础演练】1．(2013·滨州)把方程12x＝1变形为x＝2，其依据是() A．等式的性质1B．等式的性质2C．分式的基本性质D．不等式的性质1解析把方程12x＝1变形为x＝2，其依据是等式的性质2.答案B2．(2013·泰安)某电子元件厂准备生产4600个电子元件，甲车间独立生产了一半后，由于要尽快投入市场，乙车间也加入该电子元件的生产，若乙车间每天生产的电子元件是甲车间的1.3倍，结果用33天完成任务，问甲车间每天生产电子元件多少个？在这个问题中设甲车间每天生产电子元件x个，根据题意可得方程为()A.2300x＋23001.3x＝33 B.2300x＋2300x＋1.3x＝33C.2300x＋4600x＋1.3x＝33 D.4600x＋2300x＋1.3x＝33解析设甲车间每天能加工x个，则乙车间每天能加工1.3x个，根据题意可得：2300 x＋2300x＋1.3x＝33.答案B3．(2013·丽水)分式方程1x－2＝0的解是________．解析方程两边同乘以x，得1－2x＝0，解得x＝12.检验：当x＝12时，x＝12≠0，所以，原方程的解为x ＝12.答案x ＝124．(2012·宁波)分式方程x －2x ＋4＝12的解是________．解析方程的两边同乘2(x ＋4)，得2(x －2)＝x ＋4，2x －4＝x ＋4，解得x ＝8.检验：把x ＝8代入x ＋4＝12≠0.故原方程的解为x ＝8.答案x ＝85．(2013·绍兴)分式方程2xx －1＝3的解是________．解析方程两边同乘以x －1，得2x ＝3(x －1)，解得x ＝3.检验：当x ＝3时，x －1＝3－1＝2≠0，所以，原方程的解为x ＝3.答案x ＝36．(2013·滨州)解方程：3x ＋52＝2x －13.解去分母得：3(3x ＋5)＝2(2x －1)，去括号得：9x ＋15＝4x －2，移项合并得：5x ＝－17，解得：x ＝－175.7．(2010·台州)解方程：3x ＝2x －1.解方程两边同乘以x (x －1)，得3(x －1)＝2x ，解得x ＝3.经检验：x ＝3是原方程的解，所以原方程的解是x ＝3.8．(2010·义乌市)解分式方程：2x2＋1x＋2＝2x.解方程的两边同乘x＋2，得2x2＋1＝2x2＋4x，∴4x＝1，∴x＝1 4 .经检验，x＝14是原方程的解．9．(2012·北京)列方程或方程组解应用题：据林业专家分析，树叶在光合作用后产生的分泌物能够吸附空气中的一些悬浮颗粒物，具有滞尘净化空气的作用．已知一片银杏树叶一年的平均滞尘量比一片国槐树叶一年的平均滞尘量的2倍少4毫克，若一年滞尘1000毫克所需的银杏树叶的片数与一年滞尘550毫克所需的国槐树叶的片数相同，求一片国槐树叶一年的平均滞尘量．解设一片国槐树叶一年的平均滞尘量为x毫克，则一片银杏树叶一年的平均滞尘量为(2x－4)毫克，由题意得：10002x－4＝550x，解得：x＝22.经检验：x＝22是所列方程的解．答：一片国槐树叶一年的平均滞尘量为22毫克．【能力提升】10．(2013·台湾)附表为服饰店贩卖的服饰与原价对照表．某日服饰店举办大拍卖，外套依原价打六折出售，衬衫和裤子依原价打八折出售，服饰共卖出200件，共得24000元．若外套卖出x件，则依题意可列出下列哪一个一元一次方程式？()服饰原价(元)外套250衬衫125裤子125A．0.6×250x＋0.8×125(200＋x)＝24000B．0.6×250x＋0.8×125(200－x)＝24000C．0.8×125x＋0.6×250(200＋x)＝24000D．0.8×125x＋0.6×250(200－x)＝24000解析若外套卖出x 件，则衬衫和裤子卖出(200－x )件，由题意得：0．6×250x ＋0.8×125(200－x )＝24000，答案B11．(2012·山西)图1是边长为30cm 的正方形纸板，裁掉阴影部分后将其折叠成如图2所示的长方体盒子，已知该长方体的宽是高的2倍，则它的体积是________cm 3.解析长方体的高为x cm ，然后表示出其宽为30－4x ，根据题意得：30－4x ＝2x ，解得：x ＝5.故长方体的宽为10cm ，长为20cm 则长方体的体积为5×10×20＝1000cm 3.答案100012．(2012·攀枝花)若分式方程：2＋1－kx x －2＝12－x有增根，则k ＝________.解析∵2＋1－kx x －2＝12－x，去分母得：2(x －2)＋1－kx ＝－1，整理得：(2－k )x ＝2，当2－k ＝0时，此方程无解，不符合题意．∵分式方程2＋1－kx x －2＝12－x 有增根，∴x －2＝0，2－x ＝0，解得：x ＝2，把x ＝2代入(2－k )x ＝2得：k ＝1.答案113．(2010·嘉兴)解方程：x x ＋1＋x ＋1x＝2.解设x x ＋1＝y ，则原方程化为y ＋1y ＝2.整理得，y 2－2y ＋1＝0，解之得，y ＝1.当y ＝1时，xx ＋1＝1，此方程无解．故原方程无解．14．(2010·义乌市)我市举办的“义博会”是国内第三大展会，从1995年以来已成功举办了15届．(1)1995年“义博会”成交金额为1.01亿元，1999年“义博会”成交金额为35.2亿元，求1999年的成交金额比1995年的增加了几倍？(结果精确到整数)(2)2000年“义博会”的成交金额与2009年的成交金额的总和是153.99亿元，且2009年的成交金额是2000年的3倍少0.25亿元，问2009年“义博会”的成交金额是否突破了百亿元大关？解(1)(35.2－1.01)÷1.01≈34.答：1999年的成交金额比1995年约增加了34倍；(2)设2000年成交金额为x 亿元，则2009年成交金额为(3x －0.25)亿元．由题意得x ＋3x －0.25＝153.99，解得x ＝38.56，∴3x －0.25＝115.43＞100，∴2009年“义博会”的成交金额突破了百亿元大关．。
台湾第二次中考数学试题解析版.doc
山东省滨州市2011年初中毕业生统一学业考试语文参考答案及评分说明一、全卷书写（2分）书写规范、工整，卷面整洁可得2分；书写较规范、工整可得1分；书写不认真、潦草不得分。
二、积累与运用（共20分）1.ái 媚皎 zhāo 评分：共2分。
每空0.5分。
2.B 评分：共2分。
3.D 评分：共2分。
4.①明朗坚固而蓬勃生春②然后知松柏之后凋也③望之蔚然而深秀者④春潮带雨晚来急⑤长烟落日孤城闭⑥亲戚畔之天下顺之⑦几处早莺争暖树谁家春燕啄春泥评分：共7分。
每题1分，出现错别字或添字、漏字该小题不得分。
5.（1）《鲁提辖拳打镇关西》或《拳打镇关西》评分：共1分。
（2）侠肝义胆、疾恶如仇、粗中有细、有勇有谋等。
评分：共2分。
答出两点即可。
6.（1）示例：班级档案、班级宣言、班级成员寄语、班级大事记、班级毕业照等。
评分：共2分。
每个板块内容1分，只要与班级成长有关即可。
（2）示例：看一眼班级的黑板摸一把同学的桌椅听一回校园的广播想一下老师的话语评分：共2分。
每空1分，做到语意连贯，句式一致即可。
二、阅读（共38分）（一）古诗词鉴赏。
（3分）7.略。
评分：共2分。
开放性试题，描绘应表现出平也开阔、大江直流、波平浪静的景色特点，语言流畅即可。
8.思念故乡评分：共1分。
（二）阅读下面两段文言文，回答文后问题。
（10分）9.录毕/走送之/不敢稍逾约。
评分：共2分。
每对一处得1分。
10.（1）爱好（2）不（3）曾经（4）善，好评分：共2分。
每空0.5分11.（1）因此人家大多愿意把书借给我，我于是能够看到许多（各种各样的）书。
（2）真是（确实是）这样，你没有欺骗我。
评分：共4分。
每句2分，意思对即可。
12.读书方面围绕“勤奋刻苦”“博览群书”，做人方面围绕“正直”“坦诚待人”“与品德优秀的人交友”“背后不说人坏话”等要点回答即可。
评分：共2分。
每空1分，答出其中一点，言之成理即可。
（三）阅读下文，回答文后问题。
2012年台湾省中考数学试卷
2012年台湾省中考数学试卷一、选择题（共34小题，每小题3分，满分99分）1. （3分）三年甲班男、女生各有20人，如图为三年甲班男、女生身高的盒状图.若班上每位同学的身高均不相等，贝U全班身高的中位数在下列哪一个范围？（）140 ISO I 開170 IK4A. 150 〜155B. 155 〜160C. 160 〜165D. 165 〜1702. （3分）小明原有300元，如图记录了他今天所有支出，其中饼干支出的金额被涂黑.若每包饼干的售价为13元，则小明可能剩下多少元？（）R支出1金soQOO ------------------ -------120■0A. 4B. 14C. 24D. 343. （3分）解二元一次联立方程式，得y=（）A. - 4B.--C. -D. 54. （3分）已知甲、乙、丙三数，甲=5+ —，乙=3+ —，丙=1+ —，则甲、乙、丙的大小关系，下列何者正确？（）A.丙v乙v甲B.乙v甲v丙C.甲v乙v丙D.甲二乙=丙5. （3分）小美将某服饰店的促销活动内容告诉小明后，小明假设某一商品的定价为x元，并列出关系式为0.3 （2x- 100）v 1000，贝U下列何者可能是小美告诉小明的内容？（）除法，求出这三数的最小公倍数为何？（A. 12 B . 72 C. 216 D . 4327. （3分）已知某公司去年的营业额为四千零七十亿元，则此营业额可用下列何 者表示？（）A. 4.07X 109元B. 4.07X 1010元C. 4.07X 1011 元D . 4.07X 1012元8. （3分）如图为制作果冻的食谱，傅妈妈想依此食谱内容制作六人份的果冻. 若 她加入50克砂糖后，不足砂糖可依比例换成糖浆，则她需再加几小匙糖浆？呆凍〔一人扮）来凍松…30克 矽14 ....... 20克咖啡粉•…70克U :矽權20克 可換成梅漿6小地9. （3分）如图所示的方格纸上有一平行四边形 ABCD ，其顶点均在网格线的交 点上，且E 点在AD 上.今大华在方格纸网格线的交点上任取一点F ,发现△FBC 的面积比厶EBC 的面积大.判断下列哪一个图形可表示大华所取 F 点的位 置？（）A .买两件等值的商品可减 B .买两件等值的商品可减 100元，再打3折，最后不到100元，再打7折，最后不到 1000 元 1000 元 C. 买两件等值的商品可打3折，再减100元，最后不到 7折，再减100元，最后不到 6.（3分）如图是利用短除法求出三数 8、12、18的最大公因子的过程.禾U 用短 D .买两件等值的商品可打 1000 元 A . 15 B . 18 C. 21 D . 2410. （3分）小明将一正方形纸片画分成16个全等的小正方形，且如图所示为他 将其中四个小正方形涂成灰色的情形.若小明想再将一小正方形涂成灰色，第二列f 第三列 第四列f11. （3分）如图所示的直线AE 与四边形ABCD 的外接圆相切于A 点•若/DAE=12,、、三弧的度数相等，则/ ABC 的度数为何？（ ）1/ \AF )\ /\/C.D\/\F* A/\\/\/\/D.使此纸片上的灰色区域成为线对称图形, 则此小正方形的位置为何？（A .第一列第四行 C.第三列第三行B. 第二列第一行A. :;B.B fi第四行J第三行J第二行>第一行右D . 312. （3分）一纸箱内有红、黄、蓝、绿四种颜色的纸牌，且如图所示为各颜色 纸牌数量的统计图.若小华自箱内抽出一张牌，且每张牌被抽出的机会相等,则他抽出红色牌或黄色牌的机（概）率为何？（13. （3 分）计算（-100X ）X （ 5- 10）之值为何？（14. （3分）下列四个选项中，哪一个为多项式 8x 2- 10x+2的因式？（）B . 65C. 67D . 68C.D .A. 1000B. 1001C. 4999D. 5001A. 2x - 2B. 2x+2C. 4x+1D . 4x+2D . 3若在大圆上找一点 B ，使得OA=AB,则满足上述条件的BB . 1 C. 215. （3分）如图，大、小两圆的圆心均为 O 点，半径分别为3、2,且A 点为小 圆上的一固定A . 016. （3分）如图，△ ABC中，AB=AC=17 BC=16 M是厶ABC的重心，求AM的18. （3分）判断下列哪一组的a b、在坐标平面上的图形有最低点？（A. a=0, b=4，c=8 c,可使二次函数y=aX^+bx+c-5X2- 3x+7 )B. a=2，b=4，c=- 8A. 817. （3分）如图所示为魔术师在小美面前表演的经过:x,魔术师猜中的答案为y，则下列哪一B. 10C. —D.根据上图，假设小美在纸上写的数字为个图形可以表示x、y的关系？（19. （3分）如图，数轴上的A 、B 、C 、D 四点所表示的数分别为a 、b 、c 、d , 且O 为原点.根据图中各点位置，判断|a -c|之值与下列何者不同？（）A B O C；■Hl■D口£>f dA. |a|+|b|+|c| B . |a — b|+| c - b| C. | a -d| - |d - c| D . | a|+| d| - |c- d|20. （3分）下表为某公司200名职员年龄的人数分配表，其中36〜42岁及50〜 56岁的人数因污损而无法看出.若 36〜42岁及50〜56岁职员人数的相对次 数分别为a%、b%,则a+b 之值为何？（ ） 年龄 22 〜28 29 〜35 36 〜4243 〜49 50 〜5657 〜63 次数640 ■ 42 ■2A . 10B . 45C. 55D . 9921. （3分）如图，正六边形 ABCDEF 勺边长为1,连接AC 、BE DF ,求图中灰22. （3 分）有一段树干为一直圆柱体，其底面积为9 n 平方公尺，高为15公尺.若 将此树干分为两段圆柱形树干，且体积比为 2: 1，则体积较大的树干，其侧 面的表面积为多少平方公尺？（ ） A . 60 nB . 72 nC. 84 nD . 96 n23. （3 分）计算[（一）2]3X [ （―） 2]2之值为何？（ ）A . 1B . 一C. （-） 2D . （一）4 24. （3分）小华带x 元去买甜点，若全买红豆汤圆刚好可买C. a=4, b= - 4, c=8D. a=6, b=- 4, c= - 830杯，若全买豆花 色四边形的周长为何？（ ）刚好可买40杯.已知豆花每杯比红豆汤圆便宜10元，依题意可列出下列哪一个方程式？（ 25. （3分）如图，坐标平面上直线L 的方程式为3x — y=— 3.若有一直线L 的方 程式为y=a ,则a 的值在下列哪一个范围时，L 与L 的交点会在第二象限？（）AE 、BF 、CG DH 是20个箱子，依顺时针方向编号1〜20.小明在1号箱子中丢入一颗红球后，沿着圆桌依顺时针方向行走，每经过一个箱子就 依下列规则丢入一颗球：A. —— B. ——C.—D .C.— 1 v a v 0D .— 3v a v — 2之值为何？（） A . 0B . 25 C. 50 D . 80B . 3v a v 426. （3分）计算1为图2中三角柱ABCEFG 勺展开图，其中27.（3分）如图 D . 528. （3分）如图，一圆桌周围有AB 长度？（）（1）若前一个箱子丢红球，经过的箱子就丢绿球.（2）若前一个箱子丢绿球，经过的箱子就丢白球.（3）若前一个箱子丢白球，经过的箱子就丢红球.已知他沿着圆桌走了100圈，求4号箱内有几颗红球？（）A. 33B. 34C. 99D. 10029. （3 分）如图，梯形ABCD中，/ DAB=Z ABC=90, E点在CD上,且DE: EC=14. 若AB=5,BC=4 AD=8,则四边形ABCE的面积为何？（）AB CA. 24B. 25C. 26D. 2730. （3分）有一个二次函数y=x2+ax+b，其中a、b为整数.已知此函数在坐标平面上的图形与x轴交于两点，且两交点的距离为4.若此图形的对称轴为x=- 5，则此图形通过下列哪一点？（）A. （- 6，- 1）B. （-6，- 2）C. （- 6，- 3）D. （-6，- 4）31. 若一元二次方程式x2- 2x- 3599=0的两根为a、b,且a>b,则2a- b的值为（）A.- 57B. 63C. 179D. 18132. （3分）如图，边长12的正方形ABCD中，有一个小正方形EFGH其中E、F、G分别在AB、BC FD上.若BF=3则小正方形的边长为何？（）A. B. 一 C. 5 D. 633. （3分）如图，直角三角形 ABC 有一外接圆，其中/ B=90°, AB >BC,今欲在 上找一点P ,使得 =，以下是甲、乙两人的作法： 甲：（1）取AB 中点D（2）过D 作直线AC 的平行线，交 于P ,则P 即为所求 乙：（1）取AC 中点E （2）过E 作直线AB 的平行线，交 于P ，则P 即为所求对于甲、乙两人的作法，下列判断何者正确？（ ）34. （ 3分）图1的长方形 ABCD 中，E 点在AD 上，且BE=2AE 今分别以BE 、 CE 为折线，将A 、D 向BC 的方向折过去，图2为对折后A 、B 、C 、D 、E 五点均在同一平面上的位置图.若图 2中，/ AED=15，则/ BCE 的度数为何？C.甲正确，乙错误C B •两人皆错误D .甲错误，乙正确 D . 37.52012年台湾省中考数学试卷参考答案与试题解析一、选择题（共34小题，每小题3分，满分99分） 1.（3分）三年甲班男、女生各有 20人，如图为三年甲班男、女生身高的盒状 图.若班上每位同学的身高均不相等，贝U 全班身高的中位数在下列哪一个范 围？（ ）A . 150 〜155B . 155 〜160C. 160 〜165D . 165 〜170【解答】解：由图可知：男生身高的中位数约165 （cm ）, 女生身高的中位数约160 （cm ），所以全班身高的中位数在160〜165 （cm ）， 故选：C.2. （3分）小明原有300元，如图记录了他今天所有支出，其中饼干支出的金额 被涂黑.若每包饼干的售价为13元，则小明可能剩下多少元？（）1金 ®<s>:旱蚩so :牛曙 g ---- —GQ z唳番120-a*A . 4B . 14 C. 24 D . 34【解答】解：设小明买了 x 包饼干，则剩下的钱为300- （50+90+120+13X ）元, 整理后为（40- 13x ）元， 当 x=1，40 - 13x=27，朗生 •女身高（公当 x=2, 40- 13x=14, 当 x=3, 40 - 13x=1; 故选：B.3. （3分）解二元一次联立方程式 A .- 4B .--【解答】解：原方程组即： ①-②得：2y=- 8, 解得：y=- 4.故选：A .4. （3分）已知甲、乙、丙三数，甲=5+ ■/ 4= v V =5, ••• 5v 1+ —V 6, • ••丙V 乙V 甲 故选(A ).5. （3分）小美将某服饰店的促销活动内容告诉小明后，小明假设某一商品的定 价为x 元，并列出关系式为0.3 （2x - 100）v 1000,贝U 下列何者可能是小美，得 y=() C. -D . 5，乙=3+，丙=1+，则甲、乙、）C.甲v 乙v 丙D .甲二乙=丙丙的大小关系， F 列何者正确？ (A .丙v 乙v 甲 B. 乙v 甲v 丙【解答】解：：3= vv=4,• 8v 5+ v 9，• 8v 甲 v 9;■ 4= v v=5，• 7v 3+v 8，• 7v 乙v 8，告诉小明的内容？（）A.买两件等值的商品可减100元，再打3折，最后不到1000元B•买两件等值的商品可减100元，再打7折，最后不到1000元C•买两件等值的商品可打3折，再减100元，最后不到1000元D•买两件等值的商品可打7折，再减100元，最后不到1000元【解答】解：由关系式可知：0.3 （2x- 100）v 1000，由2x- 100,得出两件商品减100元，以及由0.3（2x- 100）得出买两件打3折, 故可以理解为：买两件等值的商品可减100元，再打3折，最后不到1000元. 故选：A.6. （3分）如图是利用短除法求出三数8、12、18的最大公因子的过程.禾U用短除法，求出这三数的最小公倍数为何？（）2| 8 12 1*A. 12B. 72C. 216D. 432【解答】解：如图，完成短除法如下最小公倍数为2X 2X 3X 2 X 1 X 3=72.故选：B.7. （3分）已知某公司去年的营业额为四千零七十亿元，则此营业额可用下列何者表示？（）A. 4.07X 109元B. 4.07X 1010元C. 4.07X 1011元D. 4.07X 1012元【解答】解：将四千零七十亿元可写成407000000000,407000000000=4.07X 1011，故选：C.8.（3分）如图为制作果冻的食谱，傅妈妈想依此食谱内容制作六人份的果冻. 若她加入50克砂糖后，不足砂糖可依比例换成糖浆，则她需再加几小匙糖浆？（）笨凍〔一人扮）果康粉■八*30X矽14 ........ 20克咖啡粉 (70)A. 15B. 18C. 21D. 24it:矽轉20克可換成牺漿戌小地【解答】解: 六人份需20 X 6=120克砂糖，尚需120 - 50=70克砂糖，又20克砂糖=6小匙糖浆，所求=70-20 X 6=21 （小匙）.故选：C.9. （3分）如图所示的方格纸上有一平行四边形ABCD,其顶点均在网格线的交点上，且E点在AD上.今大华在方格纸网格线的交点上任取一点F,发现△I)FBC的面积比厶EBC的面积大.判断下列哪一个图形可表示大华所取F点的位【解答】解：A、点F到边BC的距离小于点E到边BC的距离，所以△ FBC的面积＜厶EBC 的面积，故本选项错误；B 、 点F 到边BC 的距离小于点E 到边BC 的距离，所以△ FBC 的面积＜△ EBC 的 面积，故本选项错误；C 、 点F 到边BC 的距离等于点E 到边BC 的距离，所以△ FBC 的面积=△ EBC 的面 积，故本选项错误；D 、 点F 到边BC 的距离大于点E 到边BC 的距离，所以△ FBC 的面积＞△ EBC 的 面积，故本选项正确. 故选：D .10. （3分）小明将一正方形纸片画分成16个全等的小正方形，且如图所示为他 将其中四个小正方形涂成灰色的情形.若小明想再将一小正方形涂成灰色， 使此纸片上的灰色区域成为线对称图形， 则此小正方形的位置为何？（）【解答】解：根据题意得：涂成灰色的小方格在第二列第一行.故选： B.A .第一列第四行 C. 第三列第三 B. 第二列第一行第四行J第三行行第二列 第三列第四第一11. （3分）如图所示的直线AE 与四边形ABCD 的外接圆相切于A 点•若/DAE=12,三弧的度数相等，则Z ABC 的度数为何？（ ）【解答】解：作直径AF ,连接DF , ••• AE 是。
台湾中考数学真题与解析
2018年台湾中考数学真题与解读(C)由图可知男生身高的中位数约165(cm)，女生身高的中位数约160(cm)(B)设小明买了x包饼干，则剩下的钱为300－(50＋90＋120＋13x)元，整理后为(40－13x)元＝1故选(B)(A)依题意得：{ 197x ＋4y ＝11 197x ＝19－2y ⇒{197x ＋4y ＝11……○1197x ＋2y ＝19……○2 由○1－○2得：2y ＝－8，y ＝－4故选(A)(A)3＝9＜15＜16＝4 ⇒15＝3.…⇒甲＝5＋15＝8.…4＝16＜17＜25＝5 ⇒17＝4.…⇒乙＝3＋17＝7.…4＝16＜19＜25＝5 ⇒19＝4.…⇒丙＝1＋19＝5.…(A)由关系式可知2x－100 ⇒两件商品减100元0.3 ⇒打3折＜1000 ⇒不到1000元所以0.3(2x－100)＜1000即为两件商品减100元打3折不到1000元故选(A)(B)完成短除法如下8、12、18的最小公倍数为2×3×2×2×1×3＝72故选(B)(C)四千零七十亿元可写成40700000000011(C)六人份需20×6＝120克砂糖，尚需120－50＝70克砂糖(D)(D)由(A)、(B)、(C)、(D)四个图可知，(D)图上的F点到的距离＞E点到的距离(B)完成线对称图形如右则涂成灰色的小方格在第二列第一行故选(B)(D)由∠DAE ＝12°得︵AD ＝12°×2＝24°∵︵AB ＝︵BC ＝︵CD ，∴︵CD ＝(360°－24°)÷3＝112° ︵︵(B)抽出红色牌机率＝＝抽出黄色牌机率＝＝(D) (－1000)×(5－10)＝－(1000＋)×(－5)＝1000×5＋×5(A)8x2－10x＋2＝2(4x2－5x＋1)＝2(4x－1)(x－1)＝(4x－1)(2x－2) 故选(A)另解：分别将8x2－10x＋2除以四个选项可得(A)(8x2－10x＋2)÷(2x－2)＝4x－1故选(A)(C)如右图连，以A点为圆心，为半径画弧，交大圆于B1、B2两点则B1、B2即为所求(＝＝)∴满足条件的B点共有2个故选(C)(B)如右图，延长，交于N点∵＝ △ABC为等腰三角形又M是△ABC的重心∴为中线，且⊥∴＝＝＝8＝172－82＝15＝＝×15＝10故选(B)根据图(十一)，假设小美在纸上写的数字为x，魔术师猜中的答案为y，则下列哪一(D)(B)由数字乘以3可得3x加6可得3x＋6结果除以3可得(3x＋6)÷3＝x＋2再减去一开始写的数字可得x＋2－x＝2(D)y＝ax2＋bx＋c－5x2－3x＋7＝(a－5)x2＋(b－3)x＋(c＋7)若此二次函数图形有最低点则图形的开口向上⇒x2项系数为正数⇒a－5＞0，a＞5故选(D)(A)｜a－c｜＝(A)｜a｜＋｜b｜＋｜c｜＝＋＋≠(B)｜a－b｜＋｜c－b｜＝＋＝(C)｜a－d｜－｜d－c｜＝－＝(D)｜a｜＋｜d｜－｜c－d｜＝＋－＝故选(A)(A) 10 (B) 45 (C) 55 (D) 99(C)由表知36～42岁及50～56岁的职员人数共有200－6－40－42－2＝110人a%＋b%＝×100%＝55%a＋b＝55故选(C)(D)如右图∵ABCDEF为正六边形∴∠ABC＝120°，∠CBG＝60°又＝1(＝＝)∴＝32)(＝)四边形CDHG的周长＝(1＋32))×2＝2＋ 3(A)∵两段圆柱形树干的体积比为2：1∴两段圆柱形树干的柱高比为2：1则体积较大的树干柱高为15×＝10(公尺)∵圆柱体的底面积为9π平方公尺∴圆柱体的底圆半径为3公尺所求＝(2×π×3)×10＝60π(平方公尺)故选(A)(C)原式＝()6×[()－2]2(∵＝()－1∴()2＝[()－1]2＝()－2) ＝()6×()－4＝()6－4＝()2故选(C)(A)由题意知红豆汤圆每杯元，豆花每杯元又豆花每杯比红豆汤圆便宜10元即＝－10 ⇒＝＋10故选(A)(A)由L：3x－y＝－3可知，L交y轴于(0 , 3)，由图可知当0＜a＜3时(D)(C)设＝x，＝8－x则x－2＜8－x＜x＋2 由8－x＜x＋2得x＞3 由x－2＜8－x得x＜5 3＜x＜5(B)第1圈红球在1、○4、7、10、13、16、19号箱内第2圈红球在2、5、8、11、14、17、20号箱内第3圈红球在3、6、9、12、15、18号箱内第4圈红球在1、○4、7、10、13、16、19号箱内…且第1、4、7、……、100圈会在4号箱内丢一颗红球a n＝a1＋(n－1)d100＝1＋3(n－1)33＝n－1n＝34故选(B)(C)如右图，连梯形ABCD面积＝＝30△ABC面积＝×5×4＝10△ACD面积＝30－10＝20∵：＝1：4∴△ACE面积＝20×＝16∴四边形ABCE面积＝10＋16＝26故选(C)(C)∵二次函数图形的对称轴为x＝－5又图形与x轴的两个交点距离为4∴此两点的坐标为(－7 , 0)和(－3 , 0)设二次函数y＝(x＋7)(x＋3)将x＝－6代入，得y＝(－6＋7)(－6＋3)＝－3 ⇒图形会通过点(－6 ,－3)故选(C)(D)x2－2x－3599＝0⇒x2－2x＝3599⇒x2－2x＋1＝3599＋1⇒ (x－1)2＝3600⇒x－1＝60或x－1＝－60∴x＝61或x＝－59又a＞b，∴a＝61，b＝－59⇒ 2a－b＝2×61－(－59)＝181故选(D)(B)在△BEF 与△CFD 中∠1＋∠2＝∠2＋∠3＝90°⇒∠1＝∠3且∠B ＝∠C ＝90°，∴△BEF ～△CFD (AA 相似)又＝2＋2＝122＋92＝15 ∴,)＝,)，＝,15)⇒＝故选(B)(D)(1)由甲的作法，可知︵BP ≠︵CP(2)由乙的作法，连可知△BEC为等腰三角形又直线PE⊥，∴∠1＝∠2故︵BP＝︵CP∴甲错误，乙正确故选(D)(A) 30(B) 32.5(C) 35(D)∵＝2＝2，∠A＝∠A'＝90°∴△ABE、△A'BE皆为30°、60°、90°的三角形⇒∠1＝∠AEB＝60°，∠AED'＝180°－60°－60°＝60°⇒∠DED'＝∠AED＋∠AED'＝15°＋60°＝75°⇒∠2＝∠DED'＝37.5°∴∠BCE＝37.5°故选(D)。
2012年中考数学样题参考答案.doc
2012年中考数学样题参考答案选择题（每题3分，共30分）一、BADCD BADBA二、填空题（每题3分，共18分）11. 15； 12. 6； 13. （-4，3） 14.38； 15.53； 16. 4n ；三、解答题（每小题8分，共16分）17．．解：原式21=····································································· 6分3=··················································································· 8分18. 解：原式=213(3)32(2)(2)a a a a a a a +---÷-++- ······················································ 2分 =213(2)(2)32(3)a a a a a a a +-+---+-· ··········································································· 3分 1233a a a a +-=--- ······························································································ 4分 =33a - ········································································································ 6分 a 取值时只要不取2，2-，3就可以． ······························································· 7分求值正确．原式 ····························································································· 9分四、解答题（每小题9分，共18分）19．（1）200 ······································································································· 2分 （2）补充图：扇形图中补充的 跳绳25% ························································· 3分 其它20% ······································································································ 4分 条形图中补充的高为50 ···················································································· 5分（3）54 ········································································································ 7分 （4）解：1860×40%=744（人）答：最喜欢“球类”活动的学生约有744人． ······················································ 9分 20．解：（1）根据题意可列表或树状图如下：第一次第二次12341 —— （1，2） （1，3） （1，4）2 （2，1） —— （2，3） （2，4）3 （3，1） （3，2） —— （3，4） 4（4，1）（4，2）（4，3）——·············································································· 5分···························································································· 5分从表或树状图可以看出所有可能结果共有12种，且每种结果发生的可能性相同，符合条件的结果有8种， ∴P （和为奇数）23= ···················································································· 7分 （2）不公平．∵小明先挑选的概率是P （和为奇数）23=，小亮先挑选的概率是P （和为偶数）13=，∵2133≠，∴不公平． ····················································································· 9分五、解答证明题（每小题8分，共16分） 21．（1）证明：∵AD 平分∠BAC∴∠BAD=21∠BAC ． （1，2） （1，3） （1，4） 2341 （1，1） （2，3） （2，4） 1342 （3，1） （3，2） （3，4） 1243 （4，1） （4，2） （4，3）1234 第一次摸球第二次摸球∵AE 平分∠BAF ． ∴∠BAE=21∠BAF ． 2分 ∵∠BAC+∠BAF=180°∴∠BAD+∠BAE=21 （∠BAC+∠BAF ）= 21×180°=90° ∴∠DAE=90°．即DA ⊥AE ． 4分 （2）AB=DE 5分 理由是：∵AB=AC ，AD 平分∠BAC ． ∴AD ⊥BC ，即∠ADB=90°． ∵BE ⊥AE ．∴∠AEB=90° 又∵∠DAE=90°（已证），∴四边形AEBD 是矩形．故AB=DE ． 8分22、解：（1）不同．理由如下：往、返距离相等，去时用了2小时，而返回时用了2.5小时，∴往、返速度不同． ··················································································· 2分（2）设返程中y 与x 之间的表达式为y kx b =+，则120 2.505.k b k b =+⎧⎨=+⎩，解之，得48240.k b =-⎧⎨=⎩，···················································································· 5分∴48240y x =-+．（2.55x x ≤≤）（评卷时，自变量的取值范围不作要求） ······ 6分 （3）当4x =时，汽车在返程中，48424048y ∴=-⨯+=．∴这辆汽车从甲地出发4h 时与甲地的距离为48km ． ········································· 8分六、解答证明题（23小题10分,24小题12分,共22分） 23、证明：（1） 连结AC ，如图∵C 是弧BD 的中点∴∠BDC =∠DBC 1分 又∠BDC =∠BAC在三角形ABC 中，∠ACB =90°，CE ⊥AB ∴ ∠BCE=∠BAC∠BCE =∠DBC 3分 ∴ CF =BF 4分因此，CF =BF ． （2）解法一：作CG ⊥AD 于点G ， ∵C 是弧BD 的中点∴ ∠CAG =∠BAC ， 即AC 是∠BAD 的角平分线．·············· 5分 ∴ CE =CG ，AE =AG 6分 在Rt △BCE 与Rt △DCG 中，CE =CG ， CB =CD ∴Rt △BCE ≌Rt △DCG∴BE =DG 7分 ∴AE =AB -BE =AG =AD +DG 即 6-BE =2+DG∴2BE =4，即 BE =2 8分又 △BCE ∽△BAC∴ 212BC BEAB ==· 9分 32±=BC （舍去负值）∴32=BC 10分（2）解法二：∵AB 是⊙O 的直径，CE ⊥AB∴∠BEF=︒=∠90ADB ， 5分 在Rt ADB △与Rt FEB △中，∵FBE ABD ∠=∠ ∴ADB △∽FEB △，则BFABEF AD =即BFEF 62=， ∴EF BF 3= 6分 又∵CF BF =， ∴EF CF 3= 利用勾股定理得：EF EF BF BE 2222=-= 7分又∵△EBC ∽△ECA 则CEBE AE CE =，即则BE AE CE ⋅=28分 ∴BE BE EF CF ⋅-=+)6()(2即EF EF EF EF 22)226()3(2⋅-=+∴22=EF 9分 ∴3222=+=CE BE BC 10分24．解：（1）解方程01682=+-x x ，得421==x x由实数m 是方程01682=+-x x 的一个实数根，得m=4 ∴点A ，C 的坐标分别是A （4，0）和C （0，4）． 1分将A （4，0）和C （0，4）的坐标分别代人c bx x y ++-=221 得⎩⎨⎧==⇒⎩⎨⎧==++-414048c b c c b ∴抛物线的解析式为4212++-=x x y 3分 （2）由4212++-=x x y ，令y=0，得04212=++-x x ，解此方程得2,421-==x x∴点B 的坐标为B （2，0），故AB=6， S △ABC =21·AB ·CO=12 4分设AD=k （0≤k ≤6）， ∵ED ∥BC ∴△ADE ∽△ABC ，从而36)6()(222k k AB AD S S ABC ADE ===∆∆ ∴32k S ADE=∆ （5分） 同理可知，3)6(2-=∆k S BDF6分∴S 四边形DECF =S △ABC －S △ADE －S △BDF=6)3(3243222+--=+-k k k （7分） 当且仅当k =3时，S 四边形DECF 有最大值为6，此时D （1，0） 8分 （3）存在满足条件的点N ，使得∠NOB=∠AMO ，设点N （y x ,） ∵若M 是⊙G 的优弧ACO 上的一个动点∴∠NOB=∠AMO=∠ACO=45° 9分 ①当点N 在x 轴上方时，tan45°=x y xy-=⇒=-1 又∵4212++-=x x y ∴4212++-x x 3220842±=⇒=--⇒-=x x x x ∵点N 在这个抛物线位于y 轴左侧的图象上，从而有N （232,322--） 10分 ②当点N 在x 轴下方时，tan45°=x y xy=⇒=--1 又∵4212++-=x x y ∴22842122±=⇒=⇒=++-x x x x x ∵点N 在这个抛物线位于y 轴左侧的图象上，从而有N （22,22--） 12分。
2012年全国中考数学试题分类解析汇编(159套63专题)专题45_梯形(附答案)
2012年全国中考数学试题分类解析汇编(159套63专题）专题45：梯形一、选择题1. （2012广东广州3分）如图，在等腰梯形ABCD中，BC∥AD，AD=5，DC=4，DE∥AB交BC 于点E，且EC=3，则梯形ABCD的周长是【】A．26 B．25 C．21 D．202. （2012江苏无锡3分）如图，梯形ABCD中，AD∥BC，AD=3，AB=5，BC=9，CD的垂直平分线交BC于E，连接DE，则四边形ABED的周长等于【】A． 17 B．18 C．19 D．203. （2012福建漳州4分）如图，在等腰梯形ABCD中，AD∥BC，AB=DC，∠B=80o，则∠D的度数是【】A．120o B．110o C．100o D．80o4. （2012湖北十堰3分）如图，梯形ABCD中，AD∥BC，点M是AD的中点，且MB=MC，若AD=4，AB=6，BC=8，则梯形ABCD的周长为【】A．22 B．24 C．26 D．285. （2012四川宜宾3分）如图，在四边形ABCD中，DC∥AB，CB⊥AB，AB=AD，CD=12 AB，点E、F分别为AB．AD的中点，则△AEF与多边形BCDFE的面积之比为【】A．17B．16C．15D．146. （2012四川达州3分）如图，在梯形ABCD中，AD∥BC，E、F分别是AB、CD的中点，则下列结论：①EF∥AD；②S△ABO=S△DCO；③△OGH是等腰三角形；④BG=DG；⑤EG=HF。
其中正确的个数是【】A、1个B、2个C、3个D、4个7. （2012山东临沂3分）如图，在等腰梯形ABCD中，AD∥BC，对角线AC．BD相交于点O，下列结论不一定正确的是【】A．AC=BD B．OB=OC C．∠BCD=∠BDC D．∠ABD=∠ACD8. （2012山东烟台3分）如图，在平面直角坐标中，等腰梯形ABCD的下底在x轴上，且B点坐标为（4，0），D点坐标为（0，3），则AC长为【】A ．4B ．5C ．6D ．不能确定9. （2012广西北海3分）如图，梯形ABCD 中AD//BC ，对角线AC 、BD 相交于点O ，若AO∶CO ＝2：3，AD ＝4，则BC 等于：【 】A ．12B ．8C ．7D ．610. （2012广西贵港3分）如图，在直角梯形ABCD 中，AD//BC ，∠C＝90°，AD ＝5，BC＝9，以A 为中心将腰AB 顺时针旋转90°至AE ，连接DE ，则△ADE 的面积等于【 】A ．10B ．11C ．12D ．1311. （2012内蒙古呼和浩特3分）已知：在等腰梯形ABCD 中，AD∥BC，AC⊥BD，AD=3，BC=7，则梯形的面积是【 】A ．25B ．50C ．D 12. （2012黑龙江龙东地区3分）如图，已知直角梯形ABCD 中，AD∥BC，∠ABC=90°，AB=BC=2AD ，点E 、F 分别是AB 、BC 边的中点，连接AF 、CE 交于点M ，连接BM 并延长交CD 于点N ，连接DE 交AF 于点P ，则结论：①∠ABN=∠CBN； ②DE∥BN； ③△CDE 是等腰三角形；④EM 3 ：； ⑤EPM ABCD 1S S 8∆=梯形，正确的个数有【 】A. 5个B. 4个C. 3个D. 2个二、填空题1. （2012上海市4分）如图，已知梯形ABCD ，AD∥BC，BC=2AD ，如果AD=aAB=b ，那么AC = ▲ （用a b，表示）．2. （2012江苏南通3分）如图，在梯形ABCD 中，AB∥CD，∠A＋∠B＝90º，AB ＝7cm ，BC＝3cm ，AD ＝4cm ，则CD ＝ ▲ cm ．3. （2012江苏扬州3分）已知梯形的中位线长是4cm ，下底长是5cm ，则它的上底长是 ▲ cm ．4. （2012福建厦门4分）如图，在等腰梯形ABCD 中，AD∥BC，对角线AC 与BD 相交于点O ，若OB ＝3，则OC ＝ ▲ ．5. （2012湖北咸宁3分）如图，在梯形ABCD 中，AD∥BC，︒=∠90C ，BE 平分∠ABC 且交CD 于E ，E 为CD 的中点，EF∥BC 交AB 于F ，EG∥AB 交BC 于G ，当2=AD ，12=BC 时，四边形BGEF 的周长为 ▲ ．6. （2012湖北黄冈3分）如图，在梯形ABCD 中，AD∥BC ，AD=4，AB=CD=5，∠B=60°，则下底BC 的长为 ▲ .7. （2012湖南长沙3分）如图，等腰梯形ABCD 中，AD∥BC，AB=AD=2，∠B=60°，则BC 的长为▲ ．8. （2012湖南常德3分）若梯形的上底长是10厘米，下底长是30厘米，则它的中位线长为 ▲ 厘米。
【真题】台湾地区中考数学试题含答案解析(Word版)
台湾省中考数学试题(解析版)一、选择题（本大题共26小题）1．（•台湾）算式（﹣2）×|﹣5|﹣|﹣3|之值为何（）A．13 B．7 C．﹣13 D．﹣7【分析】原式先计算绝对值运算，再计算乘法运算，最后算加减运算即可得到结果．【解答】解：原式=﹣2×5﹣3=﹣10﹣3=﹣13，故选C【点评】此题考查了有理数的混合运算，熟练掌握运算法则是解本题的关键．2．（•台湾）下列哪一个选项中的等式成立（）A．=2 B．=3 C．=4 D．=5【分析】根据二次根式的性质和化简方法，逐项判断即可．【解答】解：∵=2，∴选项A符合题意；∵=3，∴选项B不符合题意；∵=16，∴选项C不符合题意；∵=25，∴选项D不符合题意．故选：A．【点评】此题主要考查了二次根式的性质和化简，要熟练掌握，化简二次根式的步骤：①把被开方数分解因式；②利用积的算术平方根的性质，把被开方数中能开得尽方的因数（或因式）都开出来；③化简后的二次根式中的被开方数中每一个因数（或因式）的指数都小于根指数2．3．（•台湾）计算6x•（3﹣2x）的结果，与下列哪一个式子相同（）A．﹣12x2+18x B．﹣12x2+3 C．16x D．6x【分析】根据单项式乘以多项式法则可得．【解答】解：6x•（3﹣2x）=18x﹣12x2，故选：A．【点评】本题主要考查整式的乘法，熟练掌握单项式乘以多项式的法则是解题的关键．4．（•台湾）若阿光以四种不同的方式连接正六边形ABCDEF的两条对角线，连接后的情形如下列选项中的图形所示，则下列哪一个图形不是轴对称图形（）A．B．C．D．【分析】根据轴对称图形的概念：如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴进行分析即可．【解答】解：A、是轴对称图形，故此选项错误；B、是轴对称图形，故此选项错误；C、不是轴对称图形，故此选项错误；D、不是轴对称图形，故此选项正确；故选：D．【点评】此题主要考查了轴对称图形，关键是掌握轴对称图形的概念．5．（•台湾）已知坐标平面上有两直线相交于一点（2，a），且两直线的方程式分别为2x+3y=7，3x﹣2y=b，其中a，b为两数，求a+b之值为何（）A．1 B．﹣1 C．5 D．﹣5【分析】把问题转化为关于a、b的方程组即可解决问题．【解答】解：由题意，解得，∴a+b=5，故选C．【点评】本题考查两条直线相交或平行的性质，二元一次方程组等知识，解题的关键是灵活运用所学知识解决问题，学会用转化的思想思考问题．6．（•台湾）阿信、小怡两人打算搭乘同一班次电车上学，若此班次电车共有5节车厢，且阿信从任意一节车厢上车的机会相等，小怡从任意一节车厢上车的机会相等，则两人从同一节车厢上车的概率为何（）A．B．C．D．【分析】根据阿信、小怡各有5节车厢可选择，共有25种，两人在不同车厢的情况数是20种，得出在同一节车厢上车的情况数是5种，根据概率公式即可得出答案．【解答】解：二人上5节车厢的情况数是：5×5=25，两人在不同车厢的情况数是5×4=20，则两人从同一节车厢上车的概率是=；故选B．【点评】此题主要考查了概率的求法．用到的知识点为：概率=所求情况数与总情况数之比．7．（•台湾）平面上有A、B、C三点，其中AB=3，BC=4，AC=5，若分别以A、B、C为圆心，半径长为2画圆，画出圆A，圆B，圆C，则下列叙述何者正确（）A．圆A与圆C外切，圆B与圆C外切B．圆A与圆C外切，圆B与圆C外离C．圆A与圆C外离，圆B与圆C外切D．圆A与圆C外离，圆B与圆C外离【分析】根据圆和圆的位置与两圆的圆心距、半径的数量之间的关系，即可判定．【解答】解：∵AC=5＞2+2，即AC＞R A+R B，∴⊙A与⊙C外离，∵BC=4=2+2，即BC=R B+R C，∴⊙B与⊙C相切．故选C．【点评】本题考查圆与圆的位置关系，记住：①两圆外离⇔d＞R+r；②两圆外切⇔d=R+r；③两圆相交⇔R﹣r＜d＜R+r（R≥r）；④两圆内切⇔d=R﹣r（R＞r）；⑤两圆内含⇔d＜R﹣r（R＞r）是解题的关键．8．（•台湾）下列选项中所表示的数，哪一个与252的最大公因数为42（）A．2×3×52×72B．2×32×5×72C．22×3×52×7 D．22×32×5×7【分析】先将42与252分别分解质因数，再找到与252的最大公因数为42的数即可．【解答】解：∵42=2×3×7，252=22×32×7，∴2×3×52×72与252的最大公因数为42．故选：A．【点评】考查了有理数的乘方，有理数的乘法，关键是将42与252分解质因数．9．（•台湾）某高中的篮球队球员中，一、二年级的成员共有8人，三年级的成员有3人，一、二年级的成员身高（单位：公分）如下：172，172，174，174，176，176，178，178若队中所有成员的平均身高为178公分，则队中三年级成员的平均身高为几公分（）A．178 B．181 C．183 D．186【分析】先求出一、二年级的成员的总共身高，再根据总数=平均数×数量可求一、二、三年级的成员的总共身高，依此可求三年级成员的总共身高，再除以3即可求解．【解答】解：172+172+174+174+176+176+178+178=1400（公分），（178×11﹣1400）÷3=（1958﹣1400）÷3=186（公分）．答：队中三年级成员的平均身高为186公分．故选：D．【点评】考查了平均数问题，关键是熟练掌握平均数的计算公式．10．（•台湾）已知在卡乐芙超市内购物总金额超过190元时，购物总金额有打八折的优惠，安妮带200元到卡乐芙超市买棒棒糖．若棒棒糖每根9元，则她最多可买多少根棒棒糖（）A．22 B．23 C．27 D．28【分析】设买x根棒棒糖，根据题意列出不等式，解不等式即可．【解答】解：设买x根棒棒糖，由题意得，9x×0.8≤200，解得，x≤，∴她最多可买27根棒棒糖，故选：C．【点评】本题考查的是一元一次不等式的应用，根据题意正确列出不等式、并正确解出不等式是解题的关键．11．（•台湾）如图，△ABC中，D，E两点分别在AB，BC上，若AD：DB=CE：EB=2：3，则△DBE与△ADC的面积比为（）A．3：5 B．4：5 C．9：10 D．15：16【分析】根据三角形面积求法进而得出S△BDC ：S△ADC=3：2，S△BDE：S△DCE=3：2，即可得出答案．【解答】解：∵AD：DB=CE：EB=2：3，∴S△BDC ：S△ADC=3：2，S△BDE：S△DCE=3：2，∴设S△BDC =3x，则S△ADC=2x，S△BED=1.8x，S△DCE=1.2x，故△DBE与△ADC的面积比为：1.8x：2x=9：10．故选：C．【点评】此题主要考查了三角形面积求法，正确利用三角形边长关系得出面积比是解题关键．12．（•台湾）一元二次方程式x2﹣8x=48可表示成（x﹣a）2=48+b的形式，其中a、b为整数，求a+b之值为何（）A．20 B．12 C．﹣12 D．﹣20【分析】将一元二次方程式x2﹣8x=48配方，可求a、b，再代入代数式即可求解．【解答】解：x2﹣8x=48，x2﹣8x+16=48+16，（x﹣4）2=48+16，a=4，b=16，a+b=20．故选：A．【点评】此题考查了配方法解一元二次方程，解题时要注意解题步骤的准确应用．选择用配方法解一元二次方程时，最好使方程的二次项的系数为1，一次项的系数是2的倍数．13．（•台湾）已知坐标平面上有一长方形ABCD，其坐标分别为A（0，0），B（2，0），C（2，1），D（0，1），今固定B点并将此长方形依顺时针方向旋转，如图所示．若旋转后C点的坐标为（3，0），则旋转后D点的坐标为何（）A．（2，2） B．（2，3） C．（3，3） D．（3，2）【分析】先根据旋转后C点的坐标为（3，0），得出点C落在x轴上，再根据AC=3，DC=2，即可得到点D的坐标为（3，2）．【解答】解：∵旋转后C点的坐标为（3，0），∴点C落在x轴上，∴此时AC=3，DC=2，∴点D的坐标为（3，2），故选：D．【点评】本题主要考查了旋转的性质以及矩形的性质的运用，解题时注意：矩形的四个角都是直角，对边相等．14．（•台湾）如图为平面上五条直线L1，L2，L3，L4，L5相交的情形，根据图中标示的角度，判断下列叙述何者正确（）A．L1和L3平行，L2和L3平行B．L1和L3平行，L2和L3不平行C．L1和L3不平行，L2和L3平行D．L1和L3不平行，L2和L3不平行【分析】根据同旁内角不互补，可得两直线不平行；根据内错角相等，可得两直线平行．【解答】解：∵92°+92°≠180°，∴L1和L3不平行，∵88°=88°，∴L2和L3平行，故选：C．【点评】本题主要考查了平行线的判定，解题时注意：同旁内角互补，两直线平行；内错角相等，两直线平行．15．（•台湾）威立到小吃店买水饺，他身上带的钱恰好等于15粒虾仁水饺或20粒韭菜水饺的价钱，若威立先买了9粒虾仁水饺，则他身上剩下的钱恰好可买多少粒韭菜水饺（）A．6 B．8 C．9 D．12【分析】可设1粒虾仁水饺为x元，1粒韭菜水饺为y元，由题意可得到y与x 之间的关系式，再利用整体思想可求得答案．【解答】解：设1粒虾仁水饺为x元，1粒韭菜水饺为y元，则由题意可得15x=20y，∴3x=4y，∴15x﹣9x=6x=2×3x=2×4y=8y，∴他身上剩下的钱恰好可买8粒韭菜水饺，故选B．【点评】本题主要考查方程的应用，利用条件找到1粒虾仁水饺和1粒韭菜水饺的价钱之间的关系是解题的关键，注意整体思想的应用．16．（•台湾）将图1中五边形纸片ABCDE的A点以BE为折线往下折，A点恰好落在CD上，如图2所示，再分别以图2的AB，AE为折线，将C，D两点往上折，使得A、B、C、D、E五点均在同一平面上，如图3所示，若图1中∠A=124°，则图3中∠CAD的度数为何（）A．56 B．60 C．62 D．68【分析】根据三角形内角和定理和折叠的性质来解答即可．【解答】解：由图（2）知，∠BAC+∠EAD=180°﹣124°=56°，所以图（3）中∠CAD=180°﹣56°×2=68°．故选：D．【点评】本题考查了多边形内角与外角，结合图形解答，需要学生具备一定的读图能力和空间想象能力．17．（•台湾）若a，b为两质数且相差2，则ab+1之值可能为下列何者（）A．392B．402C．412D．422【分析】根据选项的数值，得到ab+1的值，进一步根据平方差公式得到ab的乘积形式，再根据质数的定义即可求解．【解答】解：A、当ab+1=392时，ab=392﹣1=40×38，与a，b为两质数且相差2不符合，故本选项错误；B、当ab+1=402时，ab=402﹣1=41×39，与a，b为两质数且相差2不符合，故本选项错误；C、当ab+1=412时，ab=412﹣1=42×40，与a，b为两质数且相差2不符合，故本选项错误；D、当ab+1=422时，ab=422﹣1=43×41，正好与a，b为两质数且相差2符合，故本选项正确，故选：D．【点评】本题考查的是因式分解的应用，质数的定义，解答此类题目的关键是得到ab是哪两个相差为2的数的积．18．（•台湾）如图，O为锐角三角形ABC的外心，四边形OCDE为正方形，其中E点在△ABC的外部，判断下列叙述何者正确（）A．O是△AEB的外心，O是△AED的外心B．O是△AEB的外心，O不是△AED的外心C．O不是△AEB的外心，O是△AED的外心D．O不是△AEB的外心，O不是△AED的外心【分析】根据三角形的外心的性质，可以证明O是△ABE的外心，不是△AED的外心．【解答】解：如图，连接OA、OB、OD．∵O是△ABC的外心，∴OA=OB=OC，∵四边形OCDE是正方形，∴OA=OB=OE，∴O是△ABE的外心，∵OA=OE≠OD，∴O表示△AED的外心，故选B．【点评】本题考查三角形的外心的性质．正方形的性质等知识，解本题的关键是灵活运用所学知识解决问题，属于中考常考题型．19．（•台湾）如图为互相垂直的两直线将四边形ABCD分成四个区域的情形，若∠A=100°，∠B=∠D=85°，∠C=90°，则根据图中标示的角，判断下列∠1，∠2，∠3的大小关系，何者正确（）A．∠1=∠2＞∠3 B．∠1=∠3＞∠2 C．∠2＞∠1=∠3 D．∠3＞∠1=∠2【分析】根据多边形的内角和与外角和即可判断．【解答】解：∵（180°﹣∠1）+∠2=360°﹣90°﹣90°=180°∴∠1=∠2∵（180°﹣∠2）+∠3=360°﹣85°﹣90°=185°∴∠3﹣∠2=5°，∴∠3＞∠2∴∠3＞∠1=∠2故选（D）【点评】本题考查多边形的内角与外角，解题的关键是熟练运用多边形的内角和与外角和，本题属于基础题型．20．（•台湾）如图的数轴上有O、A、B三点，其中O为原点，A点所表示的数为106，根据图中数轴上这三点之间的实际距离进行估计，下列何者最接近B点所表示的数（）A．2×106B．4×106C．2×107D．4×108【分析】根据数轴上的数据求出OA的长度，从而估算出OB的长度，即可估算出点B表示的数，从而得解．【解答】解：由数轴的信息知：OA=106；∴B点表示的实数为：20=2×107；故选C．【点评】本题考查了数轴与有理数的加法运算，求出点D表示的数是解题的关键．21．（•台湾）如图，△ABC、△ADE中，C、E两点分别在AD、AB上，且BC与DE相交于F点，若∠A=90°，∠B=∠D=30°，AC=AE=1，则四边形AEFC的周长为何（）A．2 B．2 C．2+D．2+【分析】根据三角形的内角和得到∠AED=∠ACB=60°，根据三角形的外角的性质得到∠B=∠EFB=∠CFD=∠D，根据等腰三角形的判定得到BE=EF=CF=CD，于是得到四边形AEFC的周长=AB+AC．【解答】解：∵∠A=90°，∠B=∠D=30°，∴∠AED=∠ACB=60°，∵∠AED=∠B+∠EFB=∠ACB=∠CFD+∠D=60°，∴∠EFB=∠CFD=30°，∴∠B=∠EFB=∠CFD=∠D，∴BE=EF=CF=CD，∴四边形AEFC的周长=AB+AC，∵∠A=90°，AE=AC=1，∴AB=AD=，∴四边形AEFC的周长=2．故选B．【点评】本题考查了等腰三角形的性质，解直角三角形，三角形的外角的性质，熟练掌握等腰三角形的判定与性质是解题的关键．22．（•台湾）已知坐标平面上有两个二次函数y=a（x+1）（x﹣7），y=b（x+1）（x ﹣15）的图形，其中a、b为整数．判断将二次函数y=b（x+1）（x﹣15）的图形依下列哪一种方式平移后，会使得此两图形的对称轴重叠（）A．向左平移4单位 B．向右平移4单位C．向左平移8单位 D．向右平移8单位【分析】将二次函数解析式展开，结合二次函数的性质找出两二次函数的对称轴，二者做差后即可得出平移方向及距离．【解答】解：∵y=a（x+1）（x﹣7）=ax2﹣6ax﹣7a，y=b（x+1）（x﹣15）=bx2﹣14bx ﹣15b，∴二次函数y=a（x+1）（x﹣7）的对称轴为直线x=3，二次函数y=b（x+1）（x﹣15）的对称轴为直线x=7，∵3﹣7=﹣4，∴将二次函数y=b（x+1）（x﹣15）的图形向左平移4个单位，两图形的对称轴重叠．故选A．【点评】本题考查了二次函数图象与几何变换以及二次函数的性质，根据二次函数的性质找出两个二次函数的对称轴是解题的关键．23．（•台湾）如图为阿辉，小燕一起到商店分别买了数杯饮料与在家分饮料的经过．若每杯饮料的价格均相同，则根据图中的对话，判断阿辉买了多少杯饮料（）A．22 B．25 C．47 D．50【分析】根据题意列出算式，计算即可得到结果．【解答】解：根据题意得：[（1000+120）﹣（2000﹣1120）]÷6=40，880÷40=22（杯），则阿辉买了22杯饮料，故选A【点评】此题考查了有理数的混合运算，列出正确的算式是解本题的关键．24．（•台湾）如图，水平桌面上有个内部装水的长方体箱子，箱内有一个与底面垂直的隔板，且隔板左右两侧的水面高度为别为40公分，50公分，今将隔板抽出，若过程中箱内的水量未改变，且不计箱子及隔板厚度，则根据图中的数据，求隔板抽出后水面静止时，箱内的水面高度为多少公分（）A．43 B．44 C．45 D．46【分析】设长方形的宽为x公分，抽出隔板后之水面高度为h公分，根据题意列出方程，求出方程的解即可．【解答】解：设长方形的宽为x公分，抽出隔板后之水面高度为h公分，长方形的长为130+70=200（公分）×40+×50=200•x•h，解得：h=44，故选B．【点评】本题考查了一元一次方程的应用，能根据题意列出方程是解此题的关键．25．（•台湾）如图，某计算机中有、、三个按键，以下是这三个按键的功能．1．：将荧幕显示的数变成它的正平方根，例如：荧幕显示的数为49时，按下后会变成7．2．：将荧幕显示的数变成它的倒数，例如：荧幕显示的数为25时，按下后会变成0.04．3．：将荧幕显示的数变成它的平方，例如：荧幕显示的数为6时，按下后会变成36．若荧幕显示的数为100时，小刘第一下按，第二下按，第三下按，之后以、、的顺序轮流按，则当他按了第100下后荧幕显示的数是多少（）A．0.01 B．0.1 C．10 D．100【分析】根据题中的按键顺序确定出显示的数即可．【解答】解：根据题意得：=10，=0.1，0.12=0.01，=0.1，=10，102=100，100÷6=16…4，则第100次为0.1．故选B【点评】此题考查了计算器﹣数的平方，弄清按键顺序是解本题的关键．26．（•台湾）如图为两正方形ABCD，BPQR重叠的情形，其中R点在AD上，CD 与QR相交于S点．若两正方形ABCD、BPQR的面积分别为16、25，则四边形RBCS的面积为何（）A．8 B．C．D．【分析】根据正方形的边长，根据勾股定理求出AR，求出△ABR∽△DRS，求出DS，根据面积公式求出即可．【解答】解：∵正方形ABCD的面积为16，正方形BPQR面积为25，∴正方形ABCD的边长为4，正方形BPQR的边长为5，在Rt△ABR中，AB=4，BR=5，由勾股定理得：AR=3，∵四边形ABCD是正方形，∴∠A=∠D=∠BRQ=90°，∴∠ABR +∠ARB=90°，∠ARB +∠DRS=90°， ∴∠ABR=∠DRS ， ∵∠A=∠D ， ∴△ABR ∽△DRS ， ∴=， ∴=，∴DS=，∴阴影部分的面积S=S 正方形ABCD ﹣S △ABR ﹣S △RDS =4×4﹣﹣1××=，故选D ．【点评】本题考查了正方形的性质，相似三角形的性质和判定，能求出△ABR 和△RDS 的面积是解此题的关键．二、解答题（本大题共2小题）27．（•台湾）今有甲、乙、丙三名候选人参与某村村长选举，共发出1800张选票，得票数最高者为当选人，且废票不计入任何一位候选人之得票数内，全村设有四个投开票所，目前第一、第二、第三投开票所已开完所有选票，剩下第四投开票所尚未开票，结果如表所示： 投开票所候选人 废票 合计甲乙 丙 一 200 211 147 12 570 二2868524415630三97412057350四250（单位：票）请回答下列问题：（1）请分别写出目前甲、乙、丙三名候选人的得票数；（2）承（1），请分别判断甲、乙两名候选人是否还有机会当选村长，并详细解释或完整写出你的解题过程．【分析】（1）直接根据题意将三个投票所得所有票数相加得出答案；（2）利用（1）中所求，进而分别分析得票的张数得出答案．【解答】解：（1）由图表可得：甲得票数为：200+286+97=583；乙得票数为：211+85+41=337；丙得票数为：147+244+205=596；（2）由（1）得：596﹣583=13，即丙目前领先甲13票，所以第四投票所甲赢丙14票以上，则甲当选，故甲可能当选；596﹣337=259＞250，若第四投票所250票皆给乙，乙的总票数仍然比丙低，故乙不可能当选．【点评】此题主要考查了推理与论证，正确利用表格中数据分析得票情况是解题关键．28．（•台湾）如图，在坐标平面上，O为原点，另有A（0，3），B（﹣5，0），C （6，0）三点，直线L通过C点且与y轴相交于D点，请回答下列问题：（1）已知直线L的方程为5x﹣3y=k，求k的值．（2）承（1），请完整说明△AOB与△COD相似的理由．【分析】（1）利用函数图象上的点的特点，即可求出k的值；（2）先求出OA，OB，OC，OD，即可得出，即可得出结论．【解答】解：（1）∵直线L：5x﹣3y=k过点C（6，0），∴5×6﹣3×0=k，∴k=30，（2）由（1）知，直线L：5x﹣3y=30，∵直线L与y轴的交点为D，令x=0，∴﹣3y=30，∴y=﹣10，∴D（0，﹣10），∴OD=10，∵A（0，3），B（﹣5，0），C（6，0），∴OA=3，OB=5，OC=6，∴=，=，∴，∵∠AOB=∠COD=90°，∴△AOB∽△COD．【点评】此题是一次函数综合题，主要考查了函数图象上点的特点，相似三角形的判定，解本题的根据是求出点D的坐标．。
台湾地区中考数学试卷及答案解析（）
台湾省中考数学试卷一、选择题（1～25题）1．x=﹣3，y=1为下列哪一个二元一次方程式的解？（）A．x+2y=﹣1 B．x﹣2y=1 C．2x+3y=6 D．2x﹣3y=﹣62．算式[﹣5﹣（﹣11）]÷（×4）之值为何？（）A．1 B．16 C．﹣ D．﹣3．计算（2x+1）（x﹣1）﹣（x2+x﹣2）的结果，与下列哪一个式子相同？（）A．x2﹣2x+1 B．x2﹣2x﹣3 C．x2+x﹣3 D．x2﹣34．如图，已知扇形AOB的半径为10公分，圆心角为54°，则此扇形面积为多少平方公分？（）A．100π B．20π C．15π D．5π5．如图数轴的A、B、C三点所表示的数分别为a、b、c．若|a﹣b|=3，|b﹣c|=5，且原点O与A、B的距离分别为4、1，则关于O的位置，下列叙述何者正确？（）A．在A的左边 B．介于A、B之间 C．介于B、C之间 D．在C的右边6．多项式77x2﹣13x﹣30可因式分解成（7x+a）（bx+c），其中a、b、c均为整数，求a+b+c之值为何？（）A．0 B．10 C．12 D．227．图（一）、图（二）分别为甲、乙两班学生参加投篮测验的投进球数直方图．若甲、乙两班学生的投进球数的众数分别为a、b；中位数分别为c、d，则下列关于a、b、c、d的大小关系，何者正确？（）A．a＞b，c＞d B．a＞b，c＜d C．a＜b，c＞d D．a＜b，c＜d8．如图，有一平行四边形ABCD与一正方形CEFG，其中E点在AD上．若∠ECD=35°，∠AEF=15°，则∠B的度数为何？（）A．50 B．55 C．70 D．759．小昱和阿帆均从同一本书的第1页开始，逐页依顺序在每一页上写一个数．小昱在第1页写1，且之后每一页写的数均为他在前一页写的数加2；阿帆在第1页写1，且之后每一页写的数均为他在前一页写的数加7．若小昱在某页写的数为101，则阿帆在该页写的数为何？（）A．350 B．351 C．356 D．35810．甲箱内有4颗球，颜色分别为红、黄、绿、蓝；乙箱内有3颗球，颜色分别为红、黄、黑．小赖打算同时从甲、乙两个箱子中各抽出一颗球，若同一箱中每球被抽出的机会相等，则小赖抽出的两颗球颜色相同的机率为何？（）A． B． C． D．11．坐标平面上有一个二元一次方程式的图形，此图形通过（﹣3，0）、（0，﹣5）两点．判断此图形与下列哪一个方程式的图形的交点在第三象限？（）A．x﹣4=0 B．x+4=0 C．y﹣4=0 D．y+4=012．如图，△ABC中，D、E两点分别在AC、BC上，DE为BC的中垂线，BD为∠ADE的角平分线．若∠A=58°，则∠ABD的度数为何？（）A．58 B．59 C．61 D．6213．若一正方形的面积为20平方公分，周长为x公分，则x的值介于下列哪两个整数之间？（）A．16，17 B．17，18 C．18，19 D．19，2014．如图，圆O通过五边形OABCD的四个顶点．若=150°，∠A=65°，∠D=60°，则的度数为何？（）A．25 B．40 C．50 D．5515．如图的六边形是由甲、乙两个长方形和丙、丁两个等腰直角三角形所组成，其中甲、乙的面积和等于丙、丁的面积和．若丙的一股长为2，且丁的面积比丙的面积小，则丁的一股长为何？（）A． B． C．2﹣D．4﹣216．如图的矩形ABCD中，E点在CD上，且AE＜AC．若P、Q两点分别在AD、AE上，AP：PD=4：1，AQ：QE=4：1，直线PQ交AC于R点，且Q、R两点到CD的距离分别为q、r，则下列关系何者正确？（）A．q＜r，QE=RC B．q＜r，QE＜RC C．q=r，QE=RC D．q=r，QE＜RC17．已知a、b、c 为三正整数，且a、b的最大公因子为12，a、c的最大公因子为18．若a介于50与100之间，则下列叙述何者正确？（）A．8是a的因子，8是b的因子B．8是a的因子，8不是b的因子C．8不是a的因子，8是c的因子D．8不是a的因子，8不是c的因子18．如图，有一内部装有水的直圆柱形水桶，桶高20公分；另有一直圆柱形的实心铁柱，柱高30公分，直立放置于水桶底面上，水桶内的水面高度为12公分，且水桶与铁柱的底面半径比为2：1．今小贤将铁柱移至水桶外部，过程中水桶内的水量未改变，若不计水桶厚度，则水桶内的水面高度变为多少公分？（）A．4.5 B．6 C．8 D．919．表为小洁打算在某电信公司购买一支MAT手机与搭配一个门号的两种方案．此公司每个月收取通话费与月租费的方式如下：若通话费超过月租费，只收通话费；若通话费不超过月租费，只收月租费．若小洁每个月的通话费均为x元，x为400到600之间的整数，则在不考虑其他费用并使用两年的情况下，x至少为多少才会使得选择乙方案的总花费比甲方案便宜？（）甲方案乙方案门号的月租费（元）400 600MAT手机价格（元）15000 13000注意事项：以上方案两年内不可变更月租费A．500 B．516 C．517 D．60020．如图，以矩形ABCD的A为圆心，AD长为半径画弧，交AB于F点；再以C为圆心，CD长为半径画弧，交AB于E点．若AD=5，CD=，则EF的长度为何？（）A．2 B．3 C． D．21．坐标平面上，某二次函数图形的顶点为（2，﹣1），此函数图形与x轴相交于P、Q两点，且PQ=6．若此函数图形通过（1，a）、（3，b）、（﹣1，c）、（﹣3，d）四点，则a、b、c、d之值何者为正？（）A．a B．b C．c D．d22．如图的矩形ABCD中，E为的中点，有一圆过C、D、E三点，且此圆分别与、相交于P、Q 两点．甲、乙两人想找到此圆的圆心O，其作法如下：（甲）作∠DEC的角平分线L，作的中垂线，交L于O点，则O即为所求；（乙）连接、，两线段交于一点O，则O即为所求对于甲、乙两人的作法，下列判断何者正确？（）A．两人皆正确 B．两人皆错误C．甲正确，乙错误 D．甲错误，乙正确23．如图，正六边形ABCDEF中，P、Q两点分别为△ACF、△CEF的内心．若AF=2，则PQ的长度为何？（）A．1 B．2 C．2﹣2 D．4﹣224．如图（一），为一条拉直的细线，A、B两点在上，且： =1：3，： =3：5．若先固定B点，将折向，使得重迭在上，如图（二），再从图（二）的A点及与A点重迭处一起剪开，使得细线分成三段，则此三段细线由小到大的长度比为何？（）A．1：1：1 B．1：1：2 C．1：2：2 D．1：2：525．如图，矩形ABCD中，M、E、F三点在上，N是矩形两对角线的交点．若=24， =32，=16， =8， =7，则下列哪一条直线是A、C两点的对称轴？（）A．直线MN B．直线EN C．直线FN D．直线DN二、非选择题（第1～2题）26．如图，△ABC中，AB=AC，D点在BC上，∠BAD=30°，且∠ADC=60°．请完整说明为何AD=BD 与CD=2BD的理由．27．如图，正方形ABCD是一张边长为12公分的皮革．皮雕师傅想在此皮革两相邻的角落分别切下△PDQ与△PCR后得到一个五边形PQABR，其中PD=2DQ，PC=RC，且P、Q、R三点分别在CD、AD、BC上，如图所示．（1）当皮雕师傅切下△PDQ时，若DQ长度为x公分，请你以x表示此时△PDQ的面积．（2）承（1），当x的值为多少时，五边形PQABR的面积最大？请完整说明你的理由并求出答案．台湾省中考数学试卷参考答案与试题解析一、选择题（1～25题）1．x=﹣3，y=1为下列哪一个二元一次方程式的解？（）A．x+2y=﹣1 B．x﹣2y=1 C．2x+3y=6 D．2x﹣3y=﹣6【考点】二元一次方程的解．【分析】直接利用二元一次方程的解的定义分别代入求出答案．【解答】解：将x=﹣3，y=1代入各式，A、（﹣3）+2×1=﹣1，正确；B、（﹣3）﹣2×1=﹣5≠1，故此选项错误；C、2×（﹣3）+3‧1=﹣3≠6，故此选项错误；D、2×（﹣3）﹣3‧1=﹣9≠﹣6，故此选项错误；故选：A．【点评】此题主要考查了二元一次方程的解，正确代入方程是解题关键．2．算式[﹣5﹣（﹣11）]÷（×4）之值为何？（）A．1 B．16 C．﹣ D．﹣【考点】有理数的混合运算．【专题】计算题；实数．【分析】原式先计算括号中的运算，再计算除法运算即可得到结果．【解答】解：原式=（﹣5+11）÷（3×2）=6÷6=1，故选A【点评】此题考查了有理数的混合运算，熟练掌握运算法则是解本题的关键．3．计算（2x+1）（x﹣1）﹣（x2+x﹣2）的结果，与下列哪一个式子相同？（）A．x2﹣2x+1 B．x2﹣2x﹣3 C．x2+x﹣3 D．x2﹣3【考点】整式的混合运算．【专题】计算题；整式．【分析】原式利用多项式乘以多项式法则计算，去括号合并得到最简结果，即可作出判断．【解答】解：（2x+1）（x﹣1）﹣（x2+x﹣2）=（2x2﹣2x+x﹣1）﹣（x2+x﹣2）=2x2﹣x﹣1﹣x2﹣x+2=x2﹣2x+1，故选A【点评】此题考查了整式的混合运算，熟练掌握运算法则是解本题的关键．4．如图，已知扇形AOB的半径为10公分，圆心角为54°，则此扇形面积为多少平方公分？（）A．100π B．20π C．15π D．5π【考点】扇形面积的计算．【专题】计算题；圆的有关概念及性质．【分析】利用扇形面积公式计算即可得到结果．【解答】解：∵扇形AOB的半径为10公分，圆心角为54°，∴S==15π（平方公分），扇形AOB故选C．【点评】此题考查了扇形面积的计算，熟练掌握扇形面积公式是解本题的关键．5．如图数轴的A、B、C三点所表示的数分别为a、b、c．若|a﹣b|=3，|b﹣c|=5，且原点O与A、B的距离分别为4、1，则关于O的位置，下列叙述何者正确？（）A．在A的左边 B．介于A、B之间 C．介于B、C之间 D．在C的右边【考点】数轴；绝对值．【分析】由A、B、C三点表示的数之间的关系，可以找出向量的数值，再结合原点O与A、B的距离分别为4、1，利用向量间的关系验证的正负，由此即可得出结论．【解答】解：∵|a﹣b|=3，|b﹣c|=5，∴=3， =5，∵原点O与A、B的距离分别为4、1，∴=±1， =4．①当=﹣1时，∵=+=4﹣1=3，∴=﹣1合适；②当=1时，∵=+=4+1=5，5≠3，∴=1不合适．∴点O在点B的右侧1个单位长度处，∵点C在点B的右侧5个单位长度处，∴点O介于B、C点之间．故选C．【点评】本题考查了数值、绝对值以及向量，解题的关键是确定的符号．本题属于基础题，难度不大，利用向量来解决问题给我们带来了很大的方便，而历年中考题也时常考到，但很多版本的教材中没有讲到向量，这就需要我们同学和老师在平常的练习中理解向量的含义．6．多项式77x2﹣13x﹣30可因式分解成（7x+a）（bx+c），其中a、b、c均为整数，求a+b+c之值为何？（）A．0 B．10 C．12 D．22【考点】因式分解-十字相乘法等．【分析】首先利用十字交乘法将77x2﹣13x﹣30因式分解，继而求得a，b，c的值．【解答】解：利用十字交乘法将77x2﹣13x﹣30因式分解，可得：77x2﹣13x﹣30=（7x﹣5）（11x+6）．∴a=﹣5，b=11，c=6，则a+b+c=（﹣5）+11+6=12．故选C．【点评】此题考查了十字相乘法分解因式的知识．注意ax2+bx+c（a≠0）型的式子的因式分解：这种方法的关键是把二次项系数a分解成两个因数a1，a2的积a1•a2，把常数项c分解成两个因数c1，c2的积c1•c2，并使a1c2+a2c1正好是一次项b，那么可以直接写成结果：ax2+bx+c=（a1x+c1）（a2x+c2）．7．图（一）、图（二）分别为甲、乙两班学生参加投篮测验的投进球数直方图．若甲、乙两班学生的投进球数的众数分别为a、b；中位数分别为c、d，则下列关于a、b、c、d的大小关系，何者正确？（）A．a＞b，c＞d B．a＞b，c＜d C．a＜b，c＞d D．a＜b，c＜d【考点】众数；频数（率）分布直方图；中位数．【分析】根据众数是一组数据中出现次数最多的数据，确定众数；找中位数要把数据按从小到大的顺序排列，位于最中间的一个数（或两个数的平均数）为中位数；依此即可求解．【解答】解：由图（三）、图（四）可知a=8，b=6⇒a＞b，甲班共有5+15+20+15=55（人），乙班共有25+5+15+10=55（人），则甲、乙两班的中位数均为第28人，得c=8，d=7⇒c＞d．故选A．【点评】此题考查了众数与中位数的知识．解题的关键是熟记众数与中位数的定义．8．如图，有一平行四边形ABCD与一正方形CEFG，其中E点在AD上．若∠ECD=35°，∠AEF=15°，则∠B的度数为何？（）A．50 B．55 C．70 D．75【考点】正方形的性质；平行四边形的性质．【分析】由平角的定义求出∠CED的度数，由三角形内角和定理求出∠D的度数，再由平行四边形的对角相等即可得出结果．【解答】解：∵四边形CEFG是正方形，∴∠CEF=90°，∵∠CED=180°﹣∠AEF﹣∠CEF=180°﹣15°﹣90°=75°，∴∠D=180°﹣∠CED﹣∠ECD=180°﹣75°﹣35°=70°，∵四边形ABCD为平行四边形，∴∠B=∠D=70°（平行四边形对角相等）．故选C．【点评】本题考查了正方形的性质、平行四边形的性质、三角形内角和定理等知识；熟练掌握平行四边形和正方形的性质，由三角形内角和定理求出∠D的度数是解决问题的关键．9．小昱和阿帆均从同一本书的第1页开始，逐页依顺序在每一页上写一个数．小昱在第1页写1，且之后每一页写的数均为他在前一页写的数加2；阿帆在第1页写1，且之后每一页写的数均为他在前一页写的数加7．若小昱在某页写的数为101，则阿帆在该页写的数为何？（）A．350 B．351 C．356 D．358【考点】有理数的混合运算．【专题】计算题；规律型．【分析】根据题意确定出小昱和阿帆所写的数字，设小昱所写的第n个数为101，根据规律确定出n的值，即可确定出阿帆在该页写的数．【解答】解：小昱所写的数为 1，3，5，7，…，101，…；阿帆所写的数为 1，8，15，22，…，设小昱所写的第n个数为101，根据题意得：101=1+（n﹣1）×2，整理得：2（n﹣1）=100，即n﹣1=50，解得：n=51，则阿帆所写的第51个数为1+（51﹣1）×7=1+50×7=1+350=351．故选B【点评】此题考查了有理数的混合运算，弄清题中的规律是解本题的关键．10．甲箱内有4颗球，颜色分别为红、黄、绿、蓝；乙箱内有3颗球，颜色分别为红、黄、黑．小赖打算同时从甲、乙两个箱子中各抽出一颗球，若同一箱中每球被抽出的机会相等，则小赖抽出的两颗球颜色相同的机率为何？（）A． B． C． D．【考点】列表法与树状图法．【分析】画出树状图，得出共有12种等可能的结果，颜色相同的有2种情形，即可得出结果．【解答】解：树状图如图所示：共有12种等可能的结果，颜色相同的有2种情形，故小赖抽出的两颗球颜色相同的机率==；故选：B．【点评】本题考查的是用列表法或画树状图法求概率．列表法或画树状图法可以不重复不遗漏的列出所有可能的结果，列表法适合于两步完成的事件，树状图法适合两步或两步以上完成的事件；注意概率=所求情况数与总情况数之比．11．坐标平面上有一个二元一次方程式的图形，此图形通过（﹣3，0）、（0，﹣5）两点．判断此图形与下列哪一个方程式的图形的交点在第三象限？（）A．x﹣4=0 B．x+4=0 C．y﹣4=0 D．y+4=0【考点】坐标与图形性质．【专题】平面直角坐标系．【分析】分别作出各选项中的直线，以及通过（﹣3，0）、（0，﹣5）两点的直线，根据图象即可确定出此图形与下列方程式的图形的交点在第三象限的直线方程．【解答】解：作出选项中x﹣4=0，x+4=0，y﹣4=0，y+4=0的图象，以及通过（﹣3，0）、（0，﹣5）两点直线方程，根据图象得：通过（﹣3，0）、（0，﹣5）两点直线与y+4=0的交点在第三象限，故选D【点评】此题考查了坐标与图形性质，作出相应的图象是解本题的关键．12．如图，△ABC中，D、E两点分别在AC、BC上，DE为BC的中垂线，BD为∠ADE的角平分线．若∠A=58°，则∠ABD的度数为何？（）A．58 B．59 C．61 D．62【考点】线段垂直平分线的性质．【分析】根据线段垂直平分线的性质、角平分线的定义得到∠1=∠2=∠3，求出∠4和∠C，根据三角形内角和定理计算即可．【解答】解：∵BD是∠ADE的角平分线，∴∠1=∠2，∵DE是BC的中垂线，∴∠2=∠3，∴∠1=∠2=∠3，又∠1+∠2+∠3=180°，∴∠1=∠2=∠3=60°，∴∠4=∠C=90°﹣60°=30°，∴∠ABD=180°﹣∠A﹣∠4﹣∠C=180°﹣58°﹣30°﹣30°=62°．故选：D．【点评】本题考查的是线段垂直平分线的性质、角平分线的定义以及三角形内角和定理的应用，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键．13．若一正方形的面积为20平方公分，周长为x公分，则x的值介于下列哪两个整数之间？（）A．16，17 B．17，18 C．18，19 D．19，20【考点】估算无理数的大小．【分析】由一正方形的面积为20平方公分，周长为x公分，可求得x2=320，又由172=289，182=324，即可求得答案．【解答】解：∵周长为x公分，∴边长为公分，∴（）2=20，∴=20，∴x2=320，又∵172=289，182=324，∴172＜320＜182，即172＜x2＜182，又∵x为正整数，∴x介于17和18之间，故选B．【点评】此题考查了无理数大小的估计．注意利用数的平方大小比较是解此题的方法．14．如图，圆O通过五边形OABCD的四个顶点．若=150°，∠A=65°，∠D=60°，则的度数为何？（）A．25 B．40 C．50 D．55【考点】圆心角、弧、弦的关系．【专题】计算题；圆的有关概念及性质．【分析】连接OB，OC，由半径相等得到三角形OAB，三角形OBC，三角形OCD都为等腰三角形，根据∠A=65°，∠D=60°，求出∠1与∠2的度数，根据的度数确定出∠AOD度数，进而求出∠3的度数，即可确定出的度数．【解答】解：连接OB、OC，∵OA=OB=OC=OD，∴△OAB、△OBC、△OCD，皆为等腰三角形，∵∠A=65°，∠D=60°，∴∠1=180°﹣2∠A=180°﹣2×65°=50°，∠2=180°﹣2∠D=180°﹣2×60°=60°，∵=150°，∴∠AOD=150°，∴∠3=∠AOD﹣∠1﹣∠2=150°﹣50°﹣60°=40°，则=40°．故选B【点评】此题考查了圆心角、弧、弦的关系，弄清圆心角、弧、弦的关系是解本题的关键．15．如图的六边形是由甲、乙两个长方形和丙、丁两个等腰直角三角形所组成，其中甲、乙的面积和等于丙、丁的面积和．若丙的一股长为2，且丁的面积比丙的面积小，则丁的一股长为何？（）A． B． C．2﹣D．4﹣2【考点】一元二次方程的应用．【分析】设出丁的一股为a，表示出其它，再用面积建立方程即可．【解答】解：设丁的一股长为a，且a＜2，∵甲面积+乙面积=丙面积+丁面积，∴2a+2a=×22+×a2，∴4a=2+a2，∴a2﹣8a+4=0，∴a===4±2，∵4+2＞2，不合题意舍，4﹣2＜2，合题意，∴a=4﹣2．故选D．【点评】此题是一元二次方程的应用题，主要考查了一元二次方程的解，解本题的关键是列出一元二次方程．16．如图的矩形ABCD中，E点在CD上，且AE＜AC．若P、Q两点分别在AD、AE上，AP：PD=4：1，AQ：QE=4：1，直线PQ交AC于R点，且Q、R两点到CD的距离分别为q、r，则下列关系何者正确？（）A．q＜r，QE=RC B．q＜r，QE＜RC C．q=r，QE=RC D．q=r，QE＜RC【考点】平行线分线段成比例；矩形的性质．【分析】根据矩形的性质得到AB∥CD，根据已知条件得到，根据平行线分线段成比例定理得到PQ∥CD， =4，根据平行线间的距离相等，得到q=r，证得=，于是得到结论．【解答】解：∵在矩形ABCD中，AB∥CD，∵AP：PD=4：1，AQ：QE=4：1，∴，∴PQ∥CD，∴=4，∵平行线间的距离相等，∴q=r，∵=4，∴=，∵AE＜AC，∴QE＜CR．故选D．【点评】本题考查了平行线分线段成比例定理，矩形的性质，熟练掌握平行线分线段成比例定理是解题的关键．17．已知a、b、c 为三正整数，且a、b的最大公因子为12，a、c的最大公因子为18．若a介于50与100之间，则下列叙述何者正确？（）A．8是a的因子，8是b的因子B．8是a的因子，8不是b的因子C．8不是a的因子，8是c的因子D．8不是a的因子，8不是c的因子【考点】公因式．【专题】计算题；整式．【分析】根据a、b的最大公因子为12，a、c的最大公因子为18，得到a为12与18的公倍数，再由a的范围确定出a的值，进而表示出b，即可作出判断．【解答】解：∵（a，b）=12，（a，c）=18，∴a为12与18的公倍数，又[12，18]=36，且a介于50与100之间，∴a=36×2=72，即8是a的因子，∵（a，b）=12，∴设b=12×m，其中m为正整数，又a=72=12×6，∴m和6互质，即8不是b的因子．故选B【点评】此题考查了公因式，弄清公因式与公倍数的定义是解本题的关键．18．如图，有一内部装有水的直圆柱形水桶，桶高20公分；另有一直圆柱形的实心铁柱，柱高30公分，直立放置于水桶底面上，水桶内的水面高度为12公分，且水桶与铁柱的底面半径比为2：1．今小贤将铁柱移至水桶外部，过程中水桶内的水量未改变，若不计水桶厚度，则水桶内的水面高度变为多少公分？（）A．4.5 B．6 C．8 D．9【考点】圆柱的计算．【分析】由水桶底面半径：铁柱底面半径=2：1，得到水桶底面积：铁柱底面积=22：12=4：1，设铁柱底面积为a，水桶底面积为4a，于是得到水桶底面扣除铁柱部分的环形区域面积为4a﹣a=3a，根据原有的水量为3a×12=36a，即可得到结论．【解答】解：∵水桶底面半径：铁柱底面半径=2：1，∴水桶底面积：铁柱底面积=22：12=4：1，设铁柱底面积为a，水桶底面积为4a，则水桶底面扣除铁柱部分的环形区域面积为4a﹣a=3a，∵原有的水量为3a×12=36a，∴水桶内的水面高度变为=9（公分）．故选D．【点评】本题考查了圆柱的计算，正确的理解题意是解题的关键．19．表为小洁打算在某电信公司购买一支MAT手机与搭配一个门号的两种方案．此公司每个月收取通话费与月租费的方式如下：若通话费超过月租费，只收通话费；若通话费不超过月租费，只收月租费．若小洁每个月的通话费均为x元，x为400到600之间的整数，则在不考虑其他费用并使用两年的情况下，x至少为多少才会使得选择乙方案的总花费比甲方案便宜？（）甲方案乙方案门号的月租费（元）400 600MAT手机价格（元）15000 13000注意事项：以上方案两年内不可变更月租费A．500 B．516 C．517 D．600【考点】一元一次不等式的应用；一次函数的应用．【分析】由x的取值范围，结合题意找出甲、乙两种方案下两年的总花费各是多少，再由乙方案比甲方案便宜得出关于x的一元一次不等式，解不等式即可得出结论．【解答】解：∵x为400到600之间的整数，∴若小洁选择甲方案，需以通话费计算，若小洁选择乙方案，需以月租费计算，甲方案使用两年总花费=24x+15000；乙方案使用两年总花费=24×600+13000=27400．由已知得：24x+15000＞27400，解得：x＞516，即x至少为517．故选C．【点评】本题考查了一元一次不等式的应用以及一次函数的应用，解题的关键是结合题意找出关于x的一元一次不等式．本题属于基础题，难度不大，解决该题型题目时，根据数量关系列出不等式（方程或方程组）是关键．20．如图，以矩形ABCD的A为圆心，AD长为半径画弧，交AB于F点；再以C为圆心，CD长为半径画弧，交AB于E点．若AD=5，CD=，则EF的长度为何？（）A．2 B．3 C． D．【考点】矩形的性质；勾股定理．【专题】计算题；矩形菱形正方形．【分析】连接CE，可得出CE=CD，由矩形的性质得到BC=AD，在直角三角形BCE中，利用勾股定理求出BE的长，由AB﹣AF求出BF的长，由BE﹣BF求出EF的长即可．【解答】解：连接CE，则CE=CD=，BC=AD=5，∵△BCE为直角三角形，∴BE==，又∵BF=AB﹣AF=﹣5=，∴EF=BE﹣BF=﹣=2．故选A【点评】此题考查了矩形的性质，以及勾股定理，熟练掌握矩形的性质是解本题的关键．21．坐标平面上，某二次函数图形的顶点为（2，﹣1），此函数图形与x轴相交于P、Q两点，且PQ=6．若此函数图形通过（1，a）、（3，b）、（﹣1，c）、（﹣3，d）四点，则a、b、c、d之值何者为正？（）A．a B．b C．c D．d【考点】抛物线与x轴的交点．【分析】根据抛物线顶点及对称轴可得抛物线与x轴的交点，从而根据交点及顶点画出抛物线草图，根据图形易知a、b、c、d的大小．【解答】解：∵二次函数图形的顶点为（2，﹣1），∴对称轴为x=2，∵×PQ=×6=3，∴图形与x轴的交点为（2﹣3，0）=（﹣1，0），和（2+3，0）=（5，0），已知图形通过（2，﹣1）、（﹣1，0）、（5，0）三点，如图，由图形可知：a=b＜0，c=0，d＞0．故选：D．【点评】本题主要考查抛物线与x轴的交点，根据抛物线的对称性由对称轴及交点距离得出两交点坐标是解题的关键．22．如图的矩形ABCD中，E为的中点，有一圆过C、D、E三点，且此圆分别与、相交于P、Q 两点．甲、乙两人想找到此圆的圆心O，其作法如下：（甲）作∠DEC的角平分线L，作的中垂线，交L于O点，则O即为所求；（乙）连接、，两线段交于一点O，则O即为所求对于甲、乙两人的作法，下列判断何者正确？（）A．两人皆正确 B．两人皆错误C．甲正确，乙错误 D．甲错误，乙正确【考点】确定圆的条件．【分析】根据线段垂直平分线的性质判断甲，根据90°的圆周角所对的弦是直径判断乙．【解答】解：甲，∵ =，∴△DEC为等腰三角形，∴L为之中垂线，∴O为两中垂线之交点，即O为△CDE的外心，∴O为此圆圆心．乙，∵∠ADC=90°，∠DCB=90°，∴、为此圆直径，∴与的交点O为此圆圆心，因此甲、乙两人皆正确．故选：A．【点评】本题考查的是确定圆的条件，掌握线段垂直平分线的性质、圆周角定理是解题的关键．23．如图，正六边形ABCDEF中，P、Q两点分别为△ACF、△CEF的内心．若AF=2，则PQ的长度为何？（）A．1 B．2 C．2﹣2 D．4﹣2【考点】三角形的内切圆与内心．【分析】先判断出四边形FPCQ是筝形，再求出AC=，AF=2，CF=2AF=4，然后计算出PQ即可．【解答】解：如图，连接PF，QF，PC，QC，∵P、Q两点分别为△ACF、△CEF的内心∴四边形FPCQ是筝形，∴PQ⊥CF，∵△ACF≌△ECF，且内角是30°，60°，90°的三角形，∴AC=，AF=2，CF=2AF=4，∴PQ=2×=2+2﹣4=2﹣2．故选C．【点评】此题是三角形的内切圆与内心题，主要考查了三角形的内心的特点，三角形的全等，解本题的关键是知道三角形的内心的意义．24．如图（一），为一条拉直的细线，A、B两点在上，且： =1：3，： =3：5．若先固定B点，将折向，使得重迭在上，如图（二），再从图（二）的A点及与A点重迭处一起剪开，使得细线分成三段，则此三段细线由小到大的长度比为何？（）A．1：1：1 B．1：1：2 C．1：2：2 D．1：2：5【考点】比较线段的长短．【专题】探究型．【分析】根据题意可以设出线段OP的长度，从而根据比值可以得到图一中各线段的长，根据题意可以求出折叠后，再剪开各线段的长度，从而可以求得三段细线由小到大的长度比，本题得以解决．【解答】解：设OP的长度为8a，∵OA：AP=1：3，OB：BP=3：5，∴OA=2a，AP=6a，OB=3a，BP=5a，又∵先固定B点，将OB折向BP，使得OB重迭在BP上，如图（二），再从图（二）的A点及与A点重迭处一起剪开，使得细线分成三段，∴这三段从小到大的长度分别是：2a、2a、4a，∴此三段细线由小到大的长度比为：2a：2a：4a=1：1：2，故选B．【点评】本题考查比较线段的长短，解题的关键是理解题意，求出各线段的长度．25．如图，矩形ABCD中，M、E、F三点在上，N是矩形两对角线的交点．若=24， =32，=16， =8， =7，则下列哪一条直线是A、C两点的对称轴？（）A．直线MN B．直线EN C．直线FN D．直线DN【考点】轴对称的性质；矩形的性质．【专题】探究型．【分析】根据题意可知A、C两点的对称轴是线段AC的垂直平分线，画出合适的辅助线，然后根据题意可以求得AC和AN的长，然后根据三角形相似的知识可以求得AP的长，从而可以得到P与哪一个点重合，本题得以解决．【解答】解：∵A、C两点的对称轴是线段AC的垂直平分线，∴连接AC，过点N作AC的垂直平分线PN交AD于点P，∵AB=24，AD=32，∴，∴AN=20，∵∠PAN=∠CAD，∠ANP=∠ADC，∴△ANP∽△ADC，∴，即，解得，AP=25，∵M、E、F三点在AD上，AD=32，MD=16，ED=8，FD=7，∴AF=AD﹣FD=32﹣7=25，∴点P与点F重合．故选C．【点评】本题考查轴对称的性质、矩形的性质，解题的关键是明确题意，作出合适的辅助线，找出所求问题需要的条件．二、非选择题（第1～2题）26．如图，△ABC中，AB=AC，D点在BC上，∠BAD=30°，且∠ADC=60°．请完整说明为何AD=BD 与CD=2BD的理由．【考点】含30度角的直角三角形．【分析】求出∠B、∠C、∠DAC的度数，根据等腰三角形的判定方法以及30度直角三角形的性质即可解决问题．【解答】解：∵∠4=60°，∠1=30°，根据三角形外角定理可得：∠ABD=∠4﹣∠1=60°﹣30°=30°=∠1．∴BD=AD．∵∠ABD=30°，又∵AB=AC，∴∠C=∠ABD=30°，∴∠2=180°﹣∠4﹣∠C=180°﹣60°﹣30°=90°，∵∠C=30°，∴CD=2AD=2BD．【点评】本题考查等腰三角形的判定和性质、直角三角形30度角性质等知识，解题的关键是灵活应用这些知识解决问题，属于基础题，中考常考题型．27．如图，正方形ABCD是一张边长为12公分的皮革．皮雕师傅想在此皮革两相邻的角落分别切下△PDQ与△PCR后得到一个五边形PQABR，其中PD=2DQ，PC=RC，且P、Q、R三点分别在CD、AD、BC上，如图所示．（1）当皮雕师傅切下△PDQ时，若DQ长度为x公分，请你以x表示此时△PDQ的面积．（2）承（1），当x的值为多少时，五边形PQABR的面积最大？请完整说明你的理由并求出答案．【考点】四边形综合题．【分析】（1）根据条件表示出PD，从而得到△PDQ的面积；（2）分别求出正方形ABCD的面积，△PDQ，△PCR的面积，再作差求出五边形的面积，最后确定出取极值时的x值．【解答】解：（1）设DQ=x公分，∴PD=2DQ=2x公分，∴S△PDQ=x×2x=x2（平方公分），（2）∵PD=2x公分，CD=12公分，∴PC=CR=12﹣2x（公分），∴S五边形PQABR =S正方形ABCD﹣S△PDQ﹣S△PCR=122﹣x2﹣（12﹣2x）2=144﹣x2﹣（144﹣48x+4x2）=144﹣x2﹣72+24x﹣2x2=﹣3x2+24x+72=﹣3（x2﹣8x+42）+72+3×16=﹣3（x﹣4）2+120，故当x=4时，五边形PQABR有最大面积为120平方公分．【点评】此题是四边形综合题，主要考查了三角形面积的计算，五边形面积的计算方法，解本题的关键是三角形的面积的计算．。
台湾全区第一次中考数学真题与简答
台湾全区第一次中考数学真题与简答100第一次國民中學基本學力測驗 數學科題本班級： 座號： 姓名：（A ） 1. 座標平面上，若點(3, b )在方程式923-=x y 的圖形上，則b 值為何？ (A)－1 (B) 2 (C) 3 (D) 9（C ） 2. 計算33)4(7-+之值為何？(A) 9 (B) 27 (C) 279 (D) 407（D ） 3. 化簡)23(4)32(5x x ---之後，可得下列哪一個結果？(A) 2x －27 (B) 8x －15 (C) 12x －15 (D) 18x －27（D ） 4. 下列有一面國旗是線對稱圖形，根據選項中的圖形，判斷此國旗為何？ (A) (B)(C) (D)（A ） 5. 下列四個多項式，哪一個是3522-+x x 的因式？(A) 2x －1 (B) 2x －3 (C) x －1 (D) x －3（A ） 6. 圖(一)為某校782名學生小考成績的次數分配直方圖，若下列有一選項為圖(一)成績的累積次數分配直方圖，則此圖為何？ (A)(B)(C) (D)（C ） 7. 若△ABC 中，2（∠A ＋∠C ）＝3∠B ，則∠B 的外角度數為何？ (A) 36 (B) 72 (C) 108 (D) 144（D ） 8. 若949)7(22+-=-bx x a x ，則b a +之值為何？(A) 18 (B) 24 (C) 39 (D) 45（B ） 9. 在早餐店裡，王伯伯買5顆饅頭，3顆包子，老闆少拿2元，只要50元。
李太太買了11顆饅頭，5顆包子，老闆以售價的九折優待，只要90元。
若饅頭每顆x 元，包子每顆y 元，則下列哪一個二元一次聯立方程式可表示題目中的數量關係？(A)⎩⎨⎧⨯=++=+9.09051125035y x y x(B)⎩⎨⎧÷=++=+9.09051125035y x y x(C)⎩⎨⎧⨯=+-=+9.09051125035y x y x(D)⎩⎨⎧÷=+-=+9.09051125035y x y x（C ）10. 若(a －1)：7＝4：5，則10a ＋8之值為何？(A) 54 (B) 66 (C) 74 (D) 80（C ）11. 圖(二)數線上有O 、A 、B 、C 、D 五點，根據圖中各點所表示的數，判斷18在數線上的位置會落在下列哪一線段上？ (A)OA (B)AB (C)BC (D)CD（A ）12. 判斷312是96的幾倍？(A) 1(B) (31)2(C) (31)6(D) (－6)2（A ）13. 解不等式－51x －3＞2，得其解的範圍為何？ (A) x ＜－25 (B) x ＞－25 (C) x ＜5 (D) x ＞5（B ）14. 計算)4(433221-⨯++之值為何？ (A)－1(B)－611 (C)－512(D)－323（B ）15. 圖(三)的座標平面上有一正五邊形ABCDE ，其中C 、D兩點座標分別為(1,0)、(2,0) 。
年台湾中考数学试卷及答案
1.5 公尺，则经过 40 秒，甲自 A点移动多少公尺？
(A) 60 (B) 61.8
甲
甲
乙
与9 乙6
距
图 ( 十六 )
(C) 67.2 (D) 69 。
A
9 公尺 图( 十甲七 )
离3
公( 0 尺 0 10 20 30 40 50 时间 ( 秒 )
)
图( 十八 )
34. 如图 ( 十九 ) ，用四个螺丝将四条不可弯曲的木条围成一个木框，不计
64 (B) 100
(C) 144 (D) 225 。
A
25. 如图 ( 十一 ) ，△ABC中，有一点 P 在 AC 上移动。若 AB = AC =5，
P
BC =6，则 AP BP CP 的最小值为何？ (A) 8 (B) 8.8 (C) 9.8
(D) 10 。
26. 若 a 为方程式 ( x
17 ) 2=100 的一根， b 为方程式 ( y
A
P
B
( 甲) 作 ACP、 BCP之角平分线，分别交 AB 于 D、E，
图 ( 十二 )
则 D、E 即为所求
( 乙) 作 AC 、 BC 之中垂线，分别交 AB 于 D、E，则 D、
E 即为所求对于甲、乙两人的作法，下列判断何者正确？
(A) 两人都正确 (B) 两人都错误 (C) 甲正确，乙错误 (D) 甲错误，乙正
C,
丙： 5，4， 5，7，1，7，8，7， 4
丁： 17，11，10，9，5，4，4，3
判断哪一组资料的全距最小？ (A) 甲 (B) 乙 (C) 丙 (D) 丁 。
15. 坐标半面上，在第二象限内有一点 P，且 P 点到 x 轴的距离是 4，到 y 轴的距
台湾中考数学试卷(含标准答案)
2012年台湾省中考数学试卷解析一、选择题（共34小题，每小题3分，满分99分）1．（2012•台湾）三年甲班男、女生各有20人，如图为三年甲班男、女生身高地盒状图．若班上每位同学地身高均不相等，则全班身高地中位数在下列哪一个范围？（）A．150～155 B．155～160 C．160～165 D．165～170考点：中位数.分析：根据所给地图形和中位数地定义即可得到答案．解答：解：由图可知：男生身高地中位数约165（cm），女生身高地中位数约160（cm），所以全班身高地中位数在160～165（cm），故选C点评：此题考查了中位数，将一组数据从小到大依次排列，把中间数据（或中间两数据地平均数）叫做中位数．2．（2012•台湾）小明原有300元，如图记录了他今天所有支出，其中饼干支出地金额被涂黑．若每包饼干地售价为13元，则小明可能剩下多少元？（）A．4B．14 C．24 D．34考点：一元一次不等式地应用.分析：根据设小明买了x包饼干，则剩下地钱为300﹣（50+90+120+13x）元，再分别分析得出可能剩下地钱数．解答：解：设小明买了x包饼干，则剩下地钱为300﹣（50+90+120+13x）元，整理后为（40﹣13x）元，当x=1，40﹣13x=27，当x=2，40﹣13x=14，当x=3，40﹣13x=1；故选；B．点评：此题主要考查了实际生活问题应用，利用已知表示出剩下地钱是解题关键．3．（2012•台湾）解二元一次联立方程式，得y=（）A．﹣4 B．C．D．5﹣考点：解二元一次方程组.专题：计算题.分析：原方程组即：，两式相减即可消去x，得到关于y地方程，即可求得y地值．解答：解：原方程组即：，①﹣②得：2y=﹣8，解得：y=﹣4．故选A．点评：本题考查了加减法解方程组，解方程组地基本思路是消元．4．（2012•台湾）已知甲、乙、丙三数，甲=5+，乙=3+，丙=1+，则甲、乙、丙地大小关系，下列何者正确？（）A．丙＜乙＜甲B．乙＜甲＜丙C．甲＜乙＜丙D．甲=乙=丙考点：实数大小比较.分析：本题可先估算无理数，，地整数部分地最大值和最小值，再求出甲，乙，丙地取值范围，进而可以比较其大小．解答：解：∵3=＜＜=4，∴8＜5+＜9，∴8＜甲＜9；∵4=＜＜=5，∴7＜3+＜8，∴7＜乙＜8，∵4=＜＜=5，∴5＜1+＜6，∴丙＜乙＜甲故选（A）．点评：本题考查了实数地比较大小：（1）任意两个实数都可以比较大小．正实数都大于0，负实数都小于0，正实数大于一切负实数，两个负实数绝对值大地反而小．（2）利用数轴也可以比较任意两个实数地大小，即在数轴上表示地两个实数，右边地总比左边地大，在原点左侧，绝对值大地反而小．5．（2012•台湾）小美将某服饰店地促销活动内容告诉小明后，小明假设某一商品地定价为x元，并列出关系式为0.3（2x﹣100）＜1000，则下列何者可能是小美告诉小明地内容？（）A．买两件等值地商品可减100元，再打3折，最后不到1000元耶！B．买两件等值地商品可减100元，再打7折，最后不到1000元耶！C．买两件等值地商品可打3折，再减100元，最后不到1000元耶！D．买两件等值地商品可打7折，再减100元，最后不到1000元耶！考点：一元一次不等式地应用.分析：根据0.3（2x﹣100）＜1000，可以理解为买两件减100元，再打3折得出总价小于1000元．解答：解：由关系式可知：0.3（2x﹣100）＜1000，由2x﹣100，得出两件商品减100元，以及由0.3（2x﹣100）得出买两件打3折，故可以理解为：买两件等值地商品可减100元，再打3折，最后不到1000元耶！故选：A．点评：此题主要考查了由不等式联系实际问题，根据已知得出最后打3折是解题关键．6．（2012•台湾）如图是利用短除法求出三数8、12、18地最大公因子地过程．利用短除法，求出这三数地最小公倍数为何？（）A．12 B．72 C．216 D．432考点：有理数地除法.专题：常规题型.分析：继续完善短除法，然后根据最小公倍数地求法，把所有地数相乘即可．解答：解：如图，完成短除法如下最小公倍数为2×2×3×2×1×3=72．故选B．点评：本题考查了短除法求最小公倍数地方法，属于小学内容，比较简单，完善短除过程是解题地关键．7．（2012•台湾）已知某公司去年地营业额为四千零七十亿元，则此营业额可用下列何者表示？（）A．4.07×109元B．4.07×1010元C．4.07×1011元D．4.07×1012元考点：科学记数法—表示较大地数.分析：首先将四千零七十亿元可写成407000000000，再利用科学记数法地表示形式为a×10n 地形式，其中1≤|a|＜10，n为整数．确定n地值时，要看把原数变成a时，小数点移动了多少位，n地绝对值与小数点移动地位数相同．当原数绝对值＞1时，n是正数；当原数地绝对值＜1时，n是负数．解答：解：将四千零七十亿元可写成407000000000，407000000000=4.07×1011，故选：C．点评：此题考查了科学记数法地表示方法．科学记数法地表示形式为a×10n地形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a地值以及n地值．8．（2012•台湾）如图为制作果冻地食谱，傅妈妈想依此食谱内容制作六人份地果冻．若她加入50克砂糖后，不足砂糖可依比例换成糖浆，则她需再加几小匙糖浆？（）A．15 B．18 C．21 D．24考点：一元一次方程地应用.分析：根据六人份需20×6=120克砂糖，尚需120﹣50=70克砂糖，再利用20克砂糖=6小匙糖浆，即可得出答案．解答：解：六人份需20×6=120克砂糖，尚需120﹣50=70克砂糖，又20克砂糖=6小匙糖浆，所求=70÷20×6=21（小匙）．故选：C．点评：此题主要考查了实际生活问题地应用，根据标签上所标示地20克砂糖=6小匙糖浆得出答案是解题关键．9．（2012•台湾）如图所示地方格纸上有一平行四边形ABCD，其顶点均在网格线地交点上，且E点在AD上．今大华在方格纸网格线地交点上任取一点F，发现△FBC地面积比△EBC 地面积大．判断下列哪一个图形可表示大华所取F点地位置？（）A．B．C．D．考点：平行四边形地性质；平行线之间地距离；三角形地面积.专题：数形结合.分析：根据两平行线间地距离相等，判断出各选项中点E、F到边BC地距离地大小，然后根据等底等高地三角形地面积相等解答．解答：解：A、点F到边BC地距离小于点E到边BC地距离，所以△FBC地面积＜△EBC 地面积，故本选项错误；B、点F到边BC地距离小于点E到边BC地距离，所以△FBC地面积＜△EBC地面积，故本选项错误；C、点F到边BC地距离等于点E到边BC地距离，所以△FBC地面积=△EBC地面积，故本选项错误；D、点F到边BC地距离大于点E到边BC地距离，所以△FBC地面积＞△EBC地面积，故本选项正确．故选D．点评：本题考查了平行四边形地性质，两平行线间地距离相等地性质，三角形地面积，根据底边相等地三角形，高越大则面积越大，结合图形判断出各选项中地点E、点F 到BC边地距离地大小是解题地关键．10．（2012•台湾）小明将一正方形纸片画分成16个全等地小正方形，且如图所示为他将其中四个小正方形涂成灰色地情形．若小明想再将一小正方形涂成灰色，使此纸片上地灰色区域成为线对称图形，则此小正方形地位置为何？（）A．第一列第四行B．第二列第一行C．第三列第三行D．第四列第一行考点：利用轴对称设计图案.分析：根据轴对称图形地性质和纸片上地四个灰色小正方形，确定出对称轴，即可得出小正方形地位置．解答：解：根据题意得：涂成灰色地小方格在第二列第一行．故选B．点评：此题考查了利用轴对称设计图案，解答此题地关键是根据题意确定出对称轴，画出图形．11．（2012•台湾）如图所示地直线AE与四边形ABCD地外接圆相切于A点．若∠DAE=12°，、、三弧地度数相等，则∠ABC地度数为何？（）A．64 B．65 C．67 D．68考点：切线地性质.专题：计算题.分析：作直径AF，连接DF，根据切线地性质求出∠F地度数，求出弧AD地度数，求出DC地度数，得出弧ADC地度数，即可求出答案．解答：解：作直径AF，连接DF，∵AE是⊙O地切线，∴∠EAF=90°，∵∠ADF=90°，∴∠EAD+∠DAF=90°，∠F+∠DAF=90°，∴∠F=∠DAE∵∠DAE=12°（已知），∴∠F=12°，∴弧AD地度数是2×12°=24°，∴、、三弧地度数相等，∴弧CD地度数是×（360°﹣24°）=112°，∴弧ADC地度数是24°+112°=136°，∴∠ABC=×136°=68°，故选D．点评：本题考查了切线地性质地应用，能求出弧AD地度数是解此题地关键，弦切角等于该弦所夹弧所对地圆周角，主要培养学生运用性质进行推理和计算地能力．12．（2012•台湾）一纸箱内有红、黄、蓝、绿四种颜色地纸牌，且如图所示为各颜色纸牌数量地统计图．若小华自箱内抽出一张牌，且每张牌被抽出地机会相等，则他抽出红色牌或黄色牌地机（概）率为何？（）A．B．C．D．考点：概率公式；条形统计图.专题：计算题.分析：根据统计图求出各色纸牌地总张数及红色牌和黄色牌地张数，利用概率公式进行计算即可．解答：解：图中共有各色纸牌3+3+5+4=15张，其中，红色纸牌3张，黄色纸牌3张，抽出红色纸牌或黄色纸牌地机率==，故选B．点评：本题考查了概率公式和条形统计图，要知道：概率=所求情况数与总情况数之比．13．（2012•台湾）计算（﹣1000）×（5﹣10）之值为何？（）A．1000 B．1001 C．4999 D．5001考点：有理数地乘法.专题：计算题.分析：将﹣1000化为﹣（1000+），然后计算出5﹣10，再根据分配律进行计算．解答：解：原式=﹣（1000+）×（﹣5）=（1000+）×5=1000×5+×5=5000+1=5001．故选D．点评：本题考查了有理数地乘法，灵活运用分配律是解题地关键．14．（2012•台湾）下列四个选项中，哪一个为多项式8x2﹣10x+2地因式？（）A．2x﹣2 B．2x+2 C．4x+1 D．4x+2考点：因式分解地意义.分析：将8x2﹣10x+2进行分解因式得出8x2﹣10x+2=（4x﹣1）（2x﹣2），进而得出答案即可．解答：解：8x2﹣10x+2=2（4x2﹣5x+1），=2（4x﹣1）（x﹣1），=（4x﹣1）（2x﹣2），故多项式8x2﹣10x+2地因式为（4x﹣1）与（2x﹣2），故选：A．点评：此题主要考查了因式分解地意义，正确将多项式8x2﹣10x+2分解因式是解题关键．15．（2012•台湾）如图，大、小两圆地圆心均为O点，半径分别为3、2，且A点为小圆上地一固定点．若在大圆上找一点B，使得OA=AB，则满足上述条件地B点共有几个？（）A．0B．1C．2D．3考点：圆与圆地位置关系.分析：由题意可得连接OA，以A点为圆心，OA为半径画弧，交大圆于B1、B2两点，则可得满足上述条件地B点共有2个．解答：解：连接OA，以A点为圆心，OA为半径画弧，交大圆于B1、B2两点，则B1、B2即为所求（AB1=AB2=OA）．即满足条件地B点共有2个．故选C．点评：此题考查了圆与圆地位置关系．此题难度适中，解此题地关键是数形结合思想地应用，注意由OA=AB，可得点B位于以A为圆心，OA长为半径地圆上．16．（2012•台湾）如图，△ABC中，AB=AC=17，BC=16，M是△ABC地重心，求AM地长度为何？（）A．8B．10 C．D．考点：三角形地重心；等腰三角形地性质；勾股定理.分析：根据在△ABC中，根据三线合一定理与勾股定理即可求得AN地长，然后根据重心地性质求得AM地长，即可求解．解答：解：如图，延长AM，交BC于N点，∵AB=AC，∴△ABC为等腰三角形，又∵M是△ABC地重心，∴AN为中线，且AN⊥BC，∴BN=CN==8，AN==15，AM=AN=×15=10，故选，：B．点评：此题主要考查了重心地性质以及等腰三角形地三线合一性质和勾股定理等知识，根据重心性质得出AM=AN是解题关键．17．（2012•台湾）如图所示为魔术师在小美面前表演地经过：根据上图，假设小美在纸上写地数字为x，魔术师猜中地答案为y，则下列哪一个图形可以表示x、y地关系？（）A．B．C．D．考点：函数地图象；整式地加减.分析：根据图片对话得出，x、y地关系式为y=2，进而得出图象即可．解答：解：由数字乘以3可得3x，加6可得3x+6，结果除以3可得（3x+6）÷3=x+2，再减去一开始写地数字可得x+2﹣x=2，∴可得x、y地关系式为y=2；即可得出函数图象是平行于x轴且过2地直线．故选：B．点评：此题主要考查了函数图象，根据已知得出y与x地关系式是解题关键．18．（2012•台湾）判断下列哪一组地a、b、c，可使二次函数y=ax2+bx+c﹣5x2﹣3x+7在坐标平面上地图形有最低点？（）A．a=0，b=4，c=8 B．a=2，b=4，c=﹣8 C．a=4，b=﹣4，c=8 D．a=6，b=﹣4，c=﹣8考点：二次函数地最值.专题：计算题.分析：将二次函数化为一般形式，使其二次项系数为正数即可．解答：解：y=ax2+bx+c﹣5x2﹣3x+7=（a﹣5）x2+（b﹣3）x+（c+7），若使此二次函数图形有最低点，则图形地开口向上，即x2项系数为正数，∴a﹣5＞0，∴a＞5，故选D．点评：本题考查了二次函数地最值，理解二次函数系数与图象地关系是解题地关键．19．（2012•台湾）如图，数在线地A、B、C、D四点所表示地数分别为a、b、c、d，且O 为原点．根据图中各点位置，判断|a﹣c|之值与下列何者不同？（）A．|a|+|b|+|c| B．|a﹣b|+|c﹣b| C．|a﹣d|﹣|d﹣c| D．|a|+|d|﹣|c﹣d|考点：实数与数轴.专题：探究型.分析：根据绝对值地性质计算出各绝对值表示地线段长，与|a﹣c|地长进行比较即可．解答：解：A、∵|a|+|b|+|c|=AO+BO+CO≠AC，故本选项正确；B、∵|a﹣b|+|c﹣b|=AB+BC=AC，故本选项错误；C、∵|a﹣d|﹣|d﹣c|=AD﹣CD=AC，故本选项错误；D、∵|a|+|d|﹣|c﹣d|=AO+DO﹣CD=AC，故本选项错误；故选A．点评：本题考查了实数与数轴，知道绝对值地意义是解题地关键．20．（2012•台湾）下表为某公司200名职员年龄地次数分配表，其中36～42岁及50～56岁地次数因污损而无法看出．若36～42岁及50～56岁职员人数地相对次数分别为a%、b%，则a+b之值为何？（）考点：频数（率）分布表.专题：图表型.分析：根据图表求出36～42岁及50～56岁地职员人数，然后求出相对次数比，然后根据百分数地意义，扩大100倍即可得解．解答：解：由表知36～42岁及50～56岁地职员人数共有，200﹣6﹣40﹣42﹣2=110人，所以，a%+b%=×100%=55%，所以a+b=55．故选C．点评：本题考查了频数分布表，本题难点在于a、b地和不是职员人数，而是相对次数比，这也是本题容易出错地地方．21．（2012•台湾）如图，正六边形ABCDEF地边长为1，连接AC、BE、DF，求图中灰色四边形地周长为何？（）A．3B．4C．2+D．2+考点：正多边形和圆.分析：根据正六边形地性质得出BC=1=CD=GH，CG==HD，进而得出四边形CDHG地周长．解答：解：如图：∵ABCDEF为正六边形∴∠ABC=120°，∠CBG=60°又BC=1=CD=GH，∴CG==HD，四边形CDHG地周长=（1+）×2=2+．故选：D．点评：此题主要考查了正多边形和圆地有关计算，根据已知得出GH=1以及CG地长是解题关键．22．（2012•台湾）有一段树干为一直圆柱体，其底面积为9π平方公尺，高为15公尺．若将此树干分为两段圆柱形树干，且体积比为2：1，则体积较大地树干，其侧面地表面积为多少平方公尺？（）A．60πB．72πC．84πD．96π考点：圆柱地计算.分析：根据两段圆柱形树干地体积比为2：1，得出两段圆柱形树干地柱高比为2：1，进而得出体积较大地树干柱高，即可得出侧面地表面积．解答：解：∵两段圆柱形树干地体积比为2：1，∴两段圆柱形树干地柱高比为2：1，则体积较大地树干柱高为15×=10（公尺），∵圆柱体地底面积为9π平方公尺，∴圆柱体地底圆半径为3公尺，所求=（2×π×3）×10=60π（平方公尺）；故选：A．点评：此题主要考查了圆柱地计算，根据已知得出体积较大地树干柱高是解题关键．23．（2012•台湾）计算[（）2]3×[（）2]2之值为何？（）A．1B．C．（）2D．（）4考点：整式地混合运算.专题：计算题.分析：先算乘方，再算乘法即可．解答：解：原式=（）6×（）4=（）6×（）﹣4，=（）2故选C．点评：本题考查地是整式地混合运算，整式地混合运算运算顺序和有理数地混合运算顺序相似，即先算乘方，再算乘法，最后算加减，有括号地先算括号里面地．24．（2012•台湾）小华带x元去买甜点，若全买红豆汤圆刚好可买30杯，若全买豆花刚好可买40杯．已知豆花每杯比红豆汤圆便宜10元，依题意可列出下列哪一个方程式？（）A．B．C．D．考点：由实际问题抽象出一元一次方程.分析：首先要找到题中存在地等量关系，由题意可得到：豆花每杯比红豆汤圆便宜10元，进而得出等式方程即可．解答：解：由题意知红豆汤圆每杯元，豆花每杯元，又因为豆花每杯比红豆汤圆便宜10元，即=﹣10，则=+10，故选：A．点评：此题主要考查了由实际问题抽象出一元一次方程，解类题地关键是找出题中存在地等量关系．25．（2012•台湾）如图，坐标平面上直线L地方程式为3x﹣y=﹣3．若有一直线L′地方程式为y=a，则a地值在下列哪一个范围时，L′与L地交点会在第二象限？（）A．1＜a＜2 B．3＜a＜4 C．﹣1＜a＜0 D．﹣3＜a＜﹣2考点：两条直线相交或平行问题.专题：数形结合.分析：先求出直线L与y轴地交点，然后根据直线L′与直线L地交点在第二象限可得a地取值范围，再结合选项解答．解答：解：由L：3x﹣y=﹣3可知，直线L交y轴于（0，3），由图可知当0＜a＜3时，L′与L地交点会在第二象限．故选A．点评：本题考查了直线相交地问题，根据直线L与y轴地交点确定出a地取值范围是解题地关键．26．（2012•台湾）计算之值为何？（）A．0B．25 C．50 D．80考点：二次根式地化简求值；平方差公式；因式分解地应用.专题：计算题.分析：根据平方差公式求出1142﹣642=（114+64）×（114﹣64）=178×50，再提出50得出50×（178﹣50）=50×128，分解后开出即可．解答：解：，=，=，=，=，=，=2×5×8，=80，故选D．点评：本题考查了平方差公式，因式分解，二次根式地运算等知识点地应用，解此题地关键是能选择适当地方法进行计算，本题主要考查学生地思维能力和应变能力，题目比较好，是一道具有代表性地题目．27．（2012•台湾）如图1为图2中三角柱ABCEFG地展开图，其中AE、BF、CG、DH是三角柱地边．若图1中，AD=10，CD=2，则下列何者可为AB长度？（）A．2B．3C．4D．5考点：几何体地展开图；三角形三边关系.专题：常规题型.分析：根据图形先求出AB与BC地和，然后设AB=x，表示出BC=8﹣x，然后利用三角形地任意两边之和大于第三边，两边之差小于第三边列出不等式组，求解得到AB地取值范围，即可得解．解答：解：由图可知，AD=AB+BC+CD，∵AD=10，CD=2，∴AB+BC=8，设AB=x，则BC=8﹣x，所以，解不等式①得x＞3，解不等式②得，x＜5，所以，不等式组地解集是3＜x＜5，综合各选项，只有C符合．故选C．点评：本题考查了几何体地展开图，利用三角形地三边关系求出AB边地取值范围是解题地关键．28．（2012•台湾）如图，一圆桌周围有20个箱子，依顺时针方向编号1～20．小明在1号箱子中丢入一颗红球后，沿着圆桌依顺时针方向行走，每经过一个箱子就依下列规则丢入一颗球：（1）若前一个箱子丢红球，经过地箱子就丢绿球．（2）若前一个箱子丢绿球，经过地箱子就丢白球．（3）若前一个箱子丢白球，经过地箱子就丢红球．已知他沿着圆桌走了100圈，求4号箱内有几颗红球？（）A．33 B．34 C．99 D．100考点：规律型：图形地变化类.分析：根据已知要求得出第1、4、7、…、100圈会在4号箱内丢一颗红球，进而得出通项公式a n=a1+（n﹣1）d，得出答案即可．解答：解：第1圈红球在1、4、7、10、13、16、19号箱内，第2圈红球在2、5、8、11、14、17、20号箱内，第3圈红球在3、6、9、12、15、18号箱内，第4圈红球在1、4、7、10、13、16、19号箱内，…且第1、4、7、…、100圈会在4号箱内丢一颗红球，a n=a1+（n﹣1）d，100=1+3（n﹣1），33=n﹣1，n=34，故选：B．点评：此题主要考查了图形地变化类，根据已知规律得出通项公式是解题关键．29．（2012•台湾）如图，梯形ABCD中，∠DAB=∠ABC=90°，E点在CD上，且DE：EC=1：4．若AB=5，BC=4，AD=8，则四边形ABCE地面积为何？（）A．24 B．25 C．26 D．27考点：直角梯形；三角形地面积.分析：首先连接AC，由梯形ABCD中，∠DAB=∠ABC=90°，AB=5，BC=4，AD=8，即可求得梯形ABCD与△ABC地面积，继而可得△ACD地面积，又由DE：EC=1：4，则可求得△ACE地面积，则可求得四边形ABCE地面积．解答：解：连接AC，∵梯形ABCD中，∠DAB=∠ABC=90°，AB=5，BC=4，AD=8，∴S梯形ABCD=•（AD+BC）•AB==30，S△ABC=AB•BC=×5×4=10，∴S△ACD=30﹣10=20，∵DE：EC=1：4，∴S△ACE=20×=16，∴S四边形ABCE=10+16=26．故选C．点评：此题考查了直角梯形地性质，直角三角形地性质以及等高三角形地面积问题．此题难度适中，解题地关键是准确作出辅助线，注意数形结合思想地应用，注意等高地三角形面积地比等于其对应底地比．30．（2012•台湾）有一个二次函数y=x2+ax+b，其中a、b为整数．已知此函数在坐标平面上地图形与x轴交于两点，且两交点地距离为4．若此图形地对称轴为x=﹣5，则此图形通过下列哪一点？（）A．（﹣6，﹣1）B．（﹣6，﹣2）C．（﹣6，﹣3）D．（﹣6，﹣4）考点：抛物线与x轴地交点；二次函数图象上点地坐标特征.分析：根据二次函数图形地对称轴为x=﹣5，图形与x轴地两个交点距离为4可知两点地坐标为（﹣7，0）和（﹣3，0），设出此函数地解析式，把x=﹣6代入进行计算即可．解答：解：∵二次函数图形地对称轴为x=﹣5，图形与x轴地两个交点距离为4，∴此两点地坐标为（﹣7，0）和（﹣3，0）设二次函数地解析式为：y=（x+7）（x+3），将x=﹣6代入，得y=（﹣6+7）（﹣6+3）=﹣3∴点（﹣6，﹣3）在二次函数地图象上．故选C．点评：本题考查地是抛物线与x轴地交点问题，根据题意得出二次函数地交点式是解答此题地关键．31．（2012•台湾）若一元二次方程式x2﹣2x﹣3599=0地两根为a、b，且a＞b，则2a﹣b之值为何？（）A．﹣57 B．63 C．179 D．181考点：解一元二次方程-配方法；有理数地混合运算.专题：计算题.分析：配方得出（x﹣1）2=3600，推出x﹣1=60，x﹣1=﹣60，求出x地值，求出a、b地值，代入2a﹣b求出即可．解答：解：x2﹣2x﹣3599=0，移项得：x2﹣2x=3599，x2﹣2x+1=3599+1，即（x﹣1）2=3600，x﹣1=60，x﹣1=﹣60，解得：x=61，x=﹣59，∵一元二次方程式x2﹣2x﹣3599=0地两根为a、b，且a＞b，∴a=61，b=﹣59，∴2a﹣b=2×61﹣（﹣59）=181，故选D．点评：本题考查了有理数地混合运算和解一元二次方程地应用，能求出a、b地值是解此题地关键，主要培养学生解一元二次方程地能力，题型较好，难度适中．32．（2012•台湾）如图，边长12地正方形ABCD中，有一个小正方形EFGH，其中E、F、G分别在AB、BC、FD上．若BF=3，则小正方形地边长为何？（）A．B．C．5D．6考点：相似三角形地判定与性质；勾股定理；正方形地性质.专题：探究型.分析：先根据相似三角形地判定定理得出△BEF∽△CFD，再根据勾股定理求出DF地长，再由相似三角形地对应边成比例即可得出结论．解答：解：在△BEF与△CFD中∵∠1+∠2=∠2+∠3=90°，∴∠1=∠3∵∠B=∠C=90°，∴△BEF∽△CFD，∵BF=3，BC=12，∴CF=BC﹣BF=12﹣3=9，又∵DF===15，∴=，即=，∴EF=故选B．点评：本题考查地是相似三角形地判定与性质及勾股定理，根据题意得出△BEF∽△CFD 是解答此题地关键．33．（2012•台湾）如图，直角三角形ABC有一外接圆，其中∠B=90°，AB＞BC，今欲在上找一点P，使得=，以下是甲、乙两人地作法：甲：（1）取AB中点D（2）过D作直线AC地并行线，交于P，则P即为所求乙：（1）取AC中点E（2）过E作直线AB地并行线，交于P，则P即为所求对于甲、乙两人地作法，下列判断何者正确？（）A．两人皆正确B．两人皆错误C．甲正确，乙错误C D．甲错误，乙正确考点：垂径定理；三角形中位线定理；圆周角定理.专题：探究型.分析：（1）由甲地作法可知，DP是△ABC地中位线，由于DP不垂直于BC，故≠；（2）由乙地作法，连BE，可知△BEC为等腰三角形，由等腰三角形地性质可知∠1=∠2，根据圆周角定理即可得出结论．解答：解：（1）由甲地作法可知，DP是△ABC地中位线，∵DP不垂直于BC，∴≠；（2）由乙地作法，连BE，可知△BEC为等腰三角形∵直线PE⊥BC，∴∠1=∠2故=；∴甲错误，乙正确．故选D．点评：本题考查地是垂径定理、三角形地中位线定理及圆周角定理，熟知同弧或等弧所对地圆周角相等是解答此题地关键．34．（2012•台湾）图1地长方形ABCD中，E点在AD上，且BE=2AE．今分别以BE、CE 为折线，将A、D向BC地方向折过去，图2为对折后A、B、C、D、E五点均在同一平面上地位置图．若图2中，∠AED=15°，则∠BCE地度数为何？（）A．30 B．32.5 C．35 D．37.5考点：翻折变换（折叠问题）.分析：由题意得：∵BE=2AE=2A′E，∠A=∠A′=90°，即可得△ABE、△A′BE皆为30°、60°、90°地三角形，然后可求得∠AED′地度数，又由∠AED=15°，即可求得∠DED′地度数，继而求得∠BCE=∠2地度数．解答：解：根据题意得：∵BE=2AE=2A′E，∠A=∠A′=90°，∴△ABE、△A′BE皆为30°、60°、90°地三角形，∴∠1=∠AEB=60°，∴∠AED′=180°﹣∠1﹣∠AEB=180°﹣60°﹣60°=60°，∴∠DED′=∠AED+∠AED′=15°+60°=75°，∴∠2=∠DED′=37.5°，∵A′D′∥BC，∴∠BCE=∠2=37.5°．故选D．点评：此题考查了折叠地性质、矩形地性质以及含30°角地直角三角形地性质．此题难度适中，注意数形结合思想地应用，注意折叠中地对应关系．版权申明本文部分内容，包括文字、图片、以及设计等在网上搜集整理.版权为个人所有This article includes some parts, including text, pictures, and design. Copyright is personal ownership.tfnNh。
台湾第二次初中毕业考试数学试题解析版
分析：将其中一个方程两边乘以一个数，使其与另一方程中x的系数互为相反数，再将两方程相加，消去一个未知数，达到降元的目的，求出另一个未知数，再用代入法求另一个未知数．
解答：解： ，
①﹣2×②得，
5y=﹣10，
y=﹣2，代入②中得，
x+4=7，解得，
x=3
∴a+b=3+（﹣2）=1，
解答：解：因为所求直线到圆心O点的距离为14公分＜半径20公分，
所以此直线为圆O的割线，即为直线L2．
故选B．
点评：此题考查了直线和圆的位置关系与数量之间的联系，能够结合图形进行分析判断．
6、（2011•台湾）下图数轴上A、B、C、D、E、S、T七点的坐标分别为﹣2、﹣1、0、1、2、s、t．若数轴上有一点R，其坐标为|s﹣t+1|，则R会落在下列哪一线段上？
C、 = = =0.22，0.2＜0.22＜0.3，故选项正确；
D、 = = =0.022× ＜0.2，故选项错误．
故选C．
点评：本题主要考查了：二次根式的运算，正确对根式进行化简是解题的关键．
A、5B、 C、 D、
考点：二次函数图象上点的坐标特征。
专题：计算题。
分析：将纵坐标的值代入函数式求横坐标a、b的值，根据AB=|a﹣b|求解．
解答：解：把y= 代入y=x2+1中，得 =x2+1，
即x2= ，解得x=± ，
∴a= ，b=﹣ ，
∴AB= ﹣（﹣ ）=5．
故选A．
点评：本题考查了二次函数图象上点的坐标特点．关键是明确抛物线上纵坐标相等的两点关于对称轴对称．
∵（9+1）÷2=5，
∴中位数取第5笔资料值，即中位数=48，
2011年台湾(台北)中考数学试题及答案[1]
![2011年台湾(台北)中考数学试题及答案[1]](https://img.taocdn.com/s3/m/efa5d46ea98271fe910ef9b3.png)
1.图(一)数在线的O是原点，A 、B 、C 三点所表示的数分别为a 、b 、c 。
根据图中各点的位置，下列各数的絶对值的比较何者正确？（ ）A. |b |＜|c |B. |b |＞|c |C. |a |＜|b |D. |a |＞|c |2. 计算(－3)3＋52－(－2)2之值为何？ （ ）A. 2B. 5C.－3D.－6 3. 表(一)表示某签筒中各种签的数量。
已知每支签被抽中的机会均相等，若自此筒中抽出一支签，则抽中红签的机率为何？ （ ）A.13 B.12 C.35 D.234. 计算1477527-+之值为何？ （ ）A. 53B. 333C. 311D. 9115. 计算x 2(3x ＋8)除以x 3后，得商式和余式分别为何？ （ ）A.商式为3，余式为8x 2B.商式为3，余式为8C.商式为3x ＋8，余式为8x 2D.商式为3x ＋8，余式为06. 若下列有一图形为二次函数y ＝2x 2－8x ＋6的图形，则此图为何？ （ ）7. 化简14(－4x ＋8)－3(4－5x )，可得下列哪一个结果？ （ ） A.－16x －10 B.－16x －4 C. 56x －40 D. 14x －108. 图(二)中有四条互相不平行的直线L 1、L 2、L 3、L 4所截出的七个角。
关于这七个角的度数关系，下列何者正确？ （ ） A.247∠∠∠＝＋ B.316∠∠∠＝＋ C.146180∠∠∠︒＋＋＝D.235360∠∠∠︒＋＋＝9. 图(三)的坐标平面上，有一条通过点(－3,－2)的直线L 。
若四点(－2 , a )、(0 , b )、(c , 0)、(d ,－1)在L 上，则下列数值的判断，何者正确？ （ ） A. a ＝3 B. b ＞－2 C. c ＜－3 D. d ＝22011年台湾（台北）中考数学试题 （满分136分，考试时间120分钟）10.在1～45的45个正整数中，先将45的因子全部删除，再将剩下的整数由小到大排列，求第10个数为何？（）A.13B.14C.16D.1711.计算47( 1.6) 2.54÷÷－－之值为何？（）A.－1.1B.－1.8C.－3.2D.－3.912.已知世运会、亚运会、奥运会分别于公元2009年、2010年、2012年举办。
2012年全国中考数学试题分类解析汇编(159套63专题) 专题27概率
2012年全国中考数学试题分类解析汇编(159套63专题）专题27：概率一、选择题1. （2012安徽省4分）给甲乙丙三人打电话，若打电话的顺序是任意的，则第一个打电话给甲的概率为【 】 A.61 B. 31 C.21 D.32 【答案】B 。
【考点】概率。
【分析】第1个打电话给甲、乙、丙（因为次序是任意的）的可能性是相同的，所以第一个打电话给甲的概率是13。
故选B 。
2. （2012山西省2分）在一个不透明的袋子里装有一个黑球和一个白球，它们除颜色外都相同，随机从中摸出一个球，记下颜色后放回袋子中，充分摇匀后，在随机摸出一个球，两次都摸到黑球的概率是【 】A ．B ．C ．D ．【答案】A 。
【考点】列表法或树状图法，概率。
【分析】画树状图得：∵共有4种等可能的结果，两次都摸到黑球的只有1种情况， ∴两次都摸到黑球的概率是14。
故选A 。
3. （2012山西省2分）小江玩投掷飞镖的游戏，他设计了一个如图所示的靶子，点E 、F 分别是矩形ABCD 的两边AD ．BD 上的点，EF∥AB，点M 、N 是EF 上任意两点，则投掷一次，飞镖落在阴影部分的概率是【 】A ．B ．C ．D ．【答案】C 。
【考点】几何概率。
【分析】∵ABFE ABFE DCFE DCFE11S S S S 22==分分分分分分分分分分分分分分分边内阴边边内阴边，∴ABCD 1S S 2=分分分分分阴。
∴飞镖落在阴影部分的概率是12。
故选C 。
4. （2012海南省3分）要从小强、小红和小华三人跟随机选两人作为旗手，则小强和小红同时入选的概率是【 】 A ．23 B ．13 C ．12 D ．16【答案】B 。
【考点】概率。
【分析】因为从小强、小红和小华三人跟随机选两人作为旗手，共有小强和小红、小强和小华。
小红和小华三种情况，小强和小红同时入选只有一种情况，所以小强和小红同时入选的概率是13。
故选B 。
5. （2012广东深圳3分）端午节吃粽子是中华民族的传统习俗，妈妈买了2只红豆粽、3只碱水粽、5只咸肉粽，粽子除内部馅料不同外其它均相同．小颖任意吃一个，吃到红豆粽的概率是【 】 A.110 B.15 C. 13 D. 12【答案】B 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2012年台湾省中考数学试卷解析一、选择题(共34小题,每小题3分,满分99分)1．(2012•台湾)三年甲班男、女生各有20人,如图为三年甲班男、女生身高的盒状图．若班上每位同学的身高均不相等,则全班身高的中位数在下列哪一个范围？()A．150～155 B．155～160 C．160～165 D．165～170考点: 中位数.分析:根据所给的图形和中位数的定义即可得到答案．解答:解:由图可知:男生身高的中位数约165(cm),女生身高的中位数约160(cm),所以全班身高的中位数在160～165(cm),故选C点评:此题考查了中位数,将一组数据从小到大依次排列,把中间数据(或中间两数据的平均数)叫做中位数．2．(2012•台湾)小明原有300元,如图记录了他今天所有支出,其中饼干支出的金额被涂黑．若每包饼干的售价为13元,则小明可能剩下多少元？()A．4B．14 C．24 D．34考点: 一元一次不等式的应用.分析:根据设小明买了x包饼干,则剩下的钱为300﹣(50+90+120+13x)元,再分别分析得出可能剩下的钱数．解答:解:设小明买了x包饼干,则剩下的钱为300﹣(50+90+120+13x)元,整理后为(40﹣13x)元,当x=1,40﹣13x=27,当x=2,40﹣13x=14,当x=3,40﹣13x=1；故选；B．点评:此题主要考查了实际生活问题应用,利用已知表示出剩下的钱是解题关键．3．(2012•台湾)解二元一次联立方程式,得y=()A．﹣4 B．C．D．5﹣考点: 解二元一次方程组.专题: 计算题.分析:原方程组即:,两式相减即可消去x,得到关于y的方程,即可求得y的值．解答:解:原方程组即:,①﹣②得:2y=﹣8,解得:y=﹣4．故选A．点评:本题考查了加减法解方程组,解方程组的基本思路是消元．4．(2012•台湾)已知甲、乙、丙三数,甲=5+,乙=3+,丙=1+,则甲、乙、丙的大小关系,下列何者正确？()A．丙＜乙＜甲B．乙＜甲＜丙C．甲＜乙＜丙D．甲=乙=丙考点: 实数大小比较.分析:本题可先估算无理数,,的整数部分的最大值和最小值,再求出甲,乙,丙的取值范围,进而可以比较其大小．解答:解:∵3=＜＜=4,∴8＜5+＜9,∴8＜甲＜9；∵4=＜＜=5,∴7＜3+＜8,∴7＜乙＜8,∵4=＜＜=5,∴5＜1+＜6,∴丙＜乙＜甲故选(A)．点评:本题考查了实数的比较大小:(1)任意两个实数都可以比较大小．正实数都大于0,负实数都小于0,正实数大于一切负实数,两个负实数绝对值大的反而小．(2)利用数轴也可以比较任意两个实数的大小,即在数轴上表示的两个实数,右边的总比左边的大,在原点左侧,绝对值大的反而小．5．(2012•台湾)小美将某服饰店的促销活动内容告诉小明后,小明假设某一商品的定价为x元,并列出关系式为0.3(2x﹣100)＜1000,则下列何者可能是小美告诉小明的内容？()A．买两件等值的商品可减100元,再打3折,最后不到1000元耶！B．买两件等值的商品可减100元,再打7折,最后不到1000元耶！C．买两件等值的商品可打3折,再减100元,最后不到1000元耶！D．买两件等值的商品可打7折,再减100元,最后不到1000元耶！考点: 一元一次不等式的应用.分析:根据0.3(2x﹣100)＜1000,可以理解为买两件减100元,再打3折得出总价小于1000元．解答:解:由关系式可知:0.3(2x﹣100)＜1000,由2x﹣100,得出两件商品减100元,以及由0.3(2x﹣100)得出买两件打3折,故可以理解为:买两件等值的商品可减100元,再打3折,最后不到1000元耶！故选:A．点评:此题主要考查了由不等式联系实际问题,根据已知得出最后打3折是解题关键．6．(2012•台湾)如图是利用短除法求出三数8、12、18的最大公因子的过程．利用短除法,求出这三数的最小公倍数为何？()A．12 B．72 C．216 D．432考点: 有理数的除法.专题: 常规题型.分析:继续完善短除法,然后根据最小公倍数的求法,把所有的数相乘即可．解答:解:如图,完成短除法如下最小公倍数为2×2×3×2×1×3=72．故选B．点评:本题考查了短除法求最小公倍数的方法,属于小学内容,比较简单,完善短除过程是解题的关键．7．(2012•台湾)已知某公司去年的营业额为四千零七十亿元,则此营业额可用下列何者表示？()A．4.07×109元B．4.07×1010元C．4.07×1011元D．4.07×1012元考点: 科学记数法—表示较大的数.分析:首先将四千零七十亿元可写成407000000000,再利用科学记数法的表示形式为a×10n的形式,其中1≤|a|＜10,n为整数．确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同．当原数绝对值＞1时,n是正数；当原数的绝对值＜1时,n是负数．解答:解:将四千零七十亿元可写成407000000000,407000000000=4.07×1011,故选:C．点评:此题考查了科学记数法的表示方法．科学记数法的表示形式为a×10n的形式,其中1≤|a|＜10,n为整数,表示时关键要正确确定a的值以及n的值．8．(2012•台湾)如图为制作果冻的食谱,傅妈妈想依此食谱内容制作六人份的果冻．若她加入50克砂糖后,不足砂糖可依比例换成糖浆,则她需再加几小匙糖浆？()A．15 B．18 C．21 D．24考点: 一元一次方程的应用.分析:根据六人份需20×6=120克砂糖,尚需120﹣50=70克砂糖,再利用20克砂糖=6小匙糖浆,即可得出答案．解答:解:六人份需20×6=120克砂糖,尚需120﹣50=70克砂糖,又20克砂糖=6小匙糖浆,所求=70÷20×6=21(小匙)．故选:C．点评:此题主要考查了实际生活问题的应用,根据标签上所标示的20克砂糖=6小匙糖浆得出答案是解题关键．9．(2012•台湾)如图所示的方格纸上有一平行四边形ABCD,其顶点均在网格线的交点上,且E 点在AD上．今大华在方格纸网格线的交点上任取一点F,发现△FBC的面积比△EBC的面积大．判断下列哪一个图形可表示大华所取F点的位置？()A ．B ．C ．D．考点: 平行四边形的性质；平行线之间的距离；三角形的面积.专题: 数形结合.分析:根据两平行线间的距离相等,判断出各选项中点E、F到边BC的距离的大小,然后根据等底等高的三角形的面积相等解答．解答:解:A、点F到边BC的距离小于点E到边BC的距离,所以△FBC的面积＜△EBC的面积,故本选项错误；B、点F到边BC的距离小于点E到边BC的距离,所以△FBC的面积＜△EBC的面积,故本选项错误；C、点F到边BC的距离等于点E到边BC的距离,所以△FBC的面积=△EBC的面积,故本选项错误；D、点F到边BC的距离大于点E到边BC的距离,所以△FBC的面积＞△EBC的面积,故本选项正确．故选D．点评:本题考查了平行四边形的性质,两平行线间的距离相等的性质,三角形的面积,根据底边相等的三角形,高越大则面积越大,结合图形判断出各选项中的点E、点F到BC边的距离的大小是解题的关键．10．(2012•台湾)小明将一正方形纸片画分成16个全等的小正方形,且如图所示为他将其中四个小正方形涂成灰色的情形．若小明想再将一小正方形涂成灰色,使此纸片上的灰色区域成为线对称图形,则此小正方形的位置为何？()A．第一列第四行B．第二列第一行C．第三列第三行D．第四列第一行考点: 利用轴对称设计图案.分析:根据轴对称图形的性质和纸片上的四个灰色小正方形,确定出对称轴,即可得出小正方形的位置．解答:解:根据题意得:涂成灰色的小方格在第二列第一行．故选B．点评:此题考查了利用轴对称设计图案,解答此题的关键是根据题意确定出对称轴,画出图形．11．(2012•台湾)如图所示的直线AE与四边形ABCD的外接圆相切于A点．若∠DAE=12°,、、三弧的度数相等,则∠ABC的度数为何？()A．64 B．65 C．67 D．68考点: 切线的性质.专题: 计算题.分析:作直径AF,连接DF,根据切线的性质求出∠F的度数,求出弧AD的度数,求出DC的度数,得出弧ADC的度数,即可求出答案．解答:解:作直径AF,连接DF,∵AE是⊙O的切线,∴∠EAF=90°,∵∠ADF=90°,∴∠EAD+∠DAF=90°,∠F+∠DAF=90°,∴∠F=∠DAE∵∠DAE=12°(已知),∴∠F=12°,∴弧AD的度数是2×12°=24°,∴、、三弧的度数相等,∴弧CD的度数是×(360°﹣24°)=112°,∴弧ADC的度数是24°+112°=136°,∴∠ABC=×136°=68°,故选D．点评:本题考查了切线的性质的应用,能求出弧AD的度数是解此题的关键,弦切角等于该弦所夹弧所对的圆周角,主要培养学生运用性质进行推理和计算的能力．12．(2012•台湾)一纸箱内有红、黄、蓝、绿四种颜色的纸牌,且如图所示为各颜色纸牌数量的统计图．若小华自箱内抽出一张牌,且每张牌被抽出的机会相等,则他抽出红色牌或黄色牌的机(概)率为何？()A．B．C．D．考点: 概率公式；条形统计图.专题: 计算题.分析:根据统计图求出各色纸牌的总张数及红色牌和黄色牌的张数,利用概率公式进行计算即可．解答:解:图中共有各色纸牌3+3+5+4=15张,其中,红色纸牌3张,黄色纸牌3张,抽出红色纸牌或黄色纸牌的机率==,故选B．点评:本题考查了概率公式和条形统计图,要知道:概率=所求情况数与总情况数之比．13．(2012•台湾)计算(﹣1000)×(5﹣10)之值为何？()A．1000 B．1001 C．4999 D．5001考点: 有理数的乘法.专题: 计算题.分析:将﹣1000化为﹣(1000+),然后计算出5﹣10,再根据分配律进行计算．解答:解:原式=﹣(1000+)×(﹣5)=(1000+)×5=1000×5+×5=5000+1=5001．故选D．点评:本题考查了有理数的乘法,灵活运用分配律是解题的关键．14．(2012•台湾)下列四个选项中,哪一个为多项式8x2﹣10x+2的因式？()A．2x﹣2 B．2x+2 C．4x+1 D．4x+2考点: 因式分解的意义.分析:将8x2﹣10x+2进行分解因式得出8x2﹣10x+2=(4x﹣1)(2x﹣2),进而得出答案即可．解答:解:8x2﹣10x+2=2(4x2﹣5x+1),=2(4x﹣1)(x﹣1),=(4x﹣1)(2x﹣2),故多项式8x2﹣10x+2的因式为(4x﹣1)与(2x﹣2),故选:A．点评:此题主要考查了因式分解的意义,正确将多项式8x2﹣10x+2分解因式是解题关键．15．(2012•台湾)如图,大、小两圆的圆心均为O点,半径分别为3、2,且A点为小圆上的一固定点．若在大圆上找一点B,使得OA=AB,则满足上述条件的B点共有几个？()A．0B．1C．2D．3考点: 圆与圆的位置关系.分析:由题意可得连接OA,以A点为圆心,OA为半径画弧,交大圆于B1、B2两点,则可得满足上述条件的B点共有2个．解答:解:连接OA,以A点为圆心,OA为半径画弧,交大圆于B1、B2两点,则B1、B2即为所求(AB1=AB2=OA)．即满足条件的B点共有2个．故选C．点评:此题考查了圆与圆的位置关系．此题难度适中,解此题的关键是数形结合思想的应用,注意由OA=AB,可得点B位于以A为圆心,OA长为半径的圆上．16．(2012•台湾)如图,△ABC中,AB=AC=17,BC=16,M是△ABC的重心,求AM的长度为何？()A．8B．10 C．D．考点: 三角形的重心；等腰三角形的性质；勾股定理.分析:根据在△ABC中,根据三线合一定理与勾股定理即可求得AN的长,然后根据重心的性质求得AM的长,即可求解．解答:解:如图,延长AM,交BC于N点,∵AB=AC,∴△ABC为等腰三角形,又∵M是△ABC的重心,∴AN为中线,且AN⊥BC,∴BN=CN==8,AN==15,AM=AN=×15=10,故选,:B．点评:此题主要考查了重心的性质以及等腰三角形的三线合一性质和勾股定理等知识,根据重心性质得出AM=AN是解题关键．)如图所示为魔术师在小美面前表演的经过:17．(2012•台湾A．B ．C ．D ．考点: 函数的图象；整式的加减.分析:根据图片对话得出,x、y的关系式为y=2,进而得出图象即可．解答:解:由数字乘以3可得3x,加6可得3x+6,结果除以3可得(3x+6)÷3=x+2,再减去一开始写的数字可得x+2﹣x=2,∴可得x、y的关系式为y=2；即可得出函数图象是平行于x轴且过2的直线．故选:B．点评:此题主要考查了函数图象,根据已知得出y与x的关系式是解题关键．18．(2012•台湾)判断下列哪一组的a、b、c,可使二次函数y=ax2+bx+c﹣5x2﹣3x+7在坐标平面上的图形有最低点？()A．a=0,b=4,c=8 B．a=2,b=4,c=﹣8 C．a=4,b=﹣4,c=8 D．a=6,b=﹣4,c=﹣8考点: 二次函数的最值.专题: 计算题.分析:将二次函数化为一般形式,使其二次项系数为正数即可．解答:解:y=ax2+bx+c﹣5x2﹣3x+7=(a﹣5)x2+(b﹣3)x+(c+7),若使此二次函数图形有最低点,则图形的开口向上,即x2项系数为正数,∴a﹣5＞0,∴a＞5,故选D．点评:本题考查了二次函数的最值,理解二次函数系数与图象的关系是解题的关键．19．(2012•台湾)如图,数在线的A、B、C、D四点所表示的数分别为a、b、c、d,且O为原点．根据图中各点位置,判断|a﹣c|之值与下列何者不同？()A．|a|+|b|+|c| B．|a﹣b|+|c﹣b| C．|a﹣d|﹣|d﹣c| D．|a|+|d|﹣|c﹣d|考点: 实数与数轴.专题: 探究型.分析:根据绝对值的性质计算出各绝对值表示的线段长,与|a﹣c|的长进行比较即可．解答:解:A、∵|a|+|b|+|c|=AO+BO+CO≠AC,故本选项正确；B、∵|a﹣b|+|c﹣b|=AB+BC=AC,故本选项错误；C、∵|a﹣d|﹣|d﹣c|=AD﹣CD=AC,故本选项错误；D、∵|a|+|d|﹣|c﹣d|=AO+DO﹣CD=AC,故本选项错误；故选A．点评:本题考查了实数与数轴,知道绝对值的意义是解题的关键．20．(2012•台湾)下表为某公司200名职员年龄的次数分配表,其中36～42岁及50～56岁的次数因污损而无法看出．若36～42岁及50～56岁职员人数的相对次数分别为a%、b%,则年龄22～28 29～35 36～42 43～49 50～56 57～63次数 6 40 42 2A．10 B．45 C．55 D．99考点: 频数(率)分布表.专题: 图表型.分析:根据图表求出36～42岁及50～56岁的职员人数,然后求出相对次数比,然后根据百分数的意义,扩大100倍即可得解．解答:解:由表知36～42岁及50～56岁的职员人数共有,200﹣6﹣40﹣42﹣2=110人,所以,a%+b%=×100%=55%,所以a+b=55．故选C．点评:本题考查了频数分布表,本题难点在于a、b的和不是职员人数,而是相对次数比,这也是本题容易出错的地方．21．(2012•台湾)如图,正六边形ABCDEF的边长为1,连接AC、BE、DF,求图中灰色四边形的周长为何？()A．3B．4C．2+D．2+考点: 正多边形和圆.分析:根据正六边形的性质得出BC=1=CD=GH,CG==HD,进而得出四边形CDHG的周长．解答:解:如图:∵ABCDEF为正六边形∴∠ABC=120°,∠CBG=60°又BC=1=CD=GH,∴CG==HD,四边形CDHG的周长=(1+)×2=2+．故选:D．点评:此题主要考查了正多边形和圆的有关计算,根据已知得出GH=1以及CG的长是解题关键．22．(2012•台湾)有一段树干为一直圆柱体,其底面积为9π平方公尺,高为15公尺．若将此树干分为两段圆柱形树干,且体积比为2:1,则体积较大的树干,其侧面的表面积为多少平方公尺？()A．60πB．72πC．84πD．96π考点: 圆柱的计算.分析:根据两段圆柱形树干的体积比为2:1,得出两段圆柱形树干的柱高比为2:1,进而得出体积较大的树干柱高,即可得出侧面的表面积．解答:解:∵两段圆柱形树干的体积比为2:1,∴两段圆柱形树干的柱高比为2:1,则体积较大的树干柱高为15×=10(公尺),∵圆柱体的底面积为9π平方公尺,∴圆柱体的底圆半径为3公尺,所求=(2×π×3)×10=60π(平方公尺)；故选:A．点评:此题主要考查了圆柱的计算,根据已知得出体积较大的树干柱高是解题关键．23．(2012•台湾)计算[()2]3×[()2]2之值为何？()A．1B．C．()2D．()4考点: 整式的混合运算.专题: 计算题.分析:先算乘方,再算乘法即可．解答:解:原式=()6×()4=()6×()﹣4,=()2故选C．点评:本题考查的是整式的混合运算,整式的混合运算运算顺序和有理数的混合运算顺序相似,即先算乘方,再算乘法,最后算加减,有括号的先算括号里面的．24．(2012•台湾)小华带x元去买甜点,若全买红豆汤圆刚好可买30杯,若全买豆花刚好可买40杯．已知豆花每杯比红豆汤圆便宜10元,依题意可列出下列哪一个方程式？() A．B．C．D．考点: 由实际问题抽象出一元一次方程.分析:首先要找到题中存在的等量关系,由题意可得到:豆花每杯比红豆汤圆便宜10元,进而得出等式方程即可．解答:解:由题意知红豆汤圆每杯元,豆花每杯元,又因为豆花每杯比红豆汤圆便宜10元,即=﹣10,则=+10,故选:A．点评:此题主要考查了由实际问题抽象出一元一次方程,解类题的关键是找出题中存在的等量关系．25．(2012•台湾)如图,坐标平面上直线L的方程式为3x﹣y=﹣3．若有一直线L′的方程式为y=a,则a的值在下列哪一个范围时,L′与L的交点会在第二象限？()A．1＜a＜2 B．3＜a＜4 C．﹣1＜a＜0 D．﹣3＜a＜﹣2考点: 两条直线相交或平行问题.专题: 数形结合.分析:先求出直线L与y轴的交点,然后根据直线L′与直线L的交点在第二象限可得a的取值范围,再结合选项解答．解答:解:由L:3x﹣y=﹣3可知,直线L交y轴于(0,3),由图可知当0＜a＜3时,L′与L的交点会在第二象限．故选A．点评:本题考查了直线相交的问题,根据直线L与y轴的交点确定出a的取值范围是解题的关键．26．(2012•台湾)计算之值为何？()A．0B．25 C．50 D．80考点: 二次根式的化简求值；平方差公式；因式分解的应用.专题: 计算题.分析:根据平方差公式求出1142﹣642=(114+64)×(114﹣64)=178×50,再提出50得出50×(178﹣50)=50×128,分解后开出即可．解答:解:,=,=,=,=,=,=2×5×8,=80,故选D．点评:本题考查了平方差公式,因式分解,二次根式的运算等知识点的应用,解此题的关键是能选择适当的方法进行计算,本题主要考查学生的思维能力和应变能力,题目比较好,是一道具有代表性的题目．27．(2012•台湾)如图1为图2中三角柱ABCEFG的展开图,其中AE、BF、CG、DH是三角柱的边．若图1中,AD=10,CD=2,则下列何者可为AB长度？()A．2B．3C．4D．5考点: 几何体的展开图；三角形三边关系.专题: 常规题型.分析:根据图形先求出AB与BC的和,然后设AB=x,表示出BC=8﹣x,然后利用三角形的任意两边之和大于第三边,两边之差小于第三边列出不等式组,求解得到AB的取值范围,即可得解．解答:解:由图可知,AD=AB+BC+CD,∵AD=10,CD=2,∴AB+BC=8,设AB=x,则BC=8﹣x,所以,解不等式①得x＞3,解不等式②得,x＜5,所以,不等式组的解集是3＜x＜5,综合各选项,只有C符合．故选C．点评:本题考查了几何体的展开图,利用三角形的三边关系求出AB边的取值范围是解题的关键．28．(2012•台湾)如图,一圆桌周围有20个箱子,依顺时针方向编号1～20．小明在1号箱子中丢入一颗红球后,沿着圆桌依顺时针方向行走,每经过一个箱子就依下列规则丢入一颗球:(1)若前一个箱子丢红球,经过的箱子就丢绿球．(2)若前一个箱子丢绿球,经过的箱子就丢白球．(3)若前一个箱子丢白球,经过的箱子就丢红球．已知他沿着圆桌走了100圈,求4号箱内有几颗红球？()A．33 B．34 C．99 D．100考点: 规律型:图形的变化类.分析:根据已知要求得出第1、4、7、…、100圈会在4号箱内丢一颗红球,进而得出通项公式a n=a1+(n﹣1)d,得出答案即可．解答:解:第1圈红球在1、4、7、10、13、16、19号箱内,第2圈红球在2、5、8、11、14、17、20号箱内,第3圈红球在3、6、9、12、15、18号箱内,第4圈红球在1、4、7、10、13、16、19号箱内,…且第1、4、7、…、100圈会在4号箱内丢一颗红球,a n=a1+(n﹣1)d,100=1+3(n﹣1),33=n﹣1,n=34,故选:B．点评:此题主要考查了图形的变化类,根据已知规律得出通项公式是解题关键．29．(2012•台湾)如图,梯形ABCD中,∠DAB=∠ABC=90°,E点在CD上,且DE:EC=1:4．若AB=5,BC=4,AD=8,则四边形ABCE的面积为何？()A．24 B．25 C．26 D．27考点: 直角梯形；三角形的面积.分析:首先连接AC,由梯形ABCD中,∠DAB=∠ABC=90°,AB=5,BC=4,AD=8,即可求得梯形ABCD与△ABC的面积,继而可得△ACD的面积,又由DE:EC=1:4,则可求得△ACE的面积,则可求得四边形ABCE的面积．解答:解:连接AC,∵梯形ABCD中,∠DAB=∠ABC=90°,AB=5,BC=4,AD=8,∴S梯形ABCD=•(AD+BC)•AB==30,S△ABC=AB•BC=×5×4=10,∴S△ACD=30﹣10=20,∵DE:EC=1:4,∴S△ACE=20×=16,∴S四边形ABCE=10+16=26．故选C．点评:此题考查了直角梯形的性质,直角三角形的性质以及等高三角形的面积问题．此题难度适中,解题的关键是准确作出辅助线,注意数形结合思想的应用,注意等高的三角形面积的比等于其对应底的比．30．(2012•台湾)有一个二次函数y=x2+ax+b,其中a、b为整数．已知此函数在坐标平面上的图形与x轴交于两点,且两交点的距离为4．若此图形的对称轴为x=﹣5,则此图形通过下列哪一点？()A．(﹣6,﹣1) B．(﹣6,﹣2) C．(﹣6,﹣3) D．(﹣6,﹣4)考点: 抛物线与x轴的交点；二次函数图象上点的坐标特征.分析:根据二次函数图形的对称轴为x=﹣5,图形与x轴的两个交点距离为4可知两点的坐标为(﹣7,0)和(﹣3,0),设出此函数的解析式,把x=﹣6代入进行计算即可．解答:解:∵二次函数图形的对称轴为x=﹣5,图形与x轴的两个交点距离为4, ∴此两点的坐标为(﹣7,0)和(﹣3,0)设二次函数的解析式为:y=(x+7)(x+3),将x=﹣6代入,得y=(﹣6+7)(﹣6+3)=﹣3∴点(﹣6,﹣3)在二次函数的图象上．故选C．点评:本题考查的是抛物线与x轴的交点问题,根据题意得出二次函数的交点式是解答此题的关键．31．(2012•台湾)若一元二次方程式x2﹣2x﹣3599=0的两根为a、b,且a＞b,则2a﹣b之值为何？()A．﹣57 B．63 C．179 D．181考点: 解一元二次方程-配方法；有理数的混合运算.专题: 计算题.分析:配方得出(x﹣1)2=3600,推出x﹣1=60,x﹣1=﹣60,求出x的值,求出a、b的值,代入2a ﹣b求出即可．解答:解:x2﹣2x﹣3599=0,移项得:x2﹣2x=3599,x2﹣2x+1=3599+1,即(x﹣1)2=3600,x﹣1=60,x﹣1=﹣60,解得:x=61,x=﹣59,∵一元二次方程式x2﹣2x﹣3599=0的两根为a、b,且a＞b,∴a=61,b=﹣59,∴2a﹣b=2×61﹣(﹣59)=181,故选D．点评:本题考查了有理数的混合运算和解一元二次方程的应用,能求出a、b的值是解此题的关键,主要培养学生解一元二次方程的能力,题型较好,难度适中．32．(2012•台湾)如图,边长12的正方形ABCD中,有一个小正方形EFGH,其中E、F、G分别在AB、BC、FD上．若BF=3,则小正方形的边长为何？()A．B．C．5D．6考点: 相似三角形的判定与性质；勾股定理；正方形的性质.专题: 探究型.分析:先根据相似三角形的判定定理得出△BEF∽△CFD,再根据勾股定理求出DF的长,再由相似三角形的对应边成比例即可得出结论．解答:解:在△BEF与△CFD中∵∠1+∠2=∠2+∠3=90°,∴∠1=∠3∵∠B=∠C=90°,∴△BEF∽△CFD,∵BF=3,BC=12,∴CF=BC﹣BF=12﹣3=9,又∵DF===15,∴=,即=,∴EF=故选B．点评:本题考查的是相似三角形的判定与性质及勾股定理,根据题意得出△BEF∽△CFD是解答此题的关键．33．(2012•台湾)如图,直角三角形ABC有一外接圆,其中∠B=90°,AB＞BC,今欲在上找一点P,使得=,以下是甲、乙两人的作法:甲:(1)取AB中点D(2)过D作直线AC的并行线,交于P,则P即为所求乙:(1)取AC中点E(2)过E作直线AB的并行线,交于P,则P即为所求对于甲、乙两人的作法,下列判断何者正确？()A．两人皆正确B．两人皆错误C．甲正确,乙错误C D．甲错误,乙正确考点: 垂径定理；三角形中位线定理；圆周角定理.专题: 探究型.分析:(1)由甲的作法可知,DP是△ABC的中位线,由于DP不垂直于BC,故≠；(2)由乙的作法,连BE,可知△BEC为等腰三角形,由等腰三角形的性质可知∠1=∠2,根据圆周角定理即可得出结论．解答:解:(1)由甲的作法可知,DP是△ABC的中位线,∵DP不垂直于BC,∴≠；(2)由乙的作法,连BE,可知△BEC为等腰三角形∵直线PE⊥BC,∴∠1=∠2故=；∴甲错误,乙正确．故选D．点评:本题考查的是垂径定理、三角形的中位线定理及圆周角定理,熟知同弧或等弧所对的圆周角相等是解答此题的关键．34．(2012•台湾)图1的长方形ABCD中,E点在AD上,且BE=2AE．今分别以BE、CE为折线,将A、D向BC的方向折过去,图2为对折后A、B、C、D、E五点均在同一平面上的位置图．若图2中,∠AED=15°,则∠BCE的度数为何？()A．30 B．32.5 C．35 D．37.5考点: 翻折变换(折叠问题).分析:由题意得:∵BE=2AE=2A′E,∠A=∠A′=90°,即可得△ABE、△A′BE皆为30°、60°、90°的三角形,然后可求得∠AED′的度数,又由∠AED=15°,即可求得∠DED′的度数,继而求得∠BCE=∠2的度数．解答:解:根据题意得:∵BE=2AE=2A′E,∠A=∠A′=90°,∴△ABE、△A′BE皆为30°、60°、90°的三角形,∴∠1=∠AEB=60°,∴∠AED′=180°﹣∠1﹣∠AEB=180°﹣60°﹣60°=60°,∴∠DED′=∠AED+∠AED′=15°+60°=75°,∴∠2=∠DED′=37.5°,∵A′D′∥BC,∴∠BCE=∠2=37.5°．故选D．点评:此题考查了折叠的性质、矩形的性质以及含30°角的直角三角形的性质．此题难度适中,注意数形结合思想的应用,注意折叠中的对应关系．。