自功率谱密度函数和自相关函数
功率信号的自相关函数和功率谱密度是一对傅里叶变换

功率信号的自相关函数和功率谱密度是一对傅里叶变换在信号处理领域中,功率信号的自相关函数和功率谱密度是非常重要的概念。
它们之间的关系可以通过傅里叶变换来描述,这种变换能够帮助我们更深入地理解功率信号的特性。
在本文中,我们将深入探讨功率信号的自相关函数和功率谱密度,并探讨它们与傅里叶变换之间的关系。
1. 自相关函数让我们了解一下什么是功率信号的自相关函数。
自相关函数描述了一个信号与其自身在不同时间点的相似程度。
对于功率信号x(t),它的自相关函数R_x(tau)定义如下:R_x(tau) = E[x(t)x(t+tau)]其中tau代表时间延迟,E[]代表期望操作。
自相关函数可以告诉我们信号在不同时间点上的相关性,从而帮助我们分析信号的特性。
2. 功率谱密度接下来,让我们来看看功率谱密度是如何定义的。
功率谱密度描述了信号在频率域上的能量分布。
对于功率信号x(t),其功率谱密度S_x(f)定义如下:S_x(f) = lim T->∞ E[|X(f)|^2]其中X(f)为x(t)的傅里叶变换,E[]代表期望操作。
功率谱密度可以告诉我们信号在不同频率上的能量分布情况,从而帮助我们分析信号的频谱特性。
3. 傅里叶变换的关系现在,让我们来探讨功率信号的自相关函数和功率谱密度与傅里叶变换之间的关系。
根据Wiener-Khinchin定理,功率谱密度是自相关函数的傅里叶变换,即:S_x(f) = F[R_x(tau)]其中F[]代表傅里叶变换操作。
这个定理告诉我们,通过对功率信号的自相关函数进行傅里叶变换,我们可以得到其功率谱密度,从而在频域上进行分析。
4. 个人观点和理解在我看来,功率信号的自相关函数和功率谱密度的傅里叶变换关系非常有意义。
通过对功率信号在时间域和频率域上的分析,我们可以更全面地了解信号的特性和行为。
傅里叶变换提供了一种强大的工具,使我们能够从不同的角度来理解和处理功率信号。
对于工程领域的同行们,掌握这些概念并且能够灵活运用,将有助于我们更好地设计和分析各种信号系统。
matlab 正弦波 高斯白噪声 均匀白噪声 功率谱密度 自相关函数(word文档良心出品)

现代通信原理作业一姓名:张英伟学号:133320085208036 班级:13级理工部3班利用matlab完成:●产生正弦波信号、均匀白噪声以及高斯白噪声并分别将两种噪声叠加到正弦波信号上,绘出波形。
●分别求取均匀白噪声序列和高斯白噪声序列的自相关及功率谱密度,绘出波形。
一、白噪声区别及产生方法1、定义:均匀白噪声:噪声的幅度分布服从均匀分布,功率谱密度在整个频域内均匀分布的噪声。
高斯白噪声:噪声的幅度分布服从正态分布,功率谱密度在整个频域内均匀分布的噪声。
2、matlab仿真函数:rand函数默认产生是区间在[0,1]的随机数,这里需要利用公式:z2=a+(b-(a))*rand(m,n)............(公式1)randn函数默认产生均值是0、方差是1的随机序列,所以可以用其来产生均值为0、方差为1的正态分布白噪声,即N(0,12)。
利用公式:z1=a+b*randn(1,n).................(公式2)可以产生均值为a,方差为b2 高斯白噪声,即N(a,b2)。
二、自相关函数与功率谱密度之间的关系1、功率谱密度:每单位频率波携带的功率,这被称为信号的功率谱密度。
2、自相关函数:描述随机信号X(t)在任意两个不同时刻t1,t2的取值之间的相关程度。
3、维纳-辛钦定理:由于平均值不为零的信号不是平方可积的,所以在这种情况下就没有傅里叶变换。
幸运的是维纳-辛钦定理提供了一个简单的替换方法,如果信号可以看作是平稳随机过程,那么功率谱密度就是信号自相关函数的傅里叶变换。
4、平稳随机过程:是在固定时间和位置的概率分布与所有时间和位置的概率分布相同的随机过程。
(就是指得仅一个随机过程,中途没有变成另外一个统计特性的随机过程)二、源代码及仿真结果1、正弦波x=(0:0.01:2); %采样频率100Hzy1=sin(10*pi*x); %产生频率5Hz的sin函数plot(x,y1,'b');2、高斯白噪声+正弦波z1=0.1*randn(1,201); %产生方差N(0,0.12)高斯白噪声(b=0.01/0.1/1)plot(x,z1,'b');y2=y1+z1; %叠加高斯白噪声的正弦波plot(x,y2,'b');3、均匀白噪声+正弦波z2=-.3+.6*rand(1,201); %产生-0.3到0.3的均匀白噪声plot(x,z2,'b');y3=y1+z2; %叠加均匀白噪声的正弦波plot(x,y3,'b');4、高斯白噪声序列自相关函数及功率谱密度z1=0.1*randn(1,201); %产生方差N(0,0.12)高斯白噪声[r1,lags]=xcorr(z1); %自相关函数的估计plot(lags,r1);f1=fft(r1);f2=fftshift(f1); %频谱校正l1=(0:length(f2)-1)*200/length(f2)-100; %功率谱密度x轴y4=abs(f2);plot(l1,y4);5、均匀白噪声序列自相关函数及功率谱密度z2=-.3+.6*rand(1,201); %产生-0.3到0.3的均匀白噪声[r2,lags]=xcorr(z2); %自相关函数的估计plot(lags,r2);f3=fft(r2);f4=fftshift(f3); %频谱校正l2=(0:length(f4)-1)*200/length(f4)-100; %功率谱密度x轴y5=abs(f4);plot(l2,y5);。
基于功率谱密度工程车辆驾驶室随机振动分析

基于功率谱密度工程车辆驾驶室随机振动分析彭俊;介石磊【摘要】路面随机振动激励对驾驶室结构具有一定的疲劳破坏作用,对驾驶室进行随机振动分析,可以分析随机振动载荷对驾驶室结构的影响.根据驾驶室受到的随机振动冲击情况,基于ANSYS驾驶室有限元模型,获得驾驶室的固有振动模态;并根据工程车辆的实际运行状况,选取空载30km/h、空载40km/h、重载20km/h和重载30km/h等四个主要工况进行随机振动分析.通过对驾驶室结构的ANSYS动力学仿真分析发现,结构最大应力产生在空载40km/h工况下,位置发生在上顶板与上斜梁的连接处.以此结果作为疲劳分析的前提,根据Q235钢的S-N曲线和疲劳累积损伤理论,利用Steinberg三区间法对驾驶室结构进行疲劳强度分析,结果可知,驾驶室结构的累积疲劳损伤度远远小于1,说明驾驶室结构满足疲劳强度要求,为此类设计研究提供参考.【期刊名称】《机械设计与制造》【年(卷),期】2019(000)006【总页数】4页(P120-123)【关键词】工程车辆;驾驶室;模态分析;随机振动;功率谱密度;模型【作者】彭俊;介石磊【作者单位】黄河交通学院汽车工程学院,河南焦作 454950;黄河交通学院汽车工程学院,河南焦作 454950【正文语种】中文【中图分类】TH16;U469.21 引言工程车辆工作环境恶劣,在矿区行驶时,驾驶室受到来自地面的随机振动激励,这些随机振动对驾驶室的结构具有一定的疲劳破坏作用,对驾驶室进行随机振动分析[1],可以分析随机振动载荷对驾驶室结构的影响,为驾驶室设计研究提供参考。
国内外学者驾驶室设计取得一定成果:文献[2]应用因子分析技术,根据统计规律对其内部结构进行设计分析;文献[3]结合人机工程理论,将驾驶员身体各部分与驾驶室相对位置采用数学方法进行描述,搭建系统的数学模型,采用杆状人体模型进行研究;文献[4]根据人机工程设计理论,对驾驶室操作面板及控制装置进行设计布置;文献[5]将除雪机械在视野死角与改进措施,对驾驶室座椅的空间位置设计,可满足90%以上驾驶员需要。
求随机相位余弦波t=Acosct 的自相关函数和功率谱密度共53页

15、机会是不守纪律的。——雨果
31、只有永远躺在泥坑里的人,才不会再掉进坑里。——黑格尔 32、希望的灯一旦熄灭,生活刹那间变成了一片黑暗。——普列姆昌德 33、希望是人生的乳母。——科策布 34、形成天才的决定因素应该是勤奋。——郭沫若 35、学到很多东西的诀窍相位余弦波t=Acosct 的自相关函数和功率谱密度
11、战争满足了,或曾经满足过人的 好斗的 本能, 但它同 时还满 足了人 对掠夺 ,破坏 以及残 酷的纪 律和专 制力的 欲望。 ——查·埃利奥 特 12、不应把纪律仅仅看成教育的手段 。纪律 是教育 过程的 结果, 首先是 学生集 体表现 在一切 生活领 域—— 生产、 日常生 活、学 校、文 化等领 域中努 力的结 果。— —马卡 连柯(名 言网)
随机信号及其自相关函数和功率谱密度的MATLAB实现(1)

随机信号分析专业:电子信息工程班级:电子111姓名:***学号:**********指导老师:***随机信号及其自相关函数和功率谱密度的MATLAB实现引言:现代信号分析中,对于常见的具有各态历经的平稳随机信号,不可能用清楚的数学关系式来描述,但可以利用给定的N个样本数据估计一个平稳随机信号的功率谱密度叫做功率谱估计(PSD)。
它是数字信号处理的重要研究内容之一。
功率谱估计可以分为经典功率谱估计(非参数估计)和现代功率谱估计(参数估计)。
通过实验仿真可以直观地看出以下特性:(1)功率谱估计中的相关函数法和周期图法所得到的结果是一致的,其特点是离散性大,曲线粗糙,方差较大,但是分辨率较高。
(2)平均周期图法和平滑平均周期图法的收敛性较好,曲线平滑,估计的结果方差较小,但是功率谱主瓣较宽,分辨率低。
这是由于对随机序列的分段处理引起了长度有限所带来的Gibbs现象而造成的。
(3)平滑平均周期图法与平均周期图法相比,谱估值比较平滑,但是分辨率较差。
其原因是给每一段序列用适当的窗口函数加权后,在得到平滑的估计结果的同时,使功率谱的主瓣变宽,因此分辨率有所下降。
摘要:功率谱估计(PSD)的功率谱,来讲都是重要的,是数字信号处理的重要研究内容之一。
功率谱估计可以分为经典谱估计(非参数估计)和现代谱估计(参数估计)。
前者的主要方法有BTPSD 估计法和周期图法;后者的主要方法有最大熵谱分析法(AR 模型法)、Pisarenko 谐波分解法、Prony 提取极点法、其Prony 谱线分解法以及Capon 最大似然法。
中周期图法和AR 模型法是用得较多且最具代表性的方法。
Matlab 是目前极为流行的工程数学分析软件,在它的SignalProcessingToolbox 中也对这两个方法提供了相应的工具函数,这为我们进行工程设计分析、理论学习提供了相当便捷的途径。
关键词:随机信号 自相关系数 功率谱密度实验原理:随机信号X(t)是一个随时间变化的随机变量,将X (t )离散化,即以Ts 对X (t )进行等间隔抽样,得到随机序列X(nTs),简化为X(n)。
核电子学习题解答

习题解答第一章绪论1、核信息的获取与处理主要包括哪些方面的?①时间测量。
核信息出现的时间间隔是测定核粒子的寿命或飞行速度的基本参数,目前直接测量核信息出现的时间间隔已达到皮秒级。
②核辐射强度测量。
核辐射强度是指单位时间内核信息出现的概率,对于低辐射强度的测量,要求测量仪器具有低的噪声本底,否则核信息将淹没于噪声之中而无法测量。
对于高辐射强度的测量,由于核信息十分密集,如果信号在测量仪器中堆积,有可能使一部分信号丢失而测量不到,因此要求仪器具有良好的抗信号堆积性能。
对于待测核信息的辐射强度变化范围很大的情况(如核试验物理诊断中信号强度变化范围可达105倍),如测量仪器的量程设置太小,高辐射强度的信号可能饱和;反之,如量程设置太大,低辐射强度的信号又测不到,因此对于这种场合的测量则要求测量仪器量程可自动变换。
③能谱测量。
辐射能谱上的特征是核能级跃迁及核同位素差异的重要标志,核能谱也是核辐射的基本测量内容。
精确的能谱测量要求仪器工作稳定、能量分辨力达到几个电子伏特,并具有抑制计数速率引起的峰位和能量分辨力变化等性能。
④位置测量。
基本粒子的径迹及空间位置的精确测定是判别基本粒子的种类及其主要参数的重要手段。
目前空间定位的精度可达到微米级。
⑤波形测量。
核信息波形的变化往往反映了某些核反应过程的变化,因此核信息波形的测量是研究核爆炸反应过程的重要手段,而该波形的测量往往是单次且快速(纳秒至皮秒级)的。
⑥图像测量。
核辐射信息的二维空间图像测量是近年来发展起来的新技术。
辐射图像的测量方法可分为两类:第一种是利用辐射源进行透视以摄取被测物体的图像;第二种是利用被测目标体的自身辐射(如裂变反应产生的辐射)以反映目标体本身的图像。
图像测量利用计算机对摄取的图像信息进行处理与重建,以便更准确地反映实际和提高清晰度。
CT技术就是这种处理方法的代表。
2、抗辐射加固主要涉及哪些方面?抗辐射加固的研究重点最初是寻找能减弱核辐射效应的屏蔽材料,后来在电路上采取某些抗辐射加固措施,然后逐渐将研究重点转向对器件的抗辐射加固。
随机信号分析与处理
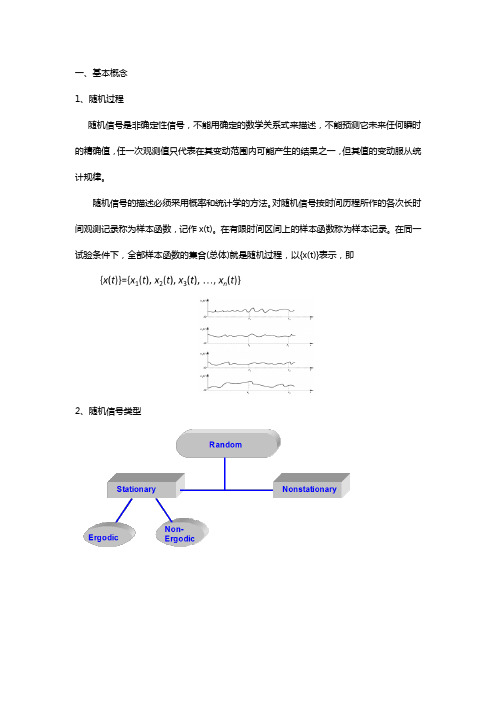
一、基本概念1、随机过程随机信号是非确定性信号,不能用确定的数学关系式来描述,不能预测它未来任何瞬时的精确值,任一次观测值只代表在其变动范围内可能产生的结果之一,但其值的变动服从统计规律。
随机信号的描述必须采用概率和统计学的方法。
对随机信号按时间历程所作的各次长时间观测记录称为样本函数,记作x(t)。
在有限时间区间上的样本函数称为样本记录。
在同一试验条件下,全部样本函数的集合(总体)就是随机过程,以{x(t)}表示,即2、随机信号类型3、平稳随机过程平稳随机过程就是统计特征参数不随时间变化而改变的随机过程。
例如,对某一随机过程的全部样本函数的集合选取不同的时间t进行计算,得出的统计参数都相同,则称这样的随机过程为平稳随机过程,否则就是非平稳随机过程。
如采样记录的均值不随时间变化4、各态历经随机过程若从平稳随机过程中任取一样本函数,如果该单一样本在长时间内的平均统计参数(时间平均)和所有样本函数在某一时刻的平均统计参数(集合平均)是一致的,则称这样的平稳随机过程为各态历经随机过程。
显然,各态历经随机过程必定是平稳随机过程,但是平稳随机过程不一定是各态历经的。
各态历经随机过程是随机过程中比较重要的一种,因为根据单个样本函数的时间平均可以描述整个随机过程的统计特性,从而简化了信号的分析和处理。
但是要判断随机过程是否各态历经的随机过程是相当困难的。
一般的做法是,先假定平稳随机过程是各态历经的,然后再根据测定的特性返回到实际中分析和检验原假定是否合理。
由大量事实证明,一般工程上遇到的平稳随机过程大多数是各态历经随机过程。
虽然有的不一定是严格的各态历经过程,但在精度许可的范围内,也可以当作各态历经随机过程来处理。
事实上,一般的随机过程需要足够多的样本(理论上应为无限多)才能描述它,而要进行大量的观测来获取足够多的样本函数是非常困难或做不到的。
在测试工作中常以一个或几个有限长度的样本记录来推断整个随机过程,以其时间平均来估计集合平均。
随机过程的自相关函数与其功率谱密度是傅里叶变换关系

随机过程的自相关函数与其功率谱密度是傅里叶变换关系随机过程是一个随时间变化的信号,每个时间点上都有一定的随机性。
我们可以用一个随机变量来描述每个时间点上的取值。
这个随机变量的集合就是一个随机过程。
自相关函数是用来描述随机过程在不同时间点上的相关性的函数。
它表示了随机过程在不同时间点上的取值之间的相关程度。
具体来说,自相关函数R(t1,t2)表示了时刻t1和t2上的信号值之间的相关性。
它的定义如下:R(t1,t2)=E[X(t1)X(t2)]其中,X(t1)和X(t2)是随机过程在时刻t1和t2上的取值,E[.]表示期望操作。
功率谱密度是用来描述随机过程在频域上的特性的函数。
它表示了随机过程在不同频率上的功率分布情况。
具体来说,功率谱密度S(f)表示了随机过程在频率f上的功率。
它的定义如下:S(f)=,F{R(t)},^2其中,R(t)是随机过程的自相关函数,F{.}表示傅里叶变换操作。
自相关函数和功率谱密度之间存在一个重要的关系,即它们通过傅里叶变换相关联。
具体来说,自相关函数是功率谱密度的傅里叶变换的模的平方,而功率谱密度是自相关函数的傅里叶变换的伪谱密度。
这个关系可以用下面的公式表示:R(t1, t2) = ∫S(f)e^(j2πft)df其中,∫表示积分操作,e^(j2πft)是复指数函数,代表了频率f上的旋转。
这个关系的意义是,自相关函数和功率谱密度提供了从时域到频域和从频域到时域的映射。
我们可以通过自相关函数计算功率谱密度,也可以通过功率谱密度计算自相关函数。
总结起来,自相关函数和功率谱密度是通过傅里叶变换相关联的重要概念。
自相关函数描述了随机过程在不同时刻上的相关性,而功率谱密度描述了随机过程在不同频率上的功率分布情况。
它们的傅里叶变换关系提供了从时域到频域和从频域到时域的映射。
这个关系在信号处理和随机过程分析中具有重要的应用价值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
∴自相关函数为: R X (τ ) =
8 − 3τ 4 − 2τ ⋅e − ⋅e 15 5
平均功率为: P = RX (0) = RX (τ )
⎡ 4 −2 τ = ⎢ ⋅e − ⋅e 15 ⎣5
三,物理功率谱密度:τ =0 Βιβλιοθήκη −3 τ ⎤⎥ ⎦τ = 0
4 8 4 = − = 5 15 15
由于实际应用中,负频率不存在,所以定义一个仅在正频率上存在 的物理功率谱密度:
既:GX (0) → ∞,GY (ω 0 ) → ∞
可以借助 δ 函数,将直流信号与周期信号在各个频率点上的无限值 δ 函数的傅氏变换 用一个δ 函数来表示,借助 ⎧
⎪ 1 ⇔ 2πδ (ω ) ⎪ ⎪ ⎨ cos(ω 0τ ) ⇔ π [δ (ω − ω 0 ) + δ (ω + ω 0 )] ⎪ π ⎪sin(ω 0τ ) ⇔ [δ (ω − ω 0 ) − δ (ω + ω 0 )] j ⎪ ⎩
FX (ω )
GX (ω )
⎧ 2GX (ω ),ω ≥ 0 FX (ω ) = ⎨ ⎩............0,ω < 0
1 RX (τ ) = 2π
∫
∞
0
FX (ω )e jωτ d ω
1 P= 2π
1 ∫-∞ GX (ω)dω = 2π
∞
∫
∞
0
1 2GX (ω )dω = 2π
∫
∞
0
FX (ω )dω
⎧ G (ω ) = ∞ R (τ )e − jωτ dτ = F [ R (τ ) ] X X ∫ −∞ X ⎪ 有: ⎨ 1 ∞ −1 jωτ ⎪ RX (τ ) = ω ω G ( ) e d F = [GX (ω )] X ∫ −∞ 2π ⎩
因为X(t) 平稳 ∴ R X (τ ),G X (ω )是偶函数。
∴ ∫ R X (τ )dτ = ∫ C 2 dτ → ∞
−∞ −∞
∞
∞
a2 Q Y (t ) = a cos(ω 0 t + θ ), RY (τ ) = cos ω 0τ 2 2 ∞ ∞ a ∴ ∫ RY (τ )dτ = ∫ cos ω 0τdτ → ∞ −∞ −∞ 2
Q R X (τ ), RY (τ ) 不满足绝对可积的条件,∴F变换不存在。
可利用δ 函数的F变换,来求⑴ ⑵两特殊信号的功率谱密度。
R X (τ ) = 1
G X (ω ) = 2πδ (ω )
0 τ RY (τ ) = cosω 0τ
ω GY (ω) = π[δ (ω − ω0 ) + δ (ω + ω0 )]
0
0
τ
−ω0
ω0
ω
) 例1 随相余弦过程 X (t ) = A cos(ω 0 t + Φ,其中 A、Φ 为常数, Φ 在 (0, 2π )上均匀分布,求X(t)的功率谱密度。
傅氏变换绝对可积的条件限制了维纳—辛钦定理的应用。
X (t ) = C ⎫ 在频域: ⑴直流信号X(t) 两者 ⑵周期信号X(t) Y (t ) = a cos(ω 0 t + θ )⎬ ⎭
⎧ω =0 仅在⎨ 频率上存在功率。 ⎩ω = ω 0
平均功率 频率点上功率 = /0 则其功率谱密度 = = →∞ 单位频带 0带宽
解:据以往结果, R (τ ) = ( A2 ) cos(ω τ ) 0 X
2
←求傅氏变换
A A GX (ω ) = ⋅ F[cos(ω0τ )] = ⋅ π [δ (ω − ω0 ) + δ (ω + ω0 )] 2 2
16 例2 已知平稳过程X(t) 具有功率谱密度: GX (ω) = 4 2 ω + 13 ω + 36 求其自相关函数,平均功率。
自功率谱密度函数和自相关函数 的关系
一、维纳—辛钦定理
对于一般随机过程X(t): G X (ω ) =
∫
∞
−∞
R X (t , t + τ )e − jωτ dτ
若 X(t)是平稳过程 则有:Q R X (t , t + τ ) = R X (τ )
∴ R X (t , t + τ ) = R X (τ ) = R X (τ )
⎧ G (ω ) = 2 ∞ R (τ ) cos ωτ dτ X X ∫ ⎪ 0 则有: ⎨ 1 ∞ ⎪ R X (τ ) = ∫0 G X (ω ) cos ωτdω π ⎩
二、维纳—辛钦定理的推广
⑴直流信号 ⑵周期信号
X (t ) = C Y (t ) = a cos(ω 0 t + θ)
2 2 在时域: Q X (t ) = C , R X (τ ) = E[ X (t ) X (t + τ )] = E[C ] = C
2
2
16 解:利用部分分式法 G X (ω ) = (ω 2 + 4)(ω 2 + 9) 16 16 4 4 8 6 5 5 = 2 − 2 = ⋅ 2 − ⋅ 2 ω + 4 ω + 9 5 ω + 4 15 ω + 9
⎡ −α τ ⎤ 利用傅氏变换对 ⎢ 2 2α 2 ⇔ e ⎥ + α ω ⎣ ⎦
