第二章 质点运动学(思考题)
大学物理第一章-质点运动学和第二章-质点动力学基础

位移的大小为
2 2 2 r x y z
z
路程是质点经过实际路径的长
度。路程是标量。
注意区分 Δ r 、r
Δr
Δr r ( A)
o x
A ΔS
B
r ( B) y
rA
o
rB
Δ
r
3. 速率和速度 速度是描述质点位置随时间变化快慢和方向的物理量。
平均速度
青年牛顿1666年6月22日至1667年3月25日两度回到乡间的老家1665年获学士学位1661年考入剑桥大学三一学院牛顿简介1667年牛顿返回剑桥大学当研究生次年获得硕士学位1669年发明了二项式定理1669年由于巴洛的推荐接受了卢卡斯数学讲座的职务全面丰收的时期16421672年进行了光谱色分析试验1672年由于制造反射望远镜的成就被接纳为伦敦皇家学会会员1680年前后提出万有引力理论1687年出版了自然哲学的数学原理牛顿简介牛顿第一定律
g
v v g
v
v g 远日点 g v
g v g g g g g v
v
近日点
v
v
思考题 质点作曲线运动,判断下列说法的正误。
r r s r
r r
s r
s r
Δr
矢量的矢积(或称叉积 、叉乘)
C A B
大小:C AB sin
方向:右手螺旋
C
B
矢积性质:A B B A A C ( A B) C A C B 可以得到:i j k , j k i , k i j . k i i 0, j j 0, k k 0
力学答案 第二章 质点运动学(思考题)

第二章 质点运动学思考题2.1质点位置矢量方向不变,质点是否作直线运动?质点沿直线运动,其位置矢量是否一定方向不变?解答:质点位置矢量方向不变,质点沿直线运动。
质点沿直线运动,质点位置矢量方向不一定不变。
如图所示。
2.2若质点的速度矢量的方向不变仅大小改变,质点作何种运动?速度矢量的大小不变而方向改变作何种运动?解答:质点的速度矢量的方向不变仅大小改变,质点作变速率直线运动;速度矢量的大小不变而方向改变作匀速率曲线运动。
2.3“瞬时速度就是很短时间内的平均速度”这一说法是否正确?如何正确表述瞬时速度的定义?我们是否能按照瞬时速度的定义通过实验测量瞬时速度? 解答:“瞬时速度就是很短时间内的平均速度”这一说法不正确。
因为瞬时速度与一定的时刻相对应。
瞬时速度的定义是质点在t 时刻的瞬时速度等于t 至t+△t 时间内平均速度t /r ∆∆,当△t →0时的极限,即dt r d t r lim v 0t=∆∆=→∆。
很难直接测量,在技术上常常用很短时间内的平均速度近似地表示瞬时速度,随着技术的进步,测量可以达到很高的精确度。
2.4试就质点直线运动论证:加速度与速度同号时,质点作加速运动;加速度与速度反号时,作减速运动。
是否可能存在这样的直线运动,质点速度逐渐增加但加速度却在减小?解答:,dt dv t v lim a xx 0t x =∆∆=→∆加速度与速度同号时,就是说,0a ,0v 0a ,0v x x x x <<>>或以0a ,0v x x >>为例,速度为正表示速度的方向与x 轴正向相同,加速度为正表示速度的增量为正,t t ∆+时刻的速度大于t 时刻的速度,质点作加速运动。
同理可说明,0a ,0v x x <<质点作加速运动。
质点在作直线运动中速度逐渐增加但加速度却在减小是可能存在的。
例如初速度为x 0v ,加速度为t 6a x -=,速度为20t0x 0x t21t 6vdt )t 6(v v -+=-+=⎰,,0v ,0a 6t x x >><时,速度逐渐增加。
质点力学思考题解答

第一章 质点力学1.1平均速度与瞬时速度有何不同?在上面情况下,它们一致?答:平均速度是运动质点在某一时间间隔t t t ∆+→内位矢大小和方向改变的平均快慢速度,其方向沿位移的方向即沿t ∆对应的轨迹割线方向;瞬时速度是运动质点在某时刻或某未知位矢和方向变化的快慢程度其方向沿该时刻质点所在点轨迹的切线方向。
在0→∆t 的极限情况,二者一致,在匀速直线运动中二者也一致的。
1.2 在极坐标系中,r v r =,θθ r v =.为什么2θ r r a r -=而非r ?为什么θθr r a 20+=而非θθ r r +?你能说出r a 中的2θ r -和θa 中另一个θ r 出现的原因和它们的物理意义吗?答:质点运动时,径向速度r V 和横向速度θV 的大小、方向都改变,而r a 中的r 只反映了rV 本身大小的改变,θa 中的θθr r +只是θV 本身大小的改变。
事实上,横向速度θV 方向的改变会引起径向速度r V 大小大改变,2θ r -就是反映这种改变的加速度分量;经向速度r V 的方向改变也引起θV 的大小改变,另一个θ r 即为反映这种改变的加速度分量,故2θ r r a r -=,.2θθθ r r a +=。
这表示质点的径向与横向运动在相互影响,它们一起才能完整地描述质点的运动变化情况1.3 在内禀方程中,n a 是怎样产生的?为什么在空间曲线中它总沿着主法线方向?当质点沿空间运动时,副法线方向的加速度b a 等于零,而作用力在副法线方向的分量b F 一般不等于零,这是不是违背了牛顿运动定律呢?答:内禀方程中,n a 是由于速度方向的改变产生的,在空间曲线中,由于a 恒位于密切面内,速度v 总是沿轨迹的切线方向,而n a 垂直于v 指向曲线凹陷一方,故n a 总是沿助法线方向。
质点沿空间曲线运动时,0,0≠=b b F a z 何与牛顿运动定律不矛盾。
因质点除受作用力F ,还受到被动的约反作用力R ,二者在副法线方向的分量成平衡力0=+b b R F ,故0=b a 符合牛顿运动率。
大学物理章质点动力学习题答案

第二章 质点动 力学2-1一物体从一倾角为30︒的斜面底部以初速v 0=10m·s -1向斜面上方冲去,到最高点后又沿斜面滑下,当滑到底部时速率v =7m·s -1,求该物体与斜面间的摩擦系数;解:物体与斜面间的摩擦力f =uN =umgcos30︒物体向斜面上方冲去又回到斜面底部的过程由动能定理得220112(1)22mv mv f s -=-⋅物体向斜面上方冲到最高点的过程由动能定理得2010sin 302mv f s mgh f s mgs -=-⋅-=-⋅-2(2)s ∴=把式2代入式1得,220.198u =2-2如本题图,一质量为m 的小球最初位于光滑圆形凹槽的A 点,然后沿圆弧ADCB 下滑,试求小球在C 点时的角速度和对圆弧表面的作用力,圆弧半径为r ;解:小球在运动的过程中受到重力G 和轨道对它的支持力T .取如图所示的自然坐标系,由牛顿定律得22sin (1)cos (2)t n dv F mg mdt v F T mg mR αα=-==-=由,,1ds rd rd v dt dt dt vαα===得代入式(), A 并根据小球从点运动到点C 始末条件进行积分有,902n (sin )m cos 3cos '3cos ,e v vdv rg d v vrv mg mg rmg αααωααα=-===+==-=-⎰⎰得则小球在点C 的角速度为=由式(2)得 T 由此可得小球对园轨道得作用力为T T 方向与反向2-3如本题图,一倾角为θ的斜面置于光滑桌面上,斜面上放一质量为m 的木块,两者间摩习题2-2图擦系数为μ,为使木块相对斜面静止,求斜面的加速度a 应满足的条件;解:如图所示()1212min max sin ,cos cos sin (1)sin cos 2(1)(2)(sin cos )(cos sin )(sin cos )()(cos sin )1(2)(1)(sin cos )(cos sin )(sin cos a a a a N mg ma ma mg uN m a ma u g u a u g u g tg u a u utg u g u a u g u a θθθθθθθθθθθθθθθθθθθθθ==∴-==±==⨯+-=+--∴==++-⨯+=-+∴=得,得,)()(cos sin )1()()11g tg u u utg g tg u g tg u a utg utg θθθθθθθθθ+=---+∴≤≤+- 2-4如本题图,A 、B 两物体质量均为m,用质量不计的滑轮和细绳连接,并不计摩擦,则A和B 的加速度大小各为多少 ; 解:如图由受力分析得(1)(2)2(3)2(4)ggA AB B A B A BA B mg T ma T mg ma a a T T a a -=-===1解得=-52=-52-5如本题图所示,已知两物体A 、B 的质量均为m=,物体A 以加速度a =s 2 运动,求物体B 与桌面间的摩擦力;滑轮与连接绳的质量不计解:分别对物体和滑轮受力分析如图,由牛顿定律和动力学方程得,()()()1f 111f (1)''(2)2'(3)'2(4)5'6'7(4)7.22A T A TB T T A B T T T T m g F m a F F m a a a F F m m m F F F F mg m m aF N-=-======-+===解得2-6质量为M 的三角形木块,放在光滑的水平桌面上,另一质量为m 的木块放在斜面上如本题图所示;如果所有接触面的摩擦均可忽略不计,求M 的加速度和m 相对M 的加速度;AB 习题2-4图习题2-5图aθ习题2-3图ma AmgT A T B a Bmg解:如图m 相对M 的相对加速度为m a ',则 cos ,sin ,mxm my m a a a a θθ''''== 在水平方向,cos mxmx Mx mx mxMx m M a a a a a a a a θ'=-''∴=+=-+在竖直方向sin mymy myma a a a θ'='∴=由牛顿定律可得,sin cos cos sin sin mx mM my m MN ma ma ma mg N ma ma N Ma θθθθθ'-==-+'-===解得θ+θθ=2sin cos sin m M mg a M , 2()sin sin m M m g a M m θθ++= 2-7在一只半径为R 的半球形碗内,有一粒质量为m 的小钢球;当钢球以角速度ω在水平面内沿碗内壁作匀速圆周运动时,它距碗底有多高解:取钢球为隔离体,受力分析如图所示,在图示坐标中列动力学方程得,2sin sin cos cos ()/n F ma mR F mg R h Rθωθθθ====-解得钢球距碗底的高度2ω-=g R h2-8光滑的水平面上放置一半径为R 的固定圆环,物体紧贴环的内侧作圆周运动,其摩擦系数为μ;物体的初速率为v 0,求:1t 时刻物体的速率;2当物体速率从v 0减少到v 0/2时,物体所经历的时间及经过的路程;解:1设物体质量为m,取图示的自然坐标系,由牛顿定律得,02222tv 2v (1)(2)(3)4dv 4dt u v N n f t f Nv F ma m R dv F m a m dtF uF v dvu R dt ===-=-=-⎰⎰0由上三式可得=()R 对()式积分得=-习题2-6图00Rv v R v tμ∴=+(2) 当物体速率从v 0减少到v 0/2时,由上式00Rv vR v tμ∴=+可得物体所经历的时间0t R v μ'=经过的路程t t 000vdt dt ln 2Rv Rs R v t μμ''=+⎰⎰==2-9从实验知道,当物体速度不太大时,可以认为空气的阻力正比于物体的瞬时速度,设其比例常数为k;将质量为m 的物体以竖直向上的初速度v 0抛出; 1试证明物体的速度为t m ktm ke v e kmg v --+-=0)1(2证明物体将达到的最大高度为)1ln(020mgkv k g m k mv H +-=3证明到达最大高度的时间为)1ln(0mgkv k mt H +=证明:由牛顿定律可得0000220200ln (1)(2),()ln(13tvv mmt t k kx mg mg kv mdv dt mg kvmg kv m mg t v e v e k mg kv kmvdvdx mg kvmg kv u du kdvk mgdu k mgdudx mdu dx mdu m u m u mv kv m g x k k mg m t k --+-=++∴==-++=-++==∴=-+=-+∴=-+=⎰⎰⎰⎰dv(1)-mg-kv=m ,dt,dv -mg-kv=mv ,dx 令,)()0ln0t ln mg kv mg kvmg kv m v k mg k +++∴=+当时,=即为到达最高点的时间2-10质量为m 的跳水运动员,从距水面距离为h 的高台上由静止跳下落入水中;把跳水运动员视为质点,并略去空气阻力;运动员入水后垂直下沉,水对其阻力为-b v 2,其中b 为一常yf =-kvmgv量;若以水面上一点为坐标原点O,竖直向下为Oy 轴,求:1运动员在水中的速率v 与y 的函数关系;2跳水运动员在水中下沉多少距离才能使其速率v 减少到落水速率v 0的1/10假定跳水运动员在水中的浮力与所受的重力大小恰好相等解:运动员入水可视为自由落体运动,所以入水时的速度为0v =入水后如图由牛顿定律的0220//0100mg-f-F=ma mg=F f=bv dv a=dt v dy (2)0.4,0.1m vy ln 5.76m b y v v by m by m dv v dy dvb mv dyb dv m vv v e m v v v ---=∴-=-=====⎰⎰b将已知条件代入上式得,m=-=2-11一物体自地球表面以速率v 0竖直上抛;假定空气对物体阻力的值为f =-km v 2,其中k 为常量,m 为物体质量;试求:1该物体能上升的高度;2物体返回地面时速度的值;解:分别对物体上抛和下落时作受力分析如图,h120m 1ln()2v 01ln()2(2)m v=v 1gyvv vvdv dy g k g k y k g k g k k g vdvdy g k k =-++∴=-+∴+=-∴+⎰⎰⎰⎰222220max 222-/0dv mvdv (1)-mg-k v =m=,dt dy v v v 物体达到最高点时,=,故v h=y =dv mvdv下落过程中,-mg+k v =m=dt dy-v v ()2-12长为60cm 的绳子悬挂在天花板上,下方系一质量为1kg 的小球,已知绳子能承受的最大张力为20N ;试求要多大的水平冲量作用在原来静止的小球上才能将绳子打断解:由动量定理得000I mv I v m∆=-∆∴=,如图受力分析并由牛顿定律得,2020220/202.47mv T mg l mv T mg lmg I l I Ns-==+≥∴+∆≥∆≥2-13一作斜抛运动的物体,在最高点炸裂为质量相等的两块,最高点距离地面为;爆炸后,第一块落到爆炸点正下方的地面上,此处距抛出点的水平距离为100m;问第二块落在距抛出点多远的地面上 设空气的阻力不计解:取如图示坐标系,根据抛体运动规律,爆炸前,物体在最高点得速度得水平分量为()1010x 2x 12y 2x 0x (1),v 2mv mv 30mv mv 414v v 100x x v x t==+=2111121物体爆炸后,第一块碎片竖直下落的运动方程为1y =h-v t-gt 2当碎片落地时,y =0,t=t 则由上式得爆炸后第一块碎片抛出得速度为1h-gt 2=()t 又根据动量守恒定律,在最高点处有1=()211=-22联立以上()-()式得爆炸后第二块碎片抛出时的速度分量分别为=2=2x 11212x 2222y 222214.7v t 5y =h+v t -60,x 500my ms v v ms gt y --====21211h-gt 2t 爆炸后第二块碎片作斜抛运动,其运动方程为x =x +()1()2落地时由式(5)和(6)可解得第二块碎片落地点得水平位置=2-14质量为M 的人手里拿着一个质量为m 的物体,此人用与水平面成θ角的速率v 0向前跳去;当他达到最高点时,他将物体以相对于人为u 的水平速率向后抛出;问:由于人抛出物体,他跳跃的距离增加了多少假设人可视为质点解:取如图所示坐标,把人和物视为一系统,当人跳跃到最高点处,在向左抛物得过程中,满足动量守恒,故有()00000m cos ()v u mu v cos m mu v v- cos m sin t g m sin x vt um gv Mv m v u v v v v v θθθθθ=+-∆∆∆+M 式中为人抛物后相对地面的水平速率,-为抛出物对地面得水平速率,得=++M人的水平速率得增量为==+M而人从最高点到地面得运动时间为=所以人跳跃后增加的距离为==(+M )2-15铁路上有一静止的平板车,其质量为M,设平板车可无摩擦地在水平轨道上运动;现有N 个人从平板车的后端跳下,每个人的质量均为m,相对平板车的速度均为u;问:在下列两种情况下,1N 个人同时跳离;2一个人、一个人地跳离,平板车的末速是多少所得的结果为何不同,其物理原因是什么解:取平板车及N 个人组成的系统,以地面为参考系,平板车的运动方向为正方向,系统在该方向上满足动量守恒;考虑N 个人同时跳车的情况,设跳车后平板车的速度为v,则由动量守恒定律得 0=Mv+Nmv -uv =Nmu/Nm+M 1又考虑N 个人一个接一个的跳车的情况;设当平板车上商有n 个人时的速度为v n ,跳下一个人后的车速为v n -1,在该次跳车的过程中,根据动量守恒有M+nmv n =M v n -1+n-1m v n -1+mv n -1-u 2 由式2得递推公式v n -1=v n +mu/M+nm 3当车上有N 个人得时即N =n,v N =0;当车上N 个人完全跳完时,车速为v 0, 根据式3有,v N-1=0+mu/Nm+Mv N-2= v N-1+mu/N-1m+M ………….v 0= v 1+mu/M+nm将上述各等式的两侧分别相加,整理后得,0n 0mu v nm,1,2,3....v vM nm M Nm n N N +≤+=∑N=1=M+由于故有,即个人一个接一个地跳车时,平板车的末速度大于N 个人同时跳下车的末速度。
大学物理第2章课后答案

大学物理第2章课后答案(总34页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--第二章 质点动力学四、习题选解2-1 光滑的水平桌面上放有三个相互接触的物体,它们的质量分别为.4,2,1321kg m kg m kg m ===(1)如图a 所示,如果用一个大小等于N 98的水平力作用于1m 的左方,求此时2m 和3m 的左边所受的力各等于多少?(2)如图b 所示,如果用同样大小的力作用于3m 的右方。
求此时2m 和3m 的左边所受的力各等于多少?(3)如图c 所示,施力情况如(1),但3m 的右方紧靠墙壁(不能动)。
求此时2m 和3m 左边所受的力各等 于多少?解:(1)三个物体受到一个水平力的作用,产生的加速度为a()a m m m F321++=232114-⋅=++=s m m m m Fa用隔离法分别画出32,m m 在水平方向的受力图(a ),题2-1(a )图由a m F =a m f f23212=- a m f323= 2332f f =N f 5623= N f 8412=(2)由()a m m m F321++=232114-⋅=++=s m m m m Fa用隔离法画出321m m m 、、在水平方向的受力图(b )由a m F = 得 ⎪⎪⎪⎩⎪⎪⎪⎨⎧====-=-3223122112121232323f f f f am f a m f f a m f F解得: N f 1412= N f 4223=题2-1(b )图(3)由于321m m m 、、都不运动,加速度0=a ,三个物体彼此的作用力都相等,都等于FN f f 982312==2-2 如图所示,一轻质弹簧连接着1m 和2m 两个物体,1m 由细线拉着在外力作用下以加速a 竖直上升。
问作用在细线上的张力是多大?在加速上升的过程中,若将线剪断,该瞬时1m 、2m 的加速度各是多大?解:(1)分别画出1m 、2m 受力的隔离体如图(a ),题2-2(a )图取向上为正方向,由牛顿第二定律⎪⎩⎪⎨⎧='=-'=--f f a m g m f a m g m f T 2211故 ()()a g m m g m g m a m a m T ++=+++=212121 (2)将线剪断,画出21m m 、的隔离体图,如图(b )题2-2(b )图取竖直向上为正方向,由牛顿第二定律得⎪⎩⎪⎨⎧='=-'=--f f a m g m f a m g m f 222111 得⎪⎩⎪⎨⎧+--==-=)(/)'(121222a g m m g a a m g m f a1a 的方向向下,2a的方向向上。
大学物理第二章质点动力学课后答案 ppt课件

m1
k
m2
A
B
大学物理第二章质点动力学课后答
20
案
解:设弹簧恢复原长时B 物体的速度为v B 0
12kx02 12m2vB20
vB0
k 3m
x0
此后系统动量守恒 m 2vB0(m 1m 2)v
v
3 4
vB0
3 4
x0
k 3m
A、B两物体速度相等时,弹簧伸长最大。
1 2m 2vB 201 2(m 1m 2)v21 2km 2 xax
(A) 2 E k
(B)
1 2
Ek
(C)
1 3
Ek
Ek
1 2
mAv2A
✓(D)
2 3 Ek
mAvA (mA mB )v
v
2mB 3mB
vA
2 3
vA
E k 总 1 2(m Am B )v 22 3m B v 2 A2 3E k
大学物理第二章质点动力学课后答
14
案
2-5 有一倔强系数为k的轻弹簧,竖直放置,下端 悬一质量为m的小球。先使弹簧为原长,而小球恰好 与地接触。再将弹簧上端缓慢地提起,直到小球刚能
vB
F t2 m2
vA
Ft2 Ft1 m2 m1m2
大学物理第二章质点动力学课后答
17
案
2-8
量为
r 一 质a 量c 为mo t的i 质b s 点s 在xi t oy j 平n (S面I)上。运式动中,a,其b位,置 是矢
正值常数, 且a > b。
(1) 求质点在A点(a,0) 和B点(0,b) 时的动能。
ABC的水平光滑轨道运动。质点越过A角时,轨道作
第2章《质点运动学》习题解答
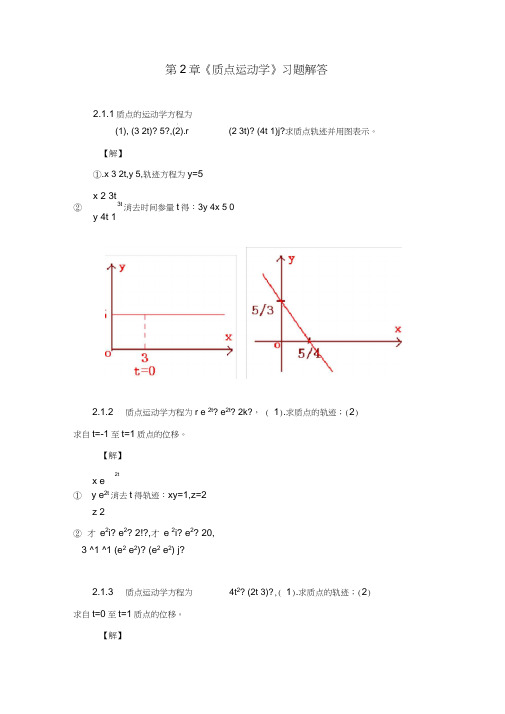
第2章《质点运动学》习题解答2.1.1质点的运动学方程为I(1), (3 2t)? 5?,(2).r(2 3t)? (4t 1)j?求质点轨迹并用图表示。
【解】①.x 3 2t,y 5,轨迹方程为y=5x 2 3t②3t消去时间参量t 得:3y 4x 5 0y 4t 12.1.2 质点运动学方程为r e 2t ? e 2t ? 2k?, ( 1).求质点的轨迹;(2)求自t=-1至t=1质点的位移。
【解】2tx e ① y e 2t 消去t 得轨迹:xy=1,z=2z 2② 才 e 2i? e 2? 2!?,才 e 2i? e 2? 20,3 ^1 ^1 (e 2 e 2)? (e 2 e 2) j?2.1.3 质点运动学方程为求自t=0至t=1质点的位移。
【解】4t 2? (2t 3)?,( 1).求质点的轨迹;(2)①.x 4t 2, y 2t 3,消去t 得轨迹方程x (y 3)2②r 0 3?』2.2.1雷达站于某瞬时测得飞机位置为R i 4100m, i 33.70,°.75s 后测得R 2 4240m, 2 29.3°, R,R 2均在铅直平面内。
求飞机瞬时速率的近似值和飞行方向(a 角)。
R i 2 R ; 2RR, cos( i 2)代入数值得: .41002 42402 -2 4100 4240cos 4.4°349.385(m)利用正弦定理可解出34.8902.2.2 一小圆柱体沿抛物线轨道运动,抛物线轨道为y x 2 / 200 (长度mm 。
第一次观察到圆柱体在349.3850.75 465.8(m/s)x=249mn 处,经过时间2ms 后圆柱体移到 x=234mn 处。
求圆柱体瞬时速度的近似4i? 5? r4? 2?t[解]19.6mm/ms152 36.22522112.502.2.3 一人在北京音乐厅内听音乐,离演奏者 17m 另一人在广州听同一 演奏的转播,广州离北京2320km 收听者离收音机2m 问谁先听到声音?声速 为340m/s,电磁波传播的速度为3.0 108m/s 。
理论力学第二章思考题及习题答案

第二章思考题2.1一均匀物体假如由几个有规则的物体并合(或剜去)而成,你觉得怎样去求它的质心? 2.2一均匀物体如果有三个对称面,并且此三对称面交于一点,则此质点即均匀物体的质心,何故?2.3在质点动力学中,能否计算每一质点的运动情况?假如质点组不受外力作用,每一质点是否都将静止不动或作匀速直线运动?2.4两球相碰撞时,如果把此两球当作质点组看待,作用的外力为何?其动量的变化如何?如仅考虑任意一球,则又如何?2.5水面上浮着一只小船。
船上一人如何向船尾走去,则船将向前移动。
这是不是与质心运动定理相矛盾?试解释之。
2.6为什么在碰撞过程中,动量守恒而能量不一定守恒?所损失的能量到什么地方去了?又在什么情况下,能量才也守恒?2.7选用质心坐标系,在动量定理中是否需要计入惯性力?2.8轮船以速度V 行驶。
一人在船上将一质量为m 的铁球以速度v 向船首抛去。
有人认为:这时人作的功为()mvV mv mV v V m +=-+222212121 你觉得这种看法对吗?如不正确,错在什么地方? 2.9秋千何以能越荡越高?这时能量的增长是从哪里来的?2.10在火箭的燃料全部燃烧完后,§2.7(2)节中的诸公式是否还能应用?为什么? 2.11多级火箭和单级火箭比起来,有哪些优越的地方?第二章思考题解答2.1.答:因均匀物体质量密度处处相等,规则形体的几何中心即为质心,故先找出各规则形体的质心把它们看作质点组,然后求质点组的质心即为整个物体的质心。
对被割去的部分,先假定它存在,后以其负质量代入质心公式即可。
2.2.答:物体具有三个对称面已足以确定该物体的规则性,该三平面的交点即为该物体的几何对称中心,又该物体是均匀的,故此点即为质心的位置。
2.3.答:对几个质点组成的质点组,理论上可以求每一质点的运动情况,但由于每一质点受到周围其它各质点的相互作用力都是相互关联的,往往其作用力难以预先知道;再者,每一质点可列出三个二阶运动微分方程,各个质点组有n 3个相互关联的三个二阶微分方程组,难以解算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章 质点运动学
思考题
2.1质点位置矢量方向不变,质点是否作直线运动?质点沿直线运动,其位置矢量是否一定方向不变?
解答:质点位置矢量方向不变,质点沿直线运动。
质点沿直线运动,质点位置矢量方向不一定不变。
如图所示。
2.2若质点的速度矢量的方向不变仅大小改变,质点作何种运动?速度矢量的大小不变而方向改变作何种运动?
解答:质点的速度矢量的方向不变仅大小改变,质点作变速率直线运动;速度矢量的大小不变而方向改变作匀速率曲线运动。
2.3“瞬时速度就是很短时间内的平均速度”这一说法是否正确?如何正确表述瞬时速度的定义?我们是否能按照瞬时速度的定义通过实验测量瞬时速度? 解答:“瞬时速度就是很短时间内的平均速度”这一说法不正确。
因为瞬时速度与一定的时刻相对应。
瞬时速度的定义是质点在t 时刻的
瞬时速度等于t 至t+△t 时间内平均速度t /r ∆∆
,当△t →0时的极
限,即
dt r d t r lim v 0t
=
∆∆=→∆。
很难直接测量,在技术上常常用很短时间内的平均速度近似地表示瞬时速度,随着技术的进步,测量可以达到很高的精确度。
2.4试就质点直线运动论证:加速度与速度同号时,质点作加速运动;加速度与速度反号时,作减速运动。
是否可能存在这样的直线运动,质点速度逐渐增加但加速度却在减小?
解答:
,dt dv t v lim a x
x 0
t x =∆∆=→∆加速度与速度同号时,就是说,0a ,0v 0a ,0v x x x x <<>>或以0a ,0v x x >>为例,
速度为正表示速度的方向与x 轴正向相同,加速度为正表示速度的增量为正,t t ∆+
时刻的速度大于t 时刻的速度,质点作加速运动。
同理可说明
,0a ,0v x x <<质点作加速运动。
质点在作直线运动中速度逐渐增加但加速度却在减小是可能存在的。
例如初速度为x 0v ,加速度为
t 6a x -=,速度为
2
0t
0x 0x t
2
1t 6v dt
)t 6(v v -+=-+=⎰,
,0v ,0a 6t x x >><时,速度逐渐增加。
2.5设质点直线运动时瞬时加速度=x a 常量,试证明在任意相等的
时间间隔内的平均加速度相等。
解答:平均加速度
121
x 2x x t t v v a --=
由瞬时加速度
,
dt a dv ,dt a dv ,dt dv a 2
1
2
x 1
x t
t x v v x x x x x ⎰⎰===
得,
121x 2x x t t v v a --=,=x a 常量,即121
x 2x x t t v v a --=
为常
量。
2.6在参照系一定的条件下,质点运动的初始条件的具体形式是否与计时起点和坐标系的选择有关? 解答:有关。
例子,以地面为参照系,研究物体的自由下落。
2.7中学时曾学过
as
2v v ,at 21t v s ,at v v 2
02t 200t =-+=+=,这几个
匀变速直线运动的公式,你能否指出在怎样的初始条件下,可得出这
几个公式。
解答:0
s ,v v ,0t
0===
2.8试画出匀变速直线运动公式(2.
3.7)和(2.3.9)的t v x -图
和t a x
-图。
)9.3.2),......(x x (a 2v v )
7.3.2,......(t a 2
1t v x x 0x 2
x 02x 2
x x 00-=-++=
解答:(1)t
a v dt dx v x x 0x +==
(2)
)x x (2v v tg a 02
x
02x x --=
α=
2.9对于抛体运动,就发射角为
2
;
,0
;
π
±
=
α
π
=
α
π
-
α
>
这几种情况说明它们各代表何种运动。
解答:①下斜抛;②平抛;③竖直上下抛。
2.10抛体运动的轨迹如图所示,试在图中用矢量表示它在A、B、C、
D、E各点处的速度和加速度。
解答:
2.11质点作上斜抛运动时,在何处的速率最大,在何处的速率最小?解答:
t
sin
g
v2
t
g
v
v
,
gt
sin
v
v,
cos
v
v
2
2
2
y
x
α
-
+
=
-
α
=
α
=
求极值,
g
sin
v
t0
α
=
时,有极小值,即最高点处速率最小。
(O、A处速率最大)
2.12试画出斜抛运动的速率—时间曲线。
解答:t sin g v 2t g v v 02
220α-+=
2.13在利用自然坐标研究曲线运动时,v v v 和、τ三个符号的含
义有什么不同?
解答:τv 为速度在切线单位矢量的投影τ=τˆv v
,它不同于速率v ,
τv 有正负,v v =τ。
v 表示的是速度,沿切线方向,有大小和方
向。
2.14质点沿圆周运动,自A 点起,从静止开始作加速运动,经B 点到C 点;从C 点开始作匀速圆周运动,经D 点直到E 点;自E 点以后作减速运动,经F 点又到A 点时速度变成零。
用矢量表示出质点在A 、B 、C 、D 、E 、F 各点的法向加速度和切向加速度的方向。
解答:
2.15什么是伽利略变换?它所包含的时空观有何特点? 解答:①伽利略变换
;v v ,v v ,v v v ;z z ,y y ,vt x x z z y y x x ='='-='='='-='
②时空观特点
同时性;等时性;等长性。
相对论中的洛伦兹变换:
,1x
c v t t ,z z ,y y ,1vt x x 222β--='='='β--='
,c /v =β当0→β该变换回到伽利略变换。
时空观特点
同时的相对性;运动的杆缩短;运动的时钟变慢。
