大连理工大学大学物理作业3(静电场三)及答案详解
辽宁大连理工大学附属高级中学必修3物理 全册全单元精选试卷检测题

辽宁大连理工大学附属高级中学必修3物理 全册全单元精选试卷检测题一、必修第3册 静电场及其应用解答题易错题培优(难)1.如图所示,一个内壁光滑的绝缘细直管竖直放置.在管子的底部固定一电荷量为Q (Q >0)的点电荷.在距离底部点电荷为h 2的管口A 处,有一电荷量为q (q >0)、质量为m 的点电荷由静止释放,在距离底部点电荷为h 1的B 处速度恰好为零.现让一个电荷量为q 、质量为3m 的点电荷仍在A 处由静止释放,已知静电力常量为k ,重力加速度为g ,则该点电荷运动过程中:(1)定性分析点电荷做何运动?(从速度与加速度分析) (2)速度最大处与底部点电荷的距离 (3)运动到B 处的速度大小【答案】(1)先做加速度减小的加速,后做加速度增大的减速运动; (2)3KQqr mg=(3)2123()3B v g h h =-【解析】 【详解】(1)由题意知,小球应先做加速运动,再做减速运动,即开始时重力应大于库仑力;而在下落中,库仑力增大,故下落时加速度先减小,后增大;即小球先做加速度减小的加速,后做加速度增大的减速运动;(2)当重力等于库仑力时,合力为零,此时速度最大,23kQqF mg r 库==解得:3kQqr mg=(3)点电荷在下落中受重力和电库仑力,由动能定理可得:mgh +W E =0;即W E =-mgh ;当小球质量变为3m 时,库仑力不变,故库仑力做功不变,由动能定理可得:3mgh-mgh=123mv 2; 解得:2123()3B v g h h =- 点睛:本题综合考查动力学知识及库仑力公式的应用,解题的关键在于明确物体的运动过程;同时还应注意点电荷由静止开始运动,故开始时重力一定大于库仑力.2.“顿牟掇芥”是两千多年前我国古人对摩擦起电现象的观察记录,经摩擦后带电的琥珀能吸起小物体,现用下述模型分析研究。
在某处固定一个电荷量为Q 的点电荷,在其正下方h 处有一个原子。
在点电荷产生的电场(场强为E )作用下,原子的负电荷中心与正电荷中心会分开很小的距离l ,形成电偶极子。
大连理工大学大学物理作业5(静电场五)及答案详解
2.一平行板电容器中充满相对介电常数为r ε的各向同性均匀电介质。
已知介质表面极化电荷面密度为σ'±,则极化电荷在电容器中产生的电场强度的大小为[ ]。
.A0σε' .B 02σε' .C 0r σεε' .D rσε' 答案:【A 】解:极化电荷也是一种电荷分布,除不能自由移动和依赖于外电场而存在外,与自由电荷没有区别。
在产生静电场方面,它们的性质是一样的。
在电容器中,正是极化电荷的存在,产生的静电场与自由电荷产生的静电场方向相反,使得电容器中总的电场强度减弱,提高了电容器储存自由电荷的能力,电容器的电容增大。
或者说,储存等量的自由电荷,添加电介质后,电场强度减弱,电容器两极的电势差减小,电容器的电容增大。
正负极化电荷产生的电场强度的大小都是0/2εσ,方向相同,所以,极化电荷产生的电场的电场强度为0/εσ。
3.在一点电荷产生的静电场中,一块电介质如图5-1放置,以点电荷q 所在处为球心作一球形闭合面,则对此球形闭合面[ ]。
.A 高斯定理成立,且可用它求出闭合面上各点的场强 .B 高斯定理成立,但不能用它求出闭合面上各点的场强 .C 由于电介质不对称分布,高斯定理不成立 .D 即使电介质对称分布,高斯定理也不成立答案:【B 】解:静电场的高斯定理,是静电场的基本规律。
无论电场分布(电荷分布)如何,无论有无电介质,也无论电介质的分布如何,都成立。
但是,只有在电场分布(电荷分布和电介质分布),在高斯面上(内)具有高度对称时,才能应用高斯定理计算高斯面上的电场强度。
否则,只能计算出穿过高斯面的电通量。
图示的高斯面上,电场强度分布不具有高度对称性,不能应用高斯定理计算高斯面上的电场强度。
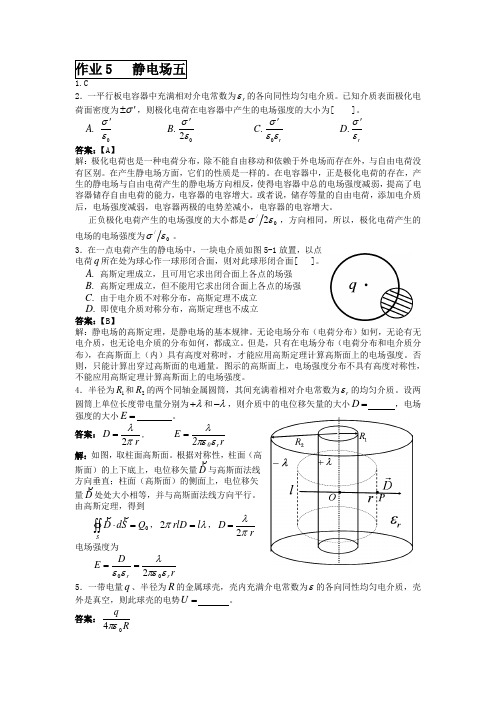
4.半径为1R 和2R 的两个同轴金属圆筒,其间充满着相对介电常数为r ε的均匀介质。
设两圆筒上单位长度带电量分别为λ+和λ-,则介质中的电位移矢量的大小D = ,电场强度的大小E = 。
大连理工大学附属中学高中物理必修三第九章《静电场及其应用》检测(答案解析)

一、选择题1.如图,三个带电小球a 、b 和c 固定在某平面上直角ΔABC 的相应顶点上,其中37B ∠=︒,小球a 所受库仑力的合力方向平行于BC 边。
设小球b 、c 所带电荷量的绝对值之比为k ,则( )A .b 、c 带同种电荷,169k =B .b 、c 带异种电荷,169k =C .b 、c 带同种电荷,6427k =D .b 、c 带异种电荷,6427k =2.如图,两个完全相同的带电小球,静止在光滑、绝缘的半圆形轨道的A 、B 两点,两小球关于过O 点的竖直半径对称,且60AOB ∠=︒。
现缓慢增大两小球的带电量,直至两小球静止在光滑的绝缘球面内的'A 、'B 处,且''120A OB ∠=︒。
则两小球电量的乘积在''A B 处是AB 处的( )A .3倍B .3倍C .33倍D .9倍 3.富兰克林提出存在正、负两种电荷,但物体通常呈电中性,这是因为( )A .物体没有电荷B .通常物体所带的正负电荷一样多C .物体很容易失去电荷D .以上说法都不正确4.如图所示,M 、N 为两个固定的等量同种正电荷,在其连线的中垂线上的P 点放一个静止的负电荷(重力不计),下列说法中正确的是( )A .从P 到O ,可能加速度越来越小,速度越来越大B .从P 到O ,可能加速度先变大,再变小,速度越来越小C .越过O 点后,加速度一直变大,速度一直变小D .越过O 点后,加速度一直变小,速度一直变小5.遵义市科技馆有一个法拉第笼(FaradayCage ),它是一个由金属制成的球形状笼子,其笼体与大地连通。
当高压电源通过限流电阻将10万伏直流高压输送给放电杆,放电杆尖端距笼体10厘米时,出现放电火花。
周日15:00限时体验时,体验者进入笼体后关闭笼门,操作员接通电源,用放电杆进行放电演示。
关于法拉第笼下列说法正确的是( )A .法拉第笼上的感应电荷均匀分布在笼体外表面上B .同一带电粒子在法拉第笼外的电势能大于在法拉第笼内部的电势能C .法拉第笼上的感应电荷在笼内产生的电场强度为零D .法拉第笼内部任意两点间的电势差为零6.下列说法正确的是( )A .静电感应时产生了电荷B .库仑首先测定了电子的电荷量C .法拉第首先提出可以用电场线描绘电场的分布D .自然界的电荷只有两种,安培把它们命名为正电荷和负电荷7.如图所示,A 、B 、C 三点为一直角三角形的三个顶点,30B ∠=︒,现在A 、B 两点放置两点电荷A q 、B q ,测得C 点场强的方向与AB 平行,且水平向左,则以下判断正确的是( )①A q 带正电 ②A q 带负电 ③B q 带正电 ④B q 带负电A .①③B .①④C .②③D .②④ 8.不属于静电的利用的是( ) A .静电除尘B .静电喷涂C .静电复印D .良好接地 9.对于FE q =和2Q E k r =两个公式,下列说法正确的是( ) A .F E q=适用于包括点电荷在内的所有场源的电场求场强,且E 的方向和试探电荷所受的F 一致B .E 随q 的增大而减小,随Q 的增大而增大C .q 表示电场中试探电荷的电荷量、Q 表示场源电荷的电荷量D .拿走电量为Q 的电荷后,场强E 保持不变10.A、B是一条电场线上的两个点,一带正电的微粒仅在电场力作用下以一定初速度从A 点沿电场线运动到B点,其速度—时间图象如图所示。
静电场作业答案

电荷体密度为,求板内sD 、d外s 场2强s的D分d 布 s内 s。q
2D ssd
d
o
s
x
D外2d, Dds2
E外20
Dd s
qi
s
s
s内
(侧视图)
2D ss2x
D内x,E内x
5. 图示一球形电容器,在外球壳的内半径b和内外 导体间的电压U维持恒定的条件下,内球半径a为 多大时,才能使内球面上的电场强度最小?这个
从电势为U的a点,移动到电势为零的bபைடு நூலகம்,若已
知小球在b点的速率为Vb,则小球在a点的速率
Va=
Vb2
2qU m
。
11. 两根互相平行的长直导线,相距为a,其上均
匀带电,电荷线密度分别为λ1和λ2,则导线单
位长度所受电场力的大小为F0= 12/20a 。
1.三图、中计所算示题为一沿 x 轴放置的长度为l的不均匀
S Q
去ΔS后球心处电场强度大小E= 4 0R2 4R2 , 其方向为 指向S 。
R
O
S
3. 在相对介电常数为εr的各向同性的电介质中,
电位移矢量与场强之间D 的关0系r是E
。
4. 两块“无限大”的带电平行电板,其电荷面密
度分别为(>0)及-2 ,如图所示,试写出各
区域的电场强度E
І区 E大小
/ 20
2. 带电细棒,其电荷线密度为 = 0(x-a), 0为 一
3. 常量。取无穷远处为电势零点,求坐标原点o
处
的解电:势U。 dU q
a
O
l
x dx
x
al dx
a 4 0 x
40l0 40a0lnaal
中国大学mooc《大学物理—相对论、电磁学(大连理工大学) 》满分章节测试答案

title大学物理—相对论、电磁学(大连理工大学) 中国大学mooc答案100分最新版content第二周相对论基础(2)相对论单元测验1、地面观察者测得地面上事件A和B同时发生,并分别处于x轴上x1和x2两点(x1< x2),则沿x 轴负向高速运动的飞船上的观察者测得此两事件中答案: B晚发生2、 p 介子静止时平均寿命为t. 用高能加速器把p 介子加速到u ,则在实验室中观测,p 介子平均一生最长行程为。
答案:3、若从一惯性系中测得宇宙飞船的长度为其固有长度的一半,则宇宙飞船相对该惯性系的速度为()。
答案:4、 K系与K¢系是坐标轴相互平行的两个惯性系,K¢系相对K系沿ox轴正方向以接近光速的速度匀速运动。
一根刚性尺静止在K¢系中,与o¢x¢轴成60°角,则在K系中观察该尺与ox轴的夹角q ,有()。
答案: q >60º5、两枚静止长度为20m 的火箭A、B,它们均以 0.9 c 的速度相对地面背向飞行。
在火箭 A上测量火箭B 的速度为()。
答案: 0.994 c6、一个静止质量是m0的粒子,以接近光速的速度v相对地面作匀速直线运动,则地面上的观测者测量其动能为( ).答案:7、由狭义相对论原理可知,相对于某些惯性系,运动物体的速度是可以达到真空中的光速的.答案: 错误8、在一惯性系中发生于同一时刻、不同地点的两个事件,在其他相对此惯性系运动的任何惯性系中一定不是同时发生的.答案: 错误9、在一惯性系中发生于同一时刻、不同地点的两个事件,在其他相对此惯性系运动的任何惯性系中可能不是同时发生的.答案: 正确10、由洛伦兹变换可得出下面的结论:有因果关系的两个事件发生的时间顺序在两个不同的惯性系中观察,有可能是颠倒的。
答案: 错误11、广义相对论的等效原理指出加速度和引力场等效.答案: 正确12、由狭义相对论原理可知:在任何一个惯性系中做光学实验都用来确定本参考系的运动速度。
大连理工大学大学物理作业5(静电场五)及答案详解

作业5 静电场五2.一平行板电容器中充满相对介电常数为r ε的各向同性均匀电介质。
已知介质表面极化电荷面密度为σ'±,则极化电荷在电容器中产生的电场强度的大小为[ ]。
.A0σε' .B 02σε' .C 0r σεε' .D rσε' 答案:【A 】解:极化电荷也是一种电荷分布,除不能自由移动和依赖于外电场而存在外,与自由电荷没有区别。
在产生静电场方面,它们的性质是一样的。
在电容器中,正是极化电荷的存在,产生的静电场与自由电荷产生的静电场方向相反,使得电容器中总的电场强度减弱,提高了电容器储存自由电荷的能力,电容器的电容增大。
或者说,储存等量的自由电荷,添加电介质后,电场强度减弱,电容器两极的电势差减小,电容器的电容增大。
正负极化电荷产生的电场强度的大小都是0/2εσ,方向相同,所以,极化电荷产生的电场的电场强度为0/εσ。
3.在一点电荷产生的静电场中,一块电介质如图5-1放置,以点电荷q 所在处为球心作一球形闭合面,则对此球形闭合面[ ]。
.A 高斯定理成立,且可用它求出闭合面上各点的场强 .B 高斯定理成立,但不能用它求出闭合面上各点的场强 .C 由于电介质不对称分布,高斯定理不成立 .D 即使电介质对称分布,高斯定理也不成立答案:【B 】解:静电场的高斯定理,是静电场的基本规律。
无论电场分布(电荷分布)如何,无论有无电介质,也无论电介质的分布如何,都成立。
但是,只有在电场分布(电荷分布和电介质分布),在高斯面上(内)具有高度对称时,才能应用高斯定理计算高斯面上的电场强度。
否则,只能计算出穿过高斯面的电通量。
图示的高斯面上,电场强度分布不具有高度对称性,不能应用高斯定理计算高斯面上的电场强度。
4.半径为1R 和2R 的两个同轴金属圆筒,其间充满着相对介电常数为r ε的均匀介质。
设两圆筒上单位长度带电量分别为λ+和λ-,则介质中的电位移矢量的大小D = ,电场强度的大小E = 。
大连理工大学大学物理作业及答案详解1-22

大连理工大学大学物理作业及答案详解作业1 (静电场一)1.关于电场强度定义式,下列说法中哪个是正确的?[ ] A .场强E 的大小与试探电荷0q 的大小成反比。
B .对场中某点,试探电荷受力F 与0q 的比值不因0q 而变。
C .试探电荷受力F 的方向就是场强E 的方向。
D .若场中某点不放试探电荷0q ,则0F =,从而0E =。
答案: 【B 】[解]定义。
场强的大小只与产生电场的电荷以及场点有关,与试验电荷无关,A 错;如果试验电荷是负电荷,则试验电荷受的库仑力的方向与电场强度方向相反,C 错;电荷产生的电场强度是一种客观存在的物质,不因试验电荷的有无而改变,D 错;试验电荷所受的库仑力与试验电荷的比值就是电场强度,与试验电荷无关,B 正确。
2.一个质子,在电场力作用下从A 点经C 点运动到B 点,其运动轨迹如图所示,已知质点运动的速率是递增的,下面关于C 点场强方向的四个图示哪个正确?[ ]答案: 【D 】[解]a m E q=,质子带正电且沿曲线作加速运动,有向心加速度和切线加速度。
存在向心加速度,即有向心力,指向运动曲线弯屈的方向,因此质子受到的库仑力有指向曲线弯屈方向的分量,而库仑力与电场强度方向平行(相同或相反),因此A 和B 错;质子沿曲线ACB 运动,而且是加速运动,所以质子受到的库仑力还有一个沿ACB 方向的分量(在C 点是沿右上方),而质子带正电荷,库仑力与电场强度方向相同,所以,C 错,D 正确。
3.带电量均为q +的两个点电荷分别位于X 轴上的a +和a -位置,如图所示,则Y 轴上各点电场强度的表示式为E = ,场强最大值的位置在y = 。
答案:j y a qyE 23220)(2+=πε,2/a y ±= [解]21E E += )(422021y a qE E +==πε关于y 轴对称:θcos 2,01E E E y x ==y a qyE y 23220)(2+==∴πε沿y 轴正向的场强最大处0=dydEy y a y y a dy dE 2)(23)(25222322⨯+-+∝-- 2/a y = 2/a y ±=处电场最强。
大连理工大学大学物理作业4(静电场四)及答案详解

作业4 静电场四它们离地球很远,内球壳用细导线穿过外球壳上得绝缘小孔与地连接,外球壳上带有正电荷,则内球壳上[ ]。
不带电荷 带正电 带负电荷外表面带负电荷,内表面带等量正电荷答案:【C 】解:如图,由高斯定理可知,内球壳内表面不带电。
否则内球壳内得静电场不为零。
如果内球壳外表面不带电(已经知道内球壳内表面不带电),则两壳之间没有电场,外球壳内表面也不带电;由于外球壳带正电,外球壳外表面带正电;外球壳外存在静电场。
电场强度由内球壳向外得线积分到无限远,不会为零。
即内球壳电势不为零。
这与内球壳接地(电势为零)矛盾。
因此,内球壳外表面一定带电。
设内球壳外表面带电量为(这也就就是内球壳带电量),外球壳带电为,则由高斯定理可知,外球壳内表面带电为,外球壳外表面带电为。
这样,空间电场强度分布,(两球壳之间:) ,(外球壳外:)其她区域(,),电场强度为零。
内球壳电势为041)11(4ˆ4ˆ4)()(403202020214324322=++-=⋅++⋅=⋅+⋅=⋅=⎰⎰⎰⎰⎰∞∞∞R Qq R R q r d r rQq r d rr q r d r E r d r E l d E U R R R R R R R πεπεπεπε则,由于,,所以即内球壳外表面带负电,因此内球壳负电。
2.真空中有一组带电导体,其中某一导体表面某处电荷面密度为,该处表面附近得场强大小为,则。
那么,就是[ ]。
该处无穷小面元上电荷产生得场 导体上全部电荷在该处产生得场 所有得导体表面得电荷在该处产生得场 以上说法都不对 答案:【C 】解:处于静电平衡得导体,导体表面附近得电场强度为,指得就是:空间全部电荷分布,在该处产生得电场,而且垂直于该处导体表面。
注意:由高斯定理可以算得,无穷小面元上电荷在表面附近产生得电场为;无限大带电平面产生得电场强度也为,但不就是空间全部电荷分布在该处产生得电场。
3.一不带电得导体球壳半径为,在球心处放一点电荷。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
作业3(静电场三)1.电场中某区域内电场线如图所示,将一点电荷从M 移到N 点则必有[ ]。
.A 电场力的功0M N A >.B 电势能M N W W >.C 电势M N U U >.D 电势M N U U <答案:【C 】解:由于静电场的无旋性,电场强度的线积分与路径无关,由M 点到N 点的线积分(即M 点与N 点之间的电势差),可以取任意路径。
现取积分路径为:由M 点到O 点,处处与电场线(电场强度方向)垂直;由O 点到N 点,处处沿着电场线。
则0=⋅=-⎰O M O M l d E U U,0>=⋅=-⎰⎰NONON O Edl l d E U U因此,M 点与N 点的电势差为0)()(>=⋅+⋅=-+-=⋅=-⎰⎰⎰⎰NONOOMN O O M N MN M Edl l d E l d E U U U U l d E U U所以,C 正确,D 错误。
由M 点到O 点,电场力所作的功为(设移动电荷量为q )⎰⋅=-=N MN M N M l d E q U U q A)( 尽管0>⋅⎰N Ml d E,但不知q 的正负,无法判断NMA 的正负。
当0>q ,即移动正电荷时,电场力作功为正,0>NM A ;如果移动的是负电荷,电场力作功为负,0<NMA 。
电势能是静电场中的带电粒子与电场共同拥有的能量。
定义为,点电荷q 在静电场中M 点时,系统拥有的电势能为:从M 点移动电荷q 到电势零点的过程中,电场力所作的功,MM M M qUl d E q A W =⋅==⎰→0,静电势能等于电荷量与电荷所在点电势的乘积。
电场力所作的功等于静电势能的减少,静电场中M 点与N 点系统的电势能之差,等于移动点电荷q 由M 点到N 点的过程中电场力所作的功)(NM NM N M N M UU q l d E q A W W -=⋅==-⎰→尽管0>-N M U U ,但电势能之差还与电荷q 有关,不能判断N M W W -的正负。
2.图中,A 、B 是真空中的两块相互平行的无限大均匀带电平面,电荷面密度分别为σ+和σ2-,若将A 板选作电势零点,则图中a 点的电势是[ ]。
.A 032d σε .B 0dσε-.C32d σε- .D3dσε答案:【C 】解:板间电场为023222εσεσεσ=--=E 。
⎰-=-=-dAa d Edl UU 023εσ解:建立直角坐标系,如图。
无限大带电平板A 、B 在两板间的电场强度分别为i E012εσ=,i i E 002)(22εσεσ=--= 两板间电场强度为i i i E E E 00021232εσεσεσ=+=+=电场强度线积分的积分路径为:由板间中点a 指向坐标原点O (板A ),则00002323)(23)(εσεσεσd dx i dx i i dx E l d E U U U d dO aO aO a aO =-=-⋅==-⋅=⋅=-=⎰⎰⎰⎰因为0=O U ,所以23εσd U a =3.如图所示,两个同心球面。
内球面半径为1R ,均匀带电荷Q ;外球面半径为2R ,是一个非常薄的导体壳,原先不带电,但与地相连接。
设地为电势零点,求在两球面之间、距离球心为r 处的的P 点的电场强度及电势。
解:取过点1P 、半径1r )(211R r R <<的同心球面为高斯面S ,⎰=⋅SQ S d E 00/ε,得到021/4επQ E r =)(211R r R <<,电场强度为02104r r Q Eπε=。
电势)11(4442121010210222R rQ dr r Q r d r r Q l d E U R rR rR PP -==⋅=⋅=⎰⎰⎰πεπεπε4.一偶极矩为l q p =的电偶极子放在场强为E 的均匀外电场中,p与E 的夹角为α。
求此电偶极子绕垂直于),(E p 平面的轴沿α增加的方向转过0180的过程中,电场力做的功。
解:设偶极子正电荷初始位置为a ,负电荷初始位置为b 。
转动后正电荷在b 处,负电荷在a 处。
如图,所作的功相当于,把正电荷q +从a 点移到b 点电场力做功)(+A 与把负电荷q -从b 点移到a 点电场力做功)(-A 之和。
⎰⋅=-=--+-=-++=b ab a a b b a l d E q U U q U U q U U q A A A2)(2))(()()()(由于ba q p =,ααcos 2cos 2222pE ba qE ab E q l d E q l d E q b ab a -=-=⋅=⋅=⋅⎰⎰故有αcos 22pE ab E q A -=⋅=。
5.均匀带电球面,半径为R ,电荷面密度为σ。
试求离球心为r 处一点P 的电势。
设()1P 点在球内。
()2P 点在球面上。
(3)P 点在球面外。
解:由于球对称性,由高斯定理求得场强分布0=→内E r (<)R ;0202020244r rR r rREεσπεπσ=⋅=→外 r (>)R 选取无限远处为电势零点,则rRrdrRr d r rR rd E l d E U rrrr022020202εσεσεσ==⋅=⋅=⋅=⎰⎰⎰⎰∞∞∞∞外外外r (>)RR l d E U Rεσ=⋅=⎰∞ 外球面球面球面内内U U l d E U Rr =+⋅=⎰'5扩展.电荷Q 均匀分布在半径为R 的球体内,试求离球心r 处()r R <的电势。
解:电荷体密度334R Qπρ=由于电场分布具有球对称性, 利用高斯定理可得3002230004 3444rQ Q r r r r rrRρππεπεπε===内r (<)Rrˆ4rˆ434rˆ42020320rQ rRrQ E πεπεπρπε===→外 r (>)R00320022323000 r 44 [3]448R R rRrRR rRQ r Q U E dl E dl r dr drRrQ r Q Qdr dr R r RrRπεπεπεπεπε∞∞∞=⋅+⋅=⋅+⋅=+=-⎰⎰⎰⎰⎰⎰外内内6.一圆盘,半径28.010R m -=⨯,均匀带电,面密度522.010C m σ--=⨯⋅ ()1求轴线上任一点的电势(该点与盘心的距离为x )。
()2由场强与电势梯度的关系,求该点电场强度。
()3计算26.010x m -=⨯的电势和场强。
解:(1)把圆盘无限分割成许多圆环,其中任一圆环半径为/R ,宽为/dR ,该圆环上的电荷量为//2dR R dS dq πσσ⋅==此圆环可以被看作无限细带电圆环,在P 点产生的电势为rdRR rdSrdq dU 0//004244πεπσπεσπε⋅===22/x Rr +=由电势叠加原理,有][22222022///0//x xR xRdR R rdR R dU U RRP -+=+===⎰⎰⎰εσεσεσ(2)由对称性知,电场沿x 方向,i xR x i dx dU i E E x ]1[2220+-=-==εσ(3)m V /1013.1260⨯=εσ。
m x 2100.6-⨯=,V U 4105.4⨯= )/(105.45m V E ⨯= 7.半径为R 的圆弧a b ,所对圆心角α,如图所示,圆弧均匀带正电,电荷线密度为λ。
试求圆弧中心处的电场强度和电势。
解:无限分割带电圆弧为许多电荷元,其中任一电荷元θλλRd dl dq ==可看成点电荷,它在O 点产生的场强为204Rdq dE πε=,电势为Rdq dU 04πε=,以x 轴为对称轴,选另一电荷元/dq 与dq 对称,dq dq =/,则有 20//4RdqdE πε=,由于对称性 0/=+yydEdE,)2/(20/R d dEdEdE xxx πεθλ==+O 点总的场强和电势为所有点电荷在该点产生的场强和电势的叠加。
2sin2cos 2cos 22020απελθπεθλθαRRd dE dEE xOx ====⎰⎰⎰i RE2sin20απελ=απελπεθλα⋅===⎰⎰0422d dU U o8.0=⋅⎰Ll d E表明静电场具有什么性质?答:静电场是无旋场。
静电场中,任意两点之间电场强度的线积分与路径无关。
静电场中,任意闭合回路电场强度的线积分为零。
静电场是保守力场,可以引入电势能和电势的概念。
9.电势为零的空间场强一定为零吗?答:不一定。
电势的零点是人为规定的,有意义的是电势差。
电势差是电场强度的线积分,线积分为零,不等于电场强度为零。
反例:如果取无限远处电势为零,则两个等量异号电荷的中垂面上各点电势为0,电场不为0(除电荷连线中点)。
再如,均匀电场E中,连线垂直于电场强度方向的两点a 和b ,电势差为零,但电场强度不为零。
10.电场强度为零的空间电势一定为零吗? 答:不一定。
电势的零点是人为规定的。
如,均匀带电球面内部各点场强为0,电势不为0。
但是,电场强度为零,线积分一定为零,空间各点电势相等,电势差为零。
例如,处于静电平衡的导体内,电场强度为零,导体是等势体。
