凸轮机构的运动仿真分析
基于TBasic的凸轮机构设计及仿真分析

T NO LOG Y TR ND凸轮机构是由凸轮、从动件和机架三个基本构件组成的高副机构。
凸轮机构在应用中的基本特点在于能使从动件获得较复杂的运动规律。
凸轮机构已经广泛应用于各种自动机械中,例如切削和加工自动机床、纺织机械、食品包装机械、印刷机、内燃机等等。
凸轮机构之所以得到如此广泛的应用,主要是由于凸轮机构可以实现各种复杂的运动要求,而且结构简单、紧凑。
对凸轮机构进行运动分析的目的是当已知各构件尺寸参数、位置参数和原动件运动规律时,研究机构其余构件上各点的轨迹、位移、速度、加速度,构件的位置、角位移、角速度和角加速度等运动参数,从而评价机构是否满足工作性能要求,机构是否发生运动干涉。
本文以滚子直动凸轮机构为例,介绍在True Basic 环境下盘形凸轮的设计及凸轮机构的运动仿真的实现方法。
1凸轮机构设计实例分析1.1已知条件已知滚子直动凸轮机构中,从动件行程h=80m m ,推程运动角d0=140°,推程采用3-4-5次多项式运动规律,远休止角dS =40°,回程运动角d0’=100°,回程用正弦加速度运动规律,近休止角dS ’=80°,偏置量e =40m m ,基圆半径rp=100mm ,滚子半径rR=20m m 。
1.2凸轮机构的数学模型1.2.1偏置直动滚子从动件盘形凸轮理论廓线偏置直动滚子从动件盘形凸轮机构,偏距e 、基圆半径rp 和从动件运动规律s=s(f)均已给定。
以凸轮回转中心为原点、从动件推程运动方向为x 轴正向建立右手直角坐标系。
为获得统一的计算公式,引入凸轮转向系数M 和从动件偏置方向系数N ,并规定;若凸轮逆时针转动,则M=+1;否则,M=-1。
如果升程时滚子中心速度矢量对轴心矩的转向与凸轮转动方向相同,则称为正偏置,N=+1;否则,称为负偏置,N =-1。
根据反转法原理,如图1所示,将点B0沿凸轮回转相反方向绕原点转过角d ,即得凸轮理论轮廓曲线上的对应点B ,其坐标为:X B =M *[(s 0+s)*sin (ζ)N*e*cos (ζ)]YB =(s0+s)*cos (ζ)-N*e*sin (ζ)上式即为凸轮理论轮廓曲线的直角坐标参数方程。
UG机械设计实例教程 第3章 凸轮机构的建模与运动仿真

推程曲线
远休止曲线
回程曲线
任务实施
1.零件造型—从动件建模
任务实施
1.零件造型—机架建模
任务实施
2.装配—凸轮机构的装配
1
2
4
3 5
任务实施
3.运动仿真-基本流程
01
确定运动构件
02
确定两构件的运动副类型
03
确定原动件,即驱动运动副
04
确定驱动参数,求解
任务实施
3.运动仿真-操作过程
1 添加连杆
2 添加运动副
3 设置机架
4 添加驱动
5 仿真计算 7 运动播放与追踪
6 仿真结果分析
第三章 凸轮机构的建模与运动仿真
技能目标
01
掌握解析法绘制凸轮轮廓曲线
02
了解凸轮轮廓曲线设计编程
03
掌握 UG 表达式参数化建模方法
04
掌握凸轮机构运动仿真的基本操作
任务引入
凸轮是一个具有轮廓曲线或凹槽的构件, 凸轮转动会带动从动件实现预期的运动规律。
1-凸轮 2-滚子 3-从动件 4-机架
设计如图所示的滚子直动从动件盘形凸轮机构。 已知凸轮 1 匀速转动, 带动滚子 2 和从动件 3 运动, 输出运动为从动件的直线往复运动。 要求将凸轮机构建模并模拟仿真其运动规律。
凸轮机构运动仿真
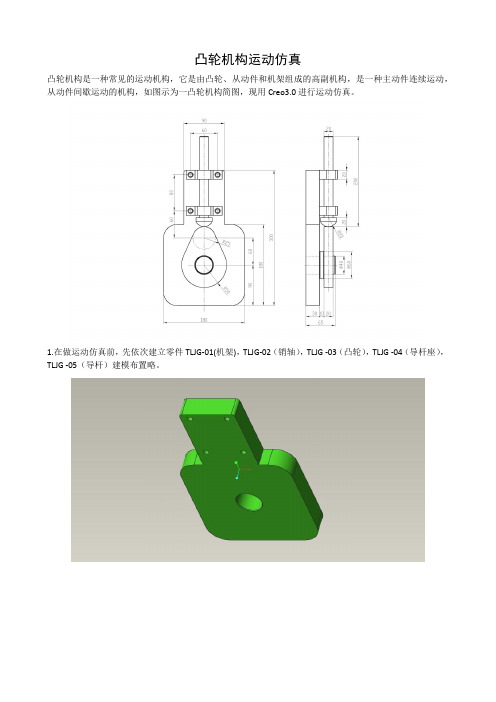
凸轮机构运动仿真凸轮机构是一种常见的运动机构,它是由凸轮、从动件和机架组成的高副机构,是一种主动件连续运动,从动件间歇运动的机构,如图示为一凸轮机构简图,现用Creo3.0进行运动仿真。
1.在做运动仿真前,先依次建立零件TLJG-01(机架),TLJG-02(销轴),TLJG -03(凸轮),TLJG -04(导杆座),TLJG -05(导杆)建模布置略。
2.打开Creo3.0,新建文件,输入名称TLJG-00,点选装配/设计,选择mmns_asm_design模板,确定,进入装配模式。
3.调入TLJG-01,选择默认装配模式,确定。
4.调入TLJG-02,重合约束:将TLJG-02的轴曲面与TLJG-01的轴孔曲面重合;TLJG-02的台阶内侧端面与TLJG-01的外侧端面重合;TLJG-02的RIGHT平面与ASM_RIGHT平面重合。
5.调入TLJG-03,销连接,轴对齐:将TLJG-03的轴孔中心线与TLJG-02的轴中心线对齐;平移:TLJG-03的内侧端面与TLJG-02的台阶外侧端面重合;旋转轴:将TLJG-03的RIGHT平面与ASM_RIGHT平面角度设为0,作为初始角度。
6.调入TLJG-04,添加3个重合约束,使TLJG-04与TLJG-01固定,再将TLJG-04阵列,数量2,距离80。
7.再调入TLJG-05,选择滑块模式,轴对齐:将TLJG-05的轴线与TLJG-04的轴孔中心线对齐;旋转:将TLJG-05的RIGHT平面与TLJG-04的RIGHT平面重合,完成。
9.进入应用程序/机构,选择凸轮模式,依次选择TLJG-03(凸轮1),TLJG-05(凸轮2)的曲面,完成。
10.新建伺服电机,类型选取TLJG-03的轴孔中心线为运动轴,轮廓选择速度,常量A为20,单位为deg/sec,即转一圈360°需要18s。
11.新建分析,首选项将结束时间设为18s,再选择电动机,运行。
如何用solidworks2016进行凸轮的运动仿真分析

如何用Solidworks2016进行凸轮的运动分析李犹胜(上海200000)0、摘要凸轮机构是机械设计中常用的结构,它的运动仿真模拟是凸轮设计过程中不可缺少的步骤。
很多专业人士都对其做了研究,但是过程趋于复杂。
较多的年轻工程师很难理解,本文通过一个简单的例子通过SolidWorks2016软件来说明凸轮机构仿真模拟的方法和步骤,浅显易懂。
1、关键词凸轮机构、运动仿真、运动分析2、概述凸轮机构一般是由凸轮、从动件和机架三个构件组成的高副机构。
凸轮通常作连续等速转动,从动件根据使用要求设计使它获得一定规律的运动。
凸轮机构能实现复杂的运动要求,广泛用于各种自动化和半自动化机械装置中,几乎所有任意动作均可经由此一机构产生[1]。
在设计凸轮机构时,凸轮机构的模拟运动分析将是一项必要而不可缺少的工作。
它也是进行凸轮外形设计的辅助手段。
本文介绍了使用solidworks2016软件进行凸轮运动分析的基本步骤和使用技巧。
3、零件建模及装配3.1、先用solidworks2016 将凸轮机构的零件建模好,作为本文的一个例子,作者建立了下列零件数模。
3.2 将上述零件导入到solidworks 2016装配体中,具体操作为:步骤1、文件、新建、选择装配图模板,进入装配体模式步骤2、导入凸轮轴(1)选择插入部件(2)在插入零部件窗口中选择“浏览”按钮。
(3)选择要插入的文件,按“打开”按钮;(4)将图形放在屏幕的任意位置,将其固定(如图2)。
步骤3、导入“凸轮”(1)重复按照步骤2的方法,将凸轮导入到装配体中。
(2)添加“同心”约束,添加后如图(3)添加“距离”约束添加后的结果如下步骤4 、导入“滚轮”(1)重复按照步骤2的方法,将滚轮导入到装配体中。
(2)添加一个“机械约束”中的“凸轮配合”约束(2)再添加一个“距离”约束到滚轮上(4)完成后的结果如下图步骤5 导入“直线运动杆”(1)重复按照步骤2的方法,将直线运动杆导入到装配体中。
凸轮机构多项式运动规律的设计方法及仿真分析

DOI:10.3969/j.issn.2095-509X.2020.08.005凸轮机构多项式运动规律的设计方法及仿真分析王㊀刚ꎬ任子文ꎬ周㊀奎(中烟机械技术中心有限责任公司ꎬ上海㊀201206)摘要:通过对基本边界条件的多项式运动规律的理论分析ꎬ推导出高次多项式运动规律的通用方程ꎬ以及各参数的计算公式ꎮ针对具有附加约束条件的凸轮机构ꎬ提出一种多项式运动规律的分段设计方法ꎬ对求解出的多项式运动规律的位移㊁速度㊁加速度进行仿真分析ꎬ并与目前通用的圆弧拼接的改进型等速运动规律进行对比ꎬ证实了该设计方法的可靠性ꎮ关键词:凸轮机构ꎻ多项式ꎻ边界条件ꎻ附加约束条件ꎻ分段求解ꎻ仿真分析中图分类号:TH112.2㊀㊀㊀文献标识码:B㊀㊀㊀文章编号:2095-509X(2020)08-0023-04㊀㊀凸轮机构是机械行业中最常用的典型机构ꎬ它可以使从动件按规定的运动规律完成动作ꎬ把回转运动转变成直线移动或摆动ꎮ然而ꎬ凸轮机构在实际运用中存在部分问题ꎬ如刚性冲击和柔性冲击ꎮ冲击不仅影响凸轮寿命ꎬ而且对主运动机构的力和功率等影响也很大ꎮ不同的运动规律所造成的冲击程度也不相同[1]ꎮ因此ꎬ对凸轮机构从动件的运动规律进行研究是十分必要的ꎮ凸轮机构从动件的运动规律包括代数多项式运动规律和三角函数式运动规律以及改进型㊁组合型运动规律ꎮ常用的代数多项式运动规律有一次多项式(等速运动规律)㊁二次多项式(等加速运动规律)以及高阶多项式运动规律ꎮ一次多项式运动规律存在刚性冲击ꎬ只能用于低速轻载的场合ꎻ二次多项式运动规律存在柔性冲击ꎬ只能用于中速轻载的场合ꎻ五次㊁七次以及更高阶的多项式运动规律既没有刚性冲击也没有柔性冲击ꎬ可用于高速场合ꎮ由于加工工艺复杂ꎬ因此高于七次的多项式运动规律很少使用ꎮ三角函数式运动规律有正弦加速度运动规律和余弦加速度运动规律等[2]ꎮ正弦加速度运动规律没有刚性冲击和柔性冲击ꎬ可用于高速场合ꎻ余弦加速度运动规律存在柔性冲击ꎬ只能用于中速轻载场合[3]ꎮ虽然正弦加速度运动规律可以用于高速场合ꎬ但在有多个特殊运动要求的情况下ꎬ正弦加速度运动规律就不太容易求解了[4]ꎬ需要采用加控制条件的多项式运动规律ꎮ为得到符合设计要求且性能更好的运动规律ꎬ本文通过对位移㊁速度以及加速度的分析ꎬ在运动过程中分段加入合适的边界条件以及其他约束条件ꎬ对多项式运动规律曲线进行分段优化设计ꎬ从而得到更精确㊁小冲击㊁无过大功率变化的改进型多项式运动规律ꎮ1 多项式运动规律的数学方程计算如图1所示ꎬ推杆位移S和凸轮转角θ存在一定的运动关系ꎬ该关系如引言所述可以有多种运动规律ꎮ图1㊀凸轮转角和推杆位移曲线㊀㊀本文论述的是多项式运动规律ꎬ其基本形式为:㊀S=C0+C1θ+C2θ2+C3θ3+ +Cmθm(1)式中:C0ꎬC1ꎬC2ꎬC3ꎬ ꎬCm为使S和S的某些导数满足运动过程规定的边界条件的待定常数ꎮ式(1)中各次幂的相继项目数应与决定凸轮运动所需的条件数相等[5]ꎮ收稿日期:2019-07-02作者简介:王刚(1987 )ꎬ男ꎬ工程师ꎬ主要研究方向为烟草包装机机械设计ꎬwang_gn@ctmtc.net.32 2020年8月㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀机械设计与制造工程㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀Aug.2020第49卷第8期㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀MachineDesignandManufacturingEngineering㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀Vol.49No.8㊀㊀对式(1)进行一次求导可得到速度方程ꎬ二次求导得到加速度方程ꎬ三次求导得到跃度方程ꎬ直到更高的阶次ꎮ在对通用机械的凸轮运动规律进行设计时ꎬ通常只需要保证速度及加速度连续即可ꎬ即设定起点和终点的约束条件为:当θ=0时ꎬS=0ꎬV=0ꎬA=0ꎻ当θ=δ时ꎬS=hꎬV=0ꎬA=0ꎮ其中δ为凸轮转角ꎬh为推杆位移ꎬV为推杆速度ꎬA为推杆加速度ꎮ由上述6个边界条件ꎬ可得该多项式方程为:㊀S=C0+C1θ+C2θ2+C3θ3+C4θ4+C5θ5(2)将方程(2)对θ求导ꎬ得V=C1+2C2θ+3C3θ2+4C4θ3+5C5θ4(3)将方程(3)对θ求导ꎬ得A=2C2+6C3θ+12C4θ2+20C5θ3(4)将6个边界条件代入方程(2)㊁(3)㊁(4)ꎬ联立求解得C0=C1=C2=0ꎻC3=10hδ3ꎻC4=-15hδ4ꎻC5=6hδ5ꎮ将C0ꎬC1ꎬC2ꎬC3ꎬC4ꎬC5的值代入式(2)㊁(3)㊁(4)ꎬ可得到位移㊁速度和加速度的运动方程为:S=h[10(θδ)3-15(θδ)4+6(θδ)5]㊀θɪ(0ꎬδ)(5)V=hδ[30(θδ)2-60(θδ)3+30(θδ)4](6)㊀A=hδ2[60(θδ)-180(θδ)2+120(θδ)3](7)通过方程(5)㊁(6)㊁(7)可以看出ꎬ速度和加速度都是连续的ꎮ根据式(5)可以写出多项式运动规律的位移方程通式[6]:S=h[Cn(θδ)n+Cn+1(θδ)n+1+ +C2n-1(θδ)2n-1](8)式中:n为起点的约束条件个数ꎮ利用终点的约束条件ꎬ即θ=δ时ꎬS=hꎬV=0ꎬA=0ꎬ ꎬ可得用于计算各系数C的线性方程组:Cn+Cn+1+ +C2n-1=1nCn+(n+1)Cn+1+ +(2n-1)C2n-1=0n(n-1)Cn+(n+1)nCn+1+ +㊀(2n-1)(2n-2)C2n-1=0ìîíïïïïï(9)运用代数运算ꎬ求得线性方程组(9)的解为:Cn=[(n+1)(n+2) (2n-1)]/㊀{[(n+1)-n][(n+2)-n] ㊀[(2n-1)-n]}Cn+1=[n(n+2) (2n-1)]/㊀{[n-(n+1)][(n+2)-(n+1)]㊀[(2n-1)-(n+1)]} C2n-1=[n(n+1)(n+2) (2n-2)]/㊀{[n-(2n-1)][(n+1)-(2n-1)] ㊀[(2n-2)-(2n-1)]}ìîíïïïïïïïïïïïïï(10)式(10)是在给定起点和终点约束条件的情况下ꎬ对高次多项式运动规律的位移㊁速度㊁加速度等进行联合求解而得到的各系数计算公式ꎮ当运动规律要求有特定的起点和终点约束条件时ꎬ只需要在式(10)中代入指定的值ꎬ便可得到相应的系数值ꎮ2㊀附加约束条件的多项式运动规律设计除了规定在边界处有一个或几个位移导数等于零的条件外ꎬ还可以给出起点或终点处一个或几个位移导数的具体数值ꎬ这种具有更多约束条件的运动规律能够严格控制凸轮机构的运动学性能[5]ꎮ现根据具体情况进行设计论述ꎮ设定升 停 回型凸轮ꎬ运动循环图如图2所示ꎬ图中δ1为凸轮升程转角ꎬδ2为停程转角ꎬδ3为回程转角ꎮ回程时ꎬ凸轮旋转δ31ꎬ推杆位移为h1ꎻ凸轮继续旋转δ32ꎬ推杆位移为h2ꎻ凸轮最后旋转δ33ꎬ推杆位移为h3ꎮ其中h1+h2+h3=hꎬδ31+δ32+δ33=δ3ꎮ图2㊀运动循环图㊀㊀升程段没有特殊的运动要求ꎬ根据多项式运动方程(8)正常求解即可ꎮ回程段时要求先进行一段加速运动ꎬ然后进行一段匀速运动ꎬ最后再进行一段减速运动ꎬ对于这样的运动特性ꎬ目前通常采用圆弧拼接的改进型等速运动规律[6]ꎮ该运动规律的缺点是加速度不连续ꎬ会造成柔性冲击ꎮ2.1㊀对升程段进行求解由于升程δ1段没有特殊要求ꎬ那么在没有刚㊁柔性冲击的条件下ꎬ可定义其边界条件为:θ=0ꎬS=0ꎬV=0ꎬA=0ꎻθ=δ1ꎬS=hꎬV=0ꎬA=0ꎮ42 2020年第49卷㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀机械设计与制造工程㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀将n=3代入式(10)ꎬ可求得各系数的值ꎬ将各系数值代入式(8)ꎬ从而得到升程段的多项式运动规律位移方程:S=h[10(θδ1)3-15(θδ1)4+6(θδ1)5](11)2.2㊀对回程段进行分段求解凸轮回程δ3段由于存在多个设计条件ꎬ采用单一的多项式运动规律显然不能满足其运动要求ꎬ因此对其进行分段求解[7]ꎮ假设推杆位移为h1时ꎬ推杆速度为v1ꎻ位移为h2时ꎬ推杆速度为v2ꎻ位移为h3时ꎬ推杆速度为v3ꎮ对h1位移段运动方程进行求解ꎬ为了保证接合处加速度曲线连续ꎬ在θ=δ31处的加速度应等于h2位移段的加速度ꎬ即A=0ꎮ为了便于计算ꎬ将升程和凸轮转角无量纲化ꎬ即令最大升程和最大凸轮转角都为1[8]ꎬ同时对速度也进行无量纲化表示ꎬ由于此时速度不为0ꎬ设定速度等于1ꎬ其边界条件为:θ=0ꎬS=0ꎬV=0ꎬA=0ꎻθ=1ꎬS=1ꎬV=1ꎬA=0ꎮ将这6个边界条件的具体值代入到式(2)㊁(3)㊁(4)ꎬ联立求解得:C0=C1=C2=0ꎻC3=6ꎻC4=-8ꎻC5=3ꎮ由此得出位移㊁速度及加速度的多项式无量纲运动方程如下:S=6θ3-8θ4+3θ5V=18θ2-32θ3+15θ4A=36θ-96θ2+60θ3{(12)只要把式(12)中的每一项Cnθn乘上hδnꎬ即hCn(θδ)nꎬ就可以把无量纲方程变换成为实际方程[4]ꎮ因此h1位移段的实际多项式方程为:S=h1[6(θδ31)3-8(θδ31)4+3(θδ31)5]V=h1δ31[18(θδ31)2-32(θδ31)3+15(θδ31)4]A=h1δ231[36 θδ31-96(θδ31)2+60(θδ31)3]ìîíïïïïïïï(13)对h2位移段运动方程进行求解ꎬ由于此段为匀速运动ꎬ因此其加速度A=0ꎬ速度V=h2δ32ꎬ位移S=h2δ32θꎮ对h3位移段运动方程进行求解ꎬ为了保证接合处速度曲线连续ꎬ此段起始速度与h2位移段的速度相等ꎬ为了保证接合处加速度曲线连续ꎬ此段起始处的加速度应等于h2位移段的加速度ꎮ于是其边界条件为:θ=0ꎬS=0ꎬV=1ꎬA=0ꎻθ=1ꎬS=1ꎬV=0ꎬA=0ꎮ运用h1位移段计算方法ꎬ可求得h3位移段的多项式方程为:S=h3[θδ33+4(θδ33)3-7(θδ33)4+3(θδ33)5]V=h3δ33[1+12(θδ33)2-28(θδ33)3+15(θδ33)4]A=h3δ233[24 θδ33-84(θδ33)2+60(θδ33)3]ìîíïïïïïïï(14)根据式(13)㊁(14)及已知条件可得出:v1=h1δ31ꎬv2=h2δ32ꎬv3=h3δ33ꎬv1=v2=v3ꎬδ31+δ32+δ33=δ3ꎮ由于h1ꎬh2ꎬh3ꎬδ3均为已知量ꎬ且h1+h2+h3=hꎬ因此可求得3个未知量:δ31=δ3h1hꎬδ32=δ3h2hꎬδ33=δ3h3hꎮ至此就求得了回程的三段多项式运动规律方程ꎮ3㊀仿真分析及应用效果在设计完多项式运动规律后ꎬ对其进行仿真分析ꎬ以确保该运动规律符合凸轮设计的基本要求以及附加的特殊需求ꎮ对各已知项进行赋值ꎬ通过第2节计算方法得出多项式运动规律方程ꎬ然后将运动规律方程导入仿真软件ꎬ并与圆弧拼接的改进型等速运动规律进行对比ꎮ图3㊀圆柱凸轮展开图㊀㊀图3中曲线1为多项式运动规律生成的滚子中心轨迹线ꎬ曲线2为用圆弧拼接的改进型等速运动规律生成的滚子中心轨迹线ꎮ两种运动规律的位移㊁速度以及加速度的运动曲线如图4ꎬ5ꎬ6所示ꎮ52 2020年第8期㊀㊀㊀㊀㊀㊀㊀㊀㊀王刚:凸轮机构多项式运动规律的设计方法及仿真分析图4㊀位移曲线图图5㊀速度曲线图图6㊀加速度曲线图㊀㊀由图可以看出ꎬ本文求解的多项式运动规律ꎬ其速度和加速度曲线在整个行程中均无突变ꎬ说明该多项式运动规律既无刚性冲击ꎬ也没有柔性冲击ꎬ同时也能严格满足回程的分段控制要求ꎮ而用圆弧拼接的改进型等速运动规律ꎬ虽然速度连续ꎬ但加速度有突变ꎬ会造成柔性冲击ꎬ而且其回程段的各参数只能趋近于要求值ꎬ做不到严格一致ꎮ因此本文多项式运动规律的设计方法是安全有效的ꎮ4㊀结束语本文在确保凸轮机构速度及加速度曲线连续的情况下ꎬ通过对边界条件赋值ꎬ求解出了多项式运动规律的位移方程通式ꎬ并根据通式推导出了各系数的计算公式ꎮ然后通过实例验证了各系数计算公式的便捷性与可靠性ꎬ并介绍了五次多项式运动规律的应用方法ꎮ同时提出了一种针对具有附加约束条件的多项式运动规律的设计方法ꎬ该方法可以针对不同的设计需求ꎬ对凸轮行程进行分段设计ꎬ在确保凸轮机构没有刚㊁柔性冲击的前提下ꎬ满足从动件的特殊动作需求ꎮ最后ꎬ通过对设计的多项式运动规律进行仿真分析ꎬ并与用圆弧拼接的改进型等速运动规律进行对比ꎬ验证了该设计方法是安全有效的ꎮ参考文献:[1]㊀孙桓ꎬ陈作模.机械原理[M].北京:高等教育出版社ꎬ2005:151-160.[2]㊀魏兵ꎬ熊禾根.机械原理[M].武汉:华中科技大学出版社ꎬ2007:110-116.[3]㊀赖晓桦.凸轮六次多项式运动规律的理论分析[J].机械传动ꎬ2010ꎬ34(9):30-32.[4]㊀石永刚ꎬ吴永芳.凸轮机构设计与应用创新[M].北京:机械工业出版社ꎬ2007:20-23.[5]㊀邹慧君ꎬ董师予.凸轮机构的现代设计[M].上海:上海交通大学出版社ꎬ1989:1-21.[6]㊀郑晨升ꎬ葛正浩.凸轮机构从动件运动规律的通用表达式[J].机械科学与技术ꎬ1996ꎬ15(1):151-155. [7]㊀朱家诚ꎬ汪进ꎬ吴天星ꎬ等.凸轮从动件运动规律的分段建模方法及设计系统研究[J].机械设计ꎬ2008ꎬ25(7):23-25. [8]㊀彭国勋ꎬ肖正杨.自动机械的凸轮机构设计[M].北京:机械工业出版社ꎬ1990:55-61.DesignmethodandsimulationanalysisofpolynomialmotionlawofcammechanismWangGangꎬRenZiwenꎬZhouKui(ChinaTobaccoMachineryTechnologyCentreCo.ꎬLtd.ꎬShanghaiꎬ201026ꎬChina)Abstract:Accordingtothetheoreticalanalysisofpolynomialmotionlawwithbasicboundaryconditionꎬthispa ̄perderivesthegeneralequationsofmotionofhigherorderpolynomialsandeachparameters'calculatingformula.Aimingatthecammechanismwithadditionalconstraintsꎬitproposesasegmenteddesignmethodwithpolynomialmotionlaw.Itcarriesoutthesimulationanalysisofthedisplacementꎬvelocityandaccelerationforsolvedpolyno ̄mialmotionlawꎬandcompareswiththecurrentgeneralcircularsplicingimprovedconstantvelocitymotionlawꎬtheresultsprovethereliabilityofthedesignmethod.Keywords:cammechanismꎻpolynomialꎻboundaryconditionꎻadditionalconstraintsꎻsegmentsolutionꎻsimula ̄tionanalysis622020年第49卷㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀机械设计与制造工程㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀。
基于Creo的凸轮机构三维参数化设计及运动仿真

基于Creo的凸轮机构三维参数化设计及运动仿真刘鹏冯立艳李静卢家宣蔡保杰冷腾飞苗伟晨(华北理工大学以升创新基地河北·唐山063210)摘要本文主要介绍用Creo对凸轮机构进行参数化设计并以圆柱槽状凸轮机构为例进行运动仿真,再通过C#软件完成人机交互,即操作人只需在程序界面输入槽状凸轮相应参数即可完成凸轮的三维建模,从而绘制出相应的位移、速度、加速度曲线进入仿真和分析环节。
这样即缩短了凸轮的设计周期提高了设计质量,并且解决了凸轮教学课程存在的设备成本高、设备数量少、实验时间和空间受限等难题。
关键词凸轮Creo参数化仿真中图分类号:TP391.9文献标识码:A1基于Creo软件下的凸轮三维建模1.1Creo环境下槽状凸轮机构三维参数化造型基本思路(1)参数化过程需准备可变参数包括行程、推程角、远休角、回程角、近休角、外径、壁厚、基底高度、凸轮高度、槽深、槽宽,以上变量成为参数组。
(2)通过根据凸轮不同运动规律编写推程、远休止、回程、近休止段凸轮轮廓线方程,本例应用的凸轮推程回程为正弦加速度运动规律。
(3)分段绘制出理论轮廓曲线,将各段曲线首尾相连封闭,即为完整的凸轮理论廓线。
(4)生成凸轮实体;加入参变量,实现参数化。
1.2三维建模具体步骤Creo是如今今应用最广的三维绘图软件之一,主要用于参数化实体设计,它所提供的功能包括实体设计、曲面设计、零件装配、建立工程图、模具设计、、电路设计、装配管件设计、加工制造和逆向工程等。
其系统特性主要包含单一数据库、全参数化、全相关、基于特征的实体建模等,不仅能实现零件的参数化设计,也可以方便地建立各零部件的通用件库和标准件库,从而提高设计的效率和质量。
1.2.1槽状凸轮机构的三位参数化建模自行设定初步参数组,注意推程角、远休角、回程角、近休角之和为360,(2)运行creo软件,新建零件,进入界面。
(3)选择【工具:程序】,出现菜单管理器,选择编辑设计,出现记事本,在IN PUT和END PUT语句中间输入语句,然后存盘,确认将所做的修改体现到模型中,最后在菜单管理器中输入设定的初步参数值。
用ADAMS进行凸轮机构模拟仿真示例

结果分析注意事项
确保模拟仿真的初始条件和参数设 置正确
注意模拟仿真的收敛性和稳定性
添加标题
添加标题
添加标题
添加标题
对比实际测试数据与模拟仿真结果, 确保一致性
考虑模拟仿真的误差和不确定性
THANK YOU
汇报人:XX
参数敏感性分析:研究模型参数对模拟仿真结果的影响,确定关键参数并分析其敏感性。
重复性验证:多次运行模拟仿真并分析结果的重复性,以评估模拟仿真的可靠性和稳定性。
模拟仿真结果优化分析
优化目标:提高凸轮机构的性能和效率
优化方法:采用多目标优化算法,对凸轮机构的关键参数进行优化 优化过程:通过ADAMS软件进行仿真实验,分析不同参数组合下的性能表 现 优化结果:得到最优参数组合,使凸轮机构性能达到最优状态
功能特点:ADAMS提供了丰富的建模工具和求解器,支持各种机械系统,包括刚体、柔性体和 刚柔耦合系统。
应用领域:广泛应用于汽车、航空航天、船舶、机械制造、能源等领域,用于产品设计和性能优 化。
优势:ADAMS提供了直观的图形界面和强大的后处理功能,使得用户可以方便地进行模型建立、 参数设置和结果分析。
对比分析不同 参数下的模拟 仿真结果,如 转速、压力角
等
输出凸轮机构 模拟仿真的最
优设计方案
总结输出凸轮 机构模拟仿真 结果对实际应 用的指导意义
用ADAMS进行凸轮机构模拟 仿真结果分析
模拟仿真结果准确性分析
对比实验:将模拟仿真结果与实际实验数据进行对比,验证模拟仿真的准确性。 误差分析:分析模拟仿真结果与实际实验数据之间的误差,判断误差是否在可接受范围内。
定义运动学参数和约束条件
设置凸轮机构运动参数
确定凸轮机构类型和尺寸 定义凸轮机构运动规律 设置凸轮机构接触参数 验证凸轮机构运动参数的正确性
凸轮机构的虚拟设计与运动仿真

凸轮机构的虚拟设计与运动仿真
首先,在进行凸轮机构的虚拟设计和运动仿真之前,需要对机构的物
理特性以及设计要求进行分析和确认。
这包括凸轮轴的几何形状、凸轮与
被控件的运动规律和传动比等。
接下来,可以使用CAD软件绘制凸轮轴和被控件的几何形状。
在绘制
凸轮轴时,可以使用CAD软件提供的几何图形工具创建具有不同形状的凸
轮剖面。
在绘制被控件时,可以创建其对应的几何模型,并与凸轮轴进行
连接。
完成几何模型的绘制后,可以使用CAD软件中的运动仿真工具来模拟
凸轮机构的运动。
首先,可以为凸轮轴设置一个恒定速度的输入条件。
然后,可以通过设置凸轮轴与被控件之间的运动关系(例如凸轮与被控件的
接触点位置)来实现凸轮机构的运动仿真。
在进行运动仿真时,可以观察凸轮机构的各个部分的运动情况,并分
析其运动特性,以评估机构的性能。
例如,可以观察被控件的运动轨迹和
速度曲线,以确定被控件是否能够按照要求进行精确的运动。
如果发现机
构存在问题,可以通过调整凸轮轴的几何形状或修改运动关系来进行优化。
除了CAD软件,还可以使用专业的凸轮机构仿真软件来进行虚拟设计
和运动仿真。
这些软件通常具有更强大的仿真功能,可以提供更准确的分
析和评估结果。
通过使用这些软件,可以更好地理解和优化凸轮机构的运
动特性,并减少实际试验的次数和费用。
总之,凸轮机构的虚拟设计与运动仿真可以通过CAD软件或专业仿真
软件来实现。
通过这种方法,可以在设计早期阶段对机构进行分析和优化,从而减少实验和测试的时间和成本,提高设计效率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
障施工能力,保证生产效率。其中与工程机械有
关的有土石方设备、运输设备、基础钻机、混凝土设备、起重
设备、道床铺装设备等。
根据中国工程机械工业协会的预测,工程机械设备需
求大约占到京沪高铁施工建设费用的 25%,按此招标总价
计算,则工程机械采购规模约为 209 亿元,平均每年的采
购额约为 42 亿元。
机械工程师 2008 年第 1 期 141
(c)设置标志点:为测量两推板间在仿真运动时的同 步距离,在与两推板滑动方向一致的直线上建立两标志 点 A001、A002,分别设在推板 1 和推板 2 上。 3 运动仿真分析及装配位置调整
(1)进入方案 scenario1,在封装选项操作中,建立两 标志点 A001 和 A002 相对距离的测量。
300
200
绘图区
100
0
0.03 0.06 0.09 0.12 0.15 时间 t/s 图7
(4)从图 3 分析,夹持段不重合,不能保证夹持时的 同步距离,需利用旋转副的关节驱动进行两凸轮相位角 的调整。
(5)进入关节仿真:根据图 3 两曲线重合时所需调整 的角度 δ,取相应的步长和步数,初步调整两凸轮相位角。 取步长为 7.2°,步数为 50,进行全循环运动仿真,列出测 量值,观察夹持同步距离的变化情况,逐步缩小步长,反 复上述过程,直到获得理想数值。另外可分别调整两拉杆 的长度,使两推板夹持器之间的距离达到烟包长度 84- 85mm 的要求。
Hale Waihona Puke 制造业信息化MANUFACTURING INFORMATIZATION 仿真 / 建模 / CAD/ CAM/ CAE/ CAP P
凸轮机构的运动仿真分析
陈建临, 王爱国 (云南烟草机械厂,昆明 650011)
摘 要:UG 的运动分析模块可以对机构进行运动仿真分析,可以分析机构中零件的位移、速度、加速度等。文中通过对
运动特性(位移、速度)已符合机构实际应用的要求。
(编辑 立 明) !!!!!!!!!! 作者简介:陈建临(1963-),女,工程师,主要从事烟机制造及设计工作。 收稿日期:2007- 01- 30
2008 年 1 月5 日,铁道工程交易中心公布 了《新建京沪高速铁路土建工程施工总价承包 招标中标结果》,总价约达 837 亿元的土建工 程“花落”6 家公司。
根据要求设立运动副并添加驱动。 (4)连杆和运动副的设置如下: (a)定义凸轮 1(包括滚子中心轨迹曲线)为连杆,并
定义它的运动副为对地静止的旋转副。驱动定义为恒定 运动,设位移为 0;加速度为 0;速度为 2400°/s(400 包/ min);定义摆杆 1(包括与其相对静止的滚子中心)、内球 头 1 为连杆,与地的运动副为旋转副,与凸轮 1 连杆的约 束为点在线上副;定义关节轴承 1 的外球头 1 为连杆,定 义它与摆杆 1 连杆之间的运动副为球面副,球面副的原 点设在球面的中心;定义关节轴承的外球头 2 和拉杆 1 为连杆,定义推板 1 和内球头 2 为连杆。外球头 2 与推板 1 之间用球面副约束;定义推板 1 对地的运动副为滑动 副;定义连杆外球头 1 和连杆外球头 2 之间的运动副为 滑动副,并设运动驱动为关节仿真。
B1 卷烟包装机 18 部件推包凸轮机构的运动仿真分析,验证了测绘凸轮曲线运动特性的正确性,求出了运动过程中两
夹持推板的同步精度数据。给出了调整两凸轮相位角的准确数值。在烟机的大修理中,可指导对机器机构的改进并验证
改进的效果,也可以指导机器的装配及调试。
关键词:烟机;凸轮机构;仿真分析
中图分类号:TH132.47
确性,求出了运动过程中两推板夹持器的位移、速度规律
及其同步运动的精度数据。给出了调整两凸轮相位角的
准确数值。类似的仿真分析在烟机的设计及大修中,有广
泛的应用前景。
1 机构简介及装配主模型
1.1 机构简介
凸轮 2
摆杆 2 凸轮 1
机构如图 1,凸轮 1 带动摆杆 1、推板 1、 拉杆 1 和关节轴承 1
截面上的中心点与实体一起放入滚子的装配引用集。
2 建立运动分析方案及连杆和运动副的设置
(1)利 用 机 构 装 配 主 模 型 进 入 运 动 分 析 菜 单 ,建 立
scenario1 新方案。
(2)连杆的设置原则:几个零件之间如果没有相对运
动,则将它们定为一个连杆。 (3)运动副设置的原则:两个有相对运动的连杆之间
位移 s/mm
108.135°。 (8)对修改后装配主模型进行运动仿真,参数设置,
得出位移曲线图 6、位移重合曲线图 7。 从图 7 可以看出,在夹持段两条位移曲线基本重合,
即两推板夹持器的相对位移很小。
300 200 100
0
0.03 0.06 0.09 0.12 0.15 时间 t/s 图6
位移 s/mm
140 机械工程师 2008 年第 1 期
制造业信息化
仿真 / 建模 / CAD/ CAM/ CAE/ CAP P MANUFACTURING INFORMATIZATION
(2)进入运动仿真分析:设置参数,取时间=0.15s(凸 轮转一圈所需时间)、步数=50。
(3)激活测量进行运动仿真,利用电子图表得出推板 1 和推板 2 的位移曲线(见图 2),理想状态下,两推板在 夹持段速度的大小和方向都应一致,即在夹持段其相对 位移应接近为 0。图 3 为两推板距离减去所夹烟包长度 后的相互位置、理想状态下,夹持阶段的曲线应重合。
(6)图 4 中的数值表为反复调整后数值,序号 35- 49 (约 108°)夹持段显示的距离偏差小于 0.4mm,较为理想。 利用两凸轮的零度线,测出此状况下的两凸轮相位角为 108.135°,如图 5。
(7)修改装配主模型,将两凸轮相位角的约束调整为
108.135°
图4
图5
4结论 调整后的装配主模型进行的运动仿真,其两推板的
京沪高铁全 长 约 1318km, 设 计 时 速 为 300 ̄350km/h,建设工期 5 年,全线封闭运行,并 在道口实现全立交。主要工程内容包括桥梁长 约 1140km, 占 正 线 长 度 86.5% ; 隧 道 长 约 16km,占正线的 1.2%;路基长度 162km,占正线 的 12.3%;全线铺设无碴轨道约 1268km,占线 路的 96.2%;有碴轨道约 50km,占线路的 3.8%。
关节轴承 2 拉杆 2
推板 2 夹紧器
摆杆 1
拉杆 1 关节轴承 1 推板 1
图1
运动,将烟包从烘干 转塔 1 推出,同时凸 轮 2 带动摆杆 2、推板 2、拉杆 2、关节轴承 2 及夹紧器运动,并将 封签封平在烟包顶口
上,两个凸轮带动两推板同步运动并夹持烟包将其推入
烘干转塔 2。机构要求两推板夹持烟包时同步运动且距
此次土建招标路段总长度为 1271km,占到 正线长度的 96.4%,标志着京沪高铁建设的大 幕全面拉开,预计整个工程在春节前开工。与普 通铁路相比,高速铁路客运专线建设需要一批 大型化、专业化、智能化的专用设备和专用的试 验、检测、测量设备,以确保技术指标的控制,保
京 沪 高 铁 大 幕 拉 开
工 程 机 械 行 业 利 好
文献标识码:A
文章编号:1002- 2333(2008)01- 0140- 02
每分钟 8000 支(400 包)的 B1 卷烟包装机有多种凸
轮机构,其运动精度直接影响设备的效率和包装的质量。
本文利用 UG 的运动分析模块对 B1 机 18 部件推包凸轮
机构进行运动仿真分析,验证了凸轮曲线运动特性的正
离保持为烟包长度(84- 85mm)。通过调整两个凸轮的相
互位置关系和拉杆的长度来达到此要求。
1.2 装配主模型
根据 B1 机 18 部件的零件图完成各个零件的三维建
模,并根据装配总图的尺寸要求,建立用作运动分析的装
配主模型,如图 1。
在装配中,将凸轮曲线和凸轮的零度线与凸轮实体
一起放入凸轮装配的引用集,将滚子在凸轮曲线平面的
