大学物理_波的衍射和折射
大学物理实验 微波光学特性及布拉格衍射

极小
类别
Xi=i
Xi=i*i
yi=Xi+1
Yi^2=Xi+1^2
Xiyi
1
1
1
22.823
520.889
22.823
2
2
4
37.225
1385.700
74.45
3
3
9
53.685
2882.079
161.055
∑
6
14
113.733
4788.668
258.328
平均
2
4.67
37.911
1596.223
根据记录数据,画出单缝衍射强度与衍射角度的关系曲线。并根据微波衍射强度一级极小角度和缝宽 ,计算微波波长 和其百分误差(表中 、 是相对于0刻度两边对应角度的电压值)。
3.微波的双缝干涉
按需要调整双缝干涉板的缝宽。将双缝缝干射板安置在支座上时,应使双缝板平面与载物圆台上 指示线一致。转动小平台使固定臂的指针在小平台的 处。此时相当于微波从双缝干涉板法线方向入射。这时让活动臂置小平台 处,调整信号使液晶显示器显示较大,然后在 线的两侧,每改变1~3度读取一次液晶显示器的读数,并记录下来,然后就可以画出双缝干涉强度与角度的关系曲线。并根据微波衍射强度一级极大角度和缝宽 ,计算微波波长 和其百分误差。
由已知的晶格常数a和微波波长λ,估算出(100)面和(110)面衍射极大的入射角;调整发射喇叭和接收喇叭的天线正对,调节衰减器;
将模型固定在载物台上,晶面法线与刻度盘0°重合,发射臂指针的读数即为入射角,将接受臂转至0°另一侧同一度数,即得到入射角等于反射角。在理论峰值附近寻找电流最大的入射角。。
原始数据记录及分析:
《大学物理》课程标准

《普通物理》课程标准1. 课程基本信息课程代码:课程归口:电子信息工程技术专业适用专业:电子信息工程技术学时数:64学分:4先修课程:高等数学2. 课程性质与地位大学物理是高等院校非物理类理工科各专业学生一门重要的通识性必修基础课。
物理学是研究物质的基本结构、基本运动形式、相互作用的自然科学。
它的基本理论渗透在自然科学的各个领域,应用于生产技术的许多部门,是其他自然科学和工程技术的基础。
课程所教授的基本概念、基本理论和基本方法是构成学生科学素养的重要组成部分,是一个科学工作者和工程技术人员所必备的。
该课程在培养学生的探索精神和创新意识等方面,具有其他课程不能替代的重要作用。
3.课程的内容与要求第一部分力学.第1章质点运动学1.1质点运动的描述1.2加速度为恒矢量时的质点运动1.3圆周运动1.4相对运动基本要求:1.深入地理解质点、位移、速度和加速度等重要概念,深入理解质点的运动。
2.分析加速度为恒矢量时的质点运动方程。
3.明确圆周运动中角位移、角速度、切向加速度、法向加速度的关系。
重点与难点:1.加速度为恒矢量时质点运动方程的描写。
2.质点圆周运动的分析。
第2章动力学基本定律2.1牛顿定律2.2物理量的单位和量纲2.3几种常见的力2.4惯性参考系力学相对性原理2.5质点和质点系的动量定理2.6动量守恒定律2.7动能定理2.8保守力与非保守力势能2.9功能原理机械能守恒定律2.10完全弹性碰撞完全非弹性碰撞2.11能量守恒定律基本要求:1.清晰的理解牛顿第一定律、牛顿第二定律和牛顿第三定律。
2.熟练掌握几种常见力。
3.掌握物理量的单位和量纲。
4.理解惯性参考系和力学相对性原理,能列举出牛顿定律应用的例子。
5.掌握质点和质点系的动量定理。
6.熟练掌握动量守恒定律和动能定理。
7.掌握功能原理和机械能守恒定律。
8.清晰分辩出完全弹性碰撞和完全非弹性碰撞重点与难点:1.牛顿三定律的应用。
2.参考系的选择。
大学物理101光的衍射(1)
解 :(1) x0
2 f
a
4.0m m
(2) 单缝衍射明纹的角位置由a
sin
(2k
1)
2
确定,得:sin 2
5 ,
2a
x2
f
tan 2
f
sin 2
5
2a
f
5.0mm
(3) 由ain (2k 1) 知: 相应于第二级、三级衍射明纹, k分别为2、3,
2
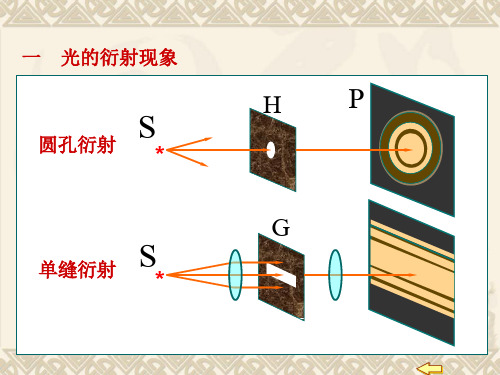
一 光的衍射现象
圆孔衍射
S
*
单缝衍射
S
*
HP
G
衍射 光在传播过程中绕过障碍物的边缘而偏离直线传 播的现象
说明
衍射现象是否明显取决于障碍物线度与波长的对 比,波长越大,障碍物越小,衍射越明显。
二 惠更斯 — 菲涅尔原理
n
S
rP *
S
t S : 时刻波阵面
S :波阵面上面元
(子波波源)
子波在 P点引起的振动振幅 s 并与 有关 .
当k=1时,λ=5000A0
当k=2时,λ=3000 A0
(3)中央明纹宽度为
x 2 f
a
5000 1010 2 1 0.5 103
在可见光范围内,入射光波长为λ=5000A0。 2 103 m
解:(1)对P点,由
(2)P点为第一级
tg x 1.5103 1.5103
f
1
明纹,k=1
sin 3 1.5103rad
2a
当θ很小, tgθ=sinθ=θ
半波带数为: 2k+1=3
由单缝衍射公式可知 2a sin 2atg 2k 1 2k
大连理工大学《大学物理-力学、振动与波动》课件-第5章

§5惠更斯原理波的衍射波的反射与折射一、惠更斯原理OS 1S 2u ∆tu ∆tS 1S 2在均匀的自由空间波传播时,任一波面上的每一点都可以看作发射子波的点波源,以后任意时刻,这些子波的包迹就是该时刻的波面。
——波沿直线传播t+∆t 时波面t 时波面t+∆t 时波面S1i 2三、波的反射与折射介质1MN反射波与入射波在同一介质中传播tu MD AN ∆==i容易算出i i '=(n 1)(n 2)A B C DMNi 1i1tu MD ∆1=tu AN ∆2=21u u AN MD =2sin i AD AN =1sin i AD MD =11u c n =22u c n =2211sin sin i n i n =介质2A B C D1122sin sin i u i u =21n =介质2相对于介质1的折射率折射波与入射波在不同介质中传播介质相对于空气的折射率声波—机械纵波一、声压媒质中有声波传播时的压力与无声波传播时的静压力之差纵波—疏密波稀疏区域:实际压力小于静压力,声压为负值稠密区域:实际压力大于静压力,声压为正值§7声波与声强级次声波可闻声超声波声压是仪器所测得的物理量定义声压:p = p -p 0对某声波媒质无声波——静压力p 0 、密度ρ0有声波——压力p 、密度ρ)(Hz ν2020000p+pV+∆V ∆V。
高二物理【波的反射、折射和衍射】

3.波的反射、折射和衍射学习目标:1.知道什么是波的反射、折射和衍射现象,知道发生明显衍射现象的条件.2.知道波发生反射现象时,反射角等于入射角.掌握入射角与折射角关系.3.了解波的衍射在生活中的应用,感受物理与生活之间的联系.一、波的反射1.反射现象波遇到介质界面会返回来继续传播的现象.2.反射角和入射角(1)入射角:入射波的波线与法线的夹角,如图中的α.(2)反射角:反射波的波线与法线的夹角,如图中的β.3.反射定律反射波线、法线、入射波线在同一平面内,且反射角等于入射角.注意:反射波与入射波的波长、频率、波速都相等,但由于反射面吸收一部分能量,反射波传播的能量将减少.二、波的折射1.波在传播过程中,从一种介质进入另一种介质时,波传播的方向发生偏折的现象叫作波的折射.2.一切波都会发生折射现象.三、波的衍射1.定义波可以绕过障碍物继续传播,这种现象叫作波的衍射.2.发生明显衍射现象的条件:只有缝、孔的宽度或障碍物的尺寸跟波长相差不多或者比波长更小时,才能观察到明显的衍射现象.3.一切波都能发生衍射,衍射是波特有的现象.1.思考判断(正确的打“√”,错误的打“×”)(1)入射波的波线与界面的夹角叫入射角.(×)(2)入射波的波长和反射波的波长相等.(√)(3)孔的尺寸比波长大得多时就不会发生衍射现象.(×)(4)衍射是波的特有现象.(√)2.(多选)下列说法正确的是()A.波发生反射时波的频率不变,波速变小,波长变短B.波发生反射时频率、波长、波速均不变C.波发生折射时的频率不变,但波长、波速发生变化D.波发生折射时波的频率、波长、波速均发生变化BC[波发生反射时因介质未变,故频率、波长、波速均不变;波发生折射时因波源不变而介质变,故频率不变,波长和波速均发生变化.B、C两项正确.] 3.(多选)一列波在传播过程中通过一个障碍物,发生了一定程度的衍射,以下哪种情况可以使衍射现象更明显()A.增大障碍物的尺寸B.减小波的频率C.缩小障碍物的尺寸D.增大波的频率BC[波在介质中传播时波速是由介质决定的,与波的频率无关,所以改变波的频率不会改变波速,但由v=λf可知,当波速一定时,减小频率则波长增大.而发生明显衍射的条件是障碍物或孔、缝的尺寸比波长小或相差不多,要使衍射现象变得明显,可以通过缩小障碍物的尺寸,同时增大波长即减小波的频率来实现,BC选项正确.]波的反射和折射(a)(b)如图(a)在水槽中,点波源所发出的圆形水波遇直线界面反射后的波形仍为同心圆形.图(b)为圆形波反射的示意图.请举例说明生活中波的反射现象.提示:①回声是声波的反射现象,原因是:对着山崖或高墙说话,声波传到山崖或高墙时,会被反射回来继续传播.②夏日的雷声轰鸣不绝,原因是:声波在云层界面多次反射.③在空房间里讲话声音更响亮,原因是:声波在房间里遇到墙壁、地面或天花板发生反射时,由于距离近,原声与回声几乎同时到达人耳.人耳只能区分相差0.1 s以上的声音,所以人在房间里讲话感觉声音比在空旷处大.如果房间里有幔帐、地毯、衣物等,它们会吸收声波,从而使声音减弱.理量也会相应发生变化,比较如下:波的反射波的折射传播方向改变,θ反=θ入改变,θ折≠θ入频率f 不变不变波速v不变改变波长λ不变改变名师点睛:(1)频率(f)由波源决定:故无论是反射波还是折射波都与入射波的频率相等,即波源的振动频率相同.(2)波速(v)由介质决定:故反射波与入射波在同一介质中传播,波速不变,折射波与入射波在不同介质中传播,波速变化.(3)据v=λf知,波长λ与波速和频率有关.反射波与入射波,频率同、波速同,故波长相同,折射波与入射波在不同介质中传播,频率同,波速不同,故波长不同.【例1】甲、乙两人站在一堵墙前面,两人相距2a,距墙均为3a.当甲开了一枪后,乙在t时间后听到第一声枪响,则乙在什么时候能听到第二声枪响()A.听不到B.甲开枪后3t时间C.甲开枪后2t时间D.甲开枪后3+72t时间思路点拨:根据反射定律画出声波传播的示意图,再用速度公式求时间.C[乙听到的第一声枪响必然是甲开枪的声音直接传到乙的耳中,故t=2a v.甲、乙二人及墙的位置如图所示,乙听到的第二声枪响必然是经墙反射传来的枪声,由反射定律可知,波线如图中AC和CB,由几何关系可得AC=CB=2a,故第二声枪响传到乙耳中的时间为t′=AC+CBv=4a v=2t.]波的反射应用技巧——回声测距利用回声测距是波的反射的一个重要应用,它的特点是声源正对障碍物,声源发出的声波与回声在同一条直线上传播.(1)若是一般情况下的反射,反射波和入射波是遵从反射定律的,可用反射定律作图后再求解.(2)利用回声测距时,要特别注意声源是否运动,若声源运动,声源发出的原声至障碍物再返回至声源的这段时间与声源的运动时间相同.(3)解决波的反射问题,关键是根据物理情景规范作出几何图形,然后利用几何知识结合物理规律进行解题.[跟进训练]1.某物体发出的声音在空气中的波长为1 m,波速为340 m/s,在海水中的波长为4.5 m.(1)该波的频率为________Hz,在海水中的波速为________ m/s.(2)若物体在海面上发出的声音经过0.5 s听到回声,则海水深为多少?(3)若物体以5 m/s的速度由海面向海底运动,则经过多长时间听到回声?[解析](1)由f=vλ得f=3401Hz=340 Hz,因波的频率不变,则在海水中的波速为v海=λ′f=4.5×340 m/s=1 530 m/s.(2)入射声波和反射声波用时相同,则海水深为h=v海t2=1 530×0.52m=382.5 m.(3)物体与声音运动的过程示意图如图所示,设听到回声的时间为t′,则v物t′+v海t′=2h代入数据解得t′=0.498 s.[答案](1)340 1 530(2)382.5 m(3)0.498 s波的衍射声波能绕过障碍物到达后面,衍射声波有什么特点?水波能到达挡板的后面,衍射水波有什么特点?提示:衍射波与原波具有相同的频率,传播过程中波形没变.(1)水波遇到障碍物的情况当障碍物较小时发现波绕过障碍物继续前进,如同障碍物不存在一样.如图甲所示,衍射现象明显.甲乙(2)水波遇到小孔的情况当孔较小时发现孔后的整个区域里传播着以孔为中心的圆形波.如图乙所示,衍射现象明显.(3)产生明显衍射的条件产生明显衍射现象,必须具备一定的条件:障碍物或孔的尺寸比波长小,或者跟波长相差不多.名师点睛:障碍物或孔的尺寸大小并不是决定衍射能否发生的条件,仅是衍射现象是否明显的条件,一般情况下,波长较大的波容易发生明显衍射现象.2.波的衍射现象分析波传到小孔(或障碍物)时,小孔(或障碍物)仿佛是一个新的波源,由它发出与原来同频率的波(称为子波),在孔后传播,于是就出现了偏离直线传播的衍射现象.波的直线传播是衍射不明显时的近似情形.【例2】(多选)如图所示是观察水面波衍射的实验装置,AC和BD是两块挡板,AB是一个孔,O是波源,图中已画出波源所在区域波的传播情况,每两条相邻波纹(图中曲线)之间距离表示一个波长,则对于波经过孔之后的传播情况,下列描述正确的是()A.此时能明显观察到波的衍射现象B.挡板前后波纹间距离相等C.如果将孔AB扩大,有可能观察不到明显的衍射现象D.如果孔的大小不变,使波源频率增大,能更明显地观察到衍射现象ABC[从题图中可以看出,孔的大小与波长相差不多,故能够发生明显的衍射现象,选项A正确;由于在同一均匀介质中,波的传播速度没有变化,又因为波的频率是一定的,又根据λ=v可得波长λ没有变化,选项B正确;当将f孔扩大后,孔的宽度和波长有可能不满足发生明显衍射的条件,选项C正确;如果孔的大小不变,使波源频率增大,则波长减小,孔的宽度将比波长大,孔的宽度和波长有可能不满足发生明显衍射现象的条件,选项D错误.]衍射现象的两点提醒(1)障碍物的尺寸的大小不是发生衍射的条件,而是发生明显衍射的条件,波长越大越易发生明显衍射现象.(2)当孔的尺寸远小于波长时,尽管衍射十分突出,但衍射波的能量很弱,也很难观察到波的衍射.[跟进训练]2.(多选)如图所示,S为在水面上振动的波源,M、N为水面上的两块挡板,其中N板可以移动,两板中间有一狭缝,此时测得A处水没有振动.为使A处水也能发生振动,可采用的方法是()A.使波源的频率增大B.使波源的频率减小C.移动N使狭缝的距离增大D.移动N使狭缝的距离减小BD[要使A处水发生振动,应使波的衍射现象更明显,而波能发生明显衍射的条件是狭缝的宽度跟波长相差不多或者比波长更小.因此可将狭缝变小,或将波长变大,而减小波源的频率可以使波长变大,故B、D正确.]1.下列现象或事实属于衍射现象的是()A.风从窗户吹进来B.雪堆积在背风的屋后C.水波前进方向上遇到凸出在水面上的小石块,小石块对波的传播没有影响D.晚上看到水中月亮的倒影C[波可以绕过障碍物继续传播的现象称为波的衍射.C与衍射现象相符.] 2.如图所示是利用发波水槽观察到的水波衍射图像,从图像可知()A.B侧波是衍射波B.A侧波速与B侧波速相等C.减小挡板间距离,衍射波的波长将减小D.增大挡板间距离,衍射现象将更明显B[小孔相当于衍射波的波源,A侧波是衍射波,A错误;在同一种介质中,波速相等,故B正确;根据波速、波长和频率的关系式v=λf,由于波速和频率不变,故波长不变,故C错误;在波长无法改变的情况下减小挡板间距会使衍射现象更明显,故D错误.]3.图中1、2、3分别代表入射波、反射波、折射波的波线,则()A.2与1的波长、频率相等,波速不等B.2与1的波速、频率相等,波长不等C.3与1的波速、频率、波长均相等D.3与1的频率相等,波速、波长均不等D[波发生反射时,在同一种介质中运动,因此波长、波速和频率不变,故选项A、B错误;波发生折射时,频率不变,波速变,波长变,故选项C错误,选项D正确.]4.(多选)关于波的反射,下列说法正确的是()A.波在反射前后,仍在同种介质中传播B.波发生反射时,波的频率不变,波速变小,波长变短C.波发生反射时,波的频率、波长、波速均不变D.波发生反射时,反射角始终等于入射角ACD[波的反射是波在介质界面上反射回同一种介质中继续传播的现象;由于传播介质不变,所以波速、频率、波长均不变.由反射定律知,反射角等于入射角.故A、C、D正确.]。
大学物理惠更斯原理波的衍射

6.5 波的干涉
6.5.1 波的叠加原理 1. 波传播的独立性原理
几列波在空间某点相遇后,每一列波都能独立地 保持自己的原有特性(频率、波长、振动方向等) 传播,就像在各自路程中,并没有遇到其它波一样.
例如: 管弦乐队合奏;
几个人同时讲话;
天空中多个无线电波.
2. 波的叠加原理
几列波在某点相遇时,该处质点的振动为各列波 单独在该点引起的振动的合振动.
水
波
通
波
过
的
狭
衍
缝
射
后
的
衍
射
讨论
1. 波的衍射现象是否明显,取决于障碍物的线度与波长的关系
小孔的直径远小于 波长时的衍射现象
小孔的直径大于 波长时的衍射现象
2. 室温下,声速为340m/s,频率20-20000Hz,波长范围:
u 0.017 ~ 17m
与障碍物尺度相当,所以声波的衍射现象较显著.
相遇前
相遇时
相遇后
6.5.2 波的干涉条件和公式
频率相同、振动 方向平行、相位 相同或相位差恒 定的两列波相遇 时,某些地方振 动始终加强,另 一些地方振动始 终减弱的现象, 称波的干涉现象.
波的相干条件:
(1) 频率相同;
S1
(2) 振动方向平行;
(3) 相位相同或相位差恒定. S2
r1
*P
r2
当(2 1) 2k 时
A = A1+ A2 —合振幅最大,同相
当(2 1) (2k 1) 时 A = |A1A2 | —合振幅最小,反相
波函数的求解:
上次课内容小结
1. 先求出某点O的振动方程: yO Acos(t )
由初始条件求振幅和初相位:
(完整word)大学物理教案 光的干涉、衍射与偏振
教学目标 掌握惠更斯-菲涅耳原理;波的干涉、衍射和偏振的特性,了解光弹性效应、电光效应和磁光效应。
掌握相位差、光程差的计算,会使用半波带法、矢量法等方法计算薄膜干涉、双缝干涉、圆孔干涉、光栅衍射。
掌握光的偏振特性、马吕斯定律和布儒斯特定律,知道起偏、检偏和各种偏振光。
教学难点 各种干涉和衍射的物理量的计算。
第十三章 光的干涉一、光线、光波、光子在历史上,光学先后被看成“光线"、“光波”和“光子”,它们各自满足一定的规律或方程,比如光线的传输满足费马原理,传统光学仪器都是根据光线光学的理论设计的。
当光学系统所包含的所有元件尺寸远大于光波长时(p k =),光的波动性就难以显现,在这种情况下,光可以看成“光线”,称为光线光学,。
光线传输的定律可以用几何学的语言表述,故光线光学又称为几何光学。
光波的传输满足麦克斯韦方程组,光子则满足量子力学的有关原理。
让电磁波的波长趋于零,波动光学就转化为光线光学,把电磁波量子化,波动光学就转化为量子光学。
二、费马原理光线将沿着两点之间的光程为极值的路线传播,即(,,)0QPn x y z ds δ=⎰三、光的干涉光矢量(电场强度矢量E )满足干涉条件的,称为干涉光。
类似于机械波的干涉,光的干涉满足:222010*********cos()r r E E E E E ϕϕ=++-1020212cos()r r E E ϕϕ-称为干涉项,光强与光矢量振幅的平方成正比,所以上式可改写为:12I I I =++(1—1)与机械波一样,只有相干电磁波的叠加才有简单、稳定的结果,对非干涉光有:1221,cos()0r r I I I ϕϕ=+-=四、相干光的研究方法(一)、光程差法两列或多列相干波相遇,在干涉处叠加波的强度由在此相遇的各个相干波的相位和场强决定。
能够产生干涉现象的最大波程差称为相干长度(coherence length )。
设光在真空中和在介质中的速度和波长分别为,c λ和,n v λ,则,n c v νλνλ==,两式相除得n vcλλ=,定义介质的折射率为: c n v=得 n nλλ=可见,一定频率的光在折射率为n 的介质中传播时波长变短,为真空中波长的1n倍.光程定义为光波在前进的几何路程d 与光在其中传播的介质折射率n 的乘积nd .则光程差为(1)nd d n d δ=-=-由光程差容易计算两列波的相位差为21212r r δϕϕϕϕϕπλ∆=-=-- (1—2)1ϕ和2ϕ是两个相干光源发出的光的初相。
(大学物理ppt)光的衍射
0
Δx
(b)当k=3时,光程差 a sin ( 2k 1 ) 7 2 2 狭缝处波阵面可分成7个半波带。
I / I0
相对光强曲线
1
明纹宽度 中央明条纹的角宽 为中央两侧第一暗条 纹之间的区域:
0.017 0.047 0 0.047
0.017
sin
-2(/a) -(/a)
/a
2(/a)
由a sin k
令k=1 半角宽
a
a
衍射屏 透镜
λ
观测屏 x2 x1 Δx Δx
Huygens-Fresnel’s principle
(1) 惠更斯原理:在波的传播过程中,波阵面(波面)(相位 相同的点构成的面)上的每一点都可看作是发射子波(次波)的 波源,在其后的任一时刻,这些子波的包迹就成为新的波阵面。
t 时刻波面
· · · · ·
t+t时刻波面
波传播方向
t + t
· ·· · · · · t · · · ·· · ·
一、衍射现象、惠更斯-菲涅耳原理 圆孔衍射
菲涅尔圆孔衍射
一、衍射现象、惠更斯-菲涅耳原理 各种孔径的夫琅禾费衍射图样 正三 边形 孔 正四 边形 孔
正六 边形 孔
正八 边形 孔
一、衍射现象、惠更斯-菲涅耳原理 圆屏衍射 R S 直边衍射 rk
P
菲涅尔圆屏衍射
直边衍射
2、惠更斯—菲涅耳原理
第 4 章 光的衍射
一、衍射现象、惠更斯-菲涅耳原理
二、单缝的夫琅禾费衍射
三、光学仪器的分辨本领
四、光栅衍射
五、光栅光谱
六、X 射线衍射
大学物理 第十二章 波动光学2
2 又,明纹所在处x满足: x tg 1.5 0.003 , f 500
2 0.5 1.5 3 104 2ax / f 107 m A λ (2k 1) 500 2k 1 2k 1
白光波长范围4000—7000Å,满足上式的波长值即为所求:
• • • •
例题:已知单缝宽a=0.5mm,透镜焦距f=50cm,今以白光垂直照 射狭缝,在观察屏上x=1.5mm处看到明纹极大,求: (1)入射光的波长及衍射级数; (2)单缝所在处的波阵面被分成的波带数目。
[解]: (1)由明纹条件: a sin (2k 1)
x 很小 。 sin ≈ tg f
sin
中央极大值对应的明条纹称 中央明纹。 中央极大值两侧的其他明条纹称次极大。
2、明暗纹中心位置坐标
(1)中央明纹中心位置 x=0
xk t g k f
tgk sin k
x xk
k
中 O 央 明 纹
k2
k 1
(1)
(2)
f
(2)暗纹中心位置坐标
由 a sin k k 及式(1)、(2) 得
二、光学仪器的分辨本领
1.22 1 D
D
瑞 利 判 据
定义
分辨本领
D R 1.22
1
刚可分辨
非相干叠加
不可分辨
瑞利判据 : 对于两个等光强的非相
干物点,若其中一点的象斑中心恰好落 在另一点的象斑的边缘(第一暗纹处), 则此两物点被认为是刚刚可以分辨。
当 再 , =3/2时,可将缝分成三个“半波带”,
B a A θ a B θ
大学物理课件光学
超快激光技术及应用领域
超快激光技术的发展历程
从纳秒到飞秒,再到阿秒的超快激光脉冲的产生和应用。
超快激光技术的应用领域
包括超快光谱学、超快化学动力学、超快生物医学成像等。
超快激光技术的挑战与前景
如提高脉冲能量、压缩脉冲宽度、拓展应用领域等。
纳米光子学及前景展望
纳米光子学的基本概念
偏振光
光振动在某一特定方向的光,在垂直于传播方向的平面 上,只沿某个特定方向振动。
马吕斯定律和布儒斯特角
马吕斯定律
描述线偏振光通过检偏器后透射光强与检偏器透振方向夹角的关系,即透射光强与夹角的余弦值的平方成正比。
布儒斯特角
当自然光在两种各向同性媒质分界面上反射、折射时,反射光和折射光都是部分偏振光。反射光中垂直振动多于 平行振动,折射光中平行振动多于垂直振动。当入射角满足某种条件时,反射光中垂直振动的光完全消失,只剩 下平行振动的光,这种光是线偏振光,而此时的入射角叫做布儒斯特角。
03 光的折射定律
光从一种介质斜射入另一种介质时,传播方向发 生改变,折射光线和入射光线分别位于法线的两 侧,且折射角与入射角满足一定的关系。
波动光学基础
光的干涉现象
当两束或多束相干光波在空间某 一点叠加时,其振幅相加而产生 的光强分布现象。干涉现象表明
了光具有波动性。
光的衍射现象
光在传播过程中遇到障碍物或小孔 时,会偏离直线传播路径而绕到障 碍物后面继续传播的现象。衍射现 象也是光波动性的表现。
衍射法测波长实验原理及操作过程
实验原理
当单色光通过单缝或小孔时, 会发生衍射现象,形成明暗相 间的衍射条纹。通过测量衍射 角或衍射条纹间距,可以计算 出单色光的波长。
