Ch4习题课
烷烃习题及答案剖析

甲烷烷烃1.复习重点1.甲烷的结构、化学性质;2.烷烃的定义、命名、同系物、同分异构体及典型的取代反应。
2.难点聚焦1.有机物:含碳.化合物叫做有机化合物...,简称有机物。
(除CO、CO2、碳酸盐、碳化物、硫氰化物、氰化物等外)它们虽然含碳,但性质和组成与无机物很相近,所以把它们看作为无机物。
也就是说,有机物一定含碳元素,但含碳元素的物质不一定是有机物。
而且有机物都是化合物,没有单质。
那么究竟哪些物质是有机物,哪些物质是无机物,有什么判断依据呢?我们可以通过有机物与无机物的主要区别加以判断。
2.有机物与无机物的主要区别性质和反应有机物无机物溶解性多数不溶于水,易溶于有机溶剂,如油脂溶于汽油,煤油溶于苯。
多数溶于水,而不溶于有机溶剂,如食盐、明矾溶于水。
耐热性多数不耐热;熔点较低,(400°C以下)。
如淀粉、蔗糖、蛋白质、脂肪受热分解;C20H42熔点36.4°C,尿素132°C。
多数耐热难熔化;熔点一般很高。
如食盐、明矾、氧化铜加热难熔,NaCl熔点801°C。
可燃性多数可以燃烧,如棉花、汽油、天然气都可以燃烧。
多数不可以燃烧,如CaCO3、MnCl2不可以燃烧。
电离性多数是非电解质,如酒精、乙醚、苯都是非电解质、溶液不电离、不导电。
多数是电解质,如盐酸、氢氧化钠、氯化镁的水溶液是强电解质。
化学反应一般复杂,副反应多,较慢,如生成乙酸乙酯的酯化反应在常温下要16年才达到平衡。
石油的形成更久一般简单,副反应少,反应快,如氯化钠和硝酸银反应瞬间完成。
3.有机物的组成C、H、O、N、S、P、卤素等元素。
构成有机物的元素只有少数几种,但有机物的种类确达三千多种?几种元素能构几千万种有机物质?(学生自学后概括)有机物种类之所以繁多主要有以下几个原因:①碳原子最外电子层上有4个电子,可形成4个共价键;②有机化合物中,碳原子不仅可以与其他原子成键,而且碳碳原子之间也可以成键;③碳与碳原子之间结合方式多种多样,可形成单键、双键或叁键,可以形成链状化合物,也可形成环状化合物;(结构图5—1)④相同组成的分子,结构可能多种多样。
电解池习题课课后作业
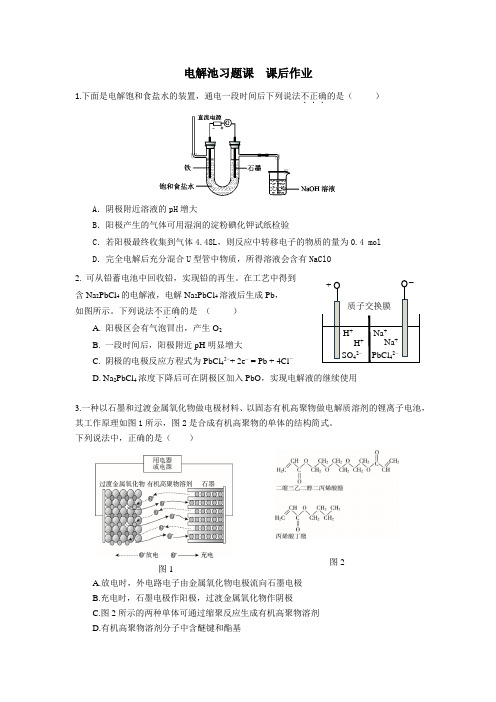
图2电解池习题课 课后作业1.下面是电解饱和食盐水的装置,通电一段时间后下列说法不正确...的是( )A .阴极附近溶液的pH 增大B .阳极产生的气体可用湿润的淀粉碘化钾试纸检验C .若阳极最终收集到气体4.48L ,则反应中转移电子的物质的量为0.4 molD .完全电解后充分混合U 型管中物质,所得溶液会含有NaClO 2. 可从铅蓄电池中回收铅,实现铅的再生。
在工艺中得到 含Na 2PbCl 4的电解液,电解Na 2PbCl 4溶液后生成Pb , 如图所示。
下列说法不正确...的是 ( ) A. 阳极区会有气泡冒出,产生O 2B. 一段时间后,阳极附近pH 明显增大C. 阴极的电极反应方程式为PbCl 42−+ 2e − = Pb + 4Cl -D. Na 2PbCl 4浓度下降后可在阴极区加入PbO ,实现电解液的继续使用3.一种以石墨和过渡金属氧化物做电极材料、以固态有机高聚物做电解质溶剂的锂离子电池,其工作原理如图1所示,图2是合成有机高聚物的单体的结构简式。
下列说法中,正确的是( )图1A.放电时,外电路电子由金属氧化物电极流向石墨电极B.充电时,石墨电极作阳极,过渡金属氧化物作阴极C.图2所示的两种单体可通过缩聚反应生成有机高聚物溶剂D.有机高聚物溶剂分子中含醚键和酯基质子交换膜 +−H + H +Na +Na + PbCl 42−SO 42−4.钠-氯化镍电池以β-Al2O3(Al2O3•x Na2O)作为固体电解质构成的一种新型电池Ni+2NaCl ), 其结构如图所示。
(2Na+NiCl2下列关于该电池的叙述错误..的是()A. 放电时NaCl在熔融电解质中生成B. 充电时阴极反应: Na+ + e- = NaC. 氯离子通过β-Al2O3(s)在两电极间移动D. 如果电池过度放电, AlCl4-可能被还原5.探究电场作用下阴阳离子的迁移。
a、b、c、d均为石墨电极,电极间距4 cm。
基础有机化学第四版上册课后练习题含答案

基础有机化学第四版上册课后练习题含答案1. 简介基础有机化学第四版上册是有机化学的入门教材,适用于大学本科有机化学及相关专业课程。
本文档提供了基础有机化学第四版上册课后练习题及答案,供学生自学、互相交流等使用。
2. 内容基础有机化学第四版上册共包含20个章节,每章都有大量习题。
本文档包含了每章的几道典型的习题和各章习题答案。
第一章有机化学概论1.1 习题1.请定义有机化学,并列举有机物的一些普遍属性。
2.请列举一些有机物与无机物的区别。
3.对于下列分子,请回答它们是无机物还是有机物:–H2O–CO2–NH3–CH4–C2H5OH1.2 答案1.有机化学是研究碳元素的化学性质和有机物的结构、性质及其反应的学科。
有机物普遍具有不稳定性、易燃性、易溶于有机溶剂、难溶于水等一些特征。
2.有机物通常是碳氢化合物,而无机物则可以是任何其他化合物,如氧化物、氧化酸、金属等。
有机物通常具有复杂结构和多样性,而无机物则具有相对较简单的结构。
–无机物–无机物–无机物–有机物–有机物第二章烷烃2.1 习题1.请回答甲烷和乙烷分别的分子式、结构式和物理状态。
2.请列举正构烷和支链烷的区别。
3.请解释链取代和环取代有区别的原因。
2.2 答案–甲烷:CH4,结构式为:H-C-H,为气体状态。
–乙烷:C2H6,结构式为:H3C-CH3,为气体状态。
1.正构烷是指所有碳原子都是直线排列的链烷,而支链烷则是一条或多条分枝链加到主链上的烷的总称。
正构烷和支链烷的物理性质有所区别,如沸点、密度等。
2.环取代和链取代不同之处在于环取代的化合物具有固定的数目和位置的取代基,而链取代化合物的取代基数目和位置可以不同。
此外,链取代的化合物可以旋转其C-C单键,而环取代的化合物不能旋转,因此,它们的空间构型也不同。
3. 结论基础有机化学是化学专业学生必修的一门课程,也是接下来有机合成和生物化学等教学内容的基础。
习题练习对于巩固和理解知识非常重要,本文档提供的基础有机化学第四版上册课后习题及答案也将对学生的学习有所帮助。
Ch4计算机网络习题课_V

Ch4习题课任兴田renxt@北京工业大学计算机学院Ch4 介质访问控制子层⏹2.N个站共享一个56kbps的纯ALOHA信道。
每个站平均每100秒输出一个1000位的帧,即使前面的帧还没有被送出去,它也这样进行(比如这些站可以将送出的帧缓存起来)。
请问N的最大值是多少?⏹对于纯ALOHA,可用的带宽是0.184*56kb/s=10.304kb/s每个站需要的带宽是1000/100=10b/s∴ N=10304/10≈1030Ch4 介质访问控制子层⏹*15.一个1km长、10Mbps的CSMA/CD LAN(不是802.3),其传播速度为200m/μs。
在这个系统中不允许使用中继器。
数据帧的长度为256位,其中包括32位的头部、校验和以及其他的开销。
在一次成功的传输之后,第一个位时槽将被预留给接收方,以便他抓住信道并发送一个32位的确认帧。
假设没有冲突,请问除去开销之后的有效数据率是多少?⏹电缆的往返传输时延为1000/200*2=10(μs)。
一个完整的传输有6个过程:发送方“抓住”电缆(10μs) (见P.208)发送数据帧(25.6μs)传输时延(5μs)接收方“抓住”电缆(10μs)发送确认帧(3.2μs)传输时延(5μs)6阶段的时间总和是58.8μs,在这期间共发送224个数据位。
所以,有效数据速率为224/58.8=3.8MbpsCh4 介质访问控制子层⏹17.一个通过以太网传送的IP分组有60字节长,其中包括所有的头部。
如果没有使用LLC的话,则以太网帧中需要填补字节吗?如果需要的话,请问需要填补多少字节?⏹最小以太帧有64字节长,包括帧头部的目的地址、源地址、类型/长度和校验和。
由于头部占18字节长,IP分组占60字节长,总的帧长度是78字节,这超过了64字节的最小帧长。
因此,不需要填充。
Ch4 介质访问控制子层⏹18.以太网帧必需至少64字节长,这样做的理由是,当电缆的另一端发生冲突的时候,传送方仍然还在发送过程中。
工程流体力学ch4-不可压缩流体的有旋流动和二维无旋流动
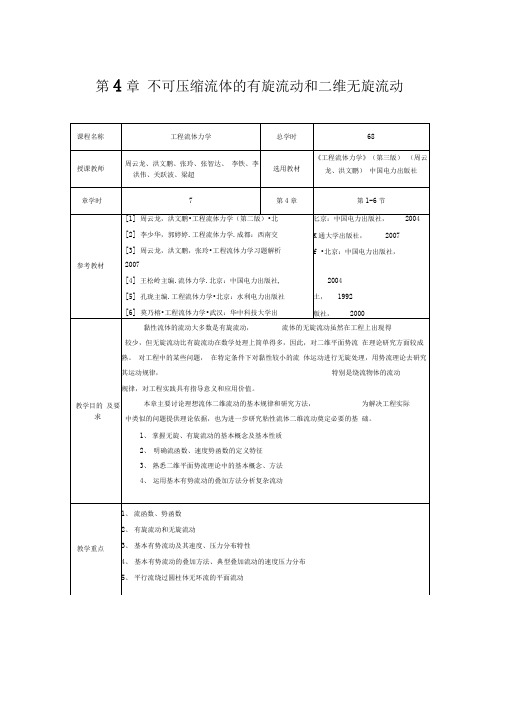
第4章不可压缩流体的有旋流动和二维无旋流动主要教学内容4.1流体微团运动分析本节教学目的:1、熟悉:流体微团的运动可以分解为移动、转动和变形运动三部分。
2、掌握:移动、转动和变形的速度表达式。
线速度V x 、V y 、V 角速度3 x 、3 y 、3 线变形、角变形知识点移动、转动和变形一、流体微团运动的分解1、平移运动如图5-2 (a )所示,平移表现为 A 点到A 点的位移,即x 方向和y 方向分别移动了 udt 、 vdt 距离,形状不变。
流体微团的平移速度为u,v,w2、线变形运动图5-2(b )表示流体微团的平面线变形。
定义单位时间内单位长度流体线段的伸长 (或缩短)量为流体微团的线变形速率。
三个方向的线变形速率分别用;xx 、 ;yy 、 ;zz 表示,则3、角变形运动图5-2(c )表示流体微团的角变形运动。
角变形速度:两正交微元流体边的夹角在单位时间内的变化量。
剪切变形速率:该夹角变化的平均值在单位时间内的变化量(角变形速度的平均值)。
过流体微团任一点 A 的三个正交微元流体面上的剪切变形速率分别为移动(move ) 转动(rotation ) 变形(reform )4、旋转运动如图5-2(d)所示。
流体微团在发生角变形的同时,还要发生旋转运动。
若d 「= d 「,则流体微团只发生角变形;若d -. =- d ‘j|,即卩::v :x = __:u.「y ,则流体微团只发生旋转,不发生角变形旋转角速度:过流体微团上 A 点的任两条正交微元流体边在其所在平面内旋转角速度 的平均值,称作 A点流体微团的旋转角速度在垂直该平面方向的分量。
用符号••表示写成矢量形式为(a) (b)i-xyL yz;yx1 ;:u :W =—I 1 T82 :-x ry1 2。
V)图5-2 流体微团平面运动的分解、表示流体微团运动特征的速度表达式 在一般情况下,流体微团的运动总是可以分解成:平移运动、旋 转运动、线变形运动及角变形运动, 与此相对应的是平移速度、旋转角速度、线变形速率和剪切变形速率。
习题课教案

习题课教案教学目标:1、通过知识的复习,使学生巩固基础知识并牢固掌握;2、引导学生分析习题,培养学生分析问题及解决问题的能力。
教学过程:一、物质分类:氧化物酸:H酸根碱: 金属离子OH_盐: 金属离子酸根离子思路:先写化学式分析:煤气:包括氢气、一氧化碳、甲烷等气体,所以是混合物。
酒精:化学式为C2H5OH,属于纯净物。
(引申:医用酒精是75%的酒精和25%的水混合而成的溶液,所以是混合物。
)二、燃烧现象的描述1、可燃物在空气、氧气中燃烧时的不同现象碳在空气中发红光、氧气中发白光、无火焰复习H2 CH4CO燃烧的火焰颜色2、烟和雾的区别烟:固体小颗粒。
如:红磷燃烧冒白烟,因为是白色固体。
雾:小液滴。
如:打开浓盐酸的瓶盖,瓶口会冒白雾,是因为从浓盐酸中挥发出来的气体与空气中的水蒸气结合形成盐酸小夜滴.三、变质和检验1、氢氧化钠固体暴露在空气中一段时间后,它会变质吗?为什么?有关化学方程式2、如何检验氢氧化钠已部分变质?分析:NaOH→Na2CO3,检验出有Na2CO3 存在,就可证明NaOH变质。
提出方案:仅用酚酞试液就可检验NaOH是否部分变质,行吗?为什么?学生讨论后得出结论:由于NaOH溶液和Na2CO3 溶液都呈碱性,都能使酚酞变红,所以不可行。
学生讨论:实验方案(包括操作、现象及结论)教师总结实验方案:①酸:稀盐酸或稀硫酸冒气泡②碱溶液:Ca(OH)2或Ba(OH)2 产生白色沉淀③盐溶液:CaCl2或BaCl2 产生白色沉淀四、水的妙用水是人类所需的六大营养素之一,且水是最常用的溶剂。
除此之外,水还有哪些妙用呢?1、除杂(原理:一种固体能溶于水,另一种固体不能溶于水)如:除去CaCO3中有少量NaCl,用试剂分析:CaCO3不能溶于水,NaCl能溶于水,加水充分溶解然后过滤,便可得到CaCO3。
2、鉴别(A、根据物质的溶解性不同B、形成溶液的颜色不同C、根据物质溶于水伴随的热量变化不同)。
分子的对称性习题课

Cl
H
CC
H
Cl
NH3
1,2 -二氯乙烯(反式) 无偶极矩—— 有对称中心,
3个σ交于C3,
有偶极矩,在C3上——
Cl
NH 3
Td C2v
C2h C3v
H3N Pt NH3 H3N Pt Cl
—— D2h
Cl
(无)
Cl
(有)
—— C2v
5、分子的旋光性 旋光性的对称性判据:
凡无对称中心 i ,对称面 和 S4n 轴的分子才可有旋 光性。
立方体群
轴向 群
Td CH4,CCl4等具有正四面体结构的分子
Oh SX6,[Fe(CN)6] 2+ 等具有正八面体结构
Cnv
C2V
H2O
C3V
NH
C4V
3F5C
Cnh
C2h (E)-1,2l-二氯乙烯
二面体群
Dn
Dnh
Dnd
比较少见
D2h
H2C=CH2
D3h
BF3等具有平面正三角形的分子
D4h
[Ni(CN)4]2- 等具有平面正方形的分子
(2) PF5 (5) XeF4
(3) CCl4 (6) PH3
一、判断题
1、凡直线分子一定具有C∞轴。 √
2、甲烷分子有对称中心。
3、分子点群是全部对称操作的集合。 √
4、非极性分子的判据之一是两个对称元素相交。
5、对称性判据不仅能告诉我们分子是否有极性,还能告诉我们偶极矩的
大小和方向。
6、镜面d一定也是镜面v 。 √ 7、如构成分子的各类原子均是成双出现的,则此分子必有对称中心 。
8、凡是四面体构型的分子一定属于 Td点群。
甲烷烷烃习题课

5、CH3CH(CH3)CH2CH3
、
C(CH3)4
练习1、下列哪些物质是属于同一物质?
(A)
(C)
(E)
(G)
C-C- C-C C ∣ C-C- C C ∣ C-C ∣ C C-C ∣ C- C
(B)
(D)
C ∣ C-C -C C C ∣ ∣ C- C
(F)
(H)
C - C- C ∣ C C- C ∣ ∣ C C
<甲烷烷烃>习题课
1.烃类的燃烧 2.烷烃的取代反应 3.同系物同分异构体的判断
1.烃类的燃烧
1.请写出烃类完全燃烧的通式。 2.请写出丙烷和辛烷分别燃烧的 化学方程式
标准状况下将35ml气态烷烃完全 燃烧,恢复到原来状况下,得到 140ml二氧化碳气体,则该烃的 分子式为( ) A、C5H12 B、C4H10 C、 C3 H6 D 、 C3 H8
原子
单质 化合物
化合物
例1、下列物质属于同位素的是: 属于同素异形体的是: 属于同系物的是: 属于同分异构体的是: ①O2和O3 ②CH3CH3和CH3CH2CH2CH3 37 35 ③ 17 和 Cl 17 Cl ④金刚石和石墨 ⑤氕、氘和氚 ⑥CH3CH2CH2CH(CH3)CH(CH3)CH3和 CH3CH2CH(CH3)CH2CH(CH3)CH3
把体积相同的甲烷和氯气充入一个集气瓶中,光 照一段时间后,发现气体的黄绿色变浅,集气瓶 壁上有淡黄绿色液滴,此时,集气瓶内的物质最 多可能有 ( ) A.四种 B.五种 C.六种 D.七种
已知甲烷分子中的氢原子可被其它原子 或原子团代替,如甲烷分子中的氢原子 被氯原子取代可得到四种物质:CH3Cl、 CH2Cl2、CHCl3、CCl4,这四种产物的 结构能充分说明甲烷分子是以碳原子为 中心的正四面体结构,而不是正方形平 面结构的是 ( ) A.CH3Cl只有一种结构 B.CH2Cl2只有一种结构 C.CHCl3只有一:烷烃分子中处于相同位置 上的氢原子称为等效氢。 同一个碳原子上的氢是等效氢 同一个碳原子上的甲基中的氢是等 效氢 处于分子中对称位置的碳上的氢原 子是等效氢
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2t 2 1 =∫ d t = 2 ∫ (1 − )dt 2 2 1+ t 1+ t = 2t − 2 arctan t + C = 2 [ 1 + sin x − arctan 1 + sin x ] + C
2 2
(1 + x 2 ) 1 − x 2 解: 令 x = sin t , 1 + x 2 = 1 + sin 2 t , d x = cos td t cos t 1 d t= ∫ dt 原式 = ∫ 2 2 (1 + sin t ) cos t 1 + sin t cos 2 t 分子分母同除以 sec 2 t 1 dt = ∫ =∫ 2 dtan t 2 2 sec t + tan t 1 + 2 tan t 1 1 = ∫ 1 + ( 2 tan t ) 2 d 2 tan t 2 2x 1 1 +C arctan = arctan( 2 tan t ) + C = 2 2 1− x2
12.
1 1− x
2
d x.
2 sin x cos x 1 + sin 2 x 2. 求不定积分 ∫ d x. 2 2 + sin x 解: 利用凑微分法 , 得
原式 =
∫
1 + sin 2 x d(1 + sin 2 x) 2 + sin 2 x
令 t = 1+ sin 2 x
三角函数有理式
多项式及 部分分式之和
简单无理函数
注意 初等函数的原函数不一定是初等函数 ,
因此不一定都能积出. 例如 , 1 − x2 sin x 2 ∫ e dx , ∫ x dx , ∫ sin x dx , ∫ ln x dx , dx 2 2 3 ∫ 1 + x 4 , ∫ 1 + x dx , ∫ 1 − k sin x dx (0 < k < 1) ,
一.基本概念 二.计算方法
1. 直接积分法
原函数与不定积分
通过简单变形, 利用基本积分公式和运算法则 求不定积分的方法 . 2. 换元积分法
∫ f ( x ) dx
第一类换元法 第二类换元法
∫ f [ϕ (t )]ϕ ′(t ) dt
(代换: x = ϕ (t ))
(注意常见的换元积分类型)
3. 分部积分法
2 x3x dx . 例1. 求 ∫ x 9 + 4x 2 3 解: 原式 = ∫ dx = ∫ dx 2x 2x 2x 3 +2 1 + ( 2) 3 d ( 2) x 1 3 = 2∫ ln 3 1 + ( 2 ) 2 x 3
x x
( 2) x 3
da x = a x ln a dx
arctan( 2 ) x 3 = +C ln 2 − ln 3
例2. 求
∫
dx 1+ e + e + e
x 6
x 2 x 3 x 6
.
解: 令 t = e , 则 x = 6 ln t , dx = 6 dt t
dt dt = 6∫ 原式 = 6 ∫ 3 2 2 (1 + t + t + t ) t (t + 1)(t + 1) t
⎛ 6 − 3 − 3t + 3 = ∫⎜ ⎝ t t +1 t2 +1
2
)
3 2
dx
xe x 9. ∫ dx 2 (1 + x )
10.设当 x ≠ 0 时, f ' ( x ) 连续,求 ' xf ( x ) − (1 + x ) f ( x ) dx . 2 x ∫ x e
2 sin x cos x 1 + sin 2 x d x. 11. 求不定积分 ∫ 2 2 + sin x
解 Q ∫ x ln(1 + x 2 )dx =
1 x2 1 2 2 2 = [(`1 + x ) ln(1 + x ) − x ] arctan x − ∫ [ln(1 + x 2 ) − ]dx 2 2 2 1+ x
x x 1 2 2 2 2 = arctan x[(`1 + x ) ln(1 + x ) − x − 3] − ln(1 + x ) + + C . 2 2 2
解
x x e (1 + 2 sin cos ) 2 2 dx 原式 = ∫ 2 x 2 cos 2 x 1 x x = ∫ (e + e tan )dx x 2 2 cos 2 2
x
x x x = ∫ e d (tan ) + ∫ e tan dx 2 2
x
x x x x x = e tan − ∫ e tan dx + ∫ e tan dx 2 2 2
3. 求不定积分 ∫
1
d x.
− 1 + C1 2
得
=
1 +C 2 2
记作
C x ≥1
∫
x − 1 dx = F (x) =
1 1 x 2 −)x + C+ C , ( −1 2 1 , 22 2
x2 + ) 1 + − 1 ( x − 1x2−+ C ,C , x < 1 2 2
注意1
⎧1, x > 0 ⎪ 符号函数 f ( x ) = sgn x = ⎨0, x = 0 ⎪ − 1, x < 0 ⎩ f ( x ) 在 ( −∞ , + ∞ ) 内不存在原函数. (反证法)
⎞ dt ⎟ ⎠ 3 = 6 ln t − 3 ln t + 1 − ln(t 2 + 1) − 3 arctan t + C 2
x x − 3 ln(e 6
=
+ 1) − 2
x 3 ln(e 3
x + 1) − 3 arctan e 6
+C
e x (1 + sin x ) 例3 求 ∫ dx . 1 + cos x
I n = ∫ sec n x dx , 证明递推公式: 例4. 设 n−2 1 n−2 In = sec x ⋅ tan x + I n−2 n −1 n −1
证: I n = ∫ sec n − 2 x ⋅ sec 2 x dx
(n ≥ 2)
= sec n − 2 x ⋅ tan x − (n − 2) ∫ sec n −3 x ⋅ sec x tan x ⋅ tan x dx = sec
u v′ dx = u v − ∫ u ′v dx ∫
使用原则: 1) 由 v′ 易求出 v ; 2)
∫ u′ v dx 比 ∫ u v′ dx 好求 .
排前者取为 u , 排后者取为 v′ .
一般经验: 按“反, 对, 幂, 指 , 三” 的顺序,
4. 几种特殊类型的积分 有理函数
分解 万能代换 根式代换 三角代换
= x + ln cos x + sin x + C a cos x + b sin x dx 的积分. 说明: 此技巧适用于形为 ∫ c cos x + d sin x
例8
求 ∫ x arctan x ln(1 + x 2 )dx .
1 ln(1 + x 2 )d (1 + x 2 ) 2∫ 1 1 2 2 2 = (1 + x ) ln(1 + x ) − x + C . 2 2 1 2 1 2 2 原式 = ∫ arctan xd [ (`1 + x ) ln(1 + x ) − x ] 2 2
( n ≥ 2)
例5. 求
∫
x − 1 dx .
解: 设 F ′( x) = x − 1 = 则 F (x) =
x −1 , 1− x ,
x ≥1
x <1
x ≥1 x <1
因 F (x) 连续 , 利用 F (1 ) = F (1− ) = F (1) , 得
1 x2 − x + C , 1 2 x − 1 x 2 + C2 , 2 +
解: 由题设 F ′( x) = f ( x) , 则 F ( x) F ′( x) = sin 2 2 x , 故 即
1 − cos 4 x F ( x) F ′( x)d x = ∫ sin 2 2 xd x = ∫ dx ∫ 2 F 2 ( x) = x − 1 sin 4 x + C 4
2
Q F (0) = 1 ,∴ C = F (0) = 1, 又 F ( x) ≥ 0 , 因此
x
x = e tan + C . 2
x
x + sin x dx . 类似地 求 ∫ 1 + cos x
解
x x x + 2 sin cos 2 2 dx 原式 = ∫ 2 x 2 cos 2 x x =∫ dx + ∫ tan dx 2 2 x 2 cos 2 x x x = x tan − ∫ tan dx + ∫ tan dx 2 2 2 x = x tan + C . 2
注意2 不连续的函数可以有原函数.如
1 1 ⎧ ⎪ 2 x sin − cos , x ≠ 0 f ( x) = ⎨ x x ⎪ 0, x=0 ⎩
每一个含有第一类间断点的函数都 没有原函数.如
例6. 设 F (x) 为 f (x) 的原函数, 且 F (0) = 1 , 当 x ≥ 0 时
