算法合集之《左偏树的特点及其应用》-讲义
左偏树

合并
C ← Merge(A,B) 将左偏树A ①与左偏树B合并为一棵新的左偏树C为 左偏树的合并。 基本的思想是,假设key(A)<key(B),则将B与A的右 子树进行合并,用合并后的左偏树作为A的右子树, 这时如果A的右子树的距离大于了左子树则交换A的 左右子树,同时更新A的距离。当然,如果A与B其 中之一为空,则可直接返回另一棵子树。 由此可见,左偏树的合并操作是递归执行的。
问题提出
我们之前所学的优先队列——二叉堆,支持的操作 有:插入、查询、删除。 如刚才当我们需要用到 合并 操作的时候,二叉堆 合并,往往会成为算法的瓶颈。 因此我们说,二叉堆不是一种可并堆。 那么,有没有一种优先队列,即支持基本的插入、 查询、删除操作,又能在较短的时间内完成两个堆 的合并呢? 这里介绍一种可合并堆:左偏树。
0 9
合并
下面是一个合并的例子:
dis key 3 1 8 1
0 5 9
0 0 20 0 50
合并
下面是一个合并的例子:
dis key 3 1 8 1
0 5 9
0 0is key 3 1 0 5 0 9 0 20 0 50
1
此时3的右子节点的 距离大于了左子节 点,所以交换
8
合并
可以发现,我们合并始终是沿着最右边的那条路径 进行的。 而一棵左偏树最右边的边数-1,便是这棵左偏树的 距离。 而一个N个节点的左偏树,其距离最多为log(n+1)-1 所以,经过的边数最多为log(n+1) 即左偏树的合并操作的复杂度为O(logN)
C
A
A.L
C.L
C.R
合并
将下图所示两个左偏树合并。
算法合集之《左偏树的特点及其应用》

左偏树的特点及其应用广东省中山市第一中学黄源河【摘要】本文较详细地介绍了左偏树的特点以及它的各种操作。
第一部分提出可并堆的概念,指出二叉堆的不足,并引出左偏树。
第二部分主要介绍了左偏树的定义和性质。
第三部分详细地介绍了左偏树的各种操作,并给出时间复杂度分析。
第四部分通过一道例题,说明左偏树在当今信息学竞赛中的应用。
第五部分对各种可并堆作了一番比较。
最后总结出左偏树的特点以及应用前景。
【关键字】左偏树可并堆优先队列【目录】一、引言 (2)二、左偏树的定义和性质 (2)2.1 优先队列,可并堆 (2)2.1.1 优先队列的定义 (2)2.1.2 可并堆的定义 (2)2.2 左偏树的定义 (3)2.3 左偏树的性质 (4)三、左偏树的操作 (6)3.1 左偏树的合并 (6)3.2 插入新节点 (8)3.3 删除最小节点 (9)3.4 左偏树的构建 (9)3.5 删除任意已知节点 (10)3.6 小结 (13)四、左偏树的应用 (15)4.1 例——数字序列(Baltic 2004) (15)五、左偏树与各种可并堆的比较 (18)5.1 左偏树的变种——斜堆 (18)5.2 左偏树与二叉堆的比较 (19)5.3 左偏树与其他可并堆的比较 (19)六、总结 (22)在线代理|网页代理|代理网页|【正文】一、引言优先队列在信息学竞赛中十分常见,在统计问题、最值问题、模拟问题和贪心问题等等类型的题目中,优先队列都有着广泛的应用。
二叉堆是一种常用的优先队列,它编程简单,效率高,但如果问题需要对两个优先队列进行合并,二叉堆的效率就无法令人满意了。
本文介绍的左偏树,可以很好地解决这类问题。
二、左偏树的定义和性质在介绍左偏树之前,我们先来明确一下优先队列和可并堆的概念。
2.1优先队列,可并堆2.1.1优先队列的定义优先队列(Priority Queue)是一种抽象数据类型(ADT),它是一种容器,里面有一些元素,这些元素也称为队列中的节点(node)。
树结构知识点总结

树结构知识点总结一、树结构的基本概念1.1 树的定义与特点树是一种递归的数据结构,它由结点和边组成,具有以下特点:(1)每个结点都有一个父结点,除了根结点;(2)每个结点可能有零个或多个子结点;(3)从根结点到任意结点之间有且仅有一条路径。
1.2 结点、父结点、子结点、根结点、叶子结点在树结构中,结点是树的基本单位,可以包含数据和指向其他结点的指针。
树结构中有一些特殊的结点概念:(1)父结点:一个结点的直接上级结点称为它的父结点;(2)子结点:一个结点的直接下级结点称为它的子结点;(3)根结点:树的顶层结点称为根结点;(4)叶子结点:没有子结点的结点称为叶子结点。
1.3 深度和高度在树结构中,深度是指从根结点到某个结点的唯一路径的长度。
而高度是指树中结点的最大深度。
1.4 子树在树结构中,一个结点以及它的子结点以及它的子结点的子结点构成的树称为子树。
1.5 有序树和无序树树结构分为有序树和无序树。
有序树中子结点的相对位置是重要的,而在无序树中子结点之间的相对位置不重要。
1.6 二叉树二叉树是一种特殊的树结构,每个结点最多有两个子结点,分别称为左子结点和右子结点。
二叉树是计算机科学中最基本的树结构之一。
1.7 二叉树的特殊类型二叉树有很多特殊类型,如满二叉树、完全二叉树、平衡二叉树、二叉搜索树等,它们在不同的场景中有着不同的应用。
1.8 树结构的表示树结构可以用不同的方式来表示,如数组表示、链表表示、层次遍历表示等。
每种表示方式都有其特点和适用场景。
二、树结构的常见应用2.1 文件系统在计算机中,文件系统通常是以树结构来表示的,每个文件夹是一个结点,而文件夹中的文件是它的子结点。
2.2 组织结构组织结构也可以用树结构来表示,每个员工是一个结点,而领导和下属的关系就是结点之间的父子关系。
2.3 数据库索引在数据库中,经常需要对数据进行索引,以提高查询的效率。
索引通常是以树结构的方式来表示的。
2.4 XML文档XML文档是一种非常常见的数据格式,它本质上就是一棵树。
离散数学PPT课件 6根树及其应用(ppt文档)
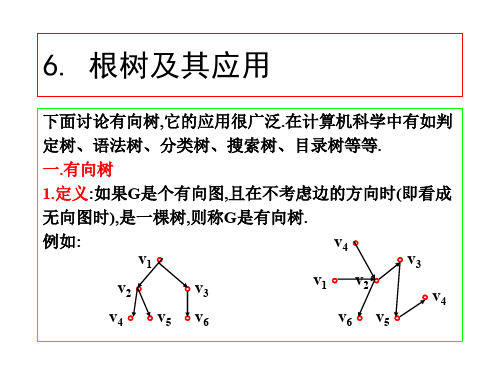
树是m叉树.
2.完全m叉树:在根树中,如果每个结点的出度都是m或者
等于0, 则称此树是完全m叉树. 3. 正则m叉树:在完全m叉树中,如果所有树叶的层次相同,
则称之为正则m叉树.
v1
v1
v1
v2
v3 v2
v3 v2
v3
v4 v5 v6 v4 v5
1.每个结点保留左儿子结点, 剪掉右边其它分支. 被剪掉 的结点如下处理.
2.同一个层次的结点, 从左到右依次画出.
r
r
a
b
c d e f g h i jk l
a
b
c d e f g
h
i j k l
八.遍历二叉树
在二叉树的一些应用中, 常常要在树中查找具有某些
3.后序遍历
⑴后序遍历左子树
⑵后序遍历右子树
⑶访问根结点.
后序遍历:32x2-×-x3x+÷+
练习: P198 — 例9.4
P204 — 9.11
九. 最优树(哈夫曼树 Huffman)
二叉树的一个重要应用就是最优树.
(3-(2×x))+((x-2)÷(3+x)
&#
+
2 x x 2 3 x
存贮时,每个结点含有三个信息: left-----是左指针,指向左子结点. data----数据 right---右指针, 指向右子结点.
left data right
表达式的存贮树:
head
(3-(2×x))+((x-2)÷(3+x)
是假的,它们的外表完全相同,只是重量有点差别.给你一
架天平找出假币.
< a:c <=
左偏堆的特点及其应用

时间复杂度:O(log n)。
空间复杂度:O(1)。
04 左偏堆的应用实例
数据压缩
数据压缩
左偏堆可以用于数据压缩,通过调整堆结构,将数据压缩成更小 的存储空间,提高存储效率。
高效压缩
由于左偏堆的特性,它可以在常数时间内完成插入和删除操作,使 得数据压缩和解压缩过程非常高效。
适用场景
适用于需要大量数据存储和传输的场景,如视频、音频、图片等数 据的压缩。
左偏堆的算法实现相对简单, 不需要复杂的操作或数据结构 。这使得它在许多情况下成为 一种实用的选择。
左偏堆只需要常数级别的额外 空间,使其在处理大规模数据 时具有较高的内存效率。
缺点分析
空间限制
不适合动态数据
左偏堆需要预先分配足够的空间来存储所 有元素,这可能在一些情况下是一个限制 因素。
由于左偏堆的特性,它可能不适合处理动 态数据集,因为每次插入或删除元素都需 要重新调整堆的结构。
1 2
PageRank算法
左偏堆可以用于实现搜索引擎的PageRank算法, 根据网页之间的链接关系计算网页的权重。
链接分析
左偏堆可以快速分析网页之间的链接关系,计算 出每个网页的PageRank值。
3
适用场景
适用于搜索引擎、网络爬虫、链接分析等场景, 用于评估网页的重要性和排名。
05 左偏堆的优缺点分析
优先队列的实现
01
02
03
优先队列
左偏堆可以用于实现优先 队列,根据元素的优先级 进行排序,使得优先级高 的元素能够优先处理。
快速插入和删除
左偏堆的插入和删除操作 非常高效,适用于需要频 繁插入和删除元素的优先 队列。
适用场景
适用于任务调度、网络流 量控制等需要处理优先级 较高的场景。
离散数学及其应用课件:树

树
图7-13 二叉树
树
例7.11 计算机中存储的文件目录,目录可以包含子目录
和文件。图7-14用多叉树表示一个文件系统。C表示根目录,
可以表示成根树,内点表示子目录,树叶表示文件或空目录。
树
图7-14 多叉树表示的文件系统
树
2.二叉树的遍历
定义7.10 对于一棵根树的每个结点都访问一次且仅一次
树
图7-16 给定单词二叉搜索树
树
7.2.3 最优二叉树及其应用
1.哈夫曼树
树
例7.14 计算图7-17所示带权二叉树的权值。
图7-17-带权二叉树
树
7.2.1 根树的概念
定义7.6 一个有向图D,如果略去有向边的方向所得的无
向图为一棵无向树,则称D为有向树。换句话说,若有向图的
基图是无向树,那么这个有向图为有向树。入度为0的顶点称
为树根(Root),入度为1且出度为0的顶点称为树叶;入度为1且
出度大于0的顶点称为内点。内点和树根统称为分支点。
有一种特殊结构的有向树叫根树。
图7-2 无向图
树
树
例7.2 设T 是一棵树,它有三个2度结点,两个3度结点,一
个4度结点,求T 的树叶数。
树
7.1.2 生成树的概念与性质
1.生成树的概念
定义7.2 设G=<V,E>是无向连通图,T 是G 的生成子图,并
且T 是树,则称T 是G的生成树(SpanningTree),记为TG 。
树
定理7.1 设G=<V,E>是n 阶无向图,G 中有m 条边,则下面
关于G 是树的命题是等价的:
(1)G 连通而不含回路;
(2)G 的每对顶点之间具有唯一的一条路径;
图解数据结构9左偏树
十三、左偏树(Leftist Tree)树这个数据结构内容真的很多,上一节所讲的二叉堆,其实就是一颗二叉树,这次讲的左偏树(又叫“左翼堆”),也是树。
二叉堆是个很不错的数据结构,因为它非常便于理解,而且仅仅用了一个数组,不会造成额外空间的浪费,但它有个缺点,那就是很难合并两个二叉堆,对于“合并”,“拆分”这种操作,我觉得最方面的还是依靠指针,改变一下指针的值就可以实现,要是涉及到元素的移动,那就复杂一些了。
左偏树跟二叉堆比起来,就是一棵真正意义上的树了,具有左右指针,所以空间开销上稍微大一点,但却带来了便于合并的便利。
BTW:写了很多很多的程序之后,我发觉“空间换时间”始终是个应该考虑的编程方法。
:)左偏左偏,给人感觉就是左子树的比重比较大了,事实上也差不多,可以这么理解:左边分量重,那一直往右,就一定能最快地找到可以插入元素的节点了。
所以可以这样下个定义:左偏树就是对其任意子树而言,往右到插入点的距离(下面简称为“距离”)始终小于等于往左到插入点的距离,当然了,和二叉堆一样,父节点的值要小于左右子节点的值。
如果节点本身不满,可插入,那距离就为0,再把空节点的距离记为-1,这样我们就得出:父节点的距离= 右子节点距离+ 1,因为右子节点的距离始终是小于等于左子节点距离的。
我把距离的值用蓝色字体标在上图中了。
左偏树并一定平衡,甚至它可以很不平衡,因为它其实也不需要平衡,它只需要像二叉堆那样的功能,再加上合并方便,现在来看左偏树的合并算法,如图:这种算法其实很适合用递归来做,但我还是用了一个循环,其实也差不多。
对于左偏树来说,这个合并操作是最重要最基本的了。
为什么?你看哦:Enqueue,我能不能看作是这个左偏树的root和一个单节点树的合并?而Dequeue,我能不能看作是把root节点取出来,然后合并root的左右子树?事实上就是这样的,我提供的代码就是这样干的。
Conclusion:左偏树比同二叉堆的优点就是方便合并,缺点是编程复杂度略高(也高不去哪),占用空间稍大(其实也大不去哪)。
离散数学第十一章 树
m 1 ) t t 1 即(
这个定理实质上可以用每局有m个选手参加的单淘汰制比赛来说明。t个叶表 示t个参赛的选手,i则表示必须按排的总的比赛局数。每一局由m个参赛者中产生 一个优胜者,最后决出一个冠军。
11.2 有向树及其应用
m叉树
例11.8 设有28盏电灯,拟公用一个电源插座,问需要多少块具有四插 座的接线板? 这个公用插座可以看成是正则四叉树的根,每个接线板看成是其它的 分枝点,灯泡看成是叶,则问题就是求总的分枝点的数目,由定理11.4可 1 以算得 i (281 ) 9 。因此,至少需要9块接线板才能达到目的。 3
图11.6
11.2 有向树及其应用
定义11.10 设<D,W>是叶加权二叉树。如果对于一切叶加权二叉树
DW ', ' 只要对于任意正实数r,D和 D ' 中权等于r的叶的数目相同,就 ', ' 的叶加权路径长度,则称 有<D,W>的叶加权路径长度不大于 DW
<D,W>为最优的。 这样,我们把求某问题的最佳算法就归结为求最优二叉树的问题。
11.1 树与生成树
生成树与最小生成树
定理11.2 无向图 为连通当且仅当 有生成树。
证明:先采用反证法来证明必要性。 若 G 不连通,则它的任何生成子图也不连通,因此不可能有生成树,与 G 有 生成树矛盾,故 G 是连通图。 再证充分性。 设 G 连通,则 G 必有连通的生成子图,令 T 是 G 的含有边数最少的生成子图, 于是 T 中必无回路(否则删去回路上的一条边不影响连通性,与 T 含边数最少矛 盾),故 T 是一棵树,即生成树。
数据结构及算法第7章 树和二叉树
LDR、LRD、DLR RDL、RLD、DRL
5.2先序遍历二叉树
先序遍历二叉树的操作定义: 当二叉树为空时,执行空操作;非空时,按如 下步骤遍历: 访问根结点。 先序遍历左子树,即先遍历左子树的根(以d1 表示),再依次先序遍历d1的左子树和右子树。 先序遍历右子树,即先序遍历右子树的根(以 d2表示),再依次先序遍历d2的左子树和右子 树。
性质3:对任何一棵二叉树T,如果其终端结点数为n0, 度为2的结点数为n2,则n0=n2+1
3.3二叉树的性质:
几种特殊形式的二叉树
满二叉树
定义: 一棵深度为 k且有2 k
1个结点的二叉树称为~
特点:每一层上的结点数都是最大结点数
完全二叉树
定义:深度为k,有n个结点的二叉树当且仅当其每一个结点 都与深度为k的满二叉树中编号从1至n的结点一一对应时, 称为~ 特点 只叶子结点只可能在层次最大的两层上出现 对任一结点,若其右分支下子孙的最大层次为l,则其左 分支下子孙的最大层次必为l 或l+1
5.1遍历二叉树的定义和方法
二叉树的遍历
先序遍历:先访问根结点,然后分别先序遍历左子树、右子树DLR 中序遍历:先中序遍历左子树,然后访问根结点,最后中序遍历右子 树:LDR 后序遍历:先后序遍历左、右子树,然后访问根结点:LRD 按层次遍历:从上到下、从左到右访问各结点
D L R
2.1二叉树
定义
定义:二叉树是n(n0)个结点的有限集,它或为空树(n=0),或由一 个根结点和两棵分别称为左子树和右子树的互不相交的二叉树构成 特点 每个结点至多有二棵子树(即不存在度大于2的结点) 二叉树的子树有左、右之分,且其次序不能任意颠倒 基本形态
树
Kruskal算法
Kruskal算法(基于避圈法思想)设G=(V,E,W) 是n阶连通带权图, (1) 在边集E中选一条具有最小权值的边e,加入 生成树T中,并将e从边集E中删去。 (2) 在边集E中选一条具有最小权值的边e,若e 和已在T中的边不构成回路,将e添加到T中,并 从边集E中删去e;若e和已在T中的边构成回路, 从边集E中删去e。 (3) 若T中的边数为n-1,算法结束,否则返回 (2)。 算法结束时,T就是G的最小生成树。
s t i j i s j t
可以用最小生成树解决这个问题。 首先可以构造一个带权完全图G=(V, E, W), 其中的每个结点是数据集D中的一个结点,即 V={ a1,a2,…an },对于任意ai, ajV,它们的距 离d(ai,aj)作为边(ai,aj)的权值。在这个带权图上 求最小生成树TG,在TG上删去权值最大的k-1条 边,成为有k个连通分支的不连通的树,这k个 连通分支就是所求聚类的k个子类 , 并且具有最大的 C1 , C2 ,...Ck 。 D ( )
(1)
(2)
(3)
(4a)
(4b)
(5)
实例
例1.3 已知无向树T中, 有1个3度顶点, 3个2度顶点, 其余结点全是树叶. T中有多少树叶?画出满足要求 的非同构的无向树.
解 设有x片树叶, 2(1+3+x-1)=13+32+x 解得x=3,故T有3片树叶. T的度数列为1, 1, 1, 2, 2, 2, 3
求生成树
求生成树的避圈法: 设图G=(V,E),|V|=n,E={e1,e2,,em}, ① 任取一条边eE,令TG={e}; ② 任取一条边eE- TG,若TG {e}无回路,则把e添加 到TG中; ③ 若 TG中的元素有n-1个,则算法结束,否则返回②。 当把n-1条边加入TG时,TG就是图G的生成树。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Merge (3, 6)
16
0 10
3? 62
12
7
18
24
8
37
17
18
26
Winter Camp 2005 演示稿
左偏树的操作 —— 合并
下面是一个合并的例子:
Merge (3, 6)
26
31
10 0
12
7
18
24
8
37
17
18
26
17
Winter Camp 2005 演示稿
左偏树的操作 —— 合并
End Function
9
Winter Camp 2005 演示稿
左偏树的操作 —— 合并
下面是一个合并的例子:
Merge (3, 6)
31
62
10 1
80
12 1
71
17 0
18 0 24 0
37 0 18 0
26 0
10
Winter Camp 2005 演示稿
左偏树的操作 —— 合并
下面是一个合并的例子:
左偏树的操作 —— 合并
下面是一个合并的例子:
Merge (8,18) Merge (8, 7) Merge (8, 6) Merge (3, 6)
8
17
NULL
18
26
13
Winter Camp 2005 演示稿
左偏树的操作 —— 合并
下面是一个合并的例子:
Merge (8, 7) Merge (8, 6) Meቤተ መጻሕፍቲ ባይዱge (3, 6)
Merge (8, 6) Merge (3, 6)
11
8 17 26
6
12
18
24
7
37
18
Winter Camp 2005 演示稿
左偏树的操作 —— 合并
下面是一个合并的例子:
Merge (8, 7) Merge (8, 6) Merge (3, 6)
8 17 26
12
7
37
18
Winter Camp 2005 演示稿
5
Winter Camp 2005 演示稿
左偏树的操作 —— 合并
合并操作是递归进行的
merge T1 a
L1
R1
T2 b
a
a<b L1
先将T1的右子 树与T2合并
L2
R2
6
合并T1和T2两 棵左偏树
merge
R1 b
L2
R2
Winter Camp 2005 演示稿
左偏树的操作 —— 合并
合并操作是递归进行的
8个节点的左偏树的最大 距离:log(8+1) -1 = 2
最右路径长度即 为左偏树的距离
Winter Camp 2005 演示稿
左偏树的操作
左偏树支持下面这些操作:
– MakeNull —— 初始化一棵空的左偏树 – Merge —— 合并两棵左偏树 – Insert —— 插入一个新节点 – Min —— 取得最小节点 – DeleteMin —— 删除最小节点 – Delete —— 删除任意已知节点 – Decrease —— 减小一个节点的键值
14
7?
0 37
81
17
18
26
Winter Camp 2005 演示稿
左偏树的操作 —— 合并
下面是一个合并的例子:
Merge (8, 6) Merge (3, 6)
15
62
12 1
71
18
24
8
37
17
18
26
Winter Camp 2005 演示稿
左偏树的操作 —— 合并
下面是一个合并的例子:
由左偏性质可知,一个节点的距离等于以该节 点为根的子树最右路径的长度。
3
Winter Camp 2005 演示稿
左偏树的性质
定理:若一棵左偏树有N个节点,则该左偏树 的距离不超过 log(N+1) -1。
A2
B1
C1
D0 E 0 H0
F0 G0
4
最右路径: A-C-G 最右路径节点数 = 3 距离 = 2
a merge
L1
R’
R1
先将T1的右子
b
树与T2合并
L2
R2
7
Winter Camp 2005 演示稿
左偏树的操作 —— 合并
合并操作是递归进行的
a
dist(R’) > dist(L1)
L1
R’
a
R’
L1
合并后的右子 树距离可能大 于左子树距离
交换左右子树 并更新根节点
距离
8
Winter Camp 2005 演示稿
合并操作都是一直沿着两棵左偏树的最 右路径进行的。
一棵N个节点的左偏树,最右路径上最 多有 log(N+1) 个节点。
因此,合并操作的时间复杂度为: O(log N1 + log N2) = O(log N)
18
Winter Camp 2005 演示稿
左偏树的操作 —— 插入
插入一个新节点
例题:数字序列
给定一个整数序列 a1 , a2 , … , an,求一 个不下降序列 b1≤b2≤…≤bn,使得数列 {ai} 和 {bi} 的各项之差的绝对值之和 |a1 b1| + |a2 - b2| + … + |an - bn| 最小。
– 把待插入节点作为一棵单节点左偏树 – 合并两棵左偏树 – 时间复杂度:O(log N)
Merge
19
Winter Camp 2005 演示稿
左偏树的操作 —— 删除
删除最小节点
– 删除根节点 – 合并左右子树 – 时间复杂度:O(log N)
Merge
20
Winter Camp 2005 演示稿
2
Winter Camp 2005 演示稿
左偏树的定义 —— 左偏性质
定义一棵左偏树中的外节点(External Node) 为 左子树或右子树为空的节点。
定义节点 i 的距离(dist(i)) 为节点 i 到它的后代 中,最近的外节点所经过的边数。
任意节点的左子节点的距离不小于右子节点的 距离(左偏性质)。
左偏树的操作 —— 合并
合并操作的代码如下:
Function Merge(A, B) If A = NULL Then return B If B = NULL Then return A If key(B) < key(A) Then swap(A, B) right(A) ← Merge(right(A), B) If dist(right(A)) > dist(left(A)) Then swap(left(A), right(A)) If right(A) = NULL Then dist(A) ← 0 Else dist(A) ← dist(right(A)) + 1 return A
算法合集之《左偏 树的特点及其应用》
精品
Winter Camp 2005 演示稿
左偏树的定义
左偏树(Leftist Tree)是一种可并堆(Mergeable Heap) ,它除了支持优先队列的三个基本操作 (插入,删除,取最小节点),还支持一个很 特殊的操作——合并操作。
左偏树是一棵堆有序(Heap Ordered)二叉树。 左偏树满足左偏性质(Leftist Property)。
