信号与系统第2章习题

合集下载

考研专业课郑君里版《信号与系统》第二章补充习题——附带答案详解

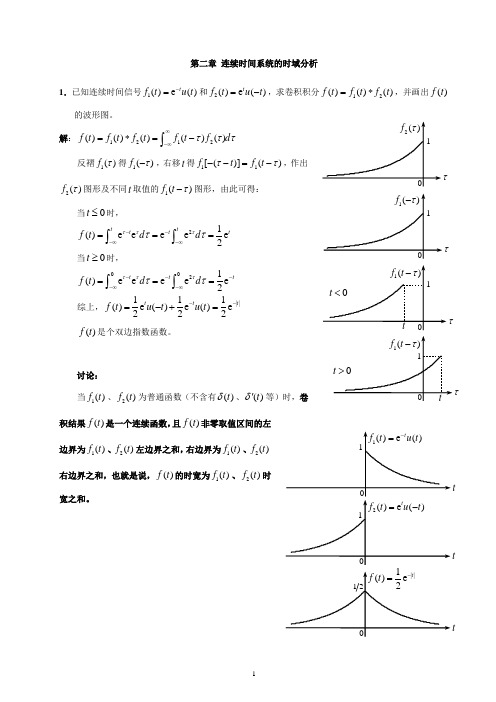
第二章连续时间系统的时域分析1．已知连续时间信号1()e ()t f t u t -=和2()e ()t f t u t =-，求卷积积分12()()()f t f t f t =*，并画出()f t 的波形图。

解：1212()()()()()f t f t f t f t f d τττ∞-∞=*=-⎰反褶1()f τ得1()f τ-，右移t 得11[()]()f t f t ττ--=-，作出2()f τ图形及不同t 取值的1()f t τ-图形，由此可得：当0t ≤时，21()e e ee e 2ttt tt f t d d τττττ---∞-∞===⎰⎰当0t ≥时，0021()e e e e e 2t t t f t d d τττττ----∞-∞===⎰⎰综上，||111()e ()e ()e 222t t t f t u t u t --=-+=()f t 是个双边指数函数。

讨论：当1()f t 、2()f t 为普通函数（不含有()t δ、()t δ'等）时，卷积结果()f t 是一个连续函数，且()f t 非零取值区间的左边界为1()f t 、2()f t 左边界之和，右边界为1()f t 、2()f t 右边界之和，也就是说，()f t 的时宽为1()f t 、2()f t 时宽之和。

τttt2．计算题图2（a ）所示函数)(1t f 和)(2t f 的卷积积分)()()(21t f t f t f *=，并画出)(t f 的图形。

解法一：图解法1212()()()()()f t f t f t f t f d τττ∞-∞=*=-⎰其中1()f t τ-的波形见题图2(b)，由此可得：当10t +≤，即1t ≤-时，()0f t = 当011t ≤+≤，即10t -≤≤时，120()2(1)t f t d t ττ+==+⎰当11t +≥但10t -≤，即01t ≤≤时，1()21f t d ττ==⎰当011t ≤-≤，即12t ≤≤时，121()21(1)t f t d t ττ-==--⎰当11t -≥，即2t ≥时，()0f t =综上，220,1,2(1),10()1,011(1),12t t t t f t t t t ≤-≥⎧⎪+-≤≤⎪=⎨≤≤⎪⎪--≤≤⎩ ()f t 波形见题图2(c)。

信号与系统第二章习题王老师经典解法(青岛大学)小白发布

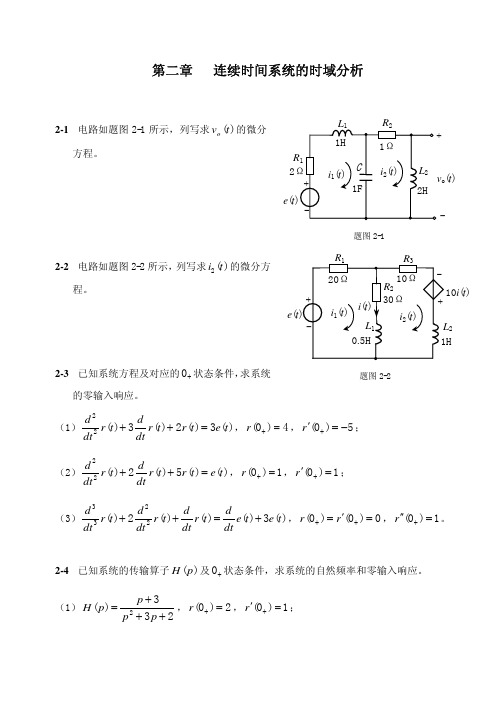
2-16 已知 f1 (t ) =
画出下列各卷积的波形。（1） s1 (t ) = f1 (t ) ∗ f 2 (t ) ；（2） s2 (t ) = f1 (t ) ∗ f 2 (t ) ∗ f 2 (t ) ；（3） s3 (t ) = f1 (t ) ∗ f 3 (t ) 。
2-17 求题图 2-17 所示电路在 e(t ) = (1 + 2e
第二章
连续时间系统的时域分析
2-1 电路如题图 2-1 所示，列写求 vo (t ) 的微分方程。
L1 1H R1 2Ω + e(t) i 1 (t )
R2 1Ω + L2 2H 题图 2-1
C
1F
i 2 (t )
vo(t)
2-2 电路如题图 2-2 所示，列写求 i2 (t ) 的微分方程。
题图 2-18
−2 t
− 1)U (t ) ，试利用卷积的性质求题
1 0 -1
e2(t)=tU(t) 1 t 0
e3(t)
t 0 1
2-19 一线性时不变的连续时间系统，其初始状态一定，当输入 e1 (t ) = δ (t ) 时，其全响应
r1 (t ) = −3e − tU (t ) ；当输入 e2 (t ) = U (t ) 时，其全响应 r2 (t ) = (1 − 5e − t )U (t ) 。求当输入 e(t ) = tU (t ) 时的全响应。
2-14 计算卷积 f (t ) = f 1 (t ) ∗ f 2 (t ) ，其中 f1 (t ) = sgn(t − 1) ， f 2 (t ) = e 2-15 求下列卷积（1） f1 (t ) = e

信号与系统第二章习题与答案

第二章习题与答案1．求以下序列的z 变换并画出零极点图和收敛域。

分析：Z 变换概念∑∞-∞=-==n nzn x z X n x Z )()()]([，n 的取值是)(n x 的有值范围。

Z 变换的收敛域是知足∞<=∑∞-∞=-M zn x n n)(的z 值范围。

解：(1) 由Z 变换的概念可知：∞====<<<<z z az a z az a z a az ,0 1, 11,1 零点为：极点为：即：且收敛域：)(21)()2(n u n x n⎪⎭⎫⎝⎛=)1(21)()3(--⎪⎭⎫⎝⎛-=n u n x n)1(,1)()4(≥=n nn x 为常数）00(0,)sin()()5(ωω≥=n n n n x 10,)()cos()()6(0<<+=r n u n Ar n x n Φω)1||()()1(<=a an x nnn nzaz X -∞-∞=⋅=∑)(nn n nn n z a za-∞=---∞=-∑∑+=1nn n nn n z a z a -∞=∞=∑∑+=01))(1()1()1)(1(1111212a z az a z a az az a za az az ---=---=-+-=-解：(2) 由z 变换的概念可知：n n nz n u z X -∞-∞=∑=)()21()( ∑∞=-=0)21(n n n z 12111--=z 211121><⋅z z 即：收敛域： 0 21==z z 零点为：极点为：解:（3）nn n z n u z X -∞-∞=∑---=)1()21()(∑--∞=--=1)21(n n n z∑∞=-=12n n n z zz212--= 12111--=z 21 12 <<z z 即：收敛域：0 21 ==z z 零点为：极点为：解： (4) ∑-⋅∞==11)(n nz n z X∑∞--=-=•••11)(1)(n n z n n dz z dX 21)(11z z z n n -=-=∑∞=-- ，1||>z。

《信号与系统分析基础》第二章部分习题参考答案

第二章部分习题参考答案2-6 试求下列各函数1()f t 与2()f t 之卷积。

121212(-)01(1) ()() ()() (0) ()()()(-) ()(-)11(1) 0(2) ()t tt t tt t f t u t f t e u t f t f t f f t d u eu t d e e d e e e t f t ααταατααταατττττττααδ-+∞-∞+∞---∞--==>*===⋅=⋅=-≥=⎰⎰⎰，解：，2121212() ()cos(45)()()()cos[()45] cos(45)(3) ()(1)[()(1)] ()(1)(2) ()()t f t t f t f t t d t f t t u t u t f t u t u t f t f t ωδτωττω+∞-∞=+*=-+=+=+--=---*⎰，解：，解：ττ222221211211()(-1)(-1)-2(-2)(-2)(-1)(-1)-(-2)(-2)2211-(-2)(-2)(-3)(-3)-(-2)(-2)(-3)(-3)22()*()()1,()0123, (1-)(1)21(1)--(12ttf t t u t t u t t u t t u t t u t t u t t u t t u t f t f t f t t f t t t dt t ft t t t τττ=+++=<=<<+=+-=++⎰222-112222212111)-222123, (1-)(1)-221()2(1)-2(1-)(-1)211121---152223, ()*()0.t t t t t t d t f t t t t t t t t t t t f t f t ττττ-+=<<+=+=+++=+++=++>=⎰121221--(4) cos , (1)-(-1)()*()()(-) [(1)-(-1)][cos(-)] cos[(1)]-cos[(-1)]f t t f t t t f t f t f f t d t t t d t t ωδδτττδδωττωω+∞∞+∞∞==+==+⋅=+⎰⎰ -212-212--2-220(5) ()(), ()sin ()()()*()()sin(-)(-) sin(-)sin t t ttt tf t e u t f t t u t f t f t f t e u t u t d e t d ee d τττττττττ+∞∞==⋅==⋅⋅⋅=⋅=⋅⎰⎰⎰-12-(-)--0022-(-)-33-2-3(6) ()2[()-(-3)], ()4()-(-2)0, ()0.02,()2488-825, 88()8(-)5, ()0.t tt t t tt t t t t f t e u t u t f t u t u t t f t t f t e d e e e t ft ed ef t e e e t f t ττττττ-==<=<<==⋅=<<===>=⎰⎰2-8 求阶跃响应为32()(21)()t t s t e e u t --=-+的LTI （线性时不变）系统对输入()()t x t e u t =的响应。

信号与系统课后答案第2章习题解

第2章习题2-1 求下列齐次微分方程在给定起始状态条件下的零输入响应（1）0)(2)(3)(22=++t y t y dt d t y dt d ；给定：2)0(,3)0(==--y dt dy ；（2）0)(4)(22=+t y t y dt d ；给定：1)0(,1)0(==--y dtd y ；（3）0)(2)(2)(22=++t y t y dt d t y dt d ；给定：2)0(,1)0(==--y dt dy ；（4）0)()(2)(22=++t y t y dt d t y dt d ；给定：2)0(,1)0(==--y dtdy ；（5）0)()(2)(2233=++t y dt d t y dt d t y dt d ；给定：2)0(,1)0(,1)0(22===---y dt d y dt d y 。

（6）0)(4)(22=+t y dt d t y dt d ；给定：2)0(,1)0(==--y dtdy 。

解：（1）微分方程的特征方程为：2320λλ++=，解得特征根：121, 2.λλ=-=- 因此该方程的齐次解为：2()t th y t Ae Be --=+.由(0)3,(0)2dy y dt--==得:3,2 2.A B A B +=--=解得:8, 5.A B ==- 所以此齐次方程的零输入响应为:2()85tty t e e--=-.（2）微分方程的特征方程为：240λ+=，解得特征根：1,22i λ=±.因此该方程的齐次解为：()cos(2)sin(2)h y t A t B t =+.由(0)1,(0)1d y y dx --==得:1A =,21B =,解得:11,2A B ==. 所以此齐次方程的零输入响应为:1()cos(2)sin(2)2y t t t =+.（3）微分方程的特征方程为：2220λλ++=，解得特征根:1,21i λ=-± 因此该方程的齐次解为：()(cos()sin())th y t e A t B t -=+.由(0)1,(0)2dy y dx--==得:1,2,A B A =-= 解得:1,3A B ==.所以齐次方程的零输入响应为:()(cos()3sin())ty t e t t -=+.（4）微分方程的特征方程为：2210λλ++=，解得二重根:1,21λ=-.因此该方程的齐次解为：()()th y t At B e -=+. 由(0)1,(0)2dy y dx--==得:1,2,B A B =-=解得:3, 1.A B == 所以该方程的零输入响应为:()(31)ty t t e -=+.（5）微分方程的特征方程为：3220λλλ++=，解得特征根: 1,21λ=-,30λ=. 因此该方程的齐次解为：()()th y t A Bt C e -=++.由22(0)1,(0)1,(0)2d d y y y dx dt---===得:1,1,22A C B C C B +=-=-=. 解得:5,3,4A B C ==-=-.所以方程的零输入响应为:()5(34)ty t t e -=-+.（6）微分方程的特征方程为：240λλ+=，解得特征根:120,4λλ==-. 因此该方程的齐次解为：4()th y t A Be -=+.由(0)1,(0)2d y y dx --==得:1,42A B B +=-=.解得:31,22A B ==-. 所以此齐次方程的零输入响应为:431()22ty t e -=-.2-2 已知系统的微分方程和激励信号，求系统的零状态响应。

信号与系统第二章典型例题

利用微分特性
f ′′(t ) =
2
2E τ τ [δ (t + ) + δ (t − ) − 2δ (t )] τ 2 2
τ τ
− jω 2E jω 2 4E ωτ ( j ω ) F (ω ) = [e + e 2 − 2] = (cos − 1) τ τ 2
8E 2 ω τ ω 2 Eτ 2 ω τ = − sin ( ) = − Sa ( ) τ 4 2 4
F1 (ω ) =
又
T 2 ωT Sa ( ) 2 4
T f 0 (t ) = f1 (t − ) 2
−j ωT 2
则：
F0 (ω ) = F1 (ω ) e
T ωT − j = Sa 2 ( )e 2 4
ωT 2
周期信号 f T (t ) 的傅里叶级数系数 C n ：
1 1 nω T − j Cn = F0 (ω ) |ω =nω1 = Sa 2 ( 1 ) e T 2 4
∴ωm
= 3000π
为从 f S (t ) 无失真恢复 f (t ) ，则
最大抽样间隔 Tmax =
π 1 = s ω m 3000
（ 3）
FS (ω ) =
1 TS
n= −∞
∑ F (ω − nω S )
∞
当 TS = Tmax 时，
FS (ω ) =
1
Tmax n =−∞
∑
∞
F (ω −
∞ 2π n) = 3000 ∑ F (ω − 6000 π ⋅ n) Tmax n =−∞
第二章典型例题
例 2-1：如图所示信号 f (t ) （ 1）求指数形和三角形傅里叶级数；（ 2）求级数 s = 1 −

奥本海姆信号与系统第二章部分习题答案

0 sin(2 t ) (t 3)dt 0
5

+ + 2.22
概率画出结果。
< 有三种解法，建议用图解法
2.22
概率画出结果。
2.28 下面均为离散时间线性时不变系统的单位脉冲响应，试判定每一系统是否是因果和/或稳定的。陈述理由。 (a)ℎ �� = (5)�� [��] (c) ℎ �� = (2)�� −��
4 5
y
长度为 M
y
x
而 N ≤n ≤N 长度为 M ，试用M 和 M 来表示 M 。
h x
(c) 考虑一个离散线性时不变系统，它具有这么一个特点，即若对全部 n ≥10, x[n] = 0 ，则对所有的 n ≥15 都有 y[n] = 0 。系统单位脉冲响应 h[n] 必须满足什么条件才有此特性？ (a) (c) (b)
(d) 有一个线性时不变系统的单位脉冲响应如图P2.44所示。为了确定 y (0) ，必须要知道在什么一个区间上的 x(t ) ？
2.50 图P2.50所示为两个系统的级联，其中一个系统 A 是线性时不变的，
y (t ) 而第二个系统 B 是系统 A 的逆系统，若 y (t )是系统 A 对 x (t )的响应，
5 �� −5 1
1 − �� cos 2��
��0 �� = ��
(a) (b) (c)
u0 (t ) cos(t )dt (t ) cos(t )dt cos(0) 1
第二章
2.4 计算并画出y[n]=x[n]*h[n]，其中

奥本海姆《信号与系统(第二版)》习题参考答案

通过整理，两种结论是一致的。
2.23
解： x (t ) =
k = −∞
∑ δ (t − kT ) ， y(t ) = x(t ) * h(t ) = x(t ) *
+∞
k = −∞
∑ δ (t − kT ) =
+∞
k = −∞
∑ x(t − kT )
+∞
（根据： x (t ) * δ (t − t 0 ) = x (t − t 0 ) ）故： (a) T=4，则 y(t)为 x(t)以周期 4 做周期拓延；
第二章作业解答
2.1
解：（a）由多项式相乘法： x[n] = {1,2,0,−1}n =0,1, 2,3
h[n] = {2,0,2}n = −1, 0,1
1 2 0 -1 2 0 2 2 4 0 -2 2 4 0 -2 2 4 2 2 0 -2
定义域为：[0-1：3+1]=[-1,4] 即： y[n] = {2,4,2,2,0,−2}n = −1, 0,1, 2,3, 4 （b）由性质：（若 x[n] * h[n] = y[n], 则：x[n] * h[n − n0 ] = y[n − n0 ] ）得：
1 τ
τ
t
（1） α ≠
β
0 t<0 ⎧ ⎪ y (t ) = x(t ) * h(t ) = ⎨ t − aτ − β ( t −τ ) e e dτ t>0 ⎪ ⎩∫0 t<0 ⎧0 = ⎨ − β t − (α − β ) t − 1] t > 0 ⎩e [e t<0 ⎧0 ⎪ −αt − βt = ⎨ e −e t>0 ⎪[ α − β ] ⎩ e −αt − e − βt =( )u (t ) β −α

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

信号与系统第2章习题
一、选择题
1、下列信号不能用复指数信号st
Ae t x =)(表示的是（）
A.冲激信号
B.直流信号
C.指数信号
D.正弦信号 2、)22(4t e t
--δ等于（）
A. t
e
4- B. )22(t -δ C.
)1(214--t e δ D. )1(2
1
4δ-e 3、积分
⎰
--+6
4
2)8(dt t e t δ等于（）
A.0
B.16
e C.1 D.)8(+t δ 4、已知信号)(t x 如下图所示，其表达式是（）
A.)3()2(2)(---+t u t u t u
B. )3(2)2()1(---+-t u t u t u
C. )3()2()(---+t u t u t u
D. )3()2()1(---+-t u t u t u 5、已知信号)(t x 如下图所示，其反转右移的信号)(1t x 是（）
A. B.
C. D.
6、如下图所示：)(t x 为原始信号，)(1t x 为变换信号，则)(1t x 的表达式是（）
A. )1(+-t x
B. )1(+t x
C. )12(+-t x
D. )12
1
(+-t x 7、若)(t x 是已录制声音的磁带，则下列表述错误的是（）
A.)(t x -表示将磁带倒转播放产生的信号
B.)2(t x 表示将磁带以二倍速度加快播放
C.)2(t x 表示原磁带放音速度降低一半播放
D.2)(t x 表示将磁带的音量放大一倍播放
8、设)(t x 表示你在山谷喊话的声音，则你耳朵听到的声音可表示为（） A.∑∞
=0)(n n
t x a
，0>n a B. ∑∞
=+0)(n n n
T t x a
，0,0>>n n T a
C.
∑∞
=-0
)(n n n
T t x a
，0,0>>n n T a D.
∑∞=-0
)(n n
T
t x ，0>n T
9、如下图所示周期信号)(~t x ，其直流分量等于（）
A.0
B.2
C.4
D.6
二、判断题
1、两个奇信号的和还是奇信号（）
2、任何信号可分解为直流分量与交流分量之和（）
3、任何信号可分解为偶分量与奇分量之和（）
4、)cos(t 是功率信号，)]()()[cos(T t u t u t --是能量信号（）
5、积分
1)(=⎰
∞
-t
d ττδ（）
6、对连续周期信号进行抽样所得离散序列一定还是周期的（）
7、设)2()(1k x k x =，则)2/()(1k x k x =（）
三、简答题
1、单位冲激信号和单位脉冲序列各有什么特性？
2、正弦信号)sin(0t ω和正弦序列)sin(0k Ω有什么区别与联系？
3、信号的时域分解有哪几种方法？
4、连续时间信号分解为冲激信号的线性组合有何实际意义？
四、计算题
教材P66习题：2-9、2-10、2-12、2-14。