13第十三章压杆稳定
建筑力学第十三章
式中 a、b是与材料性质有关的系数。
建筑力学
表 13-2 直线公式的系数 a 和 b
材料 A3 钢 优质碳钢 硅钢 铬钼钢 铸铁 强铝 松木 a(MPa) 304 461 578 9807 332.2 373 28.7 b(MPa) 1.12 2.568 3.744 5.296 1.454 2.15 0.19
建筑力学
建筑力学
2 压杆的稳定计算
1)安全系数法
建筑力学
2)折减系数法
工程中为了简便起见,对压杆的稳定计算还 常采用折减系数法。即将材料的压缩许用应力 [] 乘上一个小于 1 的折减系数 作为压杆的许用临界 应力,即: [cr] = [];
< 1,称为折减系数
按折减系数法进行压杆的稳定计算,其稳定条 件为
Pc r
2 2 2
2
建筑力学
l
i
2
压杆的长细比 或柔度
cr
E 2
计算压杆的临界应 力的欧拉公式
建筑力学
2
欧拉公式的适用范围
在推导欧拉公式时,使用了挠曲线的近似微分方程
E I v M ( x )
在推导该方程时,应用了胡克定律。因此,欧拉公式也 只有在满足胡克定律时才能适用: 2
例:长方形截面细长压杆,b/h=1/2;如果将 b改为 h
后仍为细长杆,临界力Pcr是原来的多少倍?
建筑力学
Pcr b Pcr a
4 E Ib h 2 3 Ib ( l) h 12 2 3 8 I a hb b E Ia 2 12 ( l)
2
建筑力学
2
所以,只有压杆的长细比λ≥100时,才能应用
欧拉公式计算其临界压力。
第十三章 压杆稳定

临界力为
Fccrr21c2Er A77c.r1Md4P2a 151KN
压杆2为中柔度杆,对于Q235钢,a=310MPa,b=1.24MPa,临界应力为
临界力为
σcr
Fcr
crA cr
d 2 4
414 KN
压杆3为小柔度杆,因为Q235钢为塑性材料,故其临界应力为
临界力为
σcr
Fcr
sA s
d 2 4
➢ 合理选择截面形状 应该选择Iz=Iy的截面,使压杆在各个平面内的稳定性相同。
➢ 减小压杆长度 在条件允许时,应尽量减小压杆的长度或在压杆中间增加支座。
➢ 改善支承条件 压杆与其他构件连接时,应尽可能制作成刚性连接或采用较紧 密的配合。
习题参考解答或提示
2EI ( l ) 2
μ——压杆的长度因数
➢ 杆端约束情况的简化
焊接或铆接
螺母和丝杠连接
柱形铰约束
对于与坚实的基础固结成一体的柱脚,可简化为固定端。
§13-3 欧拉公式的适用范围 中、小柔度杆的临界应力
➢ 临界应力的欧拉公式
cr
2E 2
i——压杆横截面的惯性半径,单位为mm; λ——压杆的柔度,无量纲,柔度越大,则临界应力越小,压 杆越容易失稳。
解 (1)计算各压杆的柔度 因压杆两端为铰链支承,查表得长度系数μ=1。圆形截 面对y轴和z轴的惯性矩相等,均为故圆形截Βιβλιοθήκη 的惯性半径为各压杆的柔度分别为
(2) 计算各压杆的临界应力和临界力
对于Q235钢λ p=100, λ s=60。对于压杆1,其柔度λ 1=160> λ p,所以压杆 1为大柔度杆,临界应力用欧拉公式计算。
压杆的临界力越大,稳定性越强
材料力学之压杆稳定课件

分析实验数据,得出压 杆的临界压力和失稳形式。
实验结果分析
分析压杆在不同压力 下的变形情况,判断 压杆的稳定性。
总结临界压力与失稳 形式的规律,为实际 工程应用提供依据。
对比不同长度、直径、 材料等因素对压杆稳 定性的影响。
总结词
机械装置中的压杆在承受载荷时,其稳 定性对于机械的正常运转和安全性至关 重要。
VS
详细描述
在机械装置中,如压力机、压缩机等,压 杆是重要的承载元件。通过材料力学的方 法,可以分析压杆的稳定性,确定其临界 载荷和失稳模式,从而优化机械装置的设 计,提高其稳定性和安全性。
05
压杆稳定的应用与发展
工程实例二:建筑压杆
总结词
建筑压杆在高层建筑、大跨度结构等建筑中广泛应用,其稳定性是保证建筑安全的重要 因素。
详细描述
高层建筑和大跨度结构的稳定性分析中,建筑压杆的稳定性分析占据重要地位。通过材 料力学的方法,可以对建筑压杆的承载能力和稳定性进行精确计算,从而为建筑设计提
供可靠的支持。
工程实例三:机械装置压杆
数值模拟
随着计算机技术的发展,数值模 拟方法在压杆稳定性分析中得到 广泛应用,能够更精确地预测结
构的稳定性。
材料性能研究
新型材料的不断涌现,对压杆稳定 性的影响也日益受到关注,相关研 究正在不断深入。
多因素耦合分析
在实际工程中,多种因素如载荷、 温度、腐蚀等会对压杆稳定性产生 影响,因此需要开展多因素耦合分析。
欧拉公式是由瑞士科学家欧拉提出的一个公式,用于计算等截面直杆的临界应力。 根据欧拉公式,临界应力只与压杆的材料性质和截面形状有关,而与压杆的长度 和外载大小无关。
稳定性校核
材料力学 第十三章压杆稳定

(4)若压杆在两个形心主惯性平面内的杆端约束不相
同时,该杆的临界力应按两个方向的(I/ μl)min值计算。 y z x
轴销
(5)假设压杆是均质的直杆,且只有在压杆的微弯 曲状态下仍然处于弹性状态时才是成立的;实际压杆 的临界力均小于理论值。
9l 5l
2l
稳定性
丧失原有平衡形式的现象称为失稳 失稳也是一种失效形式 理想中心受压细长压杆的临界力
§13-2
一﹑Euler公式
细长压杆的临界力
x Fcr
1.两端铰支的临界压力
M(x)=Fcrw (a)
l
E I w″= -M(x)(b) 得 E I w″= - Fcrw
w
x O y
令 k2=Fcr / EI
M(x) Fcr=F
2 0.8 160 p 0.04 i 4
l
l
2 EI 2 210 109 0.044 / 64 Fcr 102kN 2 2 (2 0.8) l
Fcr F Fst 34kN nst
例4:厂房钢柱长7m,由两根16b号Q235槽钢组成。截
稳定的。
F ≥ Fcr
F ≥ Fcr
F≥Fcr
(2)当F≥Fcr时,
在干扰力除去后,杆
干扰力
件不能恢复到原直线 位置,在曲线状态下 保持平衡。 原有的直线平衡状态是
(a)
(b)
(c)
不稳定的。
这种丧失原有平衡形式的现象称为丧失稳定性,简称失稳.
Fcr——压杆保持稳定平衡所能承受的极限压力, 即临界压力(临界荷载)。 压杆在外力作用下保持原有平衡形式的能力
第十三章压杆的稳定性

(a)
(b)
7
§ 13-2
细长压杆的临界力
w A sin kx B cos kx (c)
将边界条件x=0,w=0代入式(c)得 B=0。于是根据(c)式并利用边界条件 x=l,w=0得到
A sin kl 0
由于B=0,故上式中的A不可能等于零,则
sin kl 0
w
解得:kl 0,π, 2π,
φ28 800 C
P=30kN
1
μ1l1 0.5 900 75 i1 6 s 1 P
解: 1.根据已知条件求 s ,P cr1 304 1.12 75 220MPa
a - s 304 - 240 s 57.1 b 1.12
3
§ 13-1
压杆稳定性的概念
2. 理想中心杆件 1. 压杆轴线是理想直线即无初弯曲, 2. 压力作用线与轴线完全重合, 3. 材料是绝对均匀的。
二、失稳(屈曲)
压杆丧失其直线平衡而过渡到曲线平衡,
称为丧失稳定性,简称失稳或屈曲。
4
§ 13-1
压杆稳定性的概念
F<Fcr
F=Fcr
F>Fcr
Fcr:临界压力
F 30 103 2 48.72MPa A2 p 282 4
24
§ 13-4
压杆的稳定性计算
作业:P1076; P10916 思考:P11017; P11018
25
§ 13-4
压杆的稳定性计算
答疑通知
地点:工科二号楼A424(力学系)
时间:17周的周二下午两点;
26
§ 13-4
P=30kN
n2
第十三章-压杆稳定知识讲解

1基本概念及知识要点
1.1基本概念
理想受压直杆、理想受压直杆稳定性、屈曲、临界压力。
1.2临界压力
细长压杆(大柔度杆)用欧拉公式计算临界压力(或应力);中柔度杆用经验公式计算临界压力(或应力);小柔度杆发生强度破坏。
1.3稳定计算
为了保证受压构件不发生稳定失效,需要建立如下稳定条件,进行稳定计算:
稳定计算要求掌握安全系数法。
解析方法:稳定计算一般涉及两方面计算,即压杆临界压力计算和工作压力计算。临界压力根据柔度由相应的公式计算,工作压力根据压杆受力分析,应用平衡方程获得。
3典型问题解析
3.1临界压力
例题13.1材料、受力和约束相同,截面形式不同的四压杆如图图13-1所示,面积均为3.2×103mm2,截面尺寸分别为(1)、b=40mm、(2)、a=56.5mm、(3)、d=63.8mm、(4)、D=89.3mm,d=62.5mm。若已知材料的E=200GPa,σs=235MPa,σcr=304-1.12λ,λp=100,λs=61.4,试计算各杆的临界荷载。
解题指导:
1.计算压杆的临界压力时,需要综合考虑压杆的材料、约束、长度、惯性半径,即需要首先计算压杆的柔度,根据柔度值,代入相应的公式计算压杆的临界压力。当
λ>λP时压杆为大柔度杆,用欧拉公式计算其临界应力;
λs<λ<λP时压杆为中柔度杆,用经验公式计算其临界应力;
λ<λs时压杆为短粗杆,压杆将首先发生强度破坏。
压杆的柔度
iy=iz=i
由于
所以,λ>λP压杆为大柔度杆
用欧拉公式计算临界压力
例题13.4所示工字钢直杆在温度t1=20℃时安装,此时杆不受力,已知杆长l=6m,材料的λP=132,E= 200GPa,线膨胀系数α=12.5×10-6/℃。试问当温度升高到多少度时杆将失稳。
压杆稳定的概念

§压杆稳定的概念构件除了强度、刚度失效外,还可能发生稳定失效。
例如,受轴向压力的细长杆,当压力超过一定数值时,压杆会由原来的直线平衡形式突然变弯(图15-1a),致使结构丧失承载能力;又如,狭长截面梁在横向载荷作用下,将发生平面弯曲,但当载荷超过一定数值时,梁的平衡形式将突然变为弯曲和扭转(图15-1b);受均匀压力的薄圆环,当压力超过一定数值时,圆环将不能保持圆对称的平衡形式,而突然变为非圆对称的平衡形式(图15-1c)。
上述各种关于平衡形式的突然变化,统称为稳定失效,简称为失稳或屈曲。
工程中的柱、桁架中的压杆、薄壳结构及薄壁容器等,在有压力存在时,都可能发生失稳。
由于构件的失稳往往是突然发生的,因而其危害性也较大。
历史上曾多次发生因构件失稳而引起的重大事故。
如1907年加拿大劳伦斯河上,跨长为548米的奎拜克大桥,因压杆失稳,导致整座大桥倒塌。
近代这类事故仍时有发生。
因此,稳定问题在工程设计中占有重要地位。
“稳定”和“不稳定”是指物体的平衡性质而言。
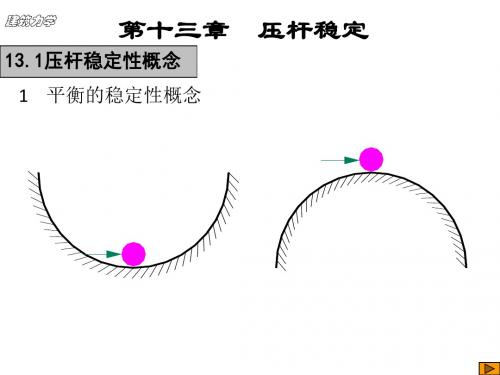
例如,图15-2a所示处于凹面的球体,其平稳是稳定的,当球受到微小干扰,偏离其平衡位置后,经过几次摆动,它会重新回到原来的平衡位置。
图15-2b所示处于凸面的球体,当球受到微小干扰,它将偏离其平衡位置,而不再恢复原位,故该球的平衡是不稳定的。
受压直杆同样存在类似的平衡性质问题。
例如,图15-3a所示下端固定、上端自由的中心受压直杆,当压力小于某一临界值时,杆件的直线平衡形式是稳定的。
此时,杆件若受到某种微小干扰,它将偏离直线平衡位置,产生微弯(15-3b);当干扰撤除后,杆件又回到原来的直线平衡位置(图15-3c)。
但当压力超过临界值时,撤除干扰后,杆件不再回到直线平衡位置,而在弯曲形式下保持平衡(图15-3d),这表明原有的直线平衡形式是不稳定的。
使中心受压直杆的直线平衡形式,由稳定平衡转变为不稳定平衡时所受的轴向压力,称为临界载荷,或简称为临界力,用表示。
压杆的稳定ppt

定义
01
边界条件是指压杆在支撑条件下的限制条件,如固定、自由、
简支等。
描述
02
不同的边界条件对压杆的稳定性产生不同的影响。例如,固定
边界条件下的压杆比自由边界条件下的压杆更稳定。
影响因素
03
边界条件对压杆稳定性的影响主要表现在支撑反力的分布和大
小上,从而影响压杆的临界载荷和屈曲载荷。
03
压杆稳定性问题的解决策略
合理选择材料和截面形状
选择高强度材料
如合金钢、不锈钢等,能够提高压杆的屈服强度和抗拉强度 ,增加压杆的稳定性。
选择合适的截面形状
如圆形、方形、工字形等,能够改变压杆的截面面积和惯性 矩,进而改变压杆的稳定性。
对压杆进行合理支撑和固定
增加支撑点
通过在压杆的适当位置增加支撑点,能够提高压杆的稳定性,防止其发生屈 曲变形。
船舶设计
在船舶设计中,压杆被用于船体结构的支撑和固定。特 别是在海洋环境中,压杆的稳定性对于抵御海浪冲击和 保证船舶的安全至关重要。
地下工程
在隧道、地铁等地下工程中,压杆被用于支撑和固定土 石方及结构物。其稳定性对于保障地下工程的稳定性和 安全性至关重要。
06
总结与展望
总结
压杆稳定的定义
压杆稳定的重要性
05
压杆稳定性问Leabharlann 的工程应用建筑结构中的压杆稳定性问题
建筑物的支撑结构
在建筑设计中,压杆常被用于支撑和固定建筑结构,如桥梁、高层建筑等。其稳定性直接 影响到建筑物的安全性和使用寿命。
抗风和抗震设计
在地震或强风天气中,建筑物的压杆稳定性显得尤为重要。压杆能够提供必要的支撑力, 帮助建筑物抵御自然灾害。
定义
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
作者:黄孟生
§13-1 压杆稳定性的概念
压杆
桁架中的压杆
高压输电线路保持相间距离的受压构件
某杆,材料σb=130MPa;截面A=2×30mm2, 长 l=300mm, 按强度条件,Fb=130×2×30=7.8kN.但 实际上只有几牛顿的力杆就折断了,为什么?
F
z y
h b
二﹑欧拉公式应用中的几个问题
(1)Fcr与EI成正比,与l2 成反比,且与杆端约束有关。 Fcr越大,压杆稳定性越好,越不容易失稳;
(2)杆端约束情况对Fcr的影响,是通过 长度系数μ来实现的。要根据实际情况选 择适当的μ 。
(3)当压杆在两个形心主惯性平面内的 杆端约束情况相同时,则失稳一定发生在 最小刚度平面,即I 最小的纵向平面。
M max F sin 300 l1 15.63kN m
max
FN A
M Wz
163MPa
s
n
168MPa
l1 A
C
l1 B
x
300
z
F
l2
d
NO.14
D
CD杆:FN 2F sin 300 25kN
l
i
1 0.55 20103 / 4
110
p
100
Fcr
2EI (l)2
2 206 109 0.0024
F
z y
h b
F
(4)若压杆在两个形心主惯性平面内的杆端约束不相 同时,该杆的临界力应按两个方向的(I/ μl)min值计算。
y z x
轴销
(5)假设压杆是均质的直杆,且只有在压杆的微弯 曲状态下仍然处于弹性状态时才是成立的;实际压杆 的临界力均小于理论值。
2l
问题的提出:
9l
5l
7l
几根材料和直径相同,但是长度不同、约束不同的压杆:
y y0
查单根16b号槽钢,得:
A = 25.15cm2, Iz0 = 934.5cm4。Iy0 = 83.4cm4 z0=1.75cm,δ = 10mm
由平行移轴公式 Iy=2[Iy0+A(z0+h/2)2]=2Iz0 h = 8.23cm
(2) 校核钢柱的稳定性和强度.
i Iz 6.1cm, l 149.2
Fcr
w Asin kx B cos kx F0 l x
Fcr
x
F0
Me
Fcr
x 0, w 0, w 0; x l, w 0;
A F0 , B F0l
kFcr
Fcr
w
F0 Fcr
1 k
sin kx l cos kx l
x
2EI
tan kl kl , kl 4.49, Fcr 0.7l 2
§13-4 压杆的稳定计算
一、压杆的稳定条件
其中:
F Fcr
nst
Fst
F---压杆的工作压力
nst---稳定安全因素
[Fst]---稳定容许压力
F cr
A nst
st
[σst]---稳定容许应力
安全因素的选取:除考虑选取强度安全因素的那些因素外,还要 考虑初曲率、材料不均匀性和荷载偏心等因素。
cr
2E 2
(2) λu <λ<λP,中柔度杆,σ cr = a- bλ ;
(3)0<λ≤λu,小柔度杆,σ cr = σu ;
σ
临
界 σu
应
力 图
σp
σ= σu λs
σcr=a-bλ
cr
2E 2
λ
λp
例1 一TC13松木压杆,两端为球铰。已知:σp=9MPa,
σb=13MPa, E=1×104MPa。压杆截面为如下两种:
能不能应用欧拉公式计算每根压杆的临界力? 每根压杆是不是都会发生失稳?
§13-3 欧拉公式的适用范围与
压杆的非弹性失稳
一、压杆的临界应力与柔度
cr
Fcr A
2 EI (l)2 A
2E (l)2
I A
i2 I A
2E 2E
l i
2
2
即
cr
2E 2
λ= μl / i ——柔度,细长比。
0.552
/ 64
52.8kN
FN
25kN
Fcr nst
29.3kN
如果CD杆为矩形截面,应如何计算?
§13-5 提高压杆稳定性的措施
一、选择合理的截面形式
1、当y、z方向约束相同,使 Iy =Iz,得:λy = λz
2、当Iy =Iz时,尽可能在面积一定的情况下,增大惯 性矩I 。
3、当y、z方向约束不同,λy = λz使 得: Iy ≠Iz,
例3 千斤顶,Q235钢,l=800mm, d=40mm,
E=210GPa, 稳定安全因素nst=3.0。试求[F]。
解:
FN F Fst
F
l
i
2 0.8 0.04
160
p
l
4
Fcr
2 EI
l 2
2 210 109 0.044
(2 0.8)2
/ 64
102kN
F Fst
cr a b, Fcr cr A
a、b为与材料有关的常数,单位:MPa。
适用范围: σP<σ cr <σ u
或 λP>λ >λ u
当λ≤λ u时,压杆为小柔度杆或短粗杆。短粗杆的破 坏是强度破坏。
显然, λ u是中柔度杆与短粗杆的分界值。
令σ cr = σ u得:
u
a
b
u
四、临界应力总图
(1) λ≥λP,大柔度杆,
Me
Fcr
A 0, B M e , w M e 1 cos kx
Fcr
Fcr
cos kl 1 , kl n , n 2, 4...
2EI
Fcr 0.5l 2
3)、一端固定,另一端铰支: M x Fcrw F0 l x
x
Fcr
F0
wl
EIw Fcrw F0 l x w kw k2 F0 l x
二、压杆的稳定计算
稳定较核; 截面设计; 求容许荷载。
1、安全因数法(nst)
F Fcr
nst
Fst
或
F cr
A nst
st
2、折减因数法
cr
nst
st
st F
A
----折减因数
st
crn nst u
0 1
与材料有关,不同的材料 不同
压杆在外力作用下保持原有平衡形式的能力
稳定性 丧失原有平衡形式的现象称为失稳
失稳也是一种失效形式 理想中心受压细长压杆的临界力
§13-2 细长压杆的临界力
一﹑Euler公式
1.两端铰支的临界压力
M(x)=Fcrw (a) E I w″= -M(x)(b)
得 E I w″= - Fcrw 令 k2=Fcr / EI 得 w″+ k2 w= 0 (c)
F=25kN,l1=1.25m,l2=0.55m,E=206GPa,
p=200MPa, s=235MPa,n=1.4,nst=1.8。求
校核该结构是否安全。
l1
A
C
l1 B
x
300
z
F
l2
d
NO.14
D
l1
A
C
l1 B
x
300
z
F
l2
d
NO.14
D
AB杆:FN F cos 300 21.65kN
l
x = 0,x=l : w =0 , M=0,w″=0
x = l/2: w=w0=wmax, 且w′=0
Fcr
Fcr
l
l
2l
Fcr
l/4
l/2
l/4
Fcr
0.7l 0.3l
μ=1
μ=2
μ=0.5
μ=0.7
2 EI Fcr 统一形式: Fcr (l)2
----欧拉公式
μ——长度系数, μl——相当长度
y z x
轴销
y z
x
轴销
解:xy面内,两端视作铰支,μ = 1,iz = 4.14 cm
z
l
iz
48.3
y z
x
轴销
xz面内,两端视作固定端,μ = 0.5,查表iy= 1.52cm
y
l
iy
65.8
压杆将在xz平面内失稳
显然 z y
而 p 100,u s 60
u p ----中长杆 cr a b 304 1.12 65.8 230.3MPa Fcr cr A 230.3106 14.3104 329.3kN
与杆发生弯曲关 与截面形状有关,(如果Iy=Iz, 且I 越大,承载力就不同了)
F
与杆的长度有关
F F1
F
实际压杆与弯曲有关的因素还有:
荷载不可避免地有一定的偏心; 杆轴线有一定初曲率; 材料本身的不均匀性。
什么是压杆的稳定性呢?
F<Fcr
F<Fcr
干扰力
F<Fcr
(1)当F<Fcr
时,撤去横向干扰力 后,压杆仍能恢复原 有的直线平衡状态。
A
i
查13-1表, =0.311, [σ]=52.9MPa,
σ=F/A=53.7MPa
σ 虽大于 [σ], 但不超过5%,故满足稳定性要求.
σ= F / Amin = 70.5 MPa< [σ]
故满足强度条件.
例5: 图示梁杆结构,材料均为Q235钢。AB梁
为14号工字钢,BC杆为 d=20mm的圆杆。已知:
