北华大学概率论数学(A卷)工科概率20090620(1)
北华大学09--10高数A卷W
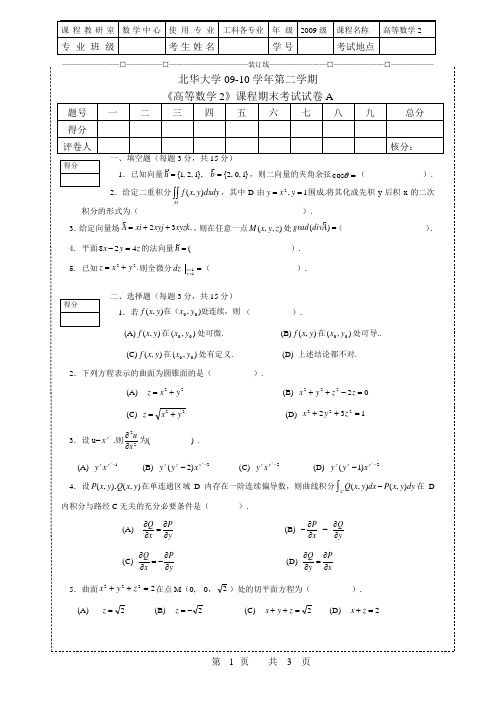
1.设 , 求 及 .
2.设 是由方程 所确定的隐函数,求 , .
3.求函数 在点M(1,0,0)处沿方向 的方向导数 .
四、(本题7分)求过点M(0,0,0)且与平面 垂直的直线的参数方程,
.
五、(本题9分)计算二重积分: .其中D为圆 围成的区域.
.
.
北华大学09-10学年第二学期《高等数学2》课程期末考试试卷A
(C) 在 处有定义.(D)上述结论都不对.
2.下列方程表示的曲面为圆锥面的是().
(A) (B)
(C) (D)
3.设u= .则 为().
(A) (B) (C) (D)
4.设 在单连通区域D内存在一阶连续偏导数,则曲线积分 在D内积分与路经C无关的充分必要条件是().教研室
数学中心
使用专业
工科各专业
年级
2009级
课程名称
高等数学2
专业班级
考生姓名
学号
考试地点
————————¤—————¤———————————装订线————————¤———————¤——————
北华大学09-10学年第二学期
《高等数学2》课程期末考试试卷A
题号
一
二
三
四
五
六
七
八
九
总分
得分
评卷人
核分:
5.曲面 在点M(0,0, )处的切平面方程为().
(A) (B) (C) (D)
北华大学09-10学年第二学期《高等数学2》课程期末考试试卷A
课程教研室
大学数学
使用专业
工科各专业
年级
2009级
课程名称
高等数学2
《概率论与数理统计》复习试卷答案.doc

北京化工大学2014——2015学年第二学期《概率论与数理统计》复习试卷一、填空题(每空3分,共18分)1.己知P(B)= 0.3, P(/luB) = 0.7,且A与B相互独立,则P⑷:0.5 。
2.设随机变量X服从参数为二项分布fi(3,p), HP{X=0}=-,则"= 1-2飞。
3.己知DX=a,DY=b,且X 和Y 相互独立,则 D (2X-Y) = 4a2+b2。
4.设样本人,…,在(/z-/?,// + P)上服从均匀分布,贝惨数//的矩估计量为X,.5.设某机器生产的零件长度(单位:cm) X〜7V(//,CT2),今抽取容量为16的样本,测得样本均值又=10 ,样本方差r =0.16 ,求//的置信度为0.95的区间估计为(9.7868,10.2131),(2)方差CT2的区间估计为(0.0873, 0.3833)(显著性水平汉=0.05)。
(保留小数点之后4位)二、(15分)甲、乙、丙3人同时各自独立地对同一0标进行射击,3人击屮目标的概率分别为0.4, 0.5, 0.7。
没1人击中R标时FI标被击毁的概率为0.2, 2人击中目标时目标被击毁的概率为0.6, 3人击中目标时,目标必定被击毁。
求1)目标被击毁的概率;2)己知目标被击毁,求由一人击中的概率。
解:设事件戌ZAC分别表示甲、乙、丙击中目标,Z)表示目标被击毁,•表示有f人击屮目标(i=l,2, 3),根据题意,P(A) = 0.4, P(5) = 0.5, P(C) = 0.7, P(£>|//,) = 0.2,P(Z)|H2) = 0.6, P(D|H3) = 1,由于事件A B,C相互独立,所以1)P(H[) = P(ABC u ABC u ABC) = 0.36, P(H2) = P(ABC U ABC U ABC) = 0.41,P(H3) = P(ABC) = 0.14,由全概率公式3p(D) = [ P(H.)P(D|H ) = 0.36x0.2 + 0.41x0.5 + 0.14x1=0.458/=12)由贝叶斯公式,所求概率为P(H1£>)_ 0.36x0.2P(HJD) == 0.1572P(D) ~ 0.458kx 1,三、(15分)已知一随机变量的密度函数为人(x)=々(4-%), 0,1) 々的取值,•2) X 的分布函数F x (x)的表达式, 3) Y = —2X +3的分布函数和密度函数。
工程数学“概率论与数理统计”测试题参考答案

工程数学“概率论与数理统计”测试题参考答案工程数学期末复习要点邹斌现在主要讨论工程数学这门课程的考核要求,08秋工程数学考试形式为半开卷,行考比例占30%,我们将分章节复习。
本课程分线性代数和概率统计两部分共7章内容。
分别是行列式、矩阵、线性方程组、矩阵的特征值及二次型、随机事件与概率、随机变量的分布和数字特征、数理统计基础。
第一部分线性代数一、行列式复习要求(1)知道n阶行列式的递归定义;(2)掌握利用性质计算行列式的方法;(3)知道克莱姆法则。
考核要求:行列式性质的计算(选择或填空)二、矩阵复习要求(1)理解矩阵的概念,了解零矩阵、单位矩阵、数量矩阵、对角矩阵、上(下)三角矩阵、对称矩阵的定义,了解初等矩阵的定义;(2)熟练掌握矩阵的加法、数乘矩阵、乘法、转置等运算;(3)掌握方阵乘积行列式定理;(4)理解可逆矩阵和逆矩阵的概念及性质,掌握矩阵可逆的充分必要条件;(5)熟练掌握求逆矩阵的初等行变换法,会用伴随矩阵法求逆矩阵,掌握求解简单的矩阵方程的方法;(6)理解矩阵秩的概念,掌握矩阵秩的求法;(7)会分块矩阵的运算。
考核要求:(1)矩阵乘法(选择或填空)(2)求逆矩阵(3阶)初等行变换法(计算题)(3)求矩阵的秩(等于阶梯形矩阵的非零行数)三、线性方程组复习要求(1)掌握向量的线性组合与线性表出的方法,了解向量组线性相关与线性无关的概念,会判别向量组的线性相关性;(2)会求向量组的极大线性无关组,了解向量组和矩阵的秩的概念,掌握求向量组的秩和矩阵的秩的方法;(3)理解线性方程组的相容性定理,理解齐次线性方程组有非零解的充分必要条件。
熟练掌握用矩阵初等行变换方法判断齐次与非齐次线性方程组解的存在性和惟一性;(4)熟练掌握齐次线性方程组基础解系和通解的求法;(5)了解非齐次线性方程组解的结构,掌握求非齐次线性方程组通解的方法。
考核要求:(1)线性相关性(选择或填空)(2)会求向量组的极大线性无关组(计算题)(3)线性方程组的判定定理(选择或填空)(4)熟练掌握齐次和非齐次方程组的基础解系和通解的求法(计算题)四、矩阵的特征值及二次型复习要求(1)理解矩阵特征值、特征多项式及特征向量的定义,掌握特征值与特征向量的求法;(2)了解矩阵相似的定义,相似矩阵的性质;(3)知道正交矩阵的定义和性质;(4)理解二次型定义、二次型的矩阵表示、二次型的标准形,掌握用配方法化二次型为标准形的方法;(5)了解正定矩阵的概念,会判定矩阵的正定性。
北民大概率论期末考试试题

北方民族大学试题课程代码:24100082 课程:概率论与数理统计(A 卷)一、填空题:(每小题3分,共30分)1.设8.0)(,5.0)(==A B P A P ,则=)(AB P ______ 。
2.设在一次试验中,事件A 发生的概率为p,现进行n 次独立试验,则A 至少发生一次的概率为 ______ 。
3.设X 的分布律为则分布函数值=)25(F ______ 。
4.设随机变量X ~N(0,1),)x (Φ为其分布函数,则)()x x -Φ+Φ(=______ 。
5.已知连续型随机变量X 的分布函数为2200,1),1(31,31)(≥<≤<⎪⎪⎪⎩⎪⎪⎪⎨⎧+=x x x x e x F x,设X 的概率密度为)(x f ,则当=<)(,0x f x ______ 。
6.设X 服从正态分布N(μ,2σ),则=-)23(X E ______ 。
7.设随机变量X 与Y 相互独立,则X 与Y 的相关系数=XY ρ_____。
8.设随机变量X 的分布律为!3)(3k e k X P k -==,,,2,1,0 =k 则)(2X E =______ 。
X0 1 2 3 P(X=k) 0.10.30.40.29. 设随机变量X 与Y 相互独立,且,2)(,1)(==Y D X D 则=-)(Y X D ______ 。
10.若4321,,,X X X X 为来自正态分布N(0,4)的样本,则∑=41241i i X ~______ 分布 。
二、设有N 件产品,其中有D 件次品,今从中任取n 件,问其中恰有k(D k ≤)件次品的概率。
(10分)三、设随机变量X 的概率密度函数为,其他10,0,3)(2<≤⎩⎨⎧=x x x f 求: (1)X 的分布函数;(2)⎭⎬⎫⎩⎨⎧≤<-2121X P .(10分)四、设随机变量X 具有概率密度,其他,0,)(>⎩⎨⎧=-x e x f x 求随机变量2X Y =的概率密度。
北方工业大学概率论试卷及答案

p11 p1 p1 , pij pi p j , i, j 1, 2,3.
(4 分)
第 4页 共 7页
, 相互独立.
北方工业大学试卷
六、 (10 分)设二维随机变量 ( X , Y ) 的概率密度为
1 ( x y ), f ( x, y) 8 0,
0 x 2 ,0 y 2 其它
求 E ( X ), E (Y ), D( X ), D(Y ), E ( XY ), COV ( X , Y ), XY 解:
解: (1) E ( X )
0
2
2
0
xf ( x , y )dxdy
2
0
2
2
0
1 7 x (x y)dxdy 8 6
格率为 98%,乙厂产品合格率为 85%,现从市场任意购买一节电池,求:
(1)所购买的电池是合格品的概率? (2)若已知所购买的电池是合格品,该电池是甲厂生产的概率? 解:
A={甲厂生产}
B={乙厂生产}
C={合格}, (1 分) (1 分) (1 分)
则 P ( A) 0.8 , P ( B ) 0.2 ,
XY
Cov ( X , Y ) D( X ) D(Y )
1 / 36 1 / 11 11 / 36
1 x , 0 x 1 七、 (10 分)设总体 X 概率密度为 f ( x ) , 1 未知, 其他 0,
X 1 , X 2 , X n 为来自总体的一个样本. 求参数 的矩估计量和极大似然估计
2
2
0
yf ( x , y )dxdy
2
概率论09-10A附答案

概率论09-10A附答案(总4页)重庆理工大学考试试卷2009~ 2010 学年第 2 学期班级 学号 姓名 考试科目 概率与数理统计 A 卷 闭卷 一、 单项选择题(每小题2分,共22分)1、设事件A 与B 互为对立事件,且()0,()0,P A P B >>则下列命题不成立的是( )A 、A 与B 不相容 B 、A 与B 相互独立C 、A 与B 不独立D 、A B 与互不相容2、设()F x 是连续型随机变量X 的分布函数,12,x x 为任意两实数,且12x x <,则( )不一定成立 A 、()F x 在1x 点连续 B 、12()()F x F x ≤ C 、12()()F x F x < D 、{}2112()()F x F x P x x x -=<≤3、设随机变量X 的分布函数为()⎪⎩⎪⎨⎧>≤≤<=1110003x x x x x F ,则()E X =( ) A 、⎰+∞04dx x B 、+⎰14dx x ⎰+∞1xdx C 、⎰133dx x D 、⎰+∞33dx x4、设127,,,X X X 取自总体2~(0,0.5)X N ,则7214i i P X =⎧⎫>=⎨⎬⎩⎭∑( )(22220.050.0250.010.05(7)14.067,(7)16.012,(7)18.474,(6)12.592χχχχ====)A 、0.5B 、0.025C 、0.05D 、0.015、每张彩票中奖的概率为0.1,某人购买了20张号码杂乱的彩票,设中奖的张数为X ,则X 服从( )分布。
A 、01- B 、 二项 C 、泊松 D 、指数.6、由()()()E XY E X E Y =可断定( ) A 、X 与Y 相互独立B 、X 与Y 不独立C 、X 与Y 不相关D 、X 与Y 相关7、设商店售盐,每包重量是一个随机变量,其数学期望为1kg ,方差为0.0005kg ,500包这种食盐总重量在499~501kg 之间的概率为( ).A 、2(1)1Φ-B 、1(2)-ΦC 、1(1)-ΦD 、2(2)1Φ-8、将n 只球随机地投入n 只盒子中,则每只盒子中各有一只球的概率为( )。
概率论与数理统计试卷及答案

华东理工大学2008–2009学年第二学期《概率论与数理统计》课程考试试卷 A 卷 2009.7.2开课学院: 理学院 ,专业:大面积 ,考试形式:闭卷 , 所需时间:120分钟 考生姓名: 学号: 班级: 任课教师:一、(共12分)设二维随机变量),(Y X 的概率密度函数为⎩⎨⎧>>=--其他,00,0,),(2y x ke y x f y x , (1) 求常数k (3分); (2) 求}{Y X P >(3分);(3) 证明:X 与Y 相互独立(6分)。
解:(1)1),(=⎰⎰∞∞-∞∞-dxdy y x f ,……………………………………….2’102=⎰⎰∞∞--dxdy ke y x ,2=k ;………………………………………1’(2)}{Y X P >⎰⎰∞--=22xy x dxdy e dx ……………………………….2’32311=-=………………………………………………1’ (3)⎩⎨⎧≤>=⎪⎩⎪⎨⎧≤>=-∞--⎰0,00,0,00,2)(02x x e x x dy e x f xy x X ,……………………………..2’ ⎩⎨⎧≤>=⎪⎩⎪⎨⎧≤>=-∞--⎰0,00,0,00,2)(202y y e y y dx e y f yy x Y …………………………………2’ 因为)()(),(y f x f y x f Y X =,所以X 与Y 相互独立。
………………………………….2’二、(10分)某公司经销某种原料,根据历史资料表明:这种原料的市场需求量X (单位:吨)服从 (300,500)上的均匀分布。
每售出1吨该原料,公司可获利1万5千元;若积压1吨,则公司损失5千元。
问公司应该组织多少货源,可使平均收益最大?解:设公司组织货源a 吨,此时的收益额为Y (单位:千元),则)(X g Y =,且⎩⎨⎧<--≥=a X X a X a X a Y ),(5.05.1,5.1⎩⎨⎧<-≥=a X a X a X a ,5.02,5.1………………2’X 的概率密度函数为 ⎪⎩⎪⎨⎧∈=其他,0)500,300(,2001)(x x f ……………………..1’ =EY ⎰∞∞-dx x f x g )()(⎰⎰⋅+⋅-=50030020015.12001)5.02(a a dx a dx a x )300900(200122-+-=a a ……………………………………………………3’ 令0)9002(2001=+-=a da dEY ,…………………………………………………2’450=a (唯一驻点), 又0100122<-=da EY d 所以,当450=a 吨时,可以使平均收益EY 最大,即公司应该组织货源450吨。
2009理工概率统计统考题A卷(本科)

2009年文华学院概率统计统考试题 (A 卷)一.填空题(每题2分,共20分)1、事件A ,B ,C . 则用A ,B ,C 及其运算关系可将事件,“A ,B ,C 中至少有二个发生”表示为 .2、已知P(A)=0.5,P (B )=0.6,当A ,B 相互独立时,_____)B A (_____,)(=-=⋃P B A P 。
3、若随机变量X 在区间 (,)a b 上服从均匀分布,则对,(,)c c l a b ∀+∈必有概率{}P c x c l <<+ = _____________4、设X 服从正态分布(2,3)N ,则~32X -=Y .5.____________,1X P 3X P 22X P ),,B ~X =======p n p n )则()()(且(6、袋中装有5只球,编号为1,2,3,4,5,在袋中同时取出3只,以X 表示取出3只球中的最小号码。
则X 的数学期望=)(X E 。
7、设随机变量(,)X Y 的分布律为则条件概率 ===}2X |3Y {P .8.设),(Y X 在正方形区域{01;01}x y ≤≤≤≤上服从均匀分布,则)(x f X = 。
)(y f Y =9、设n 1,,X X 来自正态总体) ,(2σμN ,2S ,X 分别是样本均值与方差,则S X n )(μ-=Y ~ 。
10.设n 1,,X X 来自正态总体) ,(2σμN ,参数2 σ已知,则对于给定的α参数μ 的α-1置信区间为: 。
二:判断题: (每题2分,共10分)1.如果事件A ,B 互不相容,则必相互独立 ( )2.P (A-B )=P (A )-P (B ) ( )3.如B A ⊂则1/B P =)(A ( )4.样本是和总体同分布的,相互独立的随机变量 ( )5.样本的函数称统计量 ( )三.计算题(每小题10分,共60分)1甲袋中有4只白球,6只红球,乙袋中有3只白球,7只红球,今从甲袋任取1球放入乙袋,再从乙袋中任取1球:⑴求所取球为白球的概率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5.设 , 为其分布函数,则 .
6.设总体服从正态分布 , 是来自总体 的样本,则 .
二、单项选择题(每小题3分,共18分)
1.设 且 ,则 ().
(A)0.65;(B)0.45;(C)0.25;(D)0.95.
2.离散型随机变量 的分布函数为 ,则 ( ).
(A) ; (B) ; (C) ; (D) .
3. 设随机变量 和 相互独立,方差分别为6和3,则 =().
(A) 9;(B)27;(C) 21;(D)15.
4.对于给定的正数 , ,设 , , , 分别是 , , , 分布的上 分位数,则下面结论中不正确的是().
(A) ;(B) ;(C) ;(D) .
5.设 ( )为来自总体 的一简单随机样本,则下列估计量中不是总体期望 的无偏估计量有().
0
2
0.5
0.1
0.05
0.25
1
0.1
0.05
0.1
0.25
2
0.2
0.1
0.5
0.2
0.4
六、(本题15分)设二维随机变量 具有概率密度Байду номын сангаас ,
1.求边缘密度 ;2.问 与 是否相互独立;3.求概率 ;
4.求 , ;5.求 .
七、(本题8分)设总体 的概率密度为: ,其中 为未知参数, 为来自总体 的样本值,求 的最大似然估计值.
八、(本题7分)已知某种白炽灯泡的寿命 服从正态分布,即 ,在一批该种灯泡中随机地抽取9只测寿命,得样本平均值 小时,样本标准差 小时,求未知参数 的置信度为0.95的置信区间.
(参考数据: , , , ,结果小数点后保留两位)
(A) ;(B) ;(C) ;(D) .
6.设总体 , 为已知, 是来自总体 的样本,在给定的显著性水平 下,检验假设 , ,需要选择的检验统计量为().
(A) ;(B) ;(C) ;(D) .
三、计算题(每小题6分,共12分)
1.设一批混合麦种中一、二、三、四等品分别占94%、3%、2%、1%,四个等级的发芽率依次为0.98,0.95,0.9,0.85求这批麦种的发芽率.
北华大学08-09学年第二学期
《概率论与数理统计》课程期末考试试卷(A卷)
题号
一
二
三
四
五
六
七
八
九
总分
得分
评卷人
核分:
一、填空题(每空3分,共18分)
1.设 与 为随机事件,且 ,则 .
2.三次独立的试验中,成功的概率相同,已知至少成功一次的概率为 ,则每次试验成功的概率为.
3.设 的概率密度为: ,则 .
2.离散型随机变量 的分布函数
,求 的概率分布律.
四、(本题12分)设盒中有5个球,其中2个白球,3个红球,现从中随机取3球,设X为抽得白球数,求:1.X的概率分布律;2.至少有一只白球的概率;3. .
五、(本题10分)设离散型随机变量 的联合分布律与边缘分布律如下表,
1.求表中 的值;2.求 ;3.求协方差 .
