20131220量子力学基础-黄琼
高考物理竞赛量子力学部分第八章 散射理论ppt课件

§8.2 分波法
2020届高考物理竞赛量子力学部分第 八章 散射理论(共69张ppt)
§8.2 分波法
2020届高考物理竞赛量子力学部分第 八章 散射理论(共69张ppt)
2020届高考物理竞赛量子力学部分第 八章 散射理论(共69张ppt)
§8.2 分波法
2020届高考物理竞赛量子力学部分第 八章 散射理论(共69张ppt)
§8.3 分波法示例
2020届高考物理竞赛量子力学部分第 八章 散射理论(共69张ppt)
§8.3 分波法示例
➢球对称常势阱
2020届高考物理竞赛量子力学部分第 八章 散射理论(共69张ppt)
2020届高考物理竞赛量子力学部分第 八章 散射理论(共69张ppt)
§8.3 分波法示例
2020届高考物理竞赛量子力学部分第 八章 散射理论(共69张ppt)
2020届高考物理竞赛量子力学部分第 八章 散射理论(共69张ppt)
§8.1 散射问题的一般描述
§8.2 分波法
➢关键:
▪ 入射平面波是{p, Lz, H}的共同本征态
▪ 当势场U=U(r)时,p不再守恒,散射波是 {L^2, Lz, H}的共同本征态
▪ 当将平面波按角动量平方L^2的本征态,即球 面波展开后,对每个分波,因为是{L^2, Lz, H}的本征函数,所以在U(r)作用后,每个分 波只是向前或者向后移动
高考物理竞赛量子力学部分第八章 散射理论ppt课件
第八章 散射理论
复旦大学 苏汝铿
高考物理竞赛量子力学部分第八章 散射理论ppt课件
A bird’s eye view of RHIC
A bird’s eye view of LHC(CERN)
量子力学黄皮书讲解

量子力学黄皮书讲解量子力学黄皮书是指《The Principles of Quantum Mechanics》一书,该书是由物理学家保罗·迈尔斯于1930年代撰写的,被誉为量子力学的经典教材之一。
本文将从黄皮书的结构、内容和意义三个方面来讲解量子力学黄皮书。
黄皮书的结构非常清晰,分为10章,涵盖了量子力学的基本原理以及一些应用领域。
第一章介绍了量子力学的历史背景和基本概念,包括波粒二象性、不确定性原理等。
第二章讨论了量子力学的数学基础,包括波函数、算符和态矢量等。
第三章介绍了量子力学的测量理论,包括测量算符和测量结果的统计性质。
第四章研究了定态问题,即粒子在势场中的行为。
第五章讨论了矩阵力学,即量子力学的一个重要形式。
第六章介绍了自旋和角动量的量子力学描述。
第七章研究了量子力学的微扰理论,用于处理近似求解。
第八章讨论了量子力学的路径积分方法,是一种替代的求解方法。
第九章介绍了量子力学的相互作用理论,用于描述多粒子系统。
最后一章探讨了量子力学的统计性质,包括玻尔兹曼统计和费米-狄拉克统计。
黄皮书的内容丰富而详细,对量子力学的各个方面都进行了深入的研究。
书中引入了大量的数学工具,如线性代数、微积分等,以便读者更好地理解和应用量子力学的原理。
此外,黄皮书还介绍了一些经典的实验,如双缝实验、斯特恩-盖拉赫实验等,用于验证量子力学的预言。
在应用方面,黄皮书讨论了一些重要的问题,如氢原子的能级结构、振动子和旋转子的量子力学描述等。
此外,黄皮书还介绍了一些重要的定理和方法,如哈密顿-雅可比方程、量子力学的微扰理论和路径积分方法等。
黄皮书对于量子力学的发展和意义具有重要的影响。
该书系统地阐述了量子力学的基本原理和数学形式,为后来的研究和应用奠定了基础。
许多物理学家和科学家都通过阅读黄皮书来学习量子力学,并将其中的理论和方法应用于自己的研究中。
此外,黄皮书对于量子力学的哲学和观念也进行了一些讨论,如波粒二象性的解释、测量问题的解释等,对于理解量子力学的本质和哲学意义有一定的帮助。
第二章 晶体振动

nq Ae
q
A是振幅,ω 是角频率,q 是波数,λ 是波长,naq 是第n 个原子的位相因子,将试解代入方程求解。
m Ae
2
i t naq
Ae
m 2 eiaq eiaq 2 2 cos aq 1(利用欧拉公式)
解得
2
q
相速和群速:
a
max
4 m
相速度v p 是单色波单位时间内一定的振动位相所传播的
距离。群速度 v q 是平均频率为ω ,平均波矢为q 的波包的
传播速度,它是合成波能量和动量的传播速度。
vp f
q
d vq dq
在 q 0 的长波极限下:
v p vq v s
m sin 1 aq 2
i t n 1aq
Ae
i t n 1aq
2 Ae
i t naq
—— 色散关系 Dispersion curves
这个结果与 n 无关,说明 N 个方程都有同样结果,即所有原 子都同时以相同的频率ω和相同的振幅 A 在振动,但不同的原 子间有一个相差,相邻原子间的相差是 qa 。 该结果还表示:只要ω和q 满足上述关系,试解就是联立方程 的解。通常把ω和 q 的关系称作色散关系。
运动方程: 考虑N个质量为 m 的同种原子组成的一维单原子链。设平 衡时相邻原子间距为 a(即原胞大小),在 t 时刻第 n 个原子 偏离其平衡位置的位移为 nBiblioteka n2n1n
n1
n2
为了建立起运动方程,我们首先要对原子之间的相互作用力 做些讨论,设在平衡时,两原子的相互作用势为V(a),产生 相对位移(例如 n1 n)后势能发生变化是V(a+δ) ,将 它在平衡位置附近做泰勒展开:
量子力学黄皮书讲解

量子力学黄皮书讲解量子力学是一门研究微观世界的物理学理论,被誉为20世纪最重要的科学理论之一。
它揭示了微观粒子的奇妙行为和性质,对于理解原子、分子、光与物质相互作用等现象具有重要意义。
黄皮书是量子力学领域中一本经典的教材,以其严谨的理论推导和系统的内容向读者介绍了量子力学的基本原理和应用。
黄皮书的讲解从经典物理学的视角出发,引导读者理解量子力学的背景和发展历程。
它首先介绍了黑体辐射和光电效应的实验现象,这些实验结果无法用经典物理学的理论来解释。
为了解释这些现象,量子力学引入了“能量量子化”的概念,即能量不是连续的,而是以最小单位的量子形式存在。
这一概念颠覆了传统物理学关于能量连续性的假设,开启了全新的物理学领域。
接着,黄皮书详细介绍了波粒二象性,即微观粒子既具有波动性又具有粒子性。
这一概念由德布罗意提出,并通过实验验证。
他的实验利用电子通过晶体时的衍射现象,证明了电子具有波动性。
这一实验奠定了量子力学的基础,并为后来的发展提供了重要的实验依据。
在介绍了波粒二象性后,黄皮书探讨了量子力学中的不确定性原理。
不确定性原理由海森堡提出,它指出对于某些共轭变量,如位置和动量,无法同时精确确定其数值。
这与经典物理学中的确定性原理形成了鲜明对比。
不确定性原理揭示了微观世界的固有限制和测量的局限性,成为后来量子力学理论发展的重要基础。
黄皮书还介绍了量子力学中的波函数和算符理论。
波函数是量子力学中描述微观粒子状态的数学工具,它包含了粒子的所有可能状态和性质。
算符理论则是量子力学中处理物理量测量的数学框架,它将物理量与数学算符相联系。
通过对波函数和算符理论的深入理解,我们可以计算和预测微观粒子的行为和性质。
除了基本原理的讲解,黄皮书还涵盖了量子力学的应用领域,如原子和分子物理、固体物理、粒子物理等。
它介绍了量子力学在这些领域中的重要实验和理论成果,为读者提供了对于量子力学实际应用的深入了解。
总结起来,黄皮书是一本经典的量子力学教材,通过系统而严谨的讲解,向读者介绍了量子力学的基本原理和应用。
《固体物理·黄昆》第七章(1)(1)

(2) 从电子的热容量可获得费米面附近能态密度的信 息。
一般温度下,晶格振动的热容量比电子的热容量大得多。 在温度较高下,晶格振动的热容量是主要的,热容量基 本是一个常数。
低温范围下不能忽略电子的 热容量。
C Metal V
CVPhonon bT 3
CVElectron T
EF0 kB
物理意义:设想将EF0转换成热振动能,相当于多高
温度下的振动能。
金属:TF: 104 ~ 105 K
对于金属而言,由于T << TF总是成立的,因此,只有 费米面附近的一小部分电子可以被激发到高能态,而 离费米面较远的电子则仍保持原来(T=0)的状态, 我们称这部分电子被“冷冻”下来。因此,虽然金属 中有大量的自由电子,但是,决定金属许多性质的并 不是其全部的自由电子,而只是在费米面附近的那一 小部分。
EF
E
0 F
[1
2
12
(
kBT EF0
)2
]
温度升高,费米能 级下降
EF
EF0
[1
2
12
(
kBT
E
0 F
)
2
]
T 300 K
kBT 2.6 102 eV
kBT
E
0 F
1
EF0 ~ several eV
EF EF0
三、 电子热容量
根据电子的能量分布得电 U f (E)EN (E)dE
子总能量:
由于(-f/E)具有类似函数特征,改变积分下限并
不会改变积分值
N
Q(EF ) (
f )dE E
Q '(EF ) (E
EF )(
《固体物理学(黄昆)》课后习题答案(2)
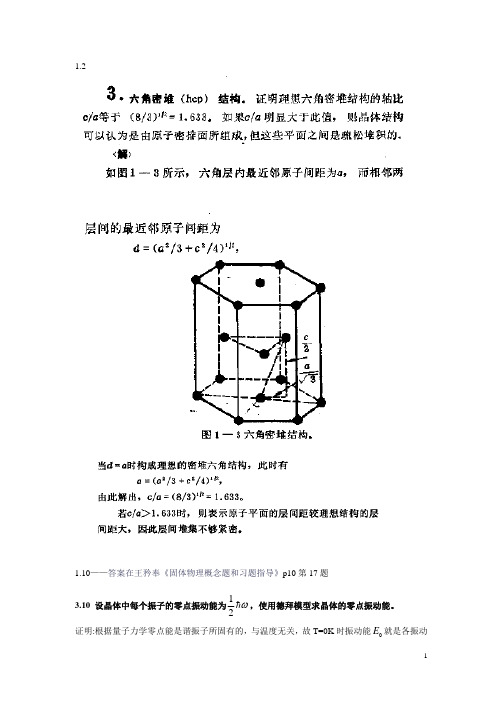
1.10——答案在王矜奉《固体物理概念题和习题指导》p10 第 17 题
3.10 设晶体中每个振子的零点振动能为
1 ,使用德拜模型求晶体的零点振动能。 2
证明:根据量子力学零点能是谐振子所固有的,与温度无关,故 T=0K 时振动能 E0 就是各振动
1
模零点能之和。 E0
m
0
E0 g d 将E0
将
M
us ueisKa e it , Vs VeisKa e it . 代入上式有
M 2u C 10 e ika V 11Cu , M 2V C eika 10 u 11CV ,
4
是 U,v 的线性齐次方程组,存在非零解的条件为
2 2 2 2 Kx , 2m 2m a 2m a
2 2 2 2 2 2 2 2 B点能量 B K x K y 2 m 2 , 所以 B / A 2 2m a a 2m a
所以 B / A 3
(c)如果二价金属具有简单立方品格结构,布里渊区如图 7—2 所示.根据自由电子理
2 2 论,自由电子的能量为 K x2 K y K z2 ,FerM 面应为球面.由(b)可知,内切于 2m
4 点的内切球的体积
3
4 3
,于是在 K 空间中,内切球内能容纳的电子数为 a
当 K= / a 时
2 20C / M , 2 2C / M ,
当 K=0 时,
2 22C / M , 2 0,
2 与 K 的关系如下图所示.这是一个双原子(例如 H 2 )晶体
黄昆版固体物理课后习题解答
《固体物理学》习题解答黄昆 原著 韩汝琦改编 (陈志远解答,仅供参考)第一章 晶体结构1.1、解:实验表明,很多元素的原子或离子都具有或接近于球形对称结构。
因此,可以把这些原子或离子构成的晶体看作是很多刚性球紧密堆积而成。
这样,一个单原子的晶体原胞就可以看作是相同的小球按点阵排列堆积起来的。
它的空间利用率就是这个晶体原胞所包含的点的数目n 和小球体积V 所得到的小球总体积nV 与晶体原胞体积Vc 之比,即:晶体原胞的空间利用率, VcnVx = (1)对于简立方结构:(见教材P2图1-1)a=2r , V=3r 34π,Vc=a 3,n=1 ∴52.06r 8r34a r 34x 3333=π=π=π= (2)对于体心立方:晶胞的体对角线BG=x 334a r 4a 3=⇒= n=2, Vc=a 3∴68.083)r 334(r 342a r 342x 3333≈π=π⨯=π⨯=(3)对于面心立方:晶胞面对角线BC=r 22a ,r 4a 2=⇒= n=4,Vc=a 374.062)r 22(r 344a r 344x 3333≈π=π⨯=π⨯= (4)对于六角密排:a=2r 晶胞面积:S=6260sin a a 6S ABO ⨯⨯=⨯∆=2a 233 晶胞的体积:V=332r 224a 23a 38a 233C S ==⨯=⨯ n=1232126112+⨯+⨯=6个 74.062r224r 346x 33≈π=π⨯= (5)对于金刚石结构,晶胞的体对角线BG=3r 8a r 24a 3=⇒⨯= n=8, Vc=a 334.063r 338r 348a r 348x 33333≈π=π⨯=π⨯=1.2、试证:六方密排堆积结构中633.1)38(a c 2/1≈=证明:在六角密堆积结构中,第一层硬球A 、B 、O 的中心联线形成一个边长a=2r 的正三角形,第二层硬球N 位于球ABO 所围间隙的正上方并与这三个球相切,于是: NA=NB=NO=a=2R.即图中NABO 构成一个正四面体。
高考物理竞赛量子力学部分 第五章 近似方法ppt课件
2020届高考物理竞赛量子力学部分 第五章 近似方法(共118张ppt)
§5.2 简并定态微扰
2020届高考物理竞赛量子力学部分 第五章 近似方法(共118张ppt)
2020届高考物理竞赛量子力学部分 第五章 近似方法(共118张ppt)
§5.2 简并定态微扰
2020届高考物理竞赛量子力学部分 第五章 近似方法(共118张ppt)
2020届高考物理竞赛量子力学部分 第五章 近似方法(共118张ppt)
§5.1 非简并定态微扰论
2020届高考物理竞赛量子力学部分 第五章 近似方法(共118张ppt)
2020届高考物理竞赛量子力学部分 第五章 近似方法(共118张ppt)源自§5.1 非简并定态微扰论
➢说明: ▪ H’<<H0是指
2020届高考物理竞赛量子力学部分 第五章 近似方法(共118张ppt)
§5.1 非简并定态微扰论
§5.1 非简并定态微扰论
§5.1 非简并定态微扰论
§5.1 非简并定态微扰论
§5.1 非简并定态微扰论
§5.1 非简并定态微扰论
§5.1 非简并定态微扰论
2020届高考物理竞赛量子力学部分 第五章 近似方法(共118张ppt)
§5.1 非简并定态微扰论
2020届高考物理竞赛量子力学部分 第五章 近似方法(共118张ppt)
2020届高考物理竞赛量子力学部分 第五章 近似方法(共118张ppt)
§5.1 非简并定态微扰论
2020届高考物理竞赛量子力学部分 第五章 近似方法(共118张ppt)
2020届高考物理竞赛量子力学部分 第五章 近似方法(共118张ppt)
§5.1 非简并定态微扰论
➢说明: ▪ 电介质在x方向加均匀弱电场E后的极化率
量子力学的物理基础
dε
= kT
− εβ
dε
8ayleigh-Jeans 公式
dE ν = ε (ν )dν =
(1.2)
这个公式与 Wien 公式的情况正好相反,它在低频部分与实验曲线符
1
合得很好,但在高频波段不但不符合,出现黑体辐射能量密度随频率 增大趋于无穷大的荒谬结果。这就是著名的所谓“紫外灾难”,是 经典物理学最早显露的困难之一。 1900 年 Planck 用一种崭新的观念来计算平均能量 ε ν 。他引入了 “能量子”的概念,即,假设黑体辐射空腔中振子的振动能量并不 象经典理论所主张的那样和振幅平方成正比并呈连续变化, 而是和振 子的频率 ν 成正比并且只能取分立值,
λ ′ − λ = λ c (1 − cosθ )
2, 第二组实验——粒子的波动性实验:电子 Young 双缝 实验、电子在晶体表面的衍射实验以及中子在晶体上的衍射 实验。
这些实验表明,原先认为是粒子的这些微观客体,其实也具有波 的性质,有时也呈现出只有波才具有的干涉、衍射现象。它们从实验 上揭示了微粒的波动性质。
P ( x ) = P1 ( x ) + P2 ( x ) + 干涉项
这一干涉项可正可负,随 x 迅速变化,从而使 P( x ) 呈现明暗相间的干 涉条纹。 如果通过缝屏的是光波、 声波, 出现这种干涉项是很自然的。 因为在 x 处的总波幅 ψ ( x ) 是由孔 1、孔 2 同时传播过来的波幅ψ 1 ( x ) 、 ψ 2 ( x ) 之和
第一章 §1.1 ,实验基础
量子力学的物理基础
1, 第一组实验 —— 光的粒子性实验: 黑体辐射、光电效应、 Compton 散射
能量分立、辐射场量子化的概念,实验揭示了光的粒子性质。 《黑体辐射谱问题》 黑体辐射谱的 Wien 经验公式(1894 年): 考虑黑体腔内辐射场。令辐射场中频率在ν 附近单位频率间隔内 的能量密度为 ε (ν ) ,则 dν 内能量密度为 dE ν = ε (ν ) dν ,该经验公式为 (1.1) dEν = ε (ν )dν = Nν εν dν = c1ν 3e − c νβ dν 这里 c1 、 c2 是两个常系数, β = 1/ kT 。此公式在短波长(高频率)区 间内与实验符合,但在中、低频区,特别是低频区与实验差别很大。 Rayleigh-Jeans 公式(1900,Rayleigh;1905,Jeans): 将腔中黑体辐射场看成大量电磁波驻波振子集合, 利用能量连续 分布的经典观念和 Maxwell - Boltzmann 分布律,即可导出黑体辐射 谱的经典理论表达式。为此令 ε (ν ) = N ν ε ν , ε ν 是频率 ν 驻波振子的平 均能量, N ν 是单位体积辐射场中频率在 ν 附近单位频率间隔内驻波振
量子力学教学改革总结详解
概况
一、近五年来主讲的主要课程
承担下列பைடு நூலகம்科课程:
1.量子力学(本科基础课,4学时/周,60学时,4届,60人/届
2.大学物理学,(本科基础课),4学时/周,120学时,5届,210-230人/届
3.光学传感器技术,专业课,4学时/周,40学时,1届,8人
4.光子材料学,专业课,4学时/周,32学时,4届,40人
3)科研促进教学,教师结合自己科研,将学科发展的前沿知识融入教学中,调动学生积极性,开拓学生思维,使课内与课外有机结合,开阔了学生的视野,提高了学习兴趣。
三、近年来的获奖和荣誉称号
1.激光激励层状材料中超声检测理论与实验研究,2007获兵器工业集团公司科学技术奖励进步奖三等奖,主要完成人
2.非球形微粒的光学测量理论及其应用技术,2005,镇江市科学技术进步三等奖,第四
3.2009年度江苏大学优秀党员
4.2011年教书育人先进个人
5.2012年江苏大学优秀教师
1-3
学术
研究
一、近年来承担的主要科研项目:
1.设计基于机电阻抗的快速自适应健康监测系统(11172114),国家自然科学基金,2012.01- 2015.12,(主持)
2.基于挠曲电效应的航空结构早期损伤监测应变梯度传感器,高等学校博士学科点专项科研基金优先发展领域课题,2013.01-2015.12,(排名3/10)
9.激光激励层状材料中超声检测理论与实验研究,国家自然科学基金项目(60208004),2003.1-2005.12,第四
10.国家自然科学基金(60578015):激光空泡发展机制、软科学效应和光学测试方法(2005-2007),排名第四,主要为理论研究、建模和数值模拟
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
o
1、 斯忒藩—玻尔兹曼定律
黑体辐射的总辐射本领(辐出度)
M B ( T ) M B ( T )d (即曲线下的面积)
0
M B ( T ) T 4
M B (T )
辐出度与黑体的热力学温度T的四次方成正比。
5.67 10 8 W m 2 K 4 — 斯忒藩常数
1100 K
o
M B (T )
(μm) 0
2、 维恩位移定律
1
2
3
4
5
6
M B ( T )
mT b
b 2.898 10 m K — 维恩常数
3
m 峰值波长
物理意义:T增加, m 减小。当绝对黑 体的温度升高时,单色辐出度最大值向 短波方向移动。
如何从理论上推导出符合实验结果的函数表达 式就成为当时物理学中引入注目的问题之一。
1921年获诺贝尔物理学奖
波尔(丹麦) 1885-1962 1922年获诺贝尔物理学奖
•1900~1926年是量子力学的酝酿时期,此时的量子力 学是半经典半量子的学说,称为旧量子论。
1929诺贝尔物理学奖
L.V.德布罗意 电子波动性的理论 研究
整个世纪以来,在辐射理论上,比 起波动的研究方法来,是过于忽视了粒 子的研究方法;在实物理论上,是否发 生了相反的错误呢?是不是我们关于粒 子图象想得太多,而过分地忽略了波的 图象呢? L.V.de Broglie
1895年,维恩(1864—1928年)从理论分 析得出,一个带有小孔的空腔的热辐 射 性能可以看作一个黑体。
一束光一旦从狭缝射入空腔后,就很难再通过 狭缝反射出来,这个空腔的开口就可以被看作 黑体。 所谓黑体是指入射的电磁波全部被吸收,既没 有反射,也没有透射( 当然黑体仍然要向外辐 射 )。
历史回顾:
1859年,柏林大学教授基尔霍 夫(1824— 1887年)根据实验的启发,提出用黑体作为理 想模型来研究热辐射。所谓黑体是指一种能够
完全吸收投射在它上面的辐射而全无反射和透
射的,看上去全黑的理想物体。
什么是黑体
记得有人在评论某人时(例如,莎士比亚的喜 剧《威尼斯商人》中的高利贷者夏洛克)人们 会称他为黑心。就是说他贪得无厌,什么都要。 若一个物体对什么光都吸收而没有反射(全部 吸收投射在它上面的辐射而无反射),我们就称这 种物体为绝对黑体。 事实上当然不存在绝对黑体,黑体是一种理想 的模型,在自然界中并不存在完全理想的黑体。 不过有的物体可以近似当做黑体处理。 黑体: 在任何温度下,全部吸收任何波长的辐 射的物体。
事实上还有第三朵小小的乌云,这就是放射性现象的发现, 它有力地表明了原子不是构成物质的基本单元,原子也是可以 分割的。
所有这些实验结果都是经典物理学无法解释的,它们使经 典物理处于十分困难境地,为摆脱这种困境,有一些思想敏锐 而又不受旧观念束缚的物理学家纷纷重新思考研究,在二十世 纪初期,建立起了近代物理的两大支柱------量子论和相对论, 并在这个基础上又建立起以研究原子的结构、性质及其运动规 律为目的的原子物理学,后来又进一步发展,相继建立起原子 核物理学和基本粒子物理学,这些内容统称为量子物理学。
用越来越广泛。
由安培、法拉第和麦克斯韦等人对电磁现象进行的
深入而系统的研究,为电动力学奠定了坚实的基础, 特别是由麦克斯韦的电磁场方程组预言了电磁波的存 在,随即被赫兹的实验所证实。后来又把牛顿、惠更 斯和菲涅耳所建立的光学也纳入了电动力学的范畴,
更是一项辉煌的成就。
因此当时许多著名的物理学家都认为物理学的基本规律都已被发现,
布方面都取决于辐射体的温度。
一、热辐射
绝对黑体辐射定律
热辐射:所有的物体都能发射热辐射,热辐射与光辐射 一样,都是一定频率范围内的电磁波。物体在不同温度 下发出电磁辐射。这种由于物质中的分子、原子受到热 激发而发射电磁波的现象称为热辐射
炼钢的好坏常常取决于炉内的温度,而温度可以从颜色中得到反 映。即如果我们知道炉内热辐射的强度分布u与波长(即颜色) 的关系,就可以把握炼钢的时机。 在天文学中,人们靠辐射的强度分布来判断星体表面的温度。 冶金学和天文学等方面的需要,大大推动了对热辐射的研究。
M B (T )
(μm)
0 1 2 3 4 5 6
维恩根据经典热力学得出一个半经验公式:维恩公式
M ( , T )
c1
5
e
c2 T
c2 1.43 10 2 米 开
c1 3.70 10 焦耳 米 / 秒
2
16
维恩公式在短波部分 与实验结果吻合得很好, M 但长波却不行。 瑞利和金斯用能量均分 定理和电磁理论得出瑞利— 金斯公式:
(μm)
1
2
3
4
5
6
M B ( T ) T
4
辐出度与黑体的热力学温度T的四次方成正比。
1879年斯忒藩从实验观察到,1884年玻尔兹曼从理论 上给出.上式称为斯忒藩—玻尔兹曼定律。
含义:它说明对于黑体, M (T ) 温度越高,辐出度越大且 1700 K 随T增高而迅速增大。
•在实验室或工厂的高温炉子 上开一小孔,小孔可看作黑 体,由小孔的热辐射特性, 就可以确定炉内的温度。
实验值
0
( , T )
瑞利-金斯
维恩理论值
M ( , T )
2ckT
4
T=1646k
瑞利—金斯公式在长波部分与实验结果比较吻合。 但在紫外区竟算得单色辐出度为无穷大—所谓的“紫 外灾难”。 利用经典理论无法解释黑体辐射现象。正如1900 年开耳文指出的晴朗的物理学理论大厦上空,飞来 “两朵乌云”之一,它动摇了经典物理的基础。
如果谁在第一次学习量子概念时,不觉 得糊涂,那末他就一点也没有懂。 -尼尔斯.玻尔
The Quantum Mechanics
主要内容:
光的量子性: 光电效应 原子的量子论:
微观粒子的波粒二象性; 德布罗意关系; 不确定关系; 波函数及其统计解释; 定态薛定谔方程; 氢原子理论; 原子的壳层结构。
指出:“但是在物理晴朗天空的远处,还有两朵小小令人不安的乌
云”,即运用当时的物理学理论所无法正确解释的两个实验现象, 一个是热辐射现象中的紫外灾难,另一个是否定绝对时空观的迈克 尔逊--莫雷实验。正是这两朵小小的乌云,冲破了经典物理学的束 缚,打消了当时绝大多数物理学家的盲目乐观情绪,为后来建立近 代物理学的理论基础作出了贡献。
单色辐出度 M ( T ) 描写物体辐射本领的物理量。类似于波强。
如果从物体单位表面上发射的、波长在 到+d之 间的辐射功率为dE ,则dE 与d之比称为单色辐出 度。
dE M d
表示在一定温度 T 下,单位时间内 从物体表面单位面积上波长在 附 近单位波长间隔内辐射出的能量。
背景知识
到十九世纪末期,物理学各个分支的发展都已日臻完善,
并不断取得新的成就。首先在牛顿力学基础上,哈密顿和拉格
朗日等人建立起来的分析力学,几乎达到无懈可击的地步,特
别是十九世纪中期,海王星的发现充分表明了牛顿力学是完美
无缺的。其次,通过克劳修斯、玻耳兹曼和吉布斯等人的巨大
努力,建立了体系完整而又严密的热力学和统计力学,并且应
0, M ,T
M B ( T )
实验值
紫 外 灾 难
维恩公式
M B ( T ) C 1 5 e
C2 T
2)在短波 波段偏离 非常大
M B ( T ) C 3 4T
瑞利--金斯公式
1)在长波部分 符合的很好
0
1
2
3
4
5
6
7
8
9
( m )
同实验数据比较,在短波区域维恩公式符合的很好,但在 长波范围则有虽不太大但却是系统的偏离。
1900.10.7,鲁本斯夫妇访问了他,并告知一重要信息: 瑞利公式在长波段与实验符合得很好,普朗克当天即用
内插法获得新的辐射公式,是普朗克为了凑合实验数据
而猜出来的。 1900.12.14,普朗克在德国赫姆霍兹研究所召开的德 国物理学会会议上宣读了一篇注定要永载史册的论文: 《正常光谱中能量分布律的理论》
1 是温度T和波长的函数,常写成 M ( , T ) 2 它描述了物体热辐射的能谱分布。
。
M B (T )
描述了物体热辐射的能谱分布。
(μm)
0
1
2
3
4
5
6
辐出度M(T):
在单位时间内,从温度为T的黑体的单位面积上 ,所辐射出的各种波长的电磁波的能量总和。
它只是热力学温度T的函数。 描写物体在温度 T 时向外辐射能量本领的物理量。
---德布罗意
1892 ——1987
海森堡(德) 1901-1976
1932年获诺贝尔物理学奖
薛定谔(奥地 利)
1887~1961
1933年获诺贝尔物理学奖
狄拉克(英) 1902~1984
1933年获诺贝尔物理学奖
•1926年,海森堡和薛定谔从不同出发点建立了 量子力学。 •1928年,狄拉克统一相对论和量子论的成就。
要求:
1.了解光电效应的规律;
2.了解波粒二象性,理解德布罗意关 系,掌握用“关系”计算波长的方法;
3.了解波函数及其统计解释; 4.理解不确定关系,会用坐标、动量 的不确定关系做估计计算; 5.知道定态薛定谔方程; 6.了解能量、角动量、空间量子化 及自旋;了解“四个量子数”。
7.理解氢原子理论;
测量黑体的辐射分布 实验装置
T
S
L
平行光管
三棱镜
