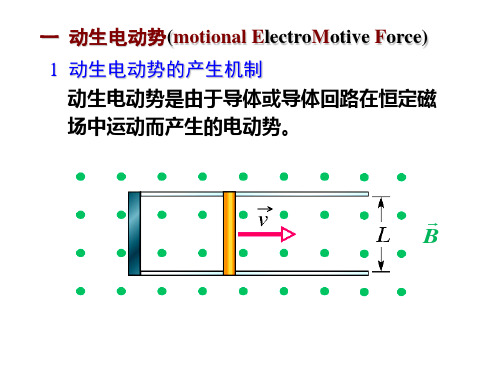
动生电动势和感生电动势
第19讲动生电动势与感生电动势
解:由 B 0, 与B同向 感生电场沿逆时针。 t
取逆时针回路, r < R 时
l Ei dl
B dS S t
l
Ei
dl
cos
0
B t
dS
cos
Ei
2
r
dB dt
r2
r dB Ei 2 dt
××××× ×××××××
r × × × × × × ×
×××××××
×R× × × × B
r > R时,
3. 动生电动势的计算
作为电源的这段运动导体杆,其中的洛仑兹力 是非静电力。
非静电力 对应的非静电场强 由电动势定义
Fk e(v B)
Ek
Fk e
v
B
i Ek dl
运动导线ab产生的动生电动势为
i
(v B) dl
l
例题1 有一半圆形金属导线在匀强磁场中作切 割磁力线运动。已知 v, B, R. 求动生电动势.
解:
d (v B)dl
dl Rd v B
vB sin900 dl cos
2
vBR cos d 2 vB2R 有效段!
b dl
d
v
0:与假定的方向相同
R
B
方向:a b
a
例题2 如图,长为L 的铜棒在匀强磁场中以角速度 ω绕 o 轴转动。求:棒中感应电动势的大小 和方向。
解:取如图所示微元(此微元暗示了假定的正方向)
C × × ×O× ×
B t
Ei Dx
L
d Ei dx cos
r dB dx cos
2 dt
r dB Ei 2 dt
逆时针
r cos h
12.2 动生电动势和感生电动势
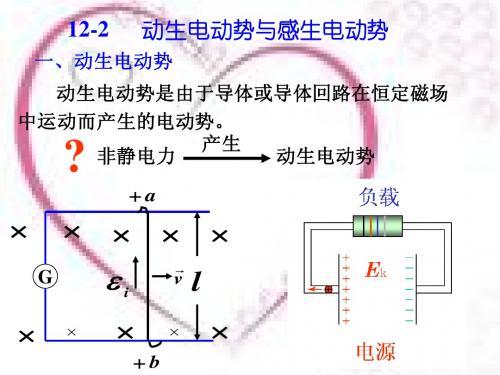
此时电荷积累停止, 两端形成稳定的电势差 两端形成稳定的电势差。 此时电荷积累停止,ab两端形成稳定的电势差。 洛仑兹力是产生动生电动势的根本原因 洛仑兹力是产生动生电动势的根本原因. 是产生动生电动势的根本原因
动生电动势的公式
非静电力
f = −e(v × B)
f 定义 Ek为非静电场强 Ek = = v ×B −e
S
A B ××× ×
ω ××v × ×
非均匀磁场
例 一直导线CD在一无限长直电流磁场中作 一直导线 在一无限长直电流磁场中作 切割磁力线运动。 切割磁力线运动。求:动生电动势。 动生电动势。 解:方法一
dε = ( v × B )⋅ dl I l dl µ0I 0 0 D sin90 dl cos180 =v C 2πl b a µ0vI dl =− 方向 D→C → 2πl µ0vI a+b dl µ0vI a + b ε =− ∫a l = − 2π ln a 2π
×××× ⊗ o ×××× B ×××× h
C
∂B ∂t
××
L
D
解:
ε i = ∫ E涡 • dl
L
r dB E涡 = 2 dt
dε = E涡 • dl r dB dl cosθ = 2 dt
h dB dl = 2 dt
⊗o
B
⊗
θ
∂B ∂t
E涡
r h
l dl
L
θ
C
D
h dB 1 dB εCD = ∫L dl = 2hL dt 2 dt
O
解:方法一 取微元
dε = ( v × B )⋅ dl
= Bvdl = Blωdl
εi = ∫ dεi = ∫0 Blωdl
动生电动势与感生电动势

【解】由于金属棒处在通电导线的非均匀磁场中,因此必
须将金属棒分成很多长度元dx,规定其方向由A指向B。这样 在每一dx处的磁场可以看作是均匀的,其磁感应强度的大小为
B 0I
2x
根据动生电动势的公式可知,dx小段上的动生电动势为
d动
(v
B)
dl
Bv
cos
dx
0I
2x
vdx
由于所有长度元上产生的动生电动势的方向都相同,所以金
d
dt
d dt
S
B
dS
又根据电动势的定义可得
L EK dl
式中,EK为感生电场的电场强度。感生电场的电场强度是 非静电性场强。
则有
L EK
dl
d dt
B dS B dS
s
s t
dB
s
S t
若闭合回路是静止的,即所包围面积S不随时间变化,即
S 0 ,则上式可写成
t
B L EK dl s t dS
性场强为
Ek
fL (e)
vB
根据电动势的定义可得,动生电动势为
a
动
L Ek
dl
(v B) dl
b
上式是动生电动势的一般表达式。由上式可知,动生电动势
的方向是非静电性场强 Ek v B 在运动导线上投影的指向。
【例9-2】如下图所示,长直导线 中通有电流I=10A,有一长l=0.1m的 金属棒AB,以v=4m·s-2的速度平行于 长直导线作匀速运动,棒离导线较近的 一端到导线的距离a=0.1m,求金属棒 中的动生电动势。
1861年,英国物理学家麦克斯韦提出感生电场的假设,认为 由于磁场变化而产生一种电场,是这个电场使导体中自由电子作 定向运动而形成电流。麦克斯韦还认为,即使没有导体,这种电 场同样存在。这种由变化磁场激发的电场称为感生电场。
动生电动势和感生电动势

Ek
1 2
B t
r
1 2
kr
2. r > R 区域
作半径为 r 的环形路径,并以逆
时针为回路绕向,则同理有
2rEk
S
B t
ds
R2k
R
o
r
r
B
1 B R2 1 R2
Ek 2 t
r
k 2r
Foundation - SJYGGF
§ 13.2 动生电动势和感生电动势
Nov 5, 2002 9/33
随时间均匀增加, dB k dt
若铝圆盘的电导率为γ,求盘内 的感应电流。
见书P212页,例4
R
解: 取半径为r、宽为dr的圆环微 元,并以逆时针方向为正方向,则 微元环中元电动势为
d L Ek dl L Ek dl
1 kr 2r dl kr2
20
o
r
dr
B
微元环中的电阻为 dR 1 2r hdr
Foundation - SJYGGF
§ 13.2 动生电动势和感生电动势
Nov 5, 2002 21/33
4) 电度表记录电量
电度表记录用电量,就是
利用通有交流电的铁心产生交
变的磁场,在缝隙处铝盘上产
o
生涡电流,涡电流的磁场与电
磁铁的磁场作用,表盘受到一
转动力矩,使表盘转动。
o’
Foundation - SJYGGF
感生电动势
1. 感生电动势——回路不动或不变,因磁场随时间变 化产生的电动势。相应的电流称为感生电流。
2. 感生电动势的起源——感生电场Ek 1) Maxwell感生电场(涡旋电场)假设
Maxwell 1861年首先从理论上预言感生电场的存在,后 被Hertz的电磁波实验所证实。Maxwell假设: 变化的磁场要在其周围空间激发一种电场——感生电场
§10-2. 动生电动势与感生电动势

(3)感生电场是无源场。
S
E dS 0.....( 4)
B t E
• 涡旋电场无源其电里力线是闭合曲线。 3、感生电动势的非静电力—感生电场对电 11 荷的作用力 F eE 。
4.感生电场和静电场的比较 (1)相同点:都对电荷有作用力。
不同点 产生的原因 电力线 静电场 电荷 电力线有头有尾
I B1 0 2d
B2 2 (d a)
0 I
I
1 : B DA 2 : B CB 回路中总感应电动势方向沿顺
时针.
1
d
B 2
a
15
10-11)
在金属杆上取距左边直导线为,则
I B1 0 2r
B B1 B2
图中电动势的方向:从负极a正极b;
b
(1)动生电动势的大小:
(3)式 (v B) dl 仅适用 a
a
f
v
于计算切割磁场线的导体中的感 应电动势。 (4)积分是沿着运动的导线进行的。
3
(5)若ab导体为闭合回路则动生电动势为: (v B) dl .....(1)
0…………(2)
10
(2)感生电场是非保守场。
d B l E dl dt SB d S S t d S........(10.4)
B dS 代入(2)式,得: S
n S l
• dS的正方向与l成右手螺旋关系
b
r Iv Iv dr d l sin 0 Iv sin dl 0 dr0 a 2 r r 2 r d 2 r 0 Iv d l sin ln 2 d v B:b a
大学物理动生电动势和感生电动势全篇

第十三章电磁感应
步骤:
dm
dt
b
a (v B) dl
1) 约定 右旋
2)求磁通
3)根据公式计算
1)取线元 dl ,并规定其方向
2)
写出
d
(v
B)
dl
3)确定积分范围,并积分
若结果 0,则
说明 实 与 相反
若结果 0,则
说明 实与 dl 相反
10 - 2 动生电动势和感生电动势
第十三章电磁感应
感生电场和静电场的对比
E静 和 Ek 均对电荷有力的作用.
静电场是保守场 L E静 dl 0
感生电场是非保守场
dΦ L Ek dl dt 0
静电场由电荷产生;感生电场是由变化的磁 场产生 .
10 - 2 动生电动势和感生电动势
第十三章电磁感应
例:将磁铁插入非金属环中,环内有无感
坩锅外的线圈中通交流电 电磁炉:交变磁场作用于金属锅底,产生
大量涡流
2. 电磁阻尼摆
涡电流的弊
热效应过强、温度过高, 易破坏绝缘,损耗电能,还可能造成事故
10 - 2 动生电动势和感生电动势
第十三章电磁感应
减少涡流 1、选择高阻值材料(硅钢、矽钢等) 2、多片铁芯组合
感生电场充当着产生感应电动势
的非静电力。
闭合回路中的感生电动势
L
Ek
dl
dΦ dt
10 - 2 动生电动势和感生电动势
第十三章电磁感应
闭合回路中的感生电动势
L
Ek
dl
dΦ dt
Φ SB dS
d
L Ek
dl
dt
B dS
S
S不变
动生和感生电动势
目录
• 动生电动势 • 感生电动势 • 比较动生和感生电动势 • 实例分析 • 问题与讨论
01
CATALOGUE
动生电动势
定义与原理
定义
动生电动势是指由导体在磁场中运动而产生的感应电动势。
原理
根据法拉第电磁感应定律,当导体在磁场中运动时,导体中 的电子会受到洛伦兹力的作用,从而在导体两端产生电动势 。
感生电动势的大小取决于磁场的变化率。如果磁场变化很快,那么产生的电动势就很大。
应用比较
动生电动势在电力生产和传输中起着关键作用。例如,发电机是通过动生电动势将机械能转化为电能 。
感生电动势在电子设备和磁性材料中有着广泛的应用。例如,变压器和电感器是通过感生电动势来改 变信号和传输能量。
04
CATALOGUE
电磁制动
在某些机械设备中,利用 动生电动势可以实现电磁 制动,达到减速或停止的 目的。
电磁感应现象
动生电动势是电磁感应现 象的一种表现形式,可以 用来解释和利用电磁感应 现象。
02
CATALOGUE
感生电动势
定义与原理
定义
感生电动势是指磁场变化时在导体中产生的电动势。
原理
根据法拉第电磁感应定律,当一个导体处于变化的磁场中时,导体中的自由电子 会受到洛伦兹力的作用,从而在导体两端产生电动势。
电子感应加速器
利用感生电动势加速带电粒子。
03
CATALOGUE
比较动生和感生电动势
产生方式比较
动生电动势
是由磁场和导线的相对运动引起的。当 导线切割磁力线时,导线两端会感应出 电动势。
VS
感生电动势
是由磁场的变化引起的。当磁场发生变化 时,附近的导体中会产生感应电流和电动 势。
动生电动势和感生电动势
动生电动势和感生电动势
d d 感应电动势 N dt dt 引起磁通量变化的原因 ?
磁场恒定,导体运动
导体不动,磁场变化
P.1
1、电动势定义
I
Ek
+
-
Ek : 非静电电场强度.
Ek dl
P.2
2、感应电动势的分类: (1)动生电动势 稳恒磁场中的导体运动 , 或者回路面积 变化、取向变化等。 (2)感生电动势: 导体不动,磁场变化。
OP
P.5
动生
OP
(v B) dl
混合积:(a b ) c
× × P ×
(vB sin ) cosdl
OP
×
× × ×
×
(v × B) ×
× ×
×
特例 B均匀,杆 l水平运动:
l×
×
× v×
× B
× O ×
OP
l
l (vB sin 900 )cos00 dl (v B) dl 0
vBl
vBdl vBl
0
P.6
2、计算方法
d动生 (v B) dl
动生
×
×
× P× B × dl
× ×
OP
(v B) dl
1 2 d BL 2 dt 1 2 BL 2
×
×
× P × × × ×
× ×
B ×
×
×
×
o
×
×
×
×
×
×
×
大学物理(8.2.2)--动生电动势感生电动势
,求金
属
杆中
的
动生
电
动B 势
。O′
距 a 点为 l 处取一线元矢d量l v r l sin
b
该,处 的 非 静 电 场 场 强 为 :
Ek
v
B
r
Ek
Ek vB lB sin
该线元运动时产生的电动势 di Ek dl
al
:di Ek dl cos(900 ) Ek dl sin lBdl sin 2
计算该线元运动时产生的电动势 di
, Ek dl
(v
B)
dl
( 3 ):计算该导线运动时产生的动生电动
势
εi
l
(v
B)
dl
i 0 电动势方向与积分路线方向相同 i 0 电动势方向与积分路线方向相反
例 8-3: 一长度为 L 的金属杆 ab 在均匀B磁场 中绕平行于磁
的
金属棒,金属棒绕其一端 O 顺时针匀速转动,转动角速度为
,
O 点至导线的垂直距离为 a ,
解
:金距1属)O选棒点O求所为:在l方M处处1向)的取当为金磁一金积属感线属分棒应元棒路内强矢转线d感度l量至应为与电B:v长动直2势l0导的aI 线,大方平小向行和,方如向图I;中
该,处 的 非 静 电 场 场 强 为 :
场方向
磁场
′ 的定轴 OO′ 转动,已知杆的角速度为 ,杆相对于 的方位角为 θ ,求金属杆中的动生电动势B 。O′
b
L
a
O
例 8-3:
感生电动势和动生电动势
小结
感生 电动 势和 动生 电动 势 感应电场:由变化的磁场激发的电 场. 感生电动势:由感应电场产生的感 : 应电动势称为感生电动势. 动生电动势:由于导体运动而产生 的感应电动势.
5感生电动势和动生电动势
一.感应电场与感生电动势 一个闭合电路静止于磁场中,由 于磁场强弱的变化,闭合电路内 产生了感应电动势.这种情况下, 哪一种作用扮演了非静电力的 角色?
磁场Байду номын сангаас强
英国物理学家麦克斯韦在他的电磁场理论 中指出,变化的磁场会在空间激发一种电场, 这种电场对电荷会产生力的作用如果此刻 周围空间存在闭合导体,导体中自由电荷会 在这种电场力的作用下定向移动,产生感应 电流,或者说产生感应电动势.变化的的磁 场能在周围空间激发电场,这种电场叫感应 电场,由感生电场产生的感应电动势称为感 感应电动势称为感 感应电动势称为 生电动势. 生电动势
导体CD在匀强磁场B中以速度V向右运动, 并且导线CD与B.V的方向相垂直,由于正电 荷随导体一起运动,因此每个电荷受到的洛
X X X L X X X C X XF洛 X X F电 X D V
伦兹力为F洛=QVB,F洛方向向上,正 电荷向上运动,使导体下端出现负电 X , X 荷,结果上端C的电势高于下端D的 X 电势,出现由C指向D的静电场,此时 电场对正电荷的作用力是向下,与洛 伦兹力方向相反,当二力互相平衡时, CD两端便产生一个稳定的电势差,
X
可见,运动的导体CD就是一个电源,C为正极,正电
荷受到洛伦兹力的作用,从D端搬到C端,这里,洛伦 兹力就相当于电源中的非静电力,根据电动势的定 义,电动势等于单位正电荷从负极通过电源内部移 动到正极非静电力所做的功,作用在单位正电荷上 的洛伦兹力 F洛
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§6-2 动生电动势和感生电动势动生电动势:回路或其一部分在磁场中的相对运动所产生的感应电动势。
感生电动势:仅由磁场的变化而产生的感应电动势。
一 动生电动势图6 - 5 动生电动势动生电动势的产生可以用洛伦兹力来解释。
长为l 的导体棒与导轨构成矩形回路abcd 平放在纸面内,均匀磁场B 垂直纸面向里。
当导体棒ab 以速度v 沿导轨向右滑动时,导体棒内自由电子也以速度v 随之一起向右运动。
每个自由电子受到的洛伦兹力为B v F ⨯-)(=e ,方向从b 指向a ,在其作用下自由电子向下运动。
如果导轨是导体,在回路中将形成沿着abcd 逆时针方向的电流。
如果导轨是绝缘体,则洛伦兹力将使自由电子在a 端累积,从而使a 端带负电,b 端带正电,在ab 棒上产生自上而下的静电场。
当作用在自由电子上的静电力与洛伦兹力大小相等时达到平衡,ab 间电压达到稳定值,b 端电势比a 端高。
这一段运动导体相当于一个电源,它的非静电力就是洛伦兹力。
电动势定义为单位正电荷从负极通过电源内部移到正极的过程中,非静电力K 所作的功,即B v F K ⨯=-=e.动生电动势为ε⎰⎰+-⋅⨯=⋅=l B v l K d )(d ba .(6.4)均匀磁场情况:若v ⊥ B , 则有ε = B l v ;若导体顺着磁场方向运动,v // B ,则有 v ⨯ B = 0,没有动生电动势产生。
因此,可以形象地说,只有当导线切割磁感应线而运动时,才产生动生电动势。
普遍情况:在任意的恒定磁场中,一个任意形状的导线线圈L (闭合的或不闭合的)在运动或发生形变时,各个线元d l 的速度v 的大小和方向都可能是不同的。
这时,在整个线圈L 中产生的动生电动势为ε l B v d )()(⋅⨯=⎰L .(6.5)图6 - 6 洛伦兹力不作功洛伦兹力对电荷不作功:洛伦兹力总是垂直于电荷的运动速度,即v ⊥F v ,因此洛伦兹力对电荷不作功。
然而,当导体棒与导轨构成回路时会有感应电流出现,这时感应电动势却是要作功的。
感应电动势作功能量的来源:在运动导体中的自由电子不但具有导体本身的运动速度v ,而且还具有相对于导体的定向运动速度u ,与此相应的洛伦兹力u ⊥F u . 自由电子所受到的总的洛伦兹力为B v u F ⨯+-)(= ev u F F +=,它与合成速度v u +垂直,总的洛伦兹力不对电子作功,即0)(=+⋅v u F .利用0=⋅v F v和0=⋅u F u ,由上式可得)(v u F +⋅0)()(=⋅+⋅=+⋅+=v F u F v u F F u v u v ,或u F v F ⋅=⋅-v u .实际上,为了使导体棒能够在磁场中以速度v 匀速运动,必须施加外力F 0,以克服洛伦兹力的一个分力u =F e -⨯u B . 利用上式的结果可以看到,F 0克服u F 所作的功为u F v F v F ⋅⋅-⋅v u ==0.外力克服洛伦兹力的一个分量u F 所作的功0⋅F v ,通过洛伦兹力的另一个分量v F 对电子的定向运动作了正功v ⋅F u ,从而全部转化成了感应电流的能量。
因此,洛伦兹力并不提供能量,而只是传递能量。
洛伦兹力在这里起了能量转化作用,其前提是运动物体中必须有能够自由移动的电荷。
二 感生电动势在磁场变化而产生感生电动势的情况下,导体回路不动,其非静电力不可能是洛伦兹力。
人们发现,不论回路的形状以及导体的性质和温度如何,只要磁场变化导致穿过回路的磁通量发生了变化,就会有数值等于/d d t Φ的感生电动势在回路中产生,说明感生电动势的产生只是由变化的磁场本身引起的。
麦克斯韦在电磁感应现象分析的基础上提出:变化的磁场在其周围空间激发一种新的电场,称为感生电场或有旋电场,用E r 表示,以区别于库仑场E c ,后者是电荷按库仑定律激发的电场。
有旋电场与库仑场都是一种客观存在的物质,它们对电荷都有作用力。
与库仑场不同的是,有旋电场不是由电荷激发的,而是由变化的磁场激发的;描述有旋电场的电场线是闭合的,从而有⎰≠⋅0d r l E ,因此有旋电场不是保守场或势场。
实际上,产生感生电动势的非静电力K 正是这一有旋电场E r ,即ε⎰-⋅=td d =d r Φl E . (6.6)三 电磁感应定律的普遍形式在普遍情况下,电场E 是库仑场E c 和有旋电场E r 的叠加,即r c E E E +=.由于库仑场是势场,⎰⋅0=d c l E ,因此感生电动势为ε⎰⎰⋅⋅+=)()(r c d =d )(L L l E l E E .(6.7)另一方面,按照法拉第电磁感应定律,有ε⎰⎰⋅-=-=)(d d d d d S ttS B Φ,式中S 是以环路L 为周界的曲面。
当环路L 不动时,可将对时间的微商与对曲面的积分的顺序颠倒,得SB l E d d )()(⋅∂∂-=⋅⎰⎰⎰S L t. (6.8)此即电磁感应定律的普遍(积分)形式,它是麦克斯韦方程组的一个方程。
根据矢量分析中的斯托克斯公式,利用导出安培环路定理的微分形式类似的方法,可以由式(6.8)得到t∂∂-⨯∇B E =, (6.9)这就是电磁感应定律的微分形式。
上式表明,即使没有导体存在,变化的磁场也会在空间激发涡旋状的感生电场。
在式(6.9)中代入磁矢势A 的定义式A B ⨯∇=,可得0)+(=∂∂⨯∇tA E .对于任何标量函数ϕ,总有0)(=∇⨯∇ϕ,所以由上式0)+(=∂∂⨯∇tA E,可得ϕ∇-∂∂-tA E =, (6.10)这就是用矢势A 和标势ϕ 表示电场强度E 的普遍表达式。
当电磁场与时间无关时,有0=∂∂ tA ,V ∇-=∇-=ϕE ,于是ϕ还原为静电势V .为了使矢势A 有确定值,对于随时间变化的电磁场,可采用 0+00=∂∂⋅∇tϕμεA(6.11)作为附加条件来限制矢势A 和标势ϕ,该条件称为洛伦兹条件或洛伦兹规范。
矢势A 和标势 ϕ 的重要性:① 四维电磁矢势)/i ,,,(c A A A z y x ϕ;② 有心力场中运动粒子的薛定谔方程为 ψϕμψ])ˆ(21[i 2q q t+-=∂∂A P,或ψϕμψ])i ()i (21[i q q q t +-∇-⋅-∇-=∂∂A A .③ 1959年,阿哈罗诺夫和玻姆从理论上指出,即使在电子的运动路径上不存在电场E 和磁场B ,但只要存在标势ϕ 和矢势A ,也会使电子波函数的相位发生变化,而这种相位变化可以通过电子波的干涉效应加以观测,这就是著名的A - B 效应。
A - B 效应表明,ϕ 和A 是比E 和B 更为基本的物理量。
四 电磁感应与相对性原理按照以上关于动生电动势和感生电动势的讨论,似乎在这两种物理情况之间存在着深刻的差异。
为了弄清它们之间的内在联系,我们现在从三个惯性系S ,'S 和"S 中静止的观测者的角度出发,考察以速度v 相对运动着的闭合回路和磁铁。
1 ) 对于S 系中的观测者来说,建立磁场B 的磁铁是静止的,导体回路以速度v 运动着,所测得的动生电动势来源于磁场B 作用于运动导体的自由电荷上的洛伦兹力,且有ε⎰⋅⨯=l B v d )(. 2 ) 对于'S 系来说,磁铁以速度 - v 运动着,使磁场B 的空间分布随时间改变,所测得的感生电动势来源于导体回路中产生的感生电场E ,且有ε⎰⋅=l E d .3 ) 对于"S 系来说,磁铁和导体回路都在运动,因而以上二者兼而有之,即导体回路中的感应电动势为ε⎰⎰⋅⋅⨯=l E l B v d '+d )''(.根据电场和磁场的相对论性变换的讨论,在不同的惯性系中所观测到的电场和磁场可以是不同的,即'B 与B ,'E 与E 都可能不同。
上述表面上看起来有着明显差异的物理情况,却有着共同的规律,它们都遵从法拉第电磁感应定律及其推广的形式,即εtd d Φ-= 和⎰⎰⎰⋅∂∂-=⋅SB l E d d t.不管磁通量Φ 变化的原因是什么,它们都是成立的。
只要磁铁和导体回路之间的相对运动相同,导体回路中的感应电动势 ε 就相同。
实际上,这是相对性原理的必然结果。
这一结果说明,磁场和电场并不是彼此无关的,它们的划分是相对的,是与惯性系的选择有关的。
1905年爱因斯坦在关于狭义相对论的著名论文“论运动物体的电动力学”中,对此作了精辟的论述。
[例题6.2] 在均匀恒定磁场B 中,一根长为L 的导体棒ab ,在垂直于磁场的平面内绕其一端作匀速转动,角速度为ω. 试求这导体棒两端的电势差U ab .[解] ( 1 ) 解法一:由于导体棒ab 在均匀磁场中匀速转动,所以棒上各处的线速度v 不同。
若在距中心为l 处取一线元d l ,则其线速度的方向既垂直于棒,又垂直于B ,大小为 v = ω l . 利用式(6.5),导体棒ab 上所产生的动生电动势为ε⎰⋅⨯=b al B v d )(B L l l v B baω221d -=-=⎰,式中的负号来源于v ⨯B 的方向与积分路径的方向相反,表示感应电动势从b 指向a 的。
于是,ab 两点间电势差为U ab = - εB L ω221=.图6 - 7 旋转的导体棒( 2 ) 解法二:为直接用式 εtd d Φ-= (6.1)来求解,设想(这种设想是有条件的!)有一回路'abb a ,'ab 是导体棒在t = 0的位置,2/2θ∆=∆L S是∆t 时间内导体棒扫过的面积。
由于回路'abb a 的绕行方向确定的面元矢量∆S 的方向与B 一致,所以回路磁通量为θΦ∆=∆=∆⋅=∆221L B S B S B ,代入式(6.1)可得εωθΦB L tLB t2221d d 21d d -=-=-=,式中的负号表示电动势 ε 的方向由b 指向a.[例题6.3 ] 交流发电机的基本原理。
[解] 一个单匝线圈abcd 可以绕固定轴在磁极N 和S 所激发的近似均匀的磁场中转动;线圈的两端分别接在两个与线圈一起转动的铜环上,铜环通过两个带有弹性的金属触头与外电路接通。
当线圈在汽轮机或水轮机的带动下在均匀磁场中匀速转动时,线圈的ab 和cd 两边切割磁感应线而产生感应电动势。
如果外电路是闭合的,则在线圈和外电路所组成的闭合回路中就会出现感应电流。
图6 - 8 交流发电机的基本原理考虑某一瞬间,线圈平面的法向n e 与B 间的夹角为θ. 由式(6. 5)可得,在边长为l的ab 和cd 两边中产生的感应电动势分别为:εab ⎰⎰=⋅⨯=lb a l B v 0d sin d )(θl B v = θsin l B v ,εcd ⎰⋅⨯=d c l B v d )(⎰-π=ll B v 0d )(sin θθsinl B v =.线圈回路中这两个电动势的方向相同,因此整个回路中的感应电动势为ε = εab + εcd = 2 vB l sin θ .设线圈旋转的角速度为ω,并取线圈平面的法线刚好处在水平位置时作为计时零点,则θ = ω t ,又因v ='l ω /2,代入上式可得ε sin BS t ωω=,式中'S l l =为线圈的面积,'l 为线圈的bc 和da 边长。
