数学期望与方差
合集下载
数学期望和方差

8 50
12
9
7 50
10
15 50
12
11
10 50
12
10 50
则这 50 个零件的平均直径为
D k P( X k ) kpk 10.14
k 8 k 8
称之为这 5 个数字的加权平均,数学期望的 概念源于此.
第四章
数学期望和方差
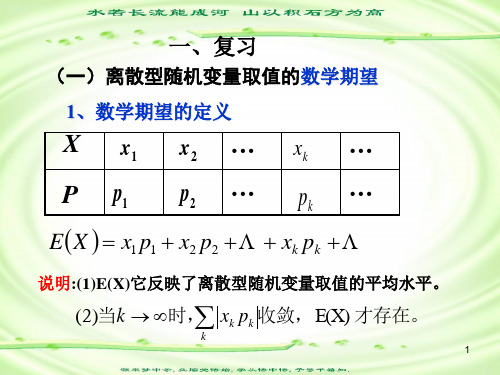
数学期望的定义
定义1.1 设离散型随机变量X 的概率分布为
证明 令g ( x ) x f ( x ).
g(x)是奇函数.
t f ( t )dt g ( t )dt .
( x ) f ( x )dx (令t x )
( x ) f ( x )dx f ( x )dx
E ( X ) xf ( x)dx
注意:随机变量的数学期望的本质就是加权 平均数,它是一个数,不再是随机变量。
第四章
数学期望和方差
常见连续型分布的数学期望 (5)指数分布E()
随机变量X的密度为:
第四章
数学期望和方差
第四章
数学期望和方差
定理1 设X的数学期望有限, 概率密度f (x) 关于
8 8
9 10 11 12 7 15 10 10 50
则这 50 个零件的平均直径为
8 8 9 7 1015 1110 1210 50 10.14cm
第四章
数学期望和方差
换个角度看,从这50个零件中任取一个,它 的尺寸为随机变量X , 则X 的概率分布为 X P 8
对称, f ( x ) f ( x ), 则E ( X ) .
12
9
7 50
10
15 50
12
11
10 50
12
10 50
则这 50 个零件的平均直径为
D k P( X k ) kpk 10.14
k 8 k 8
称之为这 5 个数字的加权平均,数学期望的 概念源于此.
第四章
数学期望和方差
数学期望的定义
定义1.1 设离散型随机变量X 的概率分布为
证明 令g ( x ) x f ( x ).
g(x)是奇函数.
t f ( t )dt g ( t )dt .
( x ) f ( x )dx (令t x )
( x ) f ( x )dx f ( x )dx
E ( X ) xf ( x)dx
注意:随机变量的数学期望的本质就是加权 平均数,它是一个数,不再是随机变量。
第四章
数学期望和方差
常见连续型分布的数学期望 (5)指数分布E()
随机变量X的密度为:
第四章
数学期望和方差
第四章
数学期望和方差
定理1 设X的数学期望有限, 概率密度f (x) 关于
8 8
9 10 11 12 7 15 10 10 50
则这 50 个零件的平均直径为
8 8 9 7 1015 1110 1210 50 10.14cm
第四章
数学期望和方差
换个角度看,从这50个零件中任取一个,它 的尺寸为随机变量X , 则X 的概率分布为 X P 8
对称, f ( x ) f ( x ), 则E ( X ) .
数学期望和方差

数学期望和方差
第四章 数学期望和方差
本 章 内 容
随机变量的平均取值 —— 数学 期望 随机变量取值平均偏离平均值的 情况 —— 方差 描述两个随机变量之间的某种关
系的数 —— 协方差与相关系数
第四章 数学期望和方差
§4.1 数学期望
引例:测量 50 个圆柱形零件直径(见下表)
尺寸(cm) 8 9 10 11 12 数量(个) 8 7 15 10 10 50
E(X) kC n kpk(1p)nk
k0
n
k
n!
pk(1p)nk
k1 k!(nk)!
nn p(n 1 )!p k 1 (1 p )(n 1 ) (k 1 )
k 1 (k 1 )(n ! k )!
n1
npCn k1pk(1p)(n1)k np
k0
第四章 数学期望和方差
(3)泊松分布
E i n1aiXiC i n1aiE (Xi)C
当X ,Y 相互独立时,
E (X Y ) = E (X )E (Y ) .
第四章 数学期望和方差
注:性质 4 的逆命题不成立,即 若E (X Y) = E(X)E(Y),X ,Y 不一定相互独立.
反例
pij X -1
Y
-1
18
0
18
第四章 数学期望和方差
若X ≥0,且EX 存在,则EX ≥0.
证明:设 X 为连续型,密度函数为f (x), 则 由X ≥0 得:
f(x)0, x0,
所以
E Xxf(x )d xxf(x )d x 0 .
0
推论: 若 X ≤Y,则 EX ≤EY.
证明:由已知 Y-X≥0,则 E(Y-X) ≥0. 而E(Y-X)=E(Y)-E(X), 所以,E(X) ≤E(Y).
第四章 数学期望和方差
本 章 内 容
随机变量的平均取值 —— 数学 期望 随机变量取值平均偏离平均值的 情况 —— 方差 描述两个随机变量之间的某种关
系的数 —— 协方差与相关系数
第四章 数学期望和方差
§4.1 数学期望
引例:测量 50 个圆柱形零件直径(见下表)
尺寸(cm) 8 9 10 11 12 数量(个) 8 7 15 10 10 50
E(X) kC n kpk(1p)nk
k0
n
k
n!
pk(1p)nk
k1 k!(nk)!
nn p(n 1 )!p k 1 (1 p )(n 1 ) (k 1 )
k 1 (k 1 )(n ! k )!
n1
npCn k1pk(1p)(n1)k np
k0
第四章 数学期望和方差
(3)泊松分布
E i n1aiXiC i n1aiE (Xi)C
当X ,Y 相互独立时,
E (X Y ) = E (X )E (Y ) .
第四章 数学期望和方差
注:性质 4 的逆命题不成立,即 若E (X Y) = E(X)E(Y),X ,Y 不一定相互独立.
反例
pij X -1
Y
-1
18
0
18
第四章 数学期望和方差
若X ≥0,且EX 存在,则EX ≥0.
证明:设 X 为连续型,密度函数为f (x), 则 由X ≥0 得:
f(x)0, x0,
所以
E Xxf(x )d xxf(x )d x 0 .
0
推论: 若 X ≤Y,则 EX ≤EY.
证明:由已知 Y-X≥0,则 E(Y-X) ≥0. 而E(Y-X)=E(Y)-E(X), 所以,E(X) ≤E(Y).
常用分布的数学期望及方差

方差的性质
方差具有可加性
对于两个独立的随机变量X和Y,有Var(X+Y) = Var(X) + Var(Y)。
方差具有对称性
对于一个常数a和随机变量X,有Var(aX) = |a|^2 * Var(X)。
方差具有非负性
对于随机变量X,有Var(X) >= 0,其中 Var(X) = 0当且仅当X是一个常数。
05 数学期望与方差的应用
在统计学中的应用
描述性统计
数学期望和方差用于描述一组数据的中心趋势和 离散程度,帮助我们了解数据的基本特征。
参数估计
通过样本数据的数学期望和方差,可以对总体参 数进行估计,如均值和方差的无偏估计。
假设检验
在假设检验中,数学期望和方差用于构建检验统 计量,判断原假设是否成立。
常见分布的数学期望
均匀分布的数学期望为
$E(X) = frac{a+b}{2}$,其中a和b是均匀分布的下限和上 限。
柯西分布的数学期望为
$E(X) = frac{pi}{beta} sinh(frac{1}{beta})$,其中β是柯西 分布的参数。
拉普拉斯分布的数学期望为
$E(X) = frac{beta}{pi} tan(frac{pi}{beta})$,其中β是拉普 拉斯分布的参数。
03
泊松分布
正态分布是一种常见的连续型随机变量 分布,其方差记作σ²。正态分布的方差 描述了随机变量取值的分散程度。
二项分布是一种离散型随机变量分布, 用于描述在n次独立重复的伯努利试验 中成功的次数。其方差记作σ²,且σ² = np(1-p),其中n是试验次数,p是单次 试验成功的概率。
泊松分布是一种离散型随机变量分布, 用于描述在一段时间内随机事件发生的 次数。其方差记作σ²,且σ² = λ,其中 λ是随机事件发生的平均速率。
数学期望与方差

因此,在对随机变量的研究中,确定某些数 字特征是重要的 .在这些数字特征中,最常用的是 数学期望、方差、协方差和相关系数
第四章 随机变量Biblioteka 数字特征第一节 随机变量的 数学期望
一、数学期望的概念
二、随机变量函数的数学期望 三、数学期望的性质
四、应用实例
下 回
停
一、数学期望的概念
1. 问题的提出 1654年, 一个名叫德.梅尔的贵族就“两个 赌徒约定赌若干局, 且谁先赢 c 局便算赢家, 若 在一赌徒胜a局 (a<c), 另一赌徒胜b局(b<c)时便 终止赌博, 问应如何分赌本” 为题求教于帕斯 卡, 帕斯卡与费马通信讨论这一问题, 于1654 年 共同建立了概率论的第一个基本概念 — 数学 期望
0 . 3 0 .1 0 . 6
8 9 10
乙射手
0 .2 0 .5 0 .3
试问哪个射手技术较好?
解 运动员的水平是通过其平均水平来衡量的, 因而甲、乙两射手的平均水平分别为
甲 : 8 0.3 9 0.1 10 0.6 9.3(环) , 乙 : 8 0.2 9 0.5 10 0.3 9.1(环), 故甲射手的技术比较好.
若级数 xk pk 绝对收敛, 即 xk pk , 则称
级数 xk pk 的和为随机变量 X 的数学期望,
k 1 k 1
k 1
PX xk pk , k 1,2,.
记为EX, 即 E X
k 1
xk pk .
比如
X的分布律为
正态分布 指数分布
1 λ
λe λx , x 0 p x x0 0,
第四章 随机变量Biblioteka 数字特征第一节 随机变量的 数学期望
一、数学期望的概念
二、随机变量函数的数学期望 三、数学期望的性质
四、应用实例
下 回
停
一、数学期望的概念
1. 问题的提出 1654年, 一个名叫德.梅尔的贵族就“两个 赌徒约定赌若干局, 且谁先赢 c 局便算赢家, 若 在一赌徒胜a局 (a<c), 另一赌徒胜b局(b<c)时便 终止赌博, 问应如何分赌本” 为题求教于帕斯 卡, 帕斯卡与费马通信讨论这一问题, 于1654 年 共同建立了概率论的第一个基本概念 — 数学 期望
0 . 3 0 .1 0 . 6
8 9 10
乙射手
0 .2 0 .5 0 .3
试问哪个射手技术较好?
解 运动员的水平是通过其平均水平来衡量的, 因而甲、乙两射手的平均水平分别为
甲 : 8 0.3 9 0.1 10 0.6 9.3(环) , 乙 : 8 0.2 9 0.5 10 0.3 9.1(环), 故甲射手的技术比较好.
若级数 xk pk 绝对收敛, 即 xk pk , 则称
级数 xk pk 的和为随机变量 X 的数学期望,
k 1 k 1
k 1
PX xk pk , k 1,2,.
记为EX, 即 E X
k 1
xk pk .
比如
X的分布律为
正态分布 指数分布
1 λ
λe λx , x 0 p x x0 0,
数学期望和方差

第四章
数学期望和方差
第四章 数学期望和方差
分布函数能够完整地描述随机变量的统计特 性,但在实际问题中,随机变量的分布函数较 难确定,而它的一些数字特征较易确定.并且 在很多实际问题中,只需知道随机变量的某些 数字特征也就够了.
另一方面,对于一些常用的重要分布,如二 项分布、泊松分布、指数分布、正态分布等, 只要知道了它们的某些数字特征,就能完全确 定其具体的分布.
8 8
9 10 11 12 7 15 10 10 50
则这 50 个零件的平均直径为
8 8 9 7 1015 1110 1210 50 10.14cm
第四章
数学期望和方差
换个角度看,从这50个零件中任取一个,它 的尺寸为随机变量X , 则X 的概率分布为 X P 8
x
| x| 但 | x | f ( x ) dx dx 发散. 2 (1 x )
它的数学期望不存在.
注:虽然f(x)是偶函数,但不能用定理1.1.
第四章
数学期望和方差
§4.2 数学期望的性质
设已知随机变量X的分布,我们需要计算的不 是X的数学期望, 而是X的某个函数的数学期望, 比如说g(X)的数学期望. 那么应该如何计算呢? 更一般的,已知随机向量(X1 , X2 …,Xn ) 的联合分布, Y= g(X1, X2 …,Xn ) 是 (X1 , X2 …,Xn ) 的函数, 需要计算Y 的数学期 望,应该如何计算呢? 我们下面就来处理这个 问题.
8 50
12
9
7 50
10
15 50
12
11
10 50
12
10 50
则这 50 个零件的平均直径为
数学期望和方差
第四章 数学期望和方差
分布函数能够完整地描述随机变量的统计特 性,但在实际问题中,随机变量的分布函数较 难确定,而它的一些数字特征较易确定.并且 在很多实际问题中,只需知道随机变量的某些 数字特征也就够了.
另一方面,对于一些常用的重要分布,如二 项分布、泊松分布、指数分布、正态分布等, 只要知道了它们的某些数字特征,就能完全确 定其具体的分布.
8 8
9 10 11 12 7 15 10 10 50
则这 50 个零件的平均直径为
8 8 9 7 1015 1110 1210 50 10.14cm
第四章
数学期望和方差
换个角度看,从这50个零件中任取一个,它 的尺寸为随机变量X , 则X 的概率分布为 X P 8
x
| x| 但 | x | f ( x ) dx dx 发散. 2 (1 x )
它的数学期望不存在.
注:虽然f(x)是偶函数,但不能用定理1.1.
第四章
数学期望和方差
§4.2 数学期望的性质
设已知随机变量X的分布,我们需要计算的不 是X的数学期望, 而是X的某个函数的数学期望, 比如说g(X)的数学期望. 那么应该如何计算呢? 更一般的,已知随机向量(X1 , X2 …,Xn ) 的联合分布, Y= g(X1, X2 …,Xn ) 是 (X1 , X2 …,Xn ) 的函数, 需要计算Y 的数学期 望,应该如何计算呢? 我们下面就来处理这个 问题.
8 50
12
9
7 50
10
15 50
12
11
10 50
12
10 50
则这 50 个零件的平均直径为
各个分布的数学期望和方差

各个分布的数学期望和方差
当数据分布比较分散(即数据在平均数附近波动较大)时,各个数据与平均数的差的
平方和较大,方差就较大;当数据分布比较集中时,各个数据与平均数的差的平方和较小。
因此方差越大,数据的波动越大;方差越小,数据的波动就越小。
样本中各数据与样本平均数的差的平方和的平均数为样本方差;样本方差的算术平方
根为样本标准差。
样本方差和样本标准差都是衡量一个样本波动大小的量,样本方差或样
本标准差越大,样本数据的波动就越大。
方差和标准差为测算线性趋势最重要、最常用的指标,它就是测算数值型数据线性程
度的最重要的方法。
标准差为方差的算术平方根,用s则表示。
连续型随机变量的数学期望与方差
(1)D( )
E[
E( )]2
[x
E( )]2
p( x)dx
(2)方差的简便计算公式
D( )=E( 2) E(2 )
x2 p(x)dx
x p( x)dx
例2 随机变量的概率密度函数
6x(1 x),当0 x 1
p(x)
0
当x 0或x 1时
求随机变量的方差。
12
4、方差的性质 设 k ,b,c均为常数,则有
E( ) xp(x)dx
15
2、数学期望的性质
(1)EaX b aEX b
(2)EaX aEX
(3)EX b EX b
(4)Eb b
(5)EX Y EX EY
(6)E( f ( )) f (x)p(x)dx
(6)E f ( ) f (xk )PK
k
16
(二)连续型随机变量ξ取值的方差
(1)D(c) 0
(2)D(k ) k 2D( ) (3)D( b) D( )
(4)D(k b) k 2D( )
13
下页
三、练习
• 课本第90页 第6题
14
四、小结 (一)连续型随机变量ξ取值的数学期望
1、连续型随机变量的数学期望的定义 p(x) 设连续型随机变量 的密度函数为
若积分 xp(x绝)d对x 收敛,则 的数学期望为:
x0 x1 x2 L xn
xi xi1 xi
b i
【xi
,
xi
)
+1
y p(x)
o
x0b0 x1 xi bi xi1
xn x
6
连续型随机变量ξ的概率分布
ξ 【x0 , x1)【x1, x2)
数学期望与方差

x
4,
x x
0 0
则 P{X 1}
1
pX (x)d x
寿命不超过1年的概率 =出售的设备在售出
11
-
e
x 4
dx
1
1
e4
04
一年之内调换的概率
PX
1
1
e4
寿命超过1年的概率 =不需调换的概率
因此出售一台设备净赢利Y 的分布律为
Y 100 100 300
内容小结
1. 数学期望是一个实数, 而非变量, 它是一种
加权平均, 与一般的平均值不同, 它从本质上
体现了随机变量 X 取可能值的真正的平均值.
2. 数学期望的性质
10 EC C;
20 ECX CX ;
30
E
n
ai
i 1
Xi
k1 k![(n 1) (k 1)]!
n1
np
(n 1)!
p qi (n1)i
i0 i![(n 1) i]!
n1
np Cni 1 p i q n1i i0
np np( p q)n1
(3) Poisson 分布: X ~ P()
E( X ) k k e e k1
10 100
X
X ki.
k 1 i1
17
例5.(续)
而X ki服从 p ek 的( 0 — 1)分布,E( X ki ) ek . i 1,2,,100, 所以
10 100
10
E(X )
E( X ki ) 100ek
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
n
(n 1)! np k p k 1q ( n1)( k 1) k![(n 1) (k 1)]! k 1
(n 1)! np p i q ( n1)i i 0 i![(n 1) i ]!
n 1
i i n 1i np C n p q 1 i 0
X
k 1 i 1
10 100
ki .
17
例5.(续)
而X ki 服从 p e k 的( 0 — 1)分布, E ( X ki ) e k . i 1,2,,100, 所以
10 100 10
E ( X ) E ( X ki ) 100e
k 1 i 1 k 1
解 设每张彩票中奖的数额为随机变量X, 则
X 10000 p 1 105
5000
1000
100
10
0
2 105
10 105 100 105 1000 105 p0
X 10000 p 1 105
5000
1000
100
10
0
2 105
10 105 100 105 1000 105 p0
每张彩票平均能得到奖金 1 2 E X 10000 5 5000 5 0 p0 10 10 0.5(元). 每张彩票平均可赚 2 0.5 0.3 1.2(元).
引例1 分赌本问题(产生背景)
A、B两人赌技相同, 各出赌金100元, 并约定 先胜三局者为胜, 取得全部 200元. 由于出现意外 情况, 在 A 胜 2 局、B 胜1局时, 不得不终止赌博, 如果要分赌金, 该如何分配才算公平?
分析 假设继续赌两局, 则结果有以下四种情况:
AA A胜B负 A胜B负 AB A胜B负 B胜A负 BA B胜A负 A胜B负 BB B胜A负 B胜A负
性质2和3
E (3 X 2 XY Y 5) 3 E ( X ) 2 E ( XY ) E (Y ) E (5)
3 10 2 E( X ) E(Y ) 3 5
30 2 10 3 3 5 92
12
性质4
数学期望不存在的实例
B. 数学期望的性质
E (C ) = C E (aX ) = a E (X )
E ( X + Y ) = E (X ) + E (Y )
E ai X i C ai E ( X i ) C i1 i1
n n
当X ,Y 相互独立时,
E ( X Y ) = E (X )E (Y ) .
但
E ( XY ) 0;
2 P( X 0) P(Y 0) 8
P( X 0, Y 0) 0
2
10
若X ≥0,且EX 存在,则EX ≥0。
证明:设 X 为连续型,密度函数为f (x), 则 由X ≥0 得:
f ( x) 0,
x0,
0
所以
EX x f ( x)dx x f ( x)dx 0 .
n 1
np( p q) n1
np
(3) Poisson 分布: X ~ P( )
E( X ) k
k 0
k
k!
e
e
(k 1)!
k 1
k 1
e e
(4) 正态分布: X ~ N (, )
2
E( X )
Remark 分布完全描述了随机变量的规律,而期望只 刻画了它的一个重要特征——“位置”特征.随 机变量以期望为“中心”而随机取值. 已知分布律可求均值.但不同的分布可有相 同的均值.
把已赌过的三局(A 胜2局、B 胜1局)与上述结果 相结合, 即A、B赌完五局: 前三局: 后二局: A胜2局B胜1局 AA
AB
A胜
BA
BB B胜
故有, 在赌技相同的情况下, A、B最终获胜的 可能性大小之比为 3:1. 1 3 即A 应获得赌金的 , 而 B 只能获得赌金的 . 4 4 因此, A 能“期望”得到的数目应 为 3 1 200 0 150(元 ), 4 4 而B 能“期望”得到的数目, 则为 1 3 200 0 50(元). 4 4
变除法为乘法和加法
Def. 1
设离散型随机变量 X 的分布律为
P{X ak } pk , k 1, 2,
E ( X ) ak P{X ak } ak pk
k k
称为 X 的数学期望或均值 Def. 2 设连续型随机变量 X 的分布密度函数为 f ( x)
其数学期望定义为 E( X )
数学期望和方差是常用的随机变量的两个数字特征
一、数学期望(mathematical expectation)
1.数学期望的概念
e.g. 小组 8 个人,英语得 90 分的 3 人,80 分的 4 人, 60 分的 1 人,求平均分数
.
90 3 80 4 60 1 3 4 1 90 80 60 3 4 1 8 8 8Leabharlann xf ( x)dx
e. g. 1
概率为
1 甲、乙两人赌博,甲赢的概率为 ,输的 3 2
,但甲赢一次可从乙处得 3 元,而输
3 一次要付给乙 1 元,求甲的平均赢利。
e. g. 2 某同学假期回家探亲,有三种方法:坐汽车, 240 元;坐火车,300 元;坐飞机,980 元.由于
各种原因,该同学采用三种路线的概率分别为: 0.3, 0.5, 0.2 。试写出差旅费 X 的概率分布,并计 算差旅费的平均值。
E ( X ) 8 0.3 2 0.7 1(万元), 存入银行的利息: 10 5% 0.5(万元), 故应选择投资.
内容小结
1. 数学期望是一个实数, 而非变量, 它是一种 加权平均, 与一般的平均值不同, 它从本质上 体现了随机变量 X 取可能值的真正的平均值. 2. 数学期望的性质 10 E C C ; 0 2 E CX C X ; n n 0 ai E X i ; 3 E a X i i i 1 i 1 0 4 X ,Y独立 E XY E X E Y .
8
注
性质 4 的逆命题不成立,即
若E (X Y) = E(X)E(Y),X ,Y 不一定相互独立.
反例
Y -1 pij X -1
18 18 18
0
18
1
18 18 18
p• j
38 28 38
0
1 pi•
0
18
38
28
38
9
XY P
-1
0
1
28
48
28
E ( X ) E (Y ) 0; E ( XY ) E ( X ) E (Y )
k
100 e
k 1
10
k
100e (1 e 1 e
10
)
18
例6. 某厂家的自动生产线, 生产一件正品的 概率为 p (0<p<1),生产一件次品的概率为 q=1-p。生产一件产品的成本为c元,正品的 价格为s元,次品不能出售。这样,厂家生产 一件正品获利s-c元, 生产一件次品亏损c 元(假定每个产品的生产过程是相互独立的 )。 若生产了N件产品,问厂家所获利润的 期望值是多少?
Y
100
1 e 4
100 300
1 1 e 4
p
则 EY 100e
1 4
1 200 1 e 4 33.64元 . .
发行彩票的创收利润
某一彩票中心发行彩票10万张, 每张2元. 设头等奖1个, 奖金 1万元, 二等奖2个, 奖金各 5千元; 三等奖10个, 奖金各1千元; 四等奖100 个, 奖金各1百元; 五等奖1000个, 奖金各10元. 每张彩票的成本费为0.3元, 请计算彩票发行单 位的创收利润.
20
四、应用实例
厂家的销售策略
1 某设备寿命X(以年计)服从 λ 的指数分布. 4 按规定: 出售的设备在售出的一年内损坏可予 以调换. 若出售一台设备赢利100元, 调换一台 设备厂方需花费300元. 求厂方出售一台设备净 赢利Y的数学期望.
1 x 4 e ,x0 p x 解 依题设, 有 X 4 x0 0,
例8 设离散型随机变量X的分布律为
k 2 1 k pk P X 1 k , k 1,2, k 2 求EX. k 1 解 由于 xk pk 1 lnk . k k 1 k 1
1 但是 xk pk . k k 1 k 1
因此彩票发行单位发行10万张彩票的创收利润为 100000 1.2 120000元 .
如何确定投资决策方向?
某人现有10万元现金, 想投资于 某项目, 为期一年. 欲估成功的机会 为30%, 并可获利8万元, 失败的机会 为70%, 将损失2万元 . 若存入银行 , 同期间的利率为 5 %, 哪一种方案可 使投资的效益较大? X 8 2 解 设X为投资利润, 则 p 0 .3 0.7
则 P{ X 1}
p X ( x ) d x 寿命不超过1年的概率 =出售的设备在售出 x 1 11 一年之内调换的概率 4 4 e dx 1 e 04 1 寿命超过1年的概率 P X 1 e 4 =不需调换的概率
1
因此出售一台设备净赢利Y 的分布律为
