07--4、电介质中的电场高斯定理
介质中的高斯定理
真空中 导体中
结论3
P与E的关系
0 0 r 1 ( r 1 ) 0 E 0 r
令 r 1 为电极化率。
1 由 P ' 和 ' 0 1 r 0 1 P ' 0 1 r 1 r r
R2
εr2
εr1 R1
R
解:E 和D 的分布具有柱对称性
D dS D 2rl l
S
D ( R1 r R2 ) 2r D E1 ( R1 r R ) 0 r1 20 r1r
D E2 0 r 2 20 r 2 r ( R r R2 )
P 0E
结论4
无介质 充满介质
充满各向同性的均匀电介质的电容器
C0
0S
C rC0
A
B
d q0 C U AB
S
q0 q S q 0 0 r 0 C U AB Ed E0 0 d d r 0 r 0S rC0 d
d
平行板电容器为例
例11.9 真空中有一半径为R,带电量为q的金属 球壳。求: (1)电场的总能量; (2)带电球壳周围空间中,多大半径球面内的 电场所具有的能量等于总能量的一半。
q
p
q
E0
E0 F
F
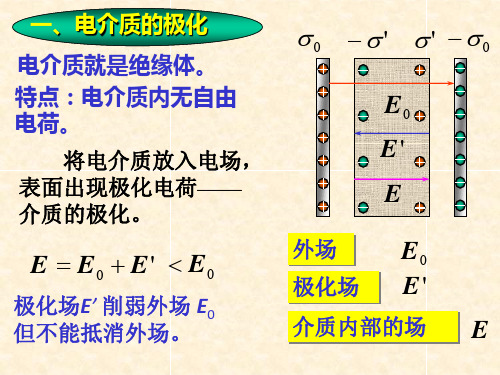
在介质表面产生极化电荷。
三、极化强度 描写电介质极化程度的物理量。 定义:单位体积内的电偶极矩矢量和。
p P V
E0
注意
1.真空中 P = 0 ,真空中无电介质。
大学物理介质中的高斯定理

r1
r2
18
例:球形电容器由半径为R1的球体和内半径为R3的导 体球壳构成,带电 q,其间有两层均匀电介质,
分界面的半径为R2,相对介电常数分别为r1和r2 。 求:E, D 和C。
解:
D
dS
4
r
2
D
q
S
R2
R1 r2
D1
q 4r 2
D2
q 4r 2
R3
r1
在界面上电位移线会发生折射
tan1 1
tan2
2
2 1
若 2 > 1 2 > 1 ,电位移线将折离法线
*
上海交通大学 董占海
28
证明:
E1t E2t D1n D2n
E1sin1 E2sin2
D1 cos 1 D2 cos 2
D1 1E1 D2 2 E2
39
思考:带电金属球 (R、Q),半个球处在电介质εr 中,则球正下方r > R 处的 E、D。
r
同上
上海交通大学 董占海
40
例5:一点电荷Q放在半无限大电介质为εr和真空的 界面处,求E、D。
解:空间的场强 = 两个点
电荷Q和q′产生的
故空间各点的E、为
r
点电荷的场,具有球
对称性
xd 2
2 DS 0 0 S0d
D
i
0
d
2
上海交通大学 董占海
d
r
0
Ox
23
xd 2
E
D
0r
0 x
电位移、介质中的高斯定理复习

E'
q'
q0
E E0 E '
E0
S
1 ( E d S q ' ) q (1) 0 内 S 0 S
S
q ' P d S 内 (3) S
S
E'
q' 1 E d S q0 S
S (1)式 0 +(3)式
S S
得介质中的高斯定理
介质中的高斯定理: 穿出某一闭合曲面的电位移矢量的通量等于 这个曲面所包围的“自由电荷”的代数和。
D d S q 0
S S
注意:1)D 是一个辅助量,场的基本量仍是场 强 E 2) D 0 E P 是 D. E 关系的普遍式。 对各向同性的介质: P e 0 E D 0E P 0 E e 0 E (1 e ) 0 E 令: r 1 e 称为相对介电常数, 0 r 称为介电常数,则: D r 0 E E
dW 1 2 1 w E DE dV 2 2 一般地,推广到任意电场(非均匀,交变场).
dV体积中的电场能量为 : dW wdV 1 2 E dV 2
1 2 整个空间中的电场能量 : W wdV E dV V V 2
例 : 求均匀带电球体內外的电场能. 已知球体带电量为Q, 半径R,內外电容率分别为 1 , 2 .
E E0 E '
0
(q
S
S
0
q'内 ) (1)
E0
S
P dS q'内 (3)
电位移介质中的高斯定理复习课件

掌握高斯定理的应用步骤
确定高斯面
根据问题的对称性选择适当的高斯面 ,高斯面应包含所有需要求解的电荷 分布。
计算电位移矢量D的通量
根据电位移的定义和性质,计算高斯 面上各点电位移矢量的通量。
应用高斯定理
将电位移矢量的通量代入高斯定理公 式中,求解出电场强度E的值。
02
高斯定理表述为"通过任意闭合曲 面的电位移通量等于该闭合曲面 所包围的体积内所含电荷量"。
高斯定理的意义
总结:高斯定理揭示了电场与电荷之 间的内在关系,是理解电场分布和电 荷相互作用的基础。
高斯定理阐明了电场线从正电荷发出 ,终止于负电荷,总电位移线闭合的 事实,对于理解电荷分布与电场的关 系至关重要。
圆柱对称分布电场的高斯定理应用
总结词
圆柱对称分布电场的高斯定理应用是指将高 斯定理应用于圆柱对称分布的电场中,以求 解电场分布和电位移矢量的方法。
详细描述
在圆柱对称分布电场中,高斯定理的应用同 样可以简化计算过程。通过将圆柱面分割成 若干个圆环,并应用高斯定理计算每个圆环 内的电位移矢量,再求和即可得到整个圆柱 面的电位移矢量。这种方法可以用于求解圆 柱形电荷、带电导体等问题的电场分布。
平面分布电场的高斯定理应用
总结词
平面分布电场的高斯定理应用是指将高斯定 理应用于平面分布的电场中,以求解电场分 布和电位移矢量的方法。
详细描述
在平面分布电场中,高斯定理的应用同样适 用。通过将平面分割成若干个小区域,并应 用高斯定理计算每个小区域内的电位移矢量 ,再求和即可得到整个平面的电位移矢量。 这种方法可以用于求解平面电荷、带电导体
电位移介质中的高斯定 理复习课件
静电场-高斯定理

电容器极板间电场分布
极板间相互作用力计算
理介
第 推质
四 章
广中 及高 应斯用定Fra bibliotek电介质极化现象及极化强度矢量引入
为了描述电介质极化 的程度和方向,引入 极化强度矢量P,其 大小与电偶极矩成正 比,方向由负电荷指 向正电荷。
在电场作用下,电介质内部正负电荷中心发生相对 位移,形成电偶极子,从而产生宏观上的电极化现 象。
高斯定理是电磁学中的基本定理之一,它表述了静电场中电场强度与电荷分布之间的关系。
高斯面选取原则及技巧
高斯面选取应遵循简单、对称、便于计算等原则。
02
在实际问题中,常根据电荷分布和电场强度的对称性来选取高斯面,以便简化计算。
03
高斯面的形状和大小应根据具体问题灵活选择,可以是平面、球面、柱面等。
高斯定理物理意义阐释
高斯定理反映了静电场的空间分布特性,即电场 强度与电荷分布之间的定量关系。
高斯定理为求解复杂静电场问题提供了一种有效 的方法,即通过选取适当的高斯面来简化计算。
高斯定理揭示了静电场的有源性,即静电场是由 电荷产生的。
高斯定理在电磁学中的地位
高斯定理是电磁学四大基本定理之一,是静 电场理论的基础。 高斯定理在电磁学中具有重要的地位,它不 仅适用于静电场,还可推广应用于恒定电场、 恒定磁场以及时变电磁场等领域。
要点一
麦克斯韦方程组
麦克斯韦方程组是描述电磁场基本规律的方程组,包括高斯定理、 安培环路定律、法拉第电磁感应定律和麦克斯韦-安培定律。
要点二
高斯定理在麦克斯韦方程组中的地 位
高斯定理是麦克斯韦方程组中的重要组成部分,它描述了电荷分 布与电场之间的关系,为电磁场理论奠定了基础。
有电介质时的高斯定理

解:( 1 )求 : D D, E , P 具有球对称性
选过场点与球面同心的 球面为S:r
S内
R
q
r
P
2 D d S D 4 r q 0
S
r
当:r R : 当: r R :
q q
0
0 q0
D=0
E=0
P=0
0
E
(1 r )q0 R P n P 2 4r R 2 (1 r )q0 q 4R R
总结
D分布
球对称 面对称 轴对称
高斯面 同心球面 垂直于板的和中心 面对称的封闭柱面 同轴封闭园柱面
由于导体为等势体:
例:设无限长同轴电缆的芯线半径为R1,外皮 的内半径为R2。芯线与外皮之间充入两层绝缘 的均匀电介质,其相对电容率分别为εr1和εr2。 两层电介质的分界面半径为R,如图。求单位 长度的电容。 解: (1) 先求 : D R2 εr1 设单位长芯线、外皮 R R1 分别带电λ、-λ εr2 D, E 具有轴对称性 选过场点与电缆同轴的单位长封闭园柱 面为高斯面:r
§9-4 有介质时的高斯定理
一、有介质时的环路定理和高斯定理:
E E0 E
L
有介质时的环路定理:
E d l 0
有介质时的高斯定理:
q内
E d S
S
q
S内
q
S
0
0
q0
1 1 S内 ) ( q0 q内 P dS 0 S内 0 0 S ( E P ) d S q 0 0
D, E , P
40 r r
电场的高斯定理及其应用

电场的高斯定理及其应用1. 高斯定理的背景高斯定理,也称为高斯电场定理,是电磁学中的基本定律之一。
它描述了电场通过任意闭合曲面的电通量与该闭合曲面内部的总电荷之间的关系。
这个定理是由德国数学家和物理学家卡尔·弗里德里希·高斯在19世纪初期提出的。
高斯定理在电磁学、物理学和工程学等领域有着广泛的应用。
2. 高斯定理的数学表述高斯定理的数学表述如下:对于任意闭合曲面S,电场通过S的电通量(记作ΦE)与曲面S内部的总电荷(记作q)之间存在以下关系:ΦE = ∫∫S E·dA = q / ε₀其中,E是电场强度,dA是曲面元素的面积向量,ε₀是真空的电介质常数(也称为电常数),其值约为8.85×10^-12 C2/N·m2。
3. 高斯定理的物理意义高斯定理的物理意义可以从两个方面来理解:(1)电场线与闭合曲面的关系:高斯定理说明,对于任意闭合曲面S,电场线通过S的电通量等于曲面S内部的总电荷。
这意味着,无论曲面S如何选择,只要它是闭合的,电场线穿过它的总通量都与曲面内部的电荷有关,而与曲面的形状和位置无关。
(2)电场的分布与电荷的关系:高斯定理表明,电场是通过闭合曲面的电通量的度量,而电通量与曲面内部的总电荷成正比。
这意味着,电场的强度和分布与曲面内部的电荷量有关,而与曲面的具体形状和位置无关。
4. 高斯定理的应用高斯定理在电场分析和计算中有着广泛的应用,下面列举几个常见的应用例子:(1)计算静电场中的电荷分布:通过高斯定理,可以计算静电场中某个闭合曲面内的电荷分布。
只需测量通过该曲面的电通量,然后根据电通量与电荷的关系,可以确定曲面内部的电荷量。
(2)设计电容器和绝缘材料:在电容器和绝缘材料的设计中,高斯定理可以用来分析电场的分布和电荷的积累。
通过合理选择闭合曲面的形状和位置,可以优化电场分布,提高电容器的性能和绝缘材料的可靠性。
(3)研究电磁波的传播:在研究电磁波的传播过程中,高斯定理可以用来分析电磁波在不同介质中的电场分布和电荷的变化。
大学物理课件-4静电场中的电介质电介质中的电场高斯定理电位移

谢谢观看
2021/3/18
26
4πe r
Q R12
2
4πR1
er
1 Q
er
在外表面上的正极化电荷的总量为
q外
外 S外
er 1 4πe r
Q R22
4πR22
er 1Q er
2021/3/18
21
例2:平行板电容器充满两层厚度 +
为 d1 和 d2 的电介质(d=d1+d2 ),
相对电容率分别为e r1 和e r2 。
S1
求:1.电介质中的电场 ;2.电容量。
2021/3/18
12
在保持电容器极板所带电量不变的情况下, 电容与电势差成反比,所以
C C0
U012 U12
er
即
C = e r C0
式中C0是电介质不存在时电容器的电容。
可见,由于电容器内充满了相对电容率为e r的 电介质, 其电容增大为原来的e r倍。
2021/3/18
13
四、电介质存在时的高斯定理
但随着外电场的增强,排列整齐的程度要增大。
无论排列整齐的程度如何,在垂直外电场的两个端面上 都产生了束缚电荷。
结论:有极分子的电极化是由于分子偶极子在外电场的作用 下发生转向的结果,故这种电极化称为转向电极化。
说明:在静电场中,两种电介质电极化的微观机
理显然不同,但是宏观结果即在电介质中出现束缚
电荷的效果时确是一样的,故在宏观讨论中不必区
在宏观上测量到的是大量分子电偶极矩的统计
平均值,为了描述电介质在外场中的行为引入电极化
强度矢量。
2021/3/18
6
为表征电介质的极化状态,定义极化强度矢量:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(5) 电位移的单位是“库仑 每平方米”,符号为:C/m2 , (这也就是电荷面密度的单位),其量纲是 I L -2T 。
例2、一金属球体,半径为R,带有电荷q0,埋在均匀“无限大” 的电介质中(介电常数为ε),求: (1)球外任意一点P的场 强;(2)与金属球接触处的电介质表面上的极化电荷。
解:由于电场具有球对称性,同时已知自由电荷的分布,所以 用有介质时的高斯定理来计算球外的场强是方便的。
(1
1
r
)
0
0
0
注意,上面得到的总电场 E 与真空中电场 E0 的关系式,
以及自由电荷面密度 σ0 与极化电荷面密度 σ’ 的关系式,并
非普适关系式,仅在均匀各向同性介质充满电场存在的空间
时才成立。
例1、平行板电容器的两极板上分别带有等值异号的电荷,面密 度为 9.0×10 –6 C/m2,在两极板间充满介电常数 3.5×10 –11 C2/ (Nm2)的电介质,求(1)自由电荷产生的场强;(2)电介 质内的场强;(3)电介质表面上的极化电荷的面密度;(4) 极化电荷所产生的场强。
0A r
q0
r
ε=ε0εr
定义电介质的介电常数与电场强度的乘积为电位移矢量,
即:
D
E时则的得高到斯有定介理质:
S
D
ds
q0(内)
(1) 我们是从平行板电容器这个特例推出有电介质的高斯
几 定理的,但它是普遍适用的,是静电场的基本规律之一;
点 (2) 电位移矢量 D 是一个辅助物理量,真正有物理意义
空
中
的
高
斯
定
理于
高
斯
面S
得
1
:
S1
E
dS
1
0
( A
1
A
2
)
E1
E2 S1
E dS
右底面
E dS
左底面
E1 A
E2 A
A
A
r1 0
r 2 0
所以
A
r1 0
A
r 2 0
1(A 0
1
A
(d1
1
d2
2
)
q S是极板上的电荷,所以电容为:
C q S 1 d1 d2
U d1 d2
c 1S 2S
1 2
(3)设电介质各个面上的极化电荷面密度分
别为 -σ 1 ’ ,+ σ 1’ ,- σ 2’ 和+σ2’(如图)
- σ 2’
-σ1’
+σ2’
+σ1’
与极板平行,面积均为 A ,上底面在正极板内,下底面在电介
质内。
这样,闭合曲面 S 内的自由电荷 q 0= σ0A ,而极化电荷
q’= -σ’A ,高斯定理写为:
代入S前E面已 d得s到的,1自0 (由电0荷A与极化电A荷) 面密度间的关系
式,有:
0A
代入高斯定理有:
A
D1 A
A
与前面的式子相比较,有D1 D2
+ +
S2
利用 D1 1E1 ,D2 2 E2 ,可求得:
E1
1
r1 0
,
E2
2
r 2 0
(2)正、负两极板间的电势差为:
U
E1d1
E2d2
(d1 1
d2 )
2
q S
无数实验证明:电场能量是定域在电场中的,哪里有电 场那里就有能量,无论这电场是稳恒不变的还是交变的。
能量是物质的固有属性(能量与物质相联系),电场具 有能量,说明电场是一种物质。
电场是一种特殊的物质。
例1、球形电容器的内、外球面半径各为 RA 和 RB,两球间充满 介电常数为ε的均匀电介质,当内、外球面各带有电荷+q 及-q 时,求电容器的总能量。
应用真空中的高斯定理于高斯面 S2 得:
E dS
S2
1 ( A 0
A
1
)
A
E dS S2
E dS
右底面
E1 A
r1 0
所 以 :A r1 0
1(A 0
A
1
)
可
得
:
1
(1
1 ) r1
D1
D2
应用
真
然后将开关拨向2 ,发现灯泡会
发光,说明带电的电容器中有能量。
1
2
设充电过程中某一时刻,极板带
电q,电势差为 uA-uB ,有 dq 的
dq
E
正电荷从负极板移到正极板,
外力所作的功为 dW =( uA – uB ) dq
dW dqU dq q 1 qdq cc
由于( uA – uB ) = q / C ,电容器在电荷从零增加至Q 的过程 中,外力所作的功,即电容器储存的能量为:
由此得: q
(1
1
r
)q0
例3、如图所示,平行板电容器两极板之间有两层电介质,电 介质表面与极板平行,介电常数分别为ε1 和ε2 ,厚度分别为 d1 和 d2 ,电容器两极板的面积为S,两极板上自由电荷面密度为 ±σ。求:
(1)两层电介质内的电位移和场强;
(2)电容器的电容;
(3)两层电介质表面的极化电荷面密度。 解:(1)设这两层电介质中的场强分别为 E1 和 E2 ,电位移分别为 D1 和 D2 ,在电介 质中作一扁盒形高斯面S1 ,其两底面与电 介质表面平行,在此高斯面内的自由电荷
1 S (Ed )2
2d
1 E 2 Sd
2
Sd 是电容器的体积,所以,有电场的空间中,单位体积 内的能量为(称为电场能量密度):
we
1 E 2
2
1 2
DE
一般情况下,有电场的空间V 中的总电场能为:
电容器的能量有两个表达式,能量是属于电荷还是属于 电场?由电磁场的传播可知这些能量是属于电场的。
分界处半径为R。 求:单位长度电缆的电容
解:设内外电缆线密度 ,在介质中做底面半径为r 长为l 的
圆柱面,有
r1
R R1 R2
r2
§7-5 电场的能量
一、带电电容器的能量
如图:书P188 图7-25 的电路,先将开关拨向1 ,使电容器
充有电量 Q ,两极间的电势差为 UA - UB
§7-4 电介质中的电场 有电介质时的高斯定理 电位移
一、电介质中的电场
附电加介电质场中之的和电(矢场量等和于)自:由电E荷产生E的0 电E场与极化电荷产生的
下面我们以平行板电容器为例求电介质中的场强:
设电容器带有电量q 0 ,其间无电介质 +σ0 -σ’ +σ’ -σ 0
时,两板间电势差为U 0,电容值为C 0; 当充满相对介电常数为εr 的电介质时, 电势差为U,电容值为C 。
极板上的自由电荷面密度为σ0 ,
相邻介质表面的极化电荷面密
++ + --
+ +σ0 - -σ’
度为 -σ’,
根据真空中的高斯定理,在
电场中任作一闭合曲面 S,通 过该闭合曲面的电通量为:
+
+
+
--
-
-
E
ds
1
S
0
q(内)
其中q(内)是曲面内所有电 荷的代数和。
为方便计,我们取如图的长方形闭合曲面 S ,其上、下底面
+ + D1
+ + E1 +
+
D2
- -
- E2 -
- S1 -
为零,由有电介质时的高斯定理得:
D dS D dS D dS D dS 0
S1
左底面
右底面
侧底面
因 侧 面 法 线nD,即dSD, 故
D
dS
说
的是电场强度矢量 E,引入 D 的好处是在高斯定理的表 达式中,不出现很难求解的极化电荷;
明:
(3)
与电力线的概念一样,我们可以引入电位移线来描述
D 矢量场,同时计算通过任意曲面的电位移通量,不过要
注意,D 线与 E 线是不同的;
(4) 引入电位移通量后,有介质时的高斯定理可以表述为: “在任意电场中,通过任意一个闭合曲面的电位移通量 等于该面所包围的自由电荷的代数和”。
0,
侧面
上式化为(其中A为扁盒形高斯面的底面积):
S1
D
dS
D
左底面
dS
D
右底面
dS
D1 A
D2 A
0
即D1 D2 两种电介质内的电位移相等。
由于:D1 1E1 D2 2 E2 所以:E 1 2 r 2 0 r 2
E dS
1
S
0
q
1
0
(q0
q)
由第一问的结论有: SE dS SEdS
- -+ + +- --++q-q+0’-++--
